Relationship Analysis between Multi-Parameters and Ferrite Number in GTAW Based on ANN Model
Abstract
:1. Introduction
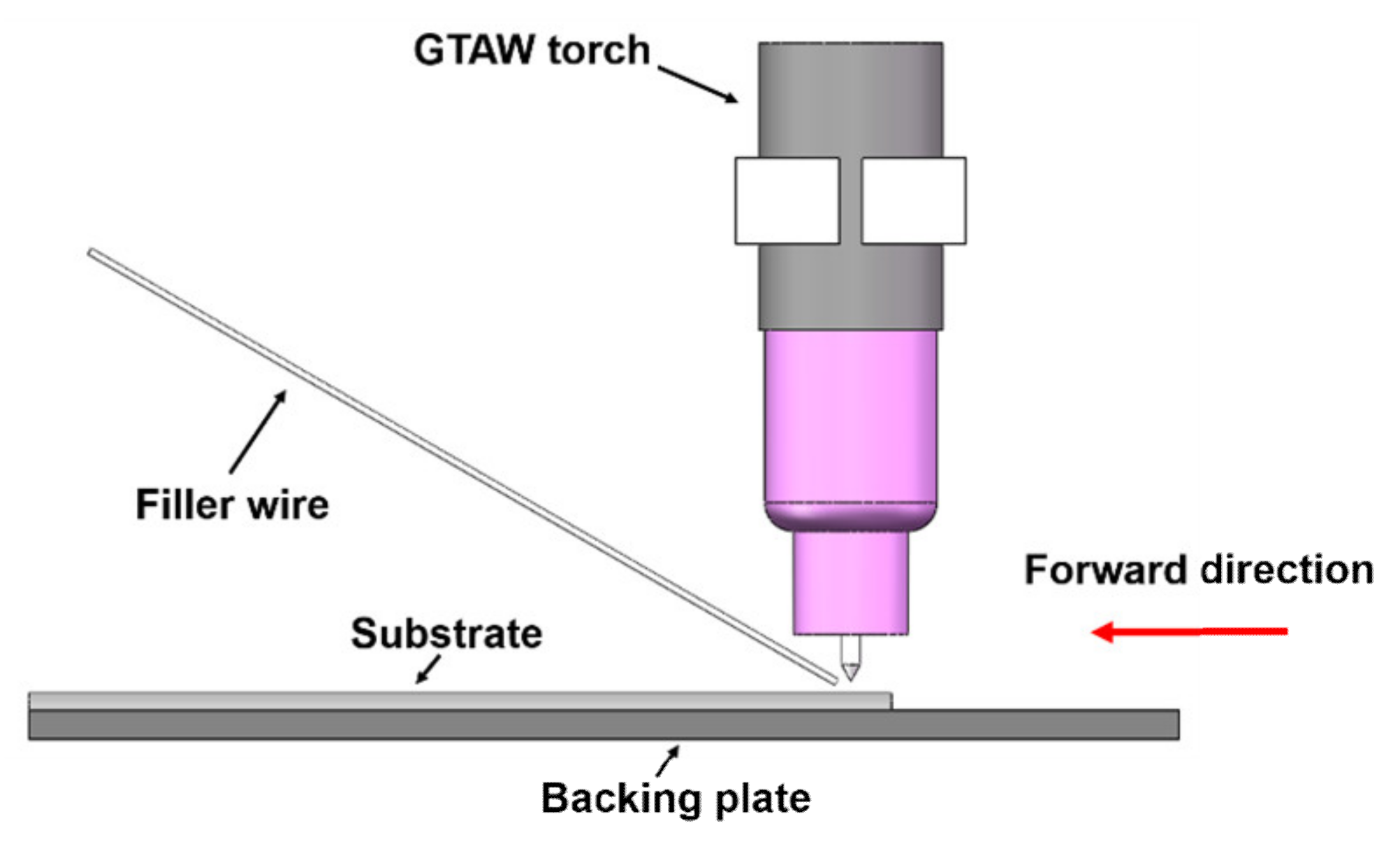
2. Materials and Methods
3. Results and Discussion
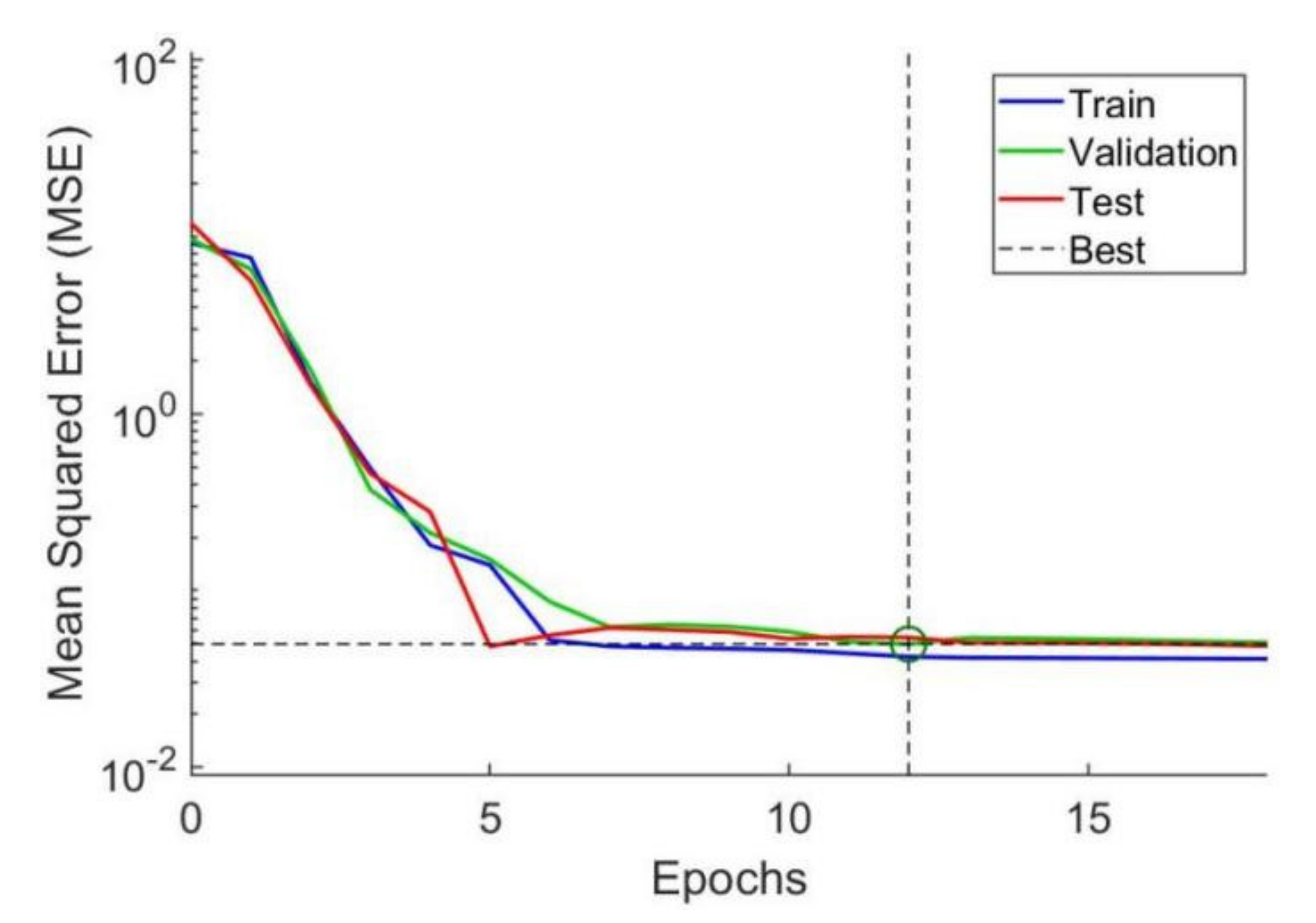
3.1. Modeling of the FN-Prediction Models
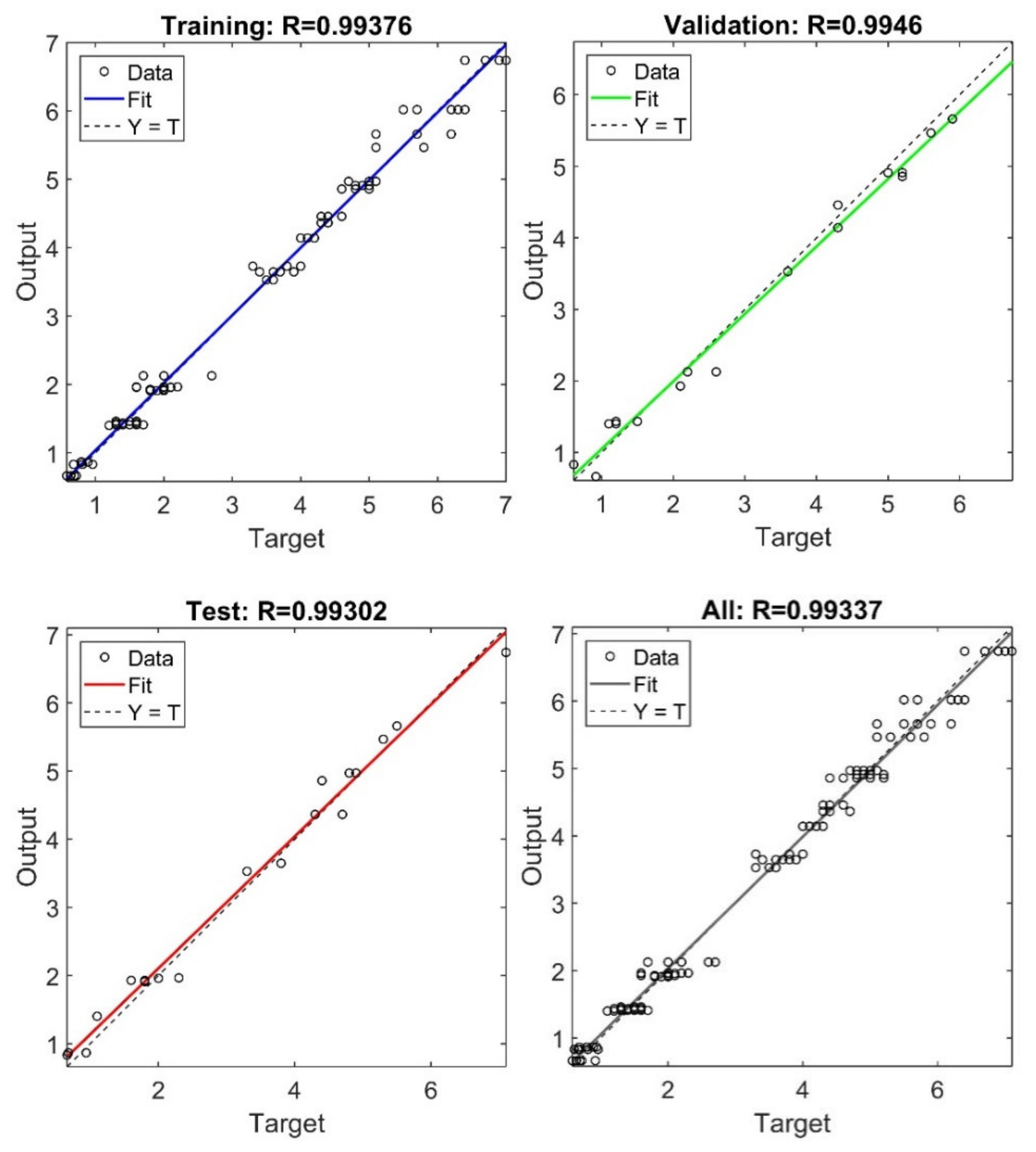
3.2. The Accuracies of the FN-Prediction Models
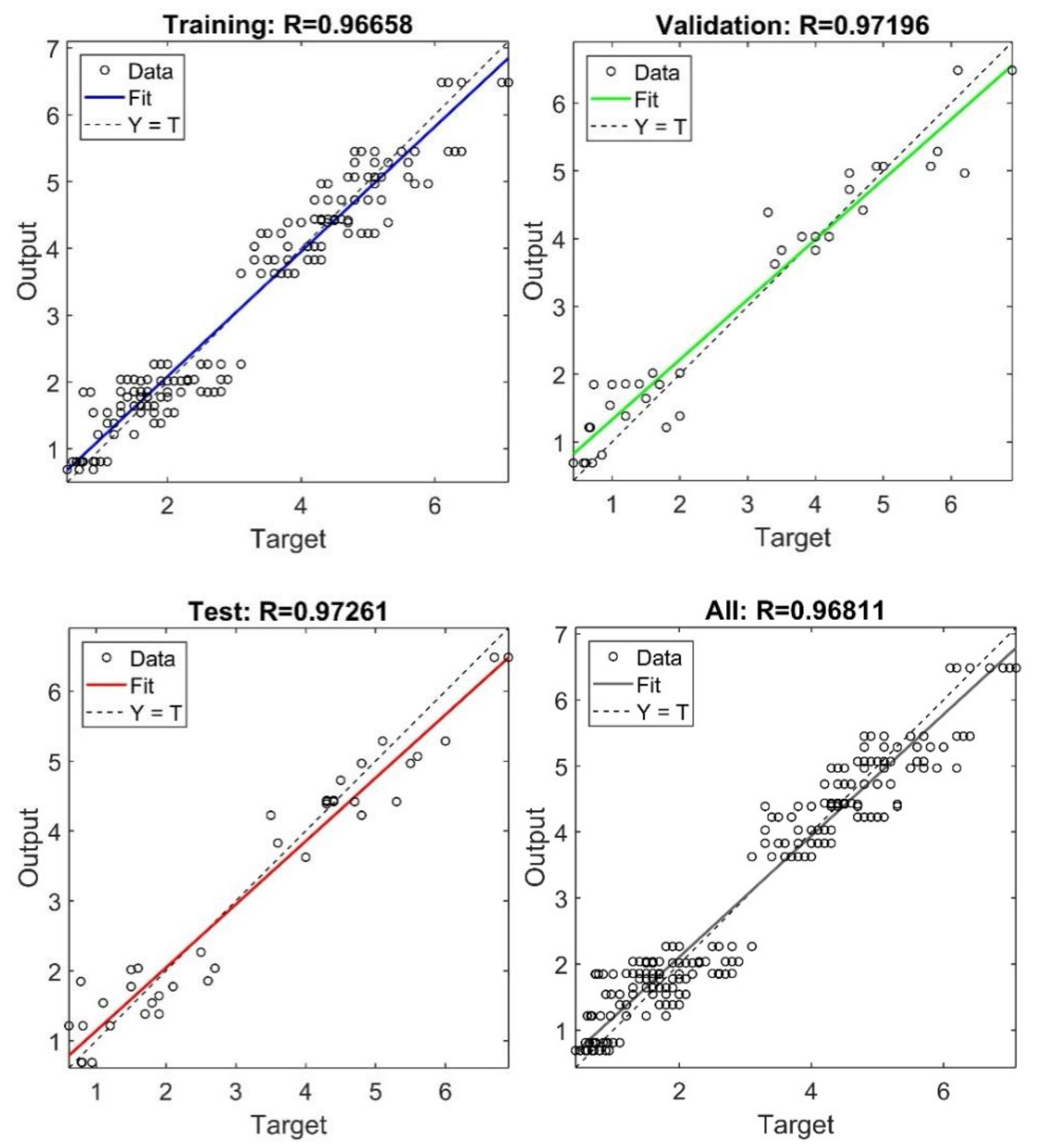
4. FN-Prediction Model under Holistic Modeling
5. Influence Analysis of Various Factors
- (1)
- Welding speed. With the increase of welding speed, heat input decreases, causing the high temperature residence time to decrease. Due to the insufficient transformation from ferrite to austenite, FN will increase. On the other hand, the increase of welding speed decreases the dilution rate of the base metal, causing the Creq/Nieq ratio to reduce, thus the FN in the weld will decrease.
- (2)
- Wire-feed rate. As wire-feed rate increases, more heat is used to melt welding consumables, resulting in a decrease in heat input and an increase in FN. On the other hand, the increase of wire-feed rate will decrease the dilution rate of the base metal, causing FN to decrease.
- (3)
- Welding current and arc length. With the increase of welding current and arc length, the heat input and dilution rate will both increase, causing FN to decrease or increase respectively.
6. Conclusions
- The ANN-based FN-prediction models trained by the orthogonal test data were stable and insensitive to different materials with different manufacturers and heat-treatment conditions. High performance can be achieved by modeling different materials separately. In the FN-prediction models for DFSS and ASIS, the correlation coefficients of total samples (R_All) reached 0.99337 and 0.98762 respectively. The effect of holistic modeling of different materials was also satisfactory, and could meet the requirements of engineering practice. In the holistic FN-prediction model, R_All reached 0.96811.
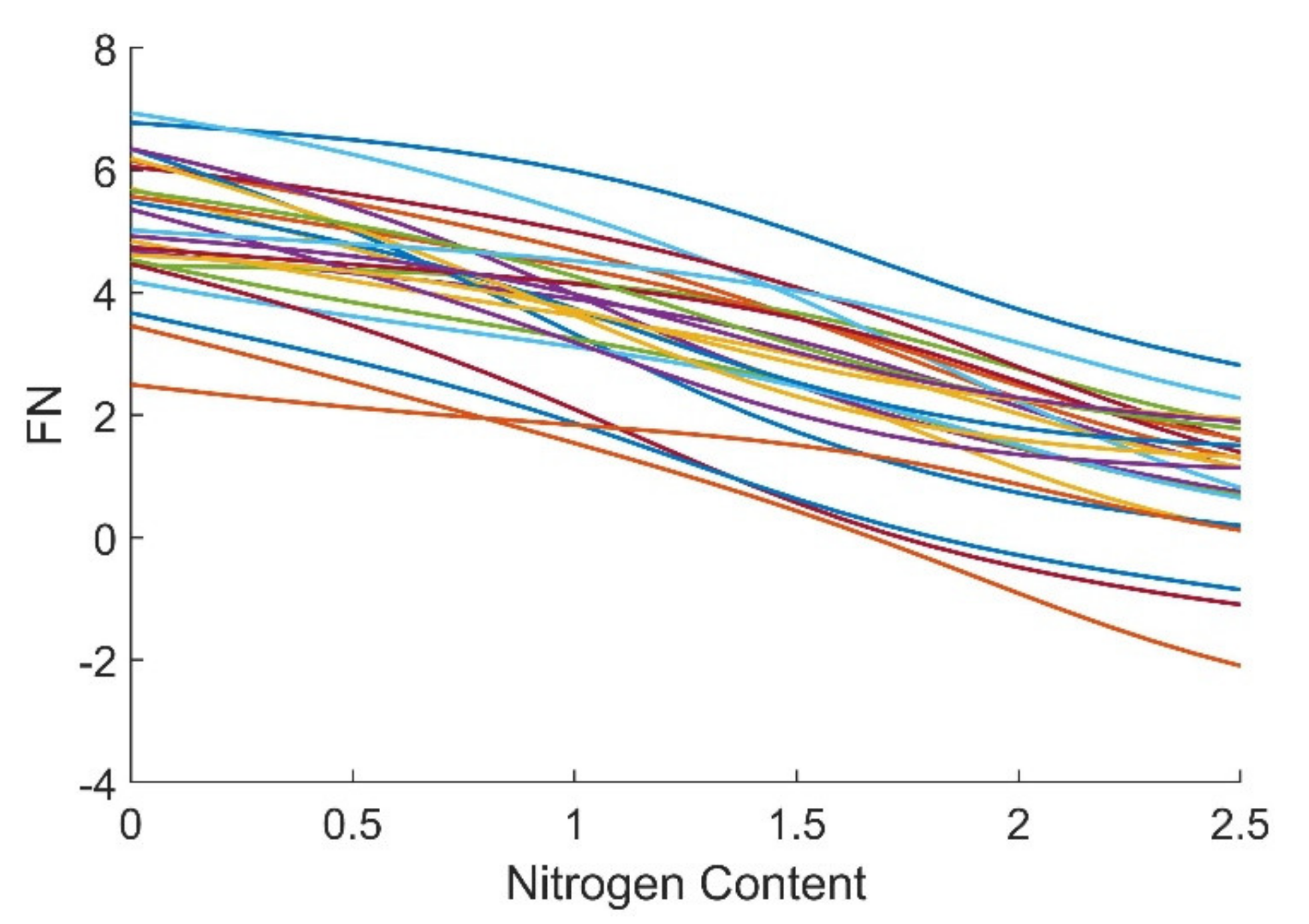
- FN decreased monotonously with the increase in nitrogen content. In production, through the FN-prediction models proposed in this paper, FN can be accurately and easily controlled by adjusting the nitrogen content in the shielding gas when other welding parameters are fixed.
- The influences of welding speed, wire-feed rate, arc length and welding current on FN were analyzed based on the FN-prediction model for DFSS. The results show that the influences of either parameters on FN were nonlinear. The FN-prediction models proposed in this paper can provide useful information to researchers about this nonlinearity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lippold, J.C.; Kotecki, D.J. Welding Metallurgy and Weldability of Stainless Steels; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2005; p. 376. [Google Scholar]
- Brooks, J.A.; Thompson, A.W. Microstructural development and solidification cracking susceptibility of austenitic stainless steel welds. Int. Mater. Rev. 1991, 36, 16–44. [Google Scholar] [CrossRef]
- Nissley, N.E.; Lippold, J.C. Development of the strain-to-fracture test for evaluating ductility-dip cracking in austenitic alloys. Weld. J. 2003, 82, 355s–364s. [Google Scholar]
- Hauser, D.; Van Echo, J.A. Effects of ferrite content in austenitic stainless steel welds. Weld. J. 1982, 61, 37s–44s. [Google Scholar]
- Lippold, J.C.; Juhas, M.C.; Dalder, E.N.C. The relationship between microstructure and fracture behavior of fully austenitic Type 316L weld filler materials at 4.2K. Metall. Trans. 1985, 16A, 1835–1848. [Google Scholar] [CrossRef]
- Kumar, S.; Shahi, A.S.; Sharma, V.; Malhotra, D. Effect of Welding Heat Input and Post-weld Thermal Aging on the Sensitization and Pitting Corrosion Behavior of AISI 304L Stainless Steel Butt Welds. JMEPEG 2021, 30, 1619–1640. [Google Scholar] [CrossRef]
- Janiczak, R.; Pańcikiewicz, K. Laser welding of austenitic ferrofluid container for the KRAKsat satellite. Weld. World 2021, 65, 1347–1357. [Google Scholar] [CrossRef]
- Rogalski, G.; Świerczyńskanska, A.S.; Landowski, M. Mechanical and Microstructural Characterization of TIG Welded Dissimilar Joints between 304L Austenitic Stainless Steel and Incoloy 800HT Nickel Alloy. Metals 2020, 10, 559. [Google Scholar] [CrossRef]
- Prabhu, R.; Alwarsamy, T. Effect of process parameters on ferrite number in cladding of 317L stainless steel by pulsed MIG welding. J. Mech. Sci. Technol. 2017, 31, 1341–1347. [Google Scholar] [CrossRef]
- Salujaa, R.; Moeed, K.M. Experimental Investigation of Solidification-Mode And Response Surface Modeling Of Ferrite-Content In Grade 304L Pulse GMA Welded Plates. Mater. Today Proc. 2019, 18, 3876–3890. [Google Scholar] [CrossRef]
- Ganesan, V.M.D.; Mathew, K.B.; Rao, S. Influence of nitrogen on tensile properties of 316LN SS. Mater. Sci. Technol. 2013, 25, 615–618. [Google Scholar] [CrossRef]
- Nage, D.D.; Raja, V.S. Effect of nitrogen addition on the stress corrosion cracking behavior of 904 L stainless steel welds in 288 °C deaerated water. Corros. Sci. 2006, 48, 2317–2331. [Google Scholar] [CrossRef]
- Singn, S.; Hurtig, K.; Andersson, J. Investigation on effect of welding parameters on solidification cracking of austenitic stainless steel 314. Procedia Manuf. 2018, 25, 351–357. [Google Scholar] [CrossRef]
- Moslemi, N.; Redzuan, N.; Ahmad, N. Effect of Current on Characteristic for 316 Stainless Steel Welded Joint Including Microstructure and Mechanical Properties. Procedia CIRP 2015, 26, 560–564. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Todd, A.P.; Allison, M.B. Effect of processing parameters on microstructure and tensile properties of austenitic stainless steel 304L made by directed energy deposition additive manufacturing. Acta Mater. 2016, 110, 226–235. [Google Scholar] [CrossRef] [Green Version]
- Schaeffler, A.L. Canstitution diagram for stainless steel weld metal. Met. Prog. 1949, 56, 680–690. [Google Scholar]
- Kotecki, D.J.; Siewert, T.A. Constitution diagram for stainless steel weld metals: A modification of the WRC-1988 diagram. Weld. J. 1992, 71, 171–s–178–s. [Google Scholar]
- Chan, B.; Pacey, J.; Bibby, M. Modelling gas metal arc weld geometry using artificial neural network technology. Can. Metall. Q. 1999, 1, 43–51. [Google Scholar] [CrossRef]
- Vora, J.; Patel, V.; Srinivasan, S.; Chaudhari, R.; Pimenov, D.; Giasin, K.; Sharma, S. Optimization of Activated Tungsten Inert Gas Welding Process Parameters Using Heat Transfer Search Algorithm: With Experimental Validation Using Case Studies. Metals 2021, 11, 981. [Google Scholar] [CrossRef]
- Vasudevan, M.; Murugananth, M.; Bhaduri, A.K. Application of Bayesian neural network for modeling and prediction of FN in austenitic stainless steel welds. In Mathematical Modeling of Weld Phenomena-VI; Institute of Material: Cambridge, UK, 2002; pp. 1079–1099. [Google Scholar]
- Bermejo, M.A. Predictive and measurement methods for delta ferrita determination in stainless steel. Weld. J. 2012, 91, 113–s–121–s. [Google Scholar]
- Pantel, T.; Sheth, S.; Modi, B.S.; Pantel, P. Experimental investigation and comparison of regression model and artificial neural network to predict weld height in MIG welding for dual plate check valve. In Proceedings of the International Conference on Advances in Materials and Product Design AMPD, Surat, India, 10–11 January 2015. [Google Scholar]
- Vitek, J.M.; Iskander, Y.S.; Oblow, E.M. Improved ferrite number prediction in stainless steel arc welds using artificial neural networks (Part 1): Neural network development. Weld. J. 2000, 79, 33–40. [Google Scholar]
- Vitek, J.M.; David, S.A.; Hinman, C.R. Improved ferrite number prediction model that accounts for cooling rate effects (Part 1): Model Development. Weld. J. 2003, 82, 10–17. [Google Scholar]
- Vasudevan, M.; Bhaduri, A.K.; Raj, B. Delta ferrite prediction in stainless steel welds using neural network analysis and comparison with other prediction methods. J. Mater. Process. Technol. 2003, 142, 20–28. [Google Scholar] [CrossRef]
- Tomaz, I.d.V.; Colaço, F.H.G.; Sarfraz, S.; Pomenov, D.; Gupta, M. Pintaude G. Investigations on quality characteristics in gas tungsten arc welding process using artificial neural network integrated with genetic algorithm. The Int. J. Adv. Manuf. Technol. 2021, 113, 3569–3583. [Google Scholar] [CrossRef]
- Shankar, V.; Mannan, S.L.; Gill, T.P.S. Effect of nitrogen addition on microstructure and fusion zone cracking in type 316L stainless steel weld metals. Mater. Sci. Eng. A 2003, 343, 170–181. [Google Scholar] [CrossRef]
- Tseng, K.H.; Hsien, K.C. Effect of Ar-N2 mixed gas on morphology and microstructure of type 316L stainless steel TIG weld metal. Adv. Mater. Res. 2011, 295, 1919–1924. [Google Scholar] [CrossRef]
- Tseng, K.; Chou, C. Effect of nitrogen addition to shielding gas on residual stress of stainless steel weldments. Sci. Technol. Weld. Join. 2002, 7, 57–62. [Google Scholar] [CrossRef]






| Abbreviations | Physical Quantities |
|---|---|
| FN | ferrite number |
| ANN | artificial neural network |
| DFSS | Dongfang Special Steel hot-rolled sheet |
| ASIS | Anshan Iron and Steel cold-rolled sheet |
| GTAW | gas tungsten rc weld |
| MSE | the mean square error |
| R_Training | the correlation coefficients of training set |
| R_Validation | the correlation coefficients of validation set |
| R_Test | the correlation coefficients of test set |
| R_All | the correlation coefficients of total samples |
| Element | C | Si | Mn | Ni | Cr | P | S | Mo | Nb | Cu | N |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Substrate | 0.024 | 0.38 | 1.42 | 8.01 | 18.28 | 0.051 | 0.024 | 0.23 | 0.0054 | 0.30 | 0.039 |
| Filling wire | 0.021 | 0.50 | 1.65 | 9.57 | 19.74 | 0.026 | 0.00074 | 0.096 | 0.012 | 0.098 | 0.013 |
| Level | Factors | ||||
|---|---|---|---|---|---|
| A Travel Speed v (mm∙s−1) | B Wire-Feed Rate (mm∙s−1) | C Welding Current (A) | D Arc Length (mm) | E Nitrogen Content (%) | |
| 1 | 4 | 12.5 | 150 | 2.5 | 0 |
| 2 | 5 | 13.5 | 165 | 3.5 | 0.5 |
| 3 | 6 | 14.5 | 180 | 4.5 | 1.0 |
| 4 | 7 | 15.5 | 195 | 5.5 | 2.0 |
| 5 | 8 | 16.5 | 210 | 6.5 | 2.5 |
| Test No. | Factors | The Average FN | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | DFSS | ASIS | |
| 1 | A1 | B1 | C1 | D1 | E1 | 6.82 | 6.28 |
| 2 | A1 | B2 | C2 | D2 | E2 | 5.48 | 5.30 |
| 3 | A1 | B3 | C3 | D3 | E3 | 3.68 | 3.60 |
| 4 | A1 | B4 | C4 | D4 | E4 | 2.02 | 1.82 |
| 5 | A1 | B5 | C5 | D5 | E5 | 1.86 | 1.07 |
| 6 | A2 | B1 | C3 | D4 | E5 | 0.74 | 1.38 |
| 7 | A2 | B2 | C4 | D5 | E1 | 6.02 | 4.88 |
| 8 | A2 | B3 | C5 | D1 | E2 | 4.98 | 5.34 |
| 9 | A2 | B4 | C1 | D2 | E3 | 4.40 | 4.44 |
| 10 | A2 | B5 | C2 | D3 | E4 | 1.94 | 1.62 |
| 11 | A3 | B1 | C5 | D2 | E4 | 1.40 | 2.24 |
| 12 | A3 | B2 | C1 | D3 | E5 | 0.71 | 0.92 |
| 13 | A3 | B3 | C2 | D4 | E1 | 4.18 | 3.86 |
| 14 | A3 | B4 | C3 | D5 | E2 | 4.40 | 4.70 |
| 15 | A3 | B5 | C4 | D1 | E3 | 3.74 | 4.80 |
| 16 | A4 | B1 | C2 | D5 | E3 | 1.48 | 1.80 |
| 17 | A4 | B2 | C3 | D1 | E4 | 1.50 | 2.62 |
| 18 | A4 | B3 | C4 | D2 | E5 | 1.16 | 1.86 |
| 19 | A4 | B4 | C5 | D3 | E1 | 5.68 | 4.48 |
| 20 | A4 | B5 | C1 | D4 | E2 | 4.80 | 4.56 |
| 21 | A5 | B1 | C4 | D3 | E2 | 3.50 | 4.08 |
| 22 | A5 | B2 | C5 | D4 | E3 | 1.88 | 2.70 |
| 23 | A5 | B3 | C1 | D5 | E4 | 0.82 | 0.57 |
| 24 | A5 | B4 | C2 | D1 | E5 | 2.24 | 0.82 |
| 25 | A5 | B5 | C3 | D2 | E1 | 4.90 | 3.52 |
| Hidden Nodes | Epoch | MSE | Gradient | R_Training | R_Validation | R_Test | R_All |
|---|---|---|---|---|---|---|---|
| 2 | 17 | 0.2350 | 0.00284 | 0.96393 | 0.96774 | 0.97223 | 0.96567 |
| 4 | 18 | 0.0708 | 0.08390 | 0.98692 | 0.98281 | 0.98905 | 0.98664 |
| 6 | 18 | 0.0411 | 0.00932 | 0.99376 | 0.99460 | 0.99302 | 0.99337 |
| 8 | 7 | 0.0365 | 3.26 × 10−11 | 0.99491 | 0.98921 | 0.98922 | 0.99340 |
| 10 | 6 | 0.0232 | 8.19 × 10−9 | 0.99653 | 0.98753 | 0.98855 | 0.99257 |
| Hidden Nodes | Epoch | MSE | Gradient | R_Training | R_Validation | R_Test | R_All |
|---|---|---|---|---|---|---|---|
| 2 | 23 | 0.3210 | 5.16 × 10−5 | 0.93982 | 0.92551 | 0.92817 | 0.93722 |
| 4 | 19 | 0.1160 | 0.03140 | 0.97718 | 0.97556 | 0.96109 | 0.97319 |
| 6 | 15 | 0.0648 | 3.25 × 10−8 | 0.98735 | 0.98270 | 0.98659 | 0.98689 |
| 8 | 9 | 0.0693 | 4.58 × 10−9 | 0.98759 | 0.98318 | 0.98876 | 0.98762 |
| 10 | 7 | 0.0688 | 5.07 × 10−9 | 0.98829 | 0.98963 | 0.98566 | 0.98740 |
| 12 | 6 | 0.0587 | 4.99 × 10−14 | 0.99017 | 0.97508 | 0.97881 | 0.98633 |
| 14 | 6 | 0.0578 | 1.10 × 10−10 | 0.99024 | 0.98843 | 0.96523 | 0.98609 |
| Hidden Nodes | Epoch | MSE | Gradient | R_Training | R_Validation | R_Test | R_All |
|---|---|---|---|---|---|---|---|
| 2 | 20 | 0.591 | 0.02000 | 0.90387 | 0.87916 | 0.88421 | 0.89614 |
| 4 | 24 | 0.194 | 0.02760 | 0.96599 | 0.96179 | 0.96448 | 0.96478 |
| 6 | 13 | 0.186 | 1.20 × 10−8 | 0.96658 | 0.97196 | 0.97261 | 0.96811 |
| 8 | 9 | 0.183 | 6.47 × 10−9 | 0.97271 | 0.95684 | 0.95878 | 0.96778 |
| 10 | 9 | 0.168 | 1.43 × 10−11 | 0.97332 | 0.95667 | 0.95227 | 0.96786 |
| Heat Input | High Temperature Residence Time | FN | |
|---|---|---|---|
| welding speed↑ | ↓ | ↓ | ↑ |
| wire-feed rate↑ | ↓ | ↓ | ↑ |
| welding current↑ | ↑ | ↑ | ↓ |
| arc length↑ | ↑ | ↑ | ↓ |
| Dilution Rate | Creq/Nieq Ratio | FN | |
|---|---|---|---|
| welding speed↑ | ↓ | ↓ | ↓ |
| wire-feed rate↑ | ↓ | ↓ | ↓ |
| welding current↑ | ↑ | ↑ | ↑ |
| arc length↑ | ↑ | ↑ | ↑ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, S.; Cheng, F.; Li, L.; Li, F.; Shao, Z.; Zhang, Y.; Wu, S. Relationship Analysis between Multi-Parameters and Ferrite Number in GTAW Based on ANN Model. Metals 2021, 11, 1429. https://doi.org/10.3390/met11091429
Cheng S, Cheng F, Li L, Li F, Shao Z, Zhang Y, Wu S. Relationship Analysis between Multi-Parameters and Ferrite Number in GTAW Based on ANN Model. Metals. 2021; 11(9):1429. https://doi.org/10.3390/met11091429
Chicago/Turabian StyleCheng, Shanghua, Fangjie Cheng, Lidong Li, Fangliang Li, Zhujing Shao, Yiqi Zhang, and Shaojie Wu. 2021. "Relationship Analysis between Multi-Parameters and Ferrite Number in GTAW Based on ANN Model" Metals 11, no. 9: 1429. https://doi.org/10.3390/met11091429
APA StyleCheng, S., Cheng, F., Li, L., Li, F., Shao, Z., Zhang, Y., & Wu, S. (2021). Relationship Analysis between Multi-Parameters and Ferrite Number in GTAW Based on ANN Model. Metals, 11(9), 1429. https://doi.org/10.3390/met11091429







