Enhancing the Lifetime of the Pneumatic Cylinder in Automatic Assembly Line Subjected to Repeated Pressure Loading
Abstract
:1. Introduction
2. Parametric ALT for Mechanical Product
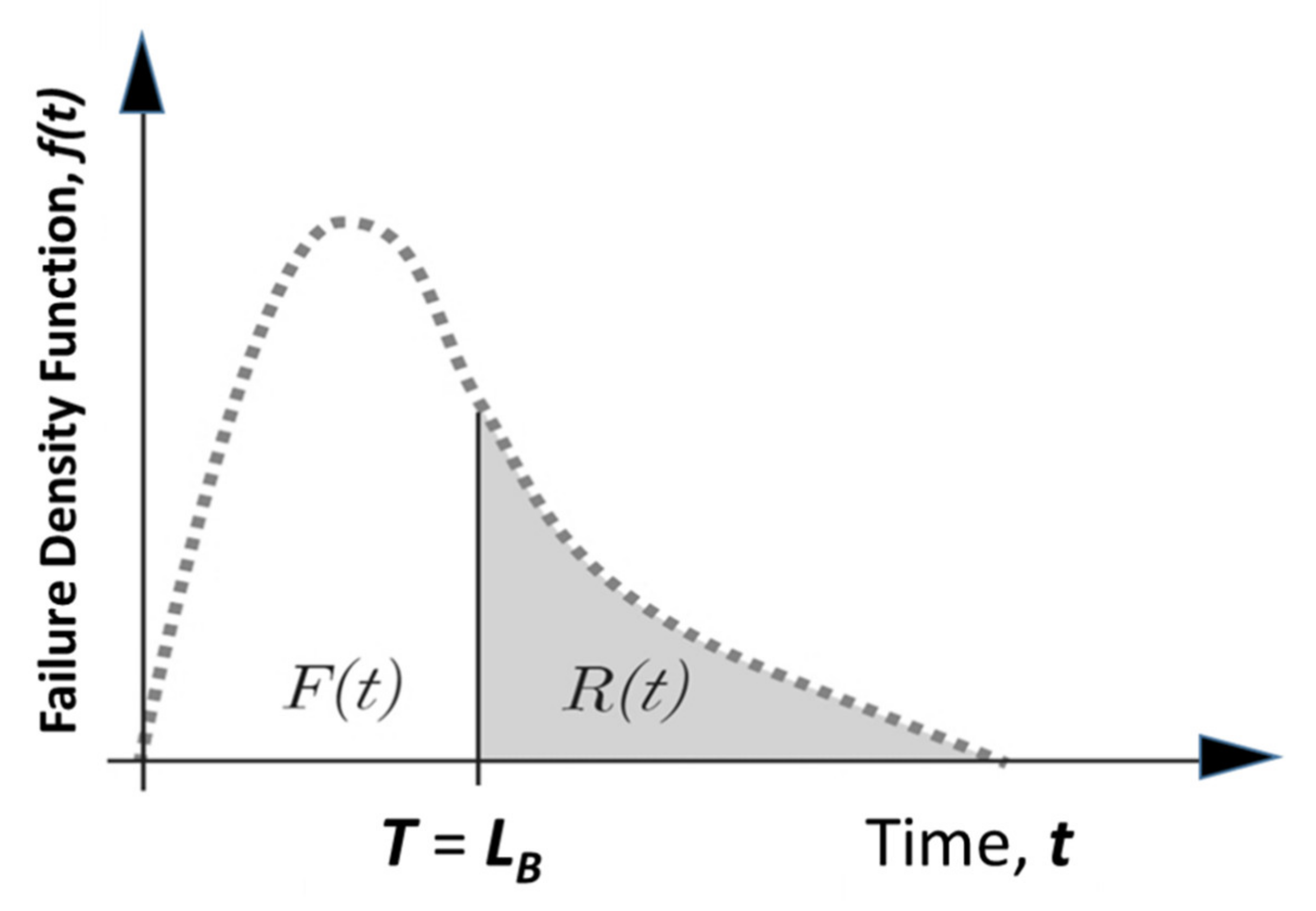
2.1. BX Lifetime Target of New System in a Mechanical System
2.2. Placing an Entire Parametric ALT Scheme
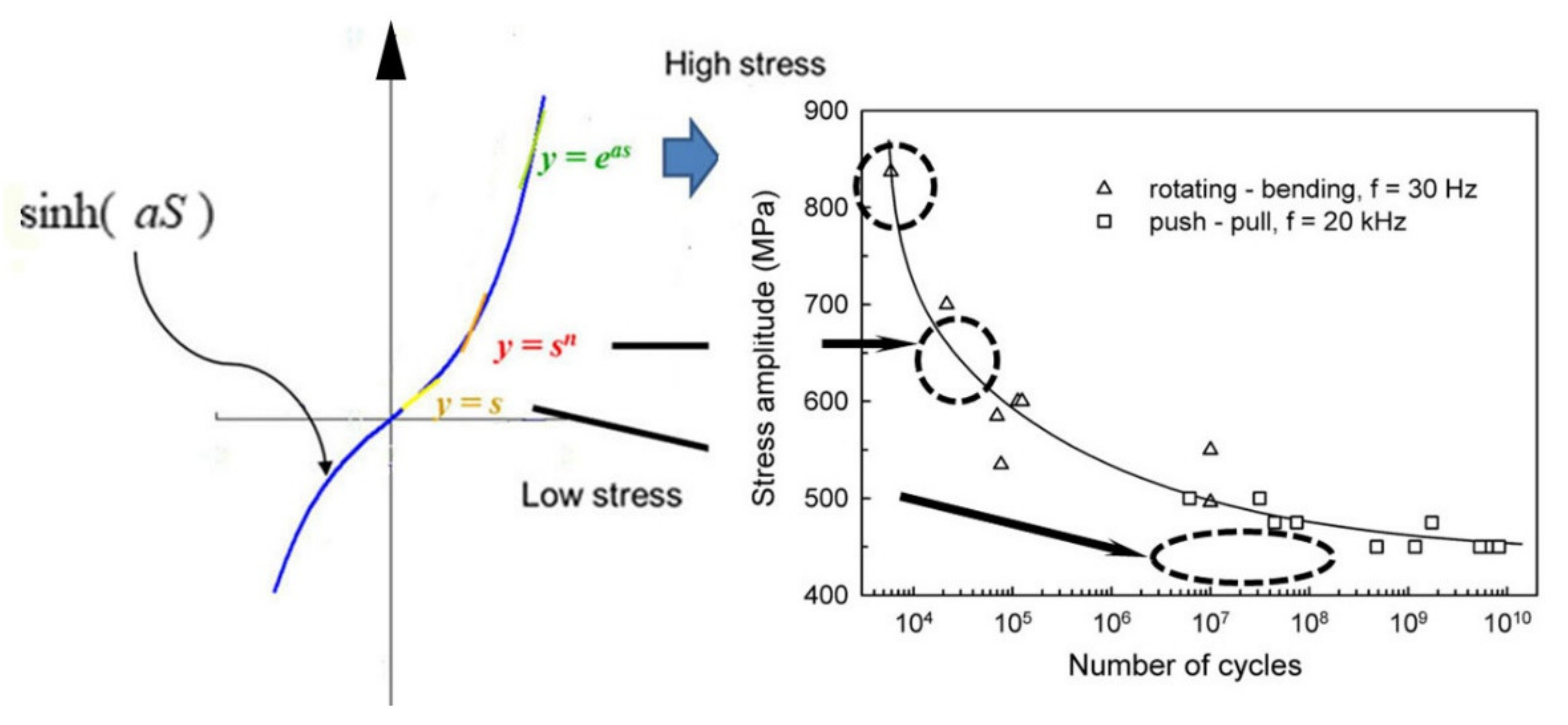
2.3. Generalized Time to Failure and Sample Size Equation for Parametric ALT
- at first has a little linear result;
- has what is judged as a medium result;
- at end is large.
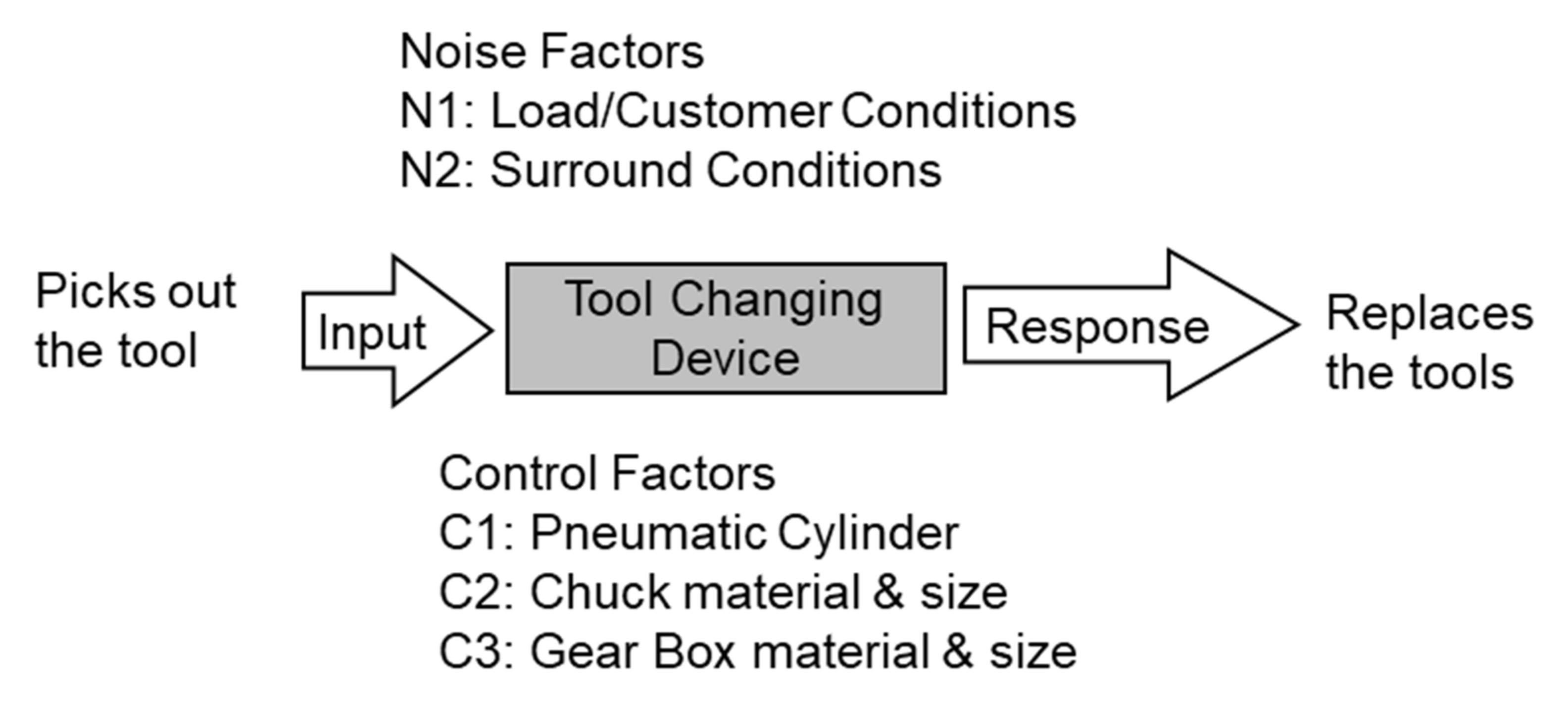
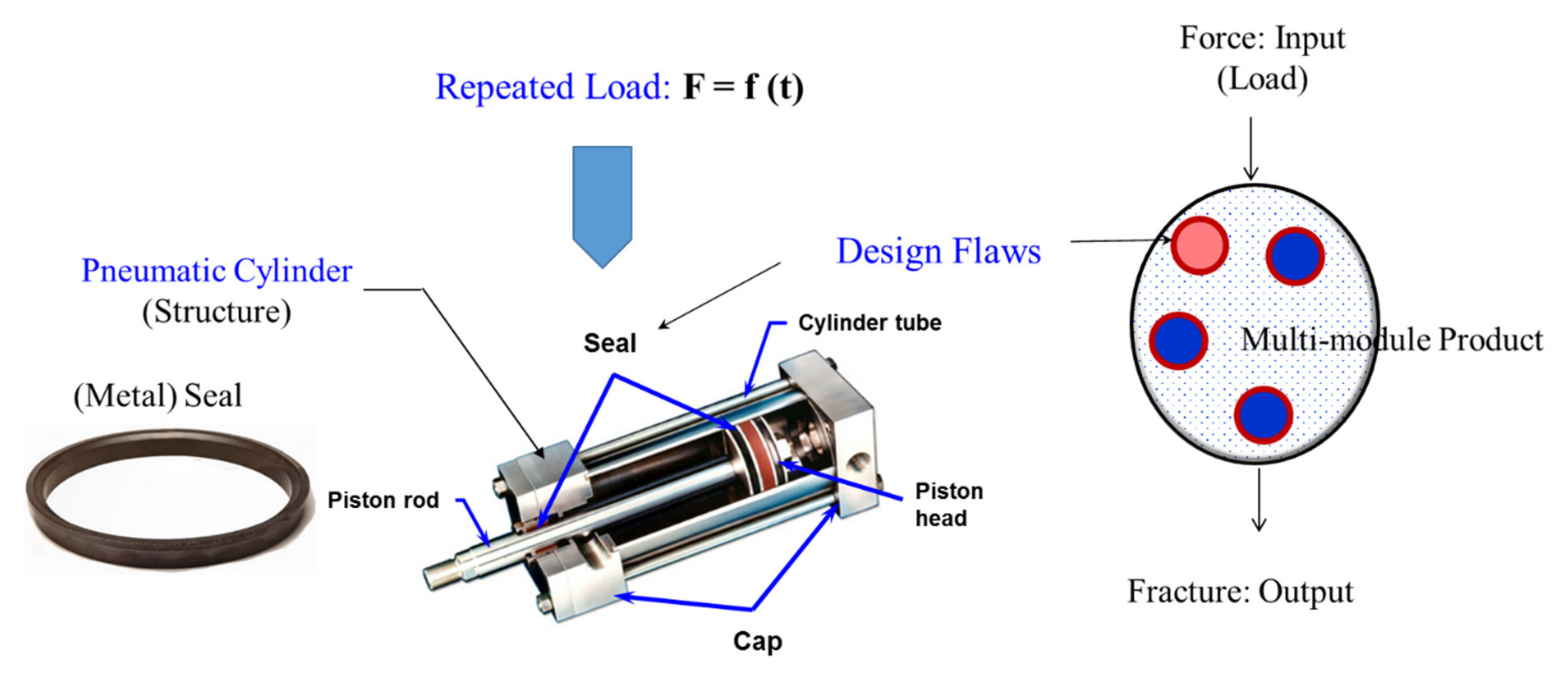
2.4. Case Study—Lifetime of a Localized Designed Pneumatic Cylinder in an Automatic Assembly Line
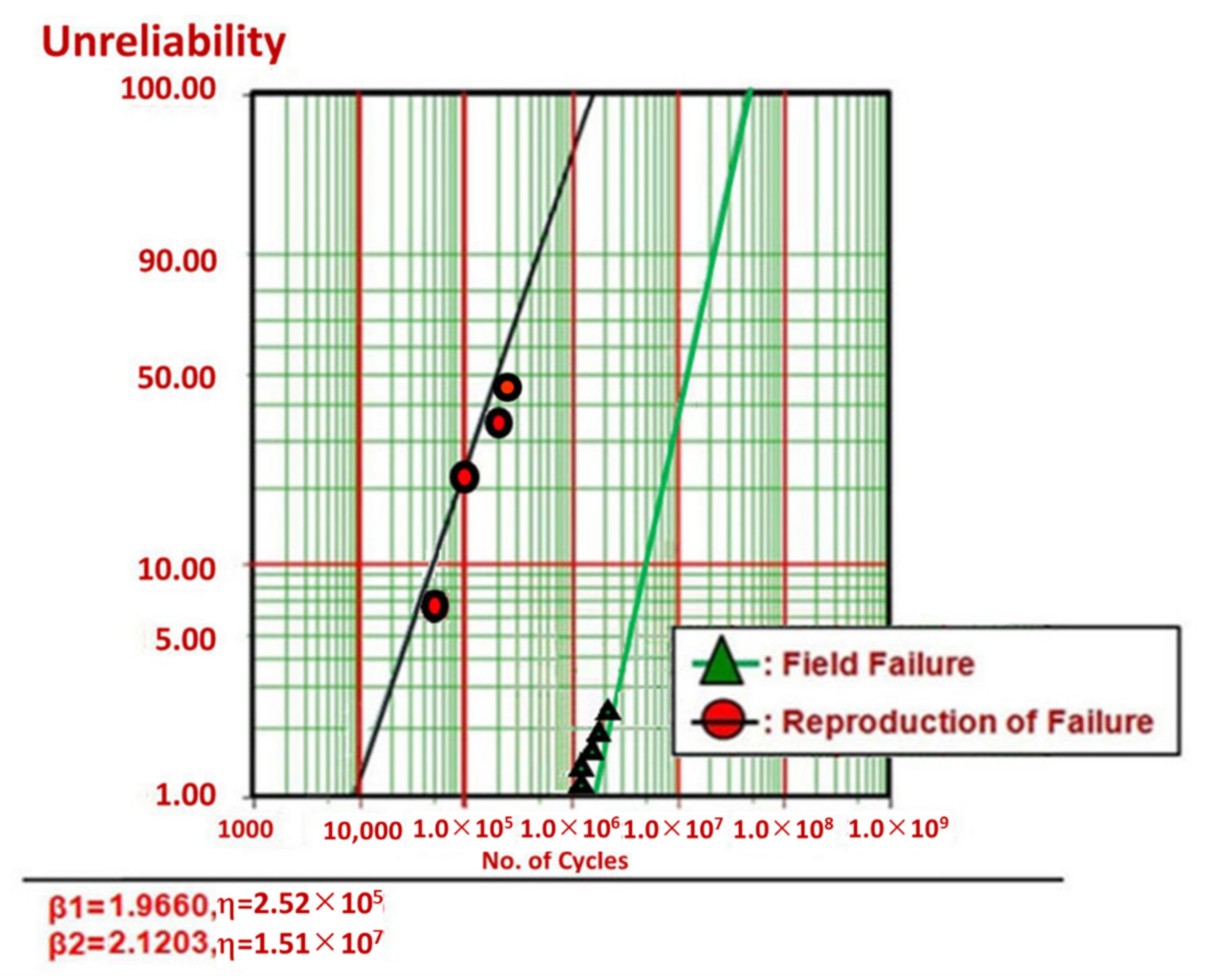
3. Results and Discussion
4. Summary and Conclusions
- ▪
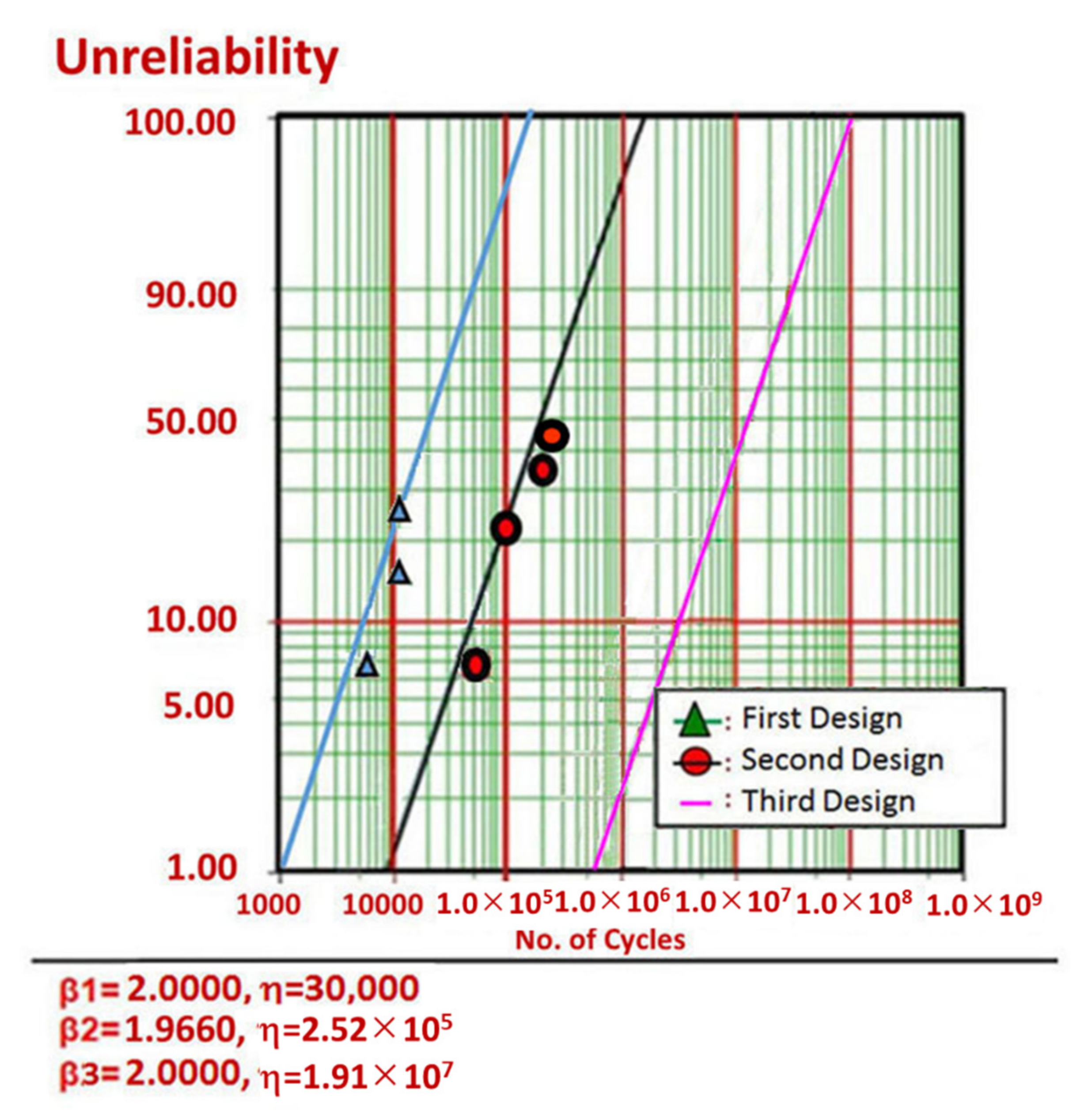
- In the second ALT, we discovered the hardening and wear of piston seal like those of market samples. It happens as follows: (1) repetitive operating stress, (2) friction heat in seal, (3) lube vaporization in seal, (4) accelerating seal hardening, and (5) accelerating seal wear. We modified the seal material, C2, from silicone rubber to (thermoset) polyurethane.
- ▪
- During the third ALT, no problems were discovered. The pneumatic cylinder systems should attain the lifetime target—B1 life of 10 years with about a 60% confidence level. By examining problematic field products and conducting parametric ALTs with design modifications, it was possible to improve the lifetime of the pneumatic cylinder.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| A BX | Cross-sectional area, cm2 Time which is a cumulated failure rate of X%: durability index |
| Ea | Activation energy, eV |
| e | Effort |
| f | Flow |
| F | Impact force, kN |
| F(t) | Unreliability |
| h | Testing cycles (or cycles) |
| h* J | Non-dimensional testing cycles, Junction function equation |
| k | Boltzmann’s constant, 8.62 × 10−5 eV/deg |
| LB | Target BX life and x = 0.01X, on the condition that x ≤ 0.2 |
| n ∆P Q | Number of test samples Pressure difference, MPa Amount of energy absorbed or released during the reaction. For the semiconductor, total number of dopants per unit area |
| R r | Ratio for minimum stress to maximum stress in stress cycle, σmin/σmax Failed numbers |
| S | Stress |
| T ti | Temperature, K Test time for each sample |
| TF | Time to failure |
| X | Accumulated failure rate, % |
| x | x = 0.01X, on condition that x ≤ 0.2. |
| Greek symbols | |
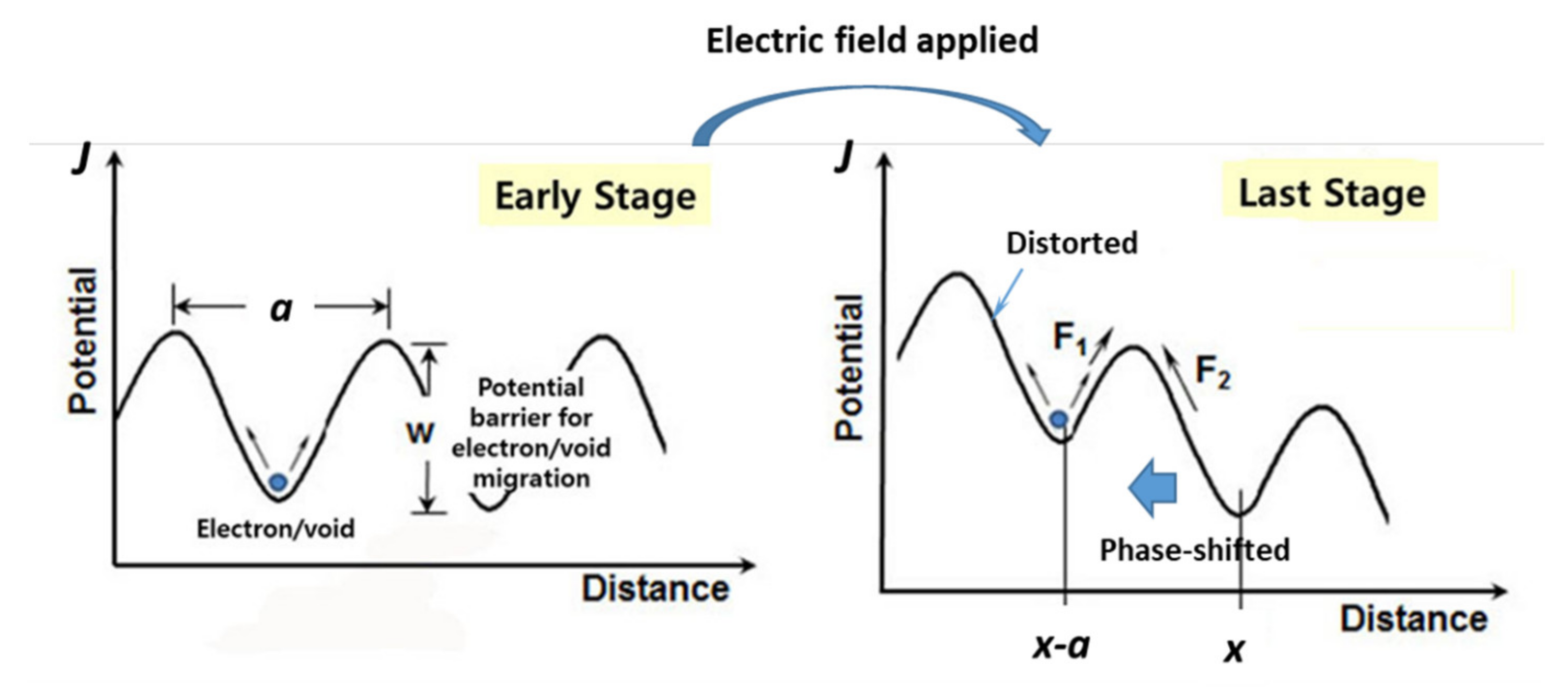
| ξ | Electrical field exerted |
| η | Characteristic life |
| λ χ2 α | Cumulative damage exponent in Palmgren–Miner’s rule Chi-square distribution Confidence level |
| Superscripts | |
| β | Shape parameter in Weibull distribution |
| n | Stress dependence, |
| Subscripts | |
| 0 | Normal stress conditions |
| 1 | Accelerated stress conditions |
Appendix A. Derivation of Sample Size Equation
References
- Magaziner, I.C.; Patinkin, M. Cold competition: GE wages the refrigerator war. Harv. Bus. Rev. 1989, 89, 114–124. [Google Scholar]
- ISO 19973-1:2015Pneumatic Fluid Power—Assessment of Component Reliability by Testing—Part 1: General Procedures, ISO: Geneva, Switzerland, 2015.
- Rogers, W.P.; Armstrong, N.A.; Acheson, D.C.; Covert, E.E.; Feynman, R.P.; Hotz, R.B.; Kutyna, D.J.; Ride, S.K.; Rummel, R.W.; Sutter, J.F.; et al. Report of the Presidential Commission on the Space Shuttle Challenger Accident; NASA: Washington, DC, USA, 1986. [Google Scholar]
- Woo, S.; O’Neal, D.; Woldemichael, D.E.; Atnaw, S.M.; Tulu, M.M. Improving the Fatigue of Newly Designed Mechanical System Subjected to Repeated Impact Loading. Metals 2021, 11, 139. [Google Scholar] [CrossRef]
- Woo, S.; O’Neal, D. Reliability Design of Mechanical Systems Such as Compressor Subjected to Repetitive Stresses. Metals 2021, 11, 1261. [Google Scholar] [CrossRef]
- Duga, J.J.; Fisher, W.H.; Buxaum, R.W.; Rosenfield, A.R.; Buhr, A.R.; Honton, E.J.; McMillan, S.C. The Economic Effects of Fracture in the United States; Final Report; Available as NBS Special Publication 647-2; Battelle Laboratories: Columbus, OH, USA, 1982. [Google Scholar]
- Fatigue. In Elements of Metallurgy and Engineering Alloys; Campbell, F.C. (Ed.) ASM International: Materials Park, OH, USA, 2008. [Google Scholar]
- Modarres, M.; Kaminskiy, M.; Krivtsov, V. Reliability Engineering and Risk Analysis: A Practical Guide, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Elsayed, E.A. Reliability Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Hahn, G.J.; Meeker, W.Q. How to Plan an Accelerated Life Test (E-Book); ASQ Quality Press: Milwaukee, WI, USA, 2004. [Google Scholar]
- McPherson, J. Accelerated testing. In Electronic Materials Handbook Volume 1: Packaging; ASM International Publishing: Materials Park, OH, USA, 1989; pp. 887–894. [Google Scholar]
- McPherson, J. Reliability Physics and Engineering: Time-to-Failure Modeling; Springer: New York, NY, USA, 2010. [Google Scholar]
- Griffith, A.A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. A 1921, 221, 163–198. [Google Scholar]
- Irwin, G. Analysis of stresses and strains near the end of a crack traversing a plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics—Fundamentals and Applications, 3rd ed.; CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- ASTM E606/E606MStandard Test Method for Strain-Controlled Fatigue Testing, ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM E399Standard Test Method for Linear-Elastic Plane-Strain Fracture Toughness of Metallic Materials, ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM E647Standard Test Method for Measurement of Fatigue Crack Growth Rates, ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM E739-10Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ε-N) Fatigue Data, ASTM International: West Conshohocken, PA, USA, 2015.
- Braco, R.; Prates, P.; Costa, J.D.M.; Berto, F. New methodology of fatigue life evaluation for multiaxially loaded notched components based on two uniaxial strain-controlled tests. Int. J. Fatigue 2018, 111, 308–320. [Google Scholar] [CrossRef]
- Weingart, R.G.; Stephen, P. Timoshenko: Father of Engineering Mechanics in the U.S. Structure Magazine, 1 August 2007. [Google Scholar]
- Sánchez, M.; Cicero, S.; Arroyo, B.; Álvarez, J.A. Coupling Finite Element Analysis and the Theory of Critical Distances to Estimate Critical Loads in Al6060-T66 Tubular Beams Containing Notches. Metals 2020, 10, 1395. [Google Scholar] [CrossRef]
- Li, Q.; Xie, L. Analysis and Optimization of Tooth Surface Contact Stress of Gears with Tooth Profile Deviations, Meshing Errors and Lead Crowning Modifications Based on Finite Element Method and Taguchi Method. Metals 2020, 10, 1370. [Google Scholar] [CrossRef]
- Hertzberg, R.W.; Vinci, R.P.; Hertzberg, J.L. Deformation and Fracture Mechanics of Engineering Materials, 6th ed.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2020. [Google Scholar]
- Zupančič, B.; Prokop, Y.; Nikonov, A. FEM analysis of dispersive elastic waves in three-layered composite plates with high contrast properties. Finite Elem. Anal. Des. 2021, 193, 103553. [Google Scholar] [CrossRef]
- Raghavan, A.; Cesnik, C.E. Review of guided-wave structural health monitoring. Shock. Vib. Dig. 2007, 39, 91–114. [Google Scholar] [CrossRef]
- IEEE Standard Glossary of Software Engineering Terminology. IEEE STD 610.12-1990. Standards Coordinating Committee of the Computer Society of IEEE. (Reaffirmed September 2002). Available online: https://ieeexplore.ieee.org/document/159342 (accessed on 31 December 1990).
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; John Wiley and Son: Hoboken, NJ, USA, 2011; p. 683. [Google Scholar]
- Grove, A. Physics and Technology of Semiconductor Device, 1st ed.; Wiley International Edition: New York, NY, USA, 1967; p. 37. [Google Scholar]
- Minges, M.L. Electronic Materials Handbook; ASM International: Cleveland, OH, USA, 1989; Volume 1, p. 888. [Google Scholar]
- Karnopp, D.C.; Margolis, D.L.; Rosenberg, R.C. System Dynamics: Modeling, Simulation, and Control of Mechatronic Systems, 6th ed.; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Wasserman, G. Reliability Verification, Testing, and Analysis in Engineering Design; Marcel Dekker: New York, NY, USA, 2003; p. 228. [Google Scholar]
- SAMSUNG Appliance Field Report Data, SRTP 97-2; SAMSUNG: Gwangju, Korea, 2003; p. 45.
- William, E.L.; David, M.; Christoper, N.M.; Stephen, W.B.; Richard, J.F.; Timothy, F.; Thomas, A.S.; Frank, W.G. Mechanical Properties of Structural Steels. NIST NCSTAR 1-3D; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2005. [Google Scholar]
- Tang, L.C. Multiple-steps Step-stress Accelerated Life Test. In Handbook of Reliability Engineering; Springer: London, UK, 2003; pp. 441–455, Chapter 24. [Google Scholar]
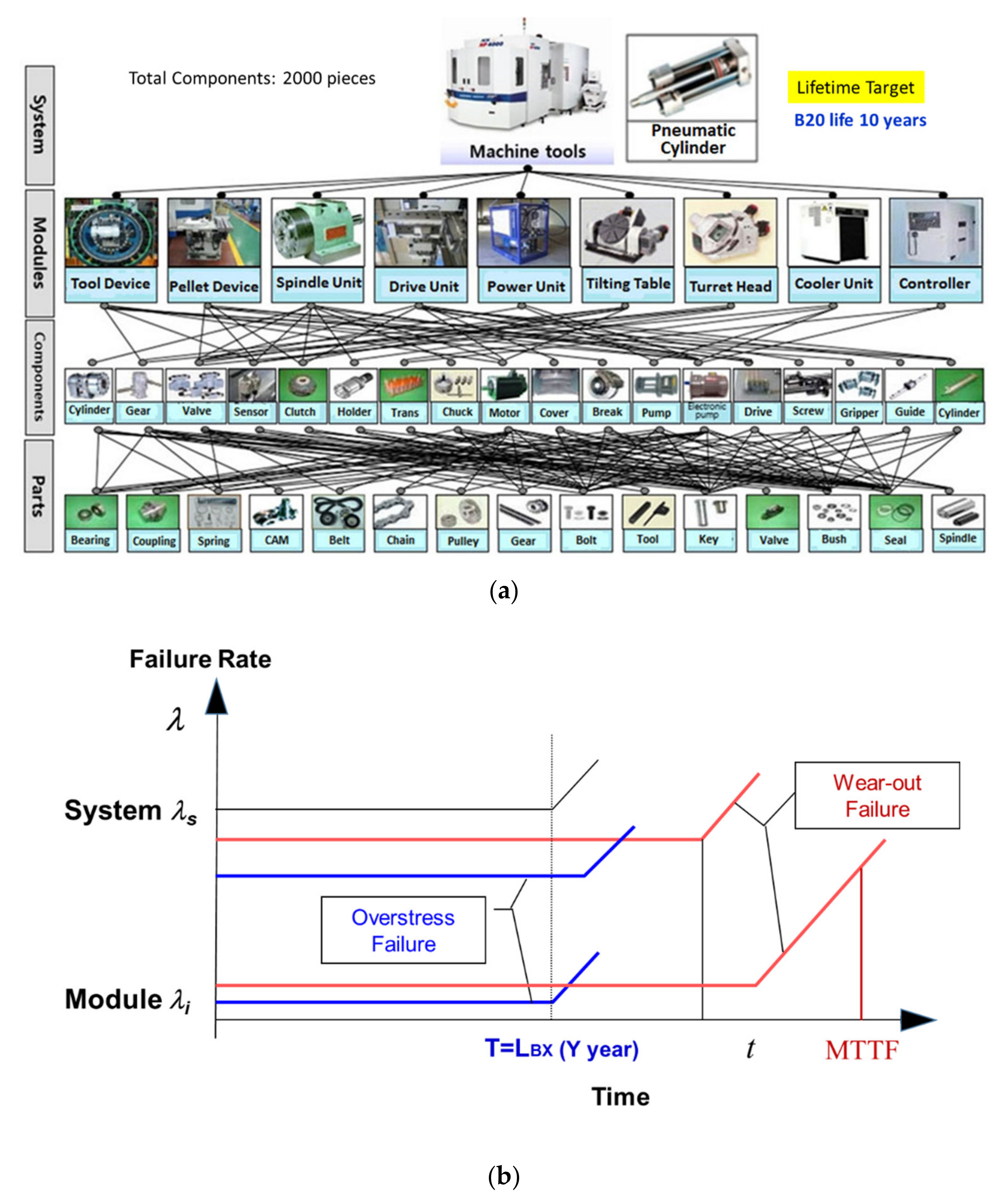
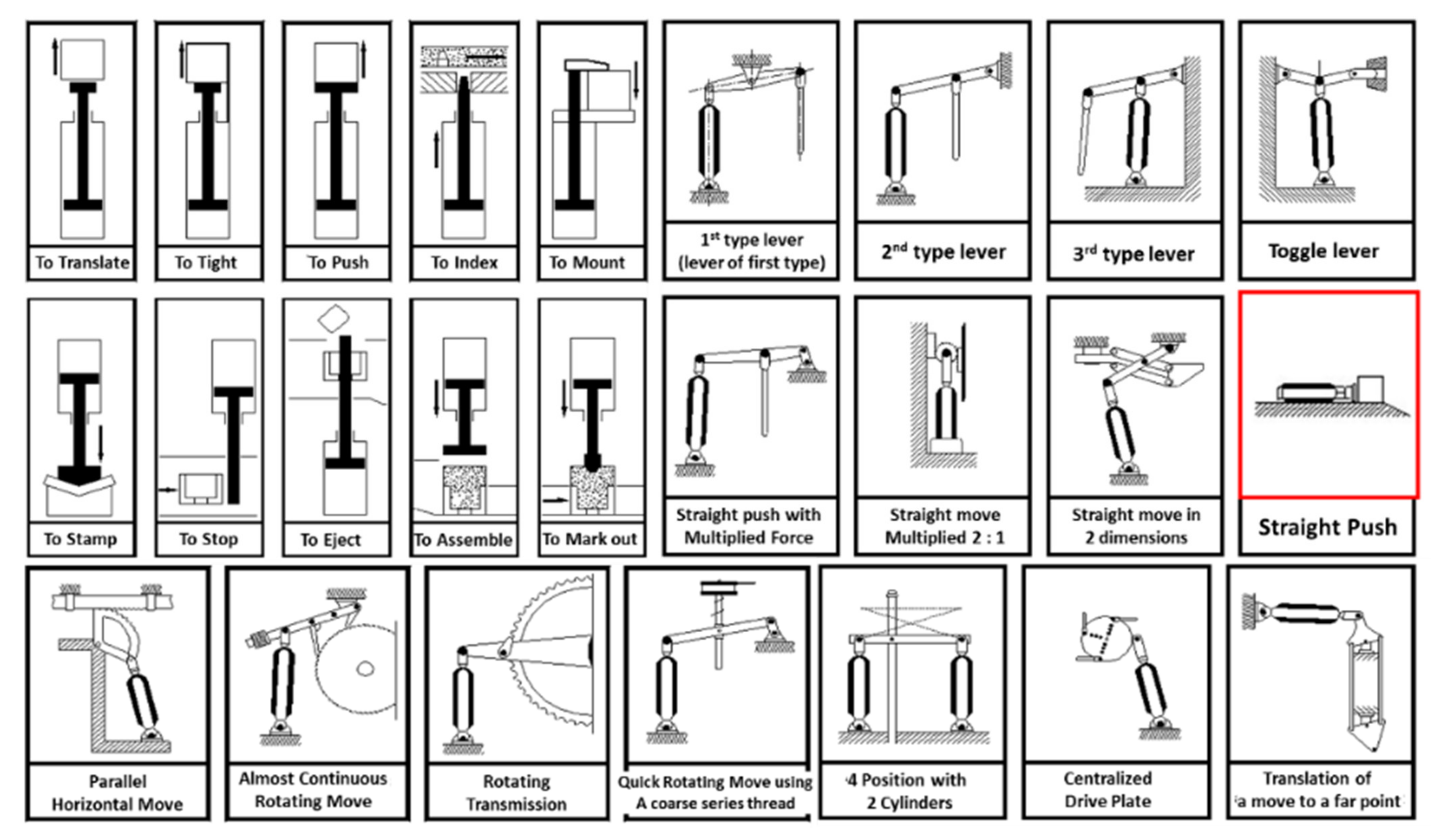






| Modules | Market Data | Anticipated Reliability | Targeted Reliability | |||||
|---|---|---|---|---|---|---|---|---|
| Failure Rate Per Year, λ (%/Year) | BX Life, LB (Year) | Failure Rate Per Year, λ (%/Year) | BX Life, LB (Year) | Failure Rate Per Year, λ (%/Year) | BX Life, LB (Year) | |||
| A | 0.24 | 4.2 | New | ×5 | 1.20 | 0.83 | 0.10 | 10(BX = 1.0) |
| B | 0.31 | 3.2 | Modified | ×2 | 0.62 | 1.61 | 0.10 | 10(BX = 1.0) |
| C | 0.15 | 6.7 | Modified | ×2 | 0.30 | 3.33 | 0.10 | 10(BX = 1.0) |
| D | 0.35 | 2.9 | Alike | ×1 | 0.35 | 2.9 | 0.10 | 10(BX = 1.0) |
| E | 0.30 | 3.3 | Alike | ×1 | 0.30 | 3.33 | 0.10 | 10(BX = 1.0) |
| Others (F/G/H/I) | 0.50 | 10.0 | Alike | ×1 | 0.50 | 10.0 | 0.50 | 10(BX = 5.0) |
| Product | 1.9 | 2.9 | - | - | 3.27 | 0.83 | 1.00 | 10(BX = 10) |
| System Attribute | Power, e(t) × f(t) | Effort, e(t) | Flow, f(t) |
|---|---|---|---|
| Translation | F × V | Force, F(t) | Velocity, V(t) |
| Rotation | Τ × ω | Torque, τ(t) | Angular velocity, ω(t) |
| Pump, compressor | ∆P × Q | Pressure difference, ∆P(t) | Volume flow rate, Q(t) |
| Electric | V × i | Voltage, V(t) | Current, i(t) |
| Magnetic | em × φ | Magneto-motive force, em(t) | Magnetic flux, φ(t) |
| System States | Worst Case | ALT | AF |
|---|---|---|---|
| Pressure (MPa) | 0.63 | 0.8 | 1.6 |
| Parametric ALT | First ALT | Second ALT | Third ALT |
|---|---|---|---|
| Original Design | Design | Final Design | |
| In 220,000 cycles, there are no issues in the pneumatic cylinder | 6000 cycles: 1/10 noise (partially cracked sample) 10,500 cycles: 1/10 noise 11,000 cycles: 1/10 noise (two chipped samples) | 50,000 cycles: 1/10 fail 100,000 cycles: 1/10 fail 110,000 cycles: 1/10 fail 115,000 cycles: 1/10 fail (hardening and wear of piston seal) | 220,000 cycles: 10/10 OK |
| Structure |   | ||
| Action plans | C1: material: Fe-36Ni Invar Alloy → Silicone rubber | C2: material: Silicone rubber → (thermoset) Polyurethane | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woo, S.; O’Neal, D.L.; Hassen, Y.M. Enhancing the Lifetime of the Pneumatic Cylinder in Automatic Assembly Line Subjected to Repeated Pressure Loading. Metals 2022, 12, 35. https://doi.org/10.3390/met12010035
Woo S, O’Neal DL, Hassen YM. Enhancing the Lifetime of the Pneumatic Cylinder in Automatic Assembly Line Subjected to Repeated Pressure Loading. Metals. 2022; 12(1):35. https://doi.org/10.3390/met12010035
Chicago/Turabian StyleWoo, Seongwoo, Dennis L. O’Neal, and Yimer Mohammed Hassen. 2022. "Enhancing the Lifetime of the Pneumatic Cylinder in Automatic Assembly Line Subjected to Repeated Pressure Loading" Metals 12, no. 1: 35. https://doi.org/10.3390/met12010035
APA StyleWoo, S., O’Neal, D. L., & Hassen, Y. M. (2022). Enhancing the Lifetime of the Pneumatic Cylinder in Automatic Assembly Line Subjected to Repeated Pressure Loading. Metals, 12(1), 35. https://doi.org/10.3390/met12010035







