Effect of Shear/Axial Stress Ratio on Multiaxial Non-Proportional Loading Fatigue Damage on AISI 303 Steel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Experimental Program
2.3. Non-Proportional Damage Parameter, Y
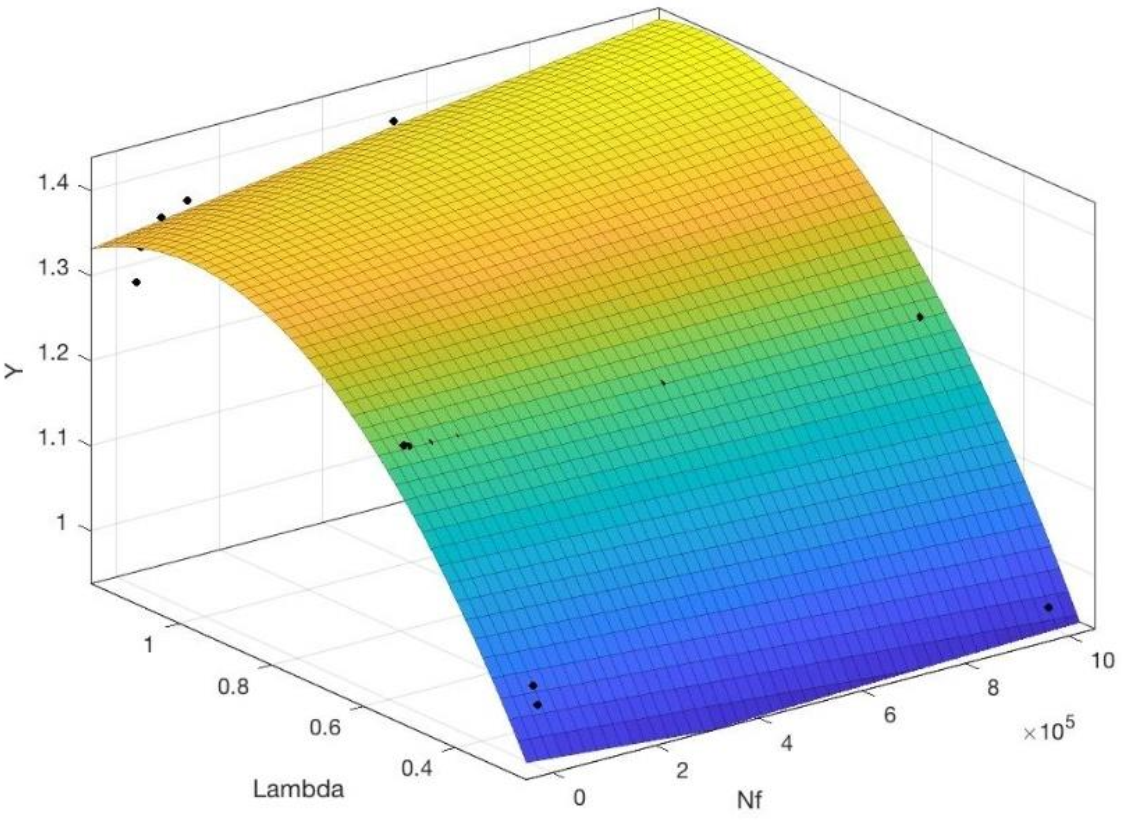
3. Results and Discussion
S-N Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Socie, D.; Marquis, G.B. Multiaxial Fatigue; Society of Automotive Engineers: Warrendale, PA, USA, 2000. [Google Scholar]
- Bernasconi, A.; Filippini, M.; Foletti, S.; Vaudo, D. Multiaxial fatigue of a railway wheel steel under non-proportional loading. Int. J. Fatigue 2006, 28, 663–672. [Google Scholar] [CrossRef]
- Itoh, T.; Sakane, M.; Ohsuga, K. Multiaxial low cycle fatigue life under non-proportional loading. Int. J. Press. Vessels Pip. 2013, 110, 50–56. [Google Scholar] [CrossRef]
- Anes, V.; Reis, L.; Li, B.; De Freitas, M. New approach to evaluate non-proportionality in multiaxial loading conditions. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 1338–1354. [Google Scholar] [CrossRef]
- Socie, D. Multiaxial Fatigue Damage Models. J. Eng. Mater. Technol. 1987, 109, 293–298. [Google Scholar] [CrossRef]
- Fatemi, A.; Shamsaei, N. Multiaxial fatigue: An overview and some approximation models for life estimation. Int. J. Fatigue 2011, 33, 948–958. [Google Scholar] [CrossRef]
- Anes, V.; Reis, L.; Li, B.; De Freitas, M. New cycle counting method for multiaxial fatigue. Int. J. Fatigue 2014, 67, 78–94. [Google Scholar] [CrossRef]
- Anes, V.; Caxias, J.; Freitas, M.; Reis, L. Fatigue damage assessment under random and variable amplitude multiaxial loading conditions in structural steels. Int. J. Fatigue 2017, 100, 591–601. [Google Scholar] [CrossRef]
- Wang, C.H.; Brown, M.W. Life prediction techniques for variable amplitude multiaxial fatigue—Part 1: Theories. J. Eng. Mater. Technol. 1996, 118, 367–370. [Google Scholar] [CrossRef]
- Carpinteri, A.; Spagnoli, A.; Vantadori, S. A review of multiaxial fatigue criteria for random variable amplitude loads. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1007–1036. [Google Scholar] [CrossRef]
- Mesa, J.; González-Quiroga, A.; Maury, H. Developing an indicator for material selection based on durability and environmental footprint: A Circular Economy perspective. Resour. Conserv. Recycl. 2020, 160, 104887. [Google Scholar] [CrossRef]
- Anes, V.; Reis, L.; Freitas, M. Multiaxial fatigue damage accumulation under variable amplitude loading conditions. Procedia Eng. 2015, 101, 117–125. [Google Scholar] [CrossRef] [Green Version]
- Fatemi, A.; Yang, L. Cumulative fatigue damage and life prediction theories: A survey of the state of the art for homogeneous materials. Int. J. Fatigue 1998, 20, 9–34. [Google Scholar] [CrossRef]
- Mei, J.; Dong, P. A new path-dependent fatigue damage model for non-proportional multi-axial loading. Int. J. Fatigue 2016, 90, 210–221. [Google Scholar] [CrossRef]
- Mei, J.; Dong, P. An equivalent stress parameter for multi-axial fatigue evaluation of welded components including non-proportional loading effects. Int. J. Fatigue 2017, 101, 297–311. [Google Scholar] [CrossRef]
- Ivashyn, U. An experimental and numerical investigation of the biaxial tensile behaviour of biomedical alloys, nitinol and SS304. PhD Thesis, University of Limerick, Limerick, Ireland, 2015. [Google Scholar]
- Reis, L.; Li, B.; De Freitas, M. Analytical and experimental studies on fatigue crack path under complex multi-axial loading. Fatigue Fract. Eng. Mater. Struct. 2006, 29, 281–289. [Google Scholar] [CrossRef]
- De Freitas, M.; Reis, L.; Li, B. Comparative study on biaxial low-cycle fatigue behaviour of three structural steels. Fatigue Fract. Eng. Mater. Struct. 2006, 29, 992–999. [Google Scholar] [CrossRef]
- Reis, L.G.; Li, B.; de Freitas, M. Crack Growth Orientation in Two Structural Materials under Multiaxial Fatigue Loading. Mater. Sci. Forum 2008, 587, 892–897. [Google Scholar] [CrossRef]
- Reis, L.; Li, B.; De Freitas, M. Crack initiation and growth path under multiaxial fatigue loading in structural steels. Int. J. Fatigue 2009, 31, 1660–1668. [Google Scholar] [CrossRef]
- Albinmousa, J.; Jahed, H. Multiaxial effects on LCF behaviour and fatigue failure of AZ31B magnesium extrusion. Int. J. Fatigue 2014, 67, 103–116. [Google Scholar] [CrossRef]
- Pujari, P. Multiaxial Fatigue Analysis—Approach Toward Real-World Life Prediction. In Proceedings of Fatigue, Durability and Fracture Mechanics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 167–183. [Google Scholar]
- de Freitas, M. Multiaxial fatigue: From materials testing to life prediction. Theor. Appl. Fract. Mech. 2017, 92, 360–372. [Google Scholar] [CrossRef]
- Pejkowski, L. On the material’s sensitivity to non-proportionality of fatigue loading. Arch. Civ. Mech. Eng. 2017, 17, 711–727. [Google Scholar] [CrossRef]
- Li, B.; Reis, L.; De Freitas, M. Simulation of cyclic stress/strain evolutions for multiaxial fatigue life prediction. Int. J. Fatigue 2006, 28, 451–458. [Google Scholar] [CrossRef]
- Li, B.; Reis, L.G.; de Freitas, M. Simulations of cyclic plasticity and fatigue behavior of structural steels under multiaxial loading. Mater. Sci. Forum 2006, 514, 1414–1418. [Google Scholar] [CrossRef]
- Marangon, C.; Lazzarin, P.; Berto, F.; Campagnolo, A. Some analytical remarks on the influence of phase angle on stress fields ahead of sharp V-notches under tension and torsion loads. Theor. Appl. Fract. Mech. 2014, 74, 64–72. [Google Scholar] [CrossRef]
- Liu, G.; Li, Z.; Li, Z.; Huang, Y. A multi-axial fatigue-oriented strategy for fatigue damage monitoring and assessment of tubular joints. Ocean Eng. 2021, 227, 108876. [Google Scholar] [CrossRef]
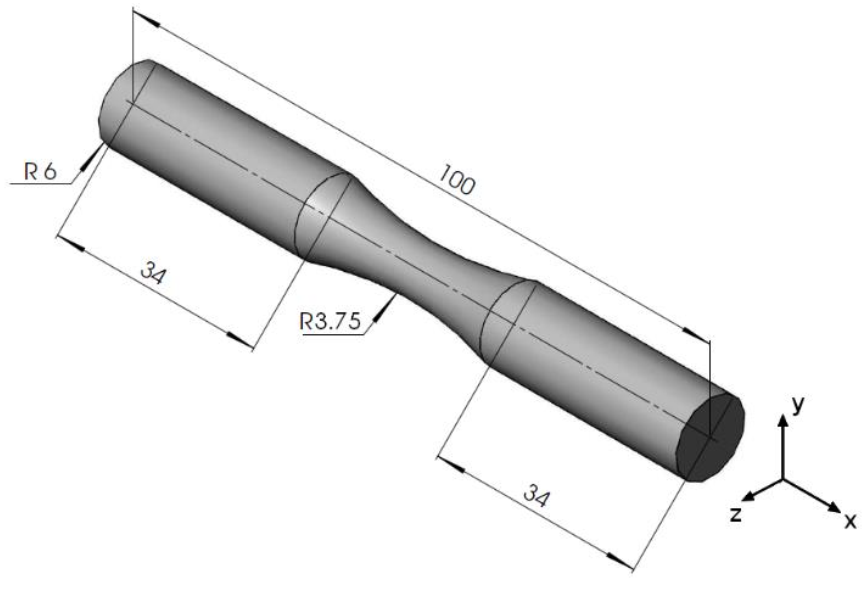


| Element | C | Si | Mn | P | S | Cr | Ni |
|---|---|---|---|---|---|---|---|
| Weight (%) | 0.12 | 1.0 | 2.0 | 0.060 | 0.25 | 18.0 | 9.0 |
| Microstructure Type | fcc |
|---|---|
| Poisson’s ratio | 0.25 |
| Density (Kg/m3) | 8000 |
| Hardness (HV) | 174 |
| Tensile strength (MPa) | 625 |
| Yield strength (MPa) | 330 |
| Elongation (%) | 28 |
| Young’s modulus (GPa) | 178 |
| σ′f—Fatigue strength coefficient (MPa) | 534 |
| b—Fatigue strength coefficient | −0.07 |
| ε′f—Fatigue ductility coefficient | 0.052 |
| c—Fatigue ductility exponent | −0.292 |
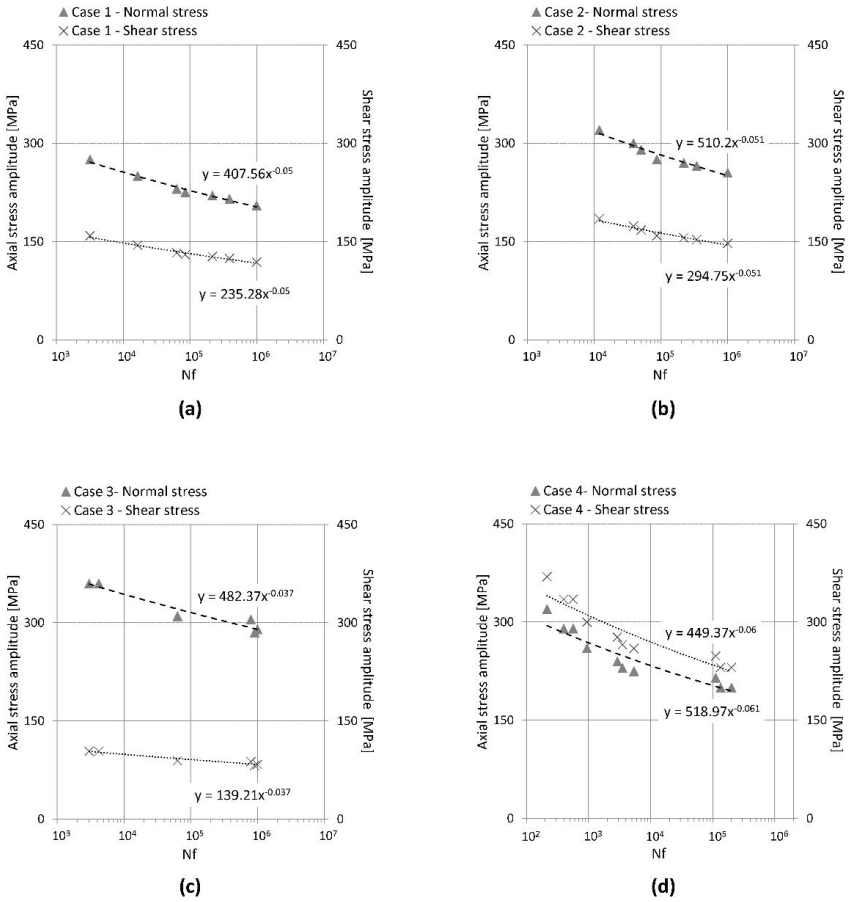
| Loading Case | Normal Stress (MPa) | Shear Stress (MPa) | Nf |
|---|---|---|---|
| Case 1 | 205 | 118.4 | 1,000,000 |
| 215 | 124.1 | 392,005 | |
| 220 | 127 | 217,075 | |
| 225 | 129.9 | 85,376 | |
| 230 | 132.8 | 63,540 | |
| 250 | 144.3 | 16,405 | |
| 275 | 158.8 | 3194 | |
| Case 2 | 255 | 147.2 | 1,000,000 |
| 265 | 153 | 342,890 | |
| 270 | 155.9 | 219,540 | |
| 275 | 158.8 | 86,926 | |
| 290 | 167.4 | 50,412 | |
| 300 | 173.2 | 38,787 | |
| 320 | 184.8 | 11,950 | |
| Case 3 | 290 | 83.7 | 1,000,000 |
| 285 | 82.3 | 911,511 | |
| 305 | 88 | 798,243 | |
| 310 | 89.5 | 63,519 | |
| 360 | 103.9 | 4200 | |
| 360 | 103.9 | 3028 | |
| Case 4 | 200 | 230.9 | 1,000,000 |
| 200 | 230.9 | 668,250 | |
| 215 | 248.3 | 557,580 | |
| 225 | 259.8 | 26,859 | |
| 230 | 265.6 | 17,520 | |
| 240 | 277.1 | 14,514 | |
| 260 | 300.2 | 4700 | |
| 290 | 334.9 | 1983 | |
| 290 | 334.9 | 2811 | |
| 320 | 369.5 | 1070 |
| Case | λ = τa/σa | Trend Line [MPa] |
|---|---|---|
| 1 | 0.57 | σa = 407.56(Nf)−0.05 |
| τa = 235.28(Nf)−0.05 | ||
| 2 | 0.57 | σa = 510.2(Nf)−0.051 |
| τa = 294.75(Nf)−0.051 | ||
| 3 | 0.29 | σa = 482.37(Nf)−0.037 |
| τa = 139.21(Nf)−0.037 | ||
| 4 | 1.15 | σa = 449.37(Nf)−0.06 |
| τa = 518.97(Nf)−0.061 |
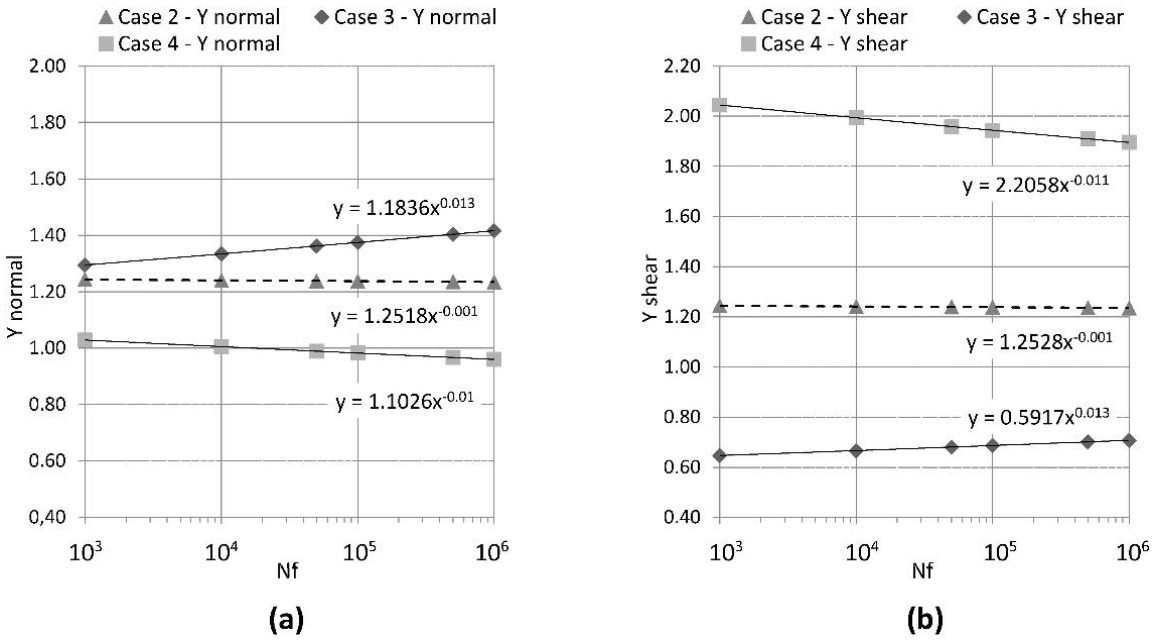
| Nf | Normal (Case 1) σa = 407.56(Nf)^(−0.05) [MPa] (1) | Shear (Case 1) τa = 235.28(Nf)^(−0.05) [MPa] (2) | Normal (Case 2) σa = 510.2(Nf)^(−0.051) [MPa] (3) | Shear (Case 2) τa = 294.75(Nf)^(−0.051) [MPa] (4) | Ynormal (3)/(1) | Yshear (4)/(2) |
|---|---|---|---|---|---|---|
| 103 | 289 | 167 | 359 | 207.23 | 1.24 | 1.24 |
| 104 | 257 | 148 | 319 | 184.27 | 1.24 | 1.24 |
| 5 × 104 | 237 | 137 | 294 | 169.75 | 1.24 | 1.24 |
| 105 | 229 | 132 | 284 | 163.85 | 1.24 | 1.24 |
| 5 × 105 | 211 | 122 | 261 | 150.94 | 1.24 | 1.24 |
| 106 | 204 | 118 | 252 | 145.70 | 1.23 | 1.24 |
| Nf | Normal (Case 1) σa = 407.56(Nf)^(−0.05) [MPa] (1) | Shear (Case 1) τa = 235.28(Nf)^(−0.05) [MPa] (2) | Normal (Case 3) σa = 482.37(Nf)^(−0.037) [MPa] (3) | Shear (Case 3) τa = 139.21(Nf)^(−0.037) [MPa] (4) | Ynormal (3)/(1) | Yshear (4)/(2) |
|---|---|---|---|---|---|---|
| 103 | 289 | 167 | 374 | 107.81 | 1.29 | 0.65 |
| 104 | 257 | 148 | 343 | 99.01 | 1.33 | 0.67 |
| 5 × 104 | 237 | 137 | 323 | 93.28 | 1.36 | 0.68 |
| 105 | 229 | 132 | 315 | 90.92 | 1.37 | 0.69 |
| 5 × 105 | 211 | 122 | 297 | 85.67 | 1.40 | 0.70 |
| 106 | 204 | 118 | 289 | 83.50 | 1.42 | 0.71 |
| Nf | Normal (Case 1) σa =407.56(Nf)^(−0.05) [MPa] (1) | Shear (Case 1) τa = 235.28(Nf)^(−0.05) [MPa] (2) | Normal (Case 4) σa = 449.37(Nf)^(−0.06) [MPa] (3) | Shear (Case 4) τa = 518.97(Nf)^(−0.061) [MPa] (4) | Ynormal (3)/(1) | Yshear (4)/(2) |
|---|---|---|---|---|---|---|
| 103 | 289 | 167 | 297 | 340.52 | 1.03 | 2.04 |
| 104 | 257 | 148 | 259 | 295.90 | 1.01 | 1.99 |
| 5 × 104 | 237 | 137 | 235 | 268.23 | 0.99 | 1.96 |
| 105 | 229 | 132 | 225 | 257.12 | 0.98 | 1.94 |
| 5 × 105 | 211 | 122 | 204 | 233.08 | 0.97 | 1.91 |
| 106 | 204 | 118 | 196 | 223.43 | 0.96 | 1.89 |
| Nf | von Mises (Case 1) [MPa] (1) | von Mises (Case 2) [MPa] (2) | von Mises (Case 3) [MPa] (3) | von Mises (Case 4) [MPa] (4) | Delta [MPa] (2)−(1) | Delta [MPa] (3)−(1) | Delta [MPa] (4)−(1) |
|---|---|---|---|---|---|---|---|
| 103 | 408 | 507 | 418 | 660 | 99 | 10 | 252 |
| 104 | 364 | 451 | 384 | 574 | 88 | 20 | 210 |
| 5 × 104 | 336 | 416 | 361 | 521 | 80 | 26 | 185 |
| 105 | 324 | 401 | 352 | 499 | 77 | 28 | 175 |
| 5 × 105 | 299 | 370 | 332 | 453 | 71 | 33 | 153 |
| 106 | 289 | 357 | 323 | 434 | 68 | 35 | 145 |
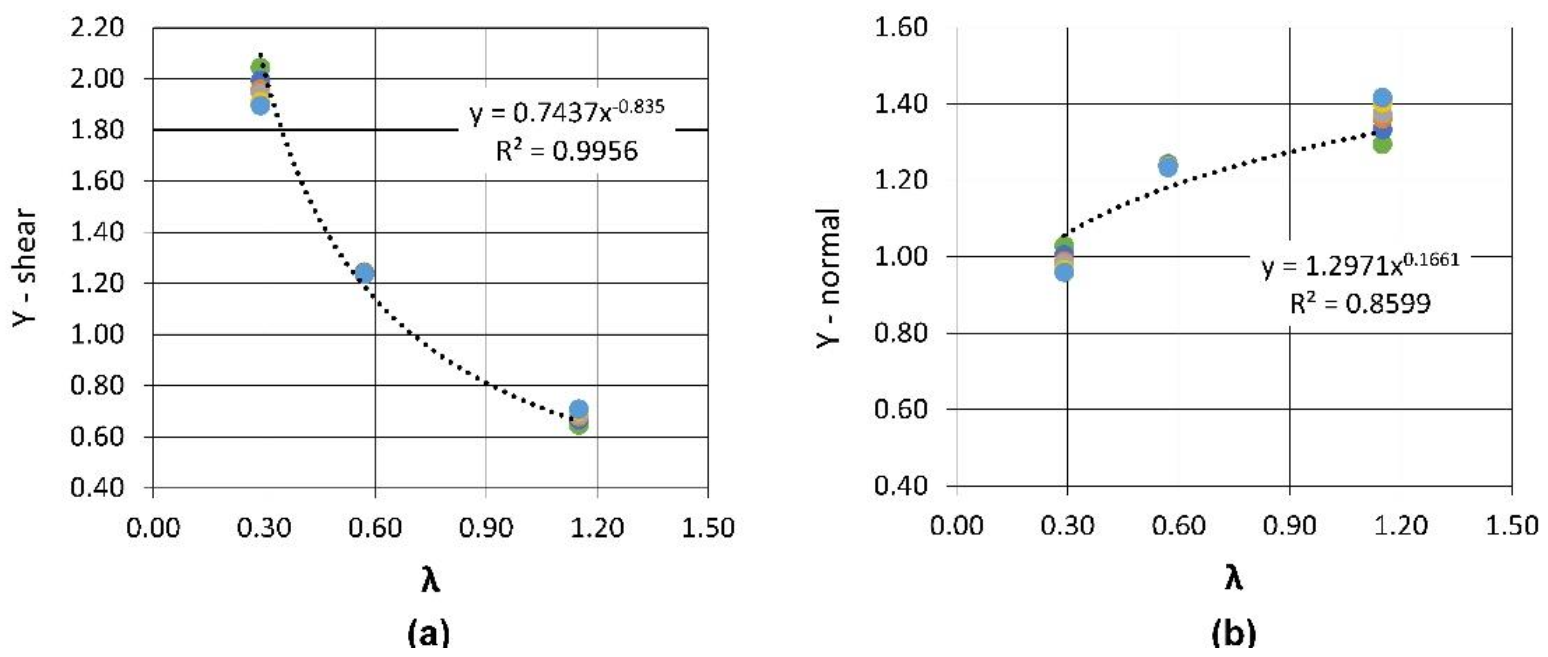
| Nf | Case 3 λ = 0.29 | Case 2 λ = 0.57 | Case 4 λ = 1.15 |
|---|---|---|---|
| 103 | 1.29 | 1.24 | 1.03 |
| 104 | 1.33 | 1.24 | 1.01 |
| 5 × 104 | 1.36 | 1.24 | 0.99 |
| 105 | 1.37 | 1.24 | 0.98 |
| 5 × 105 | 1.40 | 1.24 | 0.97 |
| 106 | 1.42 | 1.23 | 0.96 |
| Nf | Case 3 λ = 0.29 | Case 2 λ = 0.57 | Case 4 λ = 1.15 |
|---|---|---|---|
| 103 | 0.65 | 1.24 | 2.04 |
| 104 | 0.67 | 1.24 | 1.99 |
| 5 × 104 | 0.68 | 1.24 | 1.96 |
| 105 | 0.69 | 1.24 | 1.94 |
| 5 × 105 | 0.70 | 1.24 | 1.91 |
| 106 | 0.71 | 1.24 | 1.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anes, V.; Reis, L.; Freitas, M. Effect of Shear/Axial Stress Ratio on Multiaxial Non-Proportional Loading Fatigue Damage on AISI 303 Steel. Metals 2022, 12, 89. https://doi.org/10.3390/met12010089
Anes V, Reis L, Freitas M. Effect of Shear/Axial Stress Ratio on Multiaxial Non-Proportional Loading Fatigue Damage on AISI 303 Steel. Metals. 2022; 12(1):89. https://doi.org/10.3390/met12010089
Chicago/Turabian StyleAnes, Vitor, Luis Reis, and Manuel Freitas. 2022. "Effect of Shear/Axial Stress Ratio on Multiaxial Non-Proportional Loading Fatigue Damage on AISI 303 Steel" Metals 12, no. 1: 89. https://doi.org/10.3390/met12010089
APA StyleAnes, V., Reis, L., & Freitas, M. (2022). Effect of Shear/Axial Stress Ratio on Multiaxial Non-Proportional Loading Fatigue Damage on AISI 303 Steel. Metals, 12(1), 89. https://doi.org/10.3390/met12010089








