Swelling and He-Embrittlement of Austenitic Stainless Steels and Ni-Alloys in Nuclear Reactors
Abstract
:1. Introduction
1.1. Radiation Damage and Gas Atom Production
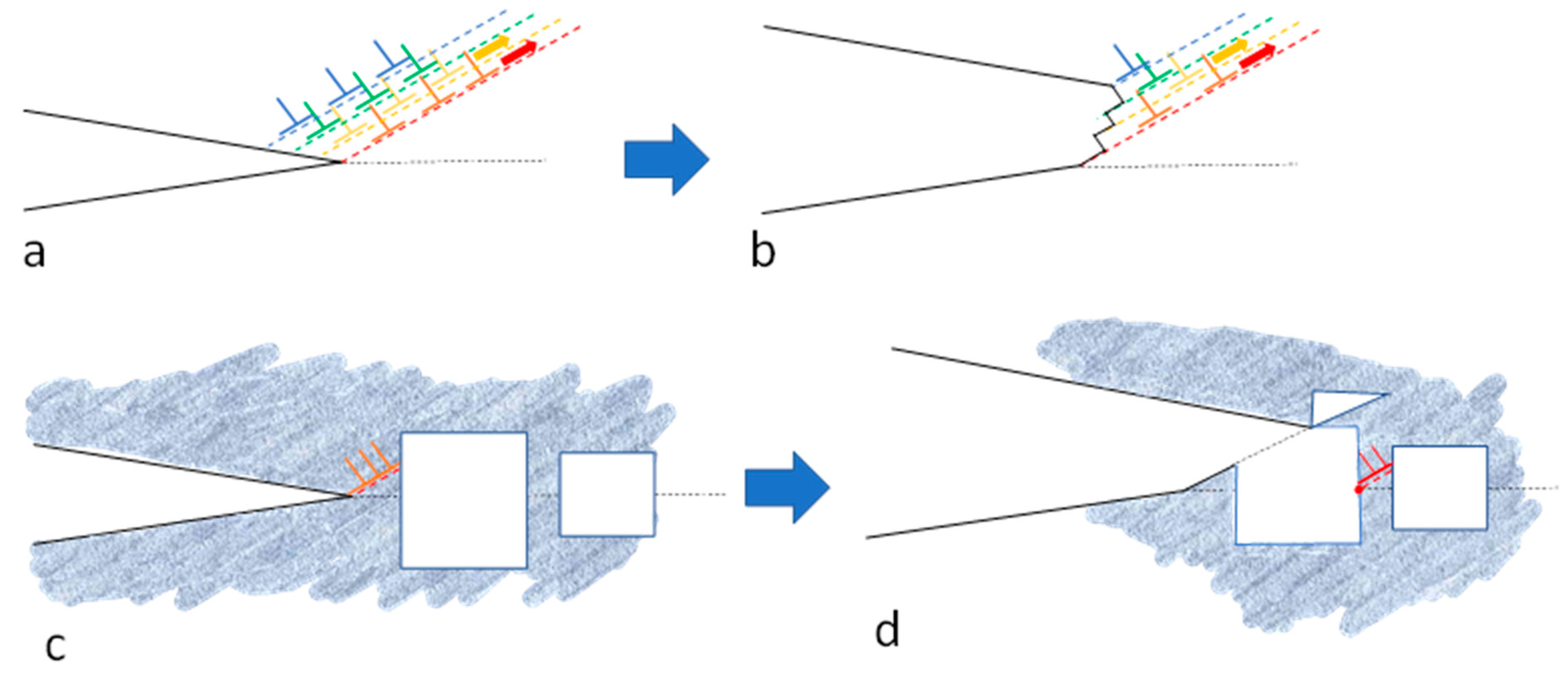
1.2. Production of Freely-Migrating Point Defects
1.2.1. FMD Production without Consideration of the 59Ni Effect
1.2.2. FMD Production with Consideration of the 59Ni Effect
2. Results
2.1. Swelling
2.2. Cavity Accumulation on Grain Boundaries
2.2.1. Theory
Dislocations
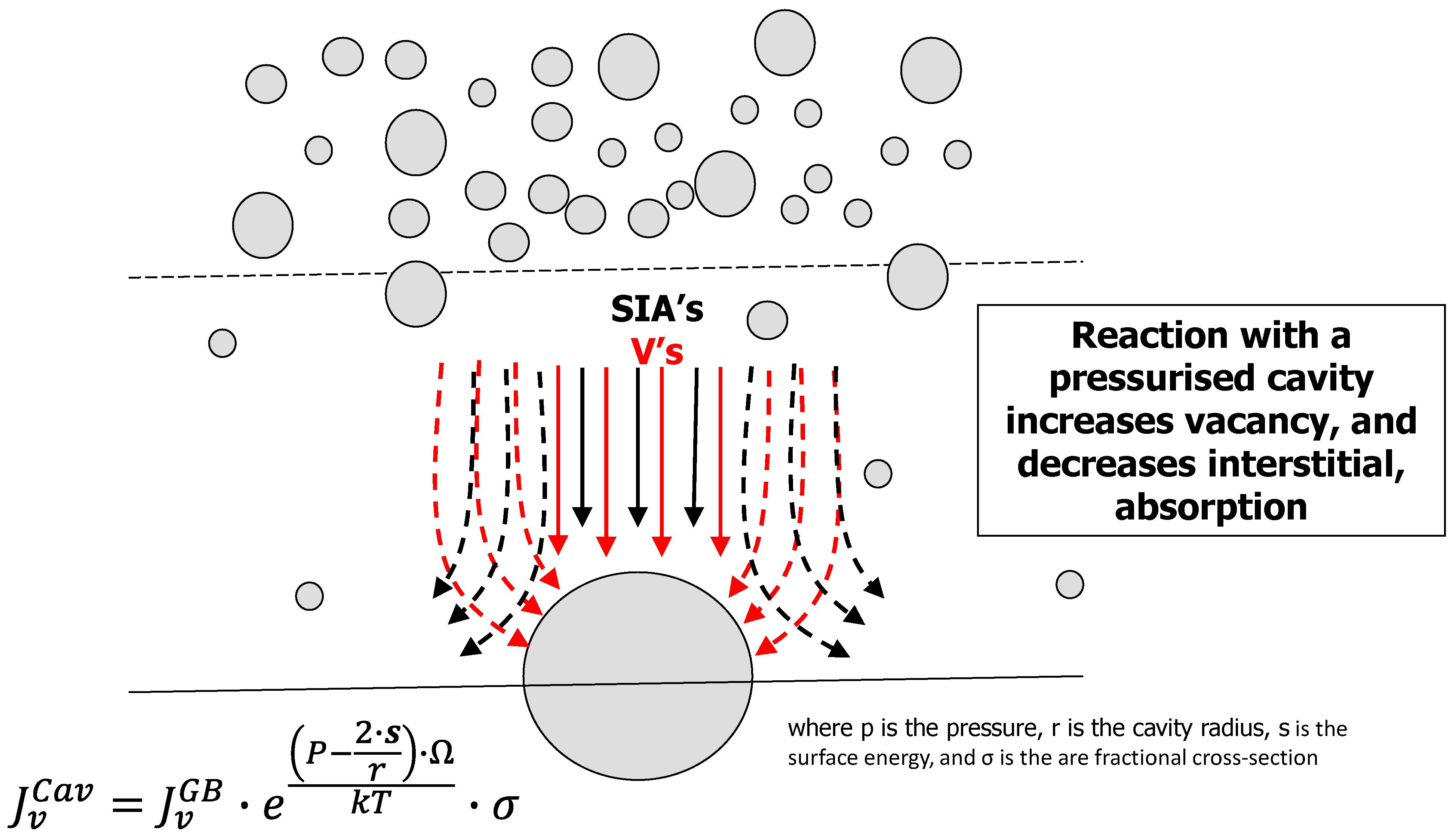
Cavities
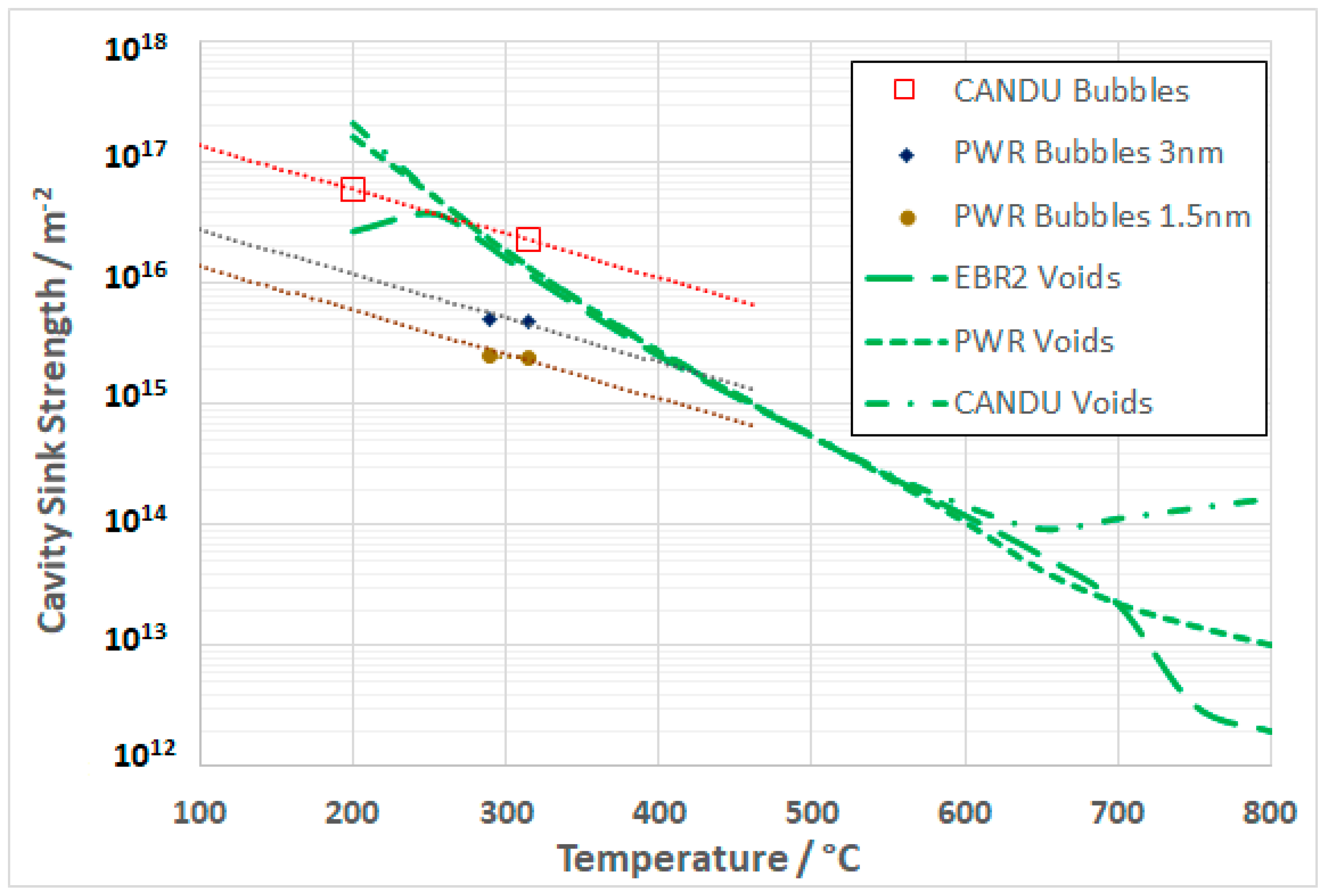
Grain Boundaries
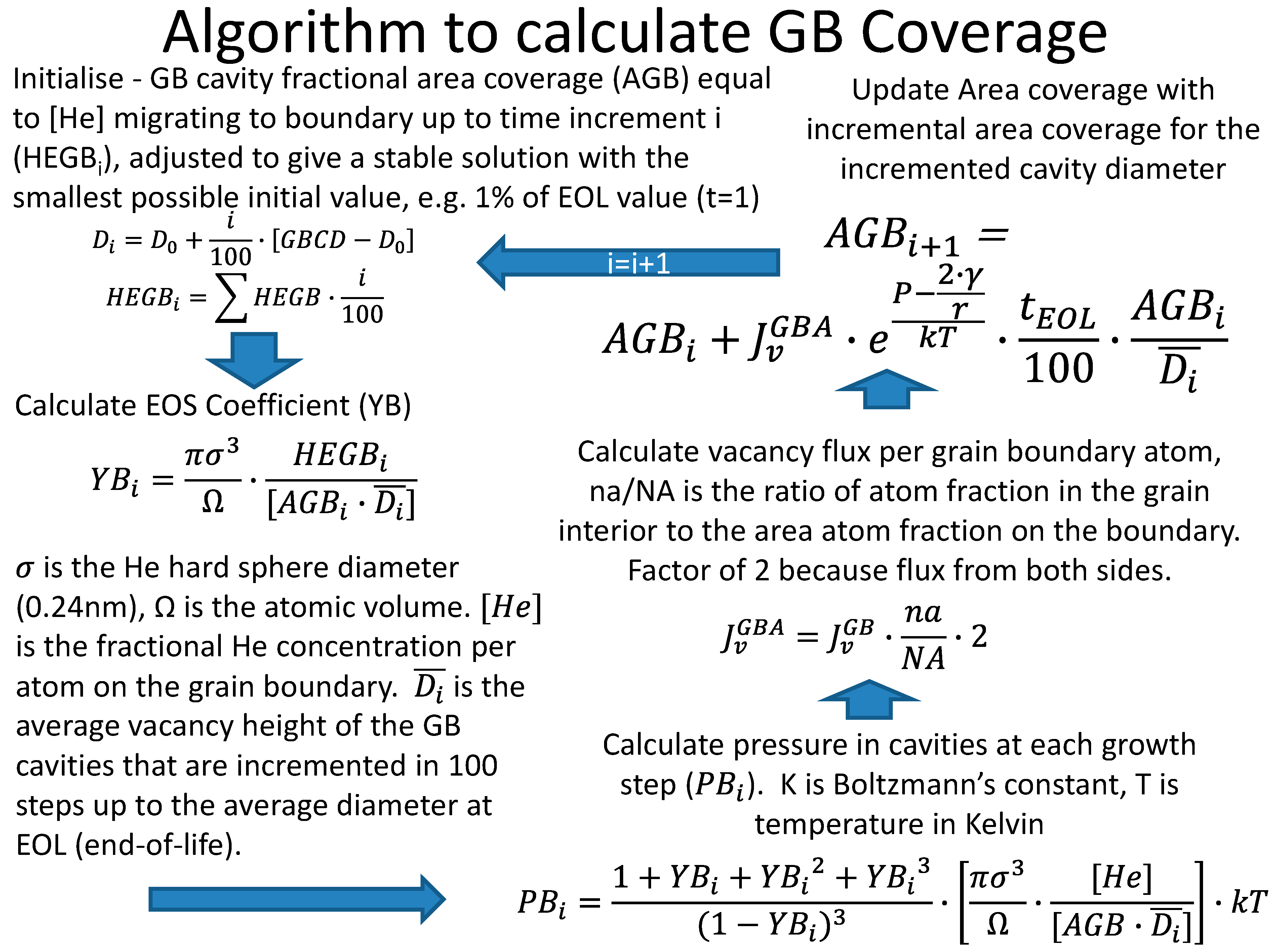
2.2.2. Model Results
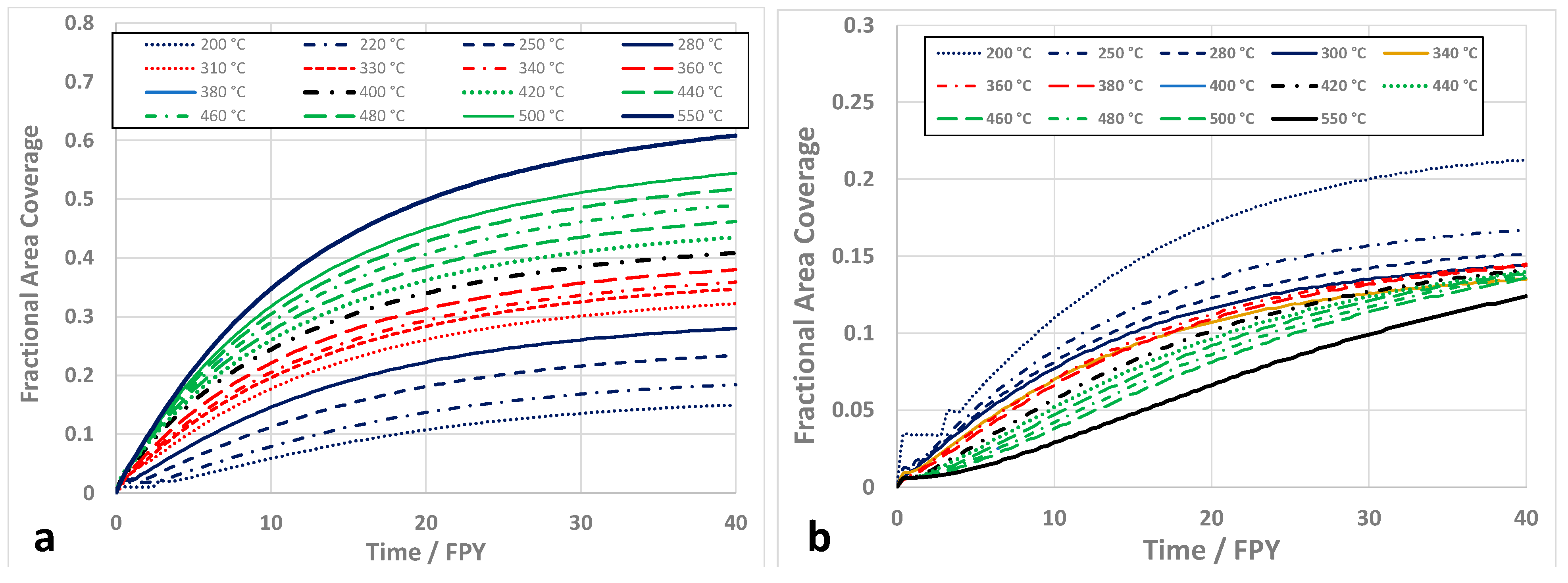
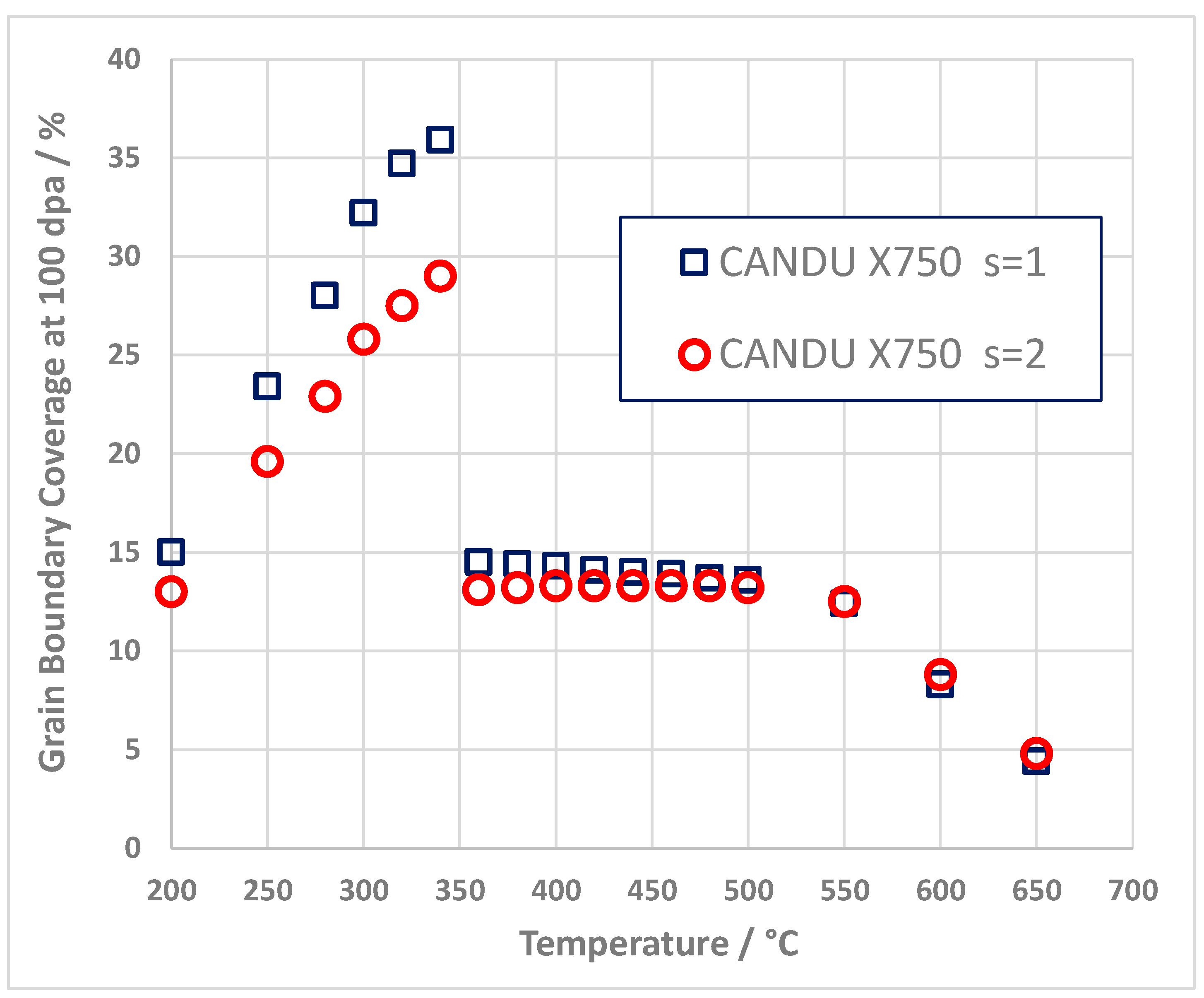
Grain Boundary Coverage for a CANDU Reactor Neutron Spectrum
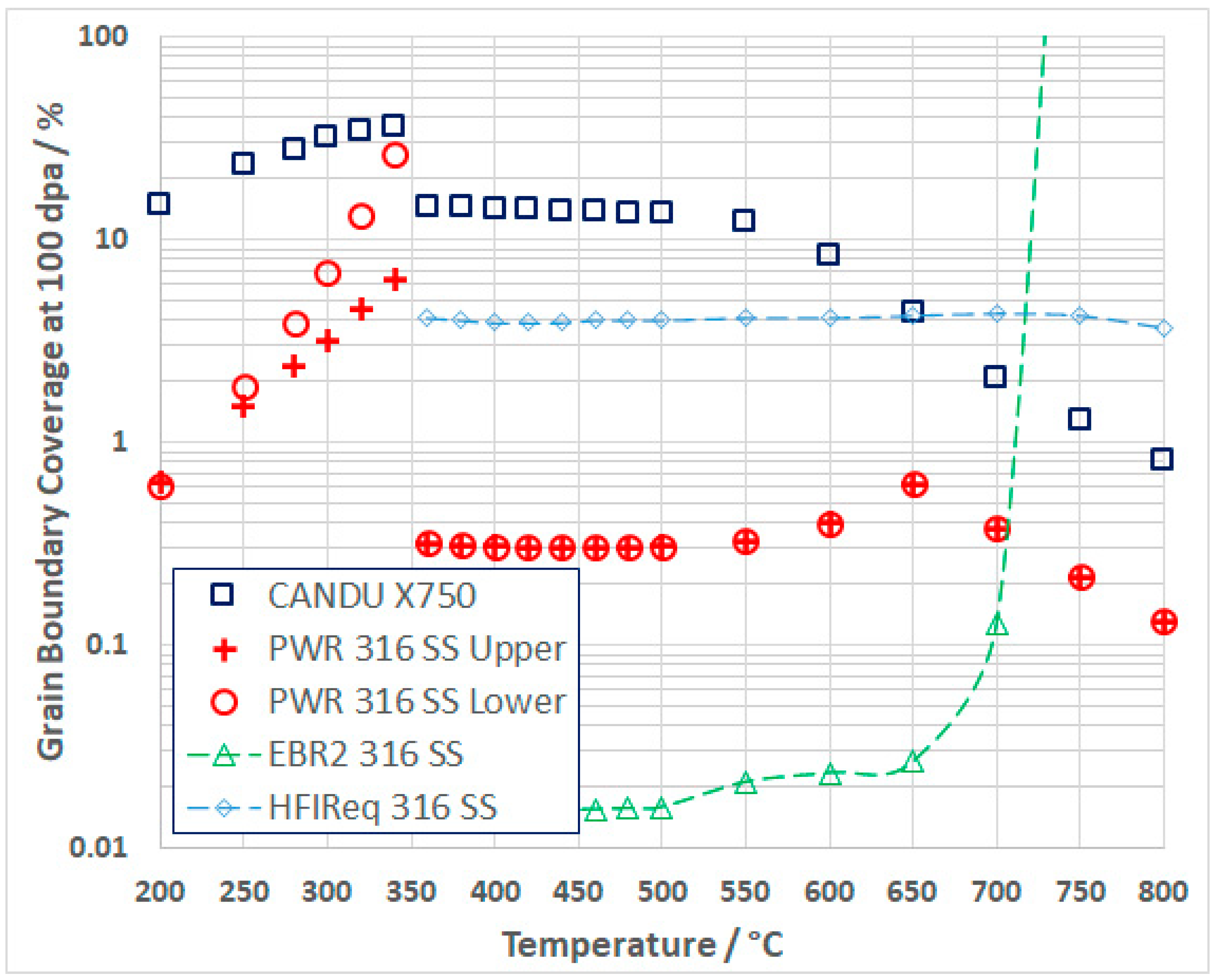
Grain Boundary Coverage for a PWR Neutron Spectrum
3. Discussion
3.1. Swelling of Austenitic Alloys
3.2. Embrittlement of Austenitic Alloys
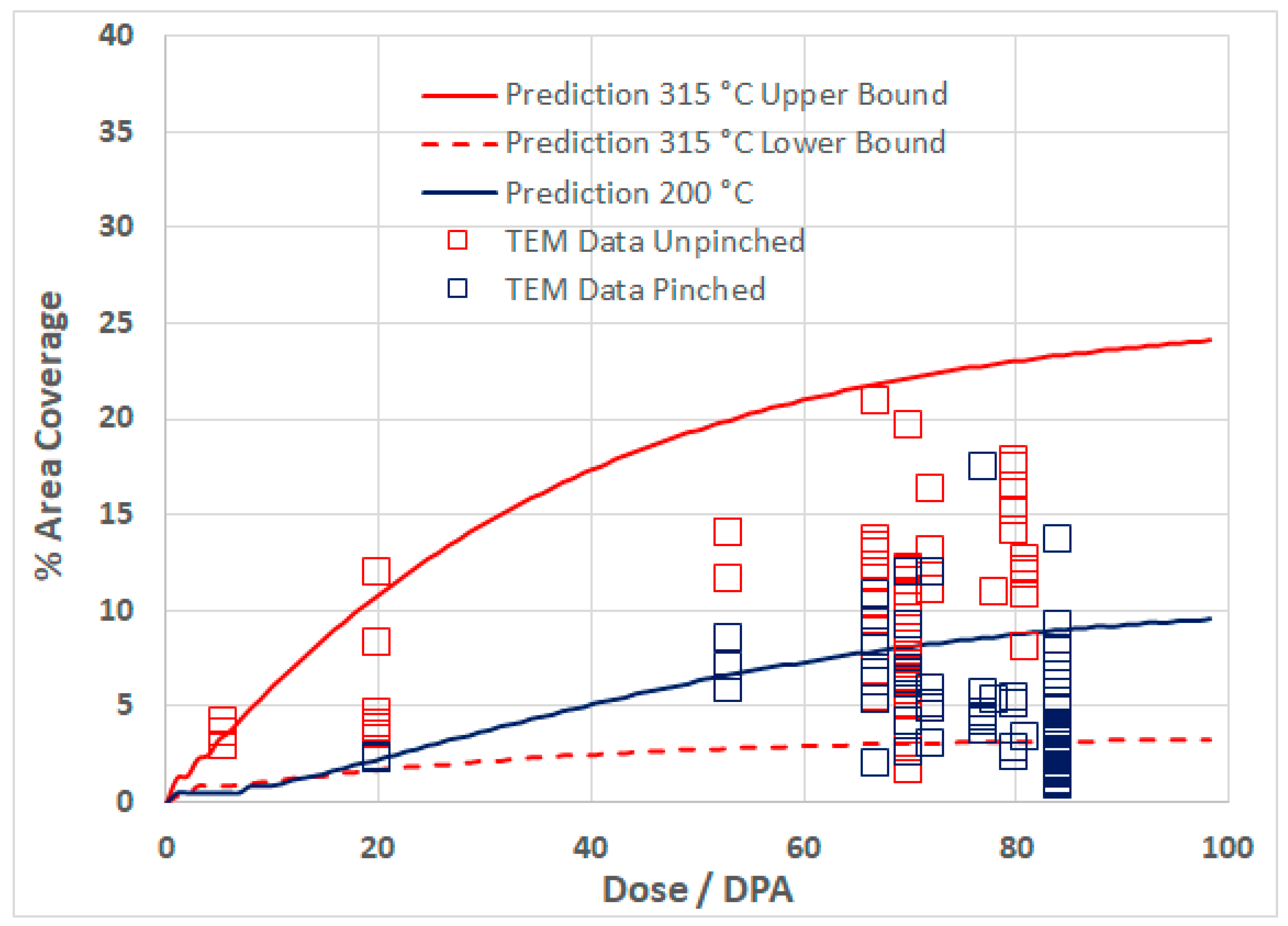
3.2.1. Grain Boundary Segregation of He Bubbles
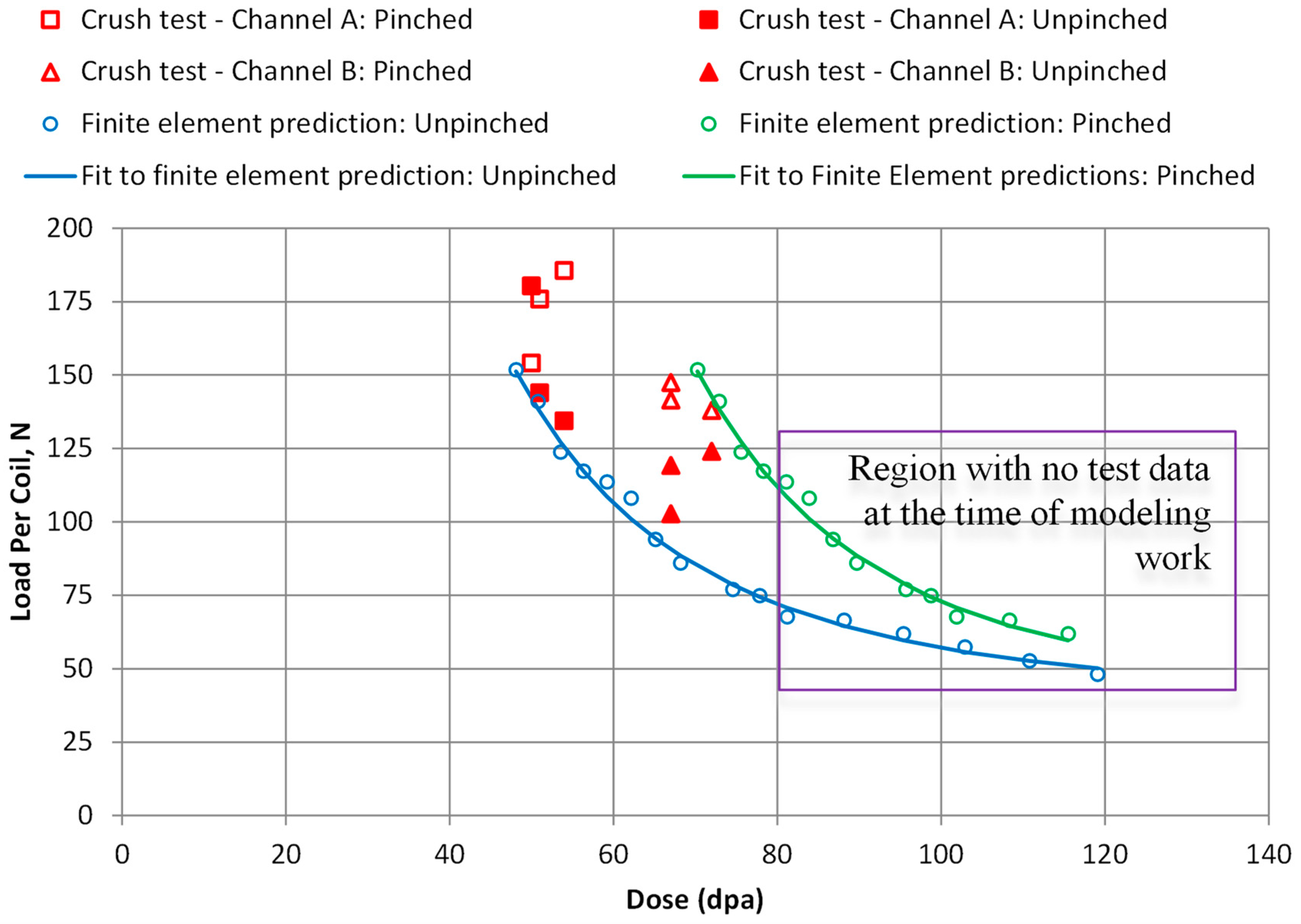
3.2.2. Inter-Granular Fracture
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| appm | atomic parts per million |
| at% | atomic% |
| BOR | a series of Russian test reactors |
| BWR | boiling water reactor |
| CANDU | a trademark of Atomic Energy of Canada Limited |
| CW | cold-worked |
| DPA or dpa | displacements per atom |
| EBR2 | experimental breeder reactor 2 |
| FCC | face-centered-cubic |
| FMD | freely migrating defects |
| FPY | full power years |
| FT | flux thimble |
| HCP | hexagonal-close-packed |
| HFIR | high flux isotope reactor |
| HWR | heavy water reactor |
| IASCC | irradiation assisted stress-corrosion-cracking |
| IGSCC | inter-granular stress-corrosion-cracking |
| INCONEL | a trademark of the special metals company |
| LMR | liquid metal (fast) reactor |
| LWR | light water reactor |
| ORNL | Oak Ridge National Laboratory |
| PKA | primary knock-on atom |
| PWR | pressurized water reactor |
| PV | pressure vessel |
| SEM | scanning electron microscope (or microscopy) |
| SFR | sodium fast reactor |
| SPECTER | a code for calculating DPA for various elements |
| SS | stainless steel |
| TDAM | energy available for creating atomic displacements for a given PKA |
| TEM | transmission electron microscope or microscopy |
| UTS | ultimate tensile strength |
| wtppm | parts per million by weight |
| wt% | weight % |
| YS | yield strength |
References
- Bhattacharya, A.; Zinkle, S.J. Cavity Swelling in Irradiated Materials. In Comprehensive Nuclear Materials, 2nd ed.; Konings, R.J.M., Stoller, R.E., Eds.; Elsevier: Oxford, UK, 2020; Chapter 12; Volume 1, pp. 406–455. [Google Scholar]
- Phillipps, K.; Sonnenberg, K. Interstitial Diffusion of He in Nickel. J. Nucl. Mater. 1983, 114, 95–97. [Google Scholar] [CrossRef]
- Phillipps, K.; Sonnenberg, K.; Williams, J.M. Diffusion of He in Nickel. J. Nucl. Mater. 1982, 107, 271–279. [Google Scholar] [CrossRef]
- Trinkaus, H.; Singh, B.N. Helium accumulation in metals during irradiation–Where do we stand? J. Nucl. Mater. 2003, 323, 229–242. [Google Scholar] [CrossRef]
- Adams, J.B.; Wolfer, W.G. On the diffusion mechanisms of helium in nickel. J. Nucl. Mater. 1988, 158, 25–29. [Google Scholar] [CrossRef]
- Hepburn, D.J.; Ferguson, D.; Gardner, S.; Ackland, G.J. First-principles study of helium, carbon, and nitrogen in austenite, dilute austenitic iron alloys, and nickel. Phys. Rev. B 2013, 88, 024115. [Google Scholar] [CrossRef] [Green Version]
- Mansur, L.K.; Yoo, M.H. Advances in the theory of swelling in irradiated metals and alloys. J. Nucl. Mater. 1979, 85–86, 523–532. [Google Scholar] [CrossRef]
- Mansur, L.K.; Coghlan, W.A. Mechanisms of helium interaction with radiation effects in metals and alloys: A review. J. Nucl. Mater. 1983, 119, 1–25. [Google Scholar] [CrossRef]
- Hishinuma, A.; Mansur, L.K. Critical radius for bias-driven swelling—A further analysis and its application to bimodal cavity size distributions. J. Nucl. Mater. 1983, 118, 91–99. [Google Scholar] [CrossRef]
- Coghlan, W.A.; Mansur, L.K. Critical radius and critical number of gas atoms for cavities containing a Van der Waals gas, for bias-driven swelling—A further analysis and its application to bimodal cavity size distributions. J. Nucl. Mater. 1984, 122–123, 495–501. [Google Scholar] [CrossRef] [Green Version]
- Stoller, R.E.; Odette, G.R. Analytical Solutions for Helium Bubble and Critical Radius Parameters Using a Hard Sphere Equation of State. J. Nucl. Mater. 1985, 131, 118–125. [Google Scholar] [CrossRef]
- Stoller, R.E.; Odette, R.G. A Comparison of the Relative Importance of Helium and Vacancy Accumulation in Void Nucleation. In Proceedings of the 13th International Symposium on Radiation Induced Changes in Microstructure, Seattle, WA, USA, 23–25 June 1986; Garner, F.A., Packan, N.H., Kumar, A.S., Eds.; ASTM STP 955, Part I. ASTM: Philadelphia, PA, USA, 1987; pp. 358–370. [Google Scholar]
- Stoller, R.E.; Odette, R.G. A Composite Model of Microstructure Evolution in Austenitic Steels Under Fast Neutron Irradiation. In Proceedings of the 13th International Symposium on Radiation Induced Changes in Microstructure, Seattle, WA, USA, 23–25 June 1986; Garner, F.A., Packan, N.H., Kumar, A.S., Eds.; ASTM STP 955, Part I. ASTM: Philadelphia, PA, USA, 1987; pp. 371–392. [Google Scholar]
- Mansur, L.K. Theory and experimental background on dimensional changes in irradiated alloys. J. Nucl. Mater. 1994, 216, 97–123. [Google Scholar] [CrossRef]
- Golubov, S.I.; Barashev, A.V.; Stoller, R.E. Radiation damage theory. In Comprehensive Nuclear Materials, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2012; pp. 357–391. [Google Scholar] [CrossRef]
- Griffiths, M. Effect of Neutron Irradiation on the Mechanical Properties, Swelling and Creep of Austenitic Stainless Steels. Materials 2021, 14, 2622. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, M.; Ramos-Nervii, J.; Greenwood, L.R. A Rate Theory Model of Radiation-Induced Swelling in an Austenitic Stainless Steel. J. Nucl. Eng. 2021, 2, 34. [Google Scholar] [CrossRef]
- Judge, C.D.; Rajakumar, H.; Korinek, A.; Botton, G.; Cole, J.; Madden, J.W.; Jackson, J.H.; Freyer, P.D.; Giannuzzi, A.L.; Griffiths, M. High Resolution Transmission Electron Microscopy of Irradiation Damage in Inconel X-750. In The Minerals, Metals & Materials Series, Proceedings of the 18th International Conference on Environmental Degradation of Materials in Nuclear Power Systems–Water Reactors, Oregon, Portland, 13–17 August 2017; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Griffiths, M.; Walters, L.; Greenwood, L.R.; Garner, F.A. Accelerated materials evaluation for nuclear applications. J. Nucl. Mater. 2017, 488, 46–62. [Google Scholar] [CrossRef]
- Greenwood, L.R. A new calculation of Thermal Neutron Damage and Helium Production in Nickel. J. Nucl. Mater. 1983, 115, 137–142. [Google Scholar] [CrossRef]
- Greenwood, L.R.; Garner, F.A. Hydrogen Generation Arising from the 59Ni (n,p) Reaction and its impact on Fission-Fusion Correlations. J. Nucl. Mater. 1996, 233–237, 1530–1534. [Google Scholar] [CrossRef]
- Greenwood, L.R.; Smither, R.K. SPECTER: Neutron Damage Calculations for Materials Irradiations, ANL/FPP/TM-197, Argonne National Laboratory. 1985. Available online: https://www-nds.iaea.org/irdf2002/codes/index.htmlx (accessed on 10 March 2014).
- MacFarlane, R.E.; Muir, D.W.; Mann, F.M. Radiation Damage Calculations with NJOY. J. Nucl. Mater. 1984, 122–123, 1041. Available online: http://t2.lanl.gov/nis/ (accessed on 2 June 2017). [CrossRef] [Green Version]
- ENDF/B-VI Nuclear Library. Available online: http://t2.lanl.gov/nis/data.shtml (accessed on 10 March 2014).
- Was, G.S. Fundamentals of Radiation Materials Science: Metals and Alloys, 2nd ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Griffiths, M. The Effect of Irradiation on Ni-containing Components in CANDU Reactor Cores: A Review. AECL Nucl. Rev. 2013, 2, 1–16, Erratum in AECL Nucl. Rev. 2014, 3, 89. [Google Scholar] [CrossRef]
- Griffiths, M. Ni-Based Alloys for Reactor Internals and Steam Generator Applications, Chapter 9. In Structural Alloys for Nuclear Energy Applications; Zinkle, S., Odette, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780123970466. [Google Scholar]
- Griffiths, M.; Boothby, R. Radiation Effects in Nickel-Based Alloys. In Reference Module in Materials Science and Materials Engineering; Comprehensive Nuclear Materials; Konings, R., Ed.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 334–371. [Google Scholar]
- Stoller, R.E.; Greenwood, L.R. An Evaluation of Through-Thickness Changes in Primary Damage Production in Commercial Reactor Pressure Vessels. Effects of Radiation on Materials: 20th International Symposium; ASTM STP, 1405; Rosinski, S.T., Grossbeck, M.L., Allen, T.R., Kumar, A.S., Eds.; American Society for Testing and Materials: West Conshohocken, PA, USA, 2002. [Google Scholar]
- Gao, F.; Wooding, S.J.; Calder, A.F.; Bacon, D.J. Computer Simulation of Displacement Cascade Damage in Metals. Mat. Res. Soc. Symp. Proc. 1995, 373, 15. [Google Scholar] [CrossRef]
- Okamoto, P.R.; Rehn, L.E.; Averback, R.S. Effects of Primary Recoil Energy on the Production Rate of Mobile Defects During Elevated Temperature Irradiation. J. Nucl. Mater. 1985, 133–134, 373–377. [Google Scholar] [CrossRef] [Green Version]
- Trinkaus, H.; Naundorf, V.; Singh, B.N.; Woo, C.H. On the experimental-determination of the migrating defect fraction under cascade damage conditions. J. Nucl. Mater. 1994, 210, 244–253. [Google Scholar] [CrossRef]
- Kwon, J.; Motta, A.T. Role of Radiation in BWR Core Shroud Cracking, Reactor Dosimetry; ASTM STP, 1398; Williams, J.G., Vehar, D.W., Ruddy, F.H., Gilliam, D.M., Eds.; American Society for Testing and Materials: West Conshohocken, PA, USA, 2000. [Google Scholar]
- Svetukhin, V.; Tikhonchev, M. Effective Atomic Displacements in α-Zirconium under Neutron Irradiation. Adv. Mater. Res. 2014, 1042, 52–57. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.; Biersack, J. SRIM—The stopping and range of ions in matter. Nucl. Instrum. Methods Phys. Res. Sect. B 2010, 268, 1818. [Google Scholar] [CrossRef] [Green Version]
- Nordlund, K.; Zinkle, S.J.; Sand, A.E.; Granberg, F.; Averback, R.S.; Stoller, R.E.; Suzudo, T.; Malerba, L.; Banhart, F.; Weber, W.J.; et al. Primary radiation damage: A review of current understanding and models. J. Nucl. Mater. 2018, 512, 450–479. [Google Scholar] [CrossRef]
- Xu, S.X.; Griffiths, M.; Scarth, D.A.; Graham, D. Microstructure-based Polycrystalline Finite Element Modeling of Inconel X-750 Irradiated in a CANDU Reactor. Eng. Fract. Mech. 2022. accepted. [Google Scholar]
- Olander, D.R. Fundamental Aspects of Nuclear Reactor Fuel Elements; TID 26711-Part 1; Technical Information Center, Office of Public Affairs, Energy Research and Development Administration: Washington, DC, USA, 1976. [Google Scholar]
- Heald, P.T.; Speight, M.V. Point Defect Behaviour in Irradiated Materials. Acta. Metall. 1975, 23, 1389. [Google Scholar] [CrossRef]
- Kohnert, A.A.; Cusentino, M.A.; Wirth, B.D. Molecular statics calculations of the biases and point defect capture volumes of small cavities. J. Nucl. Mater. 2018, 499, 480–489. [Google Scholar] [CrossRef]
- Heald, P.T.; Harbottle, J.E. Irradiation Creep due to Dislocation Climb and Glide. J. Nucl. Mater. 1977, 67, 229–233. [Google Scholar] [CrossRef]
- Harkness, S.D.; Li, C.Y. A Study of Void Formation in Fast Neutron-Irradiated Metals. Met. Trans. 1971, 2, 1457–1470. [Google Scholar] [CrossRef]
- Luo, J.; Xin, Y.; Sun, Z.; Li, Y.; Zhu, Y.; Chen, P. Formulation of voids and bubbles as biased sinks to crystalline point defects. Scripta Mater. 2021, 197, 113806. [Google Scholar] [CrossRef]
- Nabarro, F.R.N. Deformation of Crystals by the Motion of Single Point Defects; Report Conf. on Strength of Solids; The Physical Society: London, UK, 1948; Volume 75. [Google Scholar]
- Herring, C. Diffusional Viscosity of a Polycrystalline Solid. J. Appl. Phys. 1950, 21, 437. [Google Scholar] [CrossRef]
- Edwards, D.J.; Simonen, E.P.; Bruemmer, S.M.; Efsing, P. Microstructural evolution in neutron-irradiated stainless steels: Comparison of LWR and fast-reactor irradiations. In Proceedings of the 12th International Conference on Environmental Degradation of Materials in Nuclear Power System—Water Reactors, Salt Lake City, UT, USA, 14–18 August 2005; pp. 419–428. [Google Scholar]
- Garner, F.A. Radiation-Induced Damage in Austenitic Structural Steels Used in Nuclear Reactors. In Reference Module in Materials Science and Materials Engineering, 2nd ed.; Comprehensive Nuclear Materials; Konings, R., Stoller, R., Eds.; Elsevier: Oxford, UK, 2020; Volume 3, Chapter 2; pp. 57–168. [Google Scholar]
- Maziasz, P.J. Swelling and Microstructure of HFIR Irradiated Austenitic Stainless Steels, United States. 1980. Available online: https://www.osti.gov/servlets/purl/6143016 (accessed on 5 August 2022).
- Maziasz, P.J.; Grossbeck, M.L. Swelling, microstructural development and helium effects in type 316 stainless steel irradiated in HFIR and EBR-II. J. Nucl. Mater. 1981, 104, 987–991. [Google Scholar] [CrossRef] [Green Version]
- Grossbeck, M.L.; Ehrlich, K.; Wassilew, C. An assessment of tensile, irradiation creep, creep rupture, and fatigue behavior in austenitic stainless steels with emphasis on spectral effects. J. Nucl. Mater. 1990, I74, 264–281. [Google Scholar] [CrossRef]
- Mansur, L.K.; Lee, E.H.; Maziasz, P.J.; Rowcliffe, A.P. Control of Helium effects in Irradiated Materials based on Theory and Experiment. J. Nucl. Mater. 1986, 141–143, 633–646. [Google Scholar] [CrossRef] [Green Version]
- Kramer, D.; Brager, H.R.; Rhodes, C.G.; Pard, A.G. Helium embrittlement in type 304 stainless steel. J. Nucl. Mater. 1968, 25, 121–131. [Google Scholar] [CrossRef]
- Schroeder, H.; Batfalsky, P. The dependence of the high temperature mechanical properties of austenitic stainless steels on implanted helium. J. Nucl. Mater. 1983, 115, 297–306. [Google Scholar] [CrossRef]
- Fujimoto, K.; Yonezawa, T.; Wachi, E.; Yamaguchi, Y.; Nakano, M.; Shogan, R.P.; Massoud, J.P.; Mager, T.R. Effect of the accelerated irradiation and hydrogen/helium gas on IASCC characteristics for highly irradiated austenitic stainless steels. In Proceedings of the 12th International Conference on Environmental Degradation of Materials in Nuclear Power System—Water Reactors, Salt Lake City, UT, USA, 14–18 August 2005; pp. 299–310. [Google Scholar]
- Bosch, R.W.; Vankeerberghen, M.; Gérard, R.; Somville, F. Crack initiation testing of thimble tube ma-terial under PWR conditions to determine a stress threshold for IASCC. J. Nucl. Mater. 2015, 461, 112–121. [Google Scholar] [CrossRef]
- Edwards, D.J.; Garner, F.A.; Bruemmer, S.M.; Efsing, P. Nano-cavities observed in a 316 SS PWR flux thimble tube irradiated to 33 and 70 dpa. J. Nucl. Mater. 2009, 384, 249–255. [Google Scholar] [CrossRef]
- Carsughi, F.; Derz, H.; Pott, G.; Sommer, W.; Ullmaier, H. Investigations on Inconel 718 Irradiated with 800 MeV Protons. J. Nucl. Mater. 1999, 264, 78–88. [Google Scholar] [CrossRef]
- James, M.R.; Maloy, S.A.; Gac, F.D.; Sommer, W.F.; Chen, J.; Ullmaier, H. The mechanical Properties of an Alloy 718 Window after Irradiation in a Spallation Environment. J. Nucl. Mater. 2001, 296, 139–144. [Google Scholar] [CrossRef]
- Braski, D.N. The effect of neutron irradiation on vanadium alloys. J. Nucl. Mater. 1986, 141–143, 1125–1131. [Google Scholar] [CrossRef] [Green Version]
- Toloczko, M.B.; Garner, F.A.; Voyevodin, V.N.; Bryk, V.V.; Borodin, O.V.; Melnychenko, V.V.; Kalchenko, A.S. Ion-Induced Swelling of ODS Ferritic Alloy MA957 Tubing to 500 dpa. J. Nucl. Mater. 2014, 453, 323–333. [Google Scholar] [CrossRef] [Green Version]
- Neustroev, V.S.; Garner, F.A. Severe embrittlement of neutron irradiated austenitic steels arising from high void swelling. J. Nucl. Mater. 2009, 386, 157–160. [Google Scholar] [CrossRef]
- Porollo, S.I.; Vorobjev, A.N.; Konobeev, Y.V.; Dvoriashin, A.M.; Krigan, V.M.; Budylkin, N.I.; Mironova, E.G.; Garner, F.A. Swelling and void-induced embrittlement of austenitic stainless steel irradiated to 73–82 dpa at 335–365 °C. J. Nucl. Mater. 1998, 258, 1613–1617. [Google Scholar] [CrossRef]
- Hamilton, M.L.; Huang, F.H.; Yang, W.J.; Garner, F.A. Mechanical properties and fracture behavior of 20% cold-worked 316 stainless steel irradiated to very high neutron exposures. In Influence of Radiation on Material Properties, Proceedings of the 13th International Symposium (Part II); ASTM International: West Conshohocken, PA, USA, 1987; pp. 245–270. [Google Scholar]
- Rowcliffe, A.F.; Mansur, L.K.; Hoelzer, D.T.; Nanstad, R.K. Perspectives on Radiation Effects in Nickel-Base Alloys for Applications in Advanced Reactors. J. Nucl. Mater. 2009, 392, 341–352. [Google Scholar] [CrossRef]
- Judge, C.D. The Effects of Irradiation on Inconel X-750. Ph.D. Thesis, McMaster University, Hamilton, ON, Canada, November 2015. Available online: https://macsphere.mcmaster.ca/handle/11375/18091 (accessed on 9 September 2022).
- Was, G.S.; Busby, J.; Andresen, P.L. Effect of Irradiation on Stress Corrosion Cracking and Corrosion in Light Water Reactors. ASM Handb. Corros. Environ. Ind. 2006, 13C, 386–414. [Google Scholar]
- Bruemmer, S.M.; Simonen, E.P.; Scott, P.M.; Andresen, P.L.; Was, G.S.; Nelson, J.L. Radiation-induced material changes and susceptibility to intergranular failure of light-water-reactor core internals. J. Nucl. Mater. 1999, 274, 299–314. [Google Scholar] [CrossRef]
- Zhao, S.; Egami, T.; Stocks, G.M.; Zhang, Y. Effect of d electrons on defect properties in NiCoCr and NiCoFeCr concentrated solid solution alloys. Phys. Rev. Mater. 2018, 2, 013602. [Google Scholar] [CrossRef]
- Andresen, P.L.; Was, G.S. Irradiation Assisted Stress Corrosion Cracking, Comprehensive Nuclear Materials, 2nd ed.; Konings, R.J.M., Stoller, R.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Chapter 4.07; pp. 190–217. [Google Scholar]
- Fournier, L.; Sencer, B.L.; Was, G.S.; Simonen, E.P.; Bruemmer, S.M. The influence of oversized solute additions on radiation-induced changes and post-irradiation intergranular stress corrosion cracking behavior in high-purity 316 stainless steels. J. Nucl. Mater. 2003, 321, 192–209. [Google Scholar] [CrossRef]
- Schroeder, H.; Braski, D.N. The effect of implanted helium on the high temperature mechanical properties of a model austenitic Fe-17% Cr-17% Ni alloy. J. Nucl. Mater. 1983, 117, 287–294. [Google Scholar] [CrossRef]
- Schroeder, H. High temperature helium embrittlement in austenitic stainless steels correlations between microstructure and mechanical properties. J. Nucl. Mater. 1988, 155–157, 1032–1037. [Google Scholar] [CrossRef]
- Schroeder, H.; Dai, Y. Helium concentration dependence of embrittlement effects in DIN 1.4970, 13% cw austenitic stainless steel at 873 K. J. Nucl. Mater. 1992, 191–194, 781–785. [Google Scholar] [CrossRef]
- Dai, Y.; Odette, G.R.; Yamamoto, T. The Effects of Helium in Irradiated Structural Alloys, Chapter 1.07. In Basic Aspects of Radiation Effects in Solids/Basic Aspects of Multi-Scale Modeling, 2nd ed.; Comprehensive Nuclear Materials; Konings, R.J.M., Stoller, R.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 186–234. [Google Scholar]
- Demkowicz, M.J. A threshold density of helium bubbles induces a ductile-to-brittle transition at a grain boundary in nickel. J. Nucl. Mater. 2020, 533, 152118. [Google Scholar] [CrossRef]
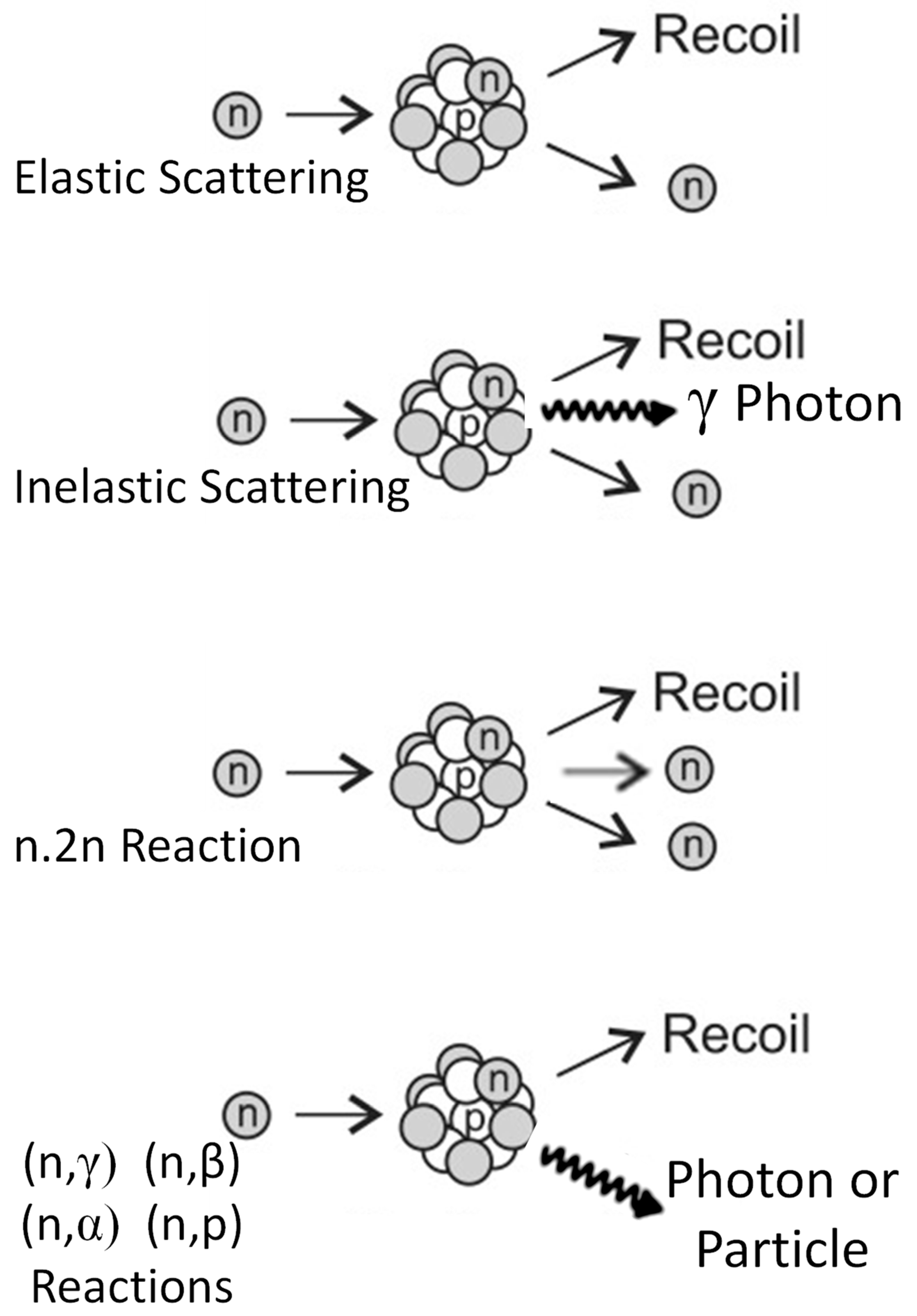
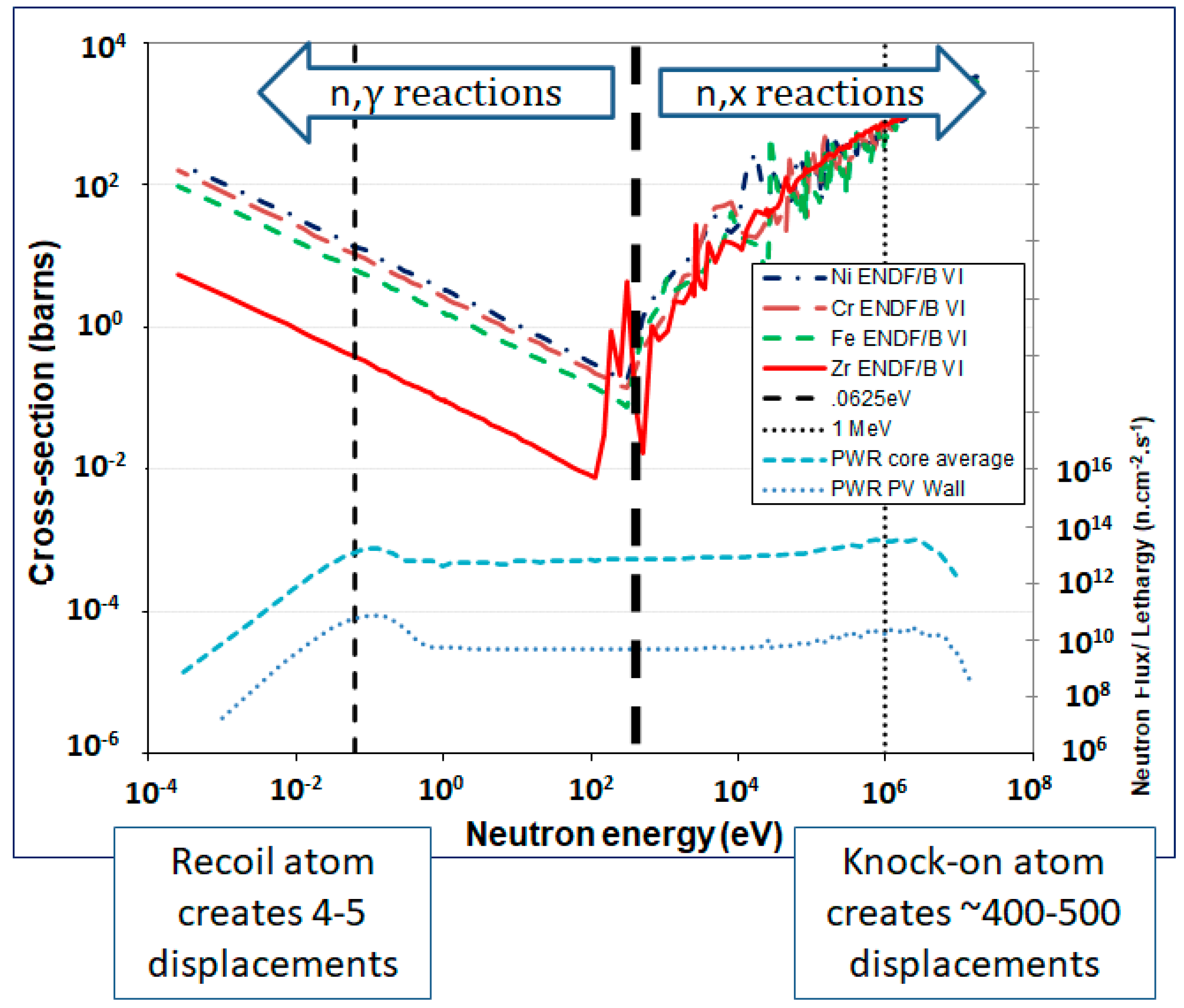
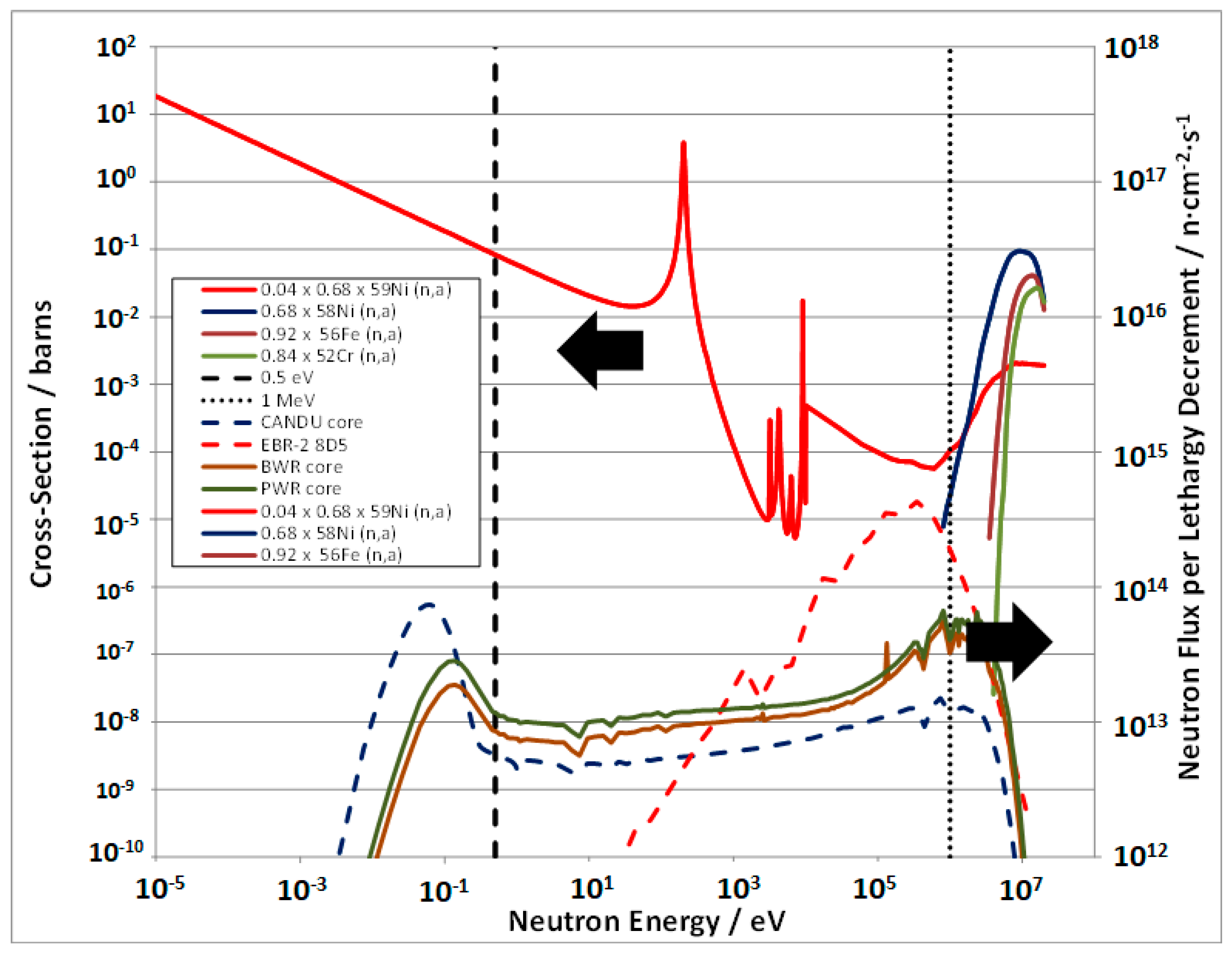
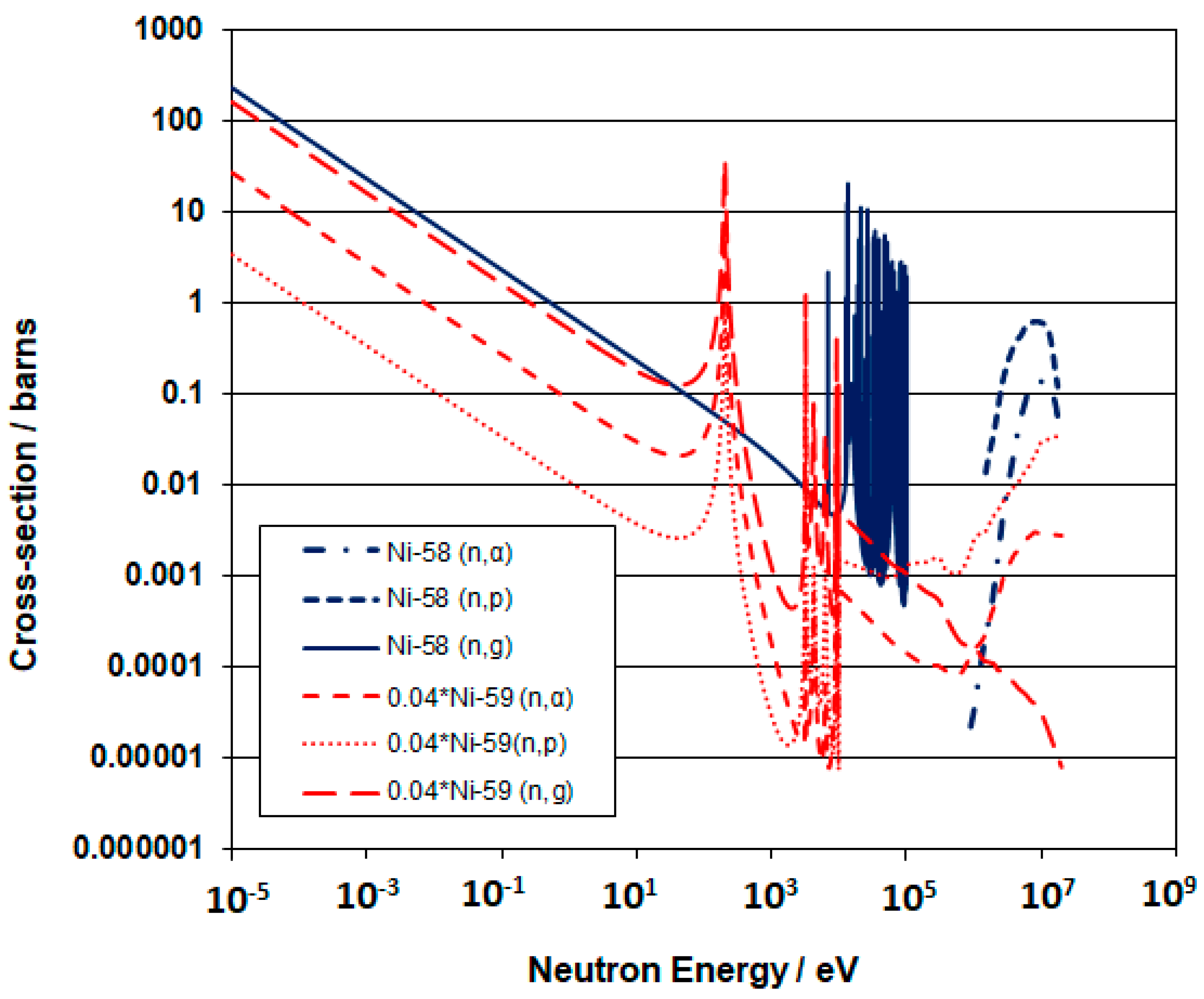

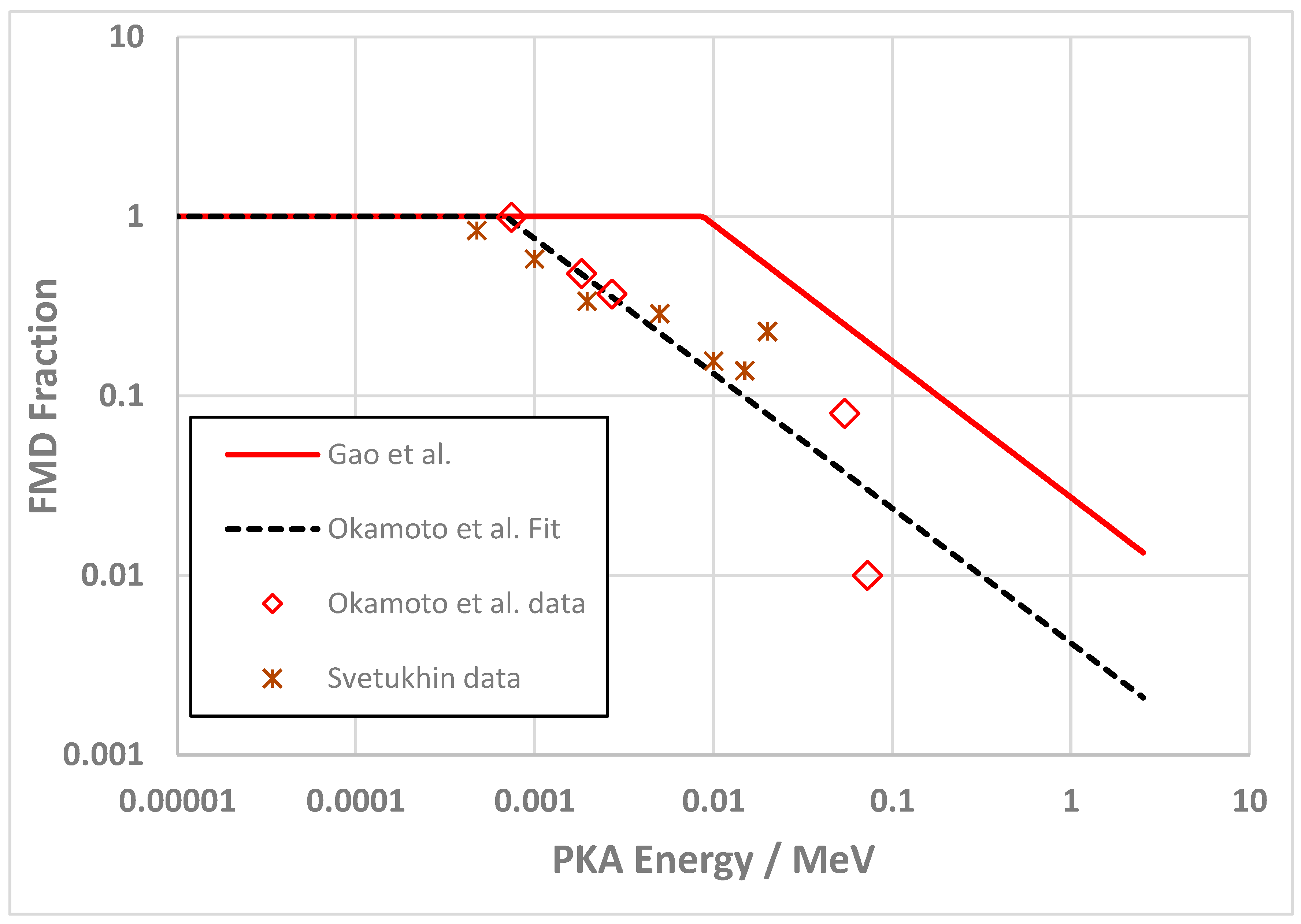
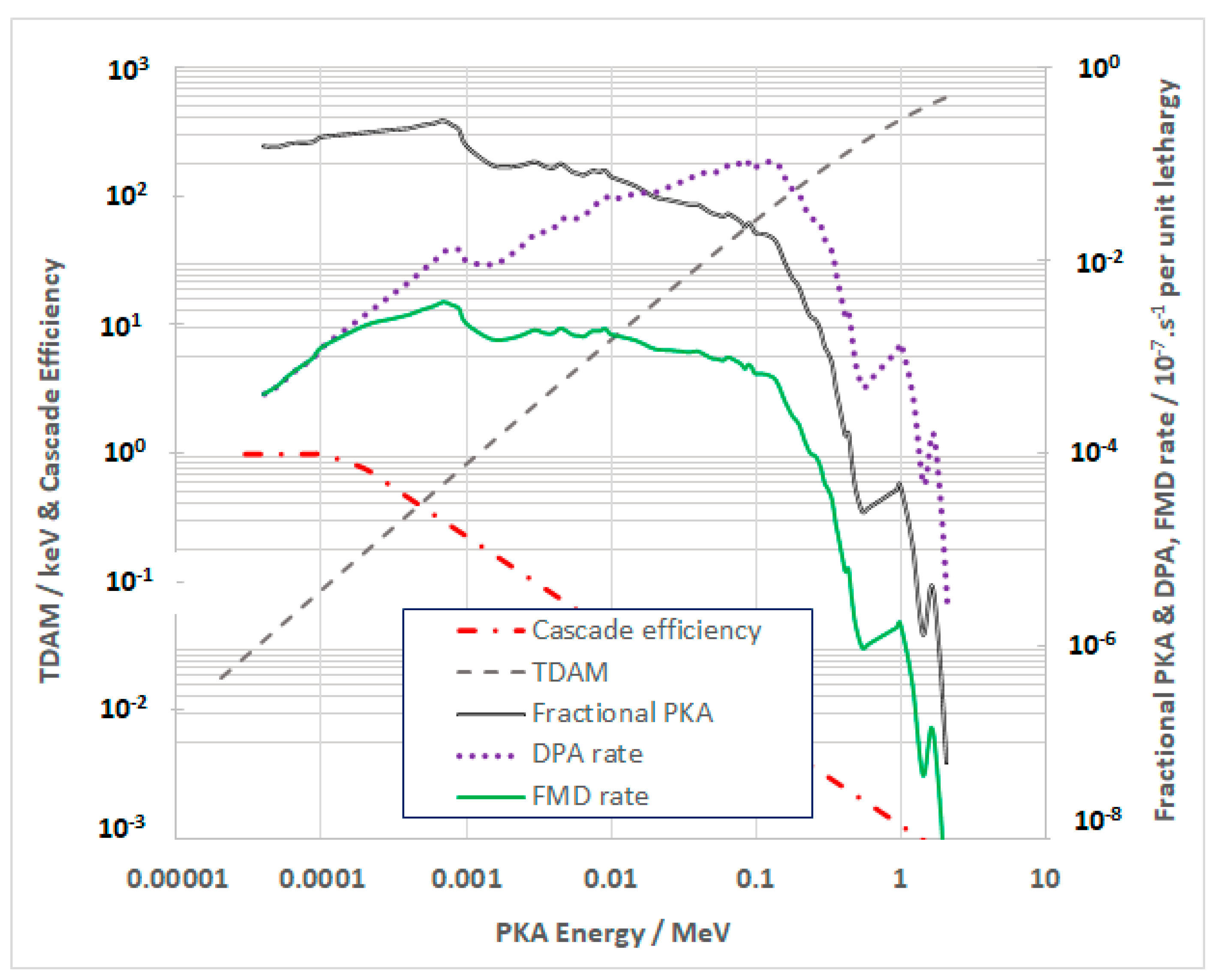
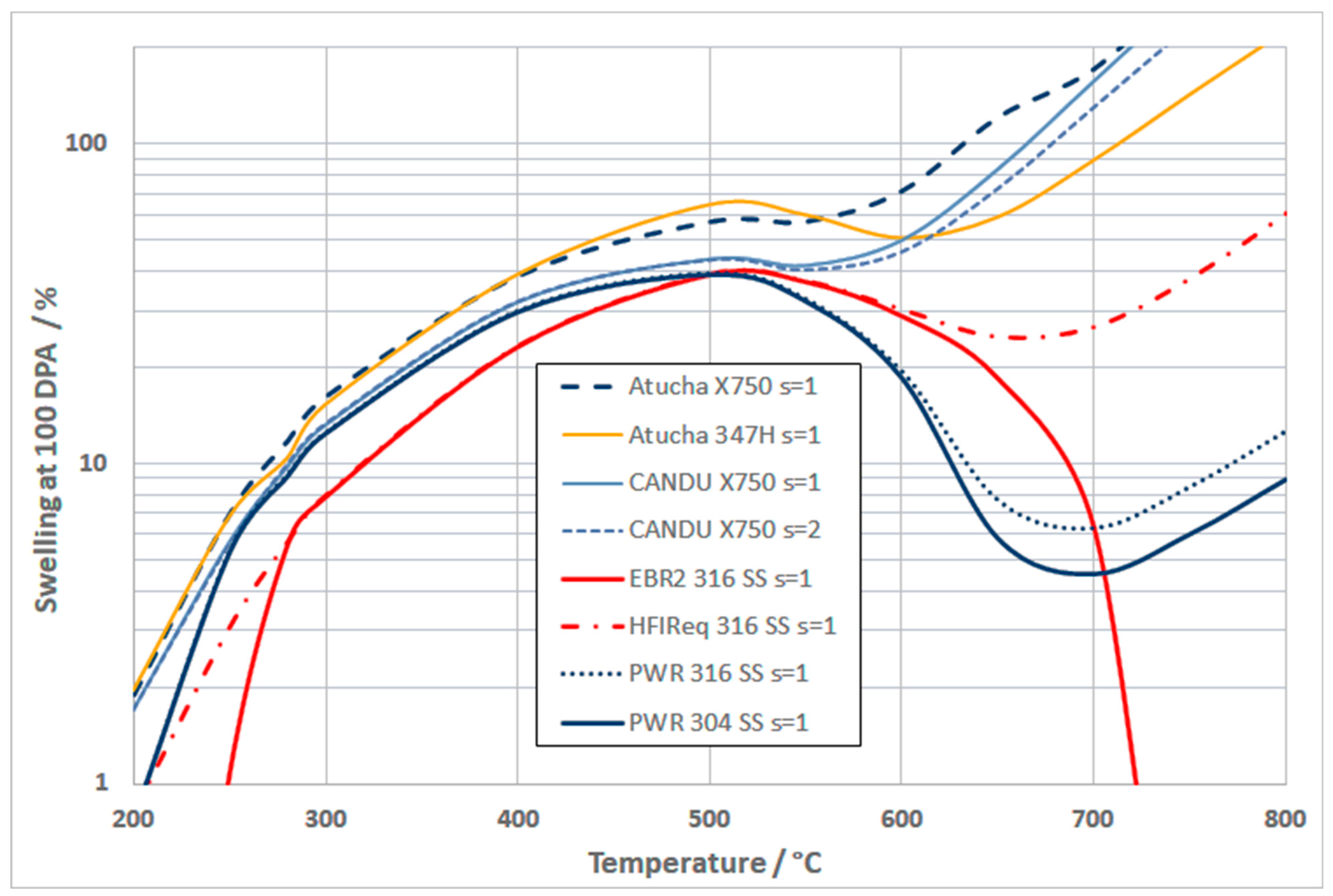

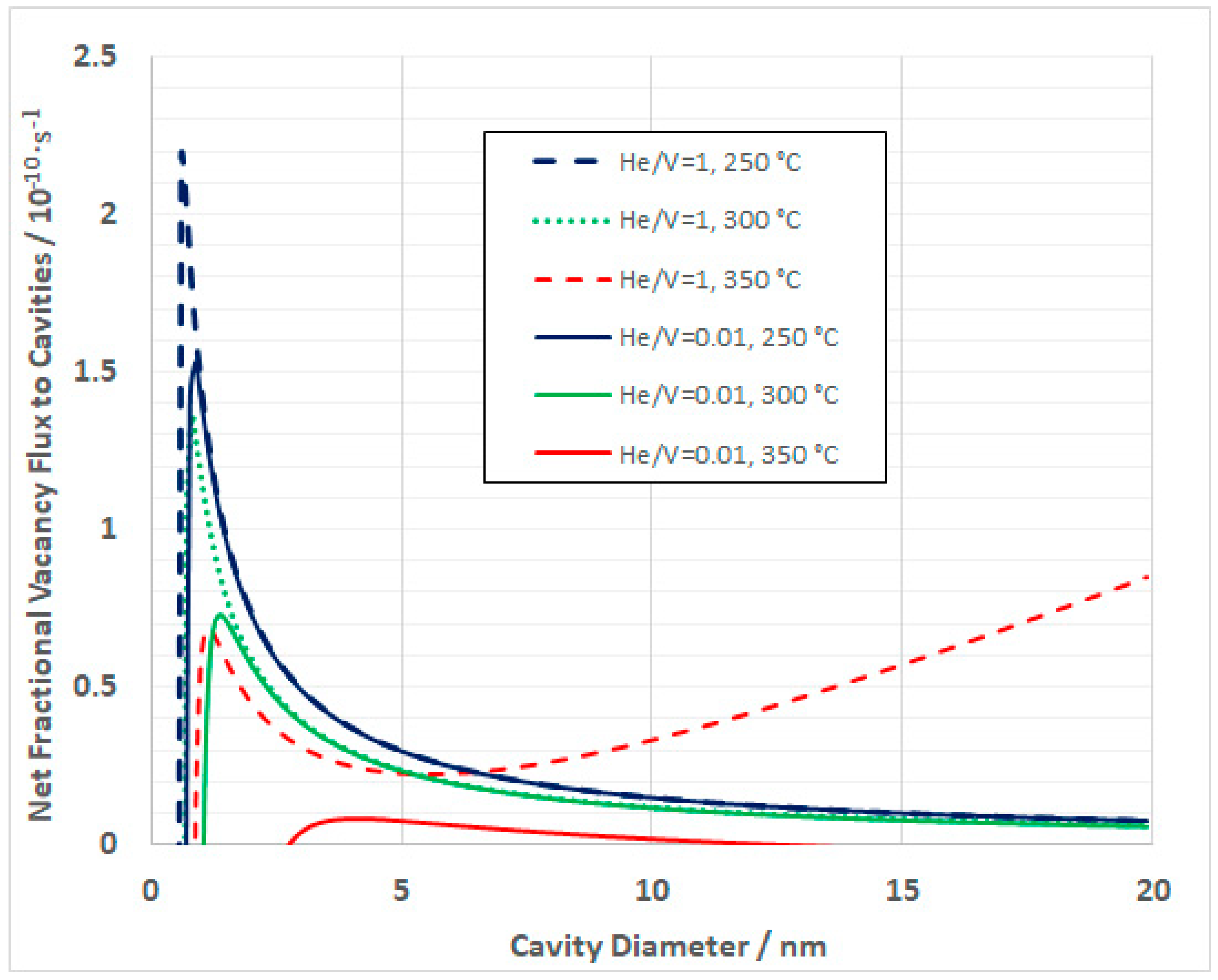

| Ni-59 Factor | Kwon and Motta [33] | Okamoto et al. [31] | ||
|---|---|---|---|---|
| Recoil keV | Displacements per Recoil | FMD Fraction per Recoil | ||
| n,a | 340 | 1760 − 180 = 1580 | 0.012 | 0.009 |
| n,p | 31 | 222 − 26 = 196 | 0.028 | 0.057 |
| n,g | 0.395 | 5 | 1 | 1 |
| Total | 1987 − 206 = 1781 | Weighted Average FMD Fraction | ||
| 0.016 | 0.017 | |||
| Reactor | Alloy | 59Ni Fraction of DPA | FMD (No 59Ni) | FMD 59Ni | Weighted Average FMD Fraction |
|---|---|---|---|---|---|
| CANDU | X750 | 0.55 | 0.142 | 0.017 | 0.073 |
| ATUCHA | X750 | 0.52 | 0.167 | 0.017 | 0.089 |
| ATUCHA | 347H | 0.17 | 0.126 | 0.017 | 0.107 |
| PWR | 316 SS | 0.02 | 0.075 | 0.017 | 0.074 |
| PWR | 304 SS | 0.01 | 0.074 | 0.017 | 0.073 |
| EBR2 | 316 SS | 0 | 0.096 | 0.017 | 0.096 |
| EBR2 | 304 SS | 0 | 0.095 | 0.017 | 0.095 |
| Reactor | Alloy | He/DPA at 100 DPA |
|---|---|---|
| CANDU | Inconel X750 | 301 |
| Atucha | Inconel X750 | 285 |
| Atucha | 347H SS | 84 |
| PWR | 316 SS | 9.9 |
| EBR2 (row 2) | 316 SS | 0.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Griffiths, M.; Xu, S.; Ramos Nervi, J.E. Swelling and He-Embrittlement of Austenitic Stainless Steels and Ni-Alloys in Nuclear Reactors. Metals 2022, 12, 1692. https://doi.org/10.3390/met12101692
Griffiths M, Xu S, Ramos Nervi JE. Swelling and He-Embrittlement of Austenitic Stainless Steels and Ni-Alloys in Nuclear Reactors. Metals. 2022; 12(10):1692. https://doi.org/10.3390/met12101692
Chicago/Turabian StyleGriffiths, Malcolm, Steven Xu, and Juan Eduardo Ramos Nervi. 2022. "Swelling and He-Embrittlement of Austenitic Stainless Steels and Ni-Alloys in Nuclear Reactors" Metals 12, no. 10: 1692. https://doi.org/10.3390/met12101692






