Mechanism Study of the Effect of Selective Laser Melting Energy Density on the Microstructure and Properties of Formed Renewable Porous Bone Scaffolds
Abstract
:1. Introduction
2. Experiment Work
2.1. Powder Materials
2.2. Model
2.3. Experimental Program Design
2.4. Analysis Methods
2.5. Finite Element Simulations
3. Results and Discussion
3.1. Phase Characterization of Bone Scaffolds
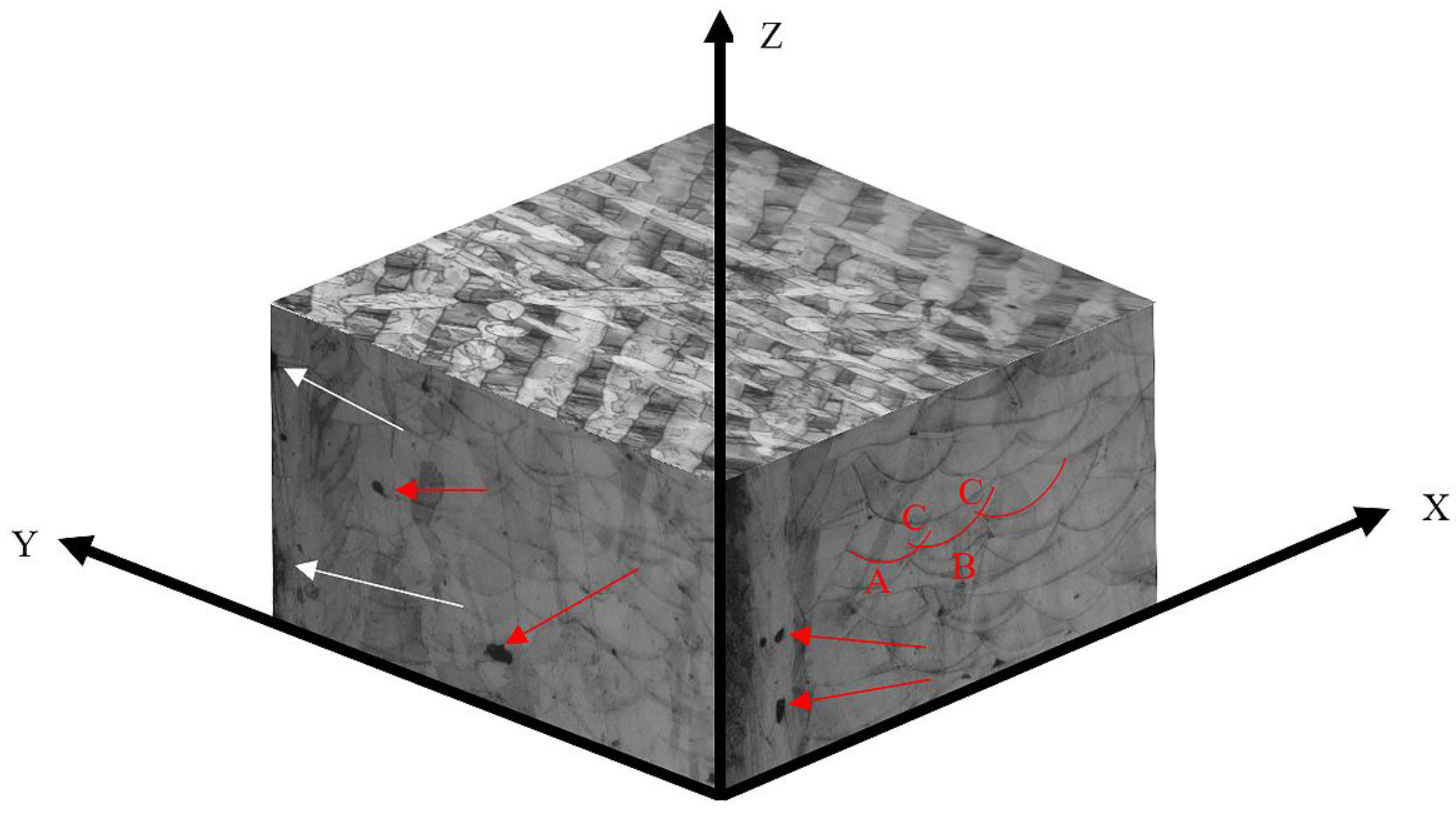
3.2. Microstructure of Bone Scaffolds
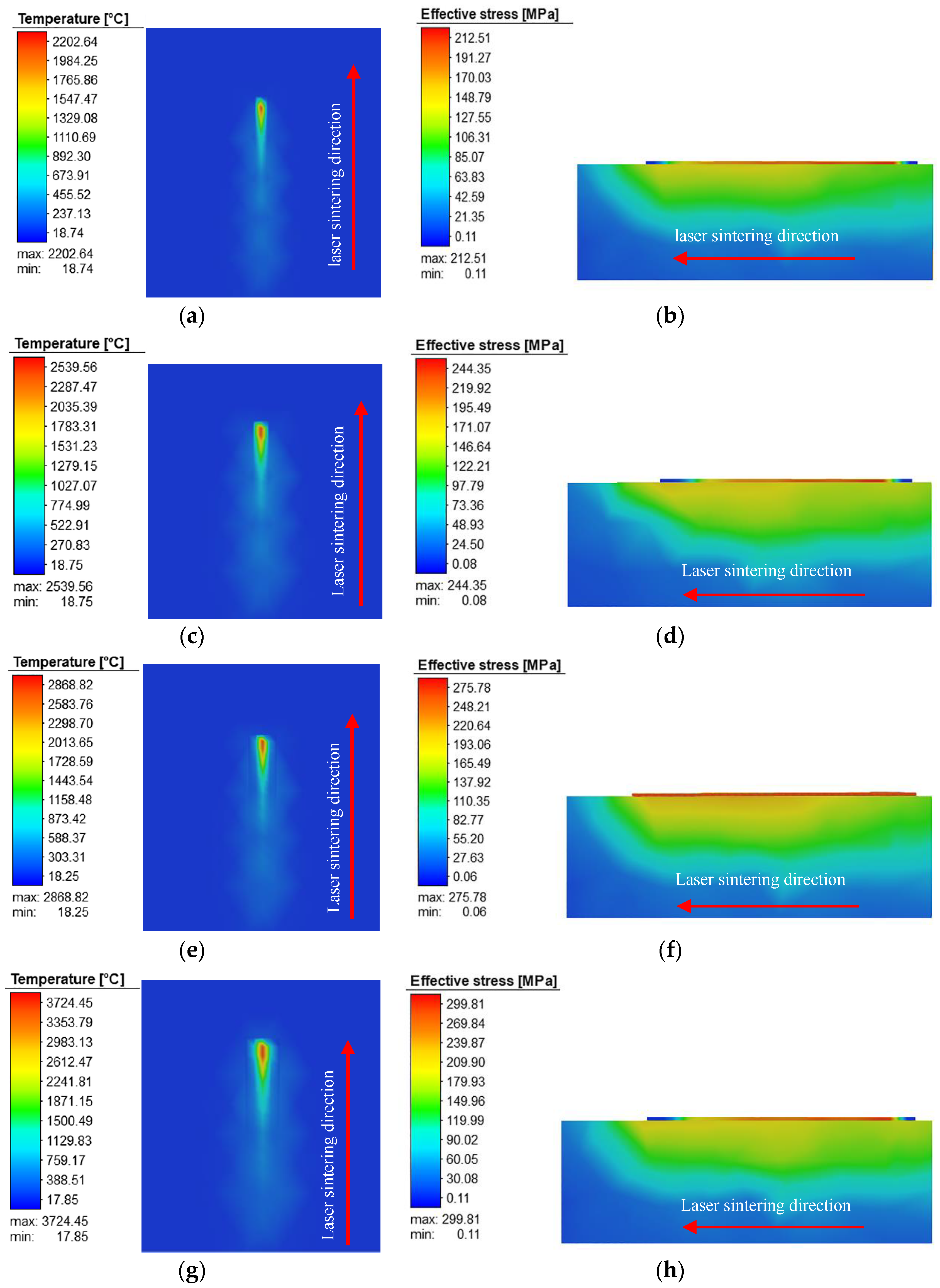
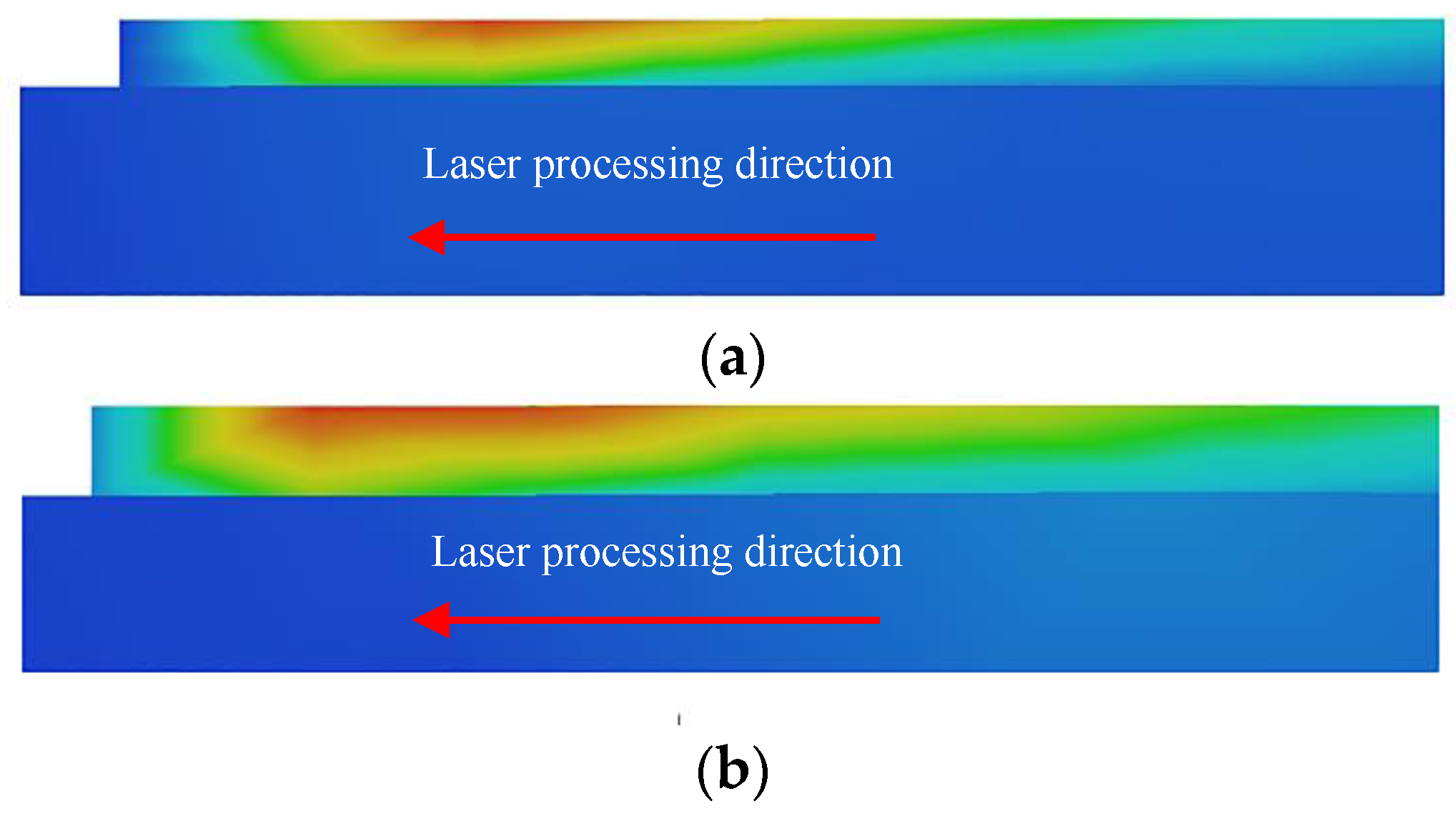
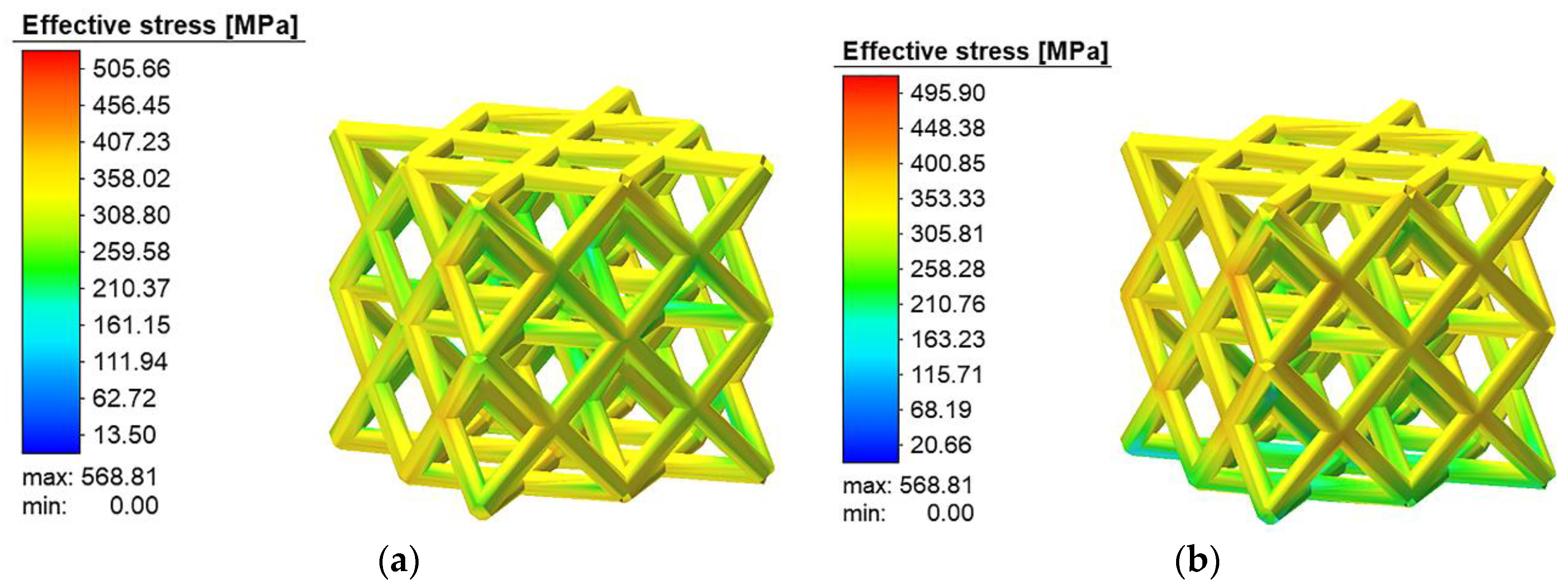
3.3. Residual Stress in Bone Scaffolds
3.4. Residual Deformation of the Bone Scaffold
3.5. Mechanical Properties of Bone Scaffolds
3.5.1. Microhardness
3.5.2. Compression Properties
3.5.3. Modulus of Elasticity of the Bone Scaffolds
4. Conclusions and Prospects
- In SLM processing, the difference in the laser energy density leads to the appearance of grain structures with different shapes and different forming angles in the melt pool. With the increase in the energy density, the direction of grain formation in the molt pool shifts from 80° to 50°. At the same time, improper energy density processing is more likely to cause deformed grains at the edge of the molt pool, which leads to cracks and holes, and reduces the mechanical properties of the porous scaffolds.
- Among the factors determining the energy density, the scanning speed of the laser and the laser power have the most significant effect on the grain size of the porous scaffolds. When the energy density increased from 41.7 to 111.1 J/mm3, the average primary dendrite spacing increased from 441 to 501 nm and this change led to a significant difference in the performance of the porous scaffolds.
- For the mechanical properties of porous scaffolds, laser processing with high energy densities (≥100.0 J/mm3) tends to achieve a lower microhardness (214.92 HV0.5) while processing with lower energy densities (<100.0 J/mm3) can increase the average microhardness by a maximum of about 9.4% in comparison, up to 237.34 HV0.5. In terms of the compressive performance, the porous bone scaffolds constructed with high energy densities were approximately 10% to 17% less than the other construction energy densities.
- The elastic modulus of the bone scaffolds was tested, and it was found that the porous bone scaffolds formed by SLM basically met the requirements for human bone implantation, but the high energy density (111.1 J/mm3) used to construct the porous bone scaffolds with an FCC structure could easily lead to a decrease in the formation accuracy of the scaffolds and make the performance of the scaffolds exceed the ideal expectations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arjunan, A.; Demetriou, M.; Baroutaji, A.; Wang, C. Mechanical performance of highly permeable laser melted Ti6Al4V bone scaffolds. J. Mech. Behav. Biomed. Mater. 2020, 102, 103517. [Google Scholar] [CrossRef]
- Bai, L.; Gong, C.; Chen, X.; Zheng, J.; Xin, L.; Xiong, Y.; Wu, X.; Hu, M.; Li, K.; Sun, Y. Quasi-Static compressive responses and fatigue behaviour of Ti-6Al-4 V graded lattice structures fabricated by laser powder bed fusion. Mater. Des. 2021, 210, 110110. [Google Scholar] [CrossRef]
- Li, J.; Jansen, J.A.; Walboomers, X.F.; van den Beucken, J.J. Mechanical aspects of dental implants and osseointegration: A narrative review. J. Mech. Behav. Biomed. Mater. 2020, 103, 103574. [Google Scholar] [CrossRef] [PubMed]
- Coffigniez, M.; Gremillard, L.; Balvay, S.; Lachambre, J.; Adrien, J.; Boulnat, X. Direct-ink writing of strong and biocompatible titanium scaffolds with bimodal interconnected porosity. Addit. Manuf. 2021, 39, 101859. [Google Scholar] [CrossRef]
- Kumar, P.; Ramamurty, U. Microstructural optimization through heat treatment for enhancing the fracture toughness and fatigue crack growth resistance of selective laser melted Ti 6Al 4V alloy. Acta Mater. 2019, 169, 45–59. [Google Scholar] [CrossRef]
- Chao, Q.; Cruz, V.; Thomas, S.; Birbilis, N.; Collins, P.; Taylor, A.; Hodgson, P.D.; Fabijanic, D. On the enhanced corrosion resistance of a selective laser melted austenitic stainless steel. Scr. Mater. 2017, 141, 94–98. [Google Scholar] [CrossRef]
- Jiang, H.-Z.; Li, Z.-Y.; Feng, T.; Wu, P.-Y.; Chen, Q.-S.; Feng, Y.-L.; Chen, L.-F.; Hou, J.-Y.; Xu, H.-J. Effect of Process Parameters on Defects, Melt Pool Shape, Microstructure, and Tensile Behavior of 316L Stainless Steel Produced by Selective Laser Melting. Acta Met. Sin. Engl. Lett. 2020, 34, 495–510. [Google Scholar] [CrossRef]
- Oliveira, J.P.; LaLonde, A.D.; Ma, J. Processing parameters in laser powder bed fusion metal additive manufacturing. Mater. Des. 2020, 193, 108762. [Google Scholar] [CrossRef]
- Liverani, E.; Toschi, S.; Ceschini, L.; Fortunato, A. Effect of selective laser melting (SLM) process parameters on microstructure and mechanical properties of 316L austenitic stainless steel. J. Mater. Process. Technol. 2017, 249, 255–263. [Google Scholar] [CrossRef]
- Sing, S.L.; An, J.; Yeong, W.Y.; Wiria, F.E. Laser and electron-beam powder-bed additive manufacturing of metallic implants: A review on processes, materials and designs. J. Orthop. Res. 2015, 34, 369–385. [Google Scholar] [CrossRef]
- Davoodi, E.; Montazerian, H.; Mirhakimi, A.S.; Zhianmanesh, M.; Ibhadode, O.; Shahabad, S.I.; Esmaeilizadeh, R.; Sarikhani, E.; Toorandaz, S.; Sarabi, S.A.; et al. Additively manufactured metallic biomaterials. Bioact. Mater. 2022, 15, 214–249. [Google Scholar] [CrossRef] [PubMed]
- Deng, F.; Liu, L.; Li, Z.; Liu, J. 3D printed Ti6Al4V bone scaffolds with different pore structure effects on bone ingrowth. J. Biol. Eng. 2021, 15, 4–16. [Google Scholar] [CrossRef] [PubMed]
- Cosma, C.; Kessler, J.; Gebhardt, A.; Campbell, I.; Balc, N. Improving the Mechanical Strength of Dental Applications and Lattice Structures SLM Processed. Materials 2020, 13, 905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Capek, J.; Machova, M.; Fousova, M.; Kubásek, J.; Vojtěch, D.; Fojt, J.; Jablonská, E.; Lipov, J.; Ruml, T. Highly porous, low elastic modulus 316L stainless steel scaffold prepared by selective laser melting. Mater. Sci. Eng. C 2016, 69, 631–639. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Zou, J.; Yang, H.-Y. Wear performance of metal parts fabricated by selective laser melting: A literature review. J. Zhejiang Univ. A 2018, 19, 95–110. [Google Scholar] [CrossRef]
- Yadollahi, A.; Shamsaei, N.; Thompson, S.M.; Seely, D.W. Effects of process time interval and heat treatment on the mechanical and microstructural properties of direct laser deposited 316L stainless steel. Mater. Sci. Eng. A 2015, 644, 171–183. [Google Scholar] [CrossRef]
- Wang, Z.; Denlinger, E.; Michaleris, P.; Stoica, A.D.; Ma, D.; Beese, A.M. Residual stress mapping in Inconel 625 fabricated through additive manufacturing: Method for neutron diffraction measurements to validate thermomechanical model predictions. Mater. Des. 2017, 113, 169–177. [Google Scholar] [CrossRef] [Green Version]
- Khorasani, M.; Ghasemi, A.; Leary, M.; Sharabian, E.; Cordova, L.; Gibson, I.; Downing, D.; Bateman, S.; Brandt, M.; Rolfe, B. The effect of absorption ratio on meltpool features in laser-based powder bed fusion of IN718. Opt. Laser Technol. 2022, 153, 108263. [Google Scholar] [CrossRef]
- Mercelis, P.; Kruth, J. Residual stresses in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2006, 12, 254–265. [Google Scholar] [CrossRef]
- Song, B.; Dong, S.; Deng, S.; Liao, H.; Coddet, C. Microstructure and tensile properties of iron parts fabricated by selective laser melting. Opt. Laser Technol. 2014, 56, 451–460. [Google Scholar] [CrossRef]
- Abe, F.; Santos, E.C.; Kitamura, Y.; Osakada, K.; Shiomi, M. Influence of forming conditions on the titanium model in rapid prototyping with the selective laser melting process. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2003, 217, 119–126. [Google Scholar] [CrossRef]
- Zhou, Y.; Abbara, E.M.; Jiang, D.; Azizi, A.; Poliks, M.D.; Ning, F. High-cycle fatigue properties of curved-surface AlSi10Mg parts fabricated by powder bed fusion additive manufacturing. Rapid Prototyp. J. 2022, 28, 1346–1360. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, S.; Ren, G.; Pan, Y.; Li, J. Optimization of Structural and Processing Parameters for Selective Laser Melting of Porous 316L Bone Scaffolds. Materials 2022, 15, 5896. [Google Scholar] [CrossRef] [PubMed]
- Giganto, S.; Martínez-Pellitero, S.; Cuesta, E.; Zapico, P.; Barreiro, J. Proposal of design rules for improving the accuracy of selective laser melting (SLM) manufacturing using benchmarks parts. Rapid Prototyp. J. 2022, 28, 1129–1143. [Google Scholar] [CrossRef]
- Moniruzzaman, M.; O'Neal, C.; Bhuiyan, A.; Egan, P.F. Design and Mechanical Testing of 3D Printed Hierarchical Lattices Using Biocompatible Stereolithography. Designs 2020, 4, 22. [Google Scholar] [CrossRef]
- Poltue, T.; Karuna, C.; Khrueaduangkham, S.; Seehanam, S.; Promoppatum, P. Design exploration of 3D-printed triply periodic minimal surface scaffolds for bone implants. Int. J. Mech. Sci. 2021, 211, 106762. [Google Scholar] [CrossRef]
- Tan, X.; Tan, Y.; Chow, C.; Tor, S.; Yeong, W. Metallic powder-bed based 3D printing of cellular scaffolds for orthopaedic implants: A state-of-the-art review on manufacturing, topological design, mechanical properties and biocompatibility. Mater. Sci. Eng. C 2017, 76, 1328–1343. [Google Scholar] [CrossRef]
- Wieding, J.; Wolf, A.; Bader, R. Numerical optimization of open-porous bone scaffold structures to match the elastic properties of human cortical bone. J. Mech. Behav. Biomed. Mater. 2014, 37, 56–68. [Google Scholar] [CrossRef] [PubMed]
- Casati, R.; Lemke, J.; Vedani, M. Microstructure and Fracture Behavior of 316L Austenitic Stainless Steel Produced by Selective Laser Melting. J. Mater. Sci. Technol. 2016, 32, 738–744. [Google Scholar] [CrossRef]
- Fischer, P.; Romano, V.; Weber, H.; Karapatis, N.; Boillat, E.; Glardon, R. Sintering of commercially pure titanium powder with a Nd:YAG laser source. Acta Mater. 2003, 51, 1651–1662. [Google Scholar] [CrossRef]
- Wang, D.; Song, C.; Yang, Y.; Bai, Y. Investigation of crystal growth mechanism during selective laser melting and mechanical property characterization of 316L stainless steel parts. Mater. Des. 2016, 100, 291–299. [Google Scholar] [CrossRef]
- Bartlett, J.L.; Croom, B.P.; Burdick, J.; Henkel, D.; Li, X. Revealing mechanisms of residual stress development in additive manufacturing via digital image correlation. Addit. Manuf. 2018, 22, 1–12. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef] [Green Version]
- Xiao, H.; Zhang, C.; Zhu, H. Effect of direct aging and annealing on the microstructure and mechanical properties of AlSi10Mg fabricated by selective laser melting. Rapid Prototyp. J. 2022, 28, 1355–2546. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, S.; Peng, Z.; Gao, Z. Effect of defects in laser selective melting of Ti-6Al-4V alloy on microstructure and mechanical properties after heat treatment. Opt. Laser Technol. 2022, 156, 108522. [Google Scholar] [CrossRef]
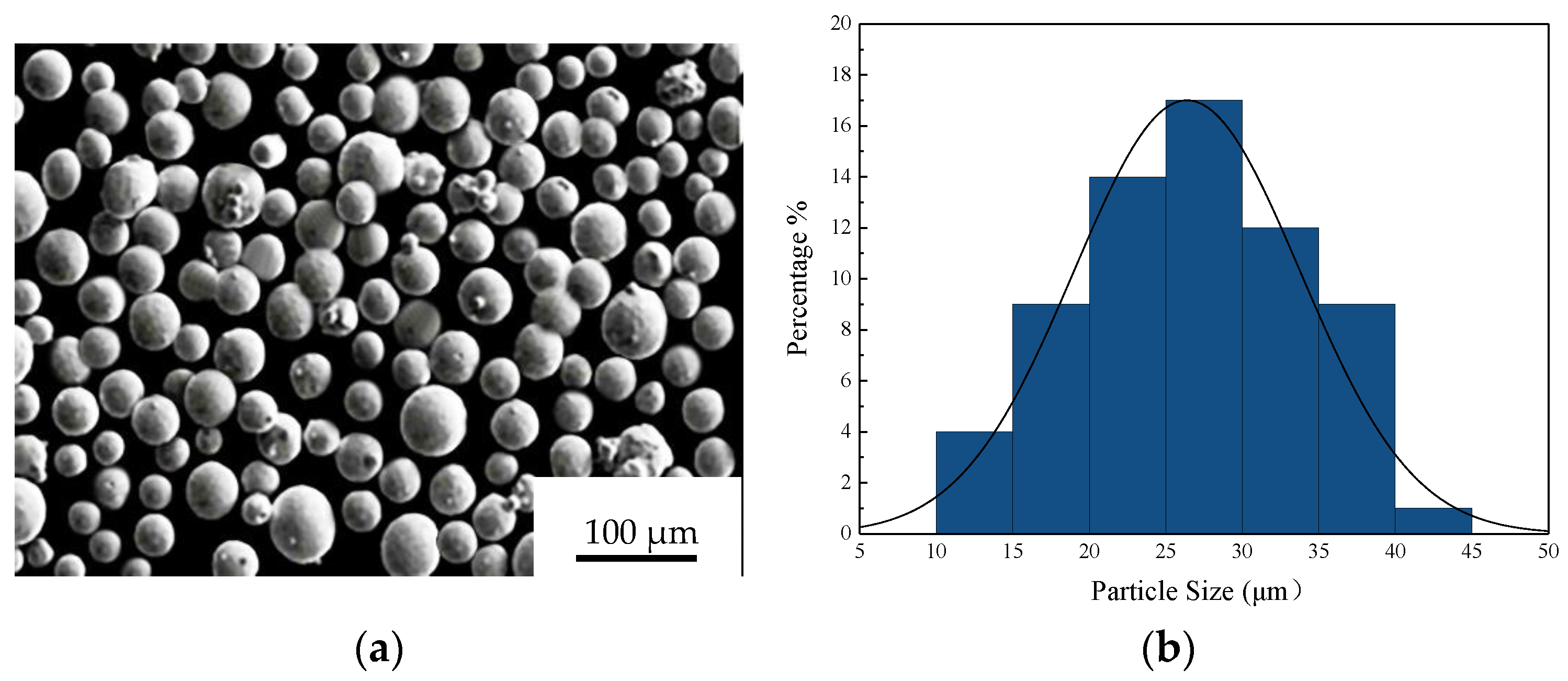
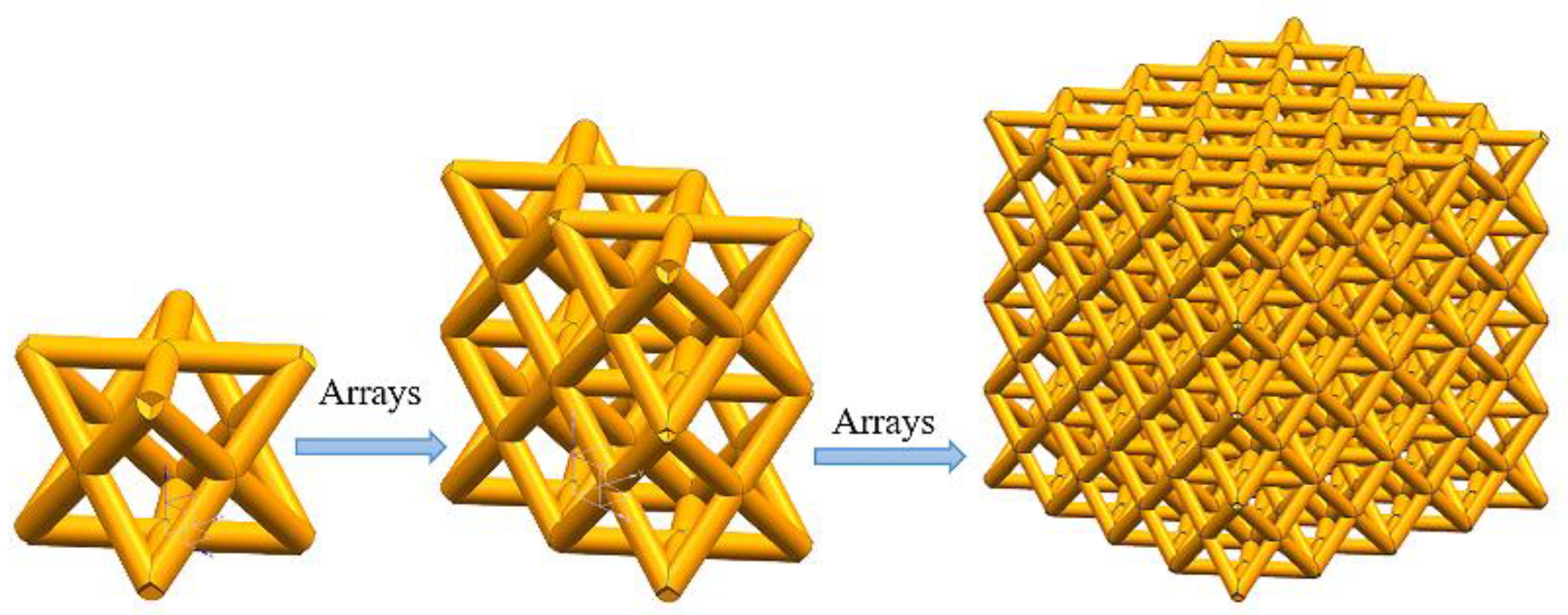
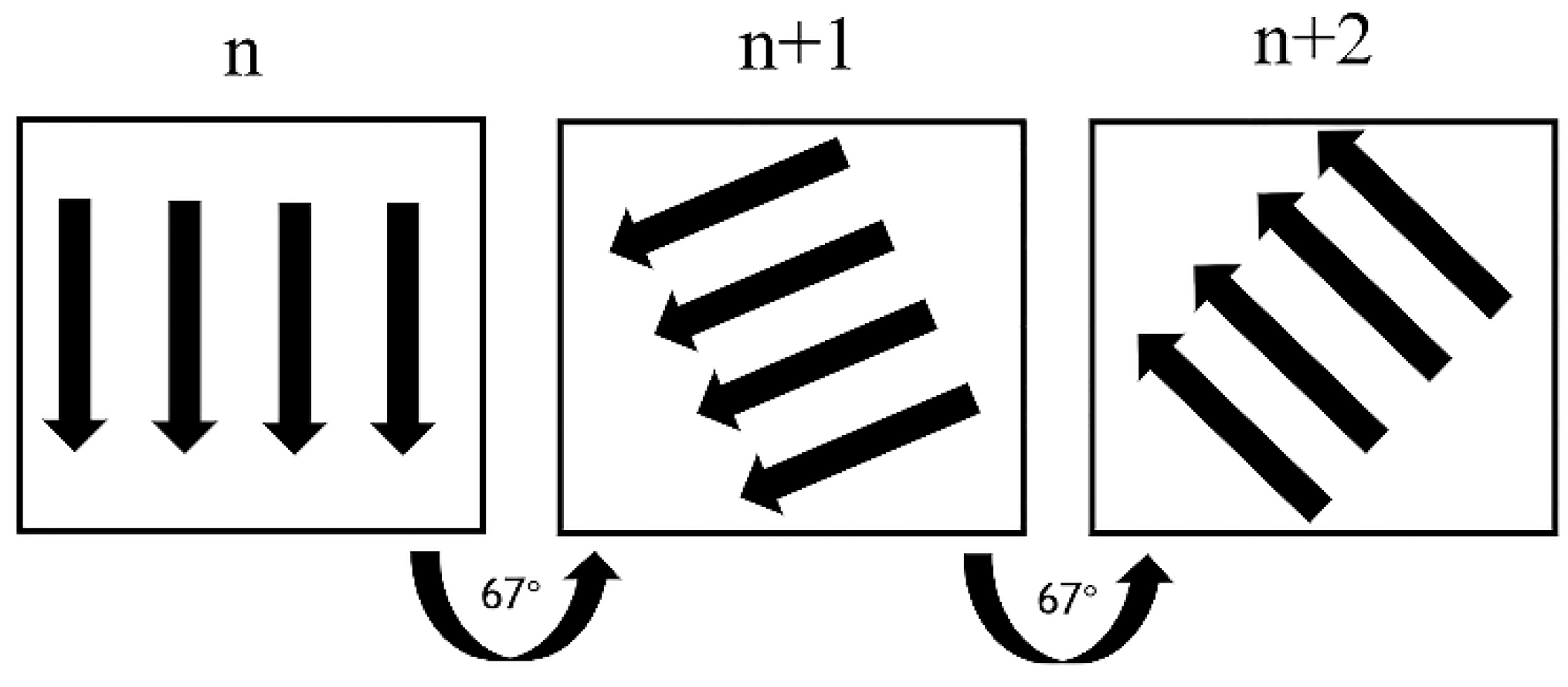
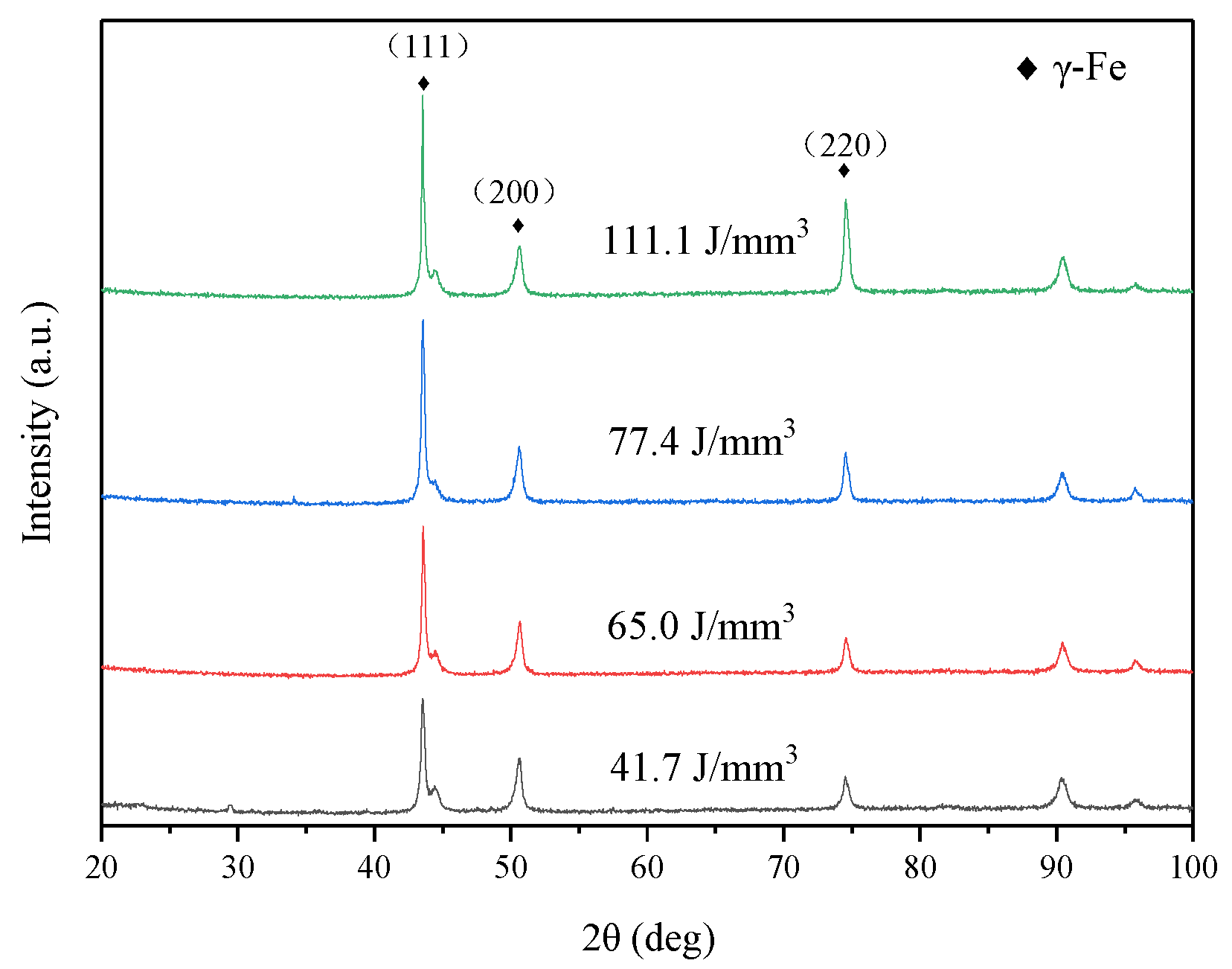


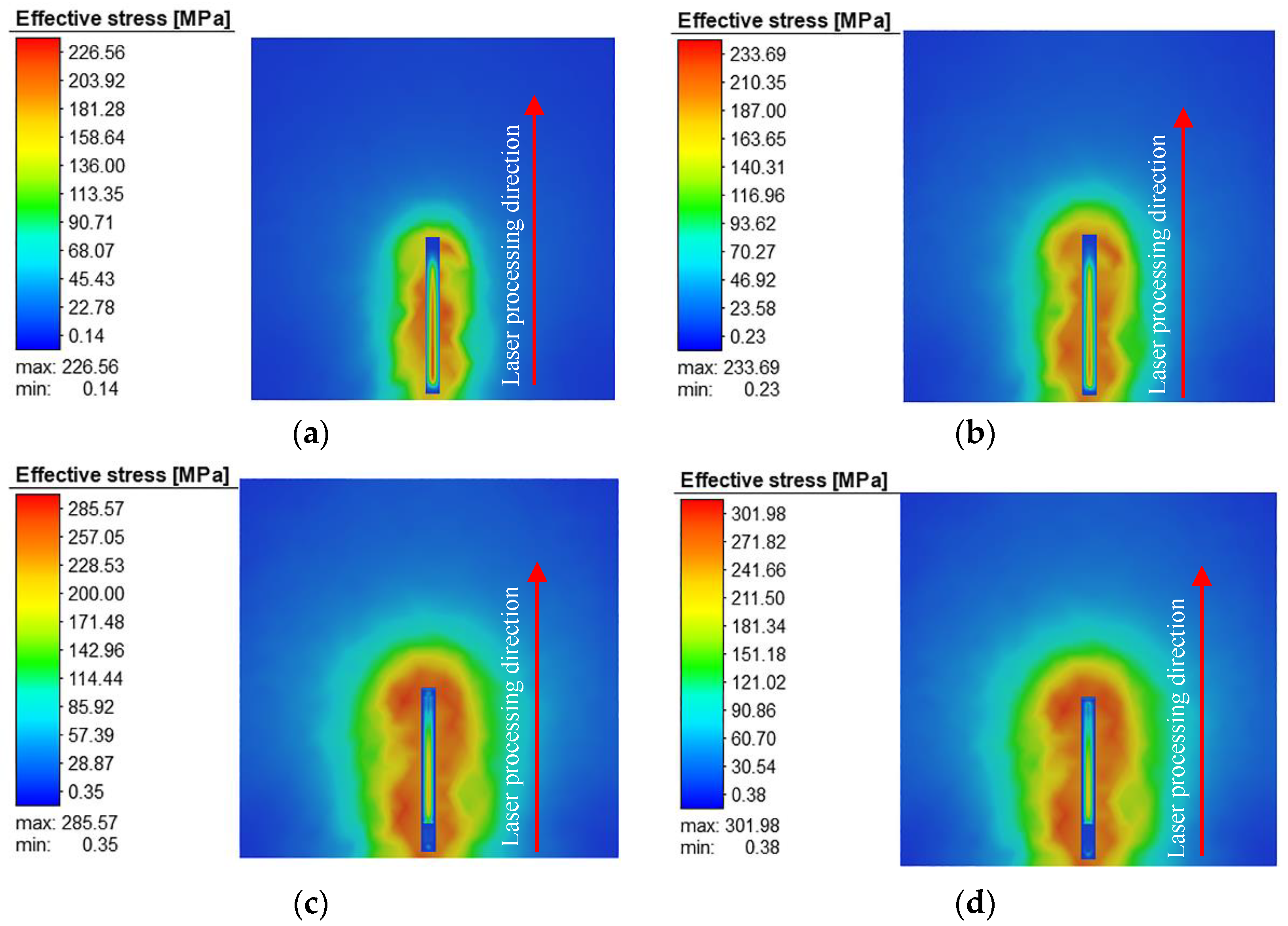
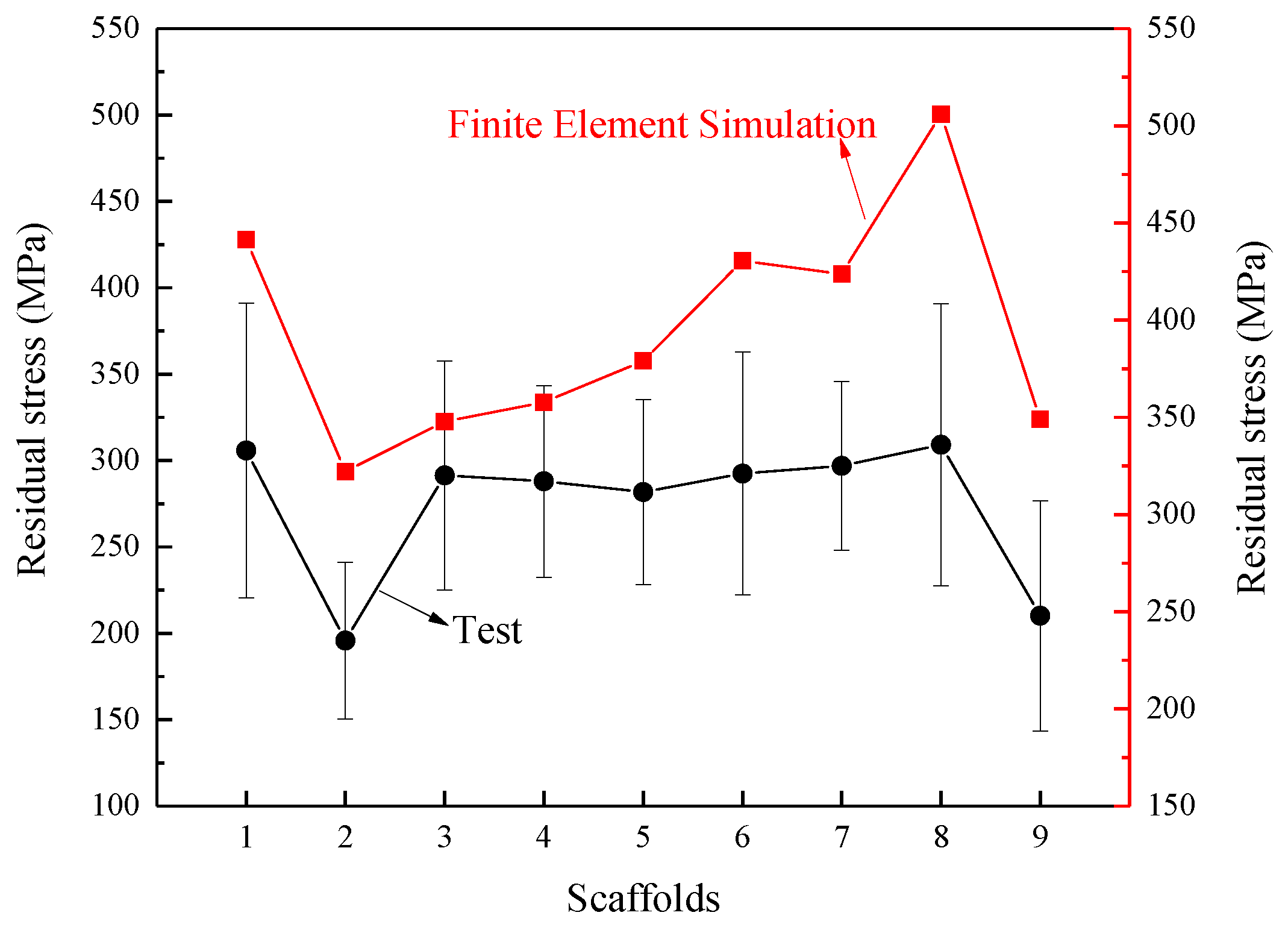
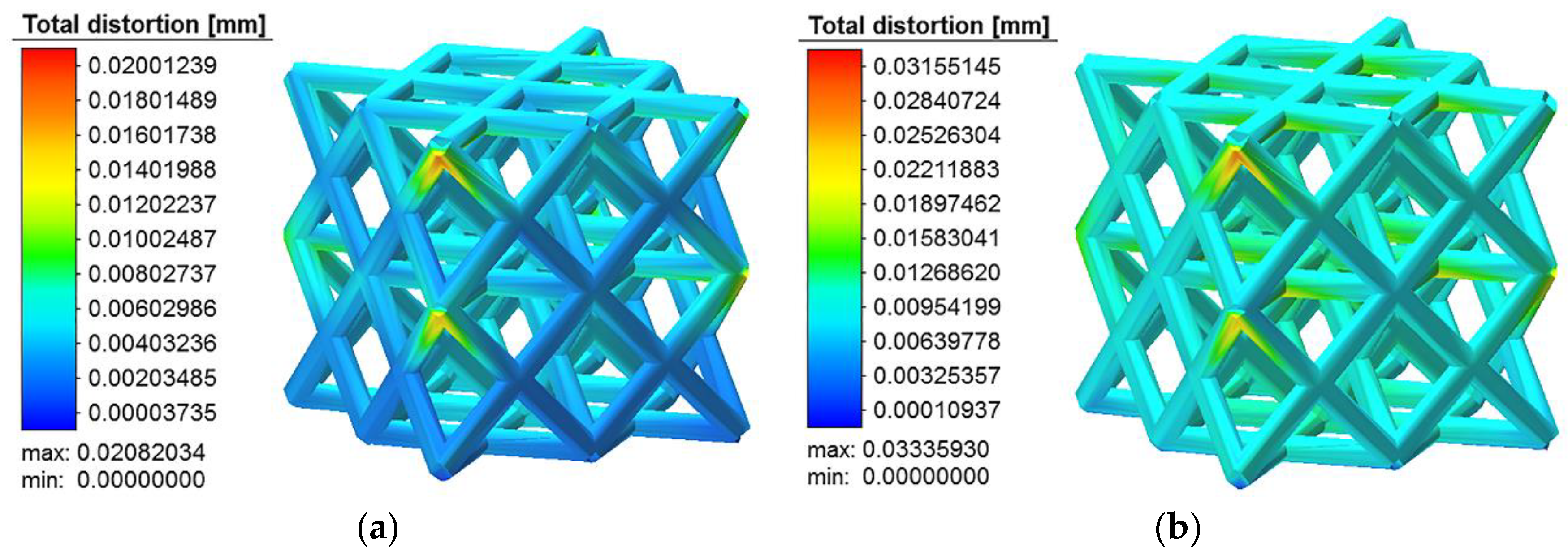

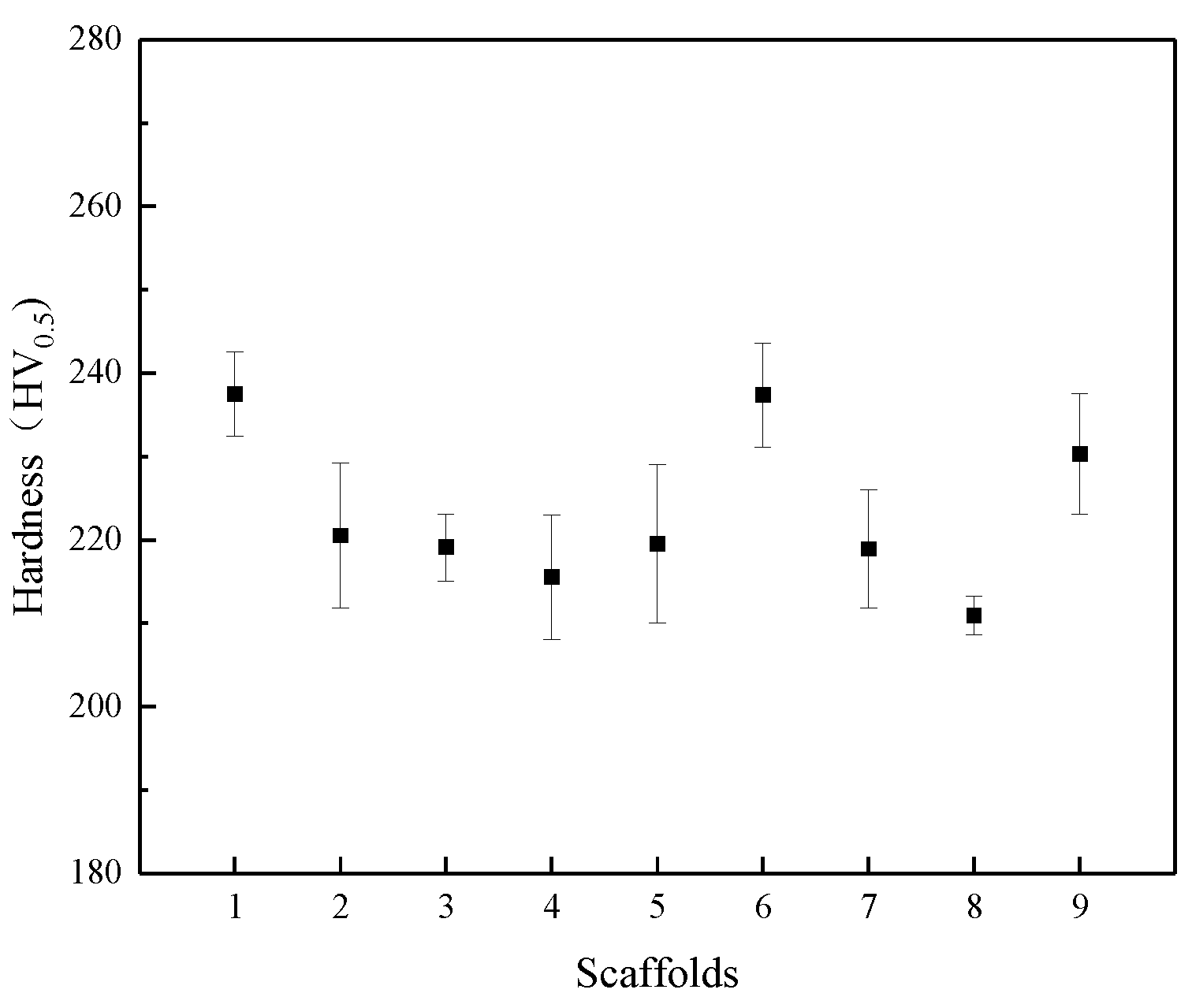

| Element | Fe | C | Mn | Si | Ni | Cr | Mo | S | P |
|---|---|---|---|---|---|---|---|---|---|
| Content (wt.%) | Balance | ≤0.03 | ≤2.0 | ≤0.75 | 12–14 | 16–18 | 2–3 | ≤0.03 | ≤0.045 |
| Route | Laser Power P (W) | Scanning Speed V (mm/s) | Hatching Spacing S (mm) | Energy Density ω (J/mm3) |
|---|---|---|---|---|
| 1 | 100 | 500 | 0.06 | 83.3 |
| 2 | 100 | 600 | 0.10 | 41.7 |
| 3 | 100 | 700 | 0.08 | 44.6 |
| 4 | 130 | 500 | 0.10 | 65.0 |
| 5 | 130 | 600 | 0.08 | 67.7 |
| 6 | 130 | 700 | 0.06 | 77.4 |
| 7 | 160 | 500 | 0.08 | 100.0 |
| 8 | 160 | 600 | 0.06 | 111.1 |
| 9 | 160 | 700 | 0.10 | 57.1 |
| Sample | 2θ Location | Intensity | Peak FWHM |
|---|---|---|---|
| Standard (PDF NO.33-0937) | 43.582 | - | - |
| 41.7 J/mm3 | 43.520 | 1891 | 0.355 |
| 65.0 J/mm3 | 43.565 | 2080 | 0.331 |
| 77.4 J/mm3 | 43.566 | 2895 | 0.317 |
| 111.1 J/mm3 | 43.565 | 3201 | 0.295 |
| Energy Density ω (J/mm3) | θ (°) |
|---|---|
| 41.7 | 80.126 |
| 44.6 | 80.013 |
| 57.1 | 53.319 |
| 65.0 | 54.201 |
| 67.7 | 52.074 |
| 77.4 | 48.490 |
| 83.3 | 46.367 |
| 100.0 | 43.647 |
| 111.1 | 50.727 |
| Porous Bone Scaffolds | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Design diameter values (μm) | 250 | 250 | 250 | 250 | 250 | 250 | 250 | 250 | 250 |
| Build diameter values (μm) | 322 ± 26 | 297 ± 15 | 310 ± 12 | 310 ± 16 | 322 ± 40 | 322 ± 20 | 328 ± 20 | 331 ± 30 | 314 ± 13 |
| Deformation Process | Initial Stage (I) | Intermediate Stage (II) | Late Stage (III) |
|---|---|---|---|
| Image |  |  |  |
| Route | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Density (g/cm3) | 2.37 | 2.36 | 2.37 | 2.37 | 2.37 | 2.38 | 2.44 | 2.47 | 2.36 |
| Modulus of elasticity (GPa) | 18.6 | 18.4 | 18.5 | 18.6 | 18.6 | 18.7 | 19.7 | 20.1 | 18.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Xu, S.; Pan, Y.; Li, J.; Li, T. Mechanism Study of the Effect of Selective Laser Melting Energy Density on the Microstructure and Properties of Formed Renewable Porous Bone Scaffolds. Metals 2022, 12, 1712. https://doi.org/10.3390/met12101712
Zhang S, Xu S, Pan Y, Li J, Li T. Mechanism Study of the Effect of Selective Laser Melting Energy Density on the Microstructure and Properties of Formed Renewable Porous Bone Scaffolds. Metals. 2022; 12(10):1712. https://doi.org/10.3390/met12101712
Chicago/Turabian StyleZhang, Sen, Shubo Xu, Yuefei Pan, Jianing Li, and Tingting Li. 2022. "Mechanism Study of the Effect of Selective Laser Melting Energy Density on the Microstructure and Properties of Formed Renewable Porous Bone Scaffolds" Metals 12, no. 10: 1712. https://doi.org/10.3390/met12101712
APA StyleZhang, S., Xu, S., Pan, Y., Li, J., & Li, T. (2022). Mechanism Study of the Effect of Selective Laser Melting Energy Density on the Microstructure and Properties of Formed Renewable Porous Bone Scaffolds. Metals, 12(10), 1712. https://doi.org/10.3390/met12101712





