Dynamical Models of Plasticity with Nonmonotonic Deformation Curves for Nanomaterials
Abstract
:1. Introduction
2. Dynamic Models of Plasticity for One-Stage Hardening or Softening Stage
2.1. Relaxation Model of Plasticity
2.2. Relaxation Model of Plasticity with Classical Hardening Law
3. Verification of Model with Experiments on Nanomaterials at Strain Rates of 10−4–10−1 s−1
3.1. Non-Monotonic Deformation Curves of Nanomaterials
3.2. Characteristic Relaxation Times and Hardening Parameters for Nanomaterials
4. Conclusions
- The relaxation model of plasticity can be applied to single-crystal nanomaterials with different values of characteristic relaxation times in the range of 10–600 s;
- The value of the hardening parameter for single-crystal nanomaterials is much higher than for nanostructured materials;
- Characteristic relaxation times of single-crystal nanomaterials were in the order of microseconds, which is several times greater than that of their coarse-grained counterparts;
- The use of the usual hardening law in the relaxation function γSH (t) allows us to consider the model in Section 2.2 with two classical hardening parameters as an alternative approach to the model in Section 2.1 with one hardening parameter;
- The characteristic relaxation times with a sample size were reduced;
- The softening and hardening effects that occur depending on the material at different strain rates are predicted by the proposed model in Section 2.1 with a fixed set of parameters (α, τ, and β).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Armstrong, R.W.; Walley, S.M. High strain rate properties of metals and alloys. Int. Mater. Rev. 2008, 53, 105–128. [Google Scholar] [CrossRef]
- Swegle, J.W.; Grady, D.E. Shock viscosity and the prediction of shock wave rise times. J. Appl. Phys. 1985, 58, 692–701. [Google Scholar] [CrossRef]
- Dehm, G. Miniaturized single-crystalline fcc metals deformed in tension: New insights in size-dependent plasticity. Prog. Mater. Sci. 2009, 54, 664–688. [Google Scholar] [CrossRef]
- Cui, Y.; Po, G.; Ghoniem, N. Temperature insensitivity of the flow stress in body-centered cubic micropillar crystals. Acta Mater. 2016, 108, 128–137. [Google Scholar] [CrossRef] [Green Version]
- Greer, J.R.; De Hosson, J.T. Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect. Prog. Mater. Sci. 2011, 56, 654–724. [Google Scholar] [CrossRef]
- Colorado, H.A.; Navarro, A.; Prikhodko, S.V.; Yang, J.M.; Ghoniem, N.; Gupta, V. Ultrahigh strain-rate bending of copper nanopillars with laser-generated shock waves. J. Appl. Phys. 2013, 114, 233510. [Google Scholar] [CrossRef]
- Petrov, Y.V.; Borodin, E.N. Relaxation mechanism of plastic deformation and its justification using the example of the sharp yield point phenomenon in whiskers. Phys. Solid State 2015, 57, 353–359. [Google Scholar] [CrossRef]
- Selyutina, N.S.; Borodin, E.N.; Petrov, Y.V. Structural–Temporal Peculiarities of Dynamic Deformation of Nanostructured and Nanoscaled Metals. Phys. Solid State 2018, 60, 1813–1820. [Google Scholar] [CrossRef]
- Gruzdkov, A.; Petrov, Y.V.; Smirnov, V.I. An invariant form of the dynamic criterion for yield of metals. Phys. Solid State 2002, 44, 2080–2082. [Google Scholar] [CrossRef]
- Gruzdkov, A.; Sitnikova, E.; Morozov, N.; Petrov, Y. Thermal Effect in Dynamic Yielding and Fracture of Metals and Alloys. Math. Mech. Solids 2009, 14, 72–87. [Google Scholar] [CrossRef]
- Petrov, Y.V.; Gruzdkov, A.A.; Sitnikova, E.V. Anomalous behavior of yield stress upon an increase in temperature under high strain rate conditions. Dokl. Phys. 2007, 52, 691–694. [Google Scholar] [CrossRef]
- Mayer, A.E.; Khishchenko, K.V.; Levashov, P.R.; Mayer, P.N. Modeling of plasticity and fracture of metals at shock loading. J. Appl. Phys. 2013, 113, 193508. [Google Scholar] [CrossRef]
- Chang, H.-J.; Segurado, J.; Molina-Aldareguía, J.M.; Soler, R.; Llorca, J. A 3D dislocation dynamics analysis of the size effect on the strength of [1 1 1] LiF micropillars at 300K and 600K. Model. Simul. Mater. Sci. Eng. 2016, 24, 035009. [Google Scholar] [CrossRef] [Green Version]
- Brenner, S.S. Tensile Strength of Whiskers. J. Appl. Phys. 1956, 27, 1484–1491. [Google Scholar] [CrossRef]
- Brown, J.A.; Ghoniem, N.M. Reversible–irreversible plasticity transition in twinned copper nanopillars. Acta Mater. 2010, 58, 886–894. [Google Scholar] [CrossRef]
- Zhang, N.; Zaeem, M.A. Competing mechanisms between dislocation and phase transformation in plastic deformation of single crystalline yttria-stabilized tetragonal zirconia nanopillars. Acta Mater. 2016, 120, 337–347. [Google Scholar] [CrossRef] [Green Version]
- Dutta, A. Compressive deformation of Fe nanopillar at high strain rate: Modalities of dislocation dynamics. Acta Mater. 2017, 125, 219–230. [Google Scholar] [CrossRef]
- Klusemann, B.; Bargmann, S.; Estrin, Y. Fourth-order strain-gradient phase mixture model for nanocrystalline fcc materials. Model. Simul. Mater. Sci. Eng. 2016, 24, 085016. [Google Scholar] [CrossRef] [Green Version]
- Barai, P.; Weng, G.J. Mechanics of very fine-grained nanocrystalline materials with contributions from grain interior, GB zone, and grain-boundary sliding. Int. J. Plast. 2009, 25, 2410–2434. [Google Scholar] [CrossRef]
- Borodin, E.; Mayer, A. A simple mechanical model for grain boundary sliding in nanocrystalline metals. Mater. Sci. Eng. A 2012, 532, 245–248. [Google Scholar] [CrossRef]
- Borodin, E.N.; Mayer, A.E. Theoretical interpretation of abnormal ultrafine-grained material deformation dynamics. Model. Simul. Mater. Sci. Eng. 2016, 24, 025013. [Google Scholar] [CrossRef]
- Upadhyay, M.; Capolungo, L.; Taupin, V.; Fressengeas, C.; Lebensohn, R. A higher order elasto-viscoplastic model using fast Fourier transforms: Effects of lattice curvatures on mechanical response of nanocrystalline metals. Int. J. Plast. 2016, 83, 126–152. [Google Scholar] [CrossRef]
- Wei, Q.; Pan, Z.; Wu, X.; Schuster, B.; Kecskes, L.; Valiev, R. Microstructure and mechanical properties at different length scales and strain rates of nanocrystalline tantalum produced by high-pressure torsion. Acta Mater. 2011, 59, 2423–2436. [Google Scholar] [CrossRef] [Green Version]
- Kim, W.; Park, K.; Yoo, S.J.; Matteini, P.; Hwang, B.; Kim, B.; Han, S.M. Deformation twinning in Au30Ag70 alloy nanowires under tensile strain. J. Alloy. Compd. 2020, 816, 152586. [Google Scholar] [CrossRef]
- Srivastava, P.; Jiang, K.; Cui, Y.; Olivera, E.; Ghoniem, N.; Gupta, V. The influence of nano/micro sample size on the strain-rate sensitivity of plastic flow in tungsten. Int. J. Plast. 2021, 136, 102854. [Google Scholar] [CrossRef]
- Rajaraman, S.; Jonnalagadda, K.N.; Ghosh, P. Indentation and Dynamic Compression Experiments on Microcrystalline and Nanocrystalline Nickel; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Berlin/Heidelberg, Germany, 2013; Volume 1, pp. 157–163. [Google Scholar] [CrossRef]
- Wei, Q.; Schuster, B.; Mathaudhu, S.; Hartwig, K.; Kecskes, L.; Dowding, R.; Ramesh, K. Dynamic behaviors of body-centered cubic metals with ultrafine grained and nanocrystalline microstructures. Mater. Sci. Eng. A 2008, 493, 58–64. [Google Scholar] [CrossRef]
- Sedlmayr, A.; Bitzek, E.; Gianola, D.S.; Richter, G.; Mönig, R.; Kraft, O. Existence of two twinning-mediated plastic deformation modes in Au nanowhiskers. Acta Mater. 2012, 60, 3985–3993. [Google Scholar] [CrossRef]
- Selyutina, N.; Borodin, E.; Petrov, Y.; Mayer, A. The definition of characteristic times of plastic relaxation by dislocation slip and grain boundary sliding in copper and nickel. Int. J. Plast. 2016, 82, 97–111. [Google Scholar] [CrossRef]
- Selyutina, N.; Petrov, Y. Comparative Analysis of Dynamic Plasticity Models. Rev. Adv. Mater. Sci. 2018, 57, 199–211. [Google Scholar] [CrossRef]
- Selyutina, N.S.; Petrov, Y.V. Instabilities of Dynamic Strain Diagrams Predicted by the Relaxation Model of Plasticity. J. Dyn. Behav. Mater. 2022, 8, 304–315. [Google Scholar] [CrossRef]
- Petrov, Y.; Karihaloo, B.; Bratov, V.; Bragov, A. Multi-scale dynamic fracture model for quasi-brittle materials. Int. J. Eng. Sci. 2012, 61, 3–9. [Google Scholar] [CrossRef]
- Petrov, Y.V.; Gruzdkov, A.; Bratov, V. Structural-temporal theory of fracture as a multiscale process. Phys. Mesomech. 2012, 15, 232–237. [Google Scholar] [CrossRef]
- Gruzdkov, A.A.; Petrov, Y.V. On temperature time correspondence in high-rate deformation of metals. Dokl. Phys. 1999, 44, 114–116. [Google Scholar]
- Meyers, M.A.; Chawla, K.K. Mechanical Behavior of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009; 882p. [Google Scholar]
- Kalpakjian, S.; Schmid, S. Manufacturing Processes for Engineering Materials, 5th ed.; Pearson Education: London, UK, 2007; 1040p. [Google Scholar]
- Cadoni, E.; D’Aiuto, F.; Albertini, C. Dynamic behavior of advanced high strength steel used in the automobile structures. DYMAT 2009, 1, 135–141. [Google Scholar]
- Li, J.; Li, Y.; Huang, C.; Suo, T. Mechanical responses and dynamic failure of nanostructure Cu–Al alloys under uniaxial compression. Mech. Mater. 2017, 114, 147–160. [Google Scholar] [CrossRef]
- Borodin, E.; Mayer, A.; Gutkin, M. Coupled model for grain rotation, dislocation plasticity and grain boundary sliding in fine-grained solids. Int. J. Plast. 2020, 134, 102776. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E. Influence of local stresses on motion of edge dislocation in aluminum. Int. J. Plast. 2018, 101, 170–187. [Google Scholar] [CrossRef]
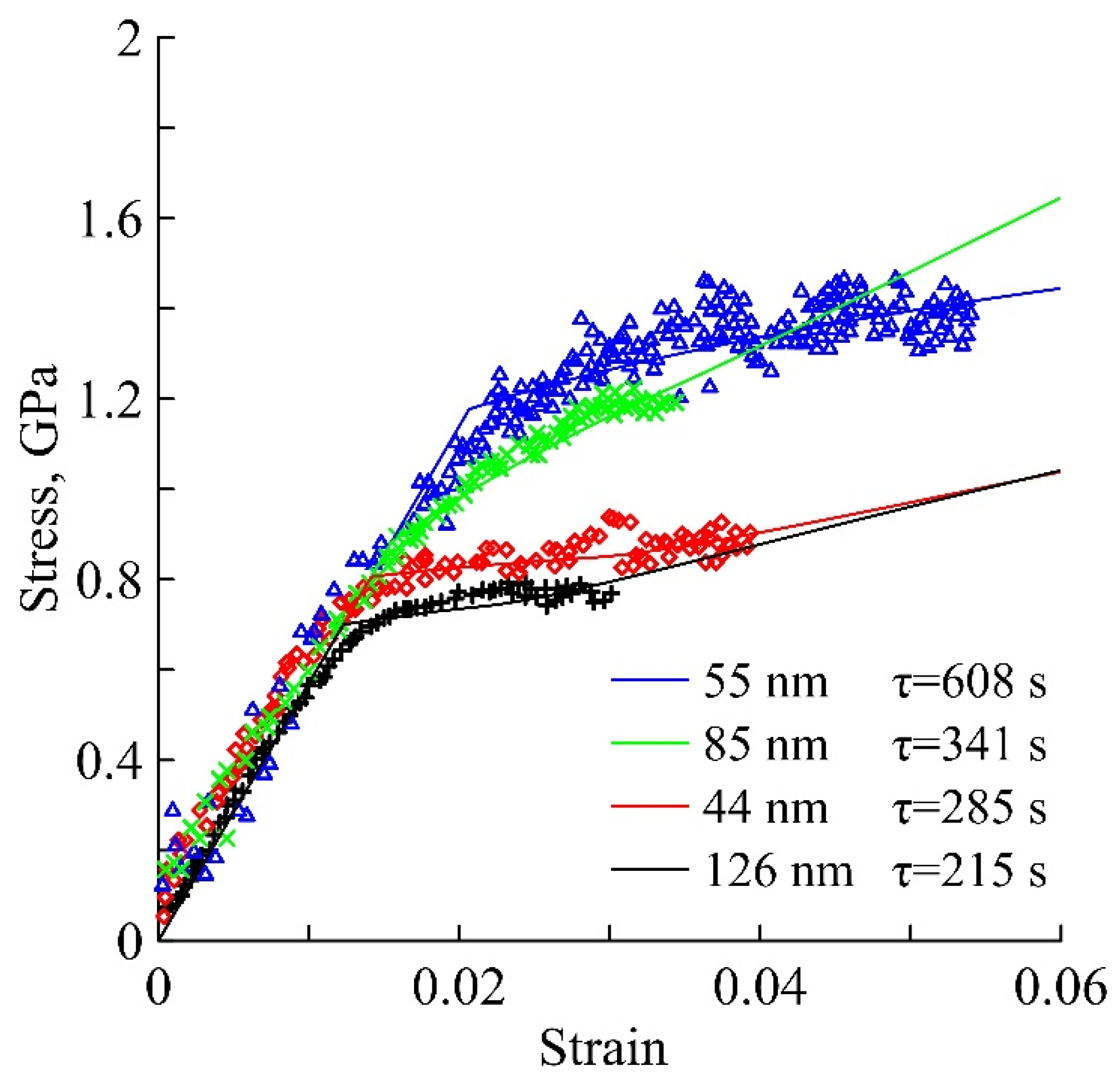
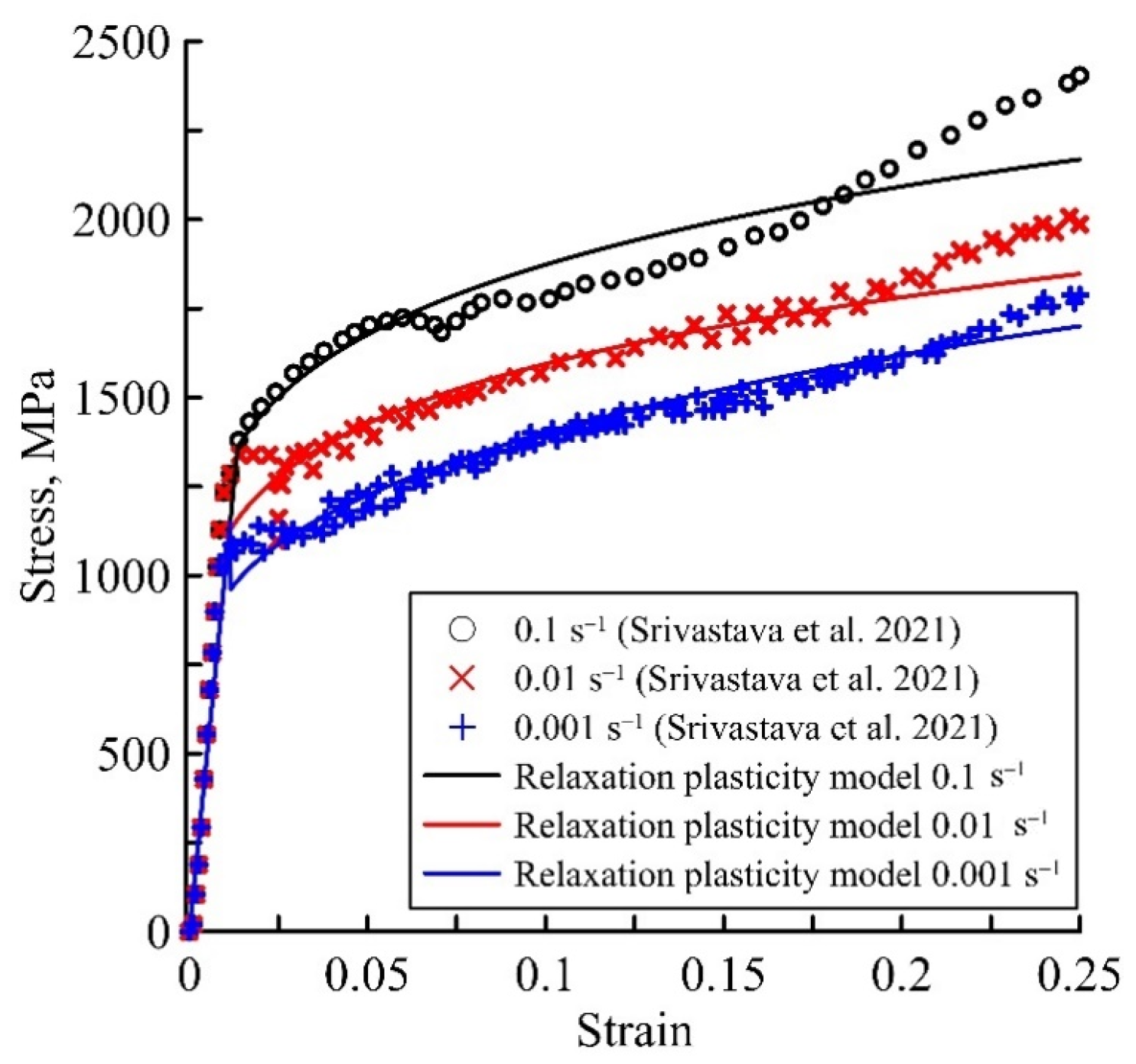
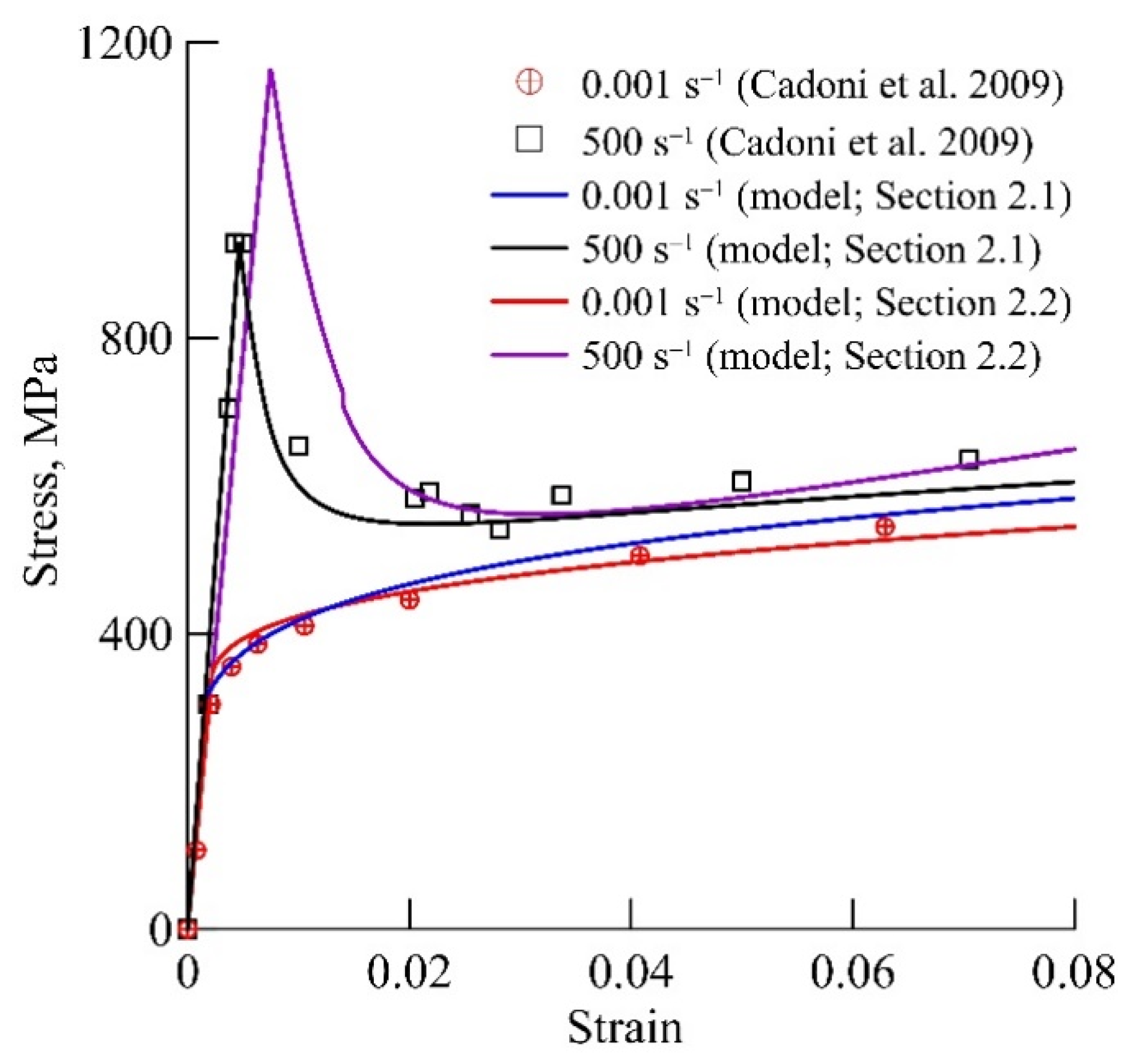
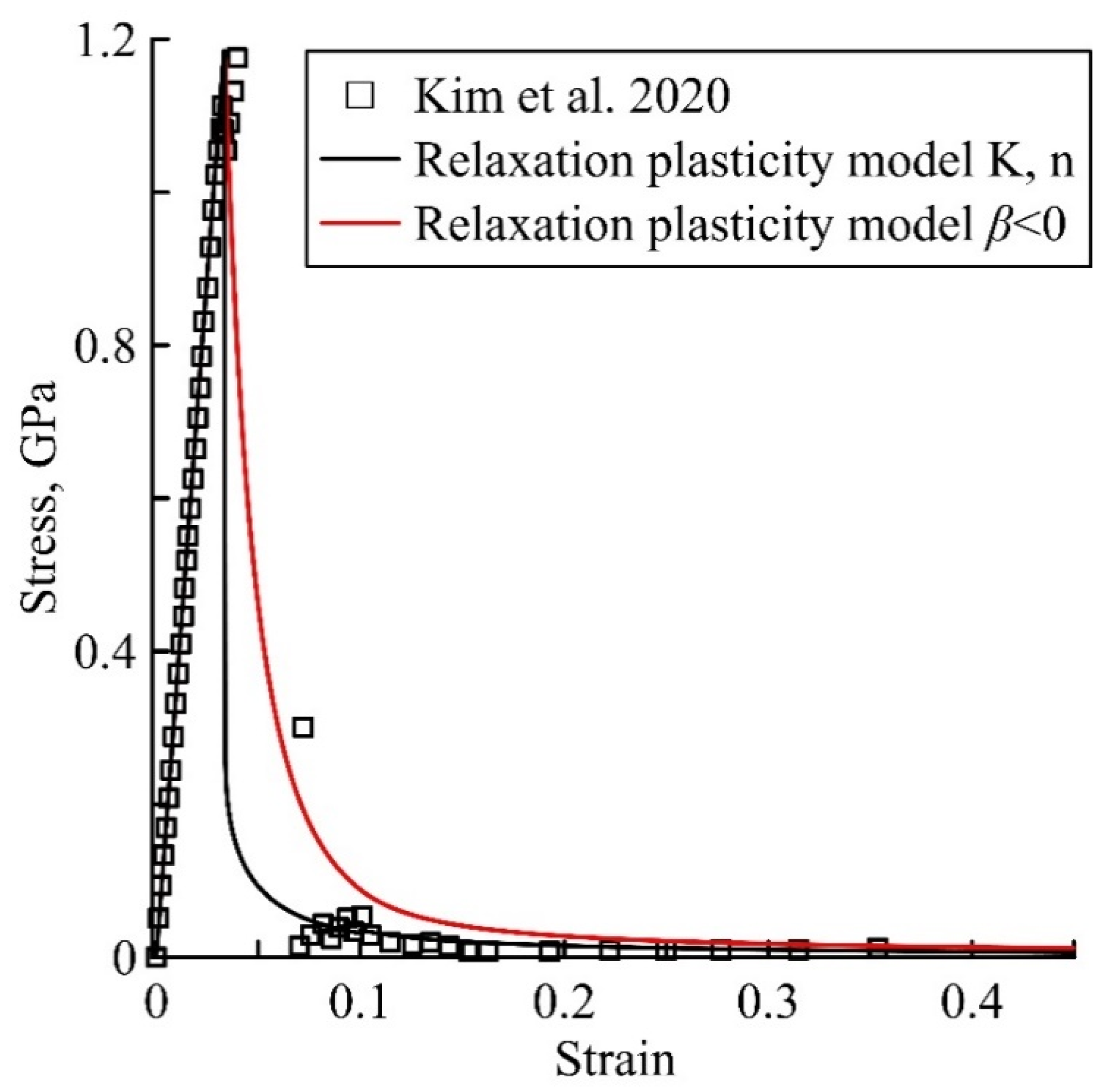
| Grain Size, nm | α | τ, s | β |
|---|---|---|---|
| 44 | 1 | 285 | 0.54 |
| 55 | 1 | 608 | 0.6 |
| 85 | 1 | 341 | 0.71 |
| 126 | 1 | 215 | 0.55 |
| Au | Au-Ag | W | |
|---|---|---|---|
| Experimental data | [28] | [24] | [25] |
| Structure type | Nanowhiskers | Nanowires | Nanopillars |
| Strain rates, s−1 | 10−4 | 0.5 × 10−3 | 10−3–10−1 |
| Type of curve | Monotonic | Nonmonotonic | Monotonic |
| Hardening type | Hardening | Softening | Hardening |
| Sample size, nm | 55 | 319 | 2000 |
| τ, s | 608 | 20 | 8 |
| β | 0.6 | −0.7 | 0.27 |
| Ta | Cu-Al | Ni | Fe | |
|---|---|---|---|---|
| Experimental data | [23] | [38] | [26] | [27] |
| Strain rates, s−1 | 10−3–104 | 10−2–104 | 10−3–104 | 10−3–104 |
| Type of curve 10−3–10−1 s−1 | Hardening | Hardening | Perfect plasticity | Perfect plasticity |
| Type of curve 103–104 s−1 | Softening | Softening | Softening | Softening |
| Sample size | d < 10 μm | 3 × 3 × 3 mm3 | d = 5 mm; l = 2.7 mm | d < 1 mm |
| Grain size, nm | 43.8 | 93 | 17 | 100–500 |
| Calculation | this paper | this paper | [29] | [31] |
| τ, μs | 4.8 | 500 | 3.3 | 190 |
| β | 0.26 | 0.04 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selyutina, N.; Borodin, E.; Petrov, Y. Dynamical Models of Plasticity with Nonmonotonic Deformation Curves for Nanomaterials. Metals 2022, 12, 1835. https://doi.org/10.3390/met12111835
Selyutina N, Borodin E, Petrov Y. Dynamical Models of Plasticity with Nonmonotonic Deformation Curves for Nanomaterials. Metals. 2022; 12(11):1835. https://doi.org/10.3390/met12111835
Chicago/Turabian StyleSelyutina, Nina, Elijah Borodin, and Yuri Petrov. 2022. "Dynamical Models of Plasticity with Nonmonotonic Deformation Curves for Nanomaterials" Metals 12, no. 11: 1835. https://doi.org/10.3390/met12111835
APA StyleSelyutina, N., Borodin, E., & Petrov, Y. (2022). Dynamical Models of Plasticity with Nonmonotonic Deformation Curves for Nanomaterials. Metals, 12(11), 1835. https://doi.org/10.3390/met12111835






