Isogeometric Analysis-Based Solidification Simulation and an Improved Way to Apply Supercooling on Droplet Boundary
Abstract
:1. Introduction
2. Mathematical Model
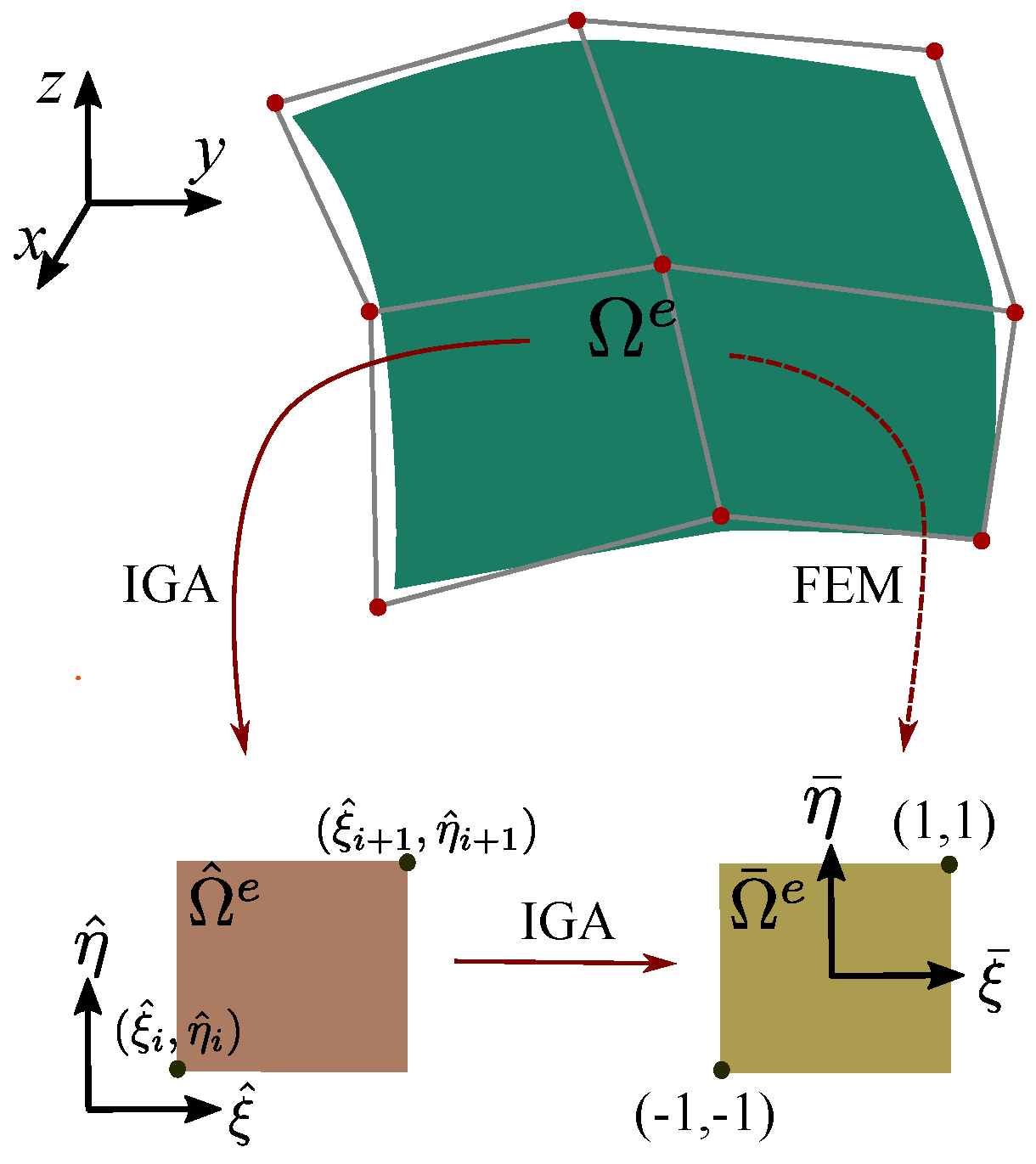
3. NURBS Shape Functions in Isogeometric Analysis
3.1. B-Splines
- •
- is a polynomial over ;
- •
- is non-negativity ;
- •
- Each p order function has continuous derivatives across the element boundary when the knot multiplicity is one for all inner knots. The first derivative of a B-spline basis function can be easily calculated from the Cox-de Boor recursion formula
- •
- If k is the multiplicity of the ith knot, is continuous.
3.2. NURBS Shape Function
3.3. Numerical Integration in IGA
4. Computational Method
4.1. Spatial Discretization
4.2. Time Discretization
5. Numerical Results
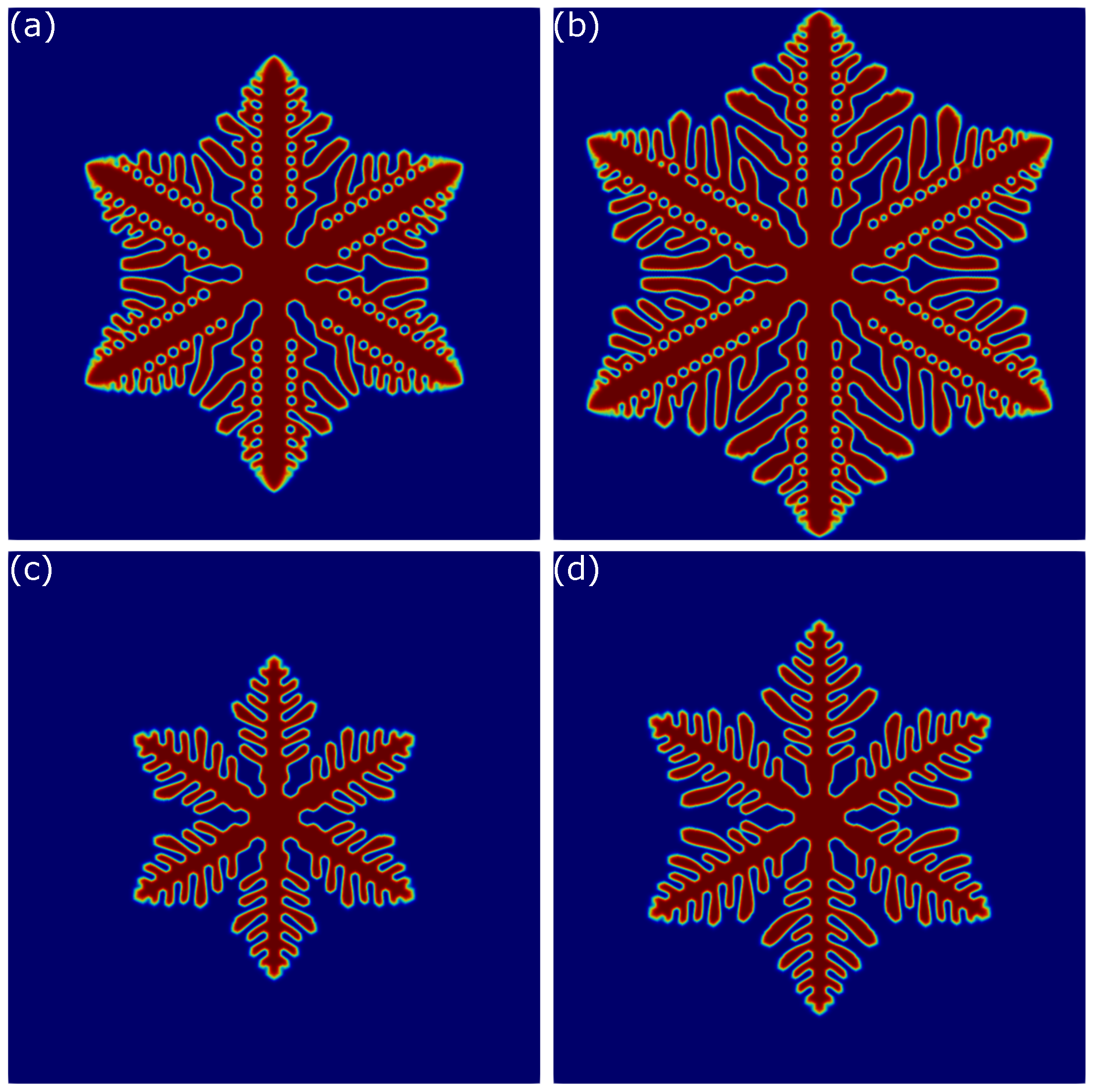
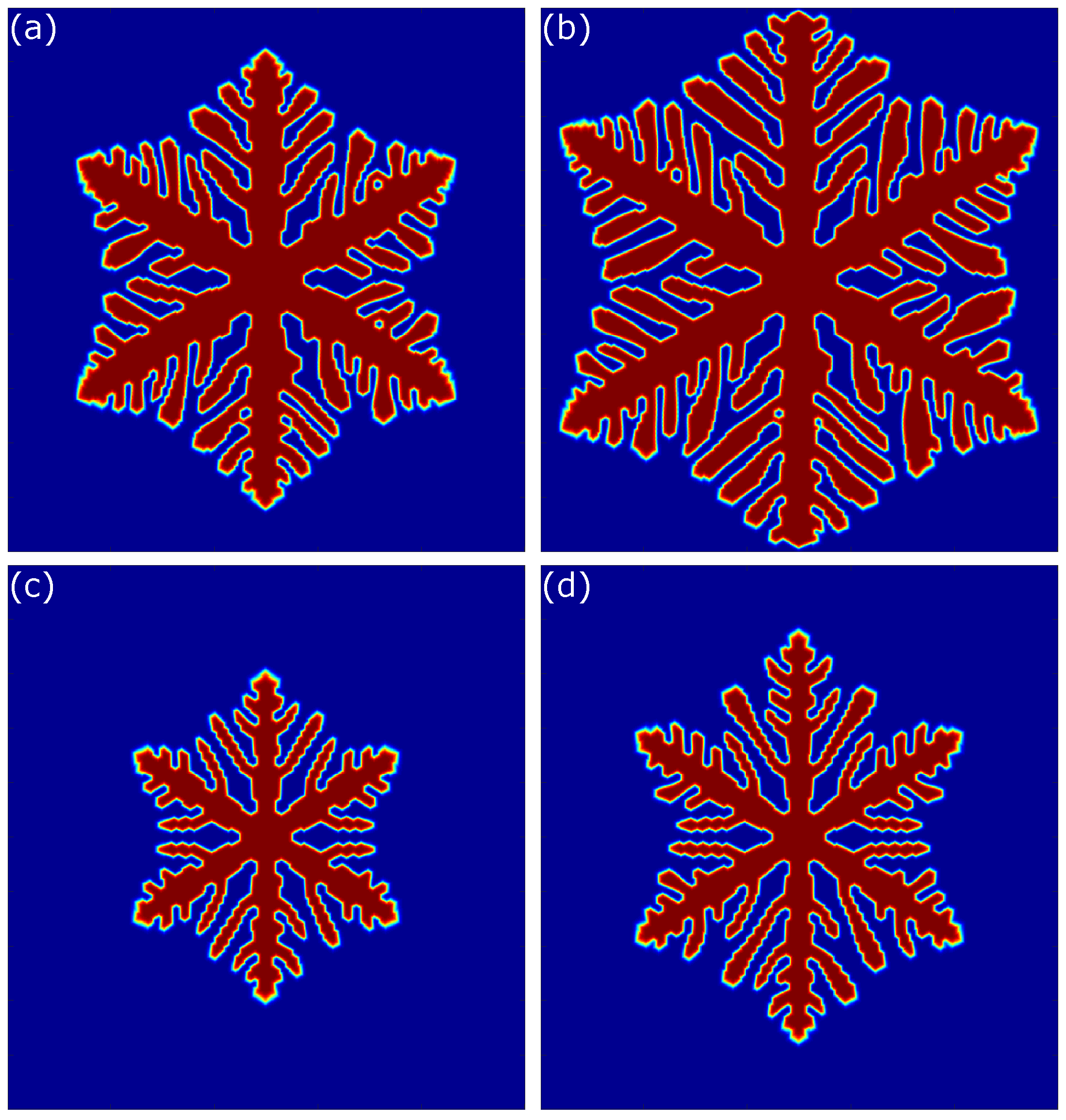
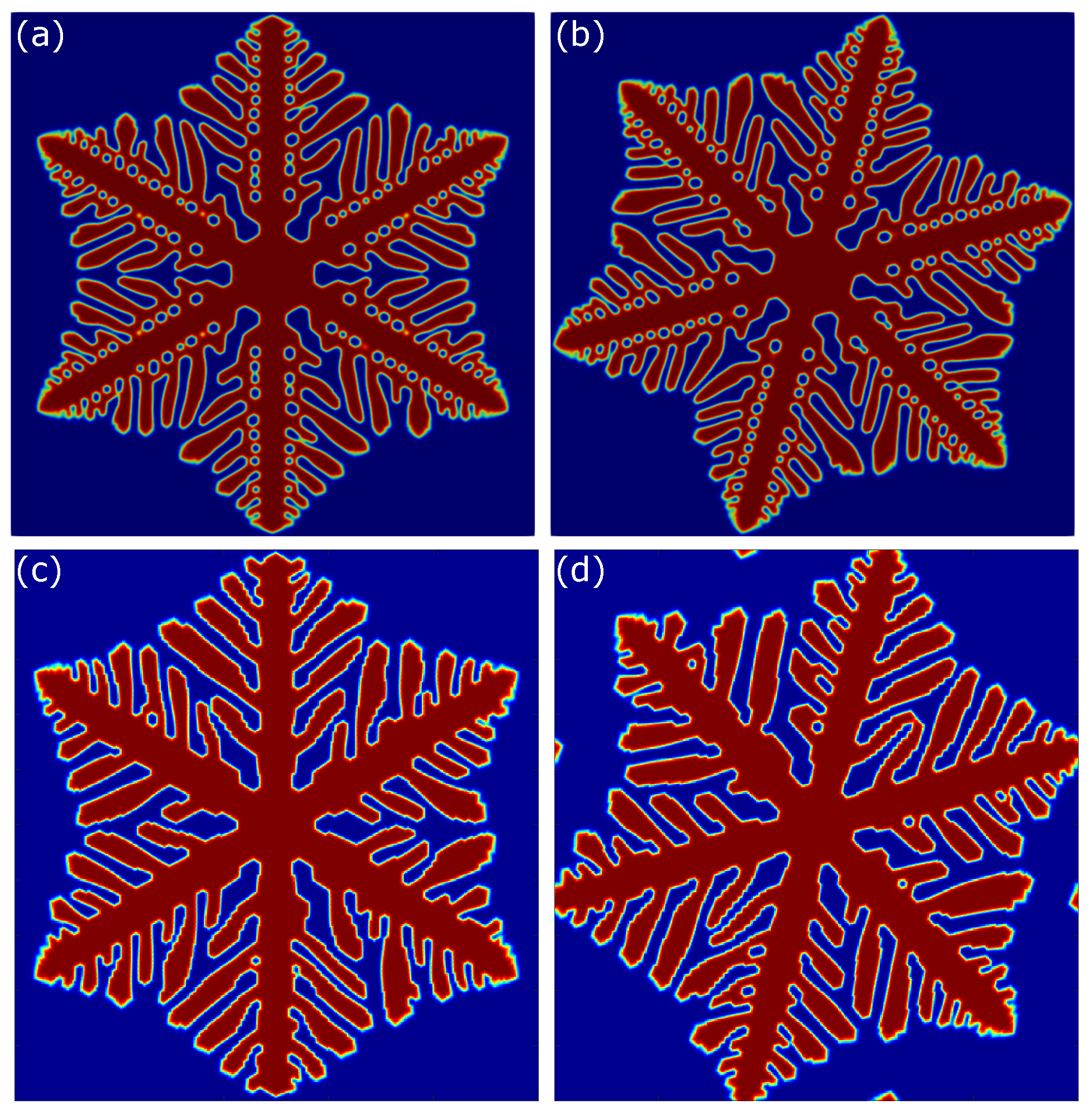
5.1. Dendritic Formation in Square Domain
5.1.1. Effect of Latent Heat
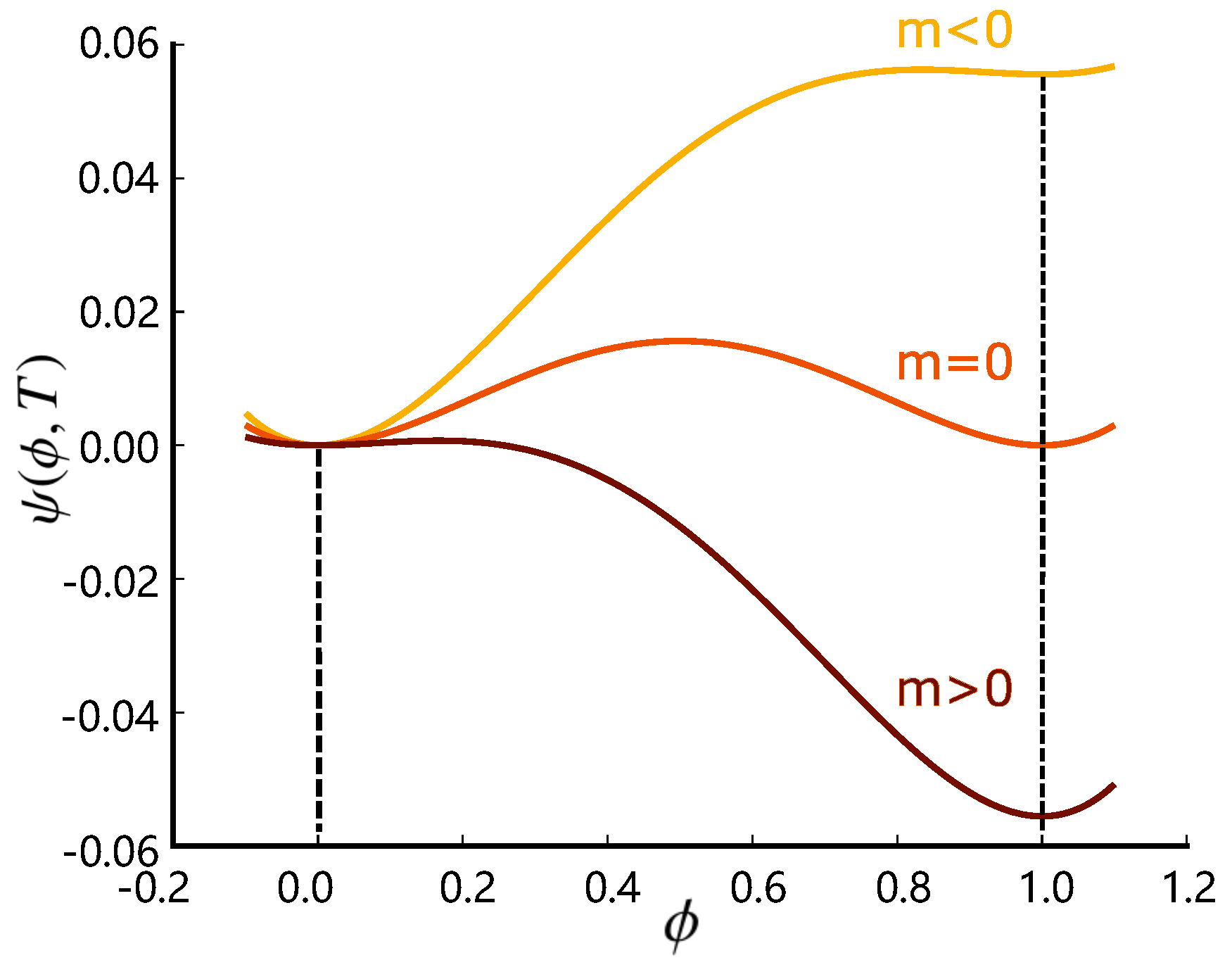
5.1.2. Effect of Anisotropy Mode
5.1.3. Effect of Initial Angle
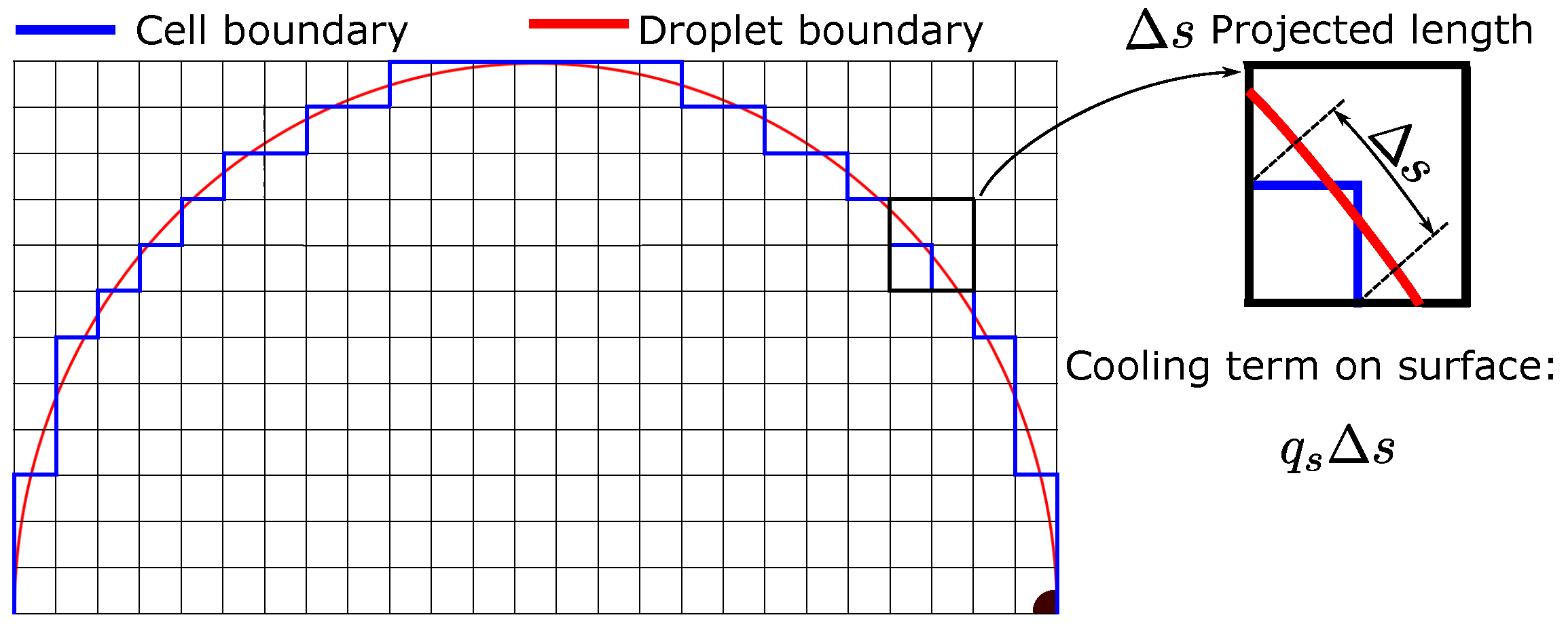
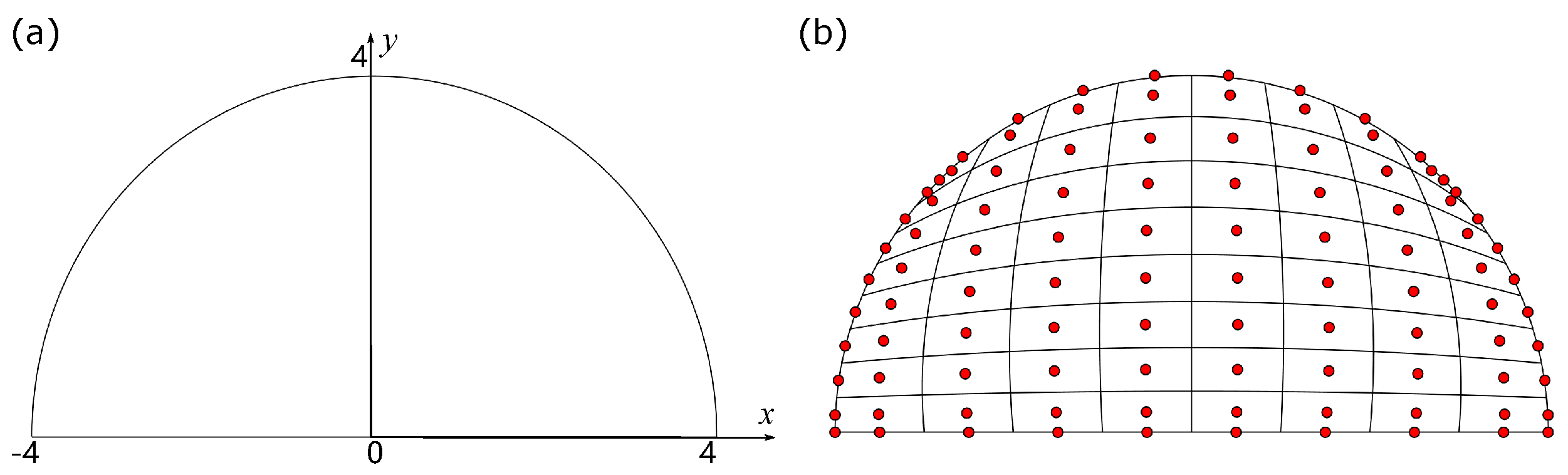
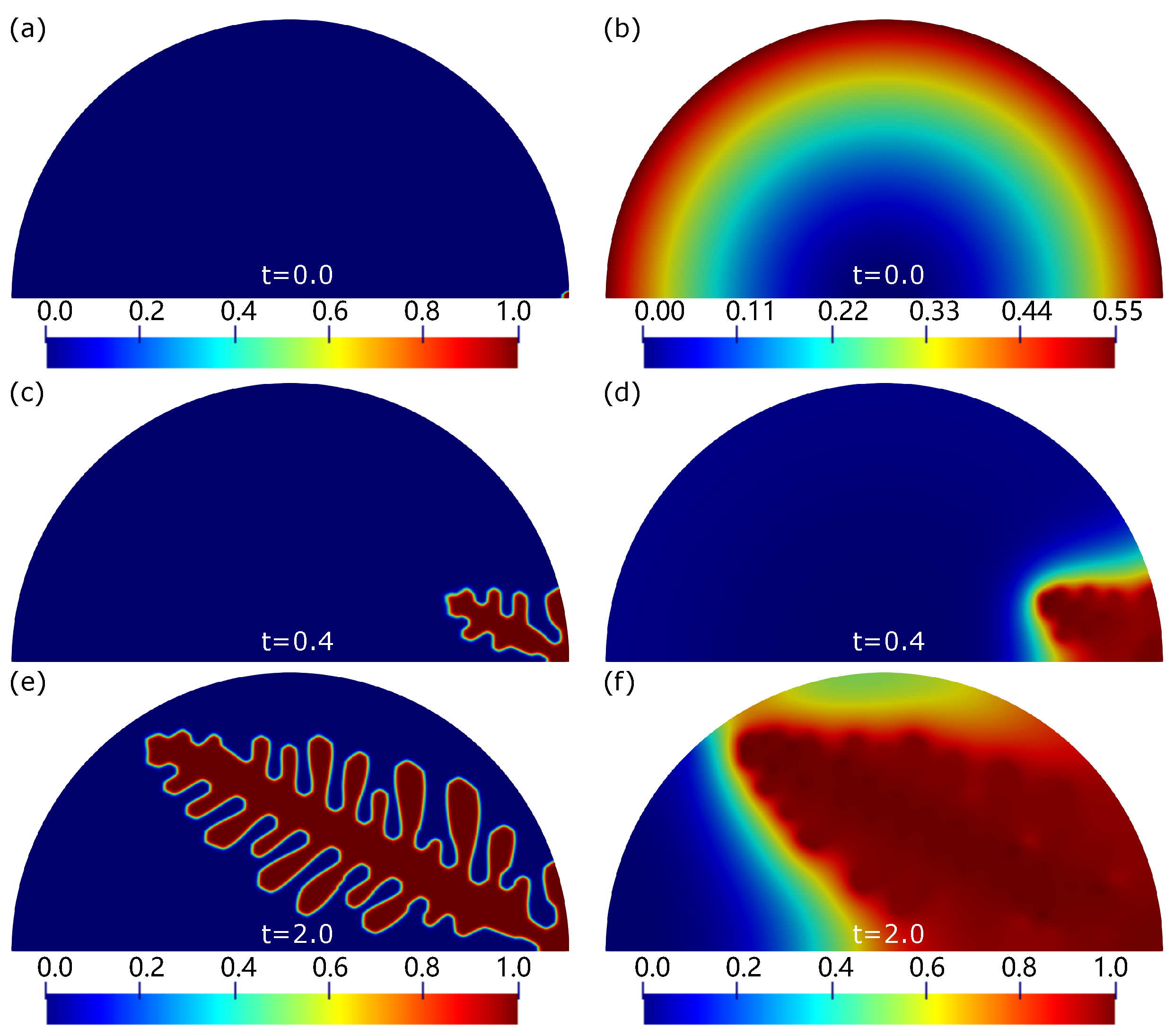
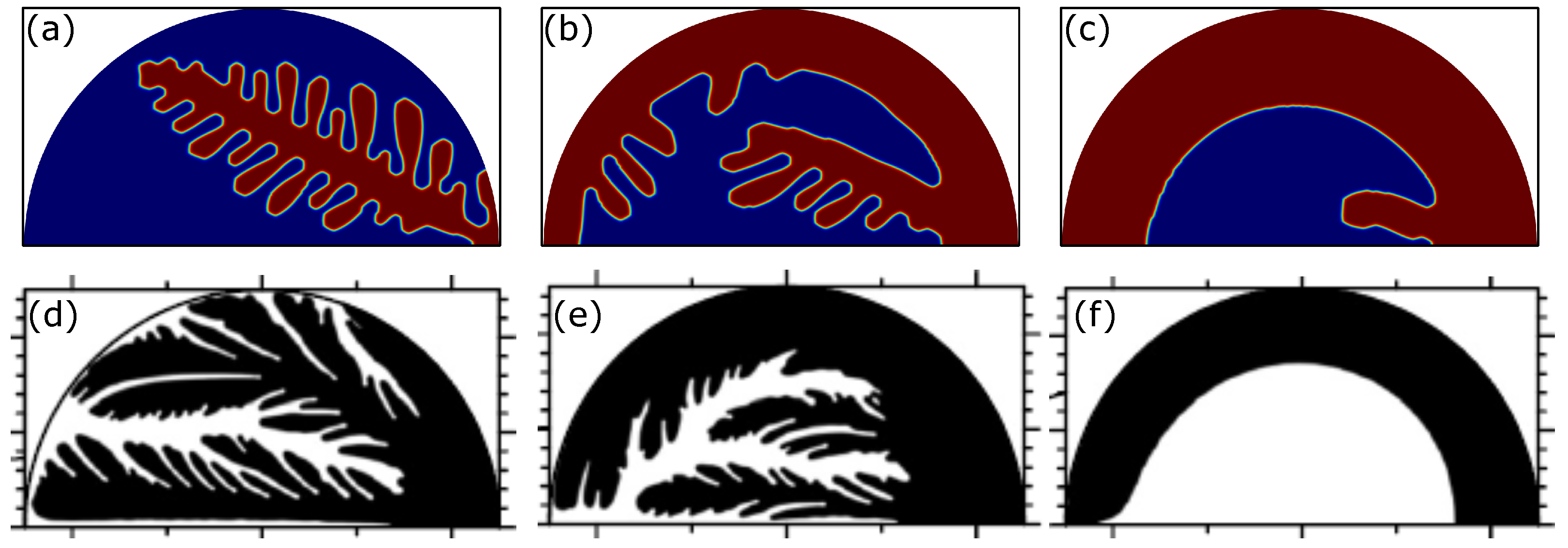
5.2. Dendrite Growth under Different Cooling Rates on Droplet Surface
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Formula Derivation
Appendix B. Movie Description
References
- Zhou, J.; Qi, L. Numerical simulation of liquid-solid extrusion process based on the mechanical model coupled with solidification. Adv. Mech. Eng. 2013, 5, 932348. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.F.; de Castro, J.A.; Ferreira, I.L. 2D phase-field simulation of the directional solidification process. Appl. Mech. Mater. 2015, 704, 17–21. [Google Scholar] [CrossRef]
- Amar, M.B.; Pomeau, Y. Theory of dendritic growth in a weakly undercooled melt. Europhys. Lett. 1986, 2, 307. [Google Scholar] [CrossRef]
- Rappaz, M.; Gandin, C.-A. Probabilistic modelling of microstructure formation in solidification processes. Acta Metall. Mater. 1993, 41, 345–360. [Google Scholar] [CrossRef]
- Miura, H.; Yokoyama, E.; Nagashima, K.; Tsukamoto, K.; Srivastava, A. Phase-field simulation for crystallization of a highly supercooled forsterite-chondrule melt droplet. J. Appl. Phys. 2010, 108, 114912. [Google Scholar] [CrossRef]
- Chen, L.Q. Phase-field models for microstructure evolution. Annu. Rev. Mater. Res. 2002, 32, 113–140. [Google Scholar] [CrossRef] [Green Version]
- Militzer, M. Phase field modeling of microstructure evolution in steels. Curr. Opin. Solid State Mater. Sci. 2011, 15, 106–115. [Google Scholar] [CrossRef]
- Elder, K.R.; Provatas, N.; Berry, J.; Stefanovic, P.; Grant, M. Phase-field crystal modeling and classical density functional theory of freezing. Phys. Rev. B 2007, 75, 064107. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Chen, J.; Lebensohn, R.A.; Ji, Y.Z.; Heo, T.W.; Bhattacharyya, S.; Chang, K.; Mathaudhu, S.; Liu, Z.K.; Chen, L.-Q. An integrated fast fourier transform-based phase-field and crystal plasticity approach to model recrystallization of three dimensional polycrystals. Comput. Meth. Appl. Mech. Eng. 2015, 285, 829–848. [Google Scholar] [CrossRef]
- Jeong, J.-H.; Goldenfeld, N.; Dantzig, J.A. Phase field model for three-dimensional dendritic growth with fluid flow. Phys. Rev. E 2001, 64, 041602. [Google Scholar] [CrossRef] [PubMed]
- Karma, A.; Kessler, D.A.; Levine, H. Phase-field model of mode III dynamic fracture. Phys. Rev. Lett. 2001, 87, 045501. [Google Scholar] [CrossRef] [Green Version]
- Borden, M.J.; Hughes, T.J.R.; Landis, C.M.; Verhoosel, C.V. A higher-order phase-field model for brittle fracture: Formulation and analysis within the isogeometric analysis framework. Comput. Meth. Appl. Mech. Eng. 2014, 273, 100–118. [Google Scholar] [CrossRef]
- Zheng, X.; Babaee, H.; Dong, S.; Chryssostomidis, C.; Karniadakis, G. A phase-field method for 3D simulation of two-phase heat transfer. Int. J. Heat Mass Transf. 2015, 82, 282–298. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Kang, J.; Guo, Z.; Han, Q. Effect of the forced flow on the permeability of dendritic networks: A study using phase-field-lattice Boltzmann method. Int. J. Heat Mass Transf. 2019, 131, 196–205. [Google Scholar] [CrossRef]
- Sedaghatkish, A.; Sadeghiseraji, J.; Jamalabadi, M.Y.A. Numerical simulation of magnetic nanofluid (MNF) film boiling on cylindrical heated magnet using phase field method. Int. J. Heat Mass Transf. 2020, 152, 119546. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, Z.; Xu, J.; Ren, Y.; Zhu, Z.; Xu, K.; Wang, Z.; Wang, C. A numerical study of picosecond laser micro-grooving of single crystalline germanium: Mechanism discussion and process simulation. J. Manuf. Process. 2021, 69, 351–367. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, C.; Mao, S.; Zhang, Z.; Zhao, D.; Xu, K.; Liu, Y.; Li, L.; Zhou, J. Localized and effcient machining of germanium based on the auto-coupling between picosecond laser irradiation and electrochemical dissolution: Mechanism validation and surface characterization. J. Manuf. Process. 2022, 77, 665–677. [Google Scholar] [CrossRef]
- Bueno, J.; Bona-Casas, C.; Bazilevs, Y.; Gomez, H. Interaction of complex fluids and solids: Theory, algorithms and application to phase-change-driven implosion. Comput. Mech. 2015, 55, 1105–1118. [Google Scholar] [CrossRef]
- Mokbel, D.; Abels, H.; Aland, S. A phase-field model for fluid–structure interaction. J. Comput. Phys. 2018, 372, 823–840. [Google Scholar] [CrossRef] [Green Version]
- Frieboes, H.B.; Jin, F.; Chuang, Y.-L.; Wise, S.M.; Lowengrub, J.S.; Cristini, V. Three-dimensional multispecies nonlinear tumor growth-II: Tumor invasion and angiogenesis. J. Theor. Biol. 2010, 264, 1254–1278. [Google Scholar] [CrossRef]
- Oden, J.T.; Hawkins-Daarud, A.J.; Prudhomme, S. General diffuse-interface theories and an approach to predictive tumor growth modeling. Math. Models Methods Appl. Sci. 2010, 20, 477–517. [Google Scholar] [CrossRef] [Green Version]
- Oden, J.T.; Prudencio, E.E.; Hawkins-Daarud, A.J. Selection and assessment of phenomenological models of tumor growth. Math. Models Methods Appl. Sci. 2013, 23, 1309–1338. [Google Scholar] [CrossRef]
- Moure, A.; Gomez, H. Computational model for amoeboid motion: Coupling membrane and cytosol dynamics. Phys. Rev. E 2016, 94, 042423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, J.; Vilanova, G.; Gomez, H. A mathematical model coupling tumor growth and angiogenesis. PLoS ONE 2016, 53, 449–464. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Vilanova, G.; Gomez, H. Full-scale, three-dimensional simulation of early-stage tumor growth: The onset of malignancy. Comput. Meth. Appl. Mech. Eng. 2016, 314, 126–146. [Google Scholar] [CrossRef]
- Xue, S.L.; Li, B.; Feng, X.Q.; Gao, H.J. A non-equilibrium thermodynamic model for tumor extracellular matrix with enzymatic degradation. J. Mech. Phys. Solids 2017, 104, 32–56. [Google Scholar] [CrossRef]
- Feng, X.Q. Advances in tumor biomechanics. J. Med. Biomech. 2019, 34, 115–120. [Google Scholar]
- Xu, J.; Vilanova, G.; Gomez, H. Phase-field model of vascular tumor growth: Three-dimensional geometry of the vascular network and integration with imaging data. Comput. Meth. Appl. Mech. Eng. 2020, 359, 112648. [Google Scholar] [CrossRef]
- Pismen, L.M. Patterns and Interfaces in Dissipative Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Steinbach, I. Phase-field models in materials science. Model. Simul. Mater. Sci. Eng. 2009, 17, 073001. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. An introduction to phase-field modeling of microstructure evolution. Calphad 2008, 32, 268–294. [Google Scholar] [CrossRef]
- Kobayashi, R.; Warren, J.A.; Carter, W.C. Vector-valued phase field model for crystallization and grain boundary formation. Phys. D Nonlinear Phenom. 1998, 119, 415–423. [Google Scholar] [CrossRef]
- Warren, J.A.; Boettinger, W.J. Prediction of dendritic growth and microsegregation patterns in a binary alloy using the phase-field method. Acta Metall. Mater. 1995, 43, 689–703. [Google Scholar] [CrossRef]
- Trivedi, R.; Kurz, W. Dendritic growth. Int. Mater. Rev. 1994, 39, 49–74. [Google Scholar] [CrossRef]
- Hughes, T.J.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Meth. Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef] [Green Version]
- Shojaee, S.; Ghelichi, M.; Izadpanah, E. Combination of isogeometric analysis and extended finite element in linear crack analysis. Struct. Eng. Mech. 2013, 48, 125–150. [Google Scholar] [CrossRef]
- Singh, S.; Singh, I.V.; Bhardwaj, G.; Mishra, B. A Bézier extraction based XIGA approach for three-dimensional crack simulations. Adv. Eng. Softw. 2018, 125, 55–93. [Google Scholar] [CrossRef]
- Chen, L.; Lingen, E.J.; de Borst, R. Adaptive hierarchical refinement of NURBS in cohesive fracture analysis. Int. J. Numer. Methods Eng. 2017, 112, 2151–2173. [Google Scholar] [CrossRef] [Green Version]
- Luu, A.-T.; Kim, N.-I.; Lee, J. NURBS-based isogeometric vibration analysis of generally laminated deep curved beams with variable curvature. Compos. Struct. 2015, 119, 150–165. [Google Scholar] [CrossRef]
- Valizadeh, N.; Natarajan, S.; Gonzalez-Estrada, O.A.; Rabczuk, T.; Bui, T.Q.; Bordas, S.P. NURBS-based finite element analysis of functionally graded plates: Static bending, vibration, buckling and flutter. Compos. Struct. 2013, 99, 309–326. [Google Scholar] [CrossRef] [Green Version]
- Faroughi, S.; Shafei, E.; Rabczuk, T. Multi-patch NURBS formulation for anisotropic variable angle tow composite plates. Compos. Struct. 2020, 241, 11196. [Google Scholar]
- Xu, G.; Mourrain, B.; Duvigneau, R.; Galligo, A. A new error assessment method in isogeometric analysis of 2D heat conduction problems. Adv. Sci. Lett. 2012, 10, 508–512. [Google Scholar] [CrossRef] [Green Version]
- Gómez, H.; Calo, V.M.; Bazilevs, Y.; Hughes, T.J.R. Isogeometric analysis of the Cahn–Hilliard phase-field model. Comput. Meth. Appl. Mech. Eng. 2008, 197, 4333–4352. [Google Scholar] [CrossRef]
- Gomez, H.; Hughes, T.J.R.; Nogueira, X.; Calo, V.M. Isogeometric analysis of the isothermal Navier–Stokes–Korteweg equations. Comput. Meth. Appl. Mech. Eng. 2010, 199, 1828–1840. [Google Scholar] [CrossRef]
- Nagy, A.P.; Abdalla, M.M.; Gürdal, Z. Isogeometric sizing and shape optimisation of beam structures. Comput. Meth. Appl. Mech. Eng. 2010, 199, 1216–1230. [Google Scholar] [CrossRef]
- Manh, N.D.; Evgrafov, A.; Gersborg, A.R.; Gravesen, J. Isogeometric shape optimization of vibrating membranes. Comput. Meth. Appl. Mech. Eng. 2011, 200, 1343–1353. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.; Mourrain, B.; Duvigneau, R.; Galligo, A. Parameterization of computational domain in isogeometric analysis: Methods and comparison. Comput. Meth. Appl. Mech. Eng. 2011, 200, 2021–2031. [Google Scholar] [CrossRef] [Green Version]
- Ashour, M.; Valizadeh, N.; Rabczuk, T. Isogeometric analysis for a phase-field constrained optimization problem of morphological evolution of vesicles in electrical fields. Comput. Meth. Appl. Mech. Eng. 2021, 377, 113669. [Google Scholar] [CrossRef]
- Dhote, R.P.; Gomez, H.; Melnik, R.N.V.; Zu, J. Isogeometric analysis of a dynamic thermo-mechanical phase-field model applied to shape memory alloys. Comput. Mech. 2014, 53, 1235–1250. [Google Scholar] [CrossRef]
- Gomez, H.; Bures, M.; Moure, A. A review on computational modelling of phase-transition problems. Philos. Trans. R. Soc. A 2019, 377, 20180203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Valizadeh, N.; Rabczuk, T. Isogeometric analysis for phase-field models of geometric PDEs and high-order PDEs on stationary and evolving surfaces. Comput. Meth. Appl. Mech. Eng. 2019, 351, 599–642. [Google Scholar] [CrossRef]
- Tsukamoto, K.; Kobatake, H.; Nagashima, K.; Satoh, H.; Yurimoto, H. Crystallization of cosmic materials in microgravity. Lunar Planet. Sci. 2001, 32, 1846. [Google Scholar]
- Kobayashi, R. A brief introduction to phase field method. AIP Conf. Proc. 2010, 1270, 282–291. [Google Scholar]
- Takaki, T. Phase-field modeling and simulations of dendrite growth. ISIJ Int. 2014, 54, 437–444. [Google Scholar] [CrossRef] [Green Version]
- Koric, S.; Thomas, B.G.; Voller, V.R. Enhanced latent heat method to incorporate superheat effects into fixed-grid multiphysics simulations. Numer. Heat Transf. Part B 2010, 57, 396–413. [Google Scholar] [CrossRef]
- de Boor, C. Package for Calculating with B-Splines. SIAM J. Numer. Anal. 1977, 14, 441–472. [Google Scholar] [CrossRef]
- Jansen, K.E.; Whiting, C.H.; Hulbert, G.M. A generalized-method for integrating the filtered Navier-Stokes equations with a stabilized finite element method. Comput. Meth. Appl. Mech. Eng. 2000, 190, 305–319. [Google Scholar] [CrossRef]
- Tiaden, J.; Nestler, B.; Diepers, H.-J.; Steinbach, I. The multiphase-field model with an integrated concept for modelling solute diffusion. Phys. D Nonlinear Phenom. 1998, 115, 73–86. [Google Scholar] [CrossRef]
- Permann, C.J.; Gaston, D.R.; Andrš, D.; Carlsen, R.W.; Kong, F.; Lindsay, A.D.; Miller, J.M.; Peterson, J.W.; Slaughter, A.E.; Stogner, R.H.; et al. MOOSE: Enabling massively parallel multiphysics simulation. SoftwareX 2020, 11, 100430. [Google Scholar] [CrossRef]
- Sanal, R. Numerical simulation of dendritic crystal growth using phase field method and investigating the effects of different physical parameter on the growth of the dendrite. arXiv 2014, 1412, 3197. [Google Scholar]
- Nguyen, V.P.; Anitescu, C.; Bordas, S.P.; Rabczuk, T. Isogeometric analysis: An overview and computer implementation aspects. Math. Comput. Simulat. 2015, 117, 89–116. [Google Scholar] [CrossRef]




| Parameters | Symbols | In Silico Values |
|---|---|---|
| Relaxation time | 0.0003 | |
| Phase width | 0.01 | |
| Anisotropy strength | 0.04 | |
| Anisotropy mode | j | 6 |
| Initial angle | ||
| Melting temperature | 1 | |
| Latent heat | K | 1.6 |
| Constant in Equation (3) | 0.9 | |
| Constant in Equation (3) | 10 |
| Method | Mesh | Processor Number | CPU Time |
|---|---|---|---|
| The proposed method | 4 | 8.2 | |
| 16 | 2.7 | ||
| 64 | 0.9 | ||
| 4 | 37 | ||
| 16 | 12 | ||
| 64 | 4.2 | ||
| 4 | 160 | ||
| 16 | 54 | ||
| 64 | 19 | ||
| FEM | 4 | 9.1 | |
| 16 | 2.9 | ||
| 64 | 1.1 | ||
| 4 | 44 | ||
| 16 | 15 | ||
| 64 | 4.8 | ||
| 4 | 173 | ||
| 16 | 62 | ||
| 64 | 23 | ||
| FDM | 1 | 52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Yan, T.; Li, Y.; Yu, Z.; Wang, Y.; Wang, Y. Isogeometric Analysis-Based Solidification Simulation and an Improved Way to Apply Supercooling on Droplet Boundary. Metals 2022, 12, 1836. https://doi.org/10.3390/met12111836
Xu J, Yan T, Li Y, Yu Z, Wang Y, Wang Y. Isogeometric Analysis-Based Solidification Simulation and an Improved Way to Apply Supercooling on Droplet Boundary. Metals. 2022; 12(11):1836. https://doi.org/10.3390/met12111836
Chicago/Turabian StyleXu, Jiangping, Tingyu Yan, Yang Li, Zhenyuan Yu, Yun Wang, and Yuan Wang. 2022. "Isogeometric Analysis-Based Solidification Simulation and an Improved Way to Apply Supercooling on Droplet Boundary" Metals 12, no. 11: 1836. https://doi.org/10.3390/met12111836
APA StyleXu, J., Yan, T., Li, Y., Yu, Z., Wang, Y., & Wang, Y. (2022). Isogeometric Analysis-Based Solidification Simulation and an Improved Way to Apply Supercooling on Droplet Boundary. Metals, 12(11), 1836. https://doi.org/10.3390/met12111836





