A Multi-Phase Modeling Framework Suitable for Dynamic Applications
Abstract
:1. Introduction
2. Methods
2.1. Traditional Model Decomposition
2.2. Multi-Phase Description of Shear Modulus and Flow Stress
2.3. Phase-Specific Shear Modulus and Strength Models
2.4. Phase-Specific Accumulated Effective Plastic Strain
2.4.1. Evolution Method
- The approach here is described in terms of volume fractions with k being the phase index, but the same approach holds for quantities that should be weighted by mass. One just uses the mass fractions instead of the volume fractions.
- We assume that volume fractions are available at the beginning and end of the time step, and . That does not amount to utilizing all of the transformation rates among the various phases. In many cases for polycrystalline metals, only two phases are exchanging mass at a given spatial location such that having the volume fractions provides complete information. The algorithm based on volume (or mass) fractions rather than rates can be simpler to implement.
- Cutoffs and thresholds can be important to numerically robust behavior of the implementation. These are particularly important in an Eulerian or Arbitrary Lagrangian–Eulerian (ALE) hydrocodes [19] given the action of the “advection” (or remap) step on the history variables. The monotonicity enforcement mentioned in the following section is similar to the monotonicity enforcement in the fixed-time mesh remap step in a hydrocode, but here the monotonicity is enforced during the time-evolution step. It can be useful to skip the contribution of phases with a tiny volume fraction, less than say .
2.4.2. Evolution Algorithm
2.4.3. Specific Examples
2.5. Multi-Phase Equation of State (EOS) and Kinetics of Transformation
2.5.1. Multi-Phase EOS with Equilibrium Phase Fractions
2.5.2. Multi-Phase EOS with Finite Rate Kinetics
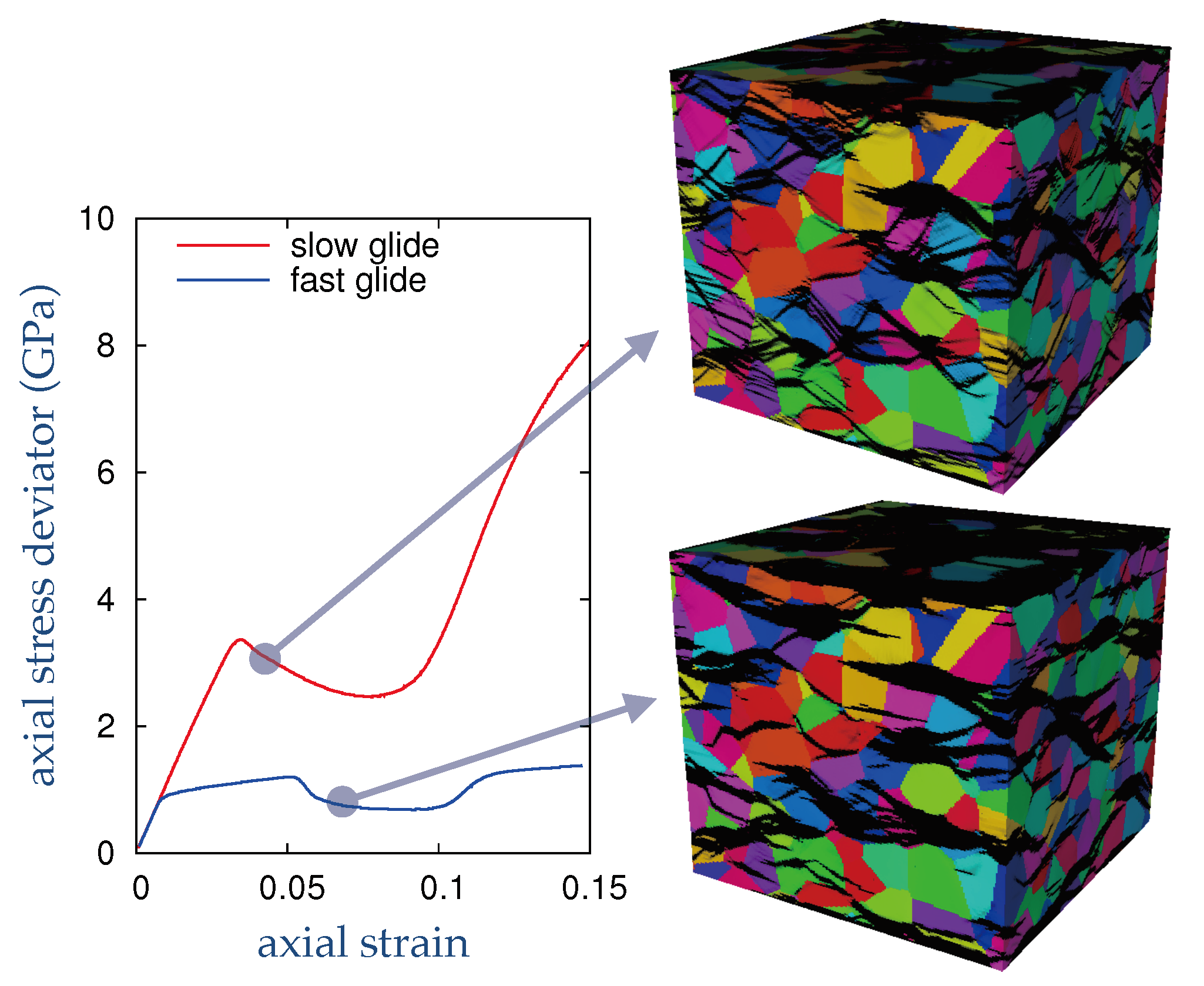
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.0597 | p | 2.82 | |
| 0.0256 | 0.00239 | ||
| 0.000675 | 0.000313 | ||
| 0.186 | 0.0355 | ||
| 0.00000136 | 0.45 | ||
| 0.45 |
References
- Hu, J.; Zhou, X.; Tan, H.; Li, J.; Dai, C. Successive phase transitions of tin under shock compression. Appl. Phys. Lett. 2008, 92, 111905. [Google Scholar] [CrossRef]
- Rigg, P.A.; Greeff, C.W.; Knudson, M.D.; Gray, G.T.; Hixson, R.S. Influence of impurities on the α to ω phase transition in zirconium under dynamic loading conditions. J. Appl. Phys. 2009, 106, 123532. [Google Scholar] [CrossRef]
- Schwager, B.; Ross, M.; Japel, S.; Boehler, R. Melting of Sn at high pressure: Comparisons with Pb. J. Chem. Phys. 2010, 133, 084501. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Bi, Y.; Li, X.; Wang, Y.; Cao, X.; Cai, L.; Wang, Z.; Meng, C. Phase diagram of tin determined by sound velocity measurements on multi-anvil apparatus up to 5 GPa and 800 K. J. Appl. Phys. 2014, 115, 164903. [Google Scholar] [CrossRef]
- Lazicki, A.; Rygg, J.R.; Coppari, F.; Smith, R.; Fratanduono, D.; Kraus, R.G.; Collins, G.W.; Briggs, R.; Braun, D.G.; Swift, D.C.; et al. X-ray Diffraction of Solid Tin to 1.2 TPa. Phys. Rev. Lett. 2015, 115, 075502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Briggs, R.; Torchio, R.; Sollier, A.; Occelli, F.; Videau, L.; Kretzschmar, N.; Wulff, M. Observation of the shock-induced β-Sn to b.c.t.-Sn transition using time-resolved X-ray diffraction. J. Synchrotron Radiat. 2019, 26, 96–101. [Google Scholar] [CrossRef]
- Schill, W.; Austin, R.; Brown, J.; Barton, N. Anelasticity and Phase Transition During Ramp-Release in Tin. J. Dyn. Behav. Mater. 2021, 7, 207–216. [Google Scholar] [CrossRef]
- Husband, R.J.; O’Bannon, E.F.; Liermann, H.P.; Lipp, M.J.; Méndez, A.S.J.; Konôpková, Z.; McBride, E.E.; Evans, W.J.; Jenei, Z. Compression-rate dependence of pressure-induced phase transitions in Bi. Sci. Rep. 2021, 11, 14859. [Google Scholar] [CrossRef]
- Sims, M.; Briggs, R.; Volz, T.J.; Singh, S.; Hamel, S.; Coleman, A.L.; Coppari, F.; Erskine, D.J.; Gorman, M.G.; Sadigh, B.; et al. Experimental and theoretical examination of shock-compressed copper through the fcc to bcc to melt phase transitions. J. Appl. Phys. 2022, 132, 075902. [Google Scholar] [CrossRef]
- Luscher, D.; Barton, N.; Crockett, S.; Wills, A.E.; Greeff, C.; Burakovsky, L.; Sjue, S. Working Draft 1.1: A Proposed Common Model of Multi-phase Strength and Equation of State for a Tri-laboratory Collaboration; Technical Report LLNL-TR-814438/LA-UR-20-26489; Lawrence Livermore National Laboratory/Los Alamos National Laboratory: Los Alamos, NM, USA, 2020. [Google Scholar] [CrossRef]
- Prime, M.B.; Arsenlis, A.; Austin, R.A.; Barton, N.R.; Battaile, C.C.; Brown, J.L.; Burakovsky, L.; Buttler, W.T.; Chen, S.R.; Dattelbaum, D.M.; et al. A Broad Study of Tantalum Strength from Ambient to Extreme Conditions. Acta Mater. 2022, 231, 117875. [Google Scholar] [CrossRef]
- Barton, N.; Benson, D.; Becker, R. Crystal level continuum modelling of phase transformations: The α↔ϵ transformation in iron. Model. Simul. Mater. Sci. Eng. 2005, 13, 707. [Google Scholar] [CrossRef]
- Zhang, W.; Jin, J.M.; Khachaturyan, A.G. Phase field microelasticity modeling of heterogeneous nucleation and growth in martensitic alloys. Acta Mater. 2007, 55, 565–574. [Google Scholar] [CrossRef]
- Denoual, A.V.C. Polymorphism of iron at high pressure: A 3D phase-field model for displacive transitions with finite elastoplastic deformations. J. Mech. Phys. Solids 2016, 92, 1–27. [Google Scholar] [CrossRef]
- Barton, N.R.; Bernier, J.V. A Method for Intragranular Orientation and Lattice Strain Distribution Determination. J. Appl. Crystallogr. 2012, 45, 1145–1155. [Google Scholar] [CrossRef]
- Krygier, A.; Powell, P.D.; McNaney, J.M.; Huntington, C.M.; Prisbrey, S.T.; Remington, B.A.; Rudd, R.E.; Swift, D.C.; Wehrenberg, C.E.; Arsenlis, A.; et al. Extreme Hardening of Pb at High Pressure and Strain Rate. Phys. Rev. Lett. 2019, 123, 205701. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, J.; Schmidt, K.; Rivera, D.; Barton, N.; Florando, J.; Kupresanin, A. A comparison of material flow strength models using Bayesian cross-validation. Comput. Mater. Sci. 2019, 169, 109098. [Google Scholar] [CrossRef]
- Barton, N.; Arsenlis, A.; Rhee, M.; Marian, J.; Bernier, J.V.; Tang, M.; Yang, L. A multi-scale strength model with phase transformation. AIP Conf. Proc. 2012, 1426, 1513–1516. [Google Scholar]
- Benson, D.J. Computational methods in Lagrangian and Eulerian hydrocodes. Comput. Methods Appl. Mech. Eng. 1992, 99, 235–394. [Google Scholar] [CrossRef]
- Luscher, D.J.; Buechler, M.A.; Walters, D.J.; Bolme, C.A.; Ramos, K.J. On computing the evolution of temperature for materials under dynamic loading. Int. J. Plast. 2018, 111, 188–210. [Google Scholar] [CrossRef]
- Preston, D.L.; Tonks, D.L.; Wallace, D.C. Model of plastic deformation for extreme loading conditions. J. Appl. Phys. 2003, 93, 211–220. [Google Scholar] [CrossRef]
- Preston, D.L.; Wallace, D.C. A model of the shear modulus. Solid State Commun. 1992, 81, 277–281. [Google Scholar] [CrossRef]
- Burakovsky, L.; Greeff, C.W.; Preston, D.L. Analytic model of the shear modulus at all temperatures and densities. Phys. Rev. B (Condens. Matter Mater. Phys.) 2003, 67, 094107. [Google Scholar] [CrossRef] [Green Version]
- Cox, G. A Multi-Phase Equation of State and Strength Model for Tin. AIP Conf. Proc. 2006, 845, 208–211. [Google Scholar]
- Rudd, R.E.; Yang, L.H.; Powell, P.D.; Graham, P.; Arsenlis, A.; Cavallo, R.M.; Krygier, A.G.; McNaney, J.M.; Prisbrey, S.T.; Remington, B.A.; et al. Modeling laser-driven high-rate plasticity in BCC lead. AIP Conf. Proc. 2018, 1979, 070027. [Google Scholar] [CrossRef]
- Steinberg, D.J.; Cochran, S.G.; Guinan, M.W. A constitutive model for metals applicable at high-strain rate. J. Appl. Phys. 1980, 51, 1498–1504. [Google Scholar] [CrossRef] [Green Version]
- Follansbee, P.S.; Kocks, U.F. A constitutive description of the deformation of copper based on the use of the mechanical threshold stress as an internal state variable. Acta Metall. 1988, 36, 81–93. [Google Scholar] [CrossRef] [Green Version]
- Barton, N.R.; Bernier, J.V.; Becker, R.; Arsenlis, A.; Cavallo, R.; Marian, J.; Rhee, M.; Park, H.S.; Remington, B.; Olson, R.T. A multi-scale strength model for extreme loading conditions. J. Appl. Phys. 2011, 109, 073501. [Google Scholar] [CrossRef]
- Austin, R.A. Elastic precursor wave decay in shock-compressed aluminum over a wide range of temperature. J. Appl. Phys. 2018, 123, 035103. [Google Scholar] [CrossRef]
- Addessio, F.; Zuo, Q.; Mason, T.; Brinson, L.C. Model for high-strain-rate deformation of uranium–niobium alloys. J. Appl. Phys. 2003, 93, 9644–9654. [Google Scholar] [CrossRef] [Green Version]
- Zuo, Q.; Harstad, E.; Addessio, F.; Greeff, C. A model for plastic deformation and phase transformations of zirconium under high-rate loading. Model. Simul. Mater. Sci. Eng. 2006, 14, 1465. [Google Scholar] [CrossRef]
- Greeff, C.; Chisolm, E.; George, D. SESAME 2161: An Explicit Multiphase Equation of State for Tin; Technical Report LA-UR-05-9414; Los Alamos National Laboratory: Los Alamos, NM, USA, 2005. [Google Scholar]
- Rehn, D.A.; Greeff, C.W.; Burakovsky, L.; Sheppard, D.G.; Crockett, S.D. Multiphase tin equation of state using density functional theory. Phys. Rev. B (Condens. Matter Mater. Phys.) 2021, 103, 184102. [Google Scholar] [CrossRef]
- Greeff, C.W. A model for phase transitions under dynamic compression. J. Dyn. Behav. Mater. 2016, 2, 452–459. [Google Scholar] [CrossRef] [Green Version]
- Myint, P.C.; Chernov, A.A.; Sadigh, B.; Benedict, L.X.; Hall, B.M.; Hamel, S.; Belof, J.L. Nanosecond Freezing of Water at High Pressures: Nucleation and Growth near the Metastability Limit. Phys. Rev. Lett. 2018, 121, 155701. [Google Scholar] [CrossRef] [Green Version]
- Anderson, W.W.; Cverna, F.; Hixson, R.S.; Vorthman, J.; Wilke, M.D.; Gray III, G.T.; Brown, K.L. Phase transition and spall behavior in β-TiN. AIP Conf. Proc. 2000, 505, 443–446. [Google Scholar]
- Cox, G.A.; Robinson, C.M. Empirical multi-phase eos modelling issues. AIP Conf. Proc. 2009, 1195, 1195–1200. [Google Scholar] [CrossRef]
- Salamat, A.; Briggs, R.; Bouvier, P.; Petitgirard, S.; Dewaele, A.; Cutler, M.E.; Corà, F.; Daisenberger, D.; Garbarino, G.; McMillan, P.F. High-pressure structural transformations of Sn up to 138 GPa: Angle-dispersive synchrotron x-ray diffraction study. Phys. Rev. B (Condens. Matter Mater. Phys.) 2013, 88, 104104. [Google Scholar] [CrossRef]
- Hinton, J.K.; Childs, C.; Smith, D.; Ellison, P.B.; Lawler, K.V.; Salamat, A. Response of the mode Grüneisen parameters with anisotropic compression: A pressure and temperature dependent Raman study of β-Sn. Phys. Rev. B (Condens. Matter Mater. Phys.) 2020, 102, 184112. [Google Scholar] [CrossRef]
- Robert, G.; Pillon, L.; Seisson, G.; Chauvin, C. Full multiphase description of materials: Application on tin. AIP Conf. Proc. 2020, 2272, 070040. [Google Scholar] [CrossRef]
- Soulard, L.; Durand, O. Observation of phase transitions in shocked tin by molecular dynamics. J. Appl. Phys. 2020, 127, 165901. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.; Fensin, S.J.; Luscher, D.J.; Prime, M.B.; Burakovsky, L.; Sjue, S.; Trujillo, C.; Martinez, D.; Jones, D.; Gray, G.T., III. Measuring and modeling the dynamic strength behavior of tin across a range of temperatures and strain rates. 2022; in preparation. [Google Scholar]
- Reisman, D.; Stoltzfus, B.; Austin, K.N.; Ao, T.; Morgan, D.; Stygar, W.A.; Cuneo, M.E.; Waisman, E.M.; Collier, L.; Haill, T.; et al. Thor: A Modern Pulsed Power Accelerator for Material Science Applications; Technical Report SAND2016-7806PE; Sandia National Laboratories: Albuquerque, NM, USA, 2016. [Google Scholar]
- Greeff, C.; Rigg, P.; Knudson, M.; Hixson, R.; Gray, G., III. Modeling dynamic phase transitions in Ti and Zr. AIP Conf. Proc. 2004, 706, 209–212. [Google Scholar]
- Barton, N.R.; Austin, R.A.; Brown, J.L.; Rhee, M. Anelastic Effects on Reverse Loading—Connection to Evolving Dislocation Structure. AIP Conf. Proc. 2020, 2272. [Google Scholar] [CrossRef]
- Huntington, C.M.; Belof, J.L.; Blobaum, K.J.M.; Cavallo, R.M.; Kostinski, N.B.; Maddox, B.R.; Park, H.S.; Plechaty, C.; Prisbrey, S.T.; Rudd, R.; et al. Investigating iron material strength up to 1 Mbar using Rayleigh-Taylor growth measurements. AIP Conf. Proc. 2017, 1793, 110007. [Google Scholar] [CrossRef] [Green Version]
- Hawreliak, J.A.; Kalantar, D.H.; Stölken, J.S.; Remington, B.A.; Lorenzana, H.E.; Wark, J.S. High-pressure nanocrystalline structure of a shock-compressed single crystal of iron. Phys. Rev. B (Condens. Matter Mater. Phys.) 2008, 78, 220101. [Google Scholar] [CrossRef]
- Amadou, N.; de Resseguier, T.; Dragon, A.; Brambrink, E. Coupling between plasticity and phase transition in shock- and ramp-compressed single-crystal iron. Phys. Rev. B (Condens. Matter Mater. Phys.) 2018, 98, 024104. [Google Scholar] [CrossRef]
- Merkel, S.; Shu, J.; Gillet, P.; Mao, H.K.; Hemley, R.J. X-ray diffraction study of the single crystal elastic moduli of ϵ-Fe up to 30 GPa. J. Geophys. Res. 2005, 110, B05201. [Google Scholar] [CrossRef] [Green Version]
- Mao, H.K.; Bassett, W.A.; Takahashi, T. Effect of pressure on crystal structure and lattice parameters of iron up to 300 kbar. J. Appl. Phys. 1967, 38, 272–276. [Google Scholar] [CrossRef]
- Liu, J.B.; Johnson, D.D. bcc-to-hcp transformation pathways for iron versus hydrostatic pressure: Coupled shuffle and shear modes. Phys. Rev. B (Condens. Matter Mater. Phys.) 2009, 79, 134113. [Google Scholar] [CrossRef]
- Dupé, B.; Amadon, B.; Pellegrini, Y.P.; Denoual, C. Mechanism for the α→ϵ phase transition in iron. Phys. Rev. B (Condens. Matter Mater. Phys.) 2013, 87, 024103. [Google Scholar] [CrossRef] [Green Version]
- Chester, S.A.; Bernier, J.V.; Barton, N.R.; Balogh, L.; Clausen, B.; Edmiston, J.K. Direct numerical simulation of deformation twinning in polycrystals. Acta Mater. 2016, 120, 348–363. [Google Scholar] [CrossRef] [Green Version]
- Wenk, H.R.; Barton, N.; Bortolotti, M.; Vogel, S.; Voltolini, M.; Lloyd, G.; Gonzalez, G. Dauphiné twinning and texture memory in polycrystalline quartz Part 3: Texture memory during phase transformation. Phys. Chem. Miner. 2009, 36, 567–583. [Google Scholar] [CrossRef]

| Phase | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| g/cm | GPa | g/cm | K | * | * | - | * | - | - | |
| 7.40 | 25.4 | 7.18 | 505.1 | 0 | 600 | 3.2 | 800 | 3.2 | 0.53 | |
| 7.82 | 26.8 | 7.585 | 595.0 | 0 | 820 | 3.2 | 2300 | 3.2 | 0.7 | |
| 10.50 | 23.0 | 9.425 | 1900.0 | 2.125 | 8.0 | 8.0 | 0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barton, N.R.; Luscher, D.J.; Battaile, C.; Brown, J.L.; Buechler, M.; Burakovsky, L.; Crockett, S.; Greeff, C.; Mattsson, A.E.; Prime, M.B.; et al. A Multi-Phase Modeling Framework Suitable for Dynamic Applications. Metals 2022, 12, 1844. https://doi.org/10.3390/met12111844
Barton NR, Luscher DJ, Battaile C, Brown JL, Buechler M, Burakovsky L, Crockett S, Greeff C, Mattsson AE, Prime MB, et al. A Multi-Phase Modeling Framework Suitable for Dynamic Applications. Metals. 2022; 12(11):1844. https://doi.org/10.3390/met12111844
Chicago/Turabian StyleBarton, Nathan R., Darby J. Luscher, Corbett Battaile, Justin L. Brown, Miles Buechler, Leonid Burakovsky, Scott Crockett, Carl Greeff, Ann E. Mattsson, Michael B. Prime, and et al. 2022. "A Multi-Phase Modeling Framework Suitable for Dynamic Applications" Metals 12, no. 11: 1844. https://doi.org/10.3390/met12111844





