Investigation of Surface Residual Stress for Medium Carbon Steel Quenched by YAG Laser with Extended Cycloidal Motion
Abstract
:1. Introduction
2. Finite Element Modeling
2.1. Governing Equations for Heat Transfer
2.2. Laser Power Simulation
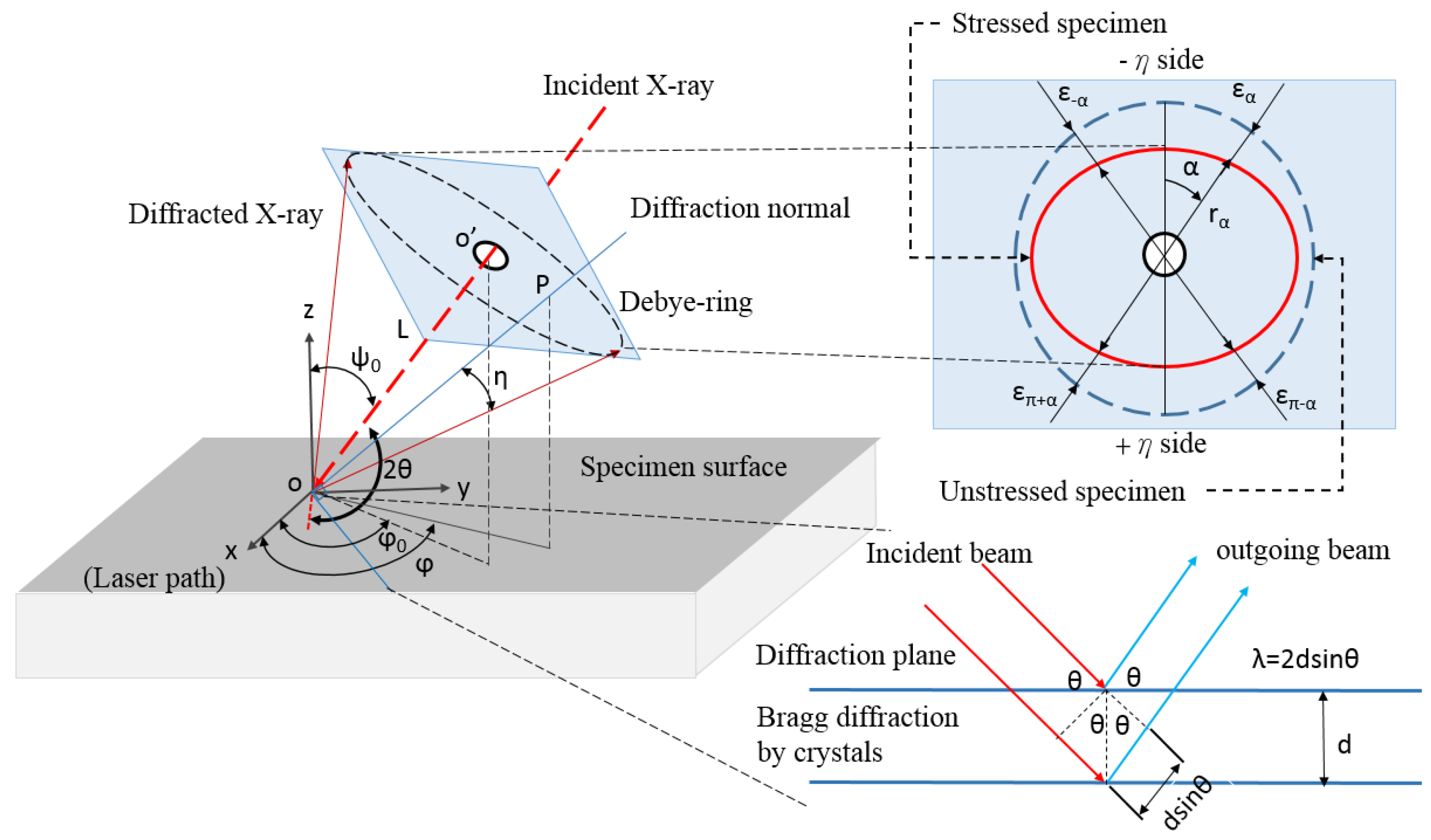
3. Experimental Setup
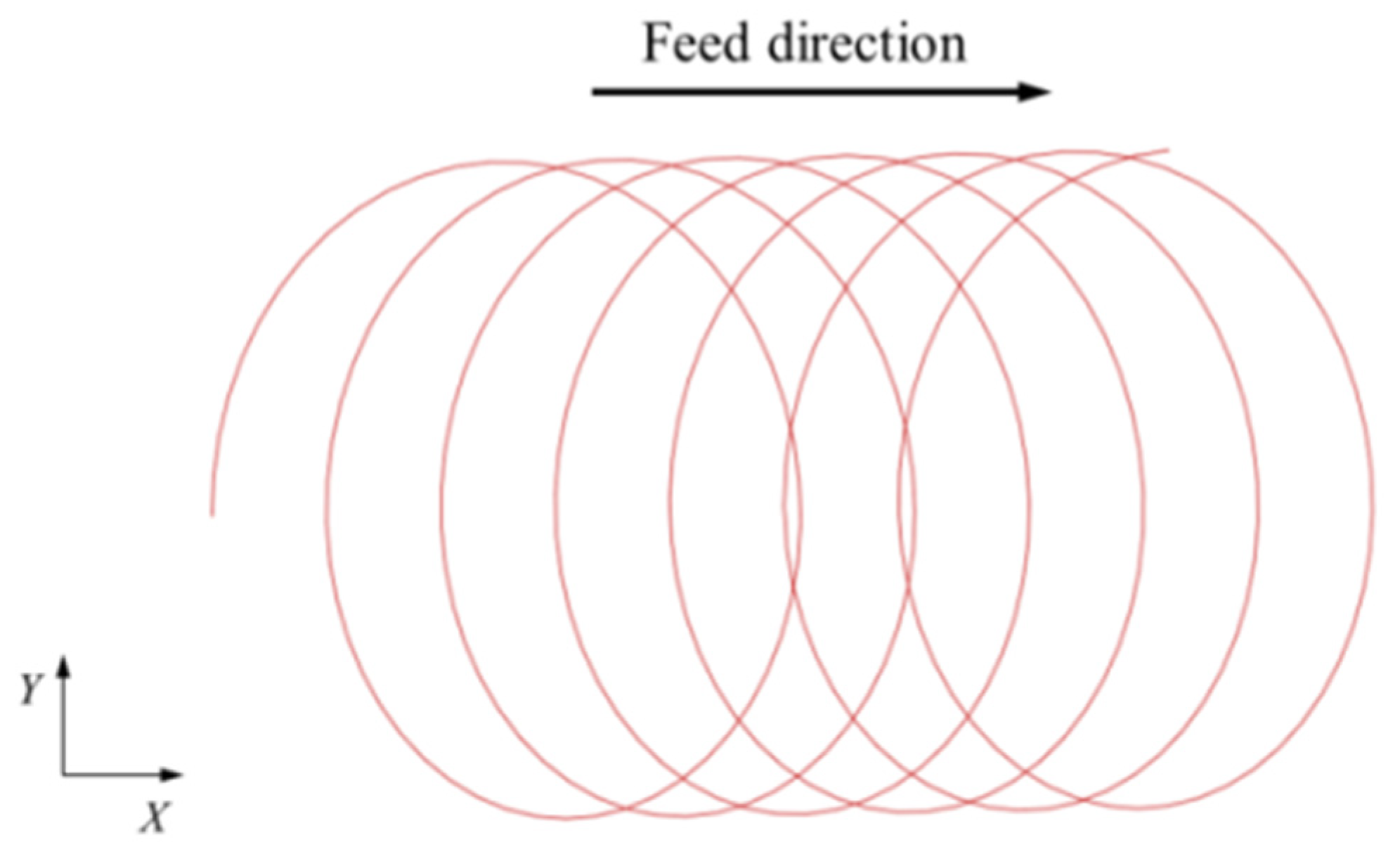
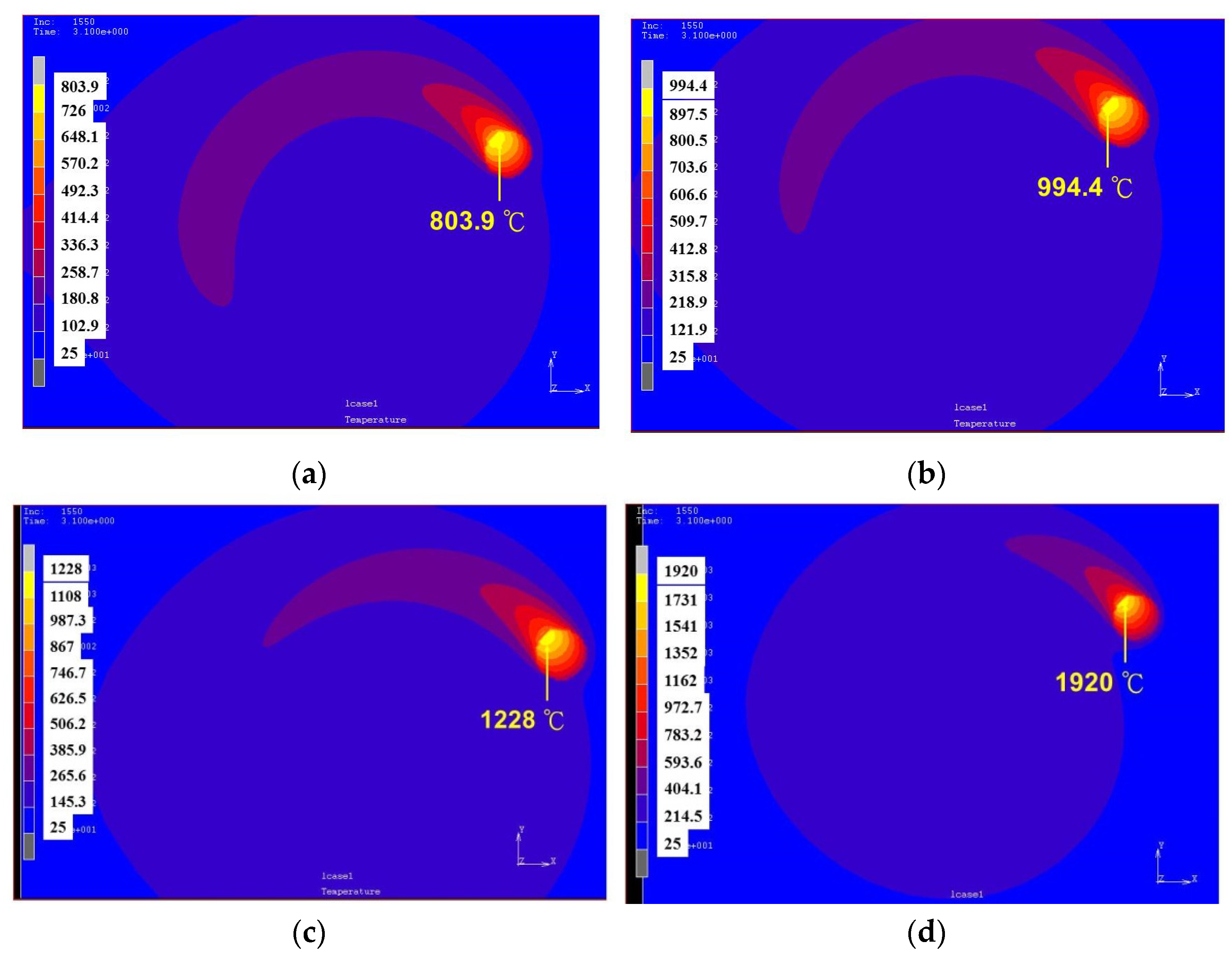
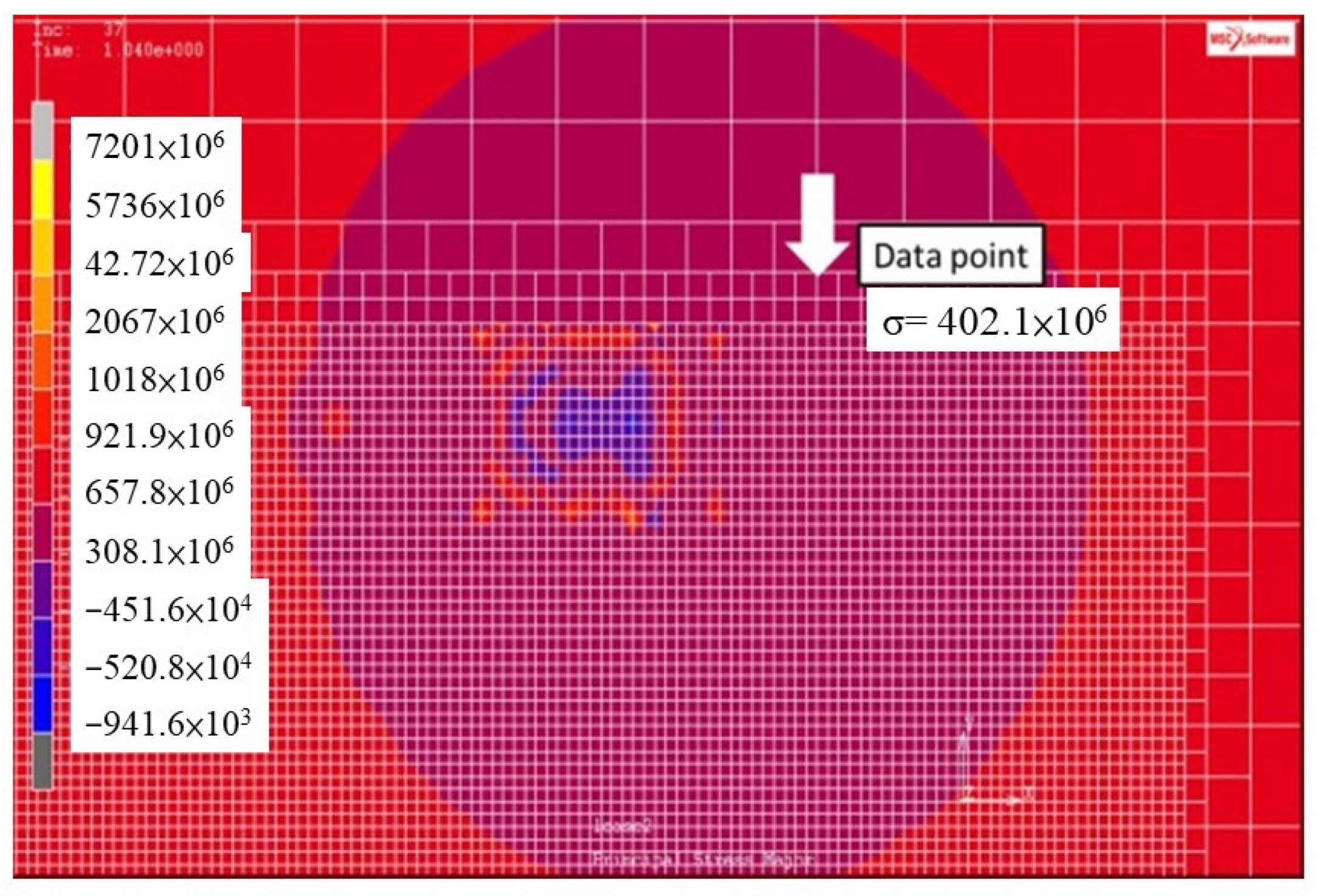
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lakhkar, R.S.; Shin, Y.C.; Krane, M.J.M. Predictive modeling of multi-Track laser hardening of AISI 4140 steel. Mater. Sci. Eng. A 2008, 480, 209–217. [Google Scholar] [CrossRef]
- Sun, P.; Li, S.; Yu, G.; He, X.; Zheng, C.; Ning, W. Laser surface hardening of 42CrMo cast steel for obtaining a wide and uniform hardened layer by shaped beams. Int. J. Adv. Manuf. Technol. 2014, 70, 787–796. [Google Scholar] [CrossRef] [Green Version]
- Barka, N.; El Ouafi, A. Effects of laser hardening process parameters on case depth of 4340 steel cylindrical specimen—A statistical analysis. J. Surf. Eng. Mater. Adv. Technol. 2015, 5, 124–135. [Google Scholar] [CrossRef] [Green Version]
- Hung, T.; Shi, H.; Kuang, J. Temperature modelling of AISI 1045 Steel during Surface Hardening Processes. Materials 2018, 11, 1815. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hung, T.; Hsu, C.; Tsai, H.; Chen, S.; Liu, Z. Temperature field numerical analysis mode and verification of quenching heat treatment using carbon steel in rotating laser scanning. Materials 2019, 12, 534. [Google Scholar] [CrossRef] [Green Version]
- Carrera-Espinoza, R.; Valerio, R.; Villasana, J.D.; Hernandez, J.A.Y.; Moreno-Garibaldi, P.; Cruz-Gomez, M.A.; Lopez, U.F. Surface laser quenching as an alternative method for conventional quenching and tempering treatment of 1538 MV steel. Adv. Mater. Sci. Eng. 2020, 2020, 7950684. [Google Scholar] [CrossRef] [Green Version]
- Maharjan, N.; Zhou, W.; Wu, N. Direct laser hardening of AISI 1020 steel under controlled gas atmosphere. Surf. Coat. Technol. 2020, 385, 125399. [Google Scholar] [CrossRef]
- Fakir, R.; Barka, N.; Brousseau, J. Case study of laser hardening process applied to 4340 steel cylindrical specimens using simulation and experimental validation. Case Stud. Therm. Eng. 2018, 11, 15–25. [Google Scholar] [CrossRef]
- Fakir, R.; Barka, N.; Brousseau, J. Servo-control applied to the parameters of the laser hardening process for a regular case depth of 4340 steel cylindrical specimen. J. Comput. Inf. Sci. Eng. 2019, 19, 031007. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, Q.; Wang, J.; Yun, X.; He, B.; Luo, J. Behaviors of 40Cr steel treated by laser quenching on impact abrasive wear. Opt. Laser Technol. 2018, 103, 118–125. [Google Scholar]
- Pan, Z.; Feng, Y.; Hung, T.P.; Jiang, Y.C.; Hsu, F.C.; Wu, L.T.; Lin, C.F.; Lu, Y.C.; Liang, S.Y. Heat affected zone in the laser-assisted milling of Inconel 718. J. Manuf. Process. 2017, 30, 141–147. [Google Scholar] [CrossRef]
- Withers, P. Residual stress and its role in failure. Rep. Prog. Phys. 2007, 70, 22–64. [Google Scholar] [CrossRef] [Green Version]
- Withers, P.J.; Bhadeshia, H.K.D.S. Residual stress part II—Nature and origins. Mater. Sci. Technol. 2013, 17, 366–375. [Google Scholar] [CrossRef]
- Withers, P.J.; Bhadeshia, H.K.D.H. Residual stress part I—Measurement techniques. Mater. Sci. Technol. 2013, 17, 355–365. [Google Scholar] [CrossRef]
- ASTM E837 Standard; Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method. American Society for Testing Materials: West Conshohocken, PA, USA, 2013.
- Pang, Y.; Zhao, J.; Chen, L.S.; Dong, J. Residual stress measurement combining blind-hole drilling and digital image correlation approach. J. Constr. Steel Res. 2021, 176, 1–9. [Google Scholar] [CrossRef]
- Tanaka, K. The method for X-ray residual stress measurement using two-dimensional detector. Mech. Eng. Rev. 2019, 6, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Taira, S.; Tanaka, K.; Yamasaki, T. A method of X-ray microbeam measurement of local stress and its application to fatigue and crack growth problems. J. Soc. Mater. Sci. Jpn. 1978, 27, 251256. (In Japanese) [Google Scholar]
- Tanaka, K. X-ray measurement of triaxial residual stress on machined surface by the method using a two-dimensional detector. J. Appl. Crystallogr. 2018, 51, 1329–1338. [Google Scholar] [CrossRef]
- Yang, Y.S.; Na, S.J. A study on residual stresses in laser surface hardening of a medium carbon steel. Surf. Coat. Technol. 1989, 38, 311–324. [Google Scholar] [CrossRef]
- Köhlera, H.; Partesa, K.; Kornmeierb, J.R.; Vollertsena, F. Residual stresses in steel specimens induced by laser cladding and their effect on fatigue strength. Phys. Procedia 2012, 39, 354–361. [Google Scholar] [CrossRef] [Green Version]
- Ganesh, P.; Kumar, H.; Kaul, R.; Kukreja, L.M. Microstructural characterization of laser surface treated AISI 1040 steel with portable X-ray stress analyzer. Surf. Eng. 2013, 29, 600–607. [Google Scholar] [CrossRef]
- Liverani, E.; Lutey, A.H.A.; Ascari, A.; Fortunato, A.; Tomesani, L. A complete residual stress model for laser surface hardening of complex medium carbon steel components. Surf. Coat. Technol. 2016, 302, 100–106. [Google Scholar] [CrossRef]
- Lopez, V.; Fernandez, B.; Bello, J.M.; Ruiz, J.; Zubir, F. Influence of Previous Structure on Laser Surface Hardening of AISI 1045 Steel. ISIJ Int. 1995, 35, 1394–1399. [Google Scholar] [CrossRef]
- MSC Software Corporation. Marc Product Documentation Volume A: Theory and User Information; MSC Software Corporation: Glen Rock, NJ, USA, 2010. [Google Scholar]
- Available online: https://mathworld.wolfram.com/ProlateCycloid.html (accessed on 8 October 2022).





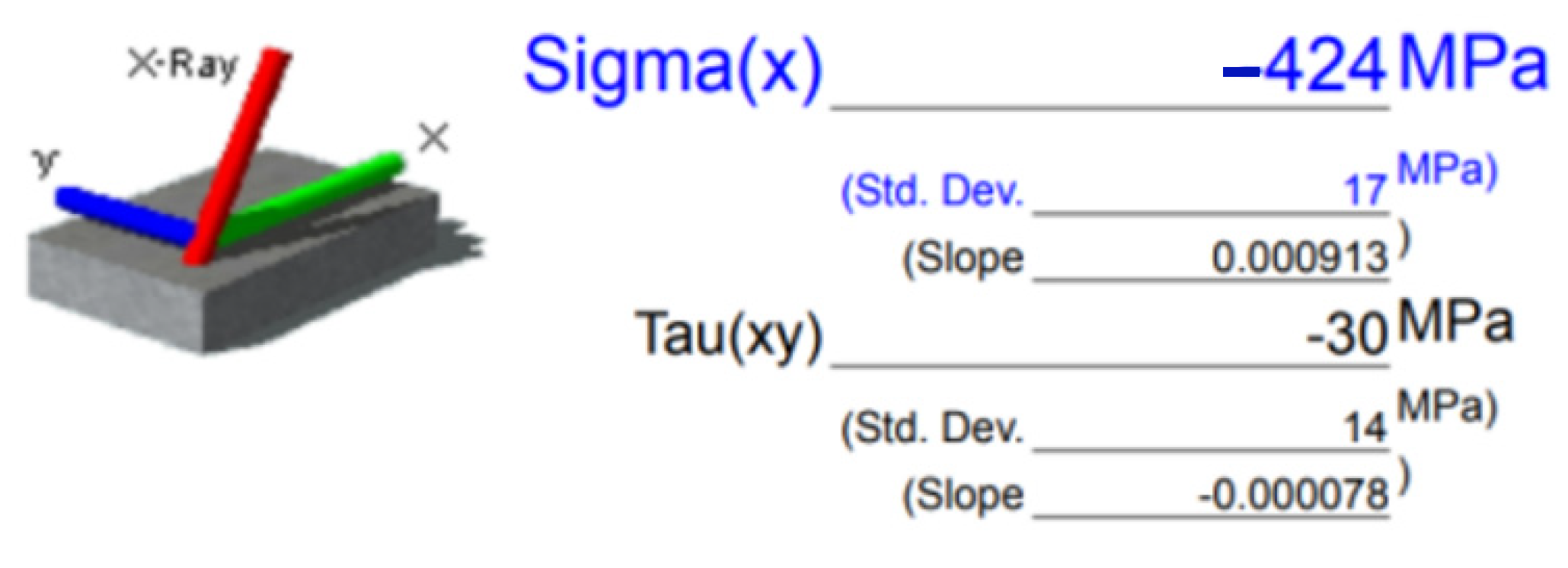
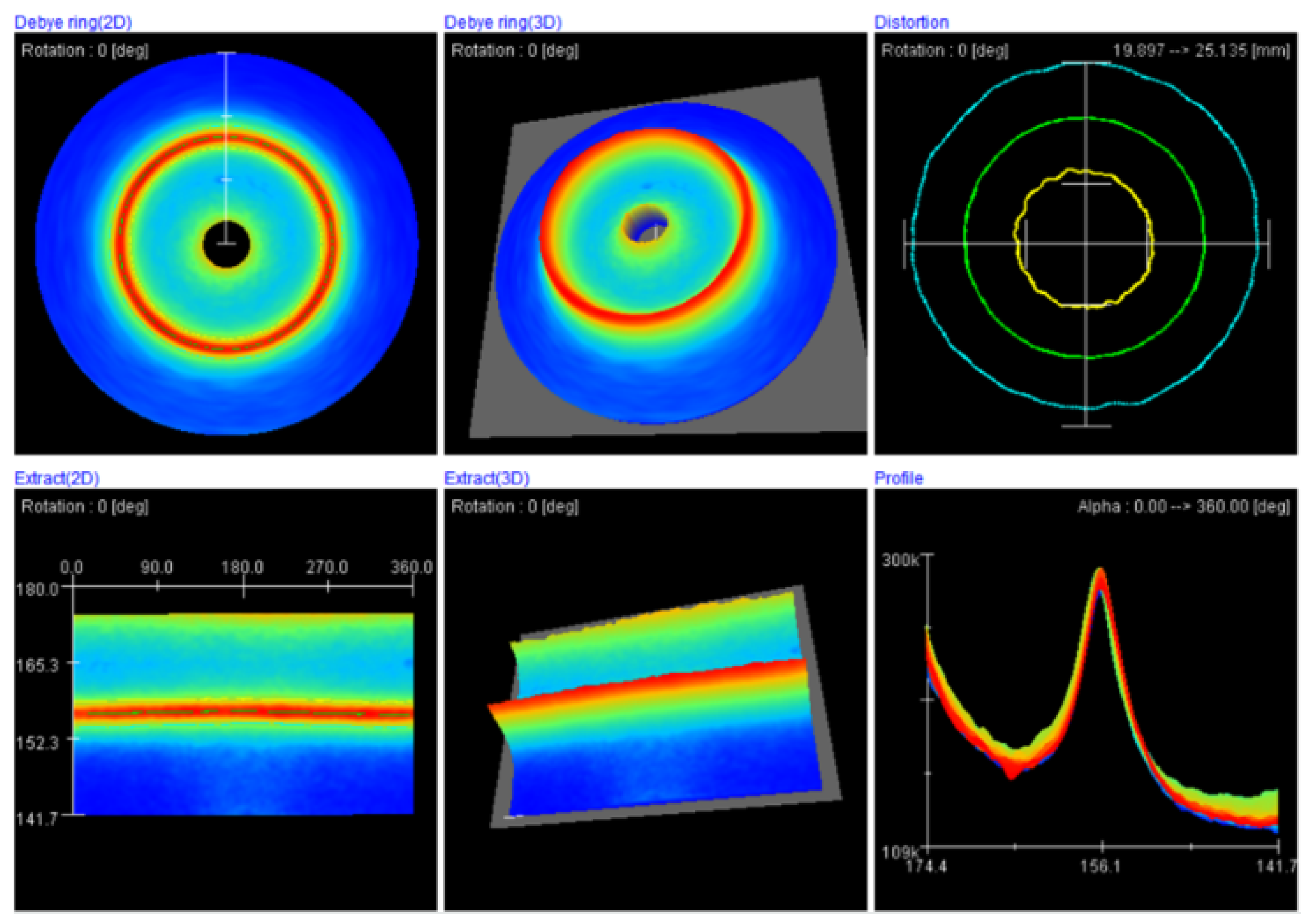

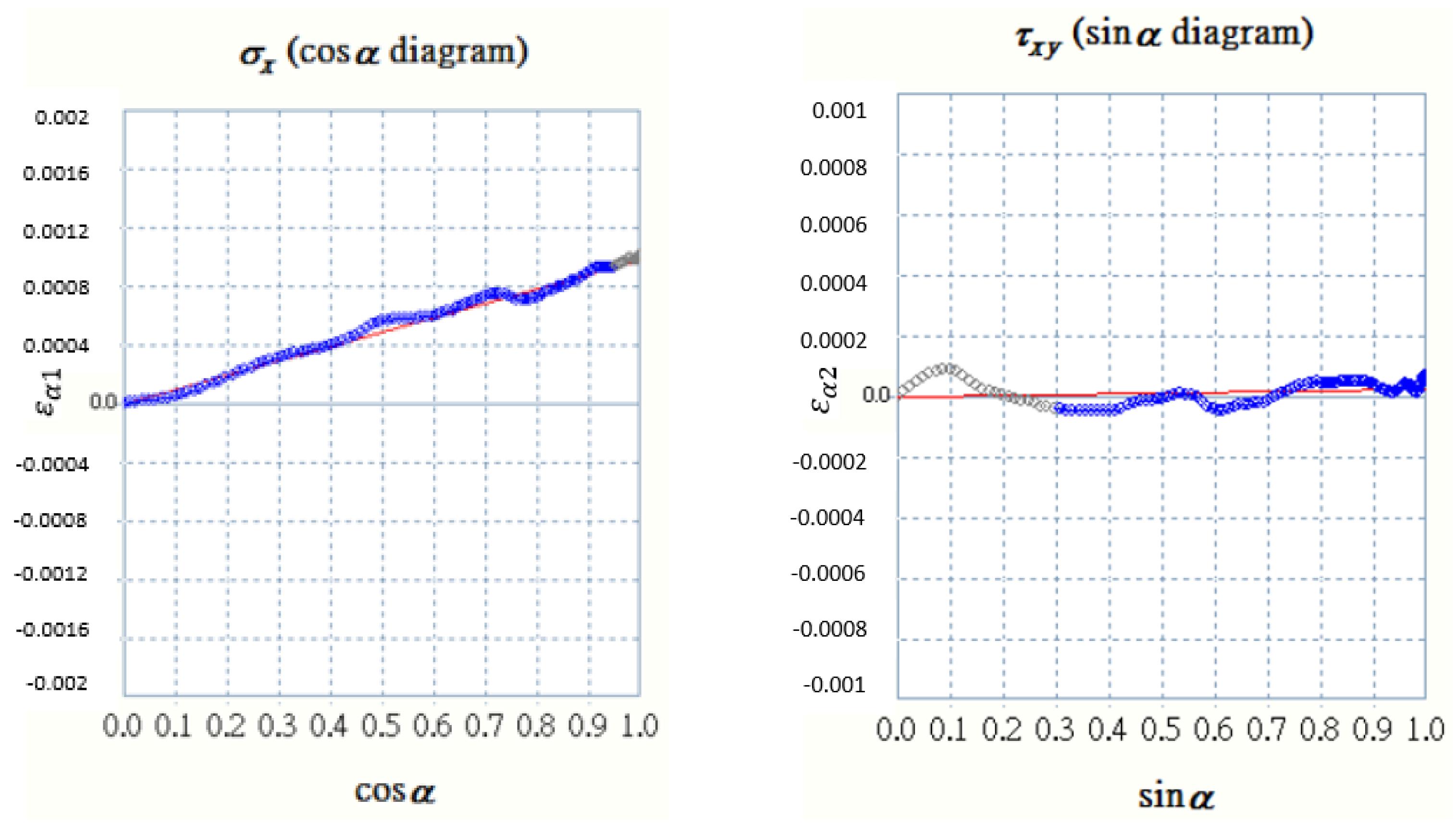
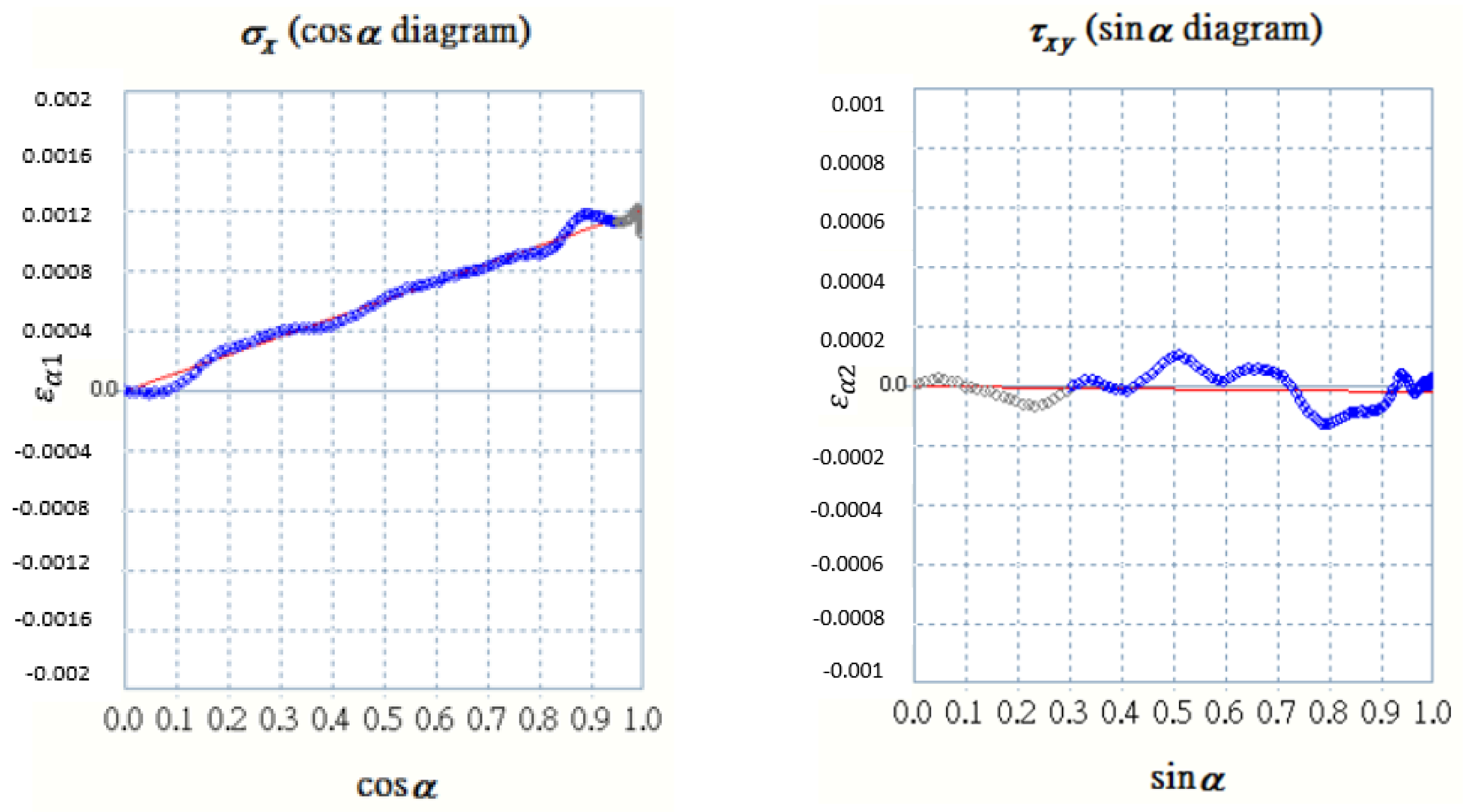

| Property | Value |
|---|---|
| Density (Kg/m3) | 7870 |
| Thermal conductivity (W/m·°C) | Temperature-dependent [5] |
| Specific heat (J/Kg·°C) | Temperature-dependent [5] |
| Young’s modulus (GPa) | Temperature-dependent [5] |
| Yield strength (MPa) | 310 |
| Coefficient of thermal expansion (μm/m·°C) | 15 |
| Poisson’s ratio | 0.27 |
| Hardening temperature Th (°C) | 760 |
| Melting temperature Tm (°C) | 1520 |
| Tempering temperature Tt (°C) | 400 |
| Item | Unit | Value |
|---|---|---|
| Measuring diameter | mm | 5 |
| X-ray irradiation time (setup) | sec | 15 |
| X-ray irradiation time (meas.) | sec | 15 |
| X-ray irradiation time (max.) | sec | 15 |
| X-ray tube current | mA | 1.50 |
| X-ray tube voltage | kV | 30.00 |
| Sample distance (monitor) | mm | 51.000 |
| Sample distance (analysis) | mm | 51.369 |
| X-ray incidence angle | deg | 35.0 |
| Offset of alpha angle | deg | 0 |
| X-ray wavelength (K-alpha) | 2.29093 | |
| X-ray wavelength (K-beta) | 2.08480 | |
| Total measurement count | - | 3099 |
| Oscillation count | - | 1 |
| X-ray tube total use time | hours | 20.05 |
| Detection sensitivity | % | 22.6 |
| Peak strength (ave.) | k | 126 |
| Level of ambient light | % | 0.3 |
| Temperature | 36.56 | |
| Valid range of alpha angle | deg | 18–90 |
| Correction coefficient (stress) | - | 0.000xx + 1.000x + 0.000 |
| Correction coefficient (FWHM) | - | 0.000xx + 1.000x + 0.000 |
| Item | Value |
|---|---|
| Name | (211) |
| Lattice constant (a) | 2.8664 () |
| Lattice constant (c) | -- |
| Wavelength | K-Alpha |
| Diffraction angle (2 theta) | |
| Diffraction lattice angle (2 eta) | |
| Interplanar spacing (d) | 1.170 |
| Diffraction plane (h, k, l) | 2, 1, 1 |
| Crystal structure | B.C.C |
| Young’s modulus (E) | 224.000 GPa |
| Poisson’s ration () | 0.280 |
| Sigma (x) stress constant (K) | −465.097 GPa |
| Tau (xy) stress constant (K) | 380.985 GPa |
| Sigma stress constant (K) | −209.661 GPa |
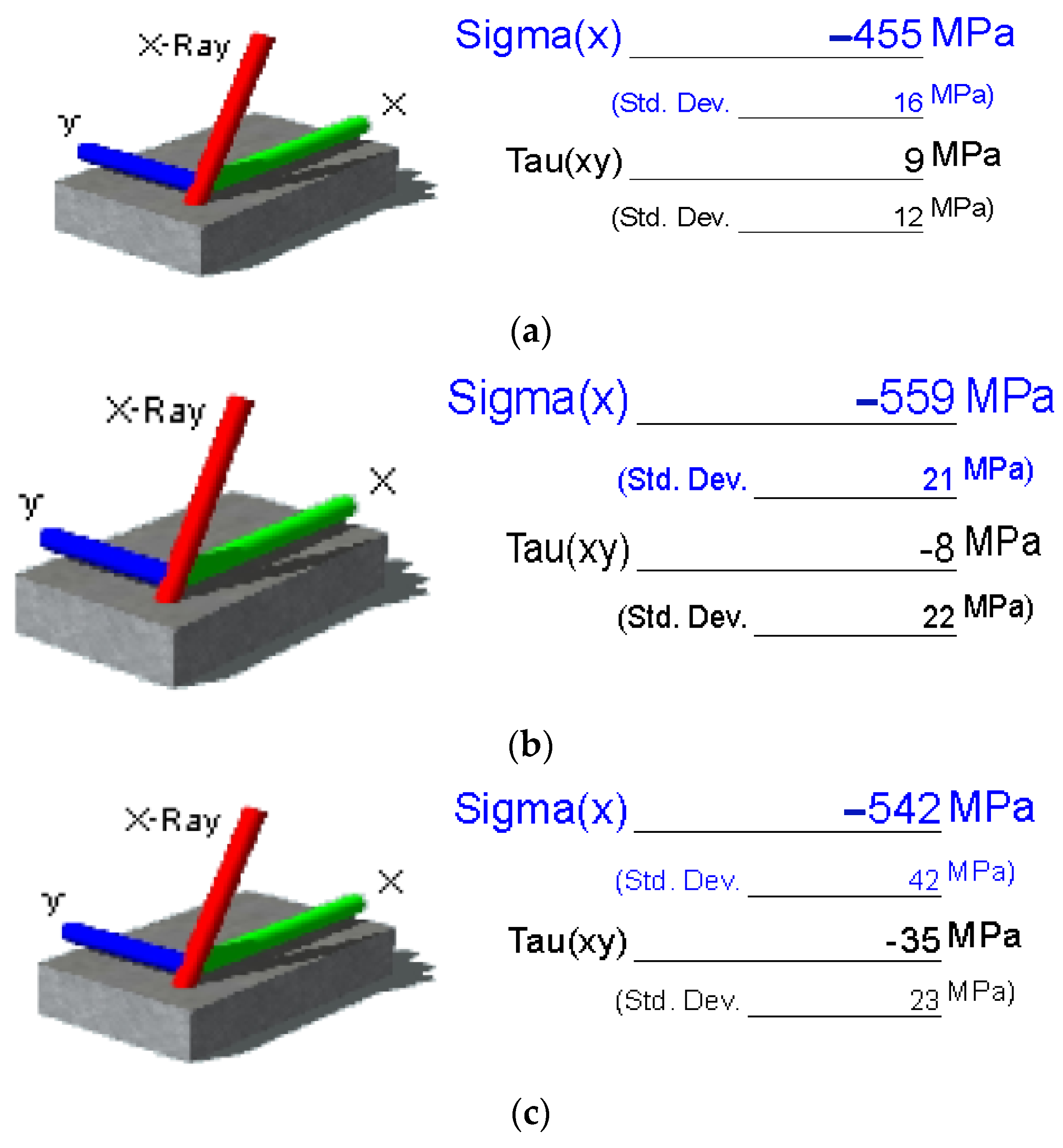
| Laser Power (W) | Experiment Normal Stress (MPa) | FEM Normal Stress (MPa) | Deviation (%) |
|---|---|---|---|
| 500 | −424 | −402.1 | 5.45 |
| 600 | −455 | −411.7 | 10.5 |
| 700 | −559 | −525.4 | 6.40 |
| 900 | −542 | −524.6 | 3.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hung, T.-P.; Tsai, H.-A.; Lin, A.-D. Investigation of Surface Residual Stress for Medium Carbon Steel Quenched by YAG Laser with Extended Cycloidal Motion. Metals 2022, 12, 1903. https://doi.org/10.3390/met12111903
Hung T-P, Tsai H-A, Lin A-D. Investigation of Surface Residual Stress for Medium Carbon Steel Quenched by YAG Laser with Extended Cycloidal Motion. Metals. 2022; 12(11):1903. https://doi.org/10.3390/met12111903
Chicago/Turabian StyleHung, Tsung-Pin, Hsiu-An Tsai, and Ah-Der Lin. 2022. "Investigation of Surface Residual Stress for Medium Carbon Steel Quenched by YAG Laser with Extended Cycloidal Motion" Metals 12, no. 11: 1903. https://doi.org/10.3390/met12111903
APA StyleHung, T.-P., Tsai, H.-A., & Lin, A.-D. (2022). Investigation of Surface Residual Stress for Medium Carbon Steel Quenched by YAG Laser with Extended Cycloidal Motion. Metals, 12(11), 1903. https://doi.org/10.3390/met12111903






