Large Linear Giant Magneto-Impedance Response of Microwire Annealed under Liquid Medium for Potential Sensor Applications
Abstract
:1. Introduction
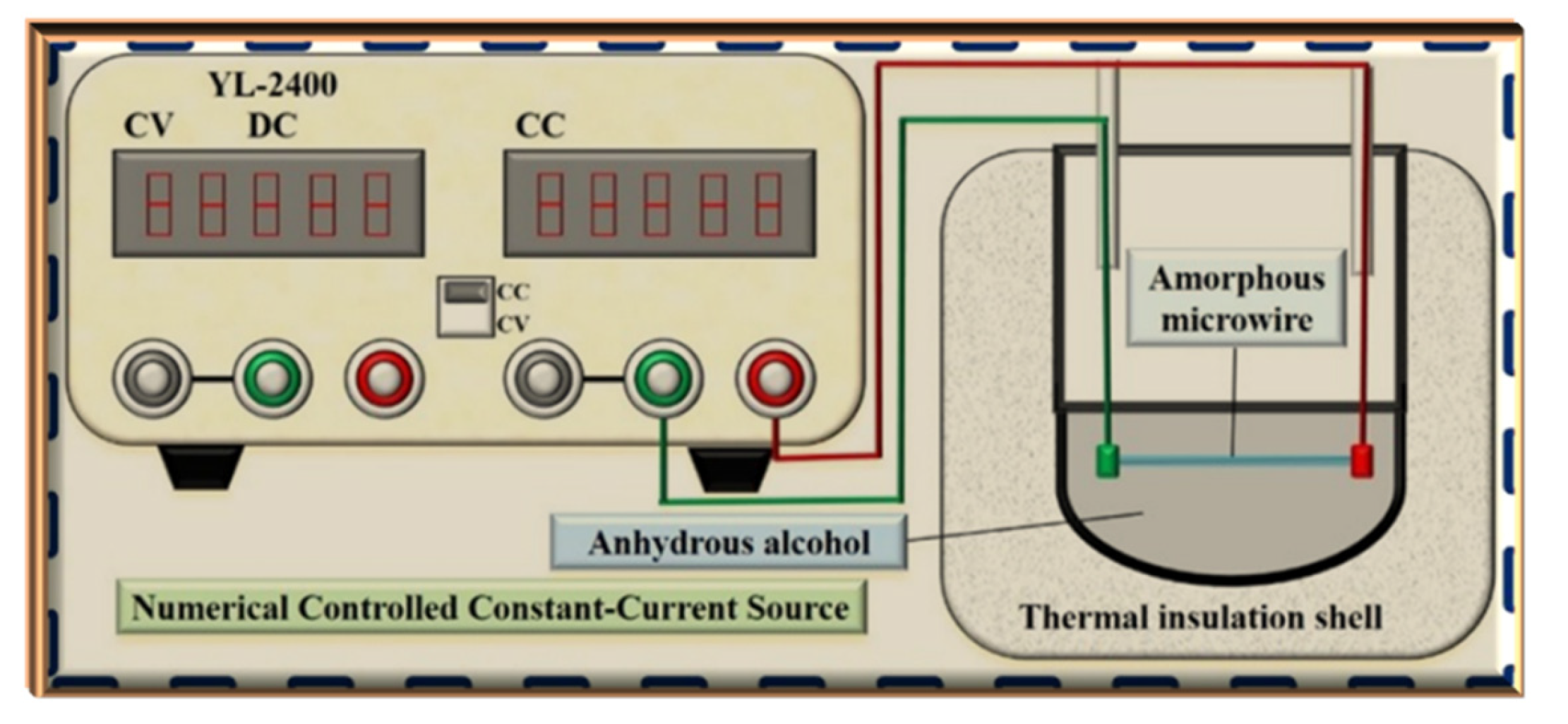
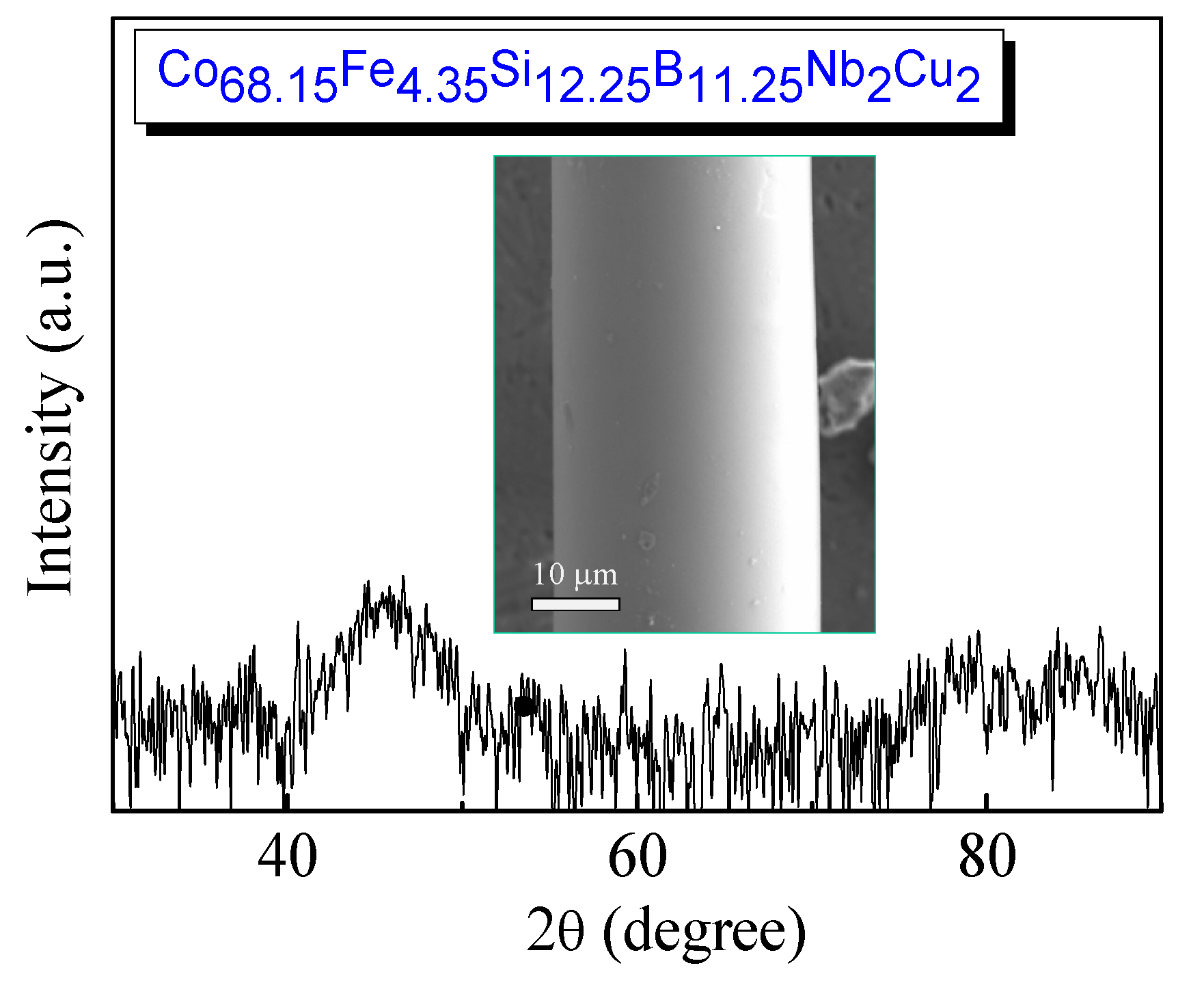
2. Experimental
3. Results
4. Conclusions
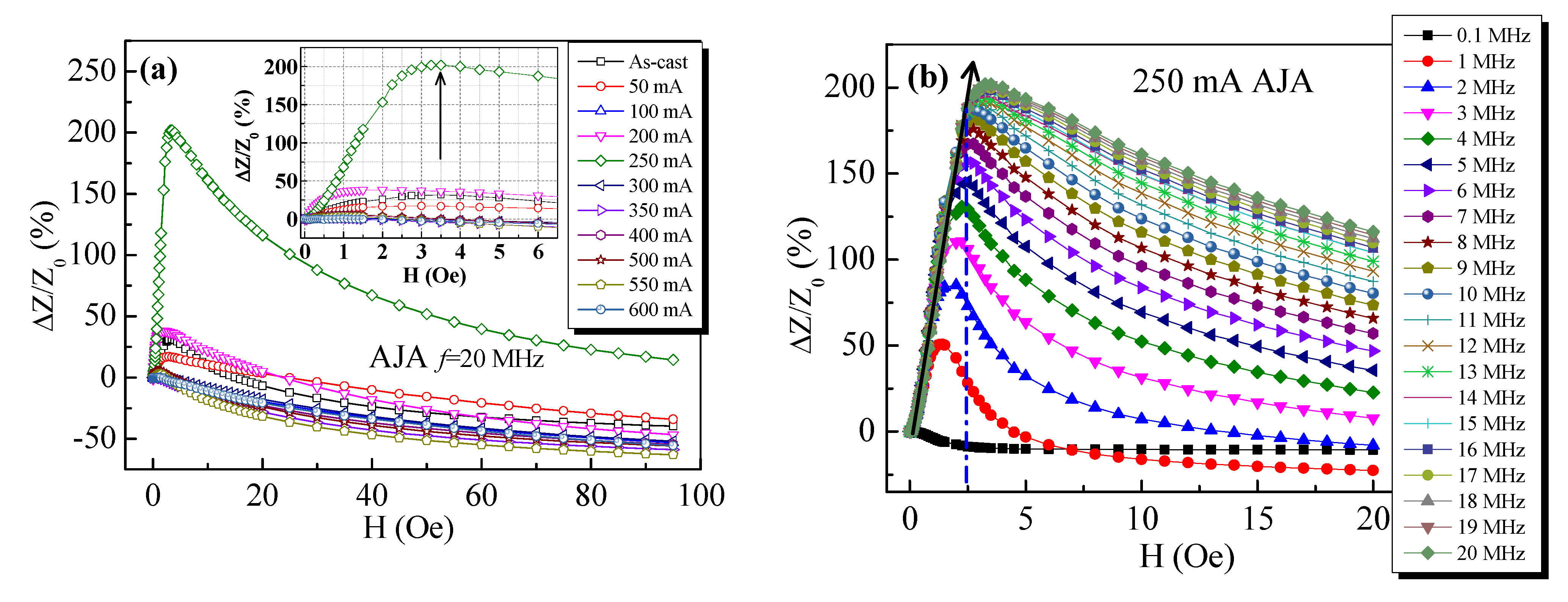
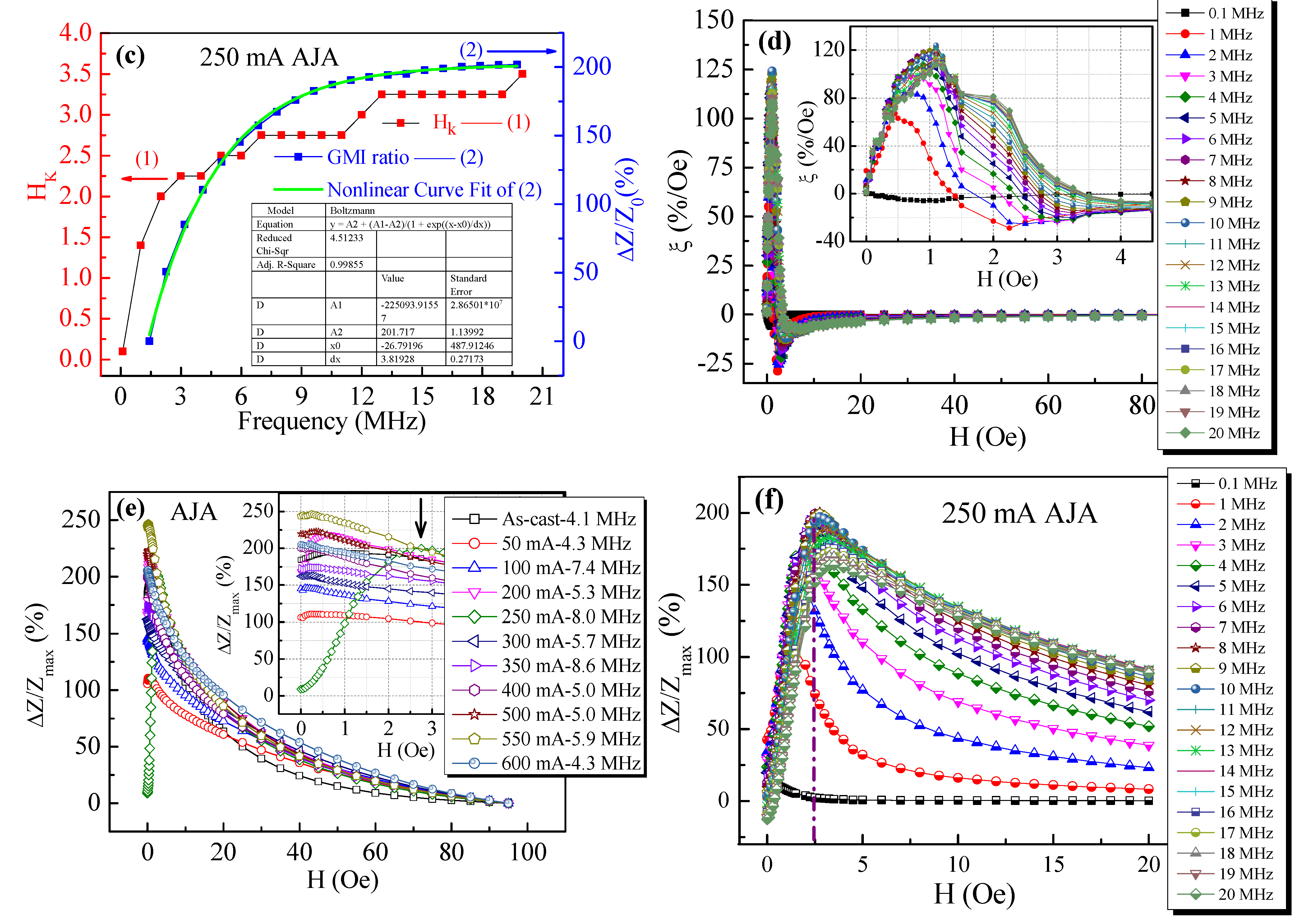
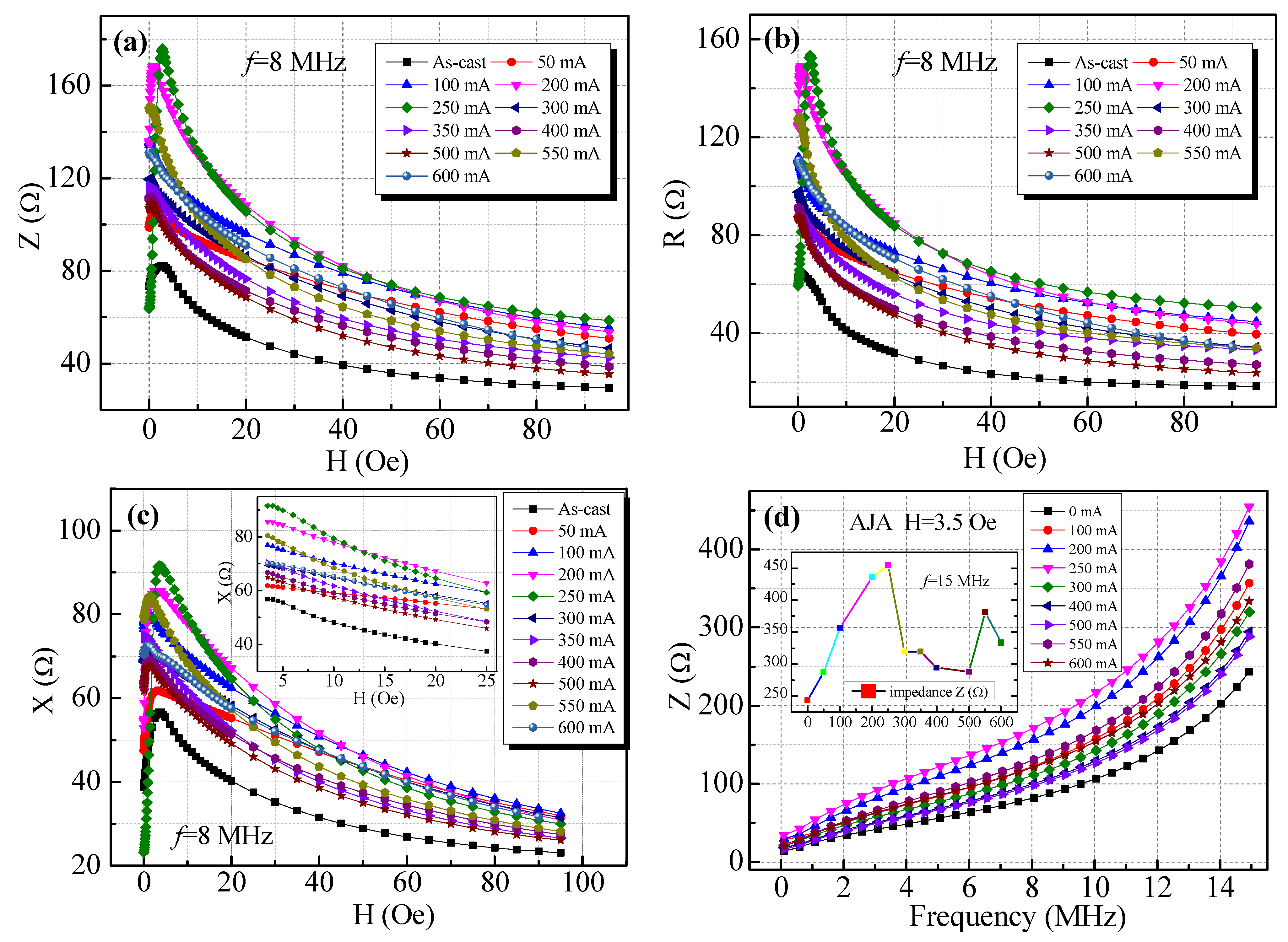
- The 250 mA AJA microwire has the characteristics of a near-linear response in the double magnetic field interval (i.e., H < 3.5 Oe and 3.5 < H < 20 Oe), which shows a promising application in the development of dual-range GMI sensors.
- The GMI effect has been improved with the ratio ΔZ/Z0(%) of 201.9% and ΔZ/Zmax(%) of 200.5% for the 250 mA AJA, simultaneously.
- The microstructure of the 250 mA AJA wires with a large number of disordered and small-sized nanocrystals embedded in an amorphous structure are good for improving the soft magnetic properties.
- The surface domains of the microwire are modified and formed a well-defined circumferential domain, which its behaviour is consistent with the improved GMI ratios for the 250 mA AJA.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Phan, M.H.; Peng, H.X. Giant magnetoimpedance materials: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 323–420. [Google Scholar] [CrossRef]
- Qin, F.X.; Peng, H.X. Ferromagnetic microwires enabled multifunctional composite materials. Prog. Mater. Sci. 2013, 58, 183–259. [Google Scholar] [CrossRef]
- Yang, H.; Chen, L.; Zhou, Y.; Cui, D.X. Giant magnetoimpedance-based microchannel system for quick and parallel genotyping of human papilloma virus type 16/18. Appl. Phys. Lett. 2010, 97, 043702. [Google Scholar] [CrossRef]
- Su, S.; Huang, Y.; Zhang, J.; Zhang, L.; Wang, H.; Ning, Z.; Sun, J. Tensile Properties of Melt-Extracted and Annealed Ni/Fe-Based Amorphous Metallic Fibers. Metals 2022, 12, 918. [Google Scholar] [CrossRef]
- Wang, C.; Cao, G.; Liu, J.; Zhang, Y.; Liu, R.; Wang, F.; Zhang, M.; Wang, L.; Zhang, B. Direct Current Annealing Modulated Ordered Structure to Optimize Tensile Mechanical Properties of Co-Based Amorphous Metallic Microwires. Metals 2022, 12, 1427. [Google Scholar] [CrossRef]
- Sun, H.; Ning, Z.; Wang, G.; Liang, W.; Shen, H.; Sun, J.; Xue, X. Tensile Strength Reliability Analysis of Cu48Zr48Al4 Amorphous Microwires. Metals 2016, 6, 296. [Google Scholar] [CrossRef] [Green Version]
- Zhukov, A.; Ipatov, M.; Corte-León, P.; Zhukova, V. Giant magnetoimpedance in rapidly quenched materials. J. Alloys Compd. 2020, 814, 152225. [Google Scholar] [CrossRef]
- Zhukov, A. Design of the Magnetic Properties of Fe-Rich, Glass-Coated Microwires for Technical Applications. Adv. Funct. Mater. 2006, 16, 675–680. [Google Scholar] [CrossRef]
- Sharko, S.A.; Serokurova, A.I.; Zubar, T.I.; Trukhanov, S.V.; Tishkevich, D.I.; Samokhvalov, A.A.; Kozlovskiy, A.L.; Zdorovets, M.V.; Panina, L.V.; Fedosyuk, V.M.; et al. Multilayer spin-valve CoFeP/Cu nanowires with giant magnetoresistance. J. Alloys Compd. 2020, 846, 156474. [Google Scholar] [CrossRef]
- Alam, J.; Nematov, M.; Yudanov, N.; Podgornaya, S.; Panina, L. High-Frequency Magnetoimpedance (MI) and Stress-MI in Amorphous Microwires with Different Anisotropies. Nanomaterials 2021, 11, 1208. [Google Scholar] [CrossRef]
- Wang, Y.F.; Thi My Duc, N.; Feng, T.F.; Wei, H.J.; Qin, F.X.; Phan, M.H. Competing ferromagnetic and antiferromagnetic interactions drive the magnetocaloric tunability in Gd55Co30NixAl15−x microwires. J. Alloys Compd. 2022, 907, 164328. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; Zhukova, V. Advances in Giant Magnetoimpedance of Materials. In Handbook of Magnetic Materials; Buschow, K.H.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 24, pp. 139–236. [Google Scholar]
- Zhukova, V.; Ipatov, M.; Zhukov, A. Thin Magnetically Soft Wires for Magnetic Microsensors. Sensors 2009, 9, 9216–9240. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.M.; Wang, Y.F.; Su, R.; Shen, H.X.; Liu, J.S.; Zhang, L.Y.; Jiang, S.D.; Sun, J.F. Tunable Linear Dependence of Giant Magnetoimpedance Response of Microwires Annealed under Fluid Oil for Sensor Applications. Phys. Status Solidi A 2021, 218, 2100154. [Google Scholar] [CrossRef]
- Chen, D.M.; Xing, D.W.; Qin, F.X.; Liu, J.S.; Shen, H.X.; Peng, H.X.; Wang, H.; Sun, J.F. Cryogenic Joule annealing induced large magnetic field response of Co-based microwires for giant magneto-impedance sensor applications. J. Appl. Phys. 2014, 116, 053907. [Google Scholar] [CrossRef]
- Wang, H.; Qin, F.X.; Xing, D.W.; Cao, F.Y.; Wang, X.D.; Peng, H.X.; Sun, J.F. Relating residual stress and microstructure to mechanical and giant magneto-impedance properties in cold-drawn Co-based amorphous microwires. Acta Mater. 2012, 60, 5425–5436. [Google Scholar] [CrossRef]
- Luo, L.; Law, J.Y.; Shen, H.; Moreno-Ramírez, L.M.; Franco, V.; Guo, S.; Duc, N.T.M.; Sun, J.; Phan, M.-H. Enhanced Magnetocaloric Properties of Annealed Melt-Extracted Mn1.3Fe0.6P0.5Si0.5 Microwires. Metals 2022, 12, 1536. [Google Scholar] [CrossRef]
- Liu, Y.; Lang, Z.; Shen, H.; Liu, J.; Sun, J. Martensitic Transition and Superelasticity of Ordered Heat Treatment Ni-Mn-Ga-Fe Microwires. Metals 2022, 12, 1546. [Google Scholar] [CrossRef]
- Shen, H.; Luo, L.; Belliveau, H.; Jiang, S.; Liu, J.; Zhang, L.; Huang, Y.; Sun, J.; Phan, M.-H. The Magnetocaloric Behaviors of Gd-based Microwire Arrays with Different Curie Temperatures. Metals 2022, 12, 1417. [Google Scholar] [CrossRef]
- Chizhik, A.; Corte-León, P.; Zhukova, V.; Gonzalez, J.; Zhukov, A. MOKE studies of magnetic microwires with longitudinally distributed properties. J. Magn. Magn. Mater. 2022, 547, 168824. [Google Scholar] [CrossRef]
- Zhukova, V.; Larin, V.S.; Zhukov, A. Stress induced magnetic anisotropy and giant magnetoimpedance in Fe-rich glass-coated magnetic microwires. J. Appl. Phys. 2003, 94, 1115–1118. [Google Scholar] [CrossRef]
- Liu, J.S.; Qin, F.X.; Chen, D.M.; Shen, H.X.; Wang, H.; Xing, D.W.; Phan, M.H.; Sun, J.F. Combined current-modulation annealing induced enhancement of giant magnetoimpedance effect of Co-rich amorphous microwires. J. Appl. Phys. 2014, 115, 17A326. [Google Scholar] [CrossRef]
- Sun, J.F.; Liu, J.S.; Xing, D.W.; Xue, X. Experimental study on the effect of alternating-current amplitude on GMI output stability of Co-based amorphous wires. Phys. Status Solidi A 2011, 208, 910–914. [Google Scholar] [CrossRef]
- Pirota, K.R.; Kraus, L.; Chiriac, H.; Knobel, M. Magnetostriction and GMI in Joule-heated CoFeSiB glass-covered microwires. J. Magn. Magn. Mater. 2001, 226–230, 730–732. [Google Scholar] [CrossRef]
- Chen, D.M.; Xing, D.W.; Qin, F.X.; Liu, J.S.; Wang, H.; Xing, D.W.; Sun, J.F. Correlation of magnetic domains, microstructure and GMI effect of Joule-annealed melt-extracted Co68.15Fe4.35Si12.25B13.75Nb1Cu0.5 microwires for double functional sensors. Phys. Status Solidi A 2013, 210, 2515–2520. [Google Scholar] [CrossRef]
- Liu, J.S.; Du, Z.X.; Jiang, S.D.; Shen, H.X.; Li, Z.; Xing, D.W.; Ma, W.; Sun, J.F. Tailoring giant magnetoimpedance effect of Co-based microwires for optimum efficiency by self-designed square-wave pulse current annealing. J. Magn. Magn. Mater. 2015, 385, 145–150. [Google Scholar] [CrossRef]
- Pirota, K.R.; Kraus, L.; Chiriac, H.; Knobel, M. Magnetic properties and giant magnetoimpedance in a CoFeSiB glass-covered microwire. J. Magn. Magn. Mater. 2000, 221, L243–L247. [Google Scholar] [CrossRef]
- Wang, H.; Qin, F.X.; Xing, D.W.; Cao, F.Y.; Peng, H.X.; Sun, J.F. Fabrication and characterization of nano/amorphous dual-phase FINEMET microwires. Mater. Sci. Eng. B 2013, 178, 1483–1490. [Google Scholar] [CrossRef]
- Rudkowski, P.; Rudkowska, G.; Ström-Olsen, J.O. The fabrication of fine metallic fibers by continuous melt-extraction and their magnetic and mechanical properties. Mater. Sci. Eng. A 1991, 133, 158–161. [Google Scholar] [CrossRef]
- Rudkowski, P.; Rudkowska, G.; Ström-Olsen, J.O.; Zeller, C.; Cordery, R. The magnetic properties of sub-20-μm metallic fibers formed by continuous melt extraction. J. Appl. Phys. 1991, 69, 5017–5019. [Google Scholar] [CrossRef]
- Kraus, L. Theory of giant magneto-impedance in the planar conductor with uniaxial magnetic anisotropy. J. Magn. Magn. Mater. 1999, 195, 764–788. [Google Scholar] [CrossRef]
- Lachowicz, H.K.; Garcia, K.L.; KuMiński, M.; Zhukov, A.; Vázquez, M. Skin-effect and circumferential permeability in micro-wires utilized in gmi-sensors. Sens. Acta. A 2005, 119, 384–389. [Google Scholar] [CrossRef]
- Chen, D.X.; Munoz, J.L.; Hernando, A.; Vázquez, M. Magnetoimpedance of metallic ferromagnetic wires. Phys. Rev. B 1998, 57, 10699–10704. [Google Scholar] [CrossRef]
- Kraus, L.; Frait, Z.; Pirota, K.R.; Chiriac, H. Giant magnetoimpedance in glass-covered amorphous microwires. J. Magn. Magn. Mater. 2003, 254, 399–403. [Google Scholar] [CrossRef]
- Herzer, G. Modern soft magnets: Amorphous and nanocrystalline materials. Acta Mater. 2013, 61, 718–734. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Liu, J.; Zhang, L.; Shen, H.; Sun, J. Large Linear Giant Magneto-Impedance Response of Microwire Annealed under Liquid Medium for Potential Sensor Applications. Metals 2022, 12, 1926. https://doi.org/10.3390/met12111926
Chen D, Liu J, Zhang L, Shen H, Sun J. Large Linear Giant Magneto-Impedance Response of Microwire Annealed under Liquid Medium for Potential Sensor Applications. Metals. 2022; 12(11):1926. https://doi.org/10.3390/met12111926
Chicago/Turabian StyleChen, Dongming, Jingshun Liu, Lunyong Zhang, Hongxian Shen, and Jianfei Sun. 2022. "Large Linear Giant Magneto-Impedance Response of Microwire Annealed under Liquid Medium for Potential Sensor Applications" Metals 12, no. 11: 1926. https://doi.org/10.3390/met12111926
APA StyleChen, D., Liu, J., Zhang, L., Shen, H., & Sun, J. (2022). Large Linear Giant Magneto-Impedance Response of Microwire Annealed under Liquid Medium for Potential Sensor Applications. Metals, 12(11), 1926. https://doi.org/10.3390/met12111926







