Elastic Thermal Deformation of an Infinite Copper Material Due to Cyclic Heat Supply Using Higher-Order Nonlocal Thermal Modeling
Abstract
:1. Introduction
2. Nonlocal Fractional Thermoviscoelastic Model
3. Statement of the Problem
The Analytical Solution in the Laplace’s Domain
4. Inversion Technique
5. Special Cases
5.1. Thermoelastic Models
5.2. Thermoviscoelastic Models
5.3. Fractional Thermoviscoelastic Models
5.4. Nonlocal Fractional Thermoviscoelastic Models:
6. Results and Discussion
- Comparing the thermoelastic properties of a material by considering the impact of higher-order parameters m and n.
- Comparing different thermoviscoelastic models including the fractional order derivatives.
- Comparing the classical and nonlocal thermoviscoelastic models.
6.1. Verification of the Results
6.2. The Influence of Time Derivatives of Higher-orders
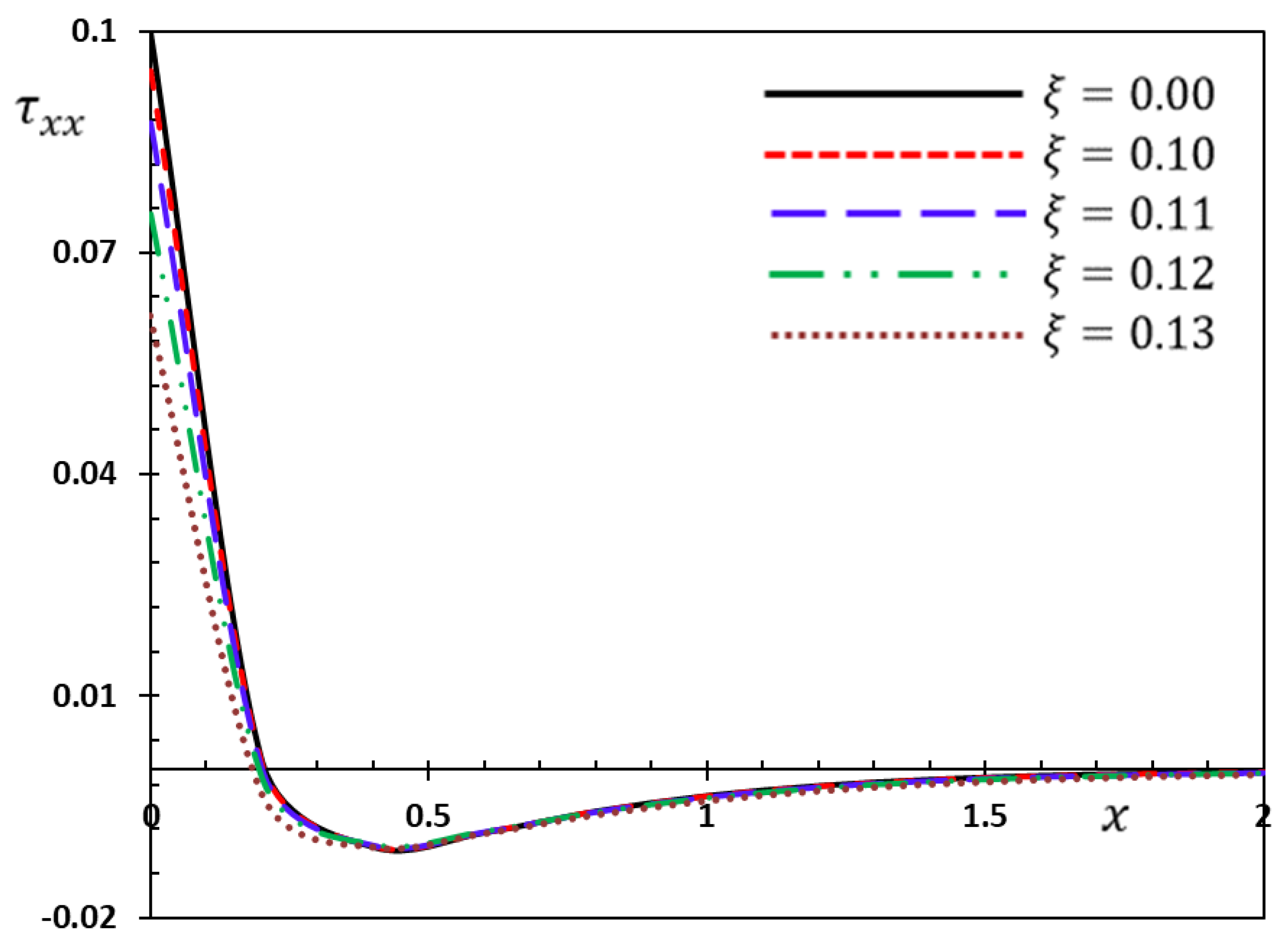
6.3. The Effect of Nonlocal Parameter
6.4. The Influence of Viscoelasticity and Various Fractional Orders
7. Conclusions
- It is necessary to consider the effect of non-local parameters to estimate the thermomechanical behavior of nanosystems.
- The selection of higher-orders may vary from case to case and some experiments must be conducted to determine the values of higher-orders terms.
- As the coefficients of higher-order derivatives increase, a specific reduction in temperature can be seen.
- The propagation of heat waves and the variation of physical variables are profoundly affected by thermoviscoelastic features of nanomaterials.
- The numerical results under the influence of models with fractional derivatives differ from those in the case of those theories including integer derivatives.
- Numerical investigations showed that the fractional derivative models may be suitable for simulating the viscoelastic materials. These results represented a significant departure from previous approaches and exhibited a transition to a new paradigm, namely the theory of nonlocal thermoviscoelasticity based on the higher-order partial differential equations.
- The nonlocal parameter may emerge as a significant criterion in categorizing particular materials when the transmission of thermal energy is of concern in miniaturized systems and devices.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abazari, A.M.; Safavi, S.M.; Rezazadeh, G.; Villanueva, L.G. Modelling the Size Effects on the Mechanical Properties of Micro/Nano Structures. Sensors 2015, 15, 28543–28562. [Google Scholar] [CrossRef] [PubMed]
- Jena, S.K.; Chakraverty, S.; Malikan, M.; Mohammad-Sedighi, H. Hygro-Magnetic Vibration of the Single-Walled Carbon Nanotube with Nonlinear Temperature Distribution Based on a Modified Beam Theory and Nonlocal Strain Gradient Model. Int. J. Appl. Mech. 2020, 12, 2050054. [Google Scholar] [CrossRef]
- Durkan, C.; Welland, M.E. Size effects in the electrical resistivity of polycrystalline nanowires. Phys. Rev. B 2000, 61, 14215–14218. [Google Scholar] [CrossRef]
- Mengotti, E.; Heyderman, L.J.; Rodríguez, A.F.; Nolting, F.; Hügli, R.V.; Braun, H.-B. Real-space observation of emergent magnetic monopoles and associated Dirac strings in artificial kagome spin ice. Nat. Phys. 2011, 7, 68–74. [Google Scholar] [CrossRef]
- Villanueva, L.G.; Karabalin, R.B.; Matheny, M.H.; Chi, D.; Sader, J.; Roukes, M.L. Nonlinearity in nanomechanical cantilevers. Phys. Rev. B 2013, 87, 024304. [Google Scholar] [CrossRef]
- Ghodrati, B.; Yaghootian, A.; Zadeh, A.G.; Mohammad-Sedighi, H. Lamb wave extraction of dispersion curves in micro/nano-plates using couple stress theories. Waves Random Complex Media 2018, 28, 15–34. [Google Scholar] [CrossRef]
- Zare, J.; Shateri, A.; Beni, Y.T.; Ahmadi, A. Vibration analysis of shell-like curved carbon nanotubes using nonlocal strain gradient theory. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Civalek, Ö.; Dastjerdi, S.; Akgöz, B. Buckling and free vibrations of CNT-reinforced cross-ply laminated composite plates. Mech. Based Des. Struct. Mach. 2020, 50, 1914–1931. [Google Scholar] [CrossRef]
- Akgoz, B.; Civalek, O. Thermo-mechanical buckling behavior of functionally graded microbeams embedded in elastic medium. Int. J. Eng. Sci. 2014, 85, 90–104. [Google Scholar] [CrossRef]
- Sae-Long, W.; Limkatanyu, S.; Sukontasukkul, P.; Damrongwiriyanupap, N.; Rungamornrat, J.; Prachasaree, W. Fourth-order strain gradient bar-substrate model with nonlocal and surface effects for the analysis of nanowires embedded in substrate media. Facta Univ. Ser. Mech. Eng. 2021, 19, 657–680. [Google Scholar] [CrossRef]
- Civalek, Ö.; Demir, C. A simple mathematical model of microtubules surrounded by an elastic matrix by nonlocal finite element method. Appl. Math. Comput. 2016, 289, 335–352. [Google Scholar] [CrossRef]
- Koutsoumaris, C.C.; Eptaimeros, K.G.; Tsamasphyros, G.J. A different approach to Eringen’s nonlocal integral stress model with applications for beams. Int. J. Solids Struct. 2017, 112, 222–238. [Google Scholar] [CrossRef]
- E Abouelregal, A. Thermoelastic fractional derivative model for exciting viscoelastic microbeam resting on Winkler foundation. J. Vib. Control 2021, 27, 2123–2135. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.-C.; Edelen, D.-B. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Inan, E.; Eringen, A. Nonlocal theory of wave propagation in thermoelastic plates. Int. J. Eng. Sci. 1991, 29, 831–843. [Google Scholar] [CrossRef]
- Sarrami-Foroushani, S.; Azhari, M. Nonlocal vibration and buckling analysis of single and multi-layered graphene sheets using finite strip method including van der Waals effects. Phys. E Low-Dimens. Syst. Nanostructures 2014, 57, 83–95. [Google Scholar] [CrossRef]
- Lim, C.; Zhang, G.; Reddy, J. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Ma, H.; Gao, X.-L.; Reddy, J. A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. J. Mech. Phys. Solids 2008, 56, 3379–3391. [Google Scholar] [CrossRef]
- Silling, S. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef] [Green Version]
- Nawaz, Y.; Arif, M.S.; Abodayeh, K. A Third-Order Two-Stage Numerical Scheme for Fractional Stokes Problems: A Comparative Computational Study. J. Comput. Nonlinear Dynam. 2022, 17, 101004. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S.; Abodayeh, K. An explicit-implicit numerical scheme for time fractional boundary layer flows. Int. J. Numer. Methods Fluids 2022, 94, 920–940. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Mohammad-Sedighi, H.; Faghidian, S.A.; Shirazi, A.H. Temperature-dependent physical characteristics of the rotating nonlocal nanobeams subject to a varying heat source and a dynamic load. Facta Univ. Ser. Mech. Eng. 2021, 19, 633–656. [Google Scholar] [CrossRef]
- Nasr, M.E.; Abouelregal, A.E.; Soleiman, A.; Khalil, K.M. Thermoelastic Vibrations of Nonlocal Nanobeams Resting on a Pasternak Foundation via DPL Model. J. Appl. Comput. Mech. 2021, 7, 34–44. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Mohammed, W.W.; Mohammad-Sedighi, H. Vibration analysis of functionally graded microbeam under initial stress via a generalized thermoelastic model with dual-phase lags. Arch. Appl. Mech 2021, 91, 2127–2142. [Google Scholar] [CrossRef]
- Abouelregal, A.; Ersoy, H.; Civalek, Ö. Solution of Moore–Gibson–Thompson Equation of an Unbounded Medium with a Cylindrical Hole. Mathematics 2021, 9, 1536. [Google Scholar] [CrossRef]
- Abouelregal, A.E. Thermomagnetic behavior of a nonlocal finite elastic rod heated by a moving heat source via a fractional derivative heat equation with a non-singular kernel. Waves Random Complex Media 2021, 1–21. [Google Scholar] [CrossRef]
- Abouelregal, A.E. A novel model of nonlocal thermoelasticity with time derivatives of higher order. Math. Methods Appl. Sci. 2020, 43, 6746–6760. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M. The Size-Dependent Thermoelastic Vibrations of Nanobeams Subjected to Harmonic Excitation and Rectified Sine Wave Heating. Mathematics 2020, 8, 1128. [Google Scholar] [CrossRef]
- E Aboueregal, A.; Sedighi, H.M. The effect of variable properties and rotation in a visco-thermoelastic orthotropic annular cylinder under the Moore–Gibson–Thompson heat conduction model. Proc. Inst. Mech. Eng. Part L: J. Mater. Des. Appl. 2021, 235, 1004–1020. [Google Scholar] [CrossRef]
- Fotouhi, M.; Fragassa, C.; Fotouhi, S.; Saghafi, H.; Minak, G. Damage Characterization of Nano-Interleaved CFRP under Static and Fatigue Loading. Fibers 2019, 7, 13. [Google Scholar] [CrossRef] [Green Version]
- Giaglianoni, W.; Cunha, M.; Bergmann, C.; Fragassa, C.; Pavlovic, A. Synthesis, Characterization and Application by HVOF of a WCCoCr/NiCr Nanocomposite as Protective Coating Against Erosive Wear. Tribol. Ind. 2018, 40, 477–487. [Google Scholar] [CrossRef]
- Fragassa, C.; Cristiano, F. Modelling the viscoelastic response of ceramic materials by commercial finite elements codes. FME Trans. 2016, 44, 58–64. [Google Scholar] [CrossRef] [Green Version]
- Tzou, D.Y. A Unified Field Approach for Heat Conduction from Macro- to Micro-Scales. J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Tzou, D.Y. The generalized lagging response in small-scale and high-rate heating. Int. J. Heat Mass Transf. 1995, 38, 3231–3240. [Google Scholar] [CrossRef]
- Tzou, D.-Y. Macro-to Microscale Heat Transfer: The Lagging Behavior; Taylor & Francis: New York, NY, USA, 1997. [Google Scholar]
- Abouelregal, A. On Green and Naghdi Thermoelasticity Model without Energy Dissipation with Higher Order Time Differential and Phase-Lags. J. Appl. Comput. Mech. 2020, 6, 445–456. [Google Scholar] [CrossRef]
- Abouelregal, A. A novel generalized thermoelasticity with higher-order time-derivatives and three-phase lags. Multidiscip. Model. Mater. Struct. 2019, 16, 689–711. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Fourier, J.B.J. Analytical Theory of Heat; Encyclopedia Britannica, Inc.: Chicago IL, USA, 1952. [Google Scholar]
- Chandrasekharaiah, D.S. Hyperbolic Thermoelasticity: A Review of Recent Literature. Appl. Mech. Rev. 1998, 51, 705–729. [Google Scholar] [CrossRef]
- Quintanilla, R.; Racke, R. A note on stability in dual-phase-lag heat conduction. Int. J. Heat Mass Transf. 2006, 49, 1209–1213. [Google Scholar] [CrossRef]
- Chiriţă, S.; Ciarletta, M.; Tibullo, V. On the thermomechanical consistency of the time differential dual-phase-lag models of heat conduction. Int. J. Heat Mass Transf. 2017, 114, 277–285. [Google Scholar] [CrossRef]
- Chiriţă, S.; Ciarletta, M.; Tibullo, V. On the wave propagation in the time differential dual-phase-lag thermoelastic model. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2015, 471, 20150400. [Google Scholar] [CrossRef]
- Chiriţă, S. High-order approximations of three-phase-lag heat conduction model: Some qualitative results. J. Therm. Stress. 2018, 41, 608–626. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J. 1985, 23, 918–925. [Google Scholar] [CrossRef]
- Bagley, R. On the equivalence of the Riemann–Liouville and the Caputo fractional order derivatives in modeling of linear viscoelastic materials. Fract. Calcul. Appl. Anal. 2007, 10, 123–126. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity—An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Taylor & Francis: London, UK, 2002. [Google Scholar]
- Caputo, M.; Fabrizio, M. On the notion of fractional derivative and applications to the hysteresis phenomena. Meccanica 2017, 52, 3043–3052. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and nonsingular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Atangana, A.; Baleanu, D. Caputo-Fabrizio Derivative Applied to Groundwater Flow within Confined Aquifer. J. Eng. Mech. 2016, 143, D4016005. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. Chaos in a simple nonlinear system with Atangana–Baleanu derivatives with fractional order. Chaos Solitons Fractals 2016, 89, 447–454. [Google Scholar] [CrossRef]
- Frederico Gastao, S.F.; Torres Delfim, F.M. Fractional optimal control in the sense of Caputo and the fractional Noether’s theorem. Int. Math. Forum 2008, 3, 1–17. [Google Scholar]
- Ezzat, M.; Youssef, H.M. State Space Approach for Conducting Magneto-Thermoelastic Medium with Variable Electrical and Thermal Conductivity Subjected to Ramp-Type Heating. J. Therm. Stress. 2009, 32, 414–427. [Google Scholar] [CrossRef]
- Youssef, H. Generalized magneto-thermoelasticity in a conducting medium with variable material properties. Appl. Math. Comput. 2006, 173, 822–833. [Google Scholar] [CrossRef]
- Abbas, I.A.; Youssef, H. Finite element analysis of two-temperature generalized magneto-thermoelasticity. Arch. Appl. Mech. 2009, 79, 917–925. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Abd-Elaziz, E.M. Effect of initial stress and Hall current on a magneto-thermoelastic porous medium with microtemperatures. Indian J. Phys. 2019, 93, 475–485. [Google Scholar] [CrossRef]
- Kaur, I.; Lata, P.; Singh, K. Effect of Hall current in transversely isotropic magneto-thermoelastic rotating medium with fractional-order generalized heat transfer due to ramp-type heat. Indian J. Phys. 2021, 95, 1165–1174. [Google Scholar] [CrossRef]
- Bachher, M.; Sarkar, N. Nonlocal theory of thermoelastic materials with voids and fractional derivative heat transfer. Waves Random Complex Media 2019, 29, 595–613. [Google Scholar] [CrossRef]
- Sarkar, N. On the discontinuity solution of the Lord–Shulman model in generalized thermoelasticity. Appl. Math. Comput. 2013, 219, 10245–10252. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Mohammad-Sedighi, H.; Shirazi, A.H.; Malikan, M.; Eremeyev, V.A. Computational analysis of an infinite magneto-thermoelastic solid periodically dispersed with varying heat flow based on non-local Moore–Gibson–Thompson approach. Contin. Mech. Thermodyn. 2021, 34, 1067–1085. [Google Scholar] [CrossRef]
- Zakian, V. Numerical inversions of Laplace transforms. Electron. Lett. 1969, 327, 120–121. [Google Scholar] [CrossRef]
- Halsted, D.J.; Brown, D.E. Zakian’s technique for inverting Laplace transform. Chem. Eng. J. 1972, 3, 312–313. [Google Scholar] [CrossRef]
- Zakian, V. Properties of IMN approximants. In Pade Approximants and Their Applications; Graves-Morris, P.R., Ed.; Academic Press: London, UK, 1973. [Google Scholar]
- Solnechnyi, E.M.; Cheremushkina, L.A. Dynamic Properties of a One-Dimensional Heat Transfer System with a Moving Heat Source. Autom. Remote Control 2022, 83, 1172–1179. [Google Scholar] [CrossRef]
- Banik, S.; Kanoria, M. Generalized thermoelastic interaction in a functionally graded isotropic unbounded medium due to varying heat source with three-phase-lag effect. Math. Mech. Solids 2012, 18, 231–245. [Google Scholar] [CrossRef]
- Das, A.; Das, B. One dimensional coupled thermoelastic problem due to periodic heating in a semi-infinite rod. IOSR J. Math. 2012, 3, 15–18. [Google Scholar]
- Kostyrko, S.; Grekov, M.; Altenbach, H. Stress concentration analysis of nanosized thin-film coating with rough interface. Contin. Mech. Thermodyn. 2019, 31, 1863–1871. [Google Scholar] [CrossRef]
- Chiriţă, S. On the time differential dual-phase-lag thermoelastic model. Meccanica 2017, 52, 349–361. [Google Scholar] [CrossRef]
- Ge, X.; Li, P.; Fang, Y.; Yang, L. Thermoelastic damping in rectangular microplate/nanoplate resonators based on modified nonlocal strain gradient theory and nonlocal heat conductive law. J. Therm. Stress. 2021, 44, 690–714. [Google Scholar] [CrossRef]
- Kumar, R.; Miglani, A.; Rani, R. Transient analysis of nonolocal microstretch thermoelastic thick circular plate with phase lags. Med. J. Model. Simul. 2018, 09, 25–42. [Google Scholar]


| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
| NFCVTE | NFVLS | NFVDPL | NHFVDPL | ||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0.0844468 | 0.0784302 | 0.0740956 | 0.0779163 | 0.0778836 | 0.0778821 | 0.077882 |
| 0.2 | 0.0198698 | 0.0204628 | 0.0208263 | 0.020509 | 0.0205119 | 0.020512 | 0.020512 |
| 0.4 | 0.00479804 | 0.00545069 | 0.00595733 | 0.00550921 | 0.00551295 | 0.00551313 | 0.00551313 |
| 0.6 | 0.00124161 | 0.00152758 | 0.00177424 | 0.00155494 | 0.0015567 | 0.00155678 | 0.00155678 |
| 0.8 | 0.000375976 | 0.000478265 | 0.000575092 | 0.000488623 | 0.000489292 | 0.000489323 | 0.000489325 |
| 1.0 | 0.000147462 | 0.000181334 | 0.000216234 | 0.000184943 | 0.000185178 | 0.000185189 | 0.000185189 |
| 1.2 | 7.54928 × 10−5 | 8.65688 × 10−5 | 9.88161 × 10−5 | 8.77989 × 10−5 | 0.000087879 | 8.78828 × 10−5 | 8.78829 × 10−5 |
| 1.4 | 0.000045809 | 4.96237 × 10−5 | 5.40217 × 10−5 | 5.00569 × 10−5 | 5.00852 × 10−5 | 5.00865 × 10−5 | 5.00866 × 10−5 |
| 1.6 | 3.00219 × 10−5 | 3.15135 × 10−5 | 3.32245 × 10−5 | 3.16817 × 10−5 | 3.16927 × 10−5 | 3.16932 × 10−5 | 3.16932 × 10−5 |
| 1.8 | 2.02587 × 10−5 | 2.09575 × 10−5 | 2.17188 × 10−5 | 2.10336 × 10−5 | 2.10386 × 10−5 | 2.10388 × 10−5 | 2.10388 × 10−5 |
| 2.0 | 1.38121 × 10−5 | 1.42001 × 10−5 | 1.45952 × 10−5 | 1.42407 × 10−5 | 1.42433 × 10−5 | 1.42434 × 10−5 | 1.42434 × 10−5 |
| NFCVTE | NFVLS | NFVDPL | NHFVDPL | ||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.2 | −0.0295324 | −0.0329637 | −0.035788 | −0.033282 | −0.0333024 | −0.0333034 | −0.0333034 |
| 0.4 | −0.0231758 | −0.0266085 | −0.0295354 | −0.0269338 | −0.0269547 | −0.0269557 | −0.0269558 |
| 0.6 | −0.0152206 | −0.0177062 | −0.0198766 | −0.0179452 | −0.0179606 | −0.0179613 | −0.0179613 |
| 0.8 | −0.00961635 | −0.0112476 | −0.0126914 | −0.0114056 | −0.0114158 | −0.0114163 | −0.0114163 |
| 1.0 | −0.00601749 | −0.00705283 | −0.00797554 | −0.00715354 | −0.00716003 | −0.00716033 | −0.00716034 |
| 1.2 | −0.00375625 | −0.00440594 | −0.00498682 | −0.00446925 | −0.00447333 | −0.00447352 | −0.00447352 |
| 1.4 | −0.00234325 | −0.00274939 | −0.00311304 | −0.002789 | −0.00279155 | −0.00279167 | −0.00279167 |
| 1.6 | −0.00146154 | −0.00171512 | −0.00194231 | −0.00173985 | −0.00174145 | −0.00174152 | −0.00174152 |
| 1.8 | −0.000911561 | −0.00106982 | −0.00121166 | −0.00108526 | −0.00108625 | −0.0010863 | −0.0010863 |
| 2.0 | −0.000568533 | −0.000667289 | −0.00075582 | −0.00067693 | −0.000677546 | −0.000677576 | −0.000677577 |
| NFCVTE | NFVLS | NFVDPL | NHFVDPL | ||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0.0887013 | 0.0941639 | 0.0985205 | 0.0946607 | 0.0946925 | 0.094694 | 0.0946941 |
| 0.2 | −0.000735809 | 0.000590091 | 0.0017973 | 0.000721137 | 0.000729581 | 0.000729978 | 0.000729992 |
| 0.4 | −0.00948806 | −0.0102996 | −0.0109006 | −0.0103704 | −0.0103749 | −0.0103751 | −0.0103751 |
| 0.6 | −0.00737191 | −0.0083814 | −0.00922206 | −0.0084758 | −0.00848186 | −0.00848214 | −0.00848215 |
| 0.8 | −0.00483203 | −0.00558685 | −0.00624065 | −0.0056591 | −0.00566374 | −0.00566396 | −0.00566397 |
| 1.0 | −0.00305141 | −0.00355059 | −0.00399112 | −0.00359889 | −0.00360199 | −0.00360214 | −0.00360215 |
| 1.2 | −0.00190921 | −0.00222671 | −0.00250938 | −0.00225758 | −0.00225957 | −0.00225966 | −0.00225966 |
| 1.4 | −0.00119173 | −0.00139109 | −0.00156928 | −0.00141052 | −0.00141177 | −0.00141183 | −0.00141183 |
| 1.6 | −0.000743429 | −0.000868077 | −0.000979677 | −0.00088023 | −0.000881016 | −0.000881053 | −0.000881054 |
| 1.8 | −0.000463694 | −0.000541523 | −0.000611258 | −0.00054912 | −0.000549605 | −0.000549628 | −0.000549629 |
| 2.0 | −0.000289205 | −0.00033778 | −0.000381319 | −0.00034252 | −0.000342825 | −0.000342839 | −0.00034284 |
| Thermoelasticity | Thermo-Viscoelasticity | Fractional Thermoviscoelasticity | |||
|---|---|---|---|---|---|
| 0.0 | 0.0781856 | 0.077936 | 0.0780195 | 0.0780846 | 0.0781426 |
| 0.2 | 0.0206431 | 0.0205212 | 0.0205463 | 0.0205781 | 0.0206058 |
| 0.4 | 0.0055038 | 0.00549451 | 0.00547669 | 0.00547944 | 0.00548102 |
| 0.6 | 0.00150279 | 0.00153666 | 0.00151044 | 0.00150223 | 0.00149423 |
| 0.8 | 0.000433526 | 0.00047608 | 0.000455001 | 0.000444614 | 0.000434965 |
| 1.0 | 0.000139912 | 0.000178855 | 0.000165263 | 0.000155729 | 0.000147098 |
| 1.2 | 5.41505 × 10−5 | 8.63547 × 10−5 | 7.89724 × 10−5 | 7.10159 × 10−5 | 6.39757 × 10−5 |
| 1.4 | 2.58301 × 10−5 | 5.13507 × 10−5 | 4.82947 × 10−5 | 4.18825 × 10−5 | 3.63333 × 10−5 |
| 1.6 | 1.45214 × 10−5 | 3.43223 × 10−5 | 3.40053 × 10−5 | 0.000028907 | 2.45912 × 10−5 |
| 1.8 | 8.97000 × 10−6 | 2.41463 × 10−5 | 2.54236 × 10−5 | 0.000021392 | 1.80528 × 10−5 |
| 2.0 | 5.79000 × 10−6 | 1.73287 × 10−5 | 1.94329 × 10−5 | 1.62522 × 10−5 | 1.36739 × 10−5 |
| Thermoelasticity | Thermo− Viscoelasticity | Fractional Thermoviscoelasticity | |||
|---|---|---|---|---|---|
| 0.0 | 0 | 0 | 0 | 0 | 0 |
| 0.2 | −0.0280434 | −0.024395 | −0.0214702 | −0.0199903 | −0.0183262 |
| 0.4 | −0.024019 | −0.0194781 | −0.0195899 | −0.0181806 | −0.0166709 |
| 0.6 | −0.0170699 | −0.0127567 | −0.0149597 | −0.0138282 | −0.0126798 |
| 0.8 | −0.0116206 | −0.00795342 | −0.0109903 | −0.0101148 | −0.00927362 |
| 1.0 | −0.00782119 | −0.00488853 | −0.00799708 | −0.0073269 | −0.0067164 |
| 1.2 | −0.00524755 | −0.00299181 | −0.00580481 | −0.00529412 | −0.00485208 |
| 1.4 | −0.00351774 | −0.0018286 | −0.00421086 | −0.00382284 | −0.00350296 |
| 1.6 | −0.00235758 | −0.00111719 | −0.0030541 | −0.00275997 | −0.00252854 |
| 1.8 | −0.00157993 | −0.000682468 | −0.00221502 | −0.00199253 | −0.00182509 |
| 2.0 | −0.00105878 | −0.00041689 | −0.00160645 | −0.00143847 | −0.00131732 |
| Thermoelasticity | Thermo− Viscoelasticity | Fractional Thermoviscoelasticity | |||
|---|---|---|---|---|---|
| 0.0 | 0.0943924 | 0.0524847 | 0.0276607 | 0.0240686 | 0.0222463 |
| 0.2 | 0.000881063 | −0.00108605 | −0.0203086 | −0.0180733 | −0.0164797 |
| 0.4 | −0.0110335 | −0.00688164 | −0.0222848 | −0.0196959 | −0.0180083 |
| 0.6 | −0.00956015 | −0.00537017 | −0.0175763 | −0.0154659 | −0.0141468 |
| 0.8 | −0.00681027 | −0.00349919 | −0.0130119 | −0.0113991 | −0.0104267 |
| 1.0 | −0.00463903 | −0.00217852 | −0.00948645 | −0.00827316 | −0.0075664 |
| 1.2 | −0.00312279 | −0.00133844 | −0.00688932 | −0.00598084 | −0.00546893 |
| 1.4 | −0.0020953 | −0.000819026 | −0.00499821 | −0.00431927 | −0.00394882 |
| 1.6 | −0.00140462 | −0.00050057 | −0.00362528 | −0.00311849 | −0.00285047 |
| 1.8 | −0.000941376 | −0.000305822 | −0.00262929 | −0.00225137 | −0.00205747 |
| 2.0 | −0.000630866 | −0.00018682 | −0.0019069 | −0.00162534 | −0.00148506 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abouelregal, A.E.; Sedighi, H.M. Elastic Thermal Deformation of an Infinite Copper Material Due to Cyclic Heat Supply Using Higher-Order Nonlocal Thermal Modeling. Metals 2022, 12, 1927. https://doi.org/10.3390/met12111927
Abouelregal AE, Sedighi HM. Elastic Thermal Deformation of an Infinite Copper Material Due to Cyclic Heat Supply Using Higher-Order Nonlocal Thermal Modeling. Metals. 2022; 12(11):1927. https://doi.org/10.3390/met12111927
Chicago/Turabian StyleAbouelregal, Ahmed E., and Hamid M. Sedighi. 2022. "Elastic Thermal Deformation of an Infinite Copper Material Due to Cyclic Heat Supply Using Higher-Order Nonlocal Thermal Modeling" Metals 12, no. 11: 1927. https://doi.org/10.3390/met12111927
APA StyleAbouelregal, A. E., & Sedighi, H. M. (2022). Elastic Thermal Deformation of an Infinite Copper Material Due to Cyclic Heat Supply Using Higher-Order Nonlocal Thermal Modeling. Metals, 12(11), 1927. https://doi.org/10.3390/met12111927






