Optimization of Process Parameters for Powder Bed Fusion Additive Manufacturing Using a Linear Programming Method: A Conceptual Framework

Abstract

At present, the selection of optimal technological parameters for laser powder bed fusion (LPBF) is determined by the requirements of the fusion process. The main parameters that are commonly varied include laser power (P), scanning speed (v), hatch spacing (h), and layer thickness (t). The productivity of the LPBF process (the increment in the fused volume of the material) is equal to the product of the last three parameters, and the mechanical properties are largely determined by the volumetric fusion energy density, which is equal to the ratio of laser power to productivity. While ensuring maximum process productivity, it is possible to obtain acceptable quality characteristics—mechanical properties, surface roughness, etc.—for a certain range of LPBF technological parameters. In these cases, several quality characteristics act as constraints on the optimization process, and productivity and the key quality characteristics become components of the objective function. Therefore, this article proposes a formalized representation of the optimization problem for the LPBF process, including the derivation of the objective function with the constraint matrix, and provides a solution to the problem using the linear programming (LP) method. The advantages of the proposed method include the guaranteed convergence of the solution with an unlimited number of constraints; the disadvantage concerns the adequacy of the solution, which is limited by a relatively narrow range of parameter changes. The proposed method was tested in determining the optimal LPBF parameters for an HN58MBYu powder LP model that included 13 constraints and an objective function with two target parameters. The obtained results made it possible to increase the productivity by 15% relative to the basic technological parameters.

1. Introduction

Additive manufacturing (AM) technologies produce three dimensional physical objects from digital information through a special technique of depositing metal on the previous layer [1,2,3,4,5]. AM is defined as “a process of joining materials to make parts from 3D model data, usually layer upon layer, as opposed to subtractive manufacturing and formative manufacturing methodologies” by ASTM and ISO standards [4]. A new approach embedded in AM makes it possible to obtain new consumer properties in as-built parts. Metal AM technology contains several processing parameters (variables), which makes it challenging to correlate them with the desired properties and quality characteristics when optimizing them. Every additive manufacturing process has its own variety of process parameters, which, in combination with material properties and environmental conditions, influence the quality of fabricated parts. The capability of AM to fabricate freeform designs makes it very suitable for the aerospace industry. Among various AM technologies, laser powder bed fusion (LPBF) provides the highest precision when forming desired part shapes [1,2]. The main parameters that are commonly varied include layer thickness (t), scanning speed (v), laser power (P), and hatch spacing (h) [6].

The correlations between the LPBF processing parameters and the various properties of the fabricated parts, such as tensile behavior [7], surface quality [8], mechanical performance [9], and fatigue properties [10], have been the subject of various studies.

To determine the optimal processing parameters, it is necessary to create AM models. Chen [3] categorized AM modeling studies into empirical, analytical, and numerical models, along with machine-learning techniques. Practical experiments suitable for empirical models are expensive, especially for metal powder [11], making the detection of parameters that influence the quality of as-built parts a more challenging task [12]. Numerous studies can be found in the literature on the application of design of experiments (DoE) methods (e.g., Taguchi, half-factorial design, central composite design, etc.) and analysis of variance (ANOVA) to define the parameters and parameter combinations that influence the types of properties of as-built parts [13,14,15]. A full factorial DoE method consists of equal numbers of replicates for all the possible combinations of the levels (values) of each of the processing parameters. The advantage of this approach is that it provides the exact response for the effects of parameters and all of the combinations of their interactions [16]. Krishnan et al. [17] used a full factorial DoE method with three levels of three factors to evaluate the most significant factor affecting the mechanical properties of LPBF-manufactured AlSi10Mg specimens. Laser power, scanning speed, and hatch spacing were among these parameters, and hatch spacing was the parameter with the most significant influence. Linares et al. used a rough and refined DoE method to target the best combination of process parameters for optimization of 17-4PH steel fatigue life [18]. However, employing a full factorial DoE method leads to high costs and time losses in the manufacturing of specimens and modeling of correlations between the characterization and the process parameters [19]. Therefore, fractional factorial DoE methods are required to evaluate the most significant process variables, such as the Taguchi method. Typically, fractional factorial DoE methods are used to analyze the most significant paired parameter interactions and their main effects [20].

The Taguchi method is one of the best experimental methodologies used to find the minimum number of experiments to be performed within the permissible factor and level limits. It provides a systematic approach for the optimization of designs in terms of quality and cost with orthogonal arrays of factors [21]. The aim of the Taguchi method is to optimize the technological parameters for the additive manufacturing of metal items, such as directed energy deposition (DED) [22,23,24], and to reduce deviations before optimizing the design to achieve average target values for the output parameters. Manjunath et al. [23] used the Taguchi L9 orthogonal die design to optimize the DED process and obtained the best interfacial adhesion between a substrate and a Colmonoy 52 SA nickel-chromium-boron hardmetal deposition material. Liu et al. [22] used a Taguchi L25 orthogonal die to achieve maximum-density AlSi10Mg parts and optimize DED process parameters, including the laser power, scanning speed, powder feed rate, and shielding gas flow. The Taguchi method has also been used to optimize the LPBF process for various materials, including titanium alloys [25,26], AlSi10Mg [10,27,28], SS316L [29,30], CoCrMo [25], and Inconel [31]. Rathod and Karia [28] reported the importance of layer thickness in determining hardness and surface roughness. Calignano et al. [27] found that scanning speed had the greatest impact on the surface roughness of LPBF components. Jiang et al. [29] investigated the effects of laser power, scanning speed, and the hatch spacing of LPBF parts on surface roughness, hardness, and density. They reported that laser power was the most important parameter influencing all the properties under study. Sathish et al. [31] used the Taguchi method to study the effect of growth orientation and heat treatment on the coefficient of friction in Inconel 718 specimens fabricated with the LPBF method.

The response surface method (RSM) uses a combination of DoE, regression analysis, and optimization methods to improve the stochastic response value [32]. The RSM can be used with full-factor DoE or fractional factorial DoE. As an optimization tool for the production of LPBF high-entropy alloys, Dada et al. [33] used a full-factor experiment along with the RSM. By changing the laser power and scanning speed, they considered the values for the microhardness of the obtained specimens as an output response. Read et al. [34] used the RSM to evaluate the best laser power, scanning speed, hatch spacing, and scanned area size to optimize the porosity level of LPBF AlSi10Mg parts. Pant et al. [35] implemented a central composition plan with the RSM to model and optimize the DED process of 316L stainless steel. Bartolomeu et al. [36] fabricated Ti-6Al-4V specimens by varying three processing parameters (laser power, scanning speed, and hatch spacing) in the LPBF process and used the RSM to analyze experimental shear stress results, hardness, and density. El-Sayed et al. [37] used the RSM to propose optimal process parameters, including laser power, scan speed, and hatch spacing, for applications involving Ti-6Al-4V medical implants and concluded that higher-density energy leads to a decrease in surface roughness and a decrease in the level of porosity. Marmarelis et al. [38] used the Taguchi method and RSM to investigate the effect of laser power, scanning speed, and hatch spacing on the density and surface roughness of AlSi10Mg specimens made using PBF and reported that groove spacing was the most significant factor in determining the output characteristics. Fotovvati et al. developed a multipurpose RSM model to optimize LPBF processing parameters for Ti-6Al-4V given all responses with equal weights. They developed an artificial neural network (ANN) model, trained it on the specimens used for the Taguchi method, and validated it on the specimens used for the RSM [39]. Wang et al. [40] combined the two methods (i.e., Taguchi and the RSM) to study the effect of laser power, scanning speed, and hatch spacing on the mechanical properties and microstructure of nickel-based superalloy specimens produced with PBF technology. They applied linear models, two-factor interaction models, and quadratic simulation to obtain response surfaces for the tensile strength of fabricated specimens and observed that quadratic simulation of this response resulted in the lowest error value among all tested models.

Researchers have adopted various methodologies to obtain better performance from a process. Unlike the Taguchi method, which is designed to optimize single response characteristics, the grey relational analysis (GRA) method is able to optimize multiple outcomes [41]. Dongari et al. [42] optimized deposition parameters for wire-arc additive manufacturing (WAAM)-fabricated Inconel 625 single beads by applying a GRA methodology. Bhadrakali et al. [43] optimized WAAM process parameters obtained for strength and hardness values using GRA followed by the Taguchi method. In previous studies, the Taguchi approach and GRA have been used to optimize the process parameters and design of support structures in a nickel–nickel chromium alloy combustion chamber [44]. A similar approach was also implemented when optimizing the LPBF parameters of bimetallic specimens from AlSi10Mg–Cr18Ni10Ti powders [45].

Machine learning (ML) methods and their combinations, which are applied for simulation and multi-response optimization of AM process parameters, are widely described in the literature [45,46,47,48,49,50,51,52,53,54]. These methods include artificial neural networks (ANNs), back-propagation neural networks (BPNs), a radial basic function (RBF) neural network based on fuzzy clustering and a pseudo-inverse method, the genetic algorithm (GA), multi-gene genetic programming (MGGP), the non-dominated genetic algorithm (NSGA-II), a multi-objective particle swarm optimizer, and an ensemble MGGP consisting of an ANN, a Bayesian classifier, and support vector regression (SVR) [12].

In addition to machine learning, robust planning and other optimization methods have also been used [55] and can be successfully adapted for multi-response optimization problems in AM.

When the quality characteristics (response parameters) of the products that are to be obtained in the AM process are multiple, some of them can then be used as constraints in multi-response optimization. In this case, to optimize the technological parameters, the classical methods of linear or nonlinear programming can be used.

The linear programming (LP)-based method is used to linearize nonlinear power system optimization problems. This method is reliable and has good convergence characteristics; however, the main shortcoming is that it can be trapped in local minima [56]. To improve the accuracy of the LP method used in this study, it was assumed that the optimization process occurs in two steps. At the first stage, the optimal parameters are determined using DoE based on the problem of minimizing porosity and, at the second stage, a multicriteria optimization problem is solved using the LP method.

Existing AM models are comprised of a set of equations relating the technological parameters of the process and the parameters of the state of the synthesized material—such as internal stresses and strains, temperature, individual structural parameters, etc.—presented in the form of analytical finite-element or empirical models. These parameters form a multi-connected area within which the area of the technological parameters that provide the multiple quality characteristics required can be defined.

The aim of this study was to develop a framework, models, and a method for determining the AM modes that make it possible to obtain a set of quality indicators at the maximum performance of the process. At the same time, some of the quality indicators can then be included in the objective function in order to maximize or minimize them; the rest can be used as constraints.

In setting the optimization problem, it was assumed that the basic (recommended) technological parameters of the LPBF were known from previous studies or from data from other sources. Thus, within a narrow range of basic technological parameters (P, v, h, t), it was necessary to determine a combination of them that would ensure maximum productivity (v·h·t) and key quality characteristics. These parameters were intended to be included in the objective function; the rest of the quality characteristics were intended to be included in the constraints. The use of the linear programming method has several advantages:

-

It ensures the convergence of the solution for any number of constraints. Any additional restriction can be easily introduced; for example, the dependence of residual porosity on a combination of P, v, h, t;

-

It facilitates constraint sensitivity analysis, which makes it possible to define critical constraints; i.e., define those constraints that have the greatest impact on the objective function. The limitations of the suggested method include the fact that the solution has acceptable adequacy only for a narrow range of changes in the basic parameters. The novelty of the proposed method for optimization is the formalization of the objective function, which consists of the process productivity and one or more key quality characteristics of choice; for example, the yield strength of the fused sample. It is preferable to obtain constraints in the form of polynomials. This makes it possible to reduce the optimization problem to a linear programming problem after taking the parameters’ logarithms.

2. Theoretical Foundations of the Optimization Method and Models

2.1. Algorithm

An enlarged optimization algorithm for determining AM modes can be represented with the following use cases.

A set of target quality indicators are defined and an objective function is formulated that includes those quality indicators that need to be maximized or minimized.

Optimal technological parameters are determined according to the most significant quality indicators. In relation to the AM process, such indicators are the parameters of the continuity of the structure of the build specimens—porosity, number, and size of microcracks. As already mentioned, the optimized technological parameters include layer thickness (t), scanning speed (v), laser power (P), and hatch spacing (h). At this stage of optimization, the optimum response parameter vector {h₀, v₀, t₀, P₀} is determined.

Using the design of experiments method and regression analysis, functional relationships are established between quality indicators and AM process parameters. The scope of these dependencies must include the vector {h₀, v₀, t₀, P₀}. To implement the proposed linear programming method, it is advisable to represent these dependencies in the form of polynomials.

The remaining quality indicators that need to be included in the optimization cycle are formalized as constraints; i.e., their values, obtained during the optimization of target indicators, should not exceed or be lower than the accepted boundary values.

An optimization problem is solved to determine the optimal technological parameters based on the objective function and constraints using the linear programming method.

It should be noted that this algorithm is applicable when the optimal values and constraints are within the scope of the dependencies obtained with the DoE method.

2.2. Object Function in General

The economic efficiency of a technological operation with fixed or slightly variable cost parameters for an operation is determined by its productivity. For laser powder melting operations, which include LPBF and L-DED processes, this performance indicator is the increment speed of the alloyed material volume V:

V = v∙h∙t,

(1)

where:

v is the scanning speed (mm/s);

h is the hatch spacing (mm);

t is the layer thickness (mm).

If we use V as an objective function, then the optimization problem of increasing economic efficiency while ensuring multiple quality indicators can be determined according to Equation (2):

$$\underset{v,h,t}{\arg \max (v\cdot h\cdot t)}\in \left\{\begin{array}{l}v,h,t|\forall (v,h,t):R_i(v,h,t,P)\le R_{i0},R_j(v,h,t,P)\ge R_{j0},\\ i=1,\dots ,I,j=1\dots J,R_{i\min }\le R_i\le R_{i\max },R_{j\min }\le R_j\le R_{j\max }\end{array}\right\},$$

(2)

where:

R_i(v,h,t,P) is the constraint function on the left with a constraint value R_i0;

R_j(v,h,t,P) is the constraint function on the right with a constraint value R_j0;

R_imin, R_imax, R_jmin, and R_jmax are area boundaries of allowable values for the functions R;

P is the laser power (W);

I and J are the number of constraints on the left and right, respectively.

As an example of a function R_i, we can give the dependence of the number of non-melts (point of non-melts), and that of the function R_j would be the dependence of the yield strength R_i on the technological parameters of fusion.

If we use a more complex functional F, which takes into account multiple quality parameters, as an objective function, then, assuming the nature of such a dependence is additive in terms of factors, we can write:

$$\underset{v,h,t,P}{\arg \max F(v,h,t,P)}\in \left\{\begin{array}{l}v,h,t,P|\forall (v,h,t,P):R_i(v,h,t,P)\le R_{i\max },R_j(v,h,t,P)\ge R_{j\min },\\ i=1,\dots ,I-n,j=1\dots J-k,R_{i\min }\le R_i\le R_{i\max },R_{j\min }\le R_j\le R_{j\max }\end{array}\right\},$$

(3)

where the function F can be defined as:

$$F(v,h,t,P)=K_V\frac{V-V_{\min }}{V_{\max }-V_{\min }}+{\displaystyle \sum _{i=1}^n{K}_i\frac{R_{i\max }-R_i}{R_{i\max }-R_{i\min }}}+{\displaystyle \sum _{j=1}^k{K}_j\frac{R_j-R_{j\min }}{R_{j\max }-R_{j\min }}},$$

(4)

where:

K_v, K_i, and K_j are the coefficients taking into account the influence (significance) of the relevant factors;

n + k + 1 is the number of analyzed factors in the functional F.

2.3. Definition of Constraints

The optimal values h₀, v₀, and P₀ correspond to the optimal value of the specific heat flux density:

q₀ ↔ {P₀, h₀, v₀, t}

The functional dependency linking these parameters is discussed below.

The heat source from the laser beam can be represented by a double ellipsoid in three dimensions with a Gaussian distribution along each axis, as proposed in the Goldak model [57]. The solution of the Gaussian dependence—for example, using the finite element method—requires the construction of a very fine grid with a thickening at the laser spot. In this case, the number of finite elements becomes extremely large. Thus, to simplify the problem, it is advisable to represent the heat source model as constant over the layer surface, changing only in the direction of depth, which gives the heat flux density equation as a function of depth in 0 < z < c [57]:

$$q(z)=\frac{2\sqrt{3}P}{\sqrt{\pi }\cdot c\cdot h^2}\exp \left(-3\frac{z^2}{c^2}\right)$$

(5)

where c is a melting pool depth.

In engineering practice, when describing LPBF or LDED technology, it is assumed that the fusion process can be described in terms of the energy density of the laser beam per unit volume of the alloyed material:

$$E=\frac{P}{h\cdot v\cdot t}$$

(6)

where t is the layer thickness in the coordinate z.

Using Equation (5), we can determine the average heat density in a layer thickness t located between two tracks with a step h:

$$Q=\frac{h}{t}{\displaystyle \underset{0}{\overset{t}{\int }}q(z)dz}=\frac{2\sqrt{3}P}{\sqrt{\pi }\cdot c\cdot h\cdot t}{\displaystyle \underset{0}{\overset{t}{\int }}\exp \left(-3\frac{z^2}{c^2}\right)dz}$$

(7)

Given that the Gaussian integral limited by the limits 0 < z < t and a—const has a solution:

$${\displaystyle \underset{0}{\overset{t}{\int }}\exp (-a\cdot z^2)dz}=\frac{\sqrt{\pi }}{2\sqrt{a}}\sqrt{\left(1-\exp (-2a\cdot t^2)\right)}$$

(8)

we will get:

$$Q=\frac{P}{h\cdot t}\cdot {\left(1-\exp \left(-6\frac{t^2}{c^2}\right)\right)}^{\frac{1}{2}}$$

(9)

Taking into account Equation (6), the average density of thermal energy per unit volume of a layer thickness t is determined by the dependence:

$$q=\frac{Q}{v}=E\cdot {\left(1-\exp \left(-6\frac{t^2}{c^2}\right)\right)}^{\frac{1}{2}}$$

(10)

Based on Equation (10), we can obtain the dependence for the optimal thermal energy density, calculated from the values of the optimum response parameter vector {h₀, v₀, t₀, P_0t}. It should be noted that the parameters h₀, v₀, t₀, and P₀ were obtained through an optimization procedure that takes into account the parameters of the continuity of the structure.

$$q_{opt}=\frac{P_{opt}}{h_{opt}{v}_{opt}{t}_{opt}}\cdot {\left(1-\exp \left(-6\frac{t_{opt}{}^2}{c^2}\right)\right)}^{\frac{1}{2}}$$

(11)

From the condition of equality of the thermal energy density for optimal technological parameters and the thermal energy density for the assigned values {h, v, t, P} according to Equation (12), we can select the increment speed of the alloyed material volume V according to Equation (13):

q(h, v, t, P) = q₀(h₀, v₀, t₀, P₀)

(12)

$$V=h\cdot v\cdot t=h_0\cdot v_0\cdot t_0\frac{P}{P_0}\cdot \sqrt{\left(1-\exp \left(-6\frac{t^2}{c^2}\right)\right)/\left(1-\exp \left(-6\frac{t_{opt}{}^2}{c^2}\right)\right)}$$

(13)

Assume that there is a constraint on the layer thickness t:

t ≤ t_max < c

(14)

In this case, the linear Equation (15) is valid, which is obtained after taking the logarithm from Equation (16) and substituting Equation (17) into it:

ln(v) + ln(h) + ln(t) − ln(P) = K_V,

(15)

where

$$\begin{array}{l}{K}_V\le K_{V\max }=\ln \left[\frac{h_0\cdot v_0\cdot t_0}{P_0}\cdot \sqrt{\left(1-\exp \left(-6\frac{t_{\max }{}^2}{c^2}\right)\right)/\left(1-\exp \left(-6\frac{t_{opt}{}^2}{c^2}\right)\right)}\right]\\ K_V\ge K_{V\min }=\ln \left[\frac{h_0\cdot v_0\cdot t_0}{P_0}\cdot \sqrt{\left(1-\exp \left(-6\frac{t_{\min }{}^2}{c^2}\right)\right)/\left(1-\exp \left(-6\frac{t_{opt}{}^2}{c^2}\right)\right)}\right]\end{array}$$

(16)

Let the remaining quality characteristics of the fusion process be described by the following polynomial dependencies:

(a) roughness:

$$R_{а}=K_r{\left(\frac{P}{v}\right)}^{a_{rp}}\cdot h^{a_{rh}}\cdot t^{a_{rt}}$$

(17)

(b) tensile strength:

$$\sigma =K_{\sigma }{\left(\frac{P}{v}\right)}^{a_{\sigma p}}\cdot h^{a_{\sigma h}}\cdot t^{a_{\sigma t}}$$

(18)

(c) percentage of elongation:

$$\delta =K_{\delta }{\left(\frac{P}{v}\right)}^{a_{\delta p}}\cdot h^{a_{\delta h}}\cdot t^{a_{\delta t}}$$

(19)

where K_i and a_ij, i = {r, σ, δ}, j = {p, h, t} are the coefficients obtained using the method of regression analysis based on the experimental results.

It is possible to specify “right” and “left” constraints on the quality characteristics:

R_a ≤ R_max,
 σ ≥ σ_min,
 δ ≥ δ_min.

(20)

The following constraints on the geometric dimensions of the alloyed layer can be added to Equation (22):

t_min ≤ t ≤ t_max
 h_min ≤ h ≤ h_max

(21)

The logarithm of the polynomial Equations (17)–(19), taking into account the constraints from Equations (20) and (21) and the previously obtained inequality from Equation (15), make it possible to obtain a system of linear constraints in the classical formulation of the linear programming problem:

A_min ∙ X + B_min ≥ 0,
 A_max ∙ X + B_max ≤ 0,

(22)

where

$$A_{\min }=\left[\begin{array}{cccc}{a}_{\sigma p}& -a_{\sigma p}& a_{\sigma h}& a_{\sigma t}\\ a_{\delta p}& -a_{\delta p}& a_{\delta h}& a_{\delta t}\\ 0& 0& 1& 0\\ \begin{array}{l}0\\ 1\\ 0\\ -1\end{array}& \begin{array}{l}0\\ 0\\ 1\\ 1\end{array}& \begin{array}{l}0\\ 0\\ 0\\ 1\end{array}& \begin{array}{l}1\\ 0\\ 0\\ 1\end{array}\end{array}\right],A_{\max }=\left[\begin{array}{cccc}{a}_{rp}& -a_{rp}& a_{rh}& a_{rt}\\ 0& 0& 1& 0\\ \begin{array}{l}0\\ 1\\ 0\end{array}& \begin{array}{l}0\\ 0\\ 1\end{array}& \begin{array}{l}0\\ 0\\ 0\end{array}& \begin{array}{l}1\\ 0\\ 0\end{array}\\ -1& 1& 1& 1\end{array}\right]$$

(23)

are the coefficient matrices for variables in constraint equations;

$$B_{\min }=\left[\begin{array}{c}\ln \left(\frac{{\sigma }_{\min }}{K_{\sigma }}\right)\\ \ln \left(\frac{{\delta }_{\min }}{K_{\delta }}\right)\\ \ln (h_{\min })\\ \begin{array}{l}\ln (t_{\min )}\\ \ln (P_{\max })\\ \ln (v_{\max })\\ K_V\min \end{array}\end{array}\right],B_{\max }=\left[\begin{array}{c}\ln \left(\frac{R_{\max }}{K_R}\right)\\ \ln (h_{\max })\\ \ln (t_{\max })\\ \begin{array}{l}\ln (P_{\max })\\ \ln (v_{\max })\\ K_V\max \end{array}\end{array}\right]$$

(24)

are the “left” and “right” constraint matrices;

$$X=\left[\begin{array}{c}\ln (P)\\ \ln (v)\\ \ln (h)\\ \ln (t)\end{array}\right]$$

(25)

is the vector of variables.

3. Validation of the Optimization Model for HN58MBYu Alloy

3.1. Objective Function Formation

The objective function F_Σ(h,v,t) can be represented as a linear combination of the productivity factor F_V(h,v,t) and the factor that is obtained by including one of the constraints in the objective function. In this case, the corresponding constraint row is excluded from the constraint matrix and coefficient matrix. For example, if the objective function includes a constraint on the minimum value of the yield strength (i.e., requirement to maximize the difference (σ − σ_min) → max), then the objective function will take the form:

F_Σ(p,h,v,t) = k_v·F_V(h,v,t) + k_σ·F_σ(p,h,v,t);
F_Σ(p,h,v,t) → max.

(26)

In expanded form, Equation (28) is written as:

$$\begin{array}{l}{F}_{\mathsf{\Sigma }}(p,h,v,t)=k_v\frac{\ln (v)+\ln (h)+\ln (t)}{M_V}+k_{\sigma }\frac{a_{\sigma p}\ln (P)-a_{\sigma p}\ln (v)+a_{\sigma h}\ln (h)+a_{\sigma t}\ln (t)}{M_{\sigma }}=\\ =\frac{k_{\sigma }{a}_{\sigma p}}{M_{\sigma }}\ln (P)+\left(\frac{k_v}{M_V}-k_{\sigma }\frac{a_{\sigma p}}{M_{\sigma }}\right)\ln (v)+\left(\frac{k_v}{M_V}+k_{\sigma }\frac{a_{\sigma h}}{M_{\sigma }}\right)\ln (h)+\left(\frac{k_v}{M_V}+k_{\sigma }\frac{a_{\sigma t}}{M_{\sigma }}\right)\ln (t)\\ ,F_{\mathsf{\Sigma }}(p,h,v,t)\to \max \\ M_V=\ln (v_{\max }\cdot h_{\max }\cdot t_{\max })\\ M_{\sigma }=a_{\sigma p}\ln (P/v{)}_{\max }+a_{\sigma h}\ln (h_{\max })+a_{\sigma t}\ln (t_{\max })\end{array}$$

(27)

where k_v and k_σ are the coefficients of influence (desirability) of the performance factor and the factor of ultimate strength for the target function. Let us take k_v = 0.3 and k_σ = 1.

3.2. Materials and Experiment Design

A total of 48 flat specimens with dimensions of 2 mm × 15 mm × 70 mm (24 pieces) and 3 mm × 15 mm × 70 mm (24 pieces) obtained using laser layer-by-layer growth (LPBF) with a Selective Laser Melting System^® 280HL (SLM Solutions GmbH, Lübek, Germany) from HN58MBYu powder in 16 modes (three specimens for each mode) were studied (Figure 1). The chemical composition of the powder is given in

Table 1. Chemical composition of nickel–chromium HN58MBYu alloy in at.%.

C	S	P	Mn	Cr	Si	Ni	Fe	Al	B	Mo	Nb	Mg	Y	La
0.05	0.011	0.012	0.49	26.4	0.8	Balance	2.7	1.29	0.002	7.6	3.1	0.02	0.02	0.03

. LPBF modes are given in

Table 2. Technological modes and test results for mechanical properties.

No.	Energy Density Е, J/mm3	Laser Power Р, W	Scanning Speed v, mm/s	Scanning Step h, mm	Layer Thickness t, mm	Sample Thickness S, mm	Tensile Strength, MPa	Relative Elongation	Ra
1	56	148	480	0.11	0.05	3	1036	21.1	4.48
2	69	215	480	0.13	0.05	2	1024	19.9	4.46
3	76	306	480	0.14	0.06	2	1020	16.2	4.58
4	63	218	480	0.12	0.06	3	1011	24.3	4.56
5	56	262	600	0.13	0.06	3	962	20.1	4.49
6	69	273	600	0.11	0.06	2	1024	19.6	4.51
7	76	274	600	0.12	0.05	2	1025	21.2	4.50
8	63	265	600	0.14	0.05	3	1013	25.1	4.47
9	56	259	660	0.14	0.05	2	1051	20.8	4.50
10	69	273	660	0.12	0.05	3	1024	23.0	4.47
11	76	331	660	0.11	0.06	3	998	22.5	4.48
12	63	299	660	0.12	0.06	2	1013	17.3	4.52
13	56	218	540	0.12	0.06	2	1055	15.9	4.59
14	69	313	540	0.14	0.06	3	980	19.6	4.60
15	76	267	540	0.13	0.05	3	1024	23.1	4.42
16	63	187	540	0.11	0.05	2	1081	19.85	4.49
max	76	331	660	0.14	0.06	3	1081	25.1	4.6
min	56	148	480	0.11	0.05	2	962	15.9	4.42

. We used a 4³ × 2² plan in a fractional factorial experiment (three factors varied at four levels, two factors varied at two levels) obtained from the D-optimal design 4⁵//D16 through equivalent transformation of the last two columns. Five parameters were changeable during the experiment: scanning speed (v), hatch spacing (h), and fusion volume energy density (VED)—all at three levels of variation—and layer thickness (t) and sample thickness—at two levels. These technological parameters were the key parameters affecting the quality characteristics. The laser power (P) values in Table 2 are given only for reference according to the dependence P = VED·v·h·t.

The produced samples were subjected to tensile tests using an Instron 5982 Testing System (ITW, Glenview, IL, USA) for uniaxial static tensile-compression examination in accordance with the recommendations of the ASTM E8/E8M standard. The roughness Ra of the samples was measured with a profilometer MarSurf PS1 (Mahr GmbH, Göttingen, Germany) in accordance with the recommendations of the ISO 13565-1 standard.

The influence of the thickness of the built specimens S on the mechanical properties was evaluated using the Mann–Whitney U-test, which showed a statistically significant effect from this factor on the tensile strength and relative elongation (

Table 3. Nonparametric analysis of the effect of sample thickness on mechanical properties.

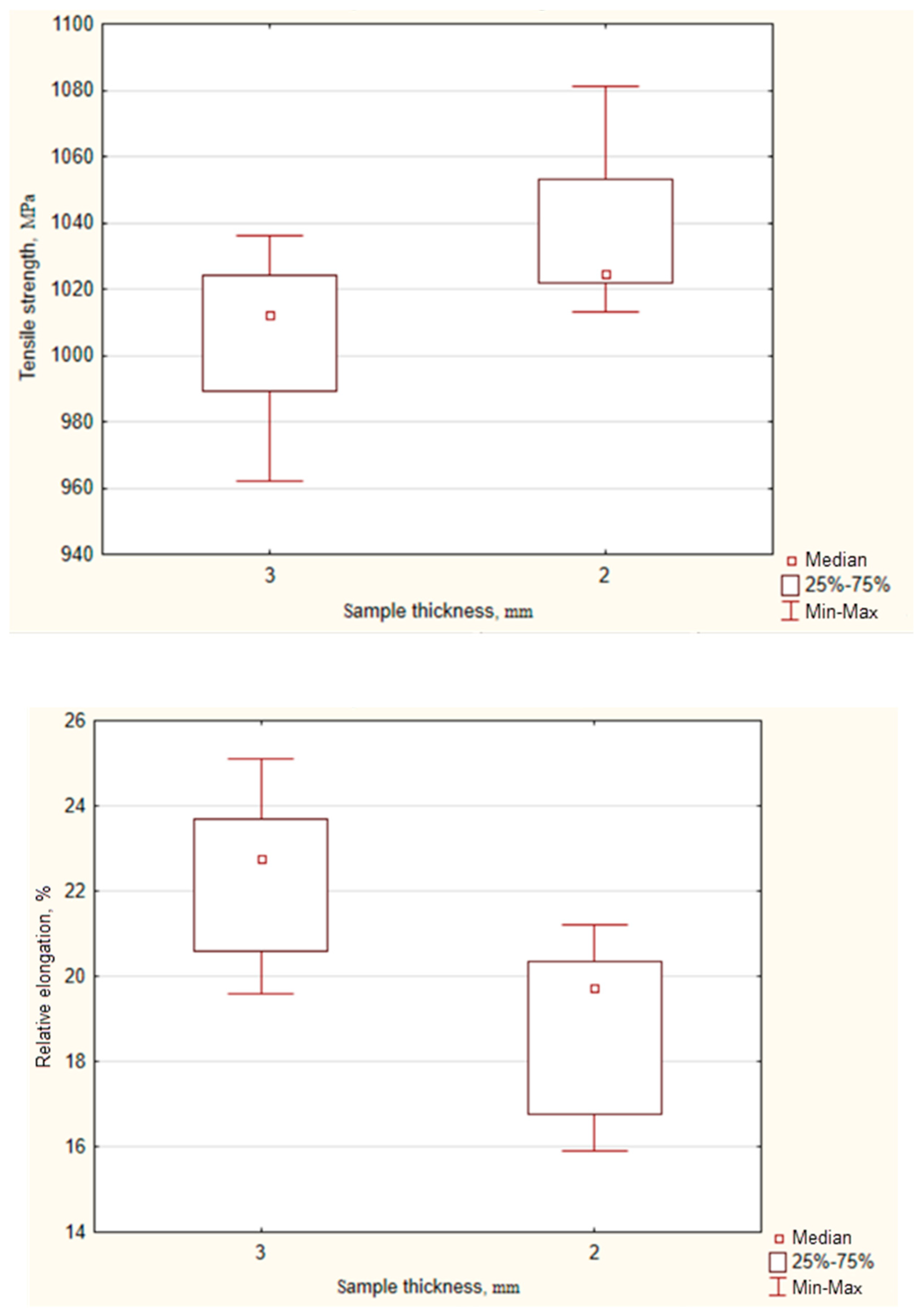
Mechanical Properties	Mann–Whitney U-Criterion	Z—Normal Distribution Function	p-Level
Tensile strength, MPa	11.50000	−2.10042	0.035693
Relative elongation, %	7.50000	2.52050	0.011719

). The influence of the factor was considered statistically significant if the p-level was <0.05.

A box plot of the mechanical property range of the built specimens grouped by thickness is shown in Figure 2.

Taking into account the fact that the thickness of the built specimens has a significant effect on the mechanical properties, the subsequent simulation was performed for each group of specimens of different thicknesses separately.

3.3. Solution of the Optimization Problem

To obtain polynomial models, eight experimental results for 3 mm thick plates were selected, the logarithmic values of the technological parameters and responses of which are given in

Table 4. Natural logarithms of factors and responses for LPBF flat specimens from HN58MBYu.

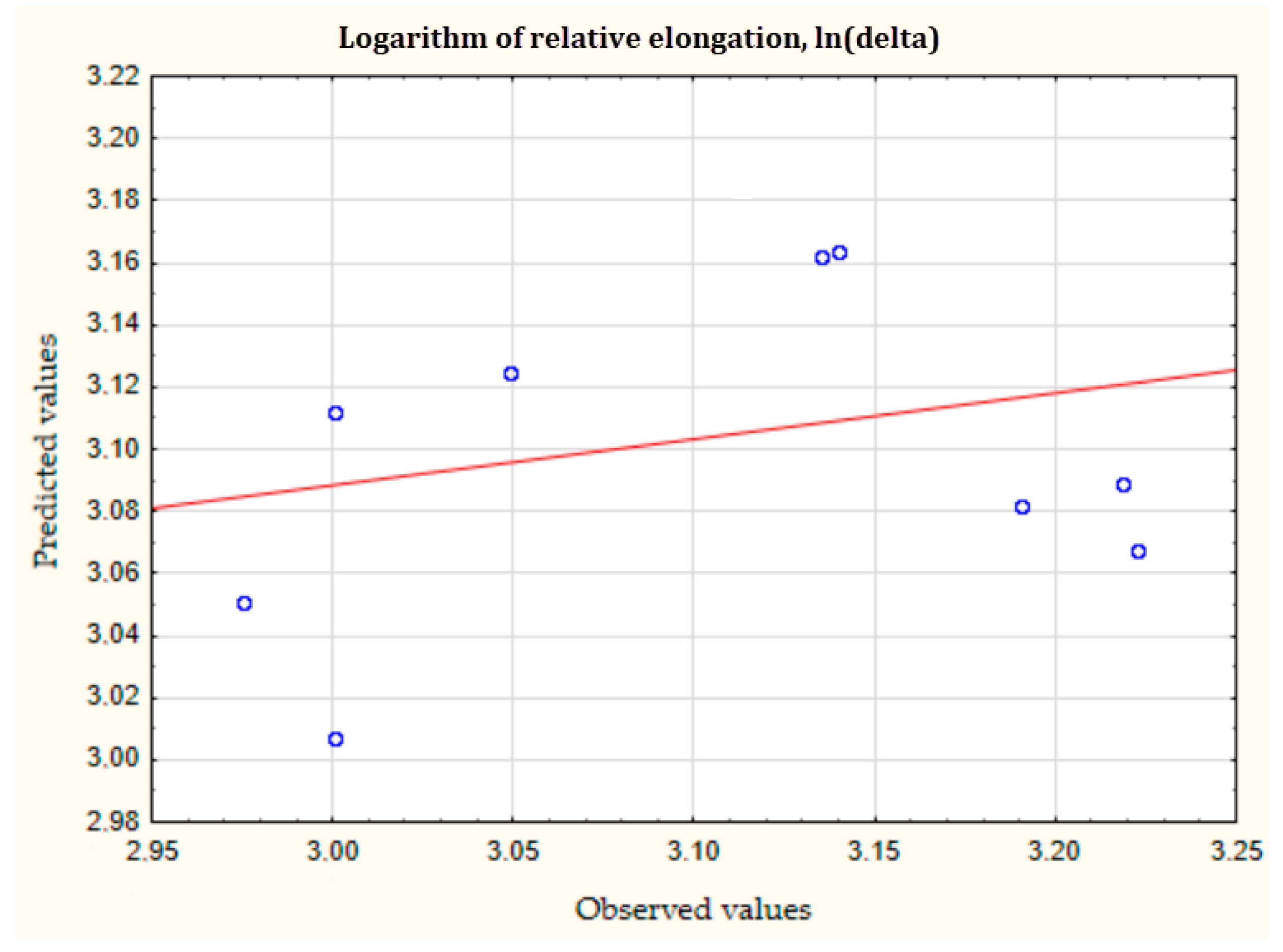
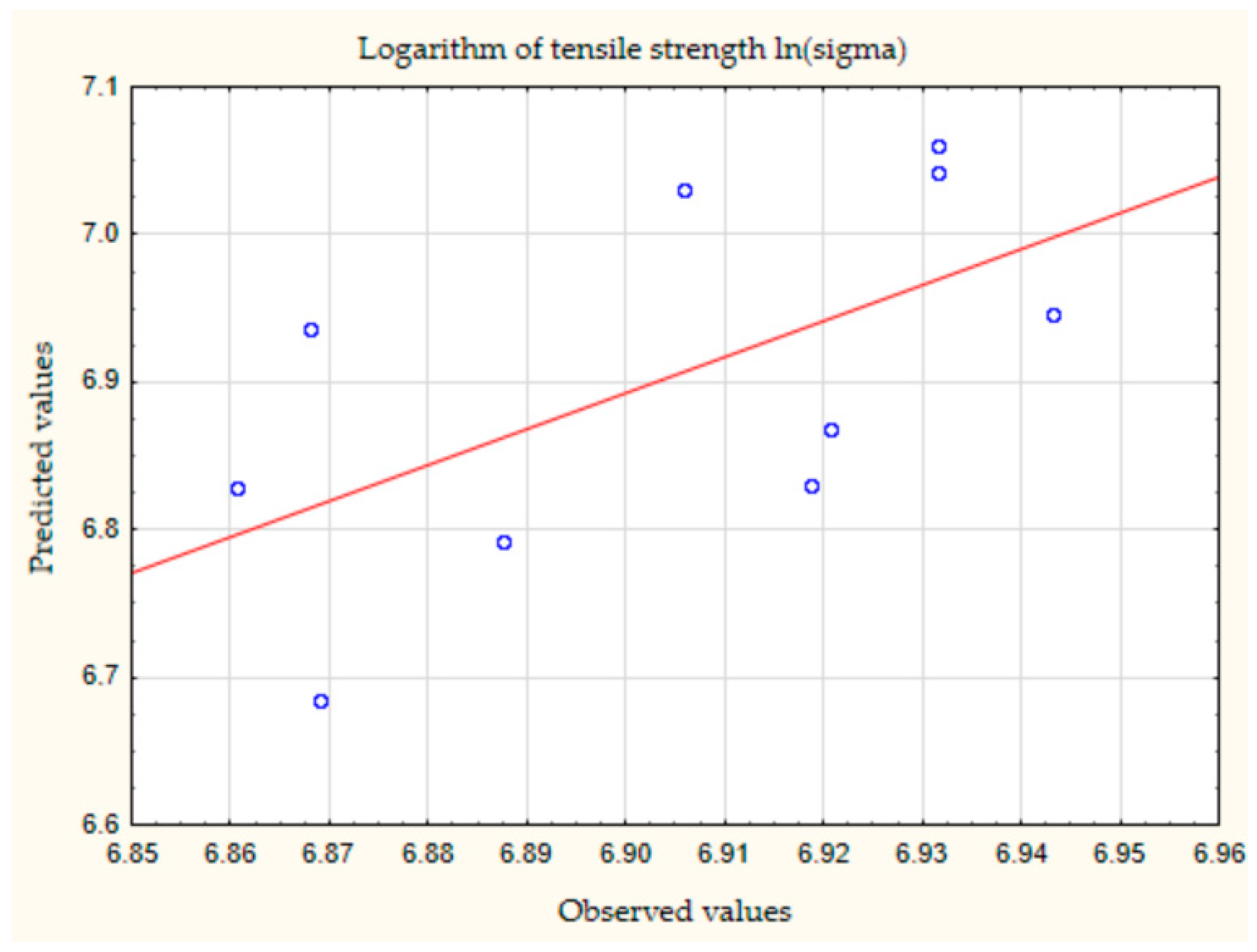
No.	Logarithm of Linear Power Density, ln(p/v)	Logarithm of Scanning Step, ln(h)	Logarithm of Thickness Layer, ln(t)	Logarithm of Tensile Strength, ln(σ)	Logarithm of Relative Elongation, ln(δ)
1	−1.17657	−2.20727	−2.99573	6.943122	3.049273
2	−0.78929	−2.12026	−2.81341	6.918695	3.190476
3	−0.82859	−2.04022	−2.81341	6.869014	3.00072
4	−0.8172	−1.96611	−2.99573	6.920672	3.222868
5	−0.88277	−2.12026	−2.99573	6.931472	3.135494
6	−0.69012	−2.20727	−2.81341	6.905753	3.113515
7	−0.54537	−1.96611	−2.81341	6.887553	2.97553
8	−0.70432	−2.04022	−2.99573	6.931472	3.139833

.

Based on the data from Table 4, the coefficients of Equations (18) and (19) were determined using the method of linear regression analysis:

$$\sigma ={\left(\frac{P}{v}\right)}^{0.75506}\cdot h^{-1.44727}\cdot t^{-1.54890}$$

(28)

$$\delta ={\left(\frac{P}{v}\right)}^{0.353741}\cdot h^{-0.763524}\cdot t^{-0.619330}$$

(29)

To analyze the roughness, we used the previously obtained dependence from Equation (30):

R_a = 5.6t^0.075

(30)

The adequacy of Equations (28) and (29) was assessed using the coefficient of determination R of the residuals (described deviations from the normal distribution). The larger the value of R, the more residuals could be explained by regression. Accordingly, for relative elongation R, residues = 0.9998; for tensile strength R, residues = 0.9997. The statistical significance and the response impact of each input parameter P/v, h, and t were assessed using an ANOVA univariate test (

Table 5. ANOVA univariate test of Equations (28) and (29).

Input Parameter	Logarithm of Tensile Strength, ln(σ)			Logarithm of Relative Elongation, ln(δ)
	Group Dispersion SS	Fisher F-Test	p-Value	SS—Dispersion in Group	Fisher F-Test	p-Value
ln(P/v)	0.134641	9.05307	0.019695	0.02955	2.497524	0.158037
ln(h)	0.255182	17.15802	0.004337	0.07102	6.002435	0.044108
ln(t)	0.612845	41.20670	0.000361	0.09798	8.280913	0.023731

). Regression coefficients were F-test-significant if the p-value < 0.05. Based on the SS values in Table 5, it was concluded that layer step t had the greatest influence on the responses, both for tensile strength and relative elongation.

The observed and predicted elongation and yield strength values are shown in Figure 3 and Figure 4.

To solve the optimization problem, it was necessary to consider the technological parameters and limitations that formed the range of acceptable values for the LPBF process with the HN58MBYu alloy. The initial data for the LP optimization process can be found in

Table 6. Data for the formation of the area of limitations.

No.	Characteristic	Type	Value
1	Yield strength (MPa)	Min	1020
2	Relative elongation	Min	20
3	Layer thickness, t (mm)	Min	0.05
4	Layer thickness, t (mm)	Max	0.06
5	Hatch spacing, h (mm)	Min	0.1
6	Hatch spacing, h (mm)	Max	0.15
7	Laser power, P (W)	Min	200
8	Laser power, P (W)	Max	300
9	Scanning speed, v (mm/s)	Min	500
10	Scanning speed, v (mm/s)	Max	640
11	Roughness, Ra (µm)	Min	12
12	Melting pool depth, c (mm)	Approximately	0.5
13	Hatch spacing, h0 (mm)	Base *	0.12
14	Scanning speed, v0 (mm/s)	Base *	540
15	Layer thickness, t0 (mm)	Base *	0.06
16	Laser power, P0 (W)	Base *	218

Base * is the mode with the most favorable microstructure in terms of continuity parameters (no pores and cracks).

. The maximum and minimum parameter values in the table had to be grouped according to the previously defined recommended base values (lines 13–16, Table 6) and they had to not go beyond the range of the experimental data (Table 2). The lower and upper limits of deviations from the recommended values were also calculated from Equation (2) and are indicated in the matrix of constraints. Figure 5 shows the scheme for measuring the melting pool depth from microstructure data. To do this, a single track (or layer) was welded onto the substrate and the value of depth c was measured from microstructure data. To reveal the microstructure of the transverse sections of the specimens, they were etched in a reagent (35 mL HCl, 24 mL HNO₃, 6 mL HF, 35 mL H₂O).

A more detailed analysis of the morphology and the depth value of the melting pool depending on the laser beam absorption ratio has been carried out in a previous study [58].

According to Table 6, we can determine the objective function with calculated coefficients using Equation (27):

F_Σ(p,h,v,t) = 0.115608064ln(P) + 0.055728722ln(v) − 0.05025458ln(h) − 0.06581634ln(t)
F_Σ(p,h,v,t) → max

(31)

Numerical values of the A_min and A_max coefficient matrices and the B_min and B_max constraint matrices are given in

Table 7. Solving the optimization problem using linear programming.

Amin					Amin∙X		Bmin
0.75506	−0.75506	−1.44727	−1.54890	=	6.927558	≥	6.927558
0.353741	−0.353741	−0.763524	−0.619330	=	3.096988	≥	2.995732
0	0	1	0	=	−1.988349	≥	−2.302585
0	0	0	1	=	−2.995732	≥	−2.995732
1	0	0	0	=	5.679789	≥	5.298317
0	1	0	0	=	6.461468	≥	6.214608
−1	1	1	1	=	−4.202402	≥	−4.202402
Amax					Amax∙X		Bmax
0	0	0	0.075	=	1.258208	≥	2.484907
0	0	1	0	=	−1.988349	≥	−1.89712
0	0	0	1	=	−2.995732	≥	−2.813411
1	0	0	0	=	5.679789	≥	5.703782
0	1	0	0	=	6.461468	≥	6.461468
−1	1	1	1	=	−4.202402	≥	−4.0266

.

Table 7 also contains the components of the product matrices A_min∙X and A_max∙X with the optimal vector X = X_opt. The values of the desired optimal components of the vector (

Table 8. Optimal components of vector X_opt.

Xopt
ln(P)	ln(v)	ln(h)	ln(t)
5.679788803	6.461468176	−1.988349345	−2.995732274

) were obtained by jointly solving Equation (27) and the constraints from Table 7 using the simplex method.

Using the exponential function with arguments from Table 5, we obtain the vector of the optimal technological modes (

Table 9. Optimal values of technological conditions for LPBF with HN58MBYu.

Laser Power, Р (W)	Scanning Speed, v (mm/s)	Scanning Step, h (mm)	Layer Thickness, t (mm)
293	640	0.14	0.05

).

4. Conclusions

• A generalized LP optimization model for determining the technological parameters of LPBF was proposed, containing:
  • An objective function in the form of additive normalized performance parameters and one of the key quality characteristics;
  • The domain of definition, formed by constraints on the limiting values of the quality characteristics (mechanical properties, surface roughness, parameters of the continuity of the material structure), which were presented as polynomial dependencies of the quality characteristics for technological parameters.
• The initial data for the LP optimization process should be grouped according to the recommended base values of layer thickness (t), scanning speed (v), laser power (P), and hatch spacing (h). The lower and upper limits of deviations from the recommended values were also calculated from Equation (2) and are indicated in the matrix of constraints. The recommended values P, v, h, and t (base point) can be obtained from previous tests or known data.
• The optimization model for determining the technological parameters of LPBF was tested with LPBF specimens from HN58MBYu. The results of the optimization made it possible to determine the optimal technological AM regimes for the formulated objective function and the assigned constraints. Since the area of constraints regarding the variation of technological parameters was rather narrow, this was justified by the use of the chosen optimization method—linear programming. Then, most of the optimal parameters took on the value of constraints. Thus, the optimal scanning speed corresponded to the maximum v_opt = v_max = 640 mm/s, which is explained by the requirements of maximum productivity; and the deposited layer thickness was the minimum t = 0.05 mm, which is explained by the requirements of minimizing the roughness. The optimum values of the laser power P = 293 W and hatching step h = 0.14 mm provide a balanced value for the fusion volume energy density E = 65.4 J/mm³, which, according to the data in Table 2, should correspond to the required mechanical properties.