Evaluation Method and Application of Cold Rolled Strip Flatness Quality Based on Multi-Objective Decision-Making
Abstract
1. Introduction
2. Pattern Recognition of Flatness Defects
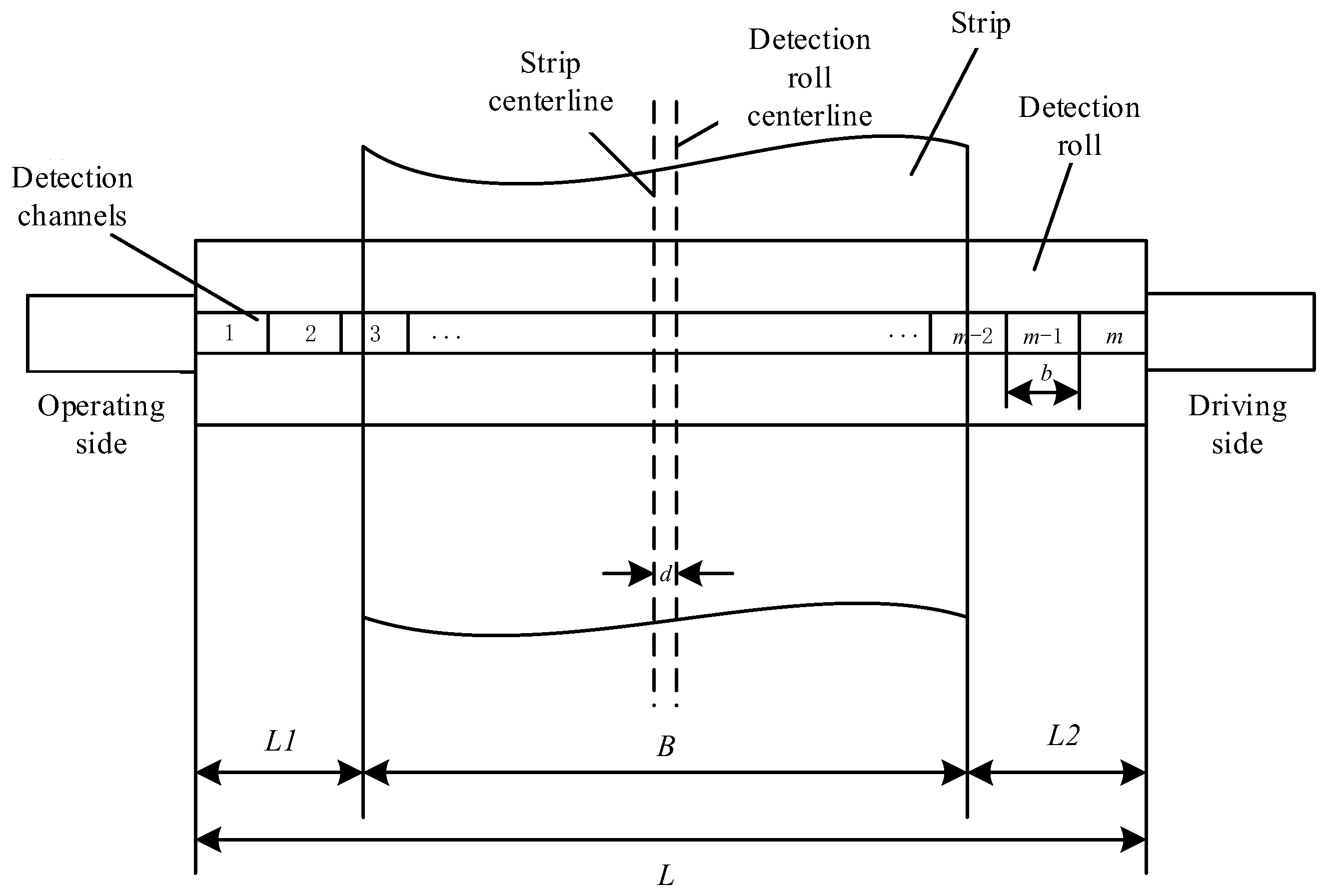
2.1. Determination of Valid Channels for Flatness Data
2.2. Extraction Algorithm of Local Wave Shapes
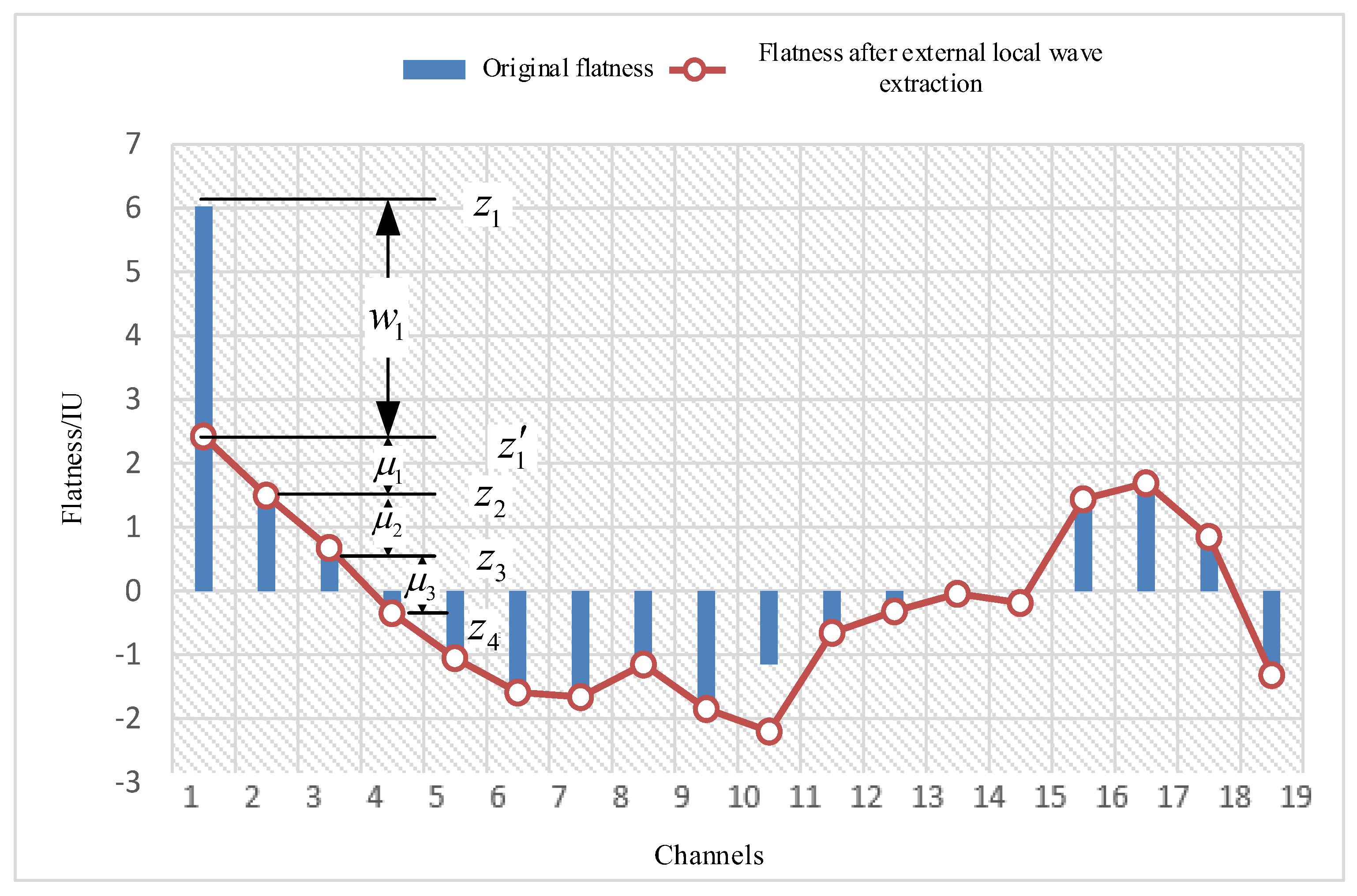
2.2.1. External Local Wave Shape Defect Recognition and Extraction
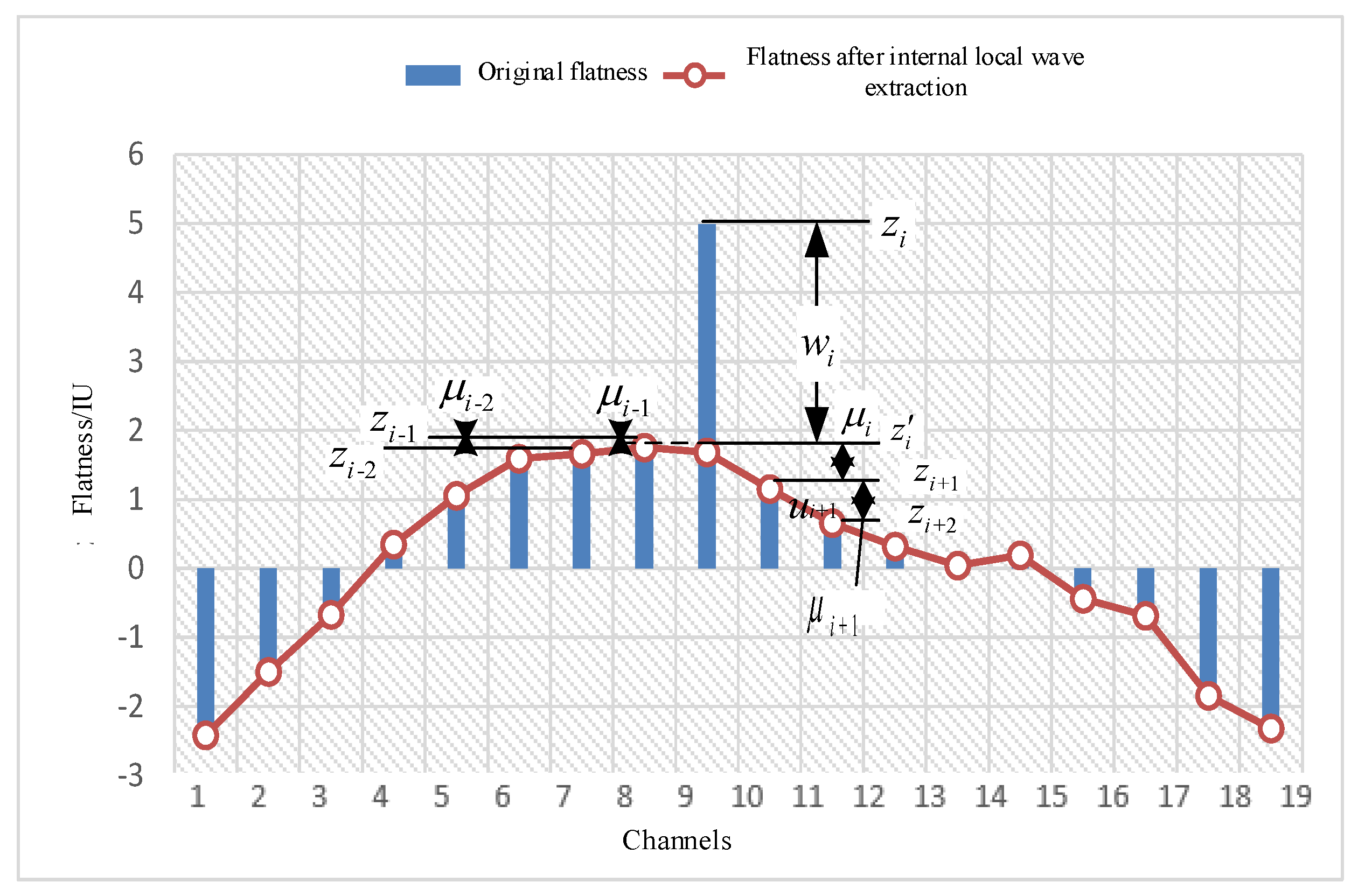
2.2.2. Internal Local Wave Shapes Defect Recognition and Extraction
2.3. Overall Flatness Recognition Algorithm
2.4. Application of Flatness Recognition Algorithm for Local and Overall Flatness
3. Rules for Determining Cold-Rolled Strip Flatness Quality
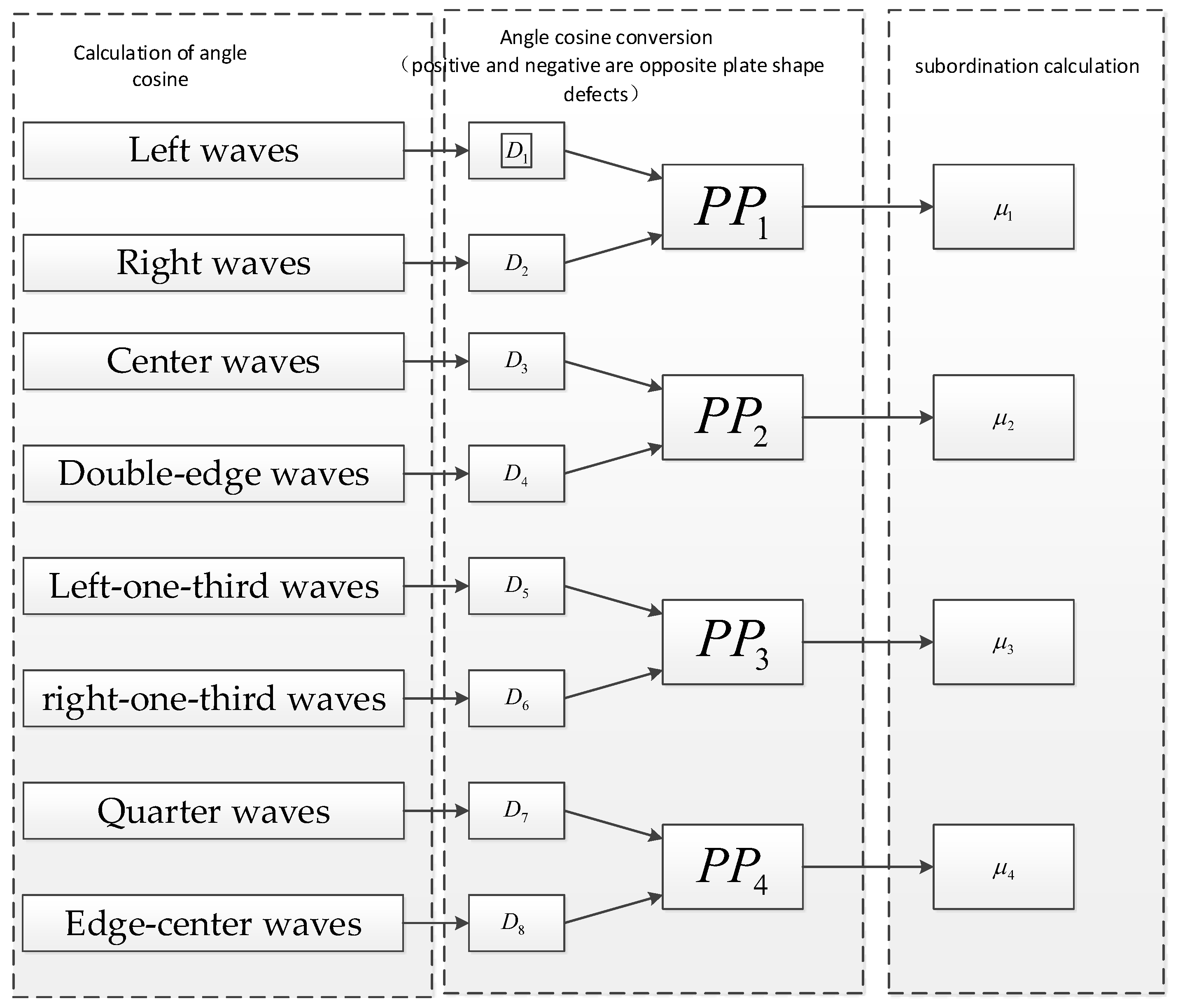
4. Comprehensive Quality Evaluation of Cold-Rolled Strip Flatness
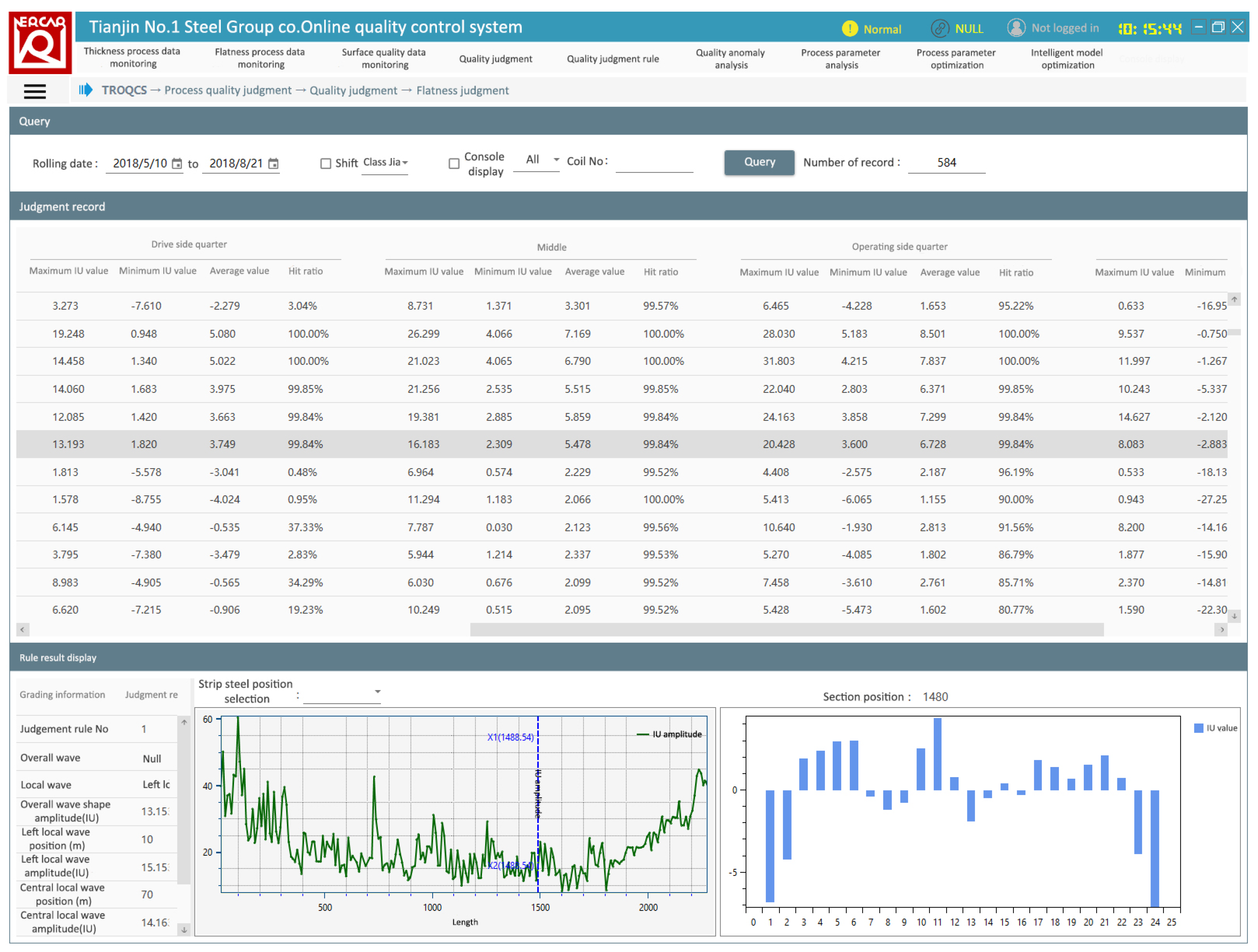
5. Application of Flatness Quality Determination in Cold Rolling
- The application of this system has improved the level of process quality data management, changed the original situation of quality data being stored piecemeal in multiple systems, and stored process quality data in the same platform after cleaning, sorting, and organizing, making it easy for users to query, download, and statistically analyze the data.
- The input of the quality judgment function significantly shortens the quality judgment time. It improves the production efficiency while avoiding the arbitrariness of manual judgment, improving the accuracy of quality judgment and realizing the decision guidance for the production post-process.
6. Conclusions
- A local wave extraction algorithm and a similar distance formula for the overall flatness pattern recognition algorithm are designed. For the recognition accuracy of local wave shape and the recognition accuracy of overall flatness defects in strip quality determination, a smooth flatness curve based on local wave shape extraction is proposed for overall flatness defect recognition. Meanwhile, the distance evaluation formula in the fuzzy classification algorithm is optimized, and the application method of cosine similarity is proposed.
- The strip stress buckling models for local and overall wave shapes were investigated by introducing the small displacement buckling theory for thin strips. The critical buckling stresses for overall and local wave shape under given conditions were calculated as the corresponding quality determination thresholds. The quality determination model of flatness containing both local and overall wave shapes was validated using field flatness data.
- A comprehensive quality determination model of the flatness was established. By using the multiobjective integrated evaluation method, we evaluated the local wave shape quality and the overall flatness quality of the strip, and the strip flatness quality was further rated using the evaluation value.
- Through C# computer programming, the determination process—such as visual display of online determination of flatness, storage and query of determination results, pattern recognition algorithm, and calculation of comprehensive quality determination— is completed, which provides a reference for the field application of cold-rolled strip flatness quality determination system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdelkhalek, S.; Zahrouni, H.; Legrand, N.; Potier-Ferry, M. Post-buckling modeling for strips under tension and residual stresses using asymptotic numerical method. Int. J. Mech. Sci. 2015, 104, 126–137. [Google Scholar] [CrossRef]
- Kpogan, K.; Zahrouni, H.; Potier-Ferry, M.; Dhia, H.B. Buckling of rolled thin sheets under residual stresses by ANM and Arlequin method. Int. J. Mater. Form. 2017, 10, 389–404. [Google Scholar] [CrossRef]
- Bao, R.R.; Zhang, J.; Li, H.B.; Jia, S.H.; Liu, H.J.; Xiao, S. Flatness pattern recognition of ultra-wide tandem cold rolling mill. Chin. J. Eng. 2015, 37, 6–11. [Google Scholar]
- Zhang, Q.D.; Chen, X.L.; Xu, J.W. Method of Flatness Defect Pattern Recognition. Iron Steel 1996, 31, 57–60. [Google Scholar]
- Dai, J.B.; Wu, W.B.; Zhang, Q.D.; Wang, J.F.; Wang, H. Recognition and Evaluation System for Strip Flatness on 2030mm Cold Tandem Mills. J. Univ. Sci. Technol. Beijing 2003, 25, 572. [Google Scholar]
- He, H.T.; Li, Y. A new flatness pattern recognition model based on cerebellar model articulation controllers network. J. Iron Steel Res. Int. 2008, 15, 32–36. [Google Scholar] [CrossRef]
- Song, J.J.; Shao, K.Y.; Chi, D.X.; Hua, J.X.; Zhang, Q. Application of wavelet analysis in recognizing the defects of plate Form in rolling process. Control. Decis. 2002, 17, 69–72. [Google Scholar]
- Zhang, X.L.; Zhang, S.Y.; Tang, G.Z.; Zhao, W.B. A novel method for flatness pattern recognition via least squares support vector regression. J. Iron Steel Res. Int. 2012, 19, 25–30. [Google Scholar] [CrossRef]
- He, H.T.; Li, N. The improved RBF Approach to Flatness Pattern Recognition Based on SVM. J. Autom. Instrum. 2007, 28, 1–4. [Google Scholar]
- Zhang, C.; Tan, J.P. Strip flatness pattern recognition based on genetic algorithms-back propagation model. J. Cent. South Univ. 2006, 37, 294–299. [Google Scholar]
- Li, X.G.; Fang, Y.M.; Liu, L. Kernel extreme learning machine for flatness pattern recognition in cold rolling mill based on particle swarm optimization. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 270. [Google Scholar] [CrossRef]
- Yang, J.; Xu, Q. Quantum ant colony optimizing theory and its application in fuzzy pattern recognition method of flatness. Int. Conf. Comput. Sci. Technol. 2017, 12508, 210–216. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.; Hu, H.Q. The shape recognition in cold strip rolling based on SVM. Appl. Mech. Mater. 2013, 427, 1687–1690. [Google Scholar] [CrossRef]
- Zhang, X.L.; Zhao, L.; Zang, J.Y.; Fan, H.M. Visualization of flatness pattern recognition based on T-S cloud inference network. J. Cent. South Univ. 2015, 22, 560–566. [Google Scholar] [CrossRef]
- Zhang, X.L.; Zhang, Z.Q. A novel method of optimal designing DHNN and applied to flatness pattern recognition. CAAI Trans. Intell. Syst. 2008, 3, 250–253. [Google Scholar]
- Wang, Y.Q.; Yin, G.F.; Sun, X.G. Research for pattern recognition of shape signal method. Chin. J. Mech. Eng. 2003, 39, 91–94. [Google Scholar] [CrossRef]
- Zhang, X.L.; Cheng, L.; Hao, S.; Gao, W.Y.; Lai, Y.J. The new method of flatness pattern recognition based on GA–RBF–ARX and comparative research. Nonlinear Dyn. 2016, 83, 3. [Google Scholar] [CrossRef]
- Jia, C.Y.; Shan, X.Y.; Liu, H.M.; Niu, Z.P. Fuzzy Neural Model for Flatness Pattern Recognition. J. Iron Steel Res. Int. 2008, 15, 33–38. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, X.L. Target Model of the Automatic Shape Control on Cold Strip Mill. J. Univ. Sci. Technol. Beijing 2003, 27, 142–145. [Google Scholar]
- Peng, Y.; Liu, H.M. Pattern Recognition Method Progress of Measured Signals of Shape in Cold Rolling. J. Yanshan Univ. 2003, 27, 142–145. [Google Scholar]
- Yang, Q.; Chen, X.L. The Deforming Route of Buckled Waves of Rolled Strip. J. Univ. Sci. Technol. Beijing 1994, 16, 53–57. [Google Scholar] [CrossRef]
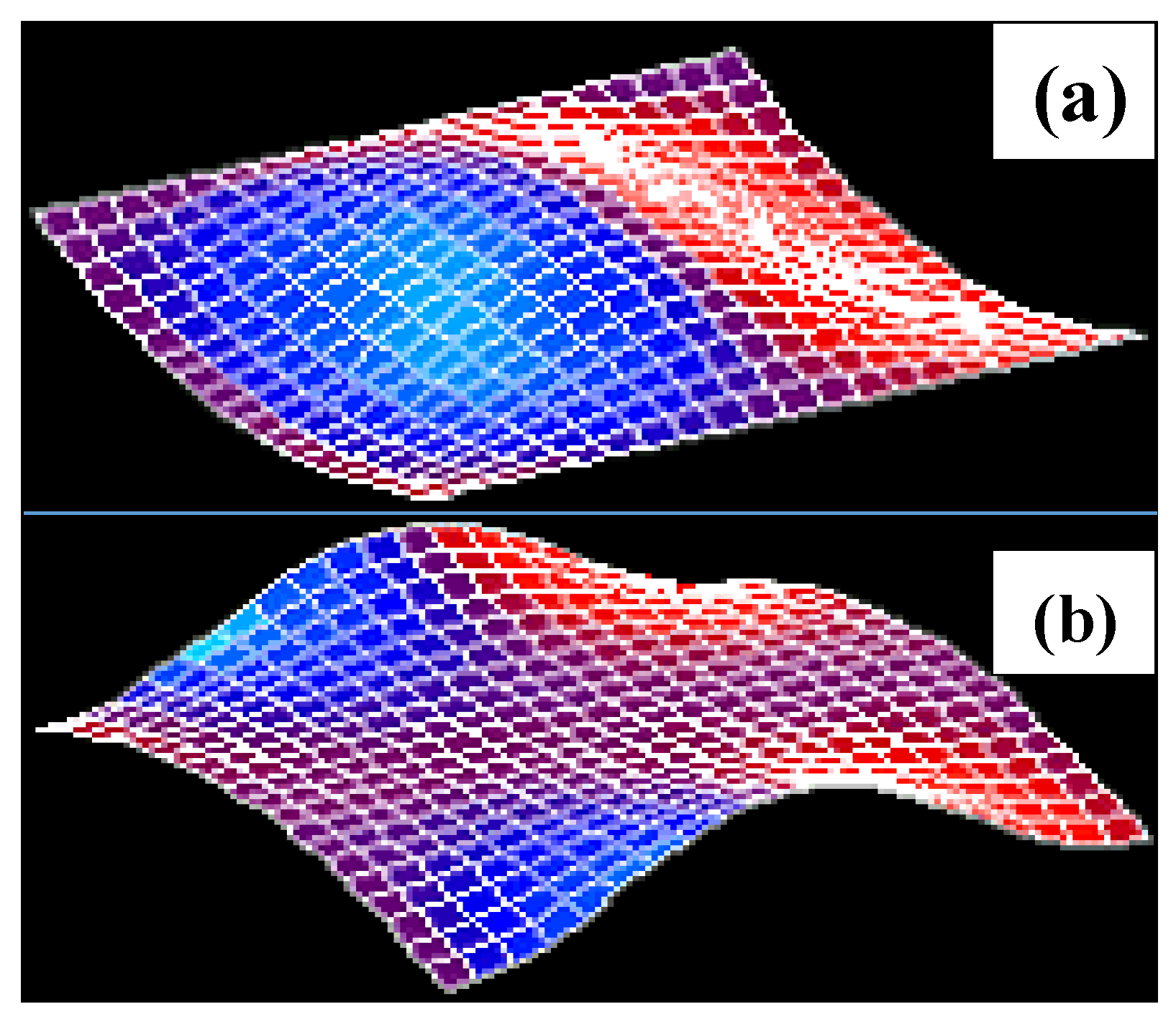



| Buckling Form | Function Name | Formula |
|---|---|---|
| External local wave buckling | Flatness stress | |
| shape wave function | ||
| Internal local wave buckling | Flatness stress | |
| shape wave function | ||
| Overall wave buckling | Flatness stress | |
| shape wave function |
| Number | Steel Grade | Thickness /mm | Width /mm | Tension /Mpa | Critical Buckling Strain Difference | |||
|---|---|---|---|---|---|---|---|---|
| Center Waves | Double-Sided Waves | Internal Local Waves | External Local Waves | |||||
| 1 | SPCC-1B | 0.28 | 909 | 10.9 | 32.37 | 28.61 | 15.07 | 17.94 |
| 2 | SPCC-1B | 0.28 | 909 | 10.2 | 30.29 | 26.78 | 14.1 | 16.78 |
| 3 | SPCC-1B | 0.32 | 904 | 10.9 | 32.37 | 28.61 | 15.09 | 17.95 |
| 4 | SPCC-1B | 0.32 | 904 | 10.9 | 32.37 | 28.61 | 15.09 | 17.95 |
| 5 | SPCC-1B | 0.66 | 904 | 10.9 | 32.38 | 28.62 | 15.16 | 17.99 |
| 6 | SPCC-1B | 0.66 | 904 | 10.9 | 32.38 | 28.62 | 15.16 | 17.99 |
| 7 | SPCC-1B | 0.37 | 904 | 10.3 | 30.59 | 27.04 | 14.27 | 16.97 |
| 8 | SPCC-1B | 0.37 | 904 | 10.1 | 29.99 | 26.51 | 13.99 | 16.64 |
| Number | Internal Local Waves | External Local Waves | Single-Edge Waves | Center Waves | Double-Edge Waves | One-Third Waves | Quarter Waves | Edge-Center Waves |
|---|---|---|---|---|---|---|---|---|
| 1 | 15.07 | 17.94 | 28.61 | 32.37 | 28.61 | 32.37 | 32.37 | 28.61 |
| 2 | 14.1 | 16.78 | 26.78 | 30.29 | 26.78 | 30.29 | 30.29 | 26.78 |
| 3 | 15.09 | 17.95 | 28.61 | 32.37 | 28.61 | 32.37 | 32.37 | 28.61 |
| 4 | 15.09 | 17.95 | 28.61 | 32.37 | 28.61 | 32.37 | 32.37 | 28.61 |
| 5 | 15.16 | 17.99 | 28.62 | 32.38 | 28.62 | 32.38 | 32.38 | 28.62 |
| 6 | 15.16 | 17.99 | 28.62 | 32.38 | 28.62 | 32.38 | 32.38 | 28.62 |
| 7 | 14.27 | 16.97 | 27.04 | 30.59 | 27.04 | 30.59 | 30.59 | 27.04 |
| 8 | 13.99 | 16.64 | 26.51 | 29.99 | 26.51 | 29.99 | 29.99 | 26.51 |
| Number | Steel Grade | w1 | w2 | Y1 | Y2 | Y3 | Y4 | λ | Grade |
|---|---|---|---|---|---|---|---|---|---|
| 1 | SPCC-1B | 29.32 | 0.00 | 2.11 | 52.28 | 25.38 | 1.44 | 0.528 | B |
| 2 | SPCC-1B | 21.11 | 0.00 | 3.68 | 35.30 | 4.47 | 13.73 | 0.523 | B |
| 3 | SPCC-1B | 20.01 | 0.00 | 5.00 | 49.98 | 2.44 | 9.38 | 0.576 | B |
| 4 | SPCC-1B | 20.11 | 0.00 | 4.94 | 38.30 | 5.90 | 6.58 | 0.548 | B |
| 5 | SPCC-1B | 17.97 | 0.00 | 3.06 | 30.36 | 2.78 | 9.81 | 0.543 | B |
| 6 | SPCC-1B | 17.67 | 0.00 | 3.98 | 27.94 | 13.01 | 16.16 | 0.456 | C |
| 7 | SPCC-1B | 33.27 | 0.00 | 6.35 | 57.88 | 6.88 | 4.36 | 0.566 | B |
| 8 | SPCC-1B | 23.43 | 0.00 | 6.04 | 45.37 | 15.68 | 5.30 | 0.528 | B |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Li, J.; Wang, X.; Yang, Q.; Wu, Z. Evaluation Method and Application of Cold Rolled Strip Flatness Quality Based on Multi-Objective Decision-Making. Metals 2022, 12, 1977. https://doi.org/10.3390/met12111977
Wang Q, Li J, Wang X, Yang Q, Wu Z. Evaluation Method and Application of Cold Rolled Strip Flatness Quality Based on Multi-Objective Decision-Making. Metals. 2022; 12(11):1977. https://doi.org/10.3390/met12111977
Chicago/Turabian StyleWang, Qiuna, Jingdong Li, Xiaochen Wang, Quan Yang, and Zedong Wu. 2022. "Evaluation Method and Application of Cold Rolled Strip Flatness Quality Based on Multi-Objective Decision-Making" Metals 12, no. 11: 1977. https://doi.org/10.3390/met12111977
APA StyleWang, Q., Li, J., Wang, X., Yang, Q., & Wu, Z. (2022). Evaluation Method and Application of Cold Rolled Strip Flatness Quality Based on Multi-Objective Decision-Making. Metals, 12(11), 1977. https://doi.org/10.3390/met12111977





