Analysis of Texture and Anisotropic Elastic Properties of Additively Manufactured Ni-Base Alloys
Abstract
1. Introduction
2. Specimen Preparation
3. Characterization Techniques
3.1. Mechanical Approaches
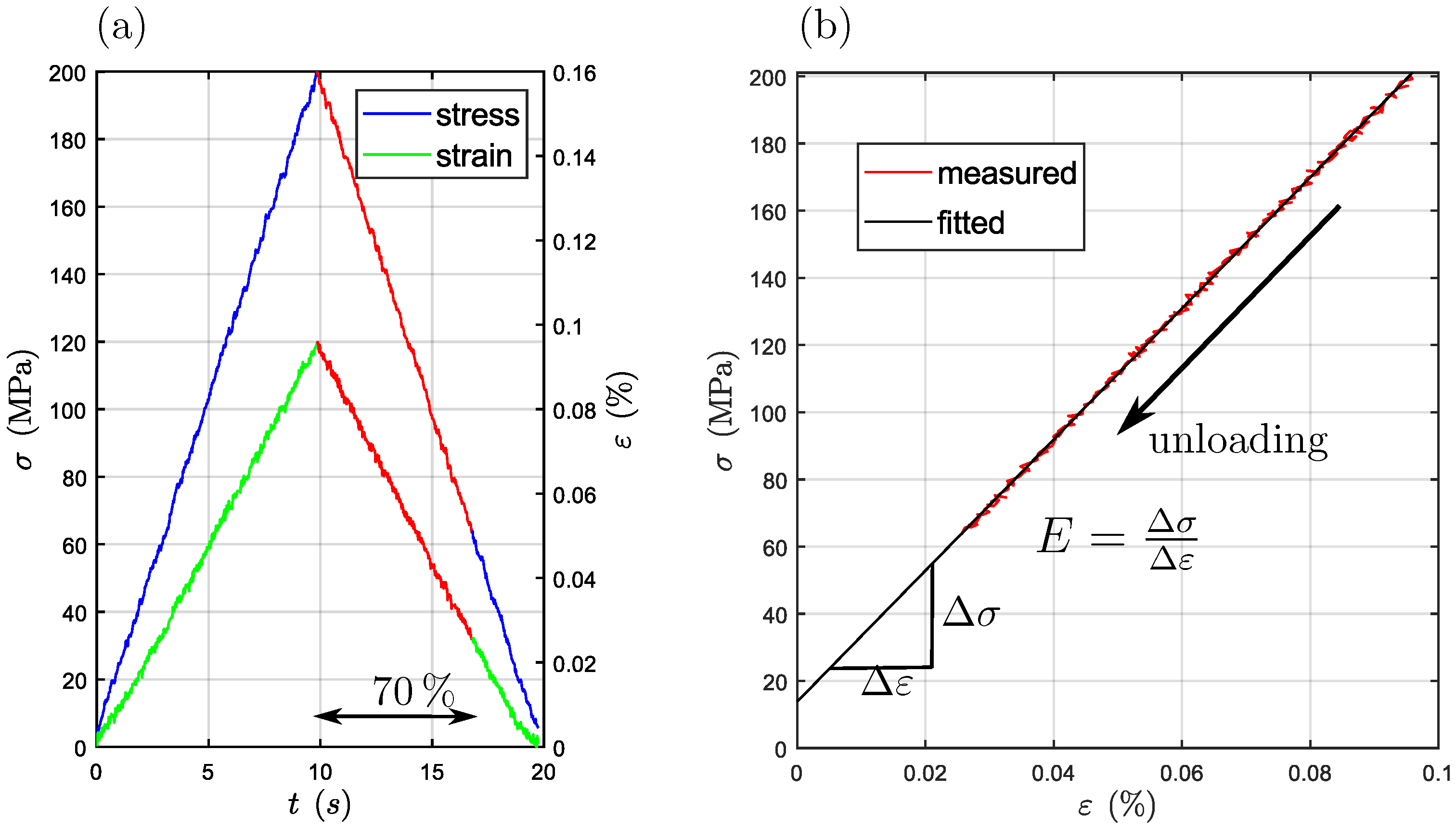
3.1.1. Tensile Loading
3.1.2. Impulse Excitation Technique
3.2. Microstructure Based Approaches
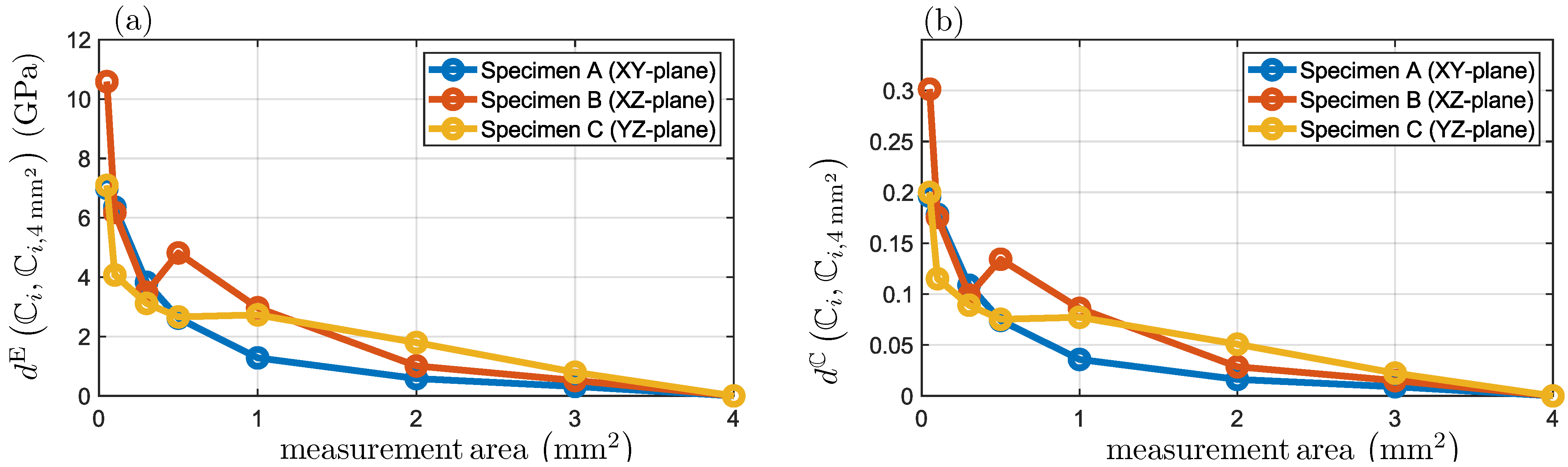
3.2.1. Electron Backscatter Diffraction
3.2.2. High Energy XRD
4. Results and Discussion
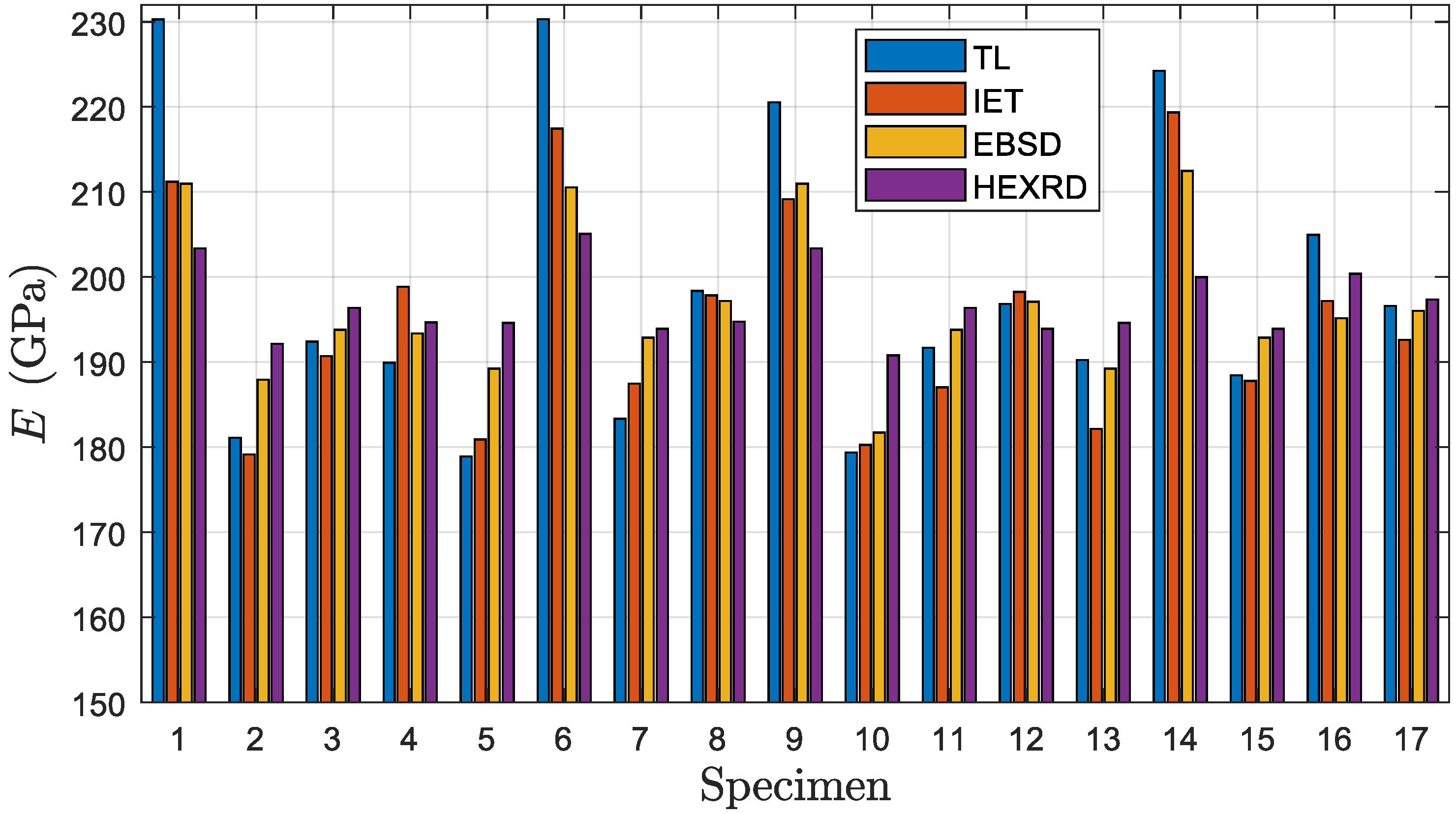
4.1. Directional Young’s Moduli
4.2. Pole Figures
4.3. Elasticity Tensors
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Fernandez-Zelaia, P.; Kirka, M.M.; Dryepondt, S.N.; Gussev, M.N. Crystallographic texture control in electron beam additive manufacturing via conductive manipulation. Mater. Des. 2020, 195, 1090–1100. [Google Scholar] [CrossRef]
- Kirka, M.M.; Lee, Y.; Greenley, D.A.; Okello, A.; Goin, M.J.; Pearce, M.T.; Dehoff, R.R. Strategy for texture management in metals additive manufacturing. JOM 2017, 69, 523–531. [Google Scholar] [CrossRef]
- Popovic, V.A.; Borisov, E.V.; Popovic, A.A.; Sufiiarov, V.S.; Masaylo, D.V.; Alzina, L. Functionally graded Inconel 718 processed by additive manufacturing: Crystallographic texture, anisotropy of microstructure and mechanical properties. Mater. Des. 2017, 114, 441–449. [Google Scholar] [CrossRef]
- Dehoff, R.R.; Kirka, M.M.; List, F.A.; Unocic, K.A.; Sames, W.J. Crystallographic texture engineering through novel melt strategies via electron beam melting: Inconel 718. Mater. Sci. Tech.-Land. 2015, 31, 939–944. [Google Scholar] [CrossRef]
- Geiger, F.; Kunze, K.; Etter, T. Tailoring the texture of IN738LC processed by selective laser melting (SLM) by specific scanning strategies. Mater. Sci. Eng. A-Struct. 2016, 661, 240–246. [Google Scholar] [CrossRef]
- Wan, H.Y.; Zhou, Z.J.; Li, C.P.; Chen, G.F.; Zhang, G.P. Effect of scanning strategy on grain structure and crystallographic texture of Inconel 718 processed by selective laser melting. J. Mater. Sci. Technol. 2018, 34, 1799–1804. [Google Scholar] [CrossRef]
- Liu, J.; To, A.C. Quantitative texture prediction of epitaxial columnar grains in additive manufacturing using selective laser melting. Addit. Manuf. 2017, 16, 58–64. [Google Scholar] [CrossRef]
- Obermayer, T.; Krempaszky, C.; Werner, E. Determination of the anisotropic elasticity tensor by mechanical spectroscopy. Contin. Mech. Therm. 2021, 34, 165–184. [Google Scholar] [CrossRef]
- Sedlák, P.; Seiner, H.; Zídek, J.; Janovská, M.; Landa, M. Determination of all 21 independent elastic coefficients of generally anisotropic solids by resonant ultrasound spectroscopy: Benchmark Examples. Exp. Mech. 2014, 54, 1073–1085. [Google Scholar] [CrossRef]
- DIN EN ISO 6892-1; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Beuth: Berlin, Germany, 2019. [CrossRef]
- ASTM E111-17; Standard Test Method for Young’s Modulus, Tangent Modulus, and Chord Modulus. American Society for Testing Materials: West Conshohocken, PA, USA, 2017. [CrossRef]
- ASTM E1876-15; Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson Ratio by Impulse Excitation of Vibration. American Society for Testing Materials: West Conshohocken, PA, USA, 2001. [CrossRef]
- Martin, G.; Ochoa, N.; Saï, K.; Hervé-Luanco, E.; Cailletaud, G. A multiscale model for the elastoviscoplastic behavior of directionally solidified alloys: Application to FE structural computations. Int. J. Solids. Struct. 2014, 51, 1175–1187. [Google Scholar] [CrossRef]
- Bachmann, F.; Hieschler, R.; Schaeben, H. Texture analysis with MTEX—Free and open source software toolbox. Solid State Phenom. 2010, 210, 63–68. [Google Scholar] [CrossRef]
- Schell, N.; King, A.; Beckmann, F.; Fischer, T.; Müller, M.; Schreyer, A. The high energy materials science beamline (HEM) at Petra III. Mater. Sci. Forum 2014, 772, 57–61. [Google Scholar] [CrossRef]
- Randau, C.; Garbe, U.; Brokmeier, H.-G. StressTextureCalculator: A software tool to exact texture, strain and microstructure information from area-detector measurements. J. Appl. Cryst. 2011, 44, 641–646. [Google Scholar] [CrossRef]
- Brydon, R.E.; Burle, J.; Coenen, W.; Gan, W.; Hofmann, M.; Katter, J.; Soinien, J.; Wuttke, J. Stress and Texture Calculator Steca, Version 2. 2018. Available online: https://github.com/scgmlz/Steca2 (accessed on 2 February 2022).
- Hieschler, R.; Schaeben, H. A novel pole figure inversion method: Specification of the MTEX algorithm. J. Appl. Cryst. 2008, 41, 1024–1037. [Google Scholar] [CrossRef]
- Morin, L.; Gilormini, P.; Derrien, K. Generalized euclidean distances for elasticity tensors. J. Elast. 2020, 138, 221–232. [Google Scholar] [CrossRef]
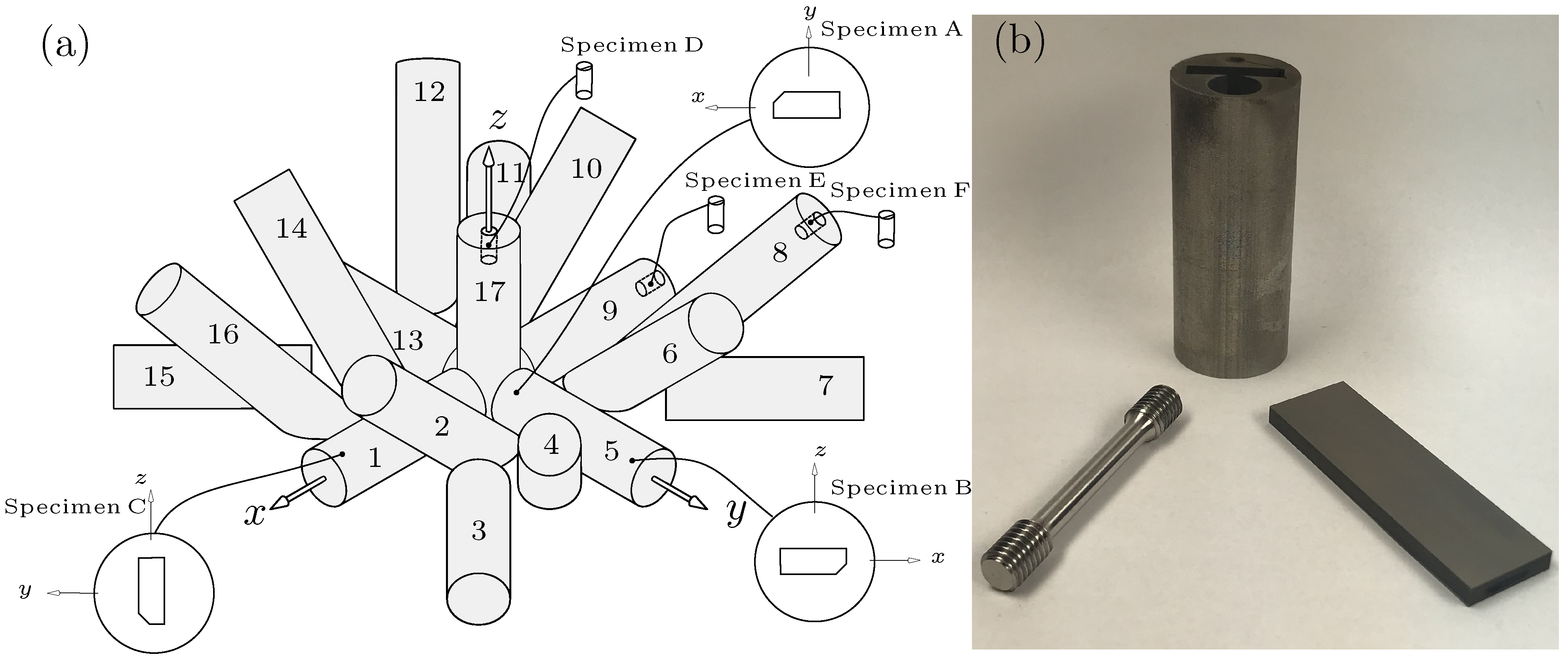




| Specimen A (-Plane) | Specimen B (-Plane) | Specimen C (-Plane) | |
|---|---|---|---|
| EBSD | HE-XRD | |||||
|---|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obermayer, T.; Krempaszky, C.; Werner, E. Analysis of Texture and Anisotropic Elastic Properties of Additively Manufactured Ni-Base Alloys. Metals 2022, 12, 1991. https://doi.org/10.3390/met12111991
Obermayer T, Krempaszky C, Werner E. Analysis of Texture and Anisotropic Elastic Properties of Additively Manufactured Ni-Base Alloys. Metals. 2022; 12(11):1991. https://doi.org/10.3390/met12111991
Chicago/Turabian StyleObermayer, Thomas, Christian Krempaszky, and Ewald Werner. 2022. "Analysis of Texture and Anisotropic Elastic Properties of Additively Manufactured Ni-Base Alloys" Metals 12, no. 11: 1991. https://doi.org/10.3390/met12111991
APA StyleObermayer, T., Krempaszky, C., & Werner, E. (2022). Analysis of Texture and Anisotropic Elastic Properties of Additively Manufactured Ni-Base Alloys. Metals, 12(11), 1991. https://doi.org/10.3390/met12111991






