Effect of Nickel Contents on Fatigue Crack Growth Rate and Fracture Toughness for Nickel Alloy Steels
Abstract
:1. Introduction
1.1. Prior Work of Fatigue and Fracture Performances for Nickel Alloy Steels
1.2. Fatigue Ductile to Brittle Transition (FDBT) Temperature
1.3. Fracture Toughness ( and CTOD)
1.4. Scope and Aim of This Paper
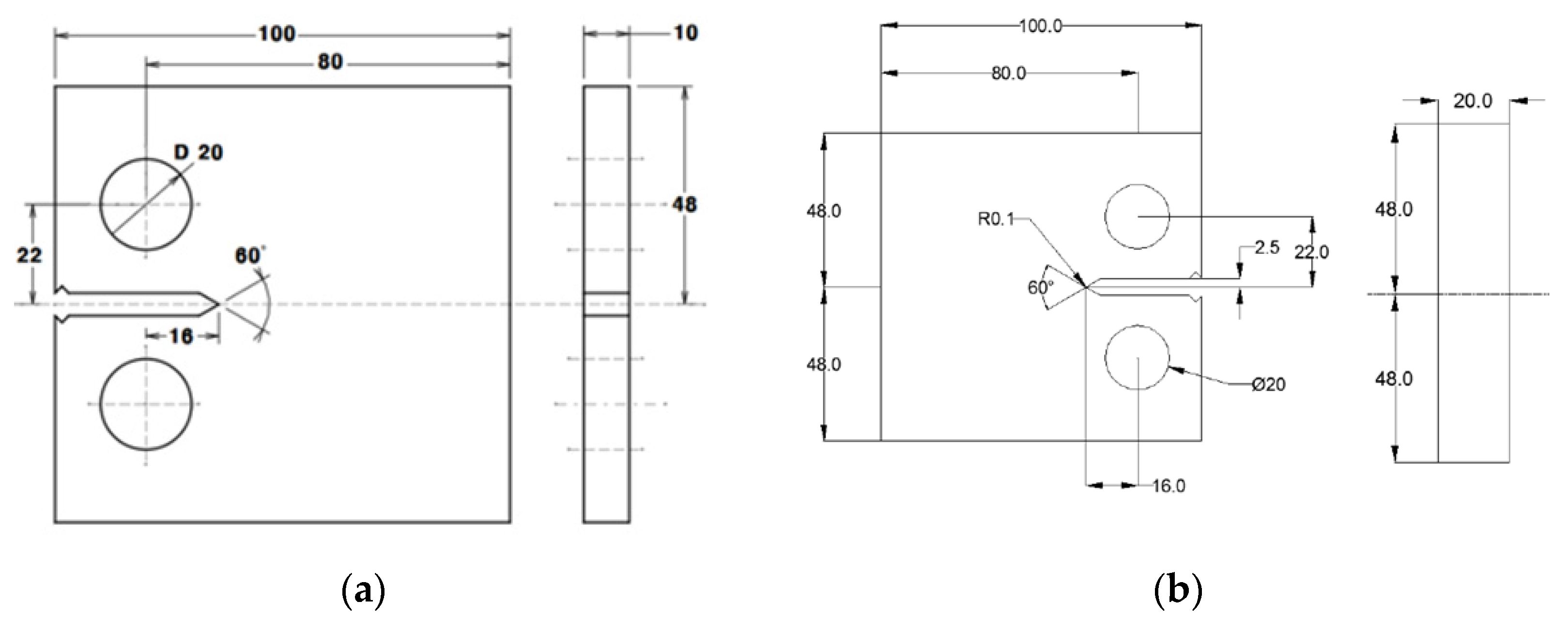
2. Materials and Methods
2.1. Materials
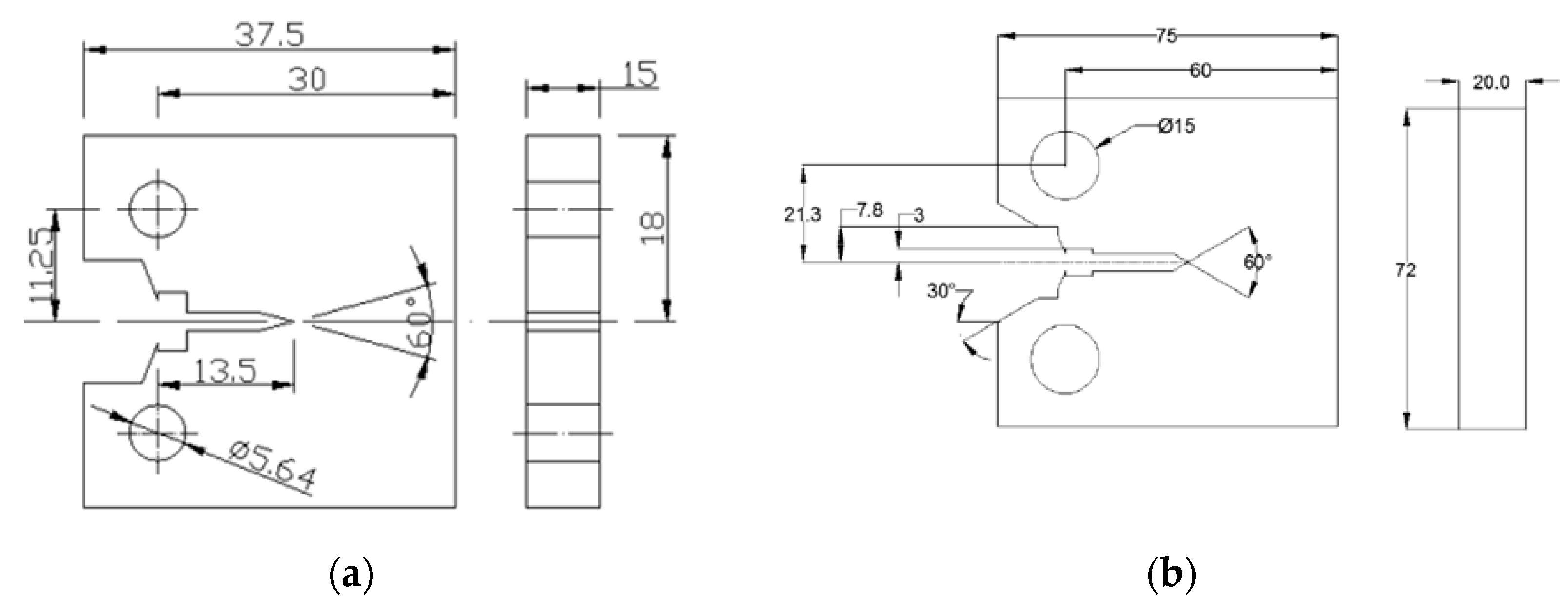
2.2. Test Condition
3. Results
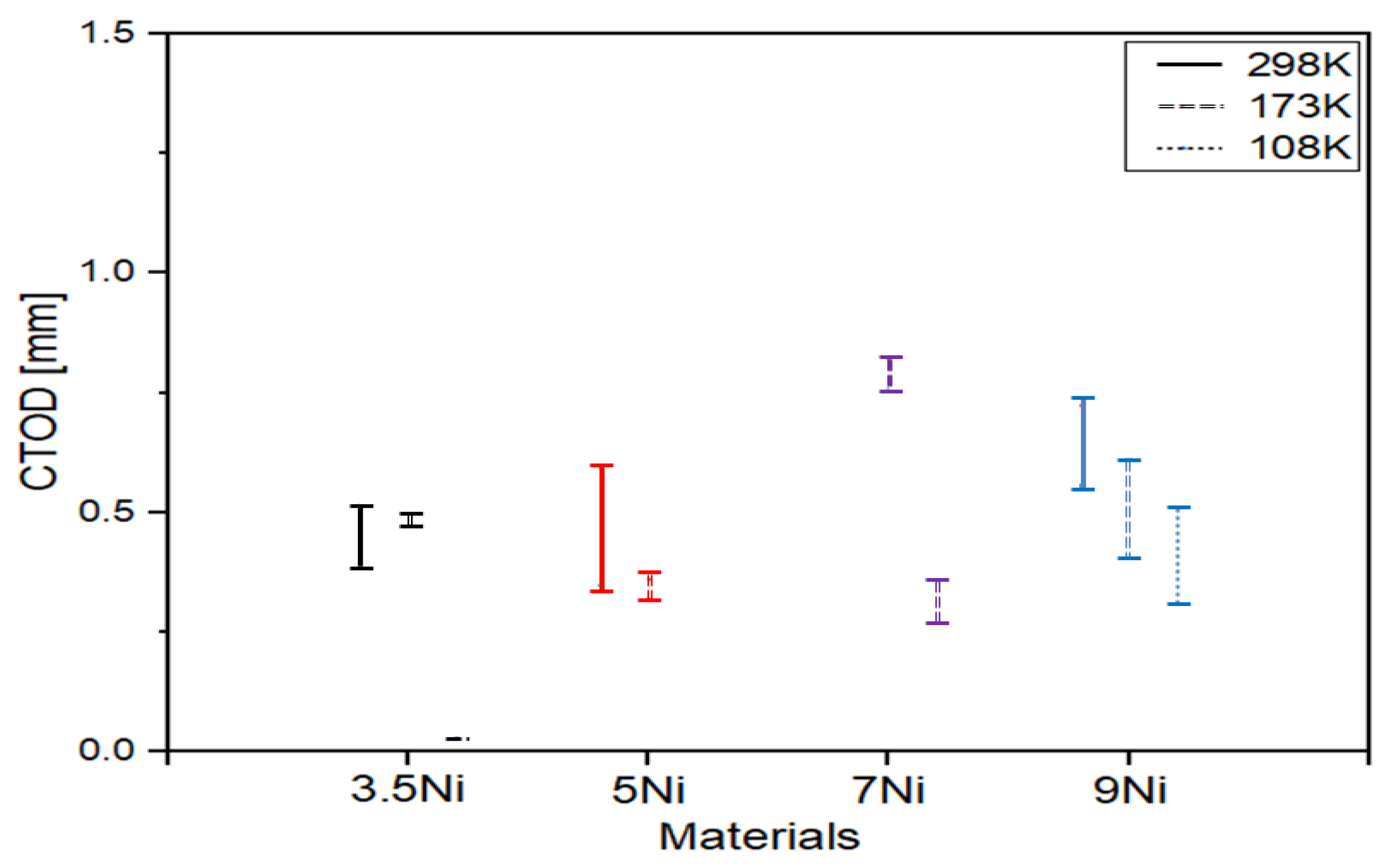
3.1. Fracture Performance (CTOD)
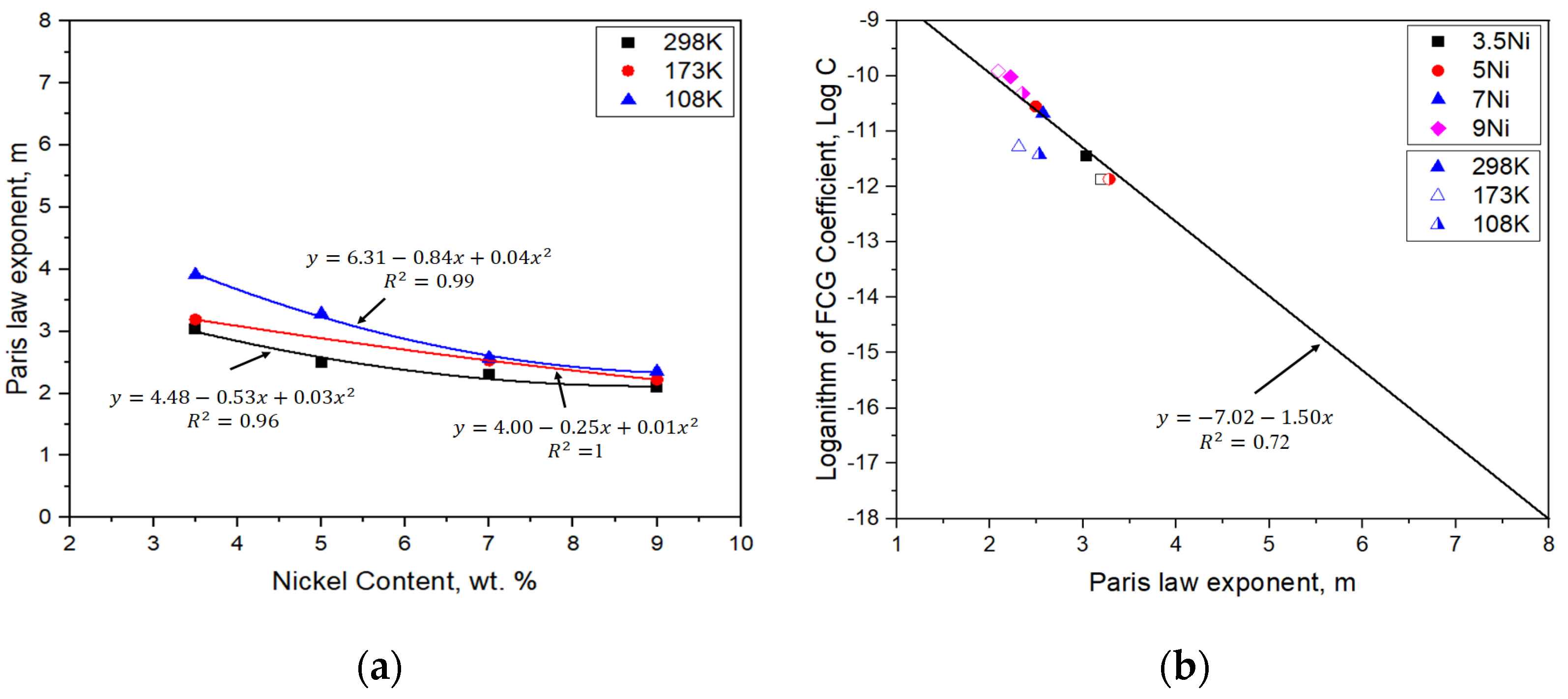
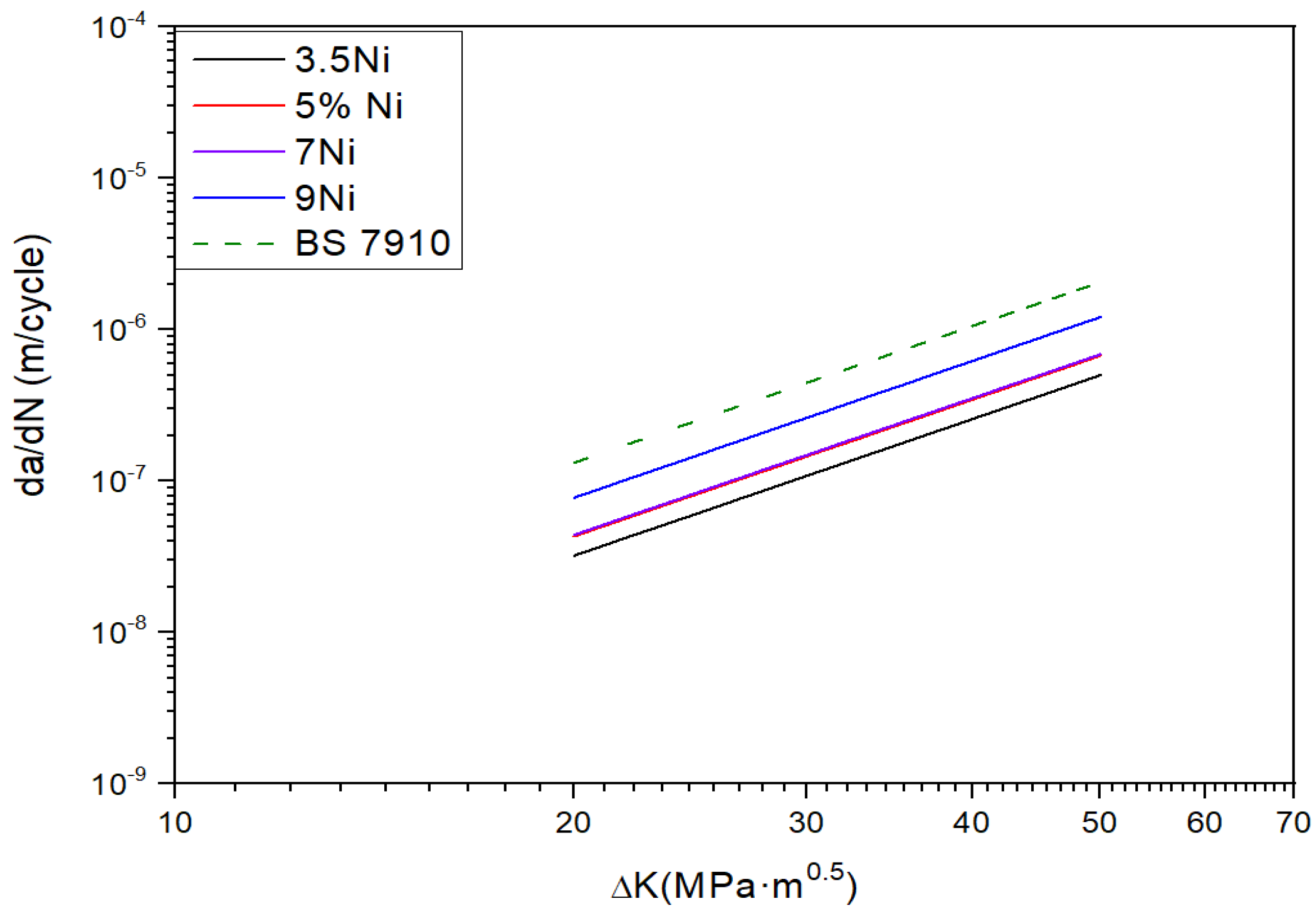
3.2. Fatigue Performance (FCGR)
4. Discussion
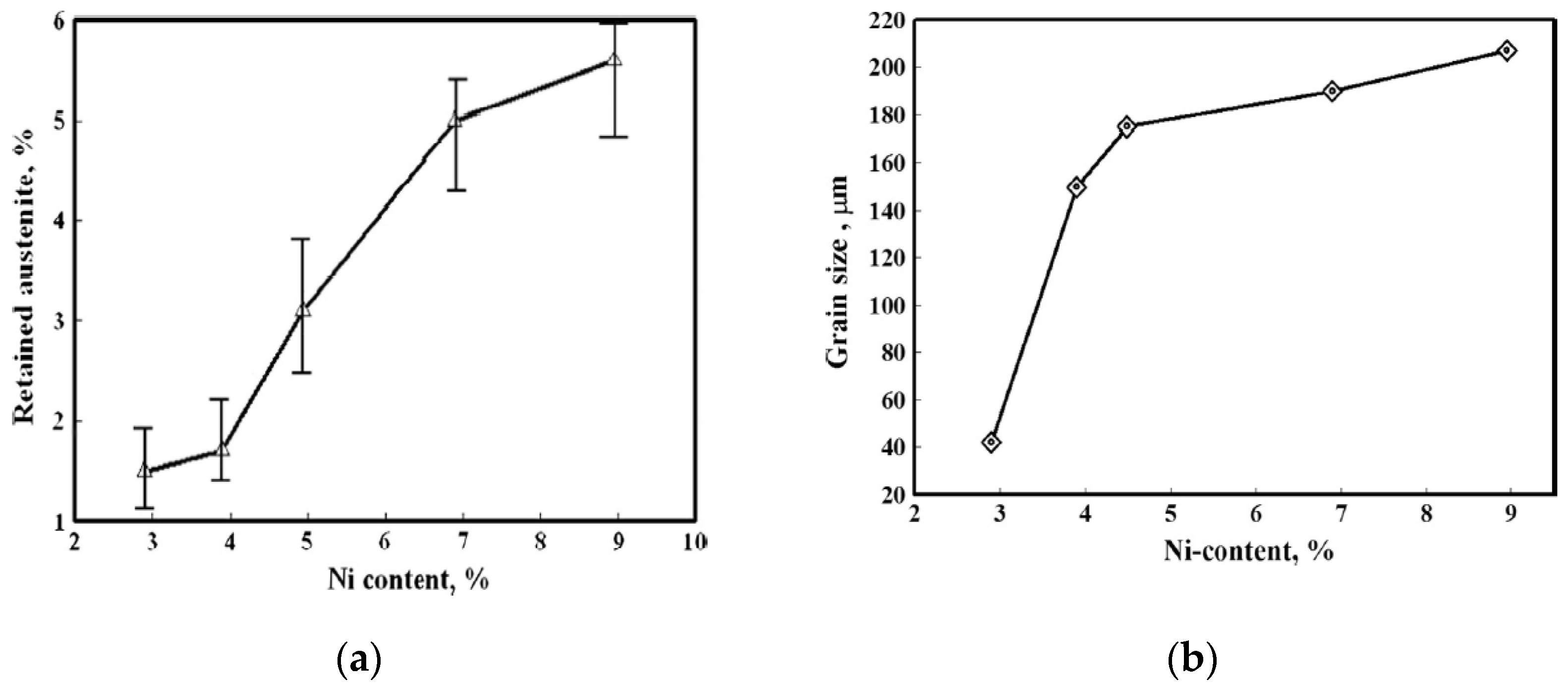
4.1. Microstructure Analysis
4.2. FDBT Temperatures for Nickel Alloy Steels
5. Conclusions
- The critical CTOD values of nickel alloy steels increase as nickel contents increase. It is well known that nickel contribute to stabilization for austenite, and the critical CTOD value increase as amount of retained austenite increase. Therefore, the critical CTOD value is influenced by nickel contents.
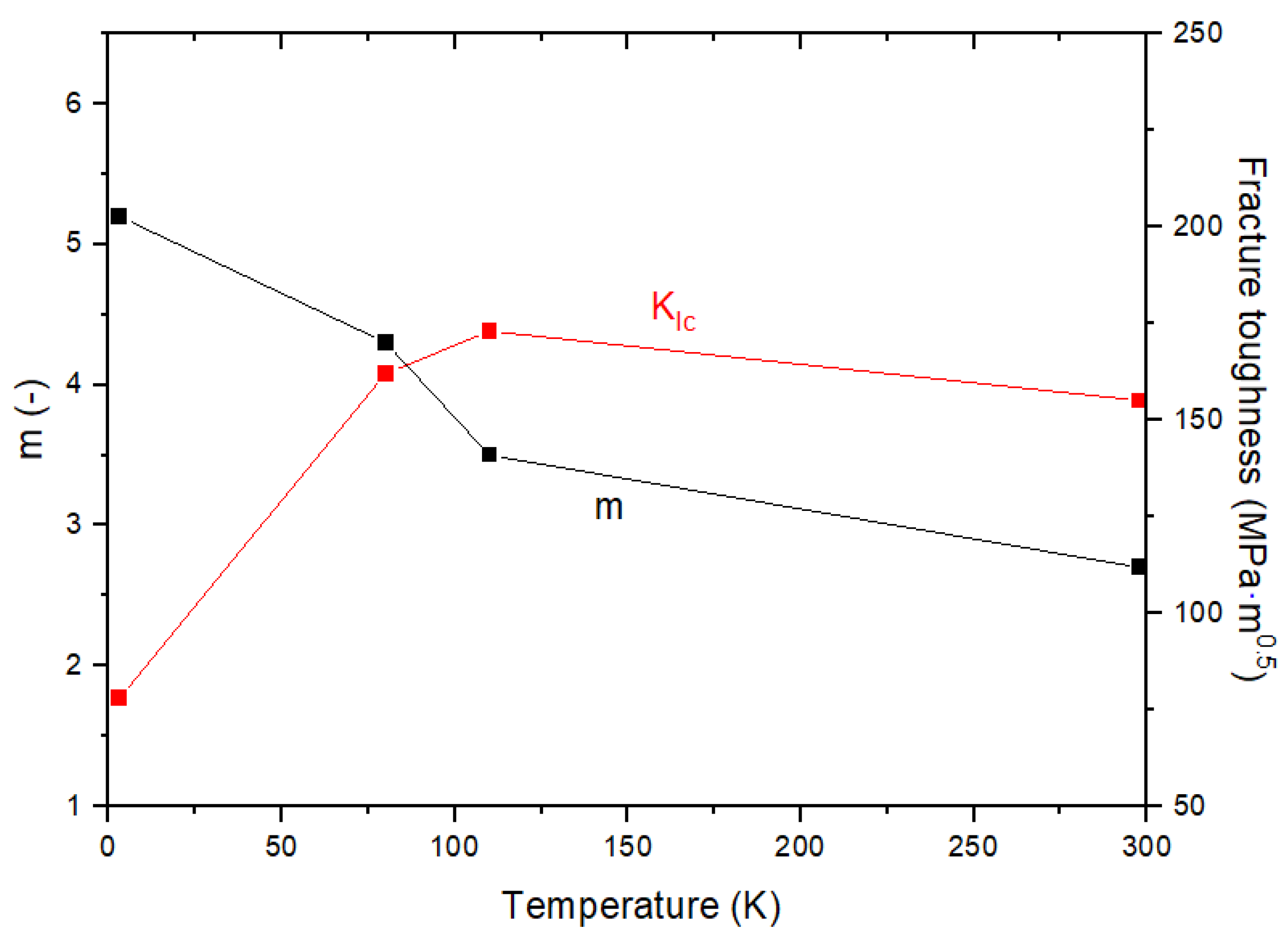
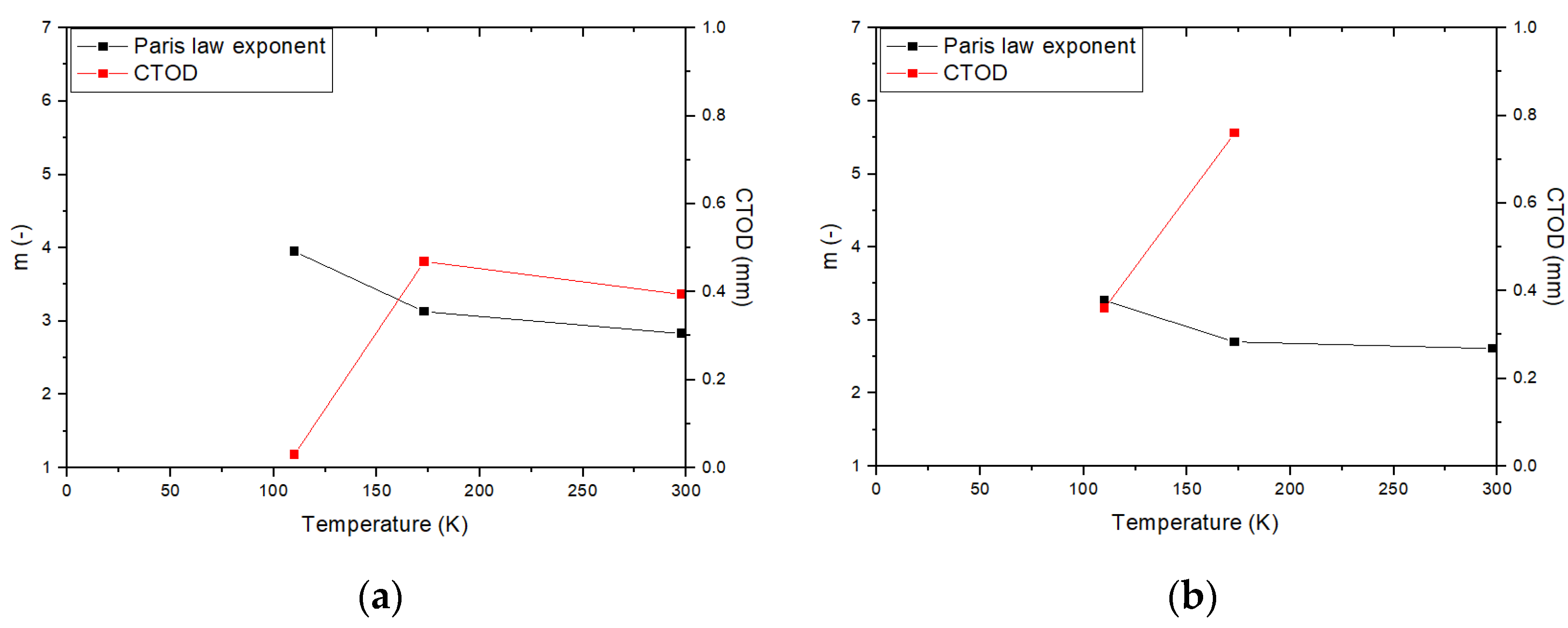
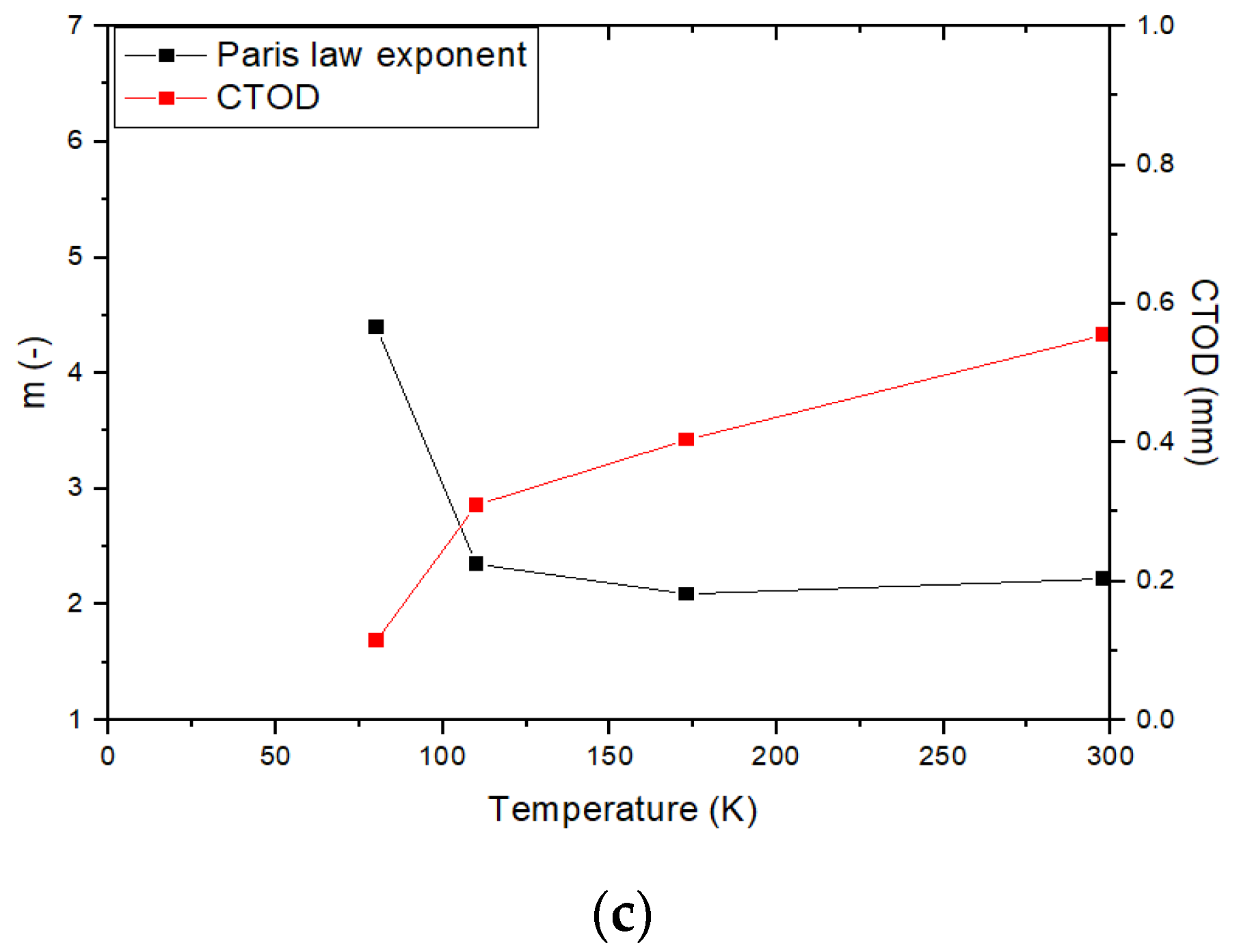
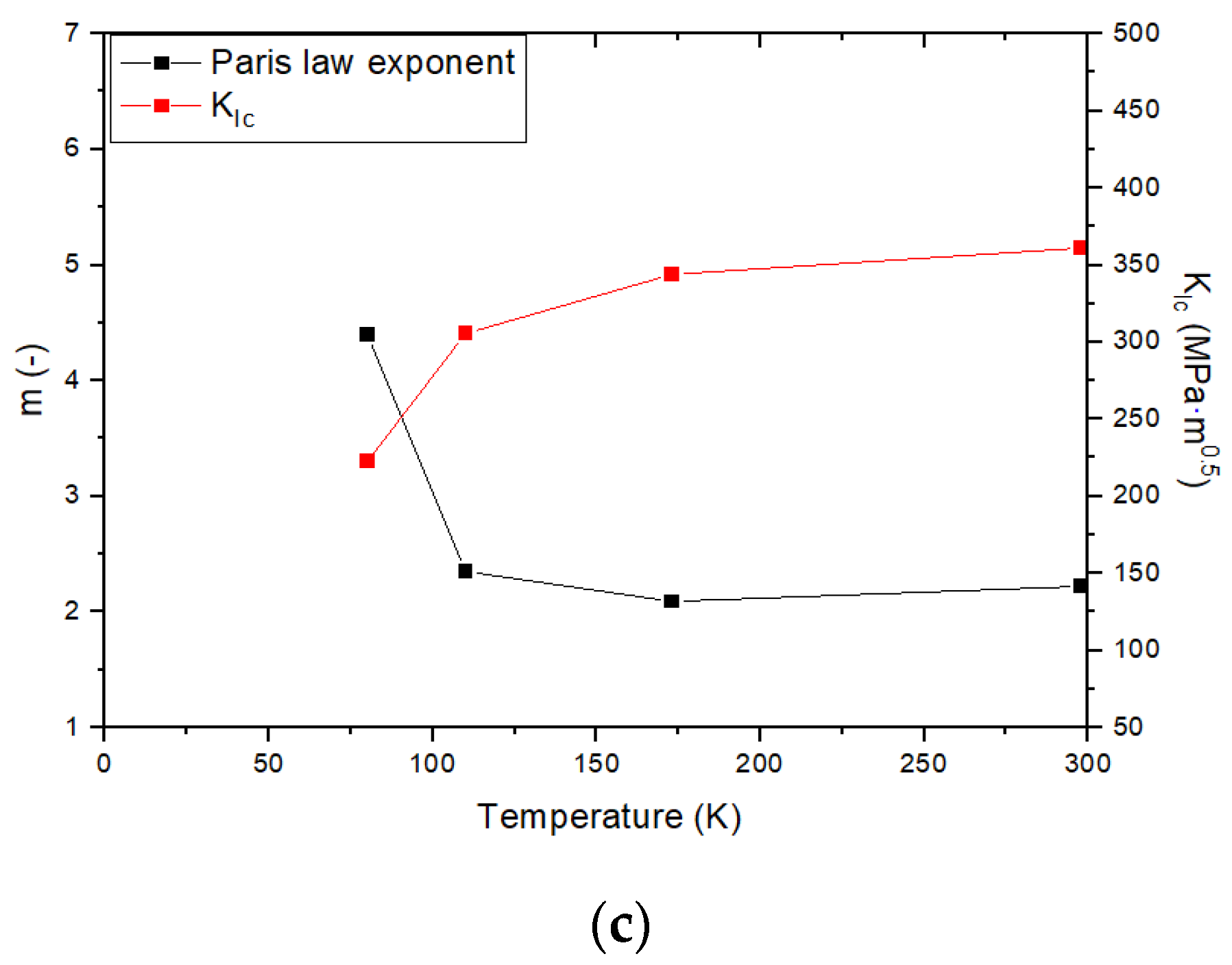
- The FCGR of nickel alloy steels increase while nickel content increase. In cases of the low nickel content in the nickel alloy steel, the factor m, the slope of the FCGR, increases further with decreasing temperature in comparison with the high nickel content of the nickel alloy steel. In addition, the factor m increases as nickel contents decrease at the same temperature. The material constants from FCGR are observed to locate within a single line except some data.
- The dimple size of 3.5Ni is smaller than that of 9Ni. In addition, the dimple size after the critical CTOD test at cryogenic temperature is smaller than that at room temperature. Therefore, the tendency of fracture toughness by nickel contents is reasonable according to analysis of dimple size. In case of fatigue striation, 3.5Ni is narrower than 9Ni. It is expected that FCGR of 9Ni is fast compared to 3.5Ni based on the fatigue striation spacing. Therefore, FCGR of nickel alloy steels obtained from this study are reasonable according to existing paper and microstructure analysis.
- Based on FDBT temperature by the relationship of the critical CTOD-m, no brittle failure exists in the fatigue and fracture performances of the nickel alloy steels at the actual operating temperature. The FDBT temperature by the critical CTOD and decreases as amount of nickel contents increase. In addition, the FDBT temperatures by are lower than thoes by the critical CTOD. The different criterion for fracture toughness parameters lead to this discrepancy. For high toughness materials, it can be inferred that , a fracture toughness parameter based on elastic fracture mechanics, does not accurately reflect the plastic deformation at the crack tip and strain hardening effect.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahssi, M.A.M.; Erden, M.A.; Acarer, M.; Çuğ, H. The Effect of Nickel on the Microstructure, Mechanical Properties and Corrosion Properties of Niobium–Vanadium Microalloyed Powder Metallurgy Steels. Materials 2020, 13, 4021. [Google Scholar] [CrossRef] [PubMed]
- Khodir, S.; Shilbayanagi, T.; Takahashi, M.; Abdel-Aleem, H.; Ikeuchi, K. Microstructural Evolution and Mechanical Properties of High Strength 3–9% Ni-steel Alloys Weld Metals Produced by Electron Beam Welding. Mater. Des. 2020, 60, 391–400. [Google Scholar] [CrossRef]
- International Association of Classification Societies. Requirement Concerning Materials and Welding; International Association of Classification Societies: London, UK, 2015. [Google Scholar]
- Revised MARPOL Annex VI, Amendments to the Annex of the Protocol of 1997 to Amend the International Convention for the Prevention of Pollution from Ships; International Maritime Organization: London, UK, 2016.
- Kim, Y.W.; Oh, D.J.; Lee, J.M.; Noh, B.J.; Sung, H.J.; Ando, R.; Matsumoto, T.; Kim, M.H. An Experimental Study for Fatigue Performance of 7% Nickel Steels for Type B Liquefied Natural Gas Carriers. J. Offshore Mech. Arct. Eng. 2016, 138, 1–6. [Google Scholar] [CrossRef]
- Yoo, C.H.; Kim, K.S.; Choung, J.M.; Kim, S.H.; You, W.H. An Experimental Study on Behaviors of IMO Type B CCS Materials at Room and Cryogenic Temperatures. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Furuya, H.; Saitoh, N.; Takahashi, Y.; Kurebayashi, K.; Kayamori, Y.; Inoue, T.; Uemori, R.; Okushima, M. Development of 6% Nickel Steel for LNG Storage Tanks. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Paris, P.C.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1960, 85, 528–534. [Google Scholar] [CrossRef]
- Walters, C.L.; Alvaro, A.; Maljaars, J. The effect of low temperatures on the fatigue crack growth of S460 structural steel. Int. J. Fatigue 2016, 82, 110–118. [Google Scholar] [CrossRef]
- Tobler, R.L.; Cheng, Y.W. Midrange fatigue crack growth data correlations for structural alloys at room and cryogenic temperatures. Fatigue Low Temp. 1985, 16, 5–30. [Google Scholar]
- Irwin, G.R. Analysis of Stresses and Strains Near the End of a Crack Traversing a Plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Williams, M.L. On the Stress Distribution at the Base of a Stationary Crack. J. Appl. Mech. 1957, 24, 109–114. [Google Scholar] [CrossRef]
- Irwin, G.R.; Kies, J.A.; Smith, H.I. Fracture Strengths Relative to Onset and Arrest of Crack Propagation. Proceeding Am. Soc. Test. Mater. 1958, 57, 640–660. [Google Scholar]
- Irwin, G.R. Plastic zone near a crack and fracture toughness. In Proceedings of the 7th Sagamore Ordnance Materials Conference, New York, NY, USA, 16–19 August 1960. [Google Scholar]
- Xian, K.Z.; James, A.J. Review of Fracture Toughness (G, K, J, CTOD, CTOA) Testing and Standardization. Eng. Fract. Mech. 2012, 85, 1–46. [Google Scholar]
- Wells, A.A. Application of fracture mechanics at and beyond general yielding. Br. Weld. J. 1963, 10, 563–570. [Google Scholar]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–108. [Google Scholar] [CrossRef]
- Goodier, J.N.; Field, F.A. Plastic Energy Dissipation in Crack Propagation; Drucker, D.C., Gilman, J.J., Eds.; The Fracture of Solids: New York, NY, USA, 1963; pp. 103–118. [Google Scholar]
- Burdekin, F.M.; Stone, D.E.W. The crack opening displacement approach to fracture mechanics in yielding materials. J. Strain Anal. Eng. Des. 1966, 1, 145–153. [Google Scholar] [CrossRef]
- Hyundai Heavy Industries Co., Ltd. Mechanical and Fatigue Properties at Room and Cryogenic Temperatures for 9% Ni Steel; Technical report; Hyundai Heavy Industries Co., Ltd.: Ulsan, Korea, 2012.
- Scheid, A.; Felix, L.M.; Martinazzi, D.; Renck, T.; Kwietniewski, C.E.F. The Microstructure Effect on the Fracture Toughness of Ferrite Ni-alloyed Steels. Mater. Sci. Eng. A 2016, 661, 96–104. [Google Scholar] [CrossRef]
- Park, J.Y.; Lee, J.M.; Kim, M.H. An Investigation of the Mechanical Properties of a Weldment of 7% Nickel Alloy Steels. Metals 2016, 6, 285. [Google Scholar] [CrossRef] [Green Version]
- BS 7448; British Standard. Method for Determination of Critical CTOD and Critical J Values of Metallic Materials. The British Standards Institution: London, UK, 1991.
- ASTM E647; Standard Test Method for Measurement of Fatigue Crack Growth Rates. American Society for Testing and Materials: West Conshohocken, PA, USA, 2013.
- Pistorius, P.C.; Toit, M.D. Low-Nickel Austenitic Stainless Steels: Metallurgical Constraints. In Proceedings of the Twelfth International Ferroalloys Congress, Helsinki, Finland, 6–9 June 2010. [Google Scholar]
- Jang, J.I.; Yang, Y.C.; Kim, W.S.; Kwon, D.G. Evaluation of Cryogenic Fracture Toughness in SMA-Welded 9% Ni Steels through Modified CTOD Test. Met. Mater. 1997, 3, 230–238. [Google Scholar] [CrossRef]
- Mchenry, H.I.; Reed, R.P. Fracture Behavior of the Heat-Affected Zone in 5% Ni Steel Weldments. Weld. Res. Suppl. 1977, 4, 104–112. [Google Scholar]
- BS 7910; Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures. British Standards Institution: London, UK, 2013.
- Park, J.J.; Kim, M.H. Investigation of Fatigue and Fracture Characteristics for Low-Temperature Metals considering the Effects of Various Alloying Components. Weld. World 2020, 64, 1691–1702. [Google Scholar] [CrossRef]
- Strife, J.R.; Passoja, D.E. The Effect of Heat Treatment on Microstructure and Cryogenic Fracture Properties in 5Ni and 9Ni Steel. Metall. Trans. A 1980, 11, 1341–1350. [Google Scholar] [CrossRef]
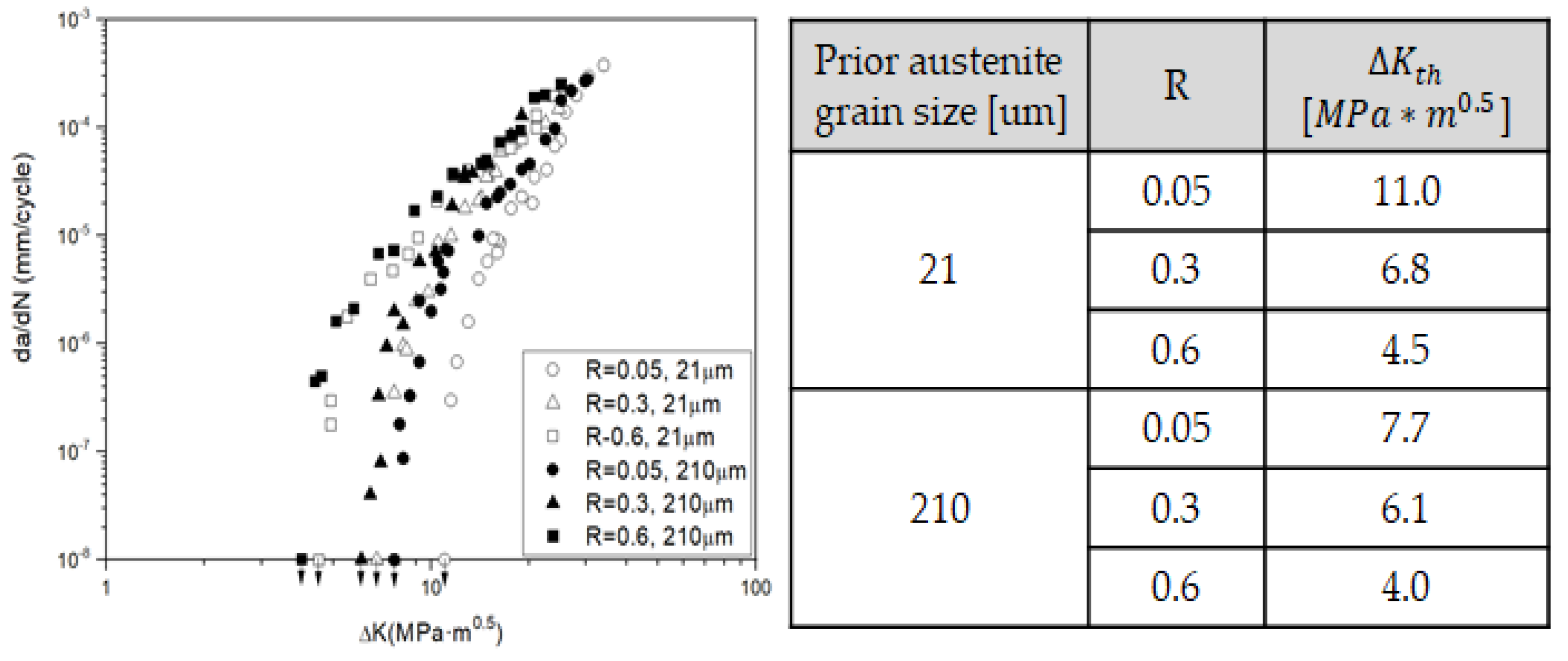
- Murakami, R.; Akizono, K. Influence of Prior Austenite Grain Size and Stress Ratio on Near Threshold Fatigue Crack Growth Behavior of High Strength Steel. J. Soc. Mater. Sci. 1980, 29, 1011–1017. [Google Scholar] [CrossRef]
- ASTM E112; Standard Test Methods for Determining Average Grain Size. American Society for Testing and Materials: West Conshohocken, PA, USA, 2010.
- Wells, A.A. Unstable Crack Propagation in Metals: Cleavage and Fast Fracture. In Proceedings of the Crack Propagation Symposium, Cranfield, UK, 26–28 September 1961. [Google Scholar]





| Minimum Design Temperature (K) | Chemical Composition | Application |
|---|---|---|
| 213 | 1.5% nickel alloy steel | Propane Gas |
| 208 | 2.25% nickel alloy steel | |
| 183 | 3.5% nickel alloy steel | Ethane Gas |
| 168 | 5% nickel alloy steel | |
| 108 | 9% nickel alloy steel | Natural Gas |
| Material | Naming | C | Mn | Si | P | S | Ni | Cr | Mo |
|---|---|---|---|---|---|---|---|---|---|
| 3.5% Ni | 3.5Ni | 0.06 | 0.54 | 0.17 | 0.005 | - | 3.58 | - | - |
| 5% Ni | 5Ni | 0.08 | 0.06 | 0.25 | 0.010 | 0.009 | 5.03 | - | 0.30 |
| 7% Ni | 7Ni | 0.04 | 0.78 | 0.06 | 0.002 | 0.004 | 7.13 | 0.46 | 0.09 |
| 9% Ni | 9Ni | 0.10 | 0.3–0.9 | 0.35 | 0.035 | 0.020 | 8.5–10 | 0.25 | 0.10 |
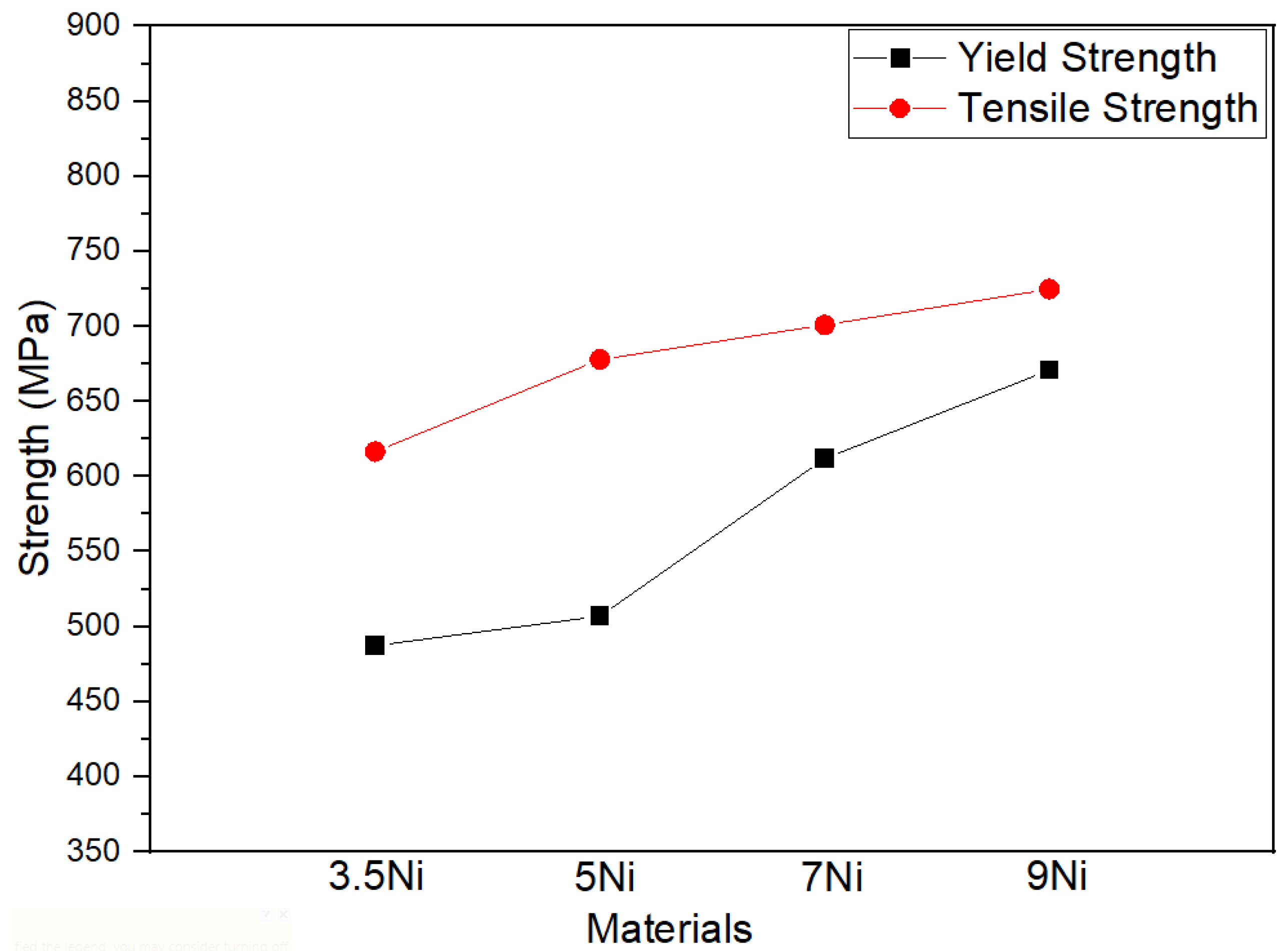
| Material | (MPa) | (MPa) |
|---|---|---|
| 3.5Ni | 487.3 | 616.8 |
| 5Ni | 507.0 | 678.0 |
| 7Ni | 612.0 | 701.0 |
| 9Ni | 670.7 | 724.9 |
| Material | C (m/cycle) | m |
|---|---|---|
| 3.5Ni | 3 | |
| 5Ni | ||
| 7Ni | ||
| 9Ni | ||
| BS 7910 |
| Material | Prior Austenite Grain Diameter (μm) |
|---|---|
| 3.5Ni | 33.3 |
| 9Ni | 98.3 |
| Material | FDBT Temperature Based on | FDBT Temperature Based on the Critical CTOD |
|---|---|---|
| 3.5Ni | 151 K | 160 K |
| 7Ni | - | 110 K |
| 9Ni | 90 K | 104 K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.Y.; Kim, B.K.; Nam, D.G.; Kim, M.H. Effect of Nickel Contents on Fatigue Crack Growth Rate and Fracture Toughness for Nickel Alloy Steels. Metals 2022, 12, 173. https://doi.org/10.3390/met12020173
Park JY, Kim BK, Nam DG, Kim MH. Effect of Nickel Contents on Fatigue Crack Growth Rate and Fracture Toughness for Nickel Alloy Steels. Metals. 2022; 12(2):173. https://doi.org/10.3390/met12020173
Chicago/Turabian StylePark, Jeong Yeol, Byoung Koo Kim, Dae Geun Nam, and Myung Hyun Kim. 2022. "Effect of Nickel Contents on Fatigue Crack Growth Rate and Fracture Toughness for Nickel Alloy Steels" Metals 12, no. 2: 173. https://doi.org/10.3390/met12020173
APA StylePark, J. Y., Kim, B. K., Nam, D. G., & Kim, M. H. (2022). Effect of Nickel Contents on Fatigue Crack Growth Rate and Fracture Toughness for Nickel Alloy Steels. Metals, 12(2), 173. https://doi.org/10.3390/met12020173






