Atomic Simulations of the Interaction between a Dislocation Loop and Vacancy-Type Defects in Tungsten
Abstract
:1. Introduction
2. Simulation Details
3. Results and Discussion
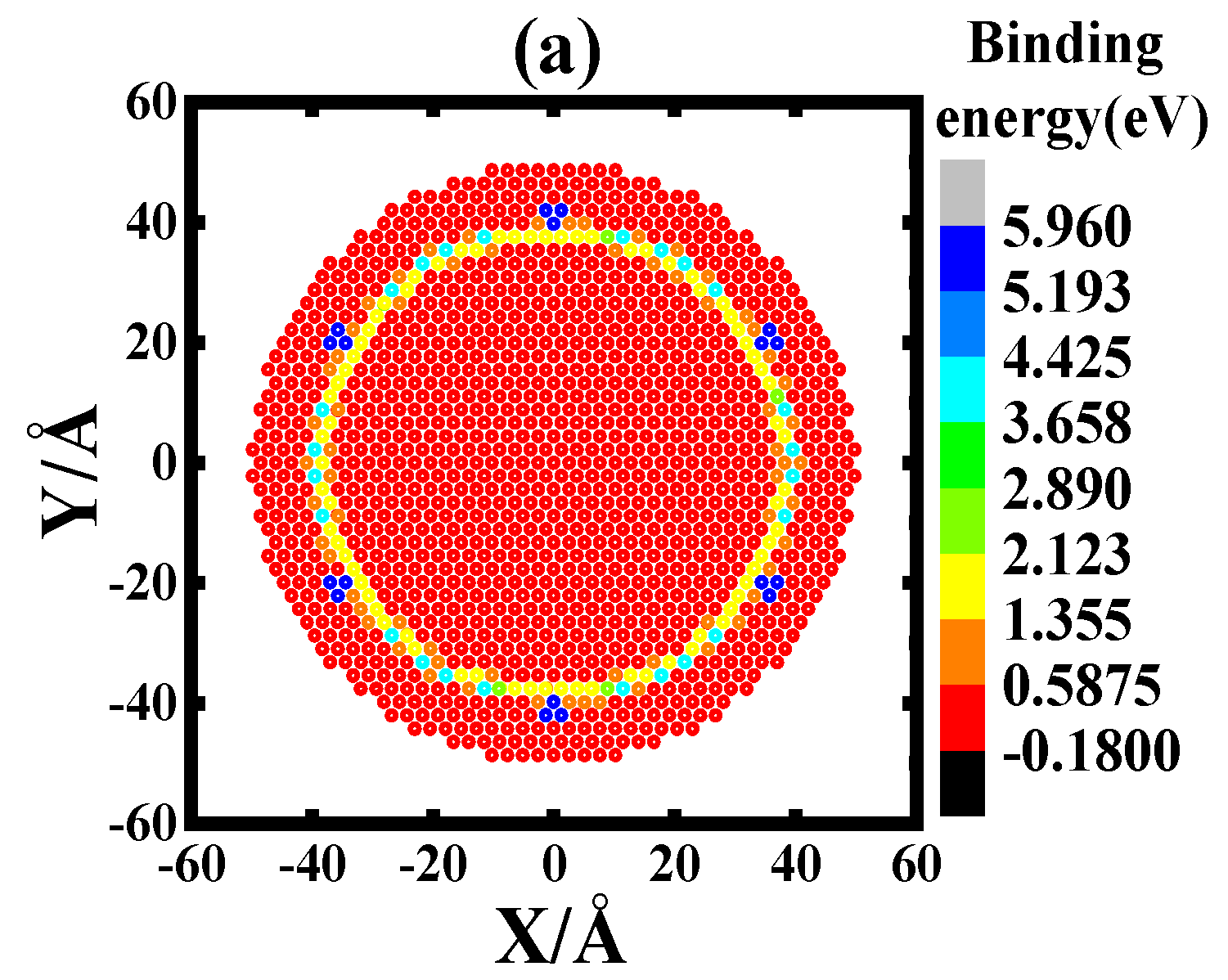
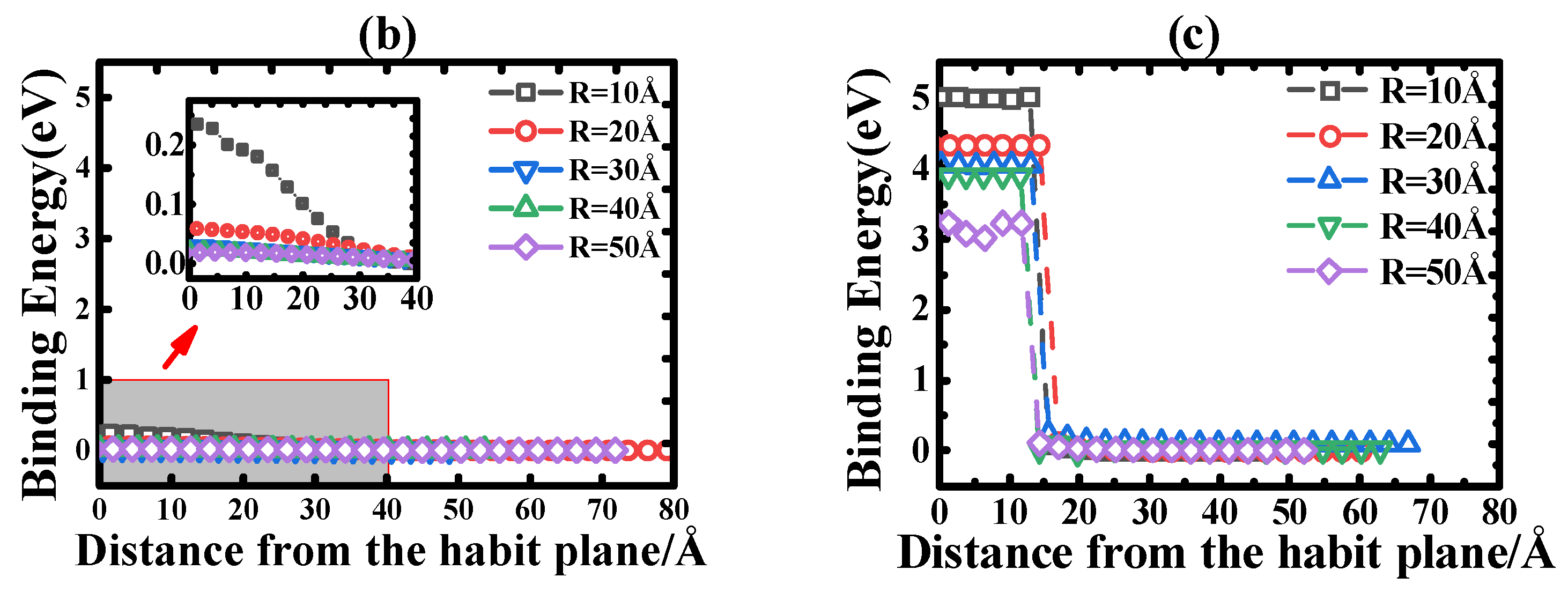
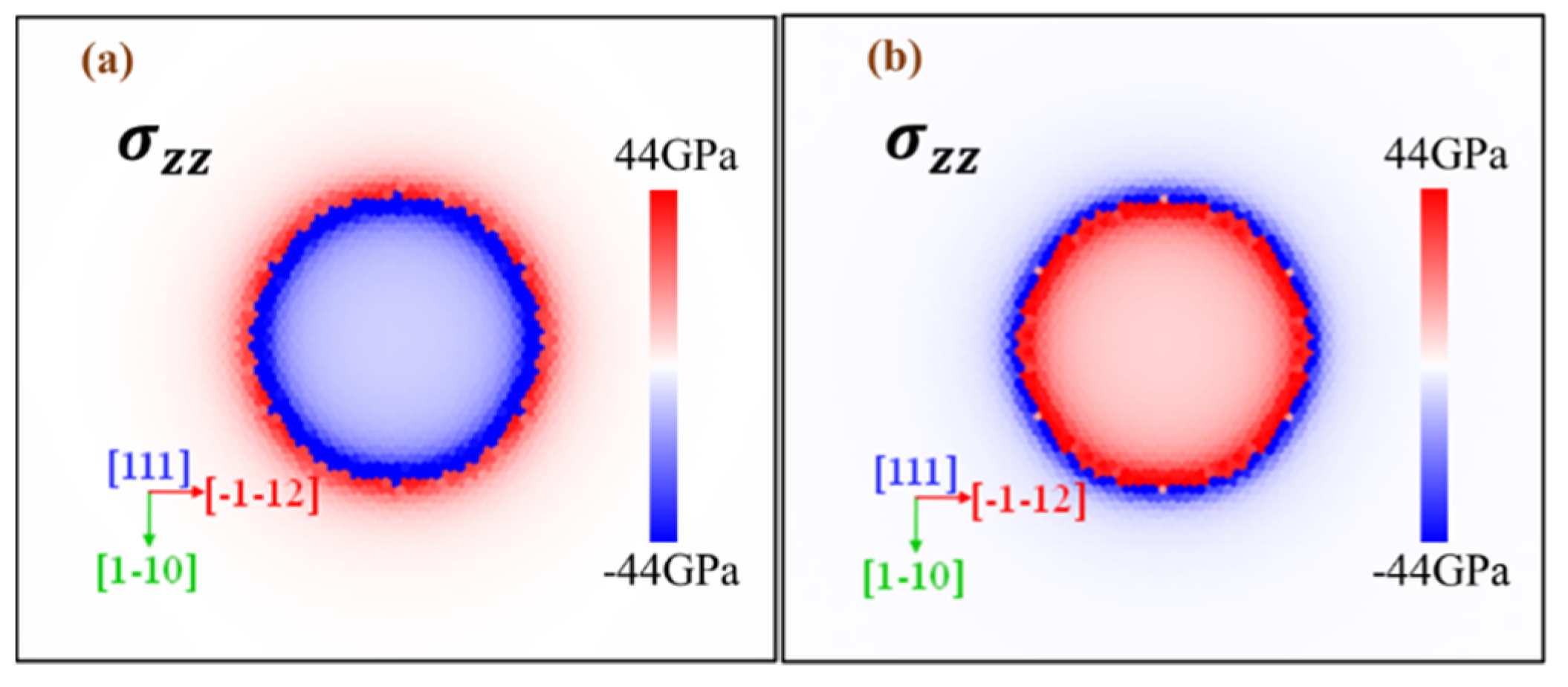
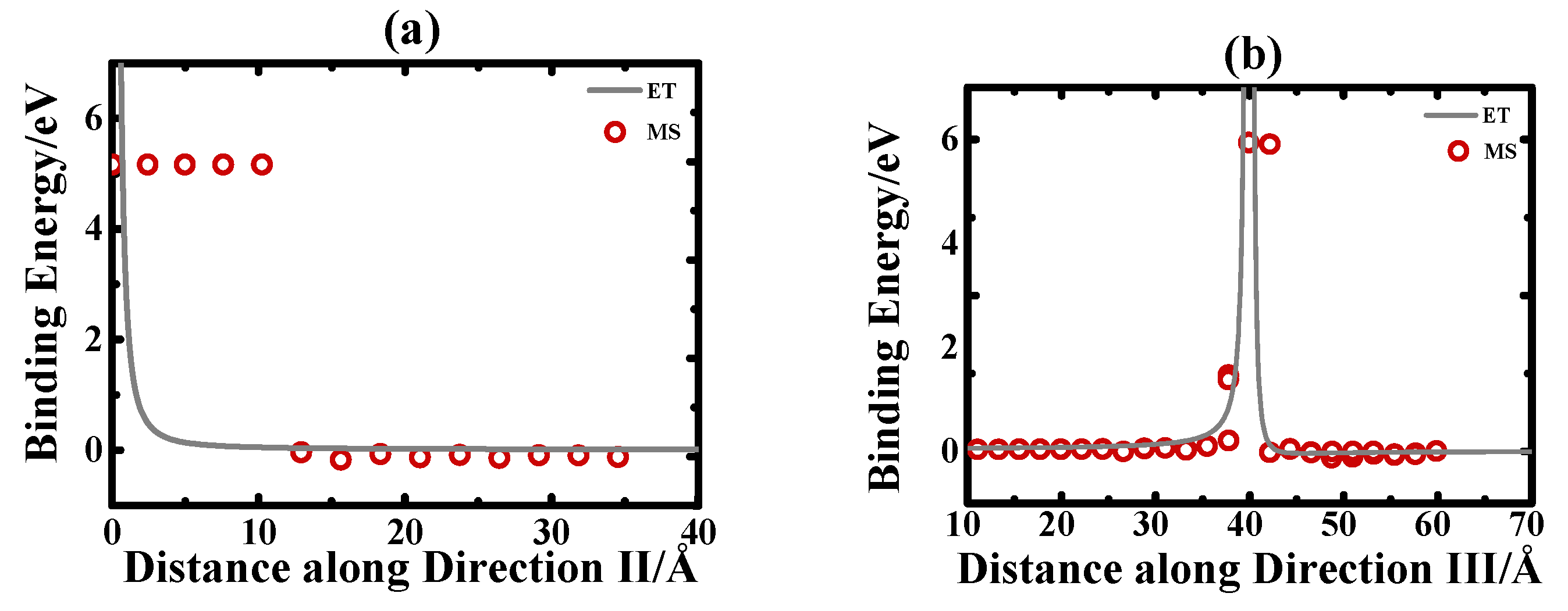
3.1. Interaction between an 1/2[111] IDL to a Vacancy
3.2. Comparison of the Binding Energies of IDL-Vacancy by Using ET and MS
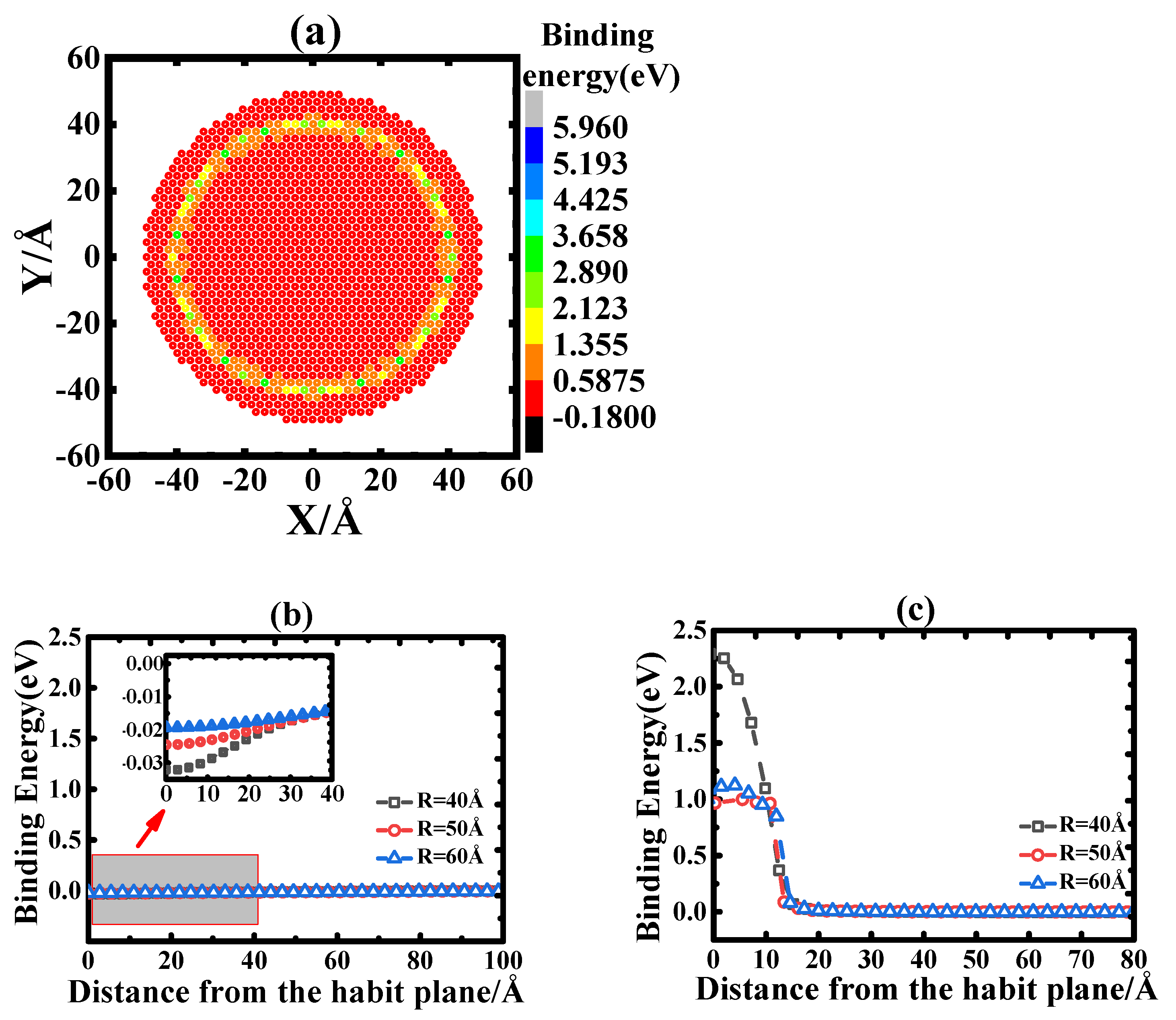
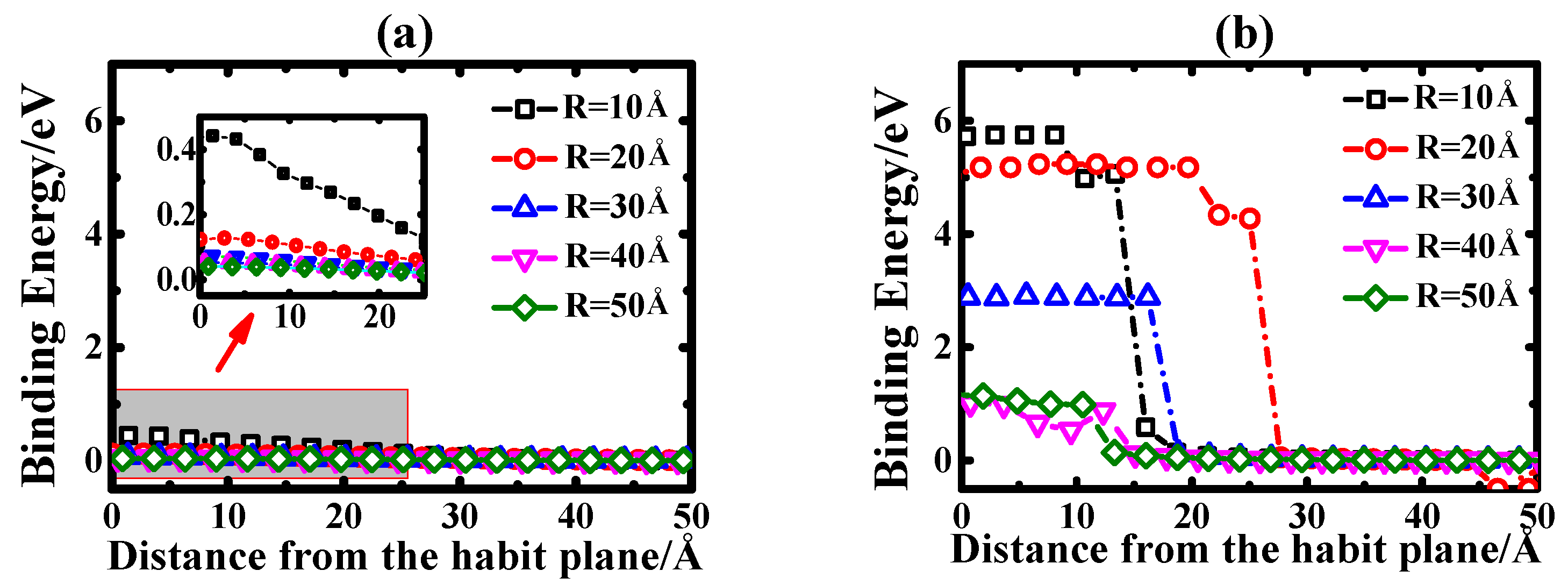
3.3. Static Interaction of an IDL to a Di-Vacancy and a Vacancy Cluster
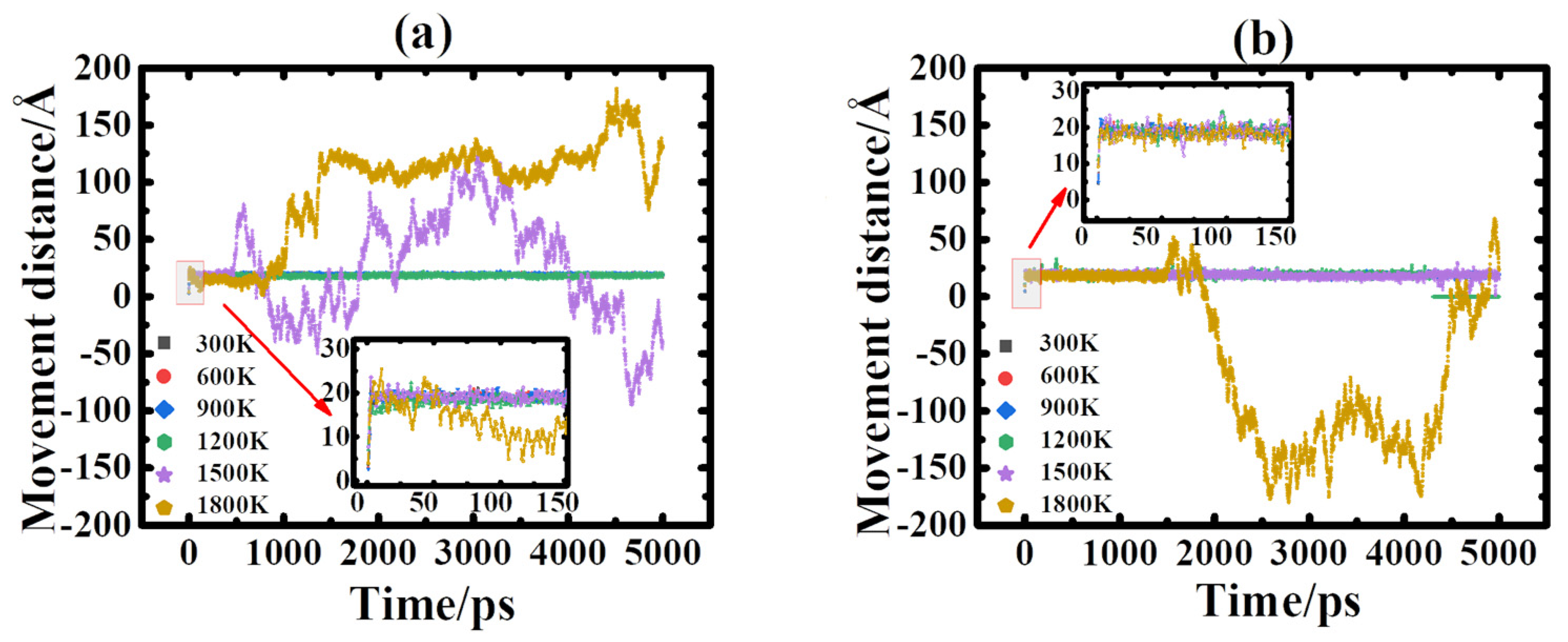
3.4. Dynamic Interaction between an IDL and a Vacancy Cluster
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bolt, H.; Brendel, A.; Levchuk, D.; Greuner, H. Materials for plasma facing components of fusion reactors. Energy Mater. 2006, 1, 121–126. [Google Scholar] [CrossRef] [Green Version]
- Federici, G.; Skinner, C.; Brooks, J.; Coad, J.; Grisolia, C.; Haasz, A.; Hassanein, A.; Philipps, V.; Pitcher, C.; Roth, J.; et al. Plasma-material interactions in current tokamaks and their implications for next step fusion reactors. Nucl. Fusion 2001, 41, 1967–2137. [Google Scholar] [CrossRef]
- Zinkle, S.; Was, G. Materials challenges in nuclear energy. Acta Mater. 2013, 61, 735–758. [Google Scholar] [CrossRef]
- Ackland, G. Controlling Radiation Damage. Science 2010, 327, 1587–1588. [Google Scholar] [CrossRef]
- Rubia, T.; Soneda, N.; Caturla, M.; Alonso, E. Defect production and annealing kinetics in elemental metals and semiconductors. J. Nucl. Mater. 1997, 251, 13–33. [Google Scholar] [CrossRef]
- Heinola, K.; Djurabekova, F.; Ahlgren, T. On the stability and mobility of di-vacancies in tungsten. Nucl. Fusion 2017, 58, 026004. [Google Scholar] [CrossRef]
- Osetsky, Y.; Bacon, D.; Serra, A.; Singh, B.; Golubov, S. Stability and mobility of defect clusters and dislocation loops in metals. J. Nucl. Mater. 1999, 276, 65–77. [Google Scholar] [CrossRef]
- Jan, F.; Robin, S.; Mason, D.; Nguyen-Manh, D. Nano-sized prismatic vacancy dislocation loops and vacancy clusters in tungsten. Nucl. Mater. Energy 2018, 16, 60–65. [Google Scholar]
- Fikar, J.; Schublin, R. Stability of small vacancy clusters in tungsten by molecular dynamics. Nucl. Instrum. Methods Phys. Res. B 2020, 464, 56–59. [Google Scholar] [CrossRef]
- Ma, P.; Mason, D.; Dudarev, S. Multiscale analysis of dislocation loops and voids in tungsten. Phys. Rev. Mater. 2020, 4, 103609. [Google Scholar] [CrossRef]
- Hasegawa, A.; Fukuda, M.; Nogami, S.; Yabuuchi, K. Neutron irradiation effects on tungsten materials. Fusion Eng. Des. 2014, 89, 1568–1572. [Google Scholar] [CrossRef]
- Yi, X.; Jenkins, M.; Hattar, K.; Edmonodson, P.; Roberts, S. Characterisation of radiation damage in W and W-based alloys from 2 MeV self-ion near-bulk implantations. Acta Mater. 2015, 92, 163–177. [Google Scholar] [CrossRef] [Green Version]
- Yi, X.; Jenkins, M.; Briceno, M.; Roberts, S.; Zhou, Z. In situ study of self-ion irradiation damage in W and W–5Re at 500 °C. Philos. Mag. 2013, 93, 1715–1738. [Google Scholar] [CrossRef]
- Dubinko, V.; Abyzov, A.; Turkin, A. Numerical evaluation of the dislocation loop bias. J. Nucl. Mater. 2005, 336, 11–21. [Google Scholar] [CrossRef]
- Wang, H.; Xu, K.; Wang, D.; Gao, N.; Li, Y.; Jin, S.; Shu, X.; Liang, L.; Lu, G. Anisotropic interaction between self-interstitial atoms and 1/2<111> pdislocation loops in tungsten. Sci. China Phys. 2021, 64, 257012. [Google Scholar] [CrossRef]
- Li, Y.; Boleininger, M.; Robertson, C.; Dupuy, L.; Dudarev, S. Diffusion and interaction of prismatic dislocation loops simulated by stochastic discrete dislocation dynamics. Phys. Rev. Mater. 2019, 3, 073805. [Google Scholar] [CrossRef]
- Shi, S.; Zhu, W.; Huang, H.; WOO, C. Interaction of Transonic Edge Dislocations with Self-interstitial Loop. Radiat. Effects Defects Solids 2010, 157, 201–208. [Google Scholar] [CrossRef]
- Singh, B.; Golubov, S.; Trinkaus, H.; Serra, A.; Osetsky, Y.; Barashev, A. Aspects of microstructure evolution under cascade damage conditions. J. Nucl. Mater. 1997, 251, 107–122. [Google Scholar] [CrossRef]
- Hull, D.; Bacon, D. Introduction to Dislocations, 5rd ed.; Elsevier Ltd.: Burlington, MA, USA, 2011; pp. 178–346. [Google Scholar]
- Bonny, G.; Terentyev, D.; Elena, J.; Zinovev, A.; Minov, B.; Zhurkin, E. Assessment of hardening due to dislocation loops in bcc iron: Overview and analysis of atomistic simulations for edge dislocations. J. Nucl. Mater. 2016, 473, 283–289. [Google Scholar] [CrossRef]
- Bacon, D.; Osetsky, Y. Dislocation-Obstacle Interactions at Atomic Level in Irradiated Metals. Math. Mech. Solids 2009, 14, 270–283. [Google Scholar] [CrossRef]
- Zhu, B.; Huang, M.; Li, Z. Atomic level simulations of interaction between edge dislocations and irradiation induced ellipsoidal voids in alpha-iron. Nucl. Instrum. Methods Phys. Res. B 2017, 397, 51–61. [Google Scholar] [CrossRef]
- Haghighat, S.; Fivel, C.; Fikar, J.; Schaeublin, R. Dislocation–void interaction in Fe: A comparison between molecular dynamics and dislocation dynamics. J. Nucl. Mater. 2009, 386, 102–105. [Google Scholar] [CrossRef]
- Pelfort, M.; Osetsky, Y.; Serra, A. Vacancy interaction with glissile interstitial clusters in bcc metals. Philos. Mag. Lett. 2001, 81, 803–811. [Google Scholar] [CrossRef]
- Puigvi, M.; Osetsky, Y.; Serra, A. Interactions between vacancy and glissile interstitial clusters in iron and copper. Mater. Sci. Eng. A 2004, 365, 101–106. [Google Scholar] [CrossRef]
- Puigvi, M.; Serra, A.; Diego, N.; Osetsky, Y.; Bacon, D. Features of the interactions between a vacancy and interstitial loops in metals. Philos. Mag. Lett. 2004, 84, 257–266. [Google Scholar] [CrossRef]
- Wang, S.; Guo, W.; Yuan, Y.; Zhu, X.; Cheng, L.; Cao, X.; Fu, E.; Shi, L.; Gao, F.; Lu, G. Evolution of vacancy defects in heavy ion irradiated tungsten exposed to helium plasma. J. Nucl. Mater. 2020, 532, 152051. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Yong, G.; Zeng, Z. Creeping Motion of Self Interstitial Atom Clusters in Tungsten. Sci. Rep. 2014, 4, 5096. [Google Scholar]
- Zhou, W.; Li, Y.; Huang, L.; Zeng, Z.; Ju, X. Dynamical behaviors of self-interstitial atoms in tungsten. J. Nucl. Mater. 2013, 437, 438–444. [Google Scholar] [CrossRef]
- Marinica, M.-C.; Ventelon, L.; Gilbert, M.; Proville, L.; Dudarev, S.; Marian, J.; Bencteux, G.; Willaime, F. Interatomic potentials for modelling radiation defects and dislocations in tungsten. J. Phys. Condens. Matter 2013, 25, 395502. [Google Scholar] [CrossRef]
- Tomas, D.; Kazuto, A.; Hirotaro, M.; Hidehiro, Y.; Minoru, I.; Kouji, M.; Masahito, U.; Sergei, D. Fast, vacancy-free climb of prismatic dislocation loops in bcc metals. Sci. Rep. 2016, 6, 30596. [Google Scholar]
- Yang, S. On The Elastic Interaction Between Dislocation Loop And Lattice Vacancy. Acta Phys. Sin. 1964, 20, 720–727. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Wang, H.; Xu, K.; Li, B.; Jin, S.; Li, X.-C.; Shu, X.; Liang, L.; Lu, G.-H. Atomic Simulations of the Interaction between a Dislocation Loop and Vacancy-Type Defects in Tungsten. Metals 2022, 12, 368. https://doi.org/10.3390/met12030368
Li L, Wang H, Xu K, Li B, Jin S, Li X-C, Shu X, Liang L, Lu G-H. Atomic Simulations of the Interaction between a Dislocation Loop and Vacancy-Type Defects in Tungsten. Metals. 2022; 12(3):368. https://doi.org/10.3390/met12030368
Chicago/Turabian StyleLi, Linyu, Hao Wang, Ke Xu, Bingchen Li, Shuo Jin, Xiao-Chun Li, Xiaolin Shu, Linyun Liang, and Guang-Hong Lu. 2022. "Atomic Simulations of the Interaction between a Dislocation Loop and Vacancy-Type Defects in Tungsten" Metals 12, no. 3: 368. https://doi.org/10.3390/met12030368
APA StyleLi, L., Wang, H., Xu, K., Li, B., Jin, S., Li, X. -C., Shu, X., Liang, L., & Lu, G. -H. (2022). Atomic Simulations of the Interaction between a Dislocation Loop and Vacancy-Type Defects in Tungsten. Metals, 12(3), 368. https://doi.org/10.3390/met12030368






