Effect of Neutron Flux on an Irradiation-Induced Microstructure and Hardening of Reactor Pressure Vessel Steels
Abstract
:1. Introduction
2. Materials and Methods
3. Results
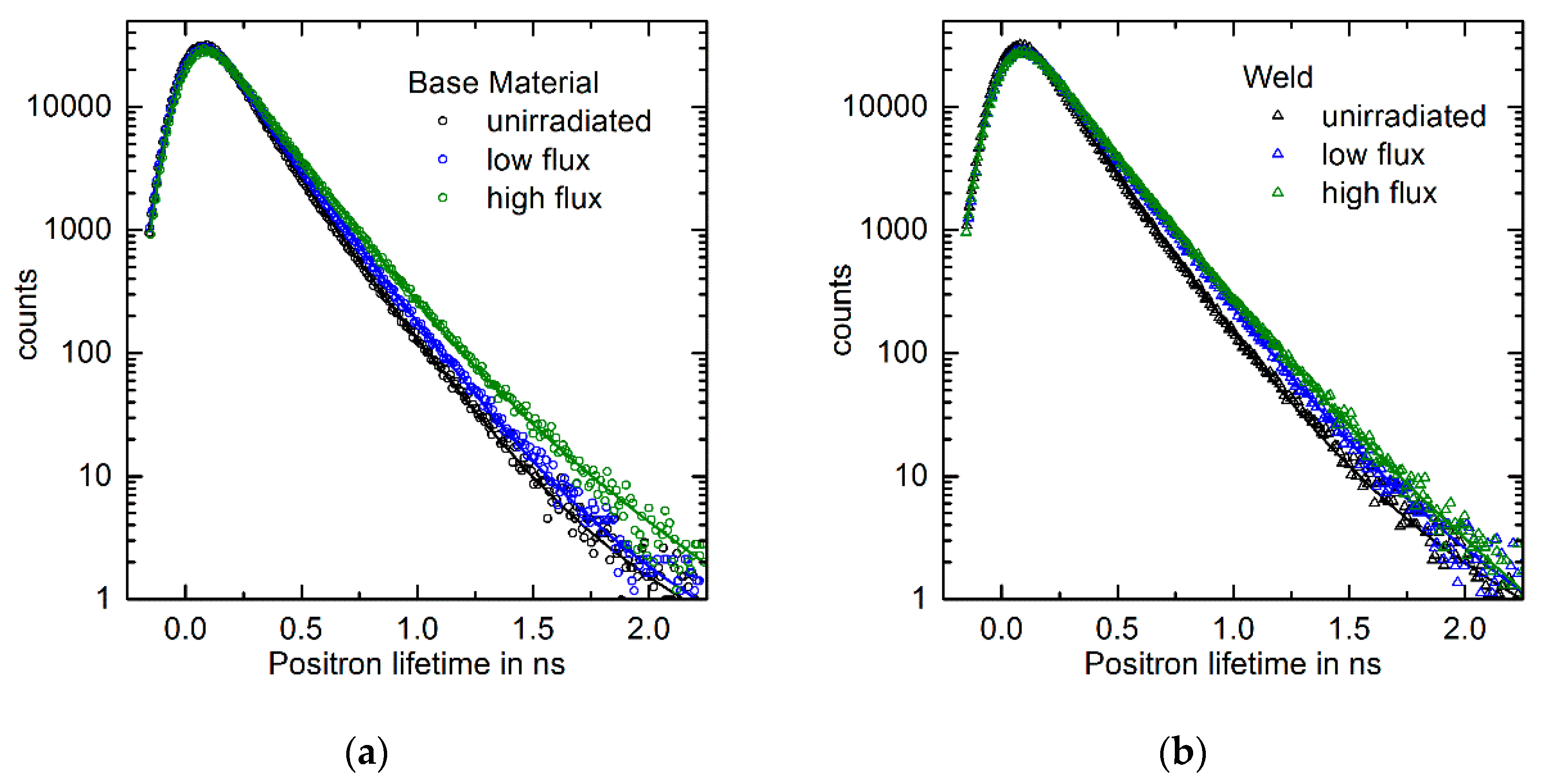
3.1. Positron Lifetime
3.2. TEM
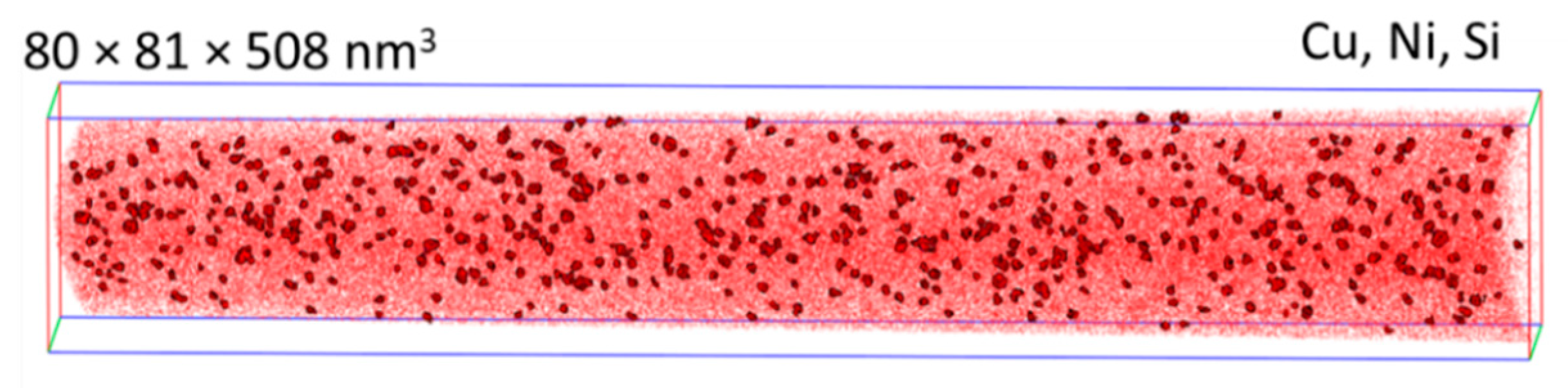
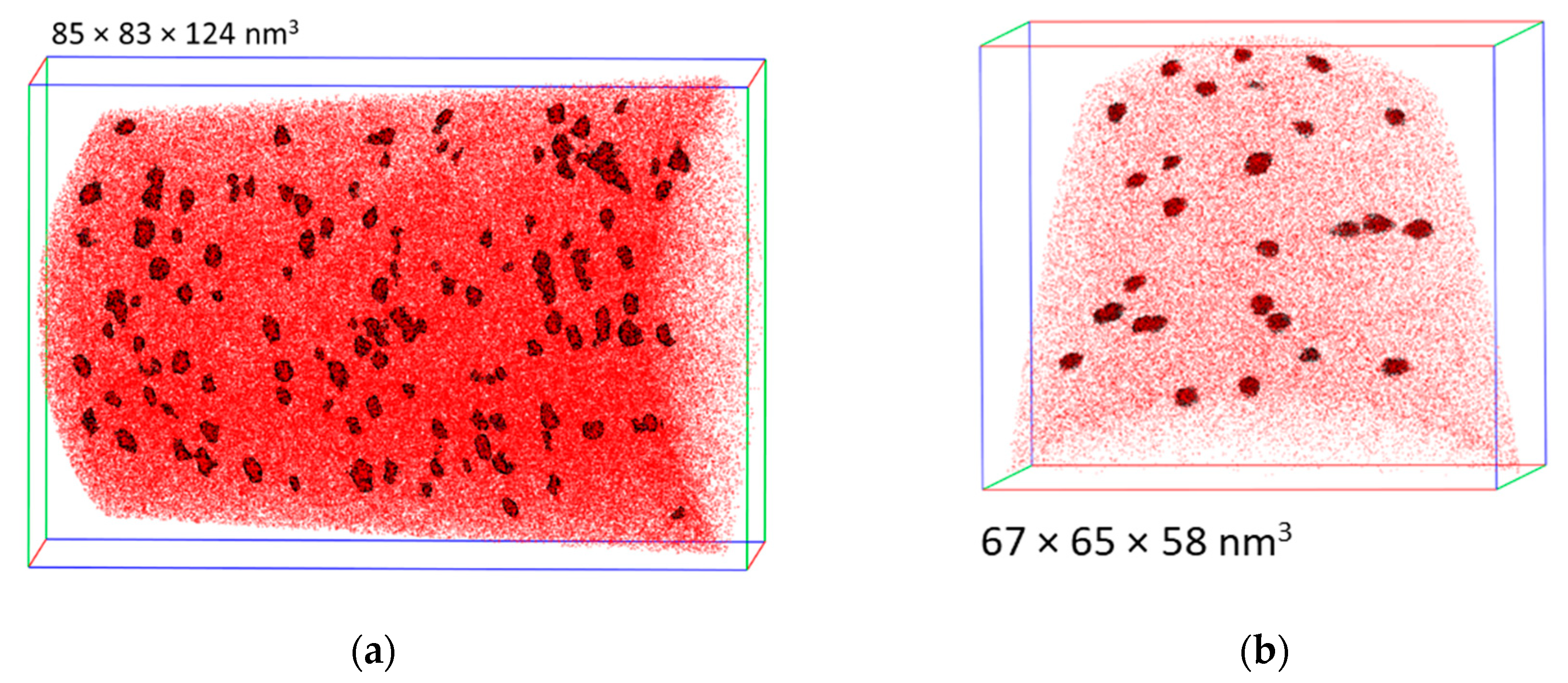
3.3. APT
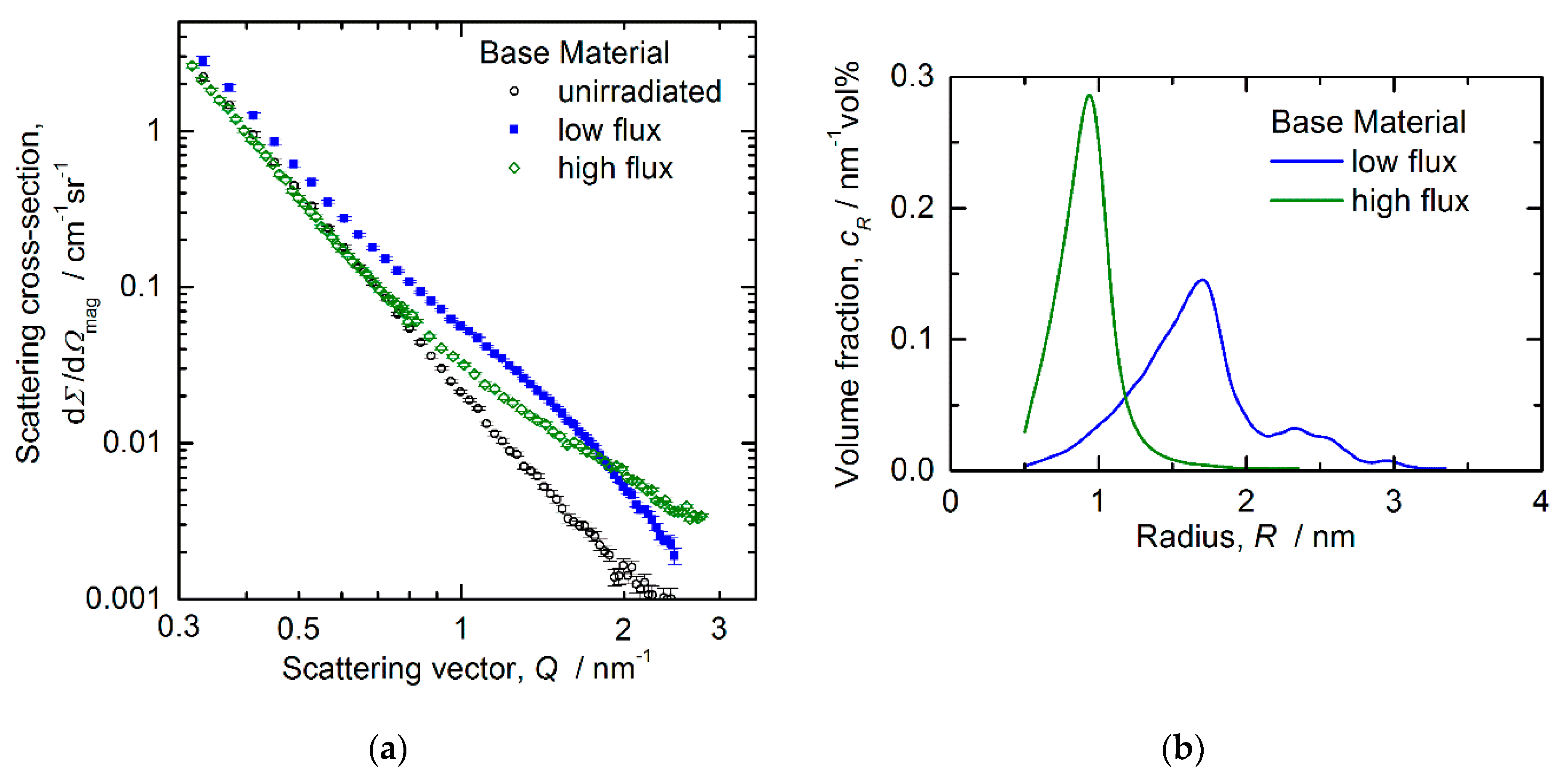
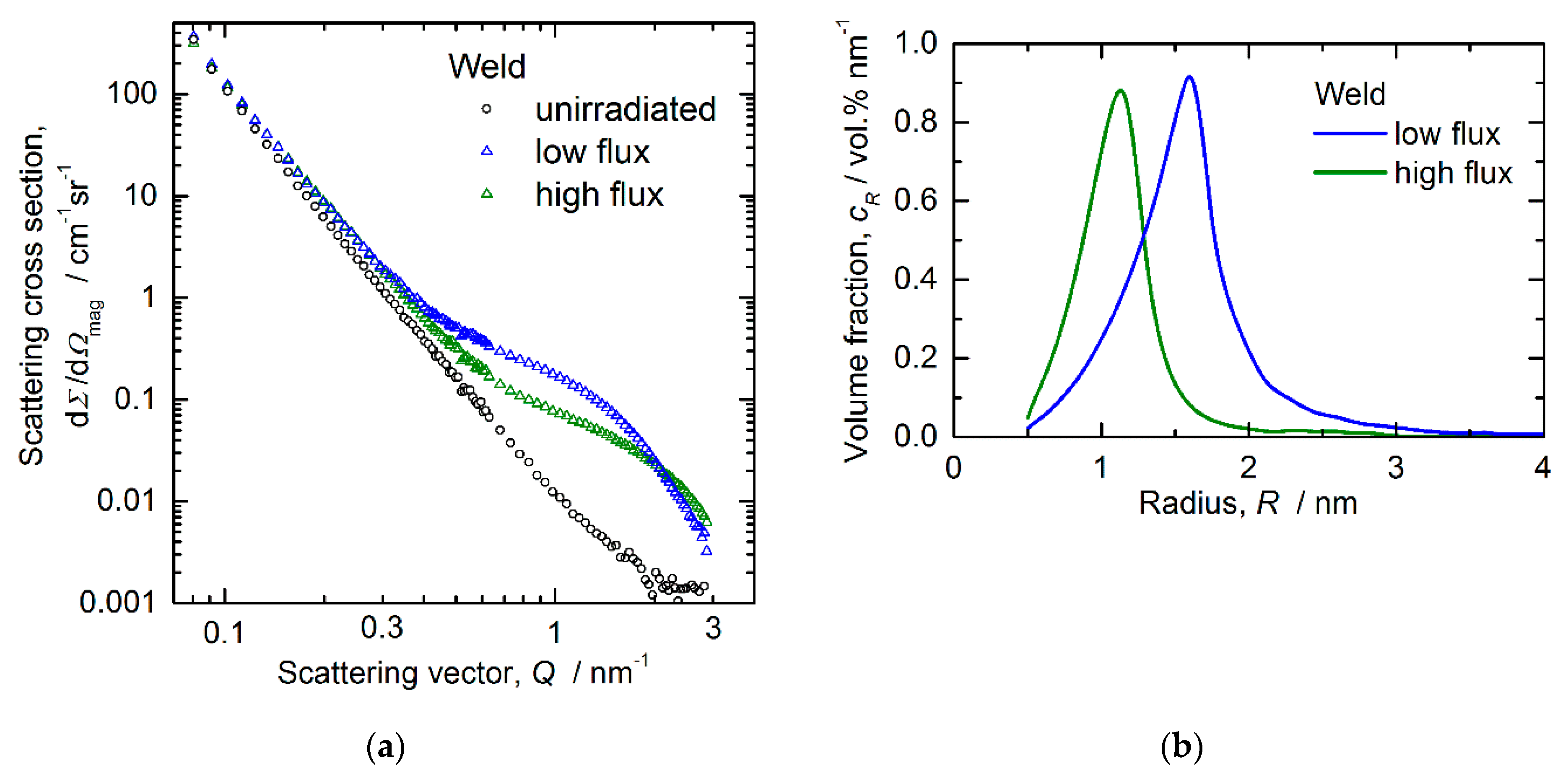
3.4. Magnetic SANS
3.5. Mechanical Properties
4. Discussion
4.1. Complementarity of Methods and Overlap of Information
- PAS is preferable to gain information about vacancy-type defects. We have found that neutron irradiation gives rise to increased concentrations of single vacancies and sub-nm vacancy clusters and that the higher flux results in higher intensities of the vacancy-cluster component.
- TEM is unique in providing insight on the formation of dislocation loops and their spatial correlations with pre-existing line dislocations. For the RPV base material (but not for the weld), the higher flux results in a lower number density of loops.
- APT resolves the composition of irradiation-induced solute atom clusters and segregations. Moreover, spatial correlations of clusters/segregations with pre-existing dislocations and grain boundaries are accessible. In short, the irradiation-induced solute atom clusters are more diluted for the high-flux condition.
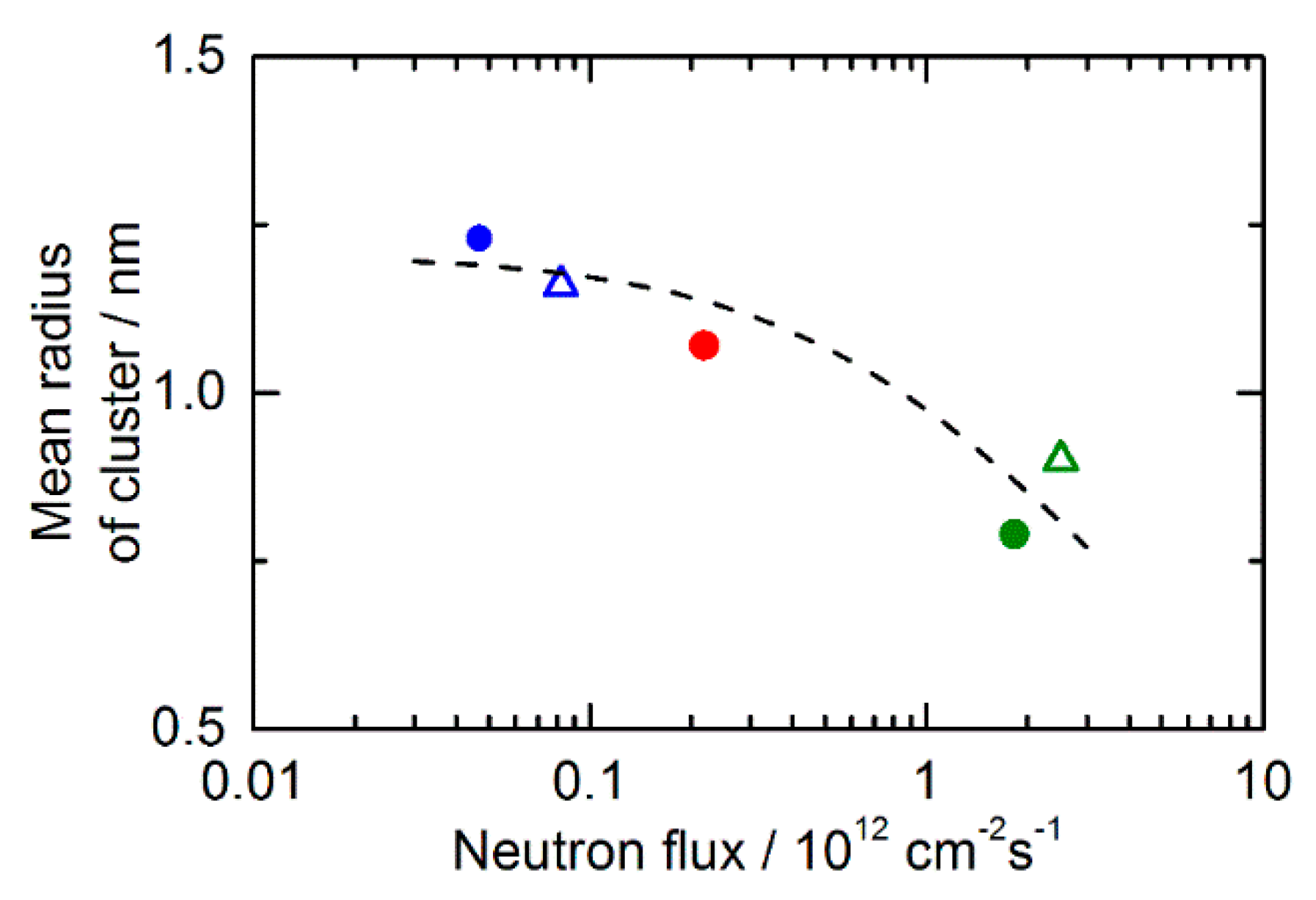
- Magnetic SANS is capable of providing macroscopically representative and statistically reliable estimates of cluster size and volume fraction. The most prominent finding is the detection of significantly smaller cluster sizes for the high-flux irradiations.
- Vacancy clusters may be associated to solute atom clusters [36]. Therefore, it is possible that the sub-nm vacancy clusters detected by PAS, although in themselves smaller than the lower detection limit of SANS, also contribute to the cluster characteristics as extracted from SANS. That means that those vacancy clusters might have slightly raised the volume fraction and reduced the A-ratio.
- Initially mobile dislocation loops may encounter solute atoms, get immobilized and turn, via solute segregation, into solute atom clusters. Indeed, this process was identified as the dominant formation mechanism of irradiation-induced solute atom clusters [5]. This means that part of the loops identified by TEM might also contribute to the estimates derived by APT or SANS for solute atom clusters.
- APT and SANS exhibit overlapping information with respect to the size and number density of solute atom clusters [11]. Moreover, the cluster composition derived from APT can be used to estimate the expected theoretical A-ratio of SANS. The latter option is not used here for the sake of conciseness.
4.2. Flux effect on Microstructure
- a higher number density of sub-nm vacancy clusters,
- a lower number density of nm-sized loops, and
- a higher number density of smaller and more diluted solute atom clusters.
- a higher number density of sub-nm vacancy clusters,
- a comparable size and number density of nm-sized loops, and
- a higher number density of smaller and more diluted solute atom clusters.
- Measurements of the concentration of single self-interstitial atoms are not available.
- Loops of diameter smaller than approximately 1.5 nm are TEM-invisible.
- Loops may transform into 3D solute atom clusters [5] (see above) and lose the loop-typical diffraction contrast.
4.3. Flux Effect on Hardening
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Odette, G.R. On the Dominant Mechanism of Irradiation Embrittlement of Reactor Pressure Vessel Steels. Scr. Metall. 1983, 17, 1183–1188. [Google Scholar] [CrossRef]
- Auger, P.; Pareige, P.; Akamatsu, M.; Blavette, D. APFIM Investigation of Clustering in Neutron-Irradiated FeCu Alloys and Pressure Vessel Steels. J. Nucl. Mater. 1995, 225, 225–230. [Google Scholar] [CrossRef]
- Odette, G.R.; Lucas, G.E. Recent Progress in Understanding Reactor Pressure Vessel Steel Embrittlement. Radiat. Eff. Defects Solids 1998, 144, 189–231. [Google Scholar] [CrossRef]
- Meslin, E.; Lambrecht, M.; Hernandez-Mayoral, M.; Bergner, F.; Malerba, L.; Pareige, P.; Radiguet, B.; Barbu, A.; Gomez-Briceno, D.; Ulbricht, A.; et al. Characterization of Neutron-Irradiated Ferritic Model Alloys and a RPV Steel from Combined APT, SANS, TEM and PAS Analyses. J. Nucl. Mater. 2010, 406, 73–83. [Google Scholar] [CrossRef]
- Castin, N.; Bonny, G.; Bakaev, A.; Bergner, F.; Domain, C.; Hyde, J.M.; Messina, L.; Radiguet, B.; Malerba, L. The Dominant Mechanisms for the Formation of Solute-Rich Clusters in Low-Cu Steels under Irradiation. Mater. Today Energy 2020, 17, 100472. [Google Scholar] [CrossRef]
- Gurovich, B.; Kuleshova, E.; Shtrombakh, Y.; Fedotova, S.; Maltsev, D.; Frolov, A.; Zabusov, O.; Erak, D.; Zhurko, D. Evolution of Structure and Properties of VVER-1000 RPV Steels under Accelerated Irradiation up to beyond Design Fluences. J. Nucl. Mater. 2015, 456, 23–32. [Google Scholar] [CrossRef]
- Boåsen, M.; Efsing, P.; Ehrnstén, U. On Flux Effects in a Low Alloy Steel from a Swedish Reactor Pressure Vessel. J. Nucl. Mater. 2017, 484, 110–119. [Google Scholar] [CrossRef]
- Kuleshova, E.A.; Gurovich, B.A.; Lavrukhina, Z.V.; Maltsev, D.A.; Fedotova, S.V.; Frolov, A.S.; Zhuchkov, G.M. Study of the Flux Effect Nature for VVER-1000 RPV Welds with High Nickel Content. J. Nucl. Mater. 2017, 483, 1–12. [Google Scholar] [CrossRef]
- Wang, K.; Guo, Y.; Song, S. Quantitative Dependence of Ductile-to-Brittle Transition on Phosphorus Grain Boundary Segregation for a Novel Ni–Cr–Mo RPV Steel. J. Mater. Res. Technol. 2021, 15, 6404–6414. [Google Scholar] [CrossRef]
- Soneda, N.; Dohi, K.; Nishida, K.; Nomoto, A.; Tomimatsu, M.; Matsuzawa, H.; Busby, J.T.; Hanson, B.; Dean, S.W. Microstructural Characterization of RPV Materials Irradiated to High Fluences at High Flux. J. ASTM Int. 2009, 6, 102128. [Google Scholar] [CrossRef]
- Meslin, E.; Radiguet, B.; Pareige, P.; Barbu, A. Kinetic of Solute Clustering in Neutron Irradiated Ferritic Model Alloys and a French Pressure Vessel Steel Investigated by Atom Probe Tomography. J. Nucl. Mater. 2010, 399, 137–145. [Google Scholar] [CrossRef]
- Lambrecht, M.; Almazouzi, A. Positron Annihilation Study of Neutron Irradiated Model Alloys and of a Reactor Pressure Vessel Steel. J. Nucl. Mater. 2009, 385, 334–338. [Google Scholar] [CrossRef]
- Cizek, J.; Procházka, I.; Kocík, J.; Keilová, E. Positron Lifetime Study of Reactor Pressure Vessel Steels. Phys. Status Solidi A 2000, 178, 651–662. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Honecker, D.; Périgo, É.A.; Bergner, F.; Disch, S.; Heinemann, A.; Erokhin, S.; Berkov, D.; Leighton, C.; Eskildsen, M.R.; et al. Magnetic Small-Angle Neutron Scattering. Rev. Mod. Phys. 2019, 91, 015004. [Google Scholar] [CrossRef] [Green Version]
- Beaven, P.A.; Frisius, F.; Kampmann, R.; Wagner, R. Analysis of Defect Microstructures in Irradiated Ferritic Alloys. In Atomic Transport and Defects in Metals by Neutron Scattering; Janot, C., Petry, W., Richter, D., Springer, T., Eds.; Springer: Berlin/Heidelberg, Germany, 1986; Volume 10, pp. 228–233. ISBN 978-3-642-71009-4. [Google Scholar]
- Hernández-Mayoral, M.; Gómez-Briceño, D. Transmission Electron Microscopy Study on Neutron Irradiated Pure Iron and RPV Model Alloys. J. Nucl. Mater. 2010, 399, 146–153. [Google Scholar] [CrossRef]
- Kirk, M.; Yi, X.; Jenkins, M. Characterization of Irradiation Defect Structures and Densities by Transmission Electron Microscopy. J. Mater. Res. 2015, 30, 1195–1201. [Google Scholar] [CrossRef]
- Odette, G.R.; Yamamoto, T.; Klingensmith, D. On the Effect of Dose Rate on Irradiation Hardening of RPV Steels. Philos. Mag. 2005, 85, 779–797. [Google Scholar] [CrossRef]
- Bergner, F.; Ulbricht, A.; Hein, H.; Kammel, M. Flux Dependence of Cluster Formation in Neutron-Irradiated Weld Material. J. Phys.-Condens. MATTER 2008, 20, 104262. [Google Scholar] [CrossRef]
- Dohi, K.; Nishida, K.; Nomoto, A.; Soneda, N.; Matsuzawa, H.; Tomimatsu, M. Effect of Neutron Flux at High Fluence on Microstructural and Hardness Changes of RPV Steels. In Proceedings of the ASME 2010 Pressure Vessels and Piping Conference, ASMEDC, Bellevue, WA, USA, 18–22 January 2010; Volume 9, pp. 95–102. [Google Scholar]
- Chaouadi, R.; Gérard, R. Confirmatory Investigations on the Flux Effect and Associated Unstable Matrix Damage in RPV Materials Exposed to High Neutron Fluence. J. Nucl. Mater. 2013, 437, 267–274. [Google Scholar] [CrossRef]
- Kryukov, A.; Blagoeva, D.; Debarberis, L. Flux Effect Analysis in WWER-440 Reactor Pressure Vessel Steels. J. Nucl. Mater. 2013, 443, 171–175. [Google Scholar] [CrossRef]
- Wagner, A.; Bergner, F.; Chaouadi, R.; Hein, H.; Hernández-Mayoral, M.; Serrano, M.; Ulbricht, A.; Altstadt, E. Effect of Neutron Flux on the Characteristics of Irradiation-Induced Nanofeatures and Hardening in Pressure Vessel Steels. Acta Mater. 2016, 104, 131–142. [Google Scholar] [CrossRef]
- Toyama, T.; Yamamoto, T.; Ebisawa, N.; Inoue, K.; Nagai, Y.; Odette, G.R. Effects of Neutron Flux on Irradiation-Induced Hardening and Defects in RPV Steels Studied by Positron Annihilation Spectroscopy. J. Nucl. Mater. 2020, 532, 152041. [Google Scholar] [CrossRef]
- Kuleshova, E.A.; Zhuchkov, G.M.; Fedotova, S.V.; Maltsev, D.A.; Frolov, A.S.; Fedotov, I.V. Precipitation Kinetics of Radiation-Induced Ni-Mn-Si Phases in VVER-1000 Reactor Pressure Vessel Steels under Low and High Flux Irradiation. J. Nucl. Mater. 2021, 553, 153091. [Google Scholar] [CrossRef]
- Altstadt, E.; Keim, E.; Hein, H.; Serrano, M.; Bergner, F.; Viehrig, H.-W.; Ballesteros, A.; Chaouadi, R.; Wilford, K. FP7 Project LONGLIFE: Overview of Results and Implications. Nucl. Eng. Des. 2014, 278, 753–757. [Google Scholar] [CrossRef]
- Hyde, J.M.; DaCosta, G.; Hatzoglou, C.; Weekes, H.; Radiguet, B.; Styman, P.D.; Vurpillot, F.; Pareige, C.; Etienne, A.; Bonny, G.; et al. Analysis of Radiation Damage in Light Water Reactors: Comparison of Cluster Analysis Methods for the Analysis of Atom Probe Data. Microsc. Microanal. 2017, 23, 366–375. [Google Scholar] [CrossRef] [Green Version]
- Selim, F.A.; Wells, D.P.; Harmon, J.F.; Kwofie, J.; Spaulding, R.; Erickson, G.; Roney, T. Bremsstrahlung-Induced Highly Penetrating Probes for Nondestructive Assay and Defect Analysis. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2002, 495, 154–160. [Google Scholar] [CrossRef]
- Butterling, M.; Anwand, W.; Cowan, T.E.; Hartmann, A.; Jungmann, M.; Krause-Rehberg, R.; Krille, A.; Wagner, A. Gamma-Induced Positron Spectroscopy (GiPS) at a Superconducting Electron Linear Accelerator. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2011, 269, 2623–2629. [Google Scholar] [CrossRef]
- Wagner, A.; Butterling, M.; Liedke, M.O.; Potzger, K.; Krause-Rehberg, R. Positron Annihilation Lifetime and Doppler Broadening Spectroscopy at the ELBE Facility; AIP Conference Proceedings 1970: Newport News, VA, USA, 2018; p. 040003. [CrossRef] [Green Version]
- Kirkegaard, P. PALSfit: A Computer Program for Analysing Positron Lifetime Spectra; Risø National Laboratory for Sustainable Energy: Roskilde, Denmark, 2009; ISBN 978-87-550-3691-8.
- Keiderling, U. The New “BerSANS-PC” Software for Reduction and Treatment of Small Angle Neutron Scattering Data. Appl. Phys. Mater. Sci. Process. 2002, 74, s1455–s1457. [Google Scholar] [CrossRef]
- Martelli, S.; Di Nunzio, P.E. Particle Size Distribution of Nanospheres by Monte Carlo Fitting of Small Angle X-Ray Scattering Curves. Part. Part. Syst. Charact. 2002, 19, 247–255. [Google Scholar] [CrossRef]
- Hernández-Mayoral, M.; Heintze, C.; Oñorbe, E. Transmission Electron Microscopy Investigation of the Microstructure of Fe–Cr Alloys Induced by Neutron and Ion Irradiation at 300 °C. J. Nucl. Mater. 2016, 474, 88–98. [Google Scholar] [CrossRef]
- Kuriplach, J.; Melikhova, O.; Domain, C.; Becquart, C.S.; Kulikov, D.; Malerba, L.; Hou, M.; Almazouzi, A.; Duque, C.A.; Morales, A.L. Vacancy-Solute Complexes and Their Clusters in Iron. Appl. Surf. Sci. 2006, 252, 3303–3308. [Google Scholar] [CrossRef] [Green Version]
- Nagai, Y.; Tang, Z.; Hassegawa, M.; Kanai, T.; Saneyasu, M. Irradiation-Induced Cu Aggregations in Fe: An Origin of Embrittlement of Reactor Pressure Vessel Steels. Phys. Rev. B 2001, 63, 134110. [Google Scholar] [CrossRef]
- Wagner, A.; Anwand, W.; Butterling, M.; Cowan, T.E.; Fiedler, F.; Fritz, F.; Kempe, M.; Krause-Rehberg, R. Positron-Annihilation Lifetime Spectroscopy Using Electron Bremsstrahlung. J. Phys. Conf. Ser. 2015, 618, 012042. [Google Scholar] [CrossRef] [Green Version]
- Soisson, F.; Barbu, A.; Martin, G. Monte Carlo Simulations of Copper Precipitation in Dilute Iron-Copper Alloys during Thermal Ageing and under Electron Irradiation. Acta Mater. 1996, 44, 3789–3800. [Google Scholar] [CrossRef]
- Odette, G.R.; Yamamoto, T.; Williams, T.J.; Nanstad, R.K.; English, C.A. On the History and Status of Reactor Pressure Vessel Steel Ductile to Brittle Transition Temperature Shift Prediction Models. J. Nucl. Mater. 2019, 526, 151863. [Google Scholar] [CrossRef]
- Bergner, F.; Ulbricht, A.; Wagner, A. Long-Term Aging Effects in RPV Steel, Scientific Report HZDR-056. 2014. Available online: https://Www.Hzdr.de/Publications/Publ-21162 (accessed on 19 January 2022).
- Christien, F.; Barbu, A. Modelling of Copper Precipitation in Iron during Thermal Aging and Irradiation. J. Nucl. Mater. 2004, 324, 90–96. [Google Scholar] [CrossRef]
- Mansur, L.K. Void Swelling in Metals and Alloys Under Irradiation: An Assessment of the Theory. Nucl. Technol. 1978, 40, 5–34. [Google Scholar] [CrossRef]
- Seeger, A.K. On the Theory of Radiation Damage and Radiation Hardening. In Proceedings of the Second United Nations International Conference on The Peaceful Uses of Atomic Energy, Geneva, Switzerland, 1–13 September 1958; 1958; Volume 6, pp. 250–273. [Google Scholar]
- Wagner, A.; Ulbricht, A.; Bergner, F.; Altstadt, E. Influence of the Copper Impurity Level on the Irradiation Response of Reactor Pressure Vessel Steels Investigated by SANS. Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. At. 2012, 280, 98–102. [Google Scholar] [CrossRef]
- Tabor, T. The Hardness of Metals; Clarendon Press: Oxford, UK, 1948. [Google Scholar]




| Material | C | Mn | Si | Cr | Ni | Mo | P | Cu |
|---|---|---|---|---|---|---|---|---|
| BH | 0.23 | 0.70 | 0.20 | 0.44 | 0.98 | 0.79 | 0.015 | 0.12 |
| BL | 0.18 | 0.81 | 0.15 | 0.40 | 0.96 | 0.53 | 0.006 | 0.09 |
| WH | 0.05 | 1.41 | 0.15 | 0.07 | 1.69 | 0.46 | 0.012 | 0.08 |
| WL | 0.06 | 1.66 | 0.21 | 0.14 | 1.2 | 0.80 | 0.016 | 0.06 |
| Material | Fluence (1019 cm−2) | Flux (1012 cm−2 s−1) | Temperature (°C) | Irradiation Facility * |
|---|---|---|---|---|
| BH | 3.9 | 1.8 | 285 | VAK |
| BL | 3.4 | 0.047 | 300 | PWR |
| WH | 5.3 | 2.3 | 285 | VAK |
| WL | 5.9 | 0.082 | 270 | BWR |
| Material/ Condition | Component 1 (108 ps, Fixed) Intensity (%) | Component 2 (175 ps, Fixed) Intensity (%) | Component 3 (Fitted) Lifetime (ps) | Component 3 Intensity (%) | Mean Lifetime (ps) |
|---|---|---|---|---|---|
| BU | 45.02 | 54.66 | 492 | 0.32 | 146 |
| BL | 22.49 | 77.07 | 462 | 0.44 | 161 |
| BH | 3.82 | 92.35 | 347 | 3.83 | 179 |
| WU | 38.76 | 60.64 | 445 | 0.60 | 151 |
| WL | 0 | 98.56 | 374 | 1.44 | 178 |
| WH | 0 | 92.08 | 282 | 7.92 | 183 |
| Material | Number of Sized Loops | Mean Diameter (nm) | Loop Density (1020 m−3) |
|---|---|---|---|
| BH | 3 | 3.8 ± 0.3 | 0.08 ± 0.04 |
| BL | 34 | 4.0 ± 0.2 | 2.0 ± 0.3 |
| WH | 33 | 3.8 ± 0.1 | 1.7 ± 0.5 |
| WL | 15 | 3.4 ± 0.9 | 1.2 ± 0.5 |
| Material | Mn | Si | Ni | P | Cu |
|---|---|---|---|---|---|
| BH | 2.6 (6.2) | 3.5 (8.7) | 6.3 (8.0) | 0.18 (32) | 5.3 (118) |
| BL | 10.8 (15) | 9.0 (36) | 21 (23) | 0.10 (100) | 6 (133) |
| WH | 3.0 (4.7) | 5.4 (10) | 7.2 (9.1) | 0.14 (77) | 1.6 (35) |
| WL | 9.1 (9.8) | 5.8 (12) | 11.5 (23) | 0.24 (40) | 8.8 (243) |
| Material | Mean Diameter (nm) | Number Density (1023 m−3) |
|---|---|---|
| BH | 2.7 | 3.7 ± 0.5 |
| BL | 3.2 | 1.1 ± 0.3 |
| WH | 2.6 | 3.1 ± 0.4 |
| WL | 2.8 | 3.0 ± 1.4 |
| Material | Mean Diameter (nm) | Volume Fraction (%) | Number Density (1023 m−3) | A-Ratio (-) |
|---|---|---|---|---|
| BH | 1.58 ± 0.04 | 0.124 ± 0.005 | 5.0 ± 0.4 | 2.6 ± 0.1 |
| BL | 2.46 ± 0.06 | 0.120 ± 0.014 | 1.1 ± 0.1 | 2.5 ± 0.1 |
| WH | 1.80 ± 0.06 | 0.534 ± 0.016 | 13.0 ± 1.5 | 2.2 ± 0.1 |
| WL | 2.32 ± 0.04 | 0.710 ± 0.002 | 7.5 ± 0.3 | 2.2 ± 0.1 |
| Material | HV10 | ΔHV10 |
|---|---|---|
| BU | 184 ± 3/196 ± 4 * | - |
| BH | 238 ± 5 | 54 ± 6 |
| BL | 220 ± 5 | 24 ± 7 |
| WU | 209 ± 3/213 ± 4 * | - |
| WH | 307 ± 8 | 98 ± 9 |
| WL | 302 ± 6 | 89 ± 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ulbricht, A.; Hernández-Mayoral, M.; Oñorbe, E.; Etienne, A.; Radiguet, B.; Hirschmann, E.; Wagner, A.; Hein, H.; Bergner, F. Effect of Neutron Flux on an Irradiation-Induced Microstructure and Hardening of Reactor Pressure Vessel Steels. Metals 2022, 12, 369. https://doi.org/10.3390/met12030369
Ulbricht A, Hernández-Mayoral M, Oñorbe E, Etienne A, Radiguet B, Hirschmann E, Wagner A, Hein H, Bergner F. Effect of Neutron Flux on an Irradiation-Induced Microstructure and Hardening of Reactor Pressure Vessel Steels. Metals. 2022; 12(3):369. https://doi.org/10.3390/met12030369
Chicago/Turabian StyleUlbricht, Andreas, Mercedes Hernández-Mayoral, Elvira Oñorbe, Auriane Etienne, Bertrand Radiguet, Eric Hirschmann, Andreas Wagner, Hieronymus Hein, and Frank Bergner. 2022. "Effect of Neutron Flux on an Irradiation-Induced Microstructure and Hardening of Reactor Pressure Vessel Steels" Metals 12, no. 3: 369. https://doi.org/10.3390/met12030369
APA StyleUlbricht, A., Hernández-Mayoral, M., Oñorbe, E., Etienne, A., Radiguet, B., Hirschmann, E., Wagner, A., Hein, H., & Bergner, F. (2022). Effect of Neutron Flux on an Irradiation-Induced Microstructure and Hardening of Reactor Pressure Vessel Steels. Metals, 12(3), 369. https://doi.org/10.3390/met12030369







