The Use of Machine-Learning Techniques in Material Constitutive Modelling for Metal Forming Processes
Abstract
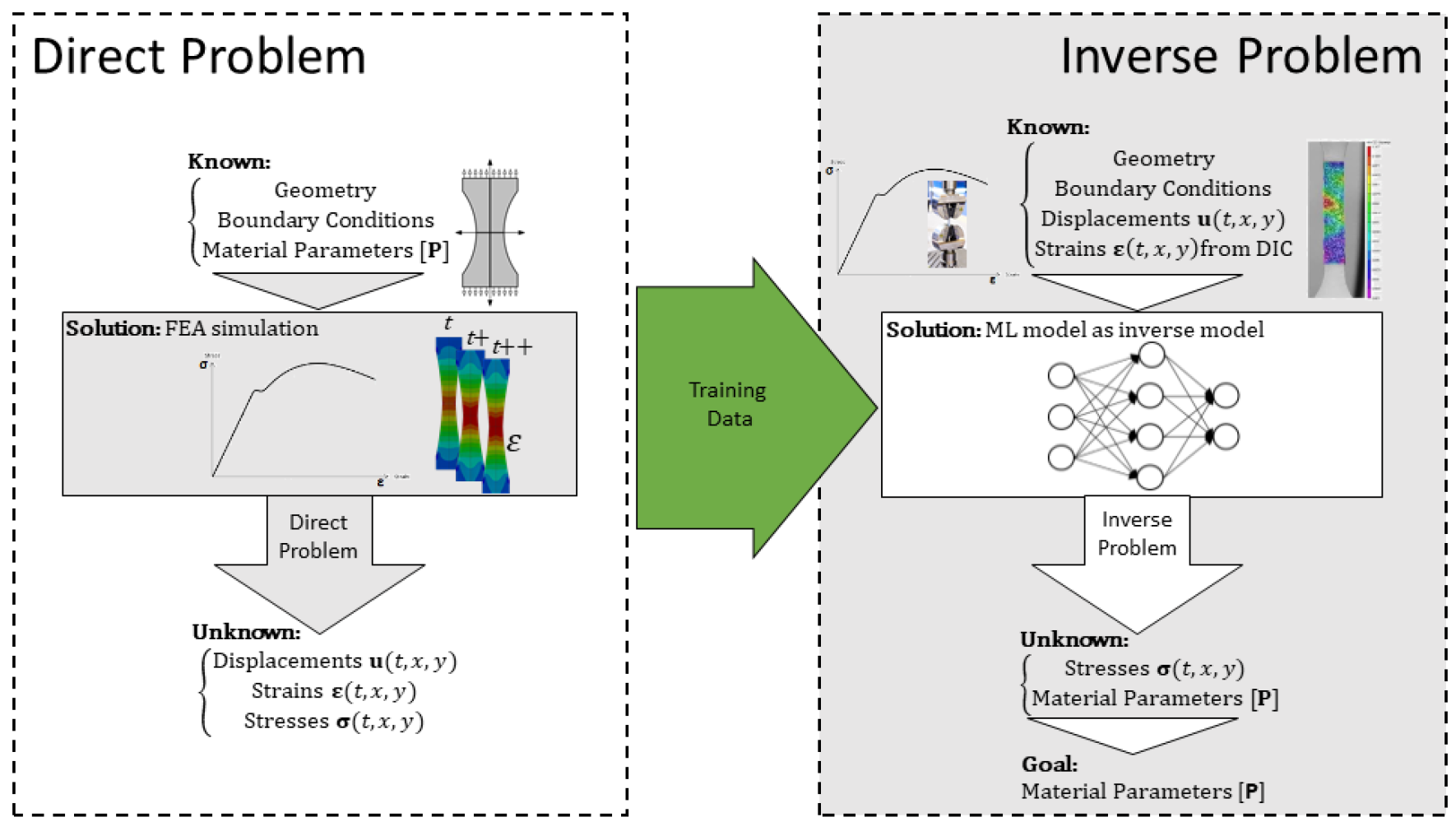
:1. Introduction
2. Classical Material Modelling
2.1. Phenomenological Approach
2.2. Elastoplasticity
3. Machine Learning Approaches for Constitutive Modelling in Metal Forming
3.1. Parameter Identification Inverse Modelling
3.2. Constitutive Model Corrector
3.3. Data-Driven Constitutive Model Using Empirical Known Concepts
3.4. General Implicit Constitutive Model Using Data-Driven Learning Approach
4. Review on Implicit Data-Driven Material Modelling
4.1. Neural Network Architectures and Generalization Capacity
- Dimensionality—where constitutive funtions are taken as members of function spaces, each of which is contained in a space of subsequently higher dimensions;
- Path-dependency—where a state of the material behavior represented with a given number of history points is a subset of another state represented with a larger number of history points.
4.2. Integration in Finite Element Analysis
4.3. Indirect/Inverse Training
5. Application Examples
5.1. Parameter Identification
5.1.1. Training the ML Using a Biaxial Cruciform Test
5.1.2. Prediction and Comparison
5.1.3. Remarks
5.2. ML Constitutive Model Using Empirical Known Concepts
5.2.1. Creating the Dataset for Trainning
5.2.2. Training the ANN Model
5.2.3. Testing the Trained Model in an FEA Simulation
5.2.4. Final Remarks
5.3. Implicit Elastoplastic Modelling Using the VFM
5.3.1. Data Generation and ANN Training
5.3.2. Results and Discussion
6. Conclusions
- ANNs provide an opportunity for a complete change of paradigm in the field of constitutive modelling. Their powerful capabilities allow material models to be devised without the need to formulate complicated symbolic expressions that, conventionally, require extensive parameter calibration procedures;
- Nevertheless, even in calibration/parameter identification procedures, the power and potential of ANNs can still be used. This paper showed that an ANN can be trained as an inverse model for parameter identification;
- ANNs are paving the way for the development of implicit material models capable of reproducing complex material behavior purely from data. Additionally, the the network architectures themselves can be designed based on the structure of existing well-known constitutive models;
- A great number of methodologies employ ANNs as “black boxes” that are not guaranteed to respect the basic laws of physics governing the dynamics of the systems, thus requiring large amounts of training to do so. This is an important issue due to the cost of data acquisition being often prohibitive and time-consuming;
- Considerable efforts have been done to improve the generalization capacity of the ANN-based implicit constitutive models, either by the development of new architectures, more robust training procedures or through the augmentation of the datasets. The use of NANNs, for example, is an interesting approach to capture the full material response, but does not solve the underlying dependency on large datasets. On the other hand, PINNs, particularly TANNs, have the potential to leverage the knowledge obtained from training data through the direct encoding of basic thermodynamic laws in the neural network, thus resulting in models able to perform very well on low data regimes. The SPD-NN goes a step further by imposing time consistency, strain energy function convexity and the Hill’s criterion, thus solving numerical instabilities derived from coupling standard ANN-based models with FEM solvers;
- Another powerful attribute of implicit constitutive models is the ease of implementation within FE subroutines. The architecture of ANNs can be stored in the code via matrices with the appropriate dimensions, containing the optimized weights obtained during training. The ANN operations are reduced to a sequence of matrix operations that provide an almost instantaneous mapping between input and output values, providing substantial gains in computational efficiency;
- A major part of the ANN-based methodologies to implicit constitutive modelling relies on labeled data pairs (strain and stress) to train the network. However, the stress tensor is not measurable in complex experimental tests, thus requiring the ANN-based model to be trained indirectly, using only measurable data, such as displacements and global force;
- Indirect training approaches for ANN-based constitutive modelling reported in the literature resort to coupling with FEA software in order for the numerical solver to impose the necessary physical and boundary contraints, while also allowing full-field data to be taken advantage of;
- A new disruptive methodology to train an ANN-based implicit constitutive model was proposed using the VFM. The new approach allows an ANN to learn both linear elastic and elastoplastic behaviors through the application of the PVW, using only measurable data, e.g., displacements and global force, to feed the training process. An interesting advantage of this new approach is that it does not require the FEM for further calculations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADAM | Adaptive moment estimation |
| ANN | Artificial neural network |
| CEGM | Constitutive equation gap method |
| CNN | Convolutional neural network |
| DIC | Digital image correlation |
| FEA | Finite element analysis |
| ECM | Equilibrium gap method |
| FEM | Finite element method |
| FEMU | Finite element model updating |
| FFNN | Feedforward neural network |
| GRU | Gated recurrent unit |
| LBFGS | Limited memory Broyden—Fletcher—Goldfarb—Shanno |
| LSTM | Long short-term memory unit |
| MAE | Mean absolute error |
| ML | Machine learning |
| MSE | Mean square error |
| NANN | Nested adaptive neural network |
| PINN | Physics-informed neural network |
| PReLU | Parametric rectified linear unit |
| ReLU | Rectified linear unit |
| RGM | Reciprocity gap method |
| RNN | Recurrent neural network |
| SELU | Scaled exponential linear unit |
| SGD | Stochastic gradient descent |
| SPD-NN | Symmetric positive definite neural network |
| TANN | Thermodynamics-based neural network |
| VFM | Virtual fields method |
Appendix A. Artificial Neural Networks
Appendix A.1. Basic Principle and Components
Appendix A.2. Network Topology

Appendix A.3. Mathematical Representation


Appendix A.4. Learning Paradigms and Training Procedures
- L1 regularization: the penalty is proportional to the L1 norm of the weighting coefficients;
- L2 regularization: the penalty is proportional to the L2 norm of the weighting coefficients.
Appendix B. Viscoplasticity
Appendix C. Virtual Fields Used to Train the Models

References
- Frank, M.; Drikakis, D.; Charissis, V. Machine-Learning Methods for Computational Science and Engineering. Computation 2020, 8, 15. [Google Scholar] [CrossRef] [Green Version]
- Martins, J.; Andrade-Campos, A.; Thuillier, S. Comparison of inverse identification strategies for constitutive mechanical models using full-field measurements. Int. J. Mech. Sci. 2018, 145, 330–345. [Google Scholar] [CrossRef]
- Andrade-Campos, A.; Thuillier, S.; Martins, J.; Carlone, P.; Tucci, F.; Valente, R.; Paulo, R.M.; de Sousa, R.J.A. Integrated Design in Welding and Incremental Forming: Material Model Calibration for Friction Stir Welded Blanks. Procedia Manuf. 2020, 47, 429–434. [Google Scholar] [CrossRef]
- Grédiac, M.; Pierron, F.; Avril, S.; Toussaint, E. The Virtual Fields Method for Extracting Constitutive Parameters From Full-Field Measurements: A Review. Strain 2006, 42, 233–253. [Google Scholar] [CrossRef] [Green Version]
- Versino, D.; Tonda, A.; Bronkhorst, C.A. Data driven modeling of plastic deformation. Comput. Methods Appl. Mech. Eng. 2017, 318, 981–1004. [Google Scholar] [CrossRef] [Green Version]
- Avril, S.; Bonnet, M.; Bretelle, A.S.; Grédiac, M.; Hild, F.; Ienny, P.; Latourte, F.; Lemosse, D.; Pagano, S.; Pagnacco, E.; et al. Overview of Identification Methods of Mechanical Parameters Based on Full-field Measurements. Exp. Mech. 2008, 48, 381. [Google Scholar] [CrossRef] [Green Version]
- Kirchdoerfer, T.; Ortiz, M. Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 2016, 304, 81–101. [Google Scholar] [CrossRef] [Green Version]
- Ibáñez, R.; Abisset-Chavanne, E.; González, D.; Duval, J.L.; Cueto, E.; Chinesta, F. Hybrid constitutive modeling: Data-driven learning of corrections to plasticity models. Int. J. Mater. Form. 2019, 12, 717–725. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.R.G.; Botti, S.; Marques, M.A.L. Recent advances and applications of machine learning in solid-state materials science. Npj Comput. Mater. 2019, 5, 2057–3960. [Google Scholar] [CrossRef]
- Jang, D.P.; Fazily, P.; Yoon, J.W. Machine learning-based constitutive model for J2- plasticity. Int. J. Plast. 2021, 138, 102919. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Lin, Y.C.; Zhang, J.; Zhong, J. Application of neural networks to predict the elevated temperature flow behavior of a low alloy steel. Comput. Mater. Sci. 2008, 43, 752–758. [Google Scholar] [CrossRef]
- González, D.; Aguado, J.V.; Cueto, E.; Abisset-Chavanne, E.; Chinesta, F. kPCA-Based Parametric Solutions Within the PGD Frameworks. Arch. Comput. Methods Eng. 2018, 25, 69–86. [Google Scholar] [CrossRef]
- Lopez, E.; Gonzalez, D.; Aguado, J.V.; Abisset-Chavanne, E.; Cueto, E.; Binetruy, C.; Chinesta, F. A Manifold Learning Approach for Integrated Computational Materials Engineering. Arch. Comput. Methods Eng. 2018, 25, 59–68. [Google Scholar] [CrossRef] [Green Version]
- Ibañez, R.; Abisset-Chavanne, E.; Aguado, J.V.; Gonzalez, D.; Cueto, E.; Chinesta, F. A Manifold Learning Approach to Data-Driven Computational Elasticity and Inelasticity. Arch. Comput. Methods Eng. 2018, 25, 47–57. [Google Scholar] [CrossRef] [Green Version]
- González, D.; Chinesta, F.; Cueto, E. Thermodynamically consistent data-driven computational mechanics. Contin. Mech. Thermodyn. 2019, 31, 239–253. [Google Scholar] [CrossRef]
- Bessa, M.; Bostanabad, R.; Liu, Z.; Hu, A.; Apley, D.W.; Brinson, C.; Chen, W.; Liu, W.K. A framework for data-driven analysis of materials under uncertainty: Countering the curse of dimensionality. Comput. Methods Appl. Mech. Eng. 2017, 320, 633–667. [Google Scholar] [CrossRef]
- Furukawa, T.; Yagawa, G. Implicit constitutive modelling for viscoplasticity using neural networks. Int. J. Numer. Methods Eng. 1998, 43, 195–219. [Google Scholar] [CrossRef]
- Man, H.; Furukawa, T. Neural network constitutive modelling for non-linear characterization of anisotropic materials. Int. J. Numer. Methods Eng. 2011, 85, 939–957. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Sidarta, D.E. New Nested Adaptive Neural Networks (NANN) for Constitutive Modeling. Comput. Geotech. 1998, 22, 29–52. [Google Scholar] [CrossRef]
- Lefik, M.; Schrefler, B.A. Artificial neural network as an incremental non-linear constitutive model for a finite element code. Comput. Methods Appl. Mech. Eng. 2003, 192, 3265–3283. [Google Scholar] [CrossRef]
- Gaspar, M.; Andrade-Campos, A. Implicit material modelling using artificial intelligence techniques. AIP Conf. Proc. 2019, 2113, 120004. [Google Scholar] [CrossRef]
- Souto, N.; Andrade-Campos, A.; Thuillier, S. A numerical methodology to design heterogeneous mechanical tests. Int. J. Mech. Sci. 2016, 107, 264–276. [Google Scholar] [CrossRef]
- Wang, K.; Sun, W.; Du, Q. A cooperative game for automated learning of elasto-plasticity knowledge graphs and models with AI-guided experimentation. Comput. Mech. 2019, 64, 467–499. [Google Scholar] [CrossRef] [Green Version]
- Simo, J.; Hughes, T. Computational Inelasticity; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Hill, R.; Orowan, E. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar] [CrossRef] [Green Version]
- Dunne, F.; Petrinic, N. Introduction to Computational Plasticity; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Crisfield, M. Non-Linear Finite Element Analysis of Solids and Structures; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- de Carvalho, R.; Valente, R.; Andrade-Campos, A. Optimization strategies for non-linear material parameters identification in metal forming problems. Comput. Struct. 2011, 89, 246–255. [Google Scholar] [CrossRef]
- Ponthot, J.P.; Kleinermann, J.P. A cascade optimization methodology for automatic parameter identification and shape/process optimization in metal forming simulation. Comput. Methods Appl. Mech. Eng. 2006, 195, 5472–5508. [Google Scholar] [CrossRef]
- Andrade-Campos, A.; Pilvin, P.; Simões, J.; Teixeira-Dias, F. Software development for inverse determination of constitutive model parameters. In Software Engineering: New Research; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2009; Chapter 6; pp. 93–124. [Google Scholar]
- Grédiac, M. Principe des travaux virtuels et identification. Comptes Rendus L’Académie Des. Sci. 1989, 309, 1–5. [Google Scholar]
- Aggarwal, C.C. Neural Networks and Deep Learning; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Chollet, F. Deep Learning with Python; Manning: Shelter Island, NY, USA, 2018. [Google Scholar]
- Ghaboussi, J.; Garrett, J.H.; Wu, X. Knowledge-Based Modeling of Material Behavior with Neural Networks. J. Eng. Mech. 1991, 117, 132–153. [Google Scholar] [CrossRef]
- Wu, X.; Ghaboussi, J. Neural Network-Based Material Modeling; Technical Report; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1995. [Google Scholar]
- Ghaboussi, J.; Sidarta, D.; Lade, P. Neural network based modelling in geomechanics. In Proceedings of the 8th International Conference on Computer Methods and Advances in Geomechanics, Morgantown, WV, USA, 22–28 May 1994. [Google Scholar]
- Ellis, G.W.; Yao, C.; Zhao, R.; Penumadu, D. Stress-Strain Modeling of Sands Using Artificial Neural Networks. J. Geotech. Eng. 1995, 121, 429–435. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Pecknold, D.A.; Zhang, M.; Haj-Ali, R.M. Autoprogressive training of neural network constitutive models. Int. J. Numer. Methods Eng. 1998, 42, 105–126. [Google Scholar] [CrossRef]
- Ping, L.; Kemin, X.; Yan, L.; Jianrong, T. Neural network prediction of flow stress of Ti-15-3 alloy under hot compression. J. Mater. Process. Technol. 2004, 148, 235–238. [Google Scholar] [CrossRef]
- Mandal, S.; Sivaprasad, P.V.; Venugopal, S.; Murthy, K.P. Artificial neural network modeling to evaluate and predict the deformation behavior of stainless steel type AISI 304L during hot torsion. Appl. Soft Comput. J. 2009, 9, 237–244. [Google Scholar] [CrossRef]
- Sun, Y.; Zeng, W.D.; Zhao, Y.Q.; Zhang, X.M.; Shu, Y.; Zhou, Y.G. Modeling constitutive relationship of Ti40 alloy using artificial neural network. Mater. Des. 2011, 32, 1537–1541. [Google Scholar] [CrossRef]
- Li, H.Y.; Hu, J.D.; Wei, D.D.; Wang, X.F.; Li, Y.H. Artificial neural network and constitutive equations to predict the hot deformation behavior of modified 2.25Cr-1Mo steel. Mater. Des. 2012, 42, 192–197. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Sobh, N.A.; Sehitoglu, H. Deep learning for plasticity and thermo-viscoplasticity. Int. J. Plast. 2021, 136, 102852. [Google Scholar] [CrossRef]
- Heider, Y.; Wang, K.; Sun, W.C. SO(3)-invariance of informed-graph-based deep neural network for anisotropic elastoplastic materials. Comput. Methods Appl. Mech. Eng. 2020, 363, 112875. [Google Scholar] [CrossRef]
- Ghavamian, F.; Simone, A. Accelerating multiscale finite element simulations of history-dependent materials using a recurrent neural network. Comput. Methods Appl. Mech. Eng. 2019, 357, 112594. [Google Scholar] [CrossRef]
- Mozaffar, M.; Bostanabad, R.; Chen, W.; Ehmann, K.; Cao, J.; Bessa, M.A. Deep learning predicts path-dependent plasticity. Proc. Natl. Acad. Sci. USA 2019, 116, 26414–26420. [Google Scholar] [CrossRef] [Green Version]
- Gorji, M.B.; Mozaffar, M.; Heidenreich, J.N.; Cao, J.; Mohr, D. On the potential of recurrent neural networks for modeling path dependent plasticity. J. Mech. Phys. Solids 2020, 143, 103972. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Masi, F.; Stefanou, I.; Vannucci, P.; Maffi-Berthier, V. Thermodynamics-based Artificial Neural Networks for constitutive modeling. J. Mech. Phys. Solids 2021, 147, 104277. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Xu, K.; Huang, D.Z.; Darve, E. Learning constitutive relations using symmetric positive definite neural networks. J. Comput. Phys. 2021, 428, 110072. [Google Scholar] [CrossRef]
- Scott Kessler, B.; El-Gizawy, A.S.; Smith, D.E. Incorporating neural network material models within finite element analysis for rheological behavior prediction. J. Press. Vessel Technol. Trans. ASME 2007, 129, 58–65. [Google Scholar] [CrossRef]
- Zhang, A.; Mohr, D. Using neural networks to represent von Mises plasticity with isotropic hardening. Int. J. Plast. 2020, 132, 102732. [Google Scholar] [CrossRef]
- Liu, X.; Tao, F.; Yu, W. A neural network enhanced system for learning nonlinear constitutive law and failure initiation criterion of composites using indirectly measurable data. Compos. Struct. 2020, 252, 112658. [Google Scholar] [CrossRef]
- Huang, D.Z.; Xu, K.; Farhat, C.; Darve, E. Learning constitutive relations from indirect observations using deep neural networks. J. Comput. Phys. 2020, 416, 109491. [Google Scholar] [CrossRef]
- Xu, K.; Tartakovsky, A.M.; Burghardt, J.; Darve, E. Learning viscoelasticity models from indirect data using deep neural networks. Comput. Methods Appl. Mech. Eng. 2021, 387, 114124. [Google Scholar] [CrossRef]
- Tao, F.; Liu, X.; Du, H.; Yu, W. Learning composite constitutive laws via coupling Abaqus and deep neural network. Compos. Struct. 2021, 272, 114137. [Google Scholar] [CrossRef]
- Liu, X.; Tao, F.; Du, H.; Yu, W.; Xu, K. Learning nonlinear constitutive laws using neural network models based on indirectly measurable data. J. Appl. Mech. Trans. ASME 2020, 87, 1–8. [Google Scholar] [CrossRef]
- Marek, A.; Davis, F.M.; Pierron, F. Sensitivity-based virtual fields for the non-linear virtual fields method. Comput. Mech. 2017, 60, 409–431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pierron, F.; Grédiac, M. The Virtual Fields Method: Extracting Constitutive Mechanical Parameters from Full-Field Deformation Measurements; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Andrade-Campos, A. Development of an Optimization Framework for Parameter Identification and Shape Optimization Problems in Engineering. Int. J. Manuf. Mater. Mech. Eng. (IJMMME) 2011, 1, 57–59. [Google Scholar] [CrossRef]
- Martins, J.; Andrade-Campos, A.; Thuillier, S. Calibration of anisotropic plasticity models using a biaxial test and the virtual fields method. Int. J. Solids Struct. 2019, 172–173, 21–37. [Google Scholar] [CrossRef]
- Scipy. scipy.integrate.odeint—SciPy v1.1.0 Reference Guide. Available online: https://docs.scipy.org/doc/scipy-1.1.0/reference/ (accessed on 15 February 2022).
- Scikit-Learn. 3.2. Tuning the Hyper-Parameters of an Estimator—Scikit-Learn 0.20.0 Documentation. Available online: https://scikit-learn.org/stable/modules/grid_search.html (accessed on 15 February 2022).
- Scikit-Learn. 3.5. Validation Curves: Plotting Scores to Evaluate Models—Scikit-Learn 0.20.1 Documentation. Available online: https://scikit-learn.org/stable/modules/learning_curve.html (accessed on 15 February 2022).
- Aquino, J.; Andrade-Campos, A.; Souto, N.; Thuillier, S. Design of heterogeneous mechanical tests—Numerical methodology and experimental validation. AIP Conf. Proc. 2018, 1960, 1–20. [Google Scholar] [CrossRef]
- Aquino, J.; Andrade-Campos, A.G.; Martins, J.M.P.; Thuillier, S. Design of heterogeneous mechanical tests: Numerical methodology and experimental validation. Strain 2019, 55, e12313. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 1026–1034. [Google Scholar] [CrossRef] [Green Version]
- Ertel, W. Introduction to Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Rosenblat, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cybenko, G. Approximation by Superpositions of a Sigmoidal Function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Bock, F.E.; Aydin, R.C.; Cyron, C.J.; Huber, N.; Kalidindi, S.R.; Klusemann, B. A Review of the Application of Machine Learning and Data Mining Approaches in Continuum Materials Mechanics. Front. Mater. 2019, 6, 110. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Haffner, P.; Bottou, L.; Bengio, Y. Object Recognition with Gradient-Based Learning. In Shape, Contour and Grouping in Computer Vision; Springer: Berlin/Heidelberg, Germany, 1999; pp. 319–345. [Google Scholar] [CrossRef]
- Alaloul, W.S.; Qureshi, A.H. Data Processing Using Artificial Neural Networks. In Dynamic Data Assimilation—Beating the Uncertainties; Harkut, D.G., Ed.; IntechOpen: London, UK, 2020. [Google Scholar]
- Ambroziak, A.; Kłosowski, P. The elasto-viscoplastic Chaboche model. Task Q. 2006, 10, 49–61. [Google Scholar]





















| Hill’48 Parameters | Reference Values |
|---|---|
| 1.680 | |
| 1.890 | |
| 2.253 |
| Constitutive Parameters | Input Space |
|---|---|
| [MPa] | 120–200 |
| n | 0.175–0.275 |
| K [MPa] | 480–570 |
| 1.0–2.5 | |
| 1.0–2.5 | |
| 1.0–2.5 |
| Layer | Neurons | Activation | Kernel_Initializer |
|---|---|---|---|
| Input | 7203 | - | - |
| Dense 1 | 7000 | tanh | Orthogonal |
| Dense 2 | 3000 | tanh | Truncated normal |
| Dense 3 | 5000 | tanh | Truncated normal |
| Dense 4 | 5000 | selu | Variance scaling |
| Dense 5 | 6000 | selu | Variance scaling |
| Output | 6 | - | - |
| [MPa] | n | K [MPa] | |||||
|---|---|---|---|---|---|---|---|
| Test 1 | Reference | 120.00 | 0.18 | 530.00 | 1.01 | 1.24 | 1.73 |
| Predicted | 120.98 | 0.18 | 536.69 | 1.06 | 1.25 | 1.71 | |
| Error [%] | 0.82 | 1.67 | 1.26 | 4.95 | 0.81 | 1.16 | |
| Test 2 | Reference | 160.00 | 0.26 | 565.00 | 1.68 | 1.89 | 2.253 |
| Predicted | 160.34 | 0.26 | 565.60 | 1.69 | 1.88 | 2.27 | |
| Error [%] | 0.21 | 1.15 | 0.11 | 0.60 | 0.53 | 0.75 | |
| Test 3 | Reference | 220.00 | 0.30 | 620.00 | 2.52 | 2.67 | 2.95 |
| Predicted | 202.61 | 0.24 | 558.54 | 2.36 | 2.30 | 2.74 | |
| Error [%] | 7.90 | 21.67 | 9.91 | 6.35 | 13.86 | 7.12 |
| [MPa] | n | K [MPa] | |||||
|---|---|---|---|---|---|---|---|
| Reference | 160.00 | 0.26 | 565.00 | 1.68 | 1.89 | 2.25 | |
| ANN approach (96 h) | Predicted | 160.34 | 0.26 | 565.60 | 1.69 | 1.88 | 2.27 |
| Error [%] | 0.21 | 1.15 | 0.11 | 0.60 | 0.53 | 0.75 | |
| VFM (<5 min) | Predicted | 159.76 | 0.26 | 566.16 | 1.67 | 1.91 | 2.24 |
| Error [%] | 0.15 | 0.44 | 0.25 | 0.16 | 1.11 | 0.26 |
| [MPa] | n | K [MPa] | |||||
|---|---|---|---|---|---|---|---|
| Test 1 | Reference | 120.00 | 0.18 | 530.00 | 1.01 | 1.24 | 1.73 |
| Predicted | 146.82 | 0.197 | 568.02 | 1.66 | 1.72 | 1.98 | |
| Error | 22.35 | 9.44 | 7.17 | 64.36 | 38.71 | 14.45 | |
| Test 2 | Reference | 160.00 | 0.26 | 565.00 | 1.68 | 1.89 | 2.25 |
| Predicted | 152.79 | 0.23 | 558.82 | 1.66 | 1.72 | 1.98 | |
| Error | 4.51 | 10.00 | 1.09 | 8.93 | 8.47 | 18.77 | |
| Test 3 | Reference | 220.00 | 0.30 | 620.00 | 2.52 | 2.67 | 2.95 |
| Predicted | 166.61 | 0.23 | 554.62 | 1.77 | 1.73 | 1.93 | |
| Error | 24.27 | 24.27 | 10.55 | 29.76 | 35.21 | 34.58 |
[MPa] | [MPa] | [MPa] | [MPa] | [MPa] | [MPa] | R [MPa] | ||
|---|---|---|---|---|---|---|---|---|
Point 1  | ANN | 283.88 | 533.31 | 69.08 | −100.18 | 101.41 | 3.49 | 81.97 |
| Experiment | 243.42 | 537.35 | 37.83 | −95.94 | 95.94 | 23.94 | 82.81 | |
| Error [%] | 16.62 | 0.75 | 82.61 | 4.42 | 5.7 | 85.42 | 1.01 | |
Point 2  | ANN | −29.96 | 180.21 | 0.96 | −64.34 | 64.08 | 1.72 | 52.49 |
| Experiment | −25.78 | 180.33 | 1.05 | −69.35 | 69.35 | 0.77 | 53.35 | |
| Error [%] | 0.16 | 0.07 | 8.57 | 7.22 | 7.60 | 0.01 | 1.61 | |
Point 3  | ANN | 0.62 | 163.06 | 7.47 | −48.62 | 48.28 | 1.25 | 51.80 |
| Experiment | −0.66 | 168.67 | 6.61 | −52.11 | 52.11 | 4.18 | 52.07 | |
| Error [%] | 193.94 | 3.33 | 13.01 | 6.7 | 7.35 | 70.1 | 0.52 |
| p | |||||
|---|---|---|---|---|---|
Point 1  | ANN | −1.162 | 1.111 | 8.266 | 1.313 |
| Experiment | −1.079 | 1.079 | 2.452 | 1.262 | |
| Error [%] | 7.69 | 2.97 | 66.29 | 4.04 | |
Point 2  | ANN | −9.948 | 1.055 | 1.798 | 1.162 |
| Experiment | −1.077 | 1.077 | 1.400 | 1.244 | |
| Error [%] | 7.63 | 2.04 | 28.43 | 6.59 | |
Point 3  | ANN | −7.230 | 7.836 | 9.220 | 8.538 |
| Experiment | −6.630 | 6.630 | 5.400 | 7.670 | |
| Error [%] | 9.05 | 18.19 | 82.93 | 11.32 |
| Virtual Field | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 0 | 0 | |||||
| 0 | 0 | |||||
| 0 | 0 | |||||
| 0 | 0 | |||||
| 0 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lourenço, R.; Andrade-Campos, A.; Georgieva, P. The Use of Machine-Learning Techniques in Material Constitutive Modelling for Metal Forming Processes. Metals 2022, 12, 427. https://doi.org/10.3390/met12030427
Lourenço R, Andrade-Campos A, Georgieva P. The Use of Machine-Learning Techniques in Material Constitutive Modelling for Metal Forming Processes. Metals. 2022; 12(3):427. https://doi.org/10.3390/met12030427
Chicago/Turabian StyleLourenço, Rúben, António Andrade-Campos, and Pétia Georgieva. 2022. "The Use of Machine-Learning Techniques in Material Constitutive Modelling for Metal Forming Processes" Metals 12, no. 3: 427. https://doi.org/10.3390/met12030427
APA StyleLourenço, R., Andrade-Campos, A., & Georgieva, P. (2022). The Use of Machine-Learning Techniques in Material Constitutive Modelling for Metal Forming Processes. Metals, 12(3), 427. https://doi.org/10.3390/met12030427







