Research on Hot Deformation Behavior of F92 Steel Based on Stress Correction
Abstract
:1. Introduction
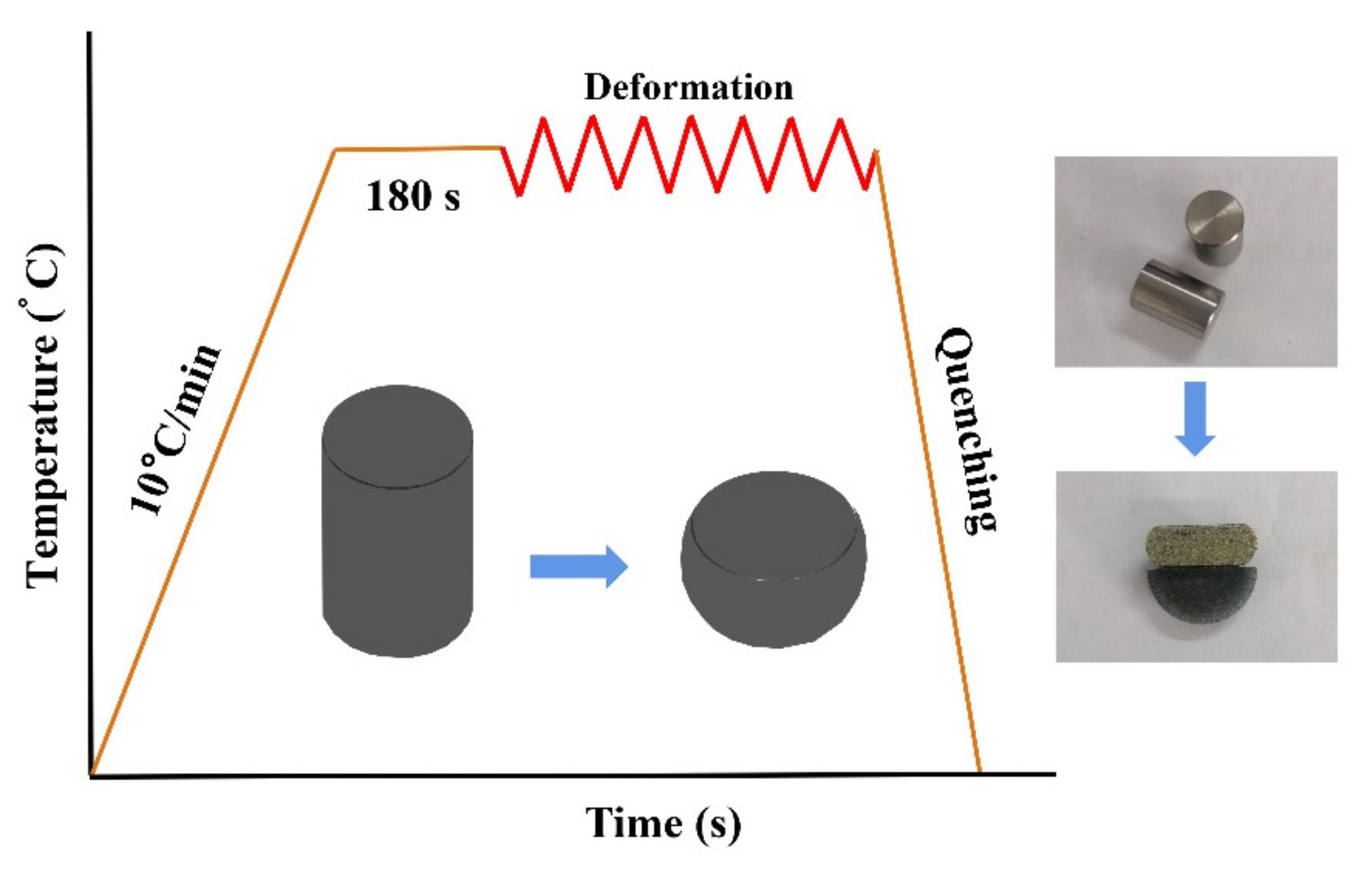
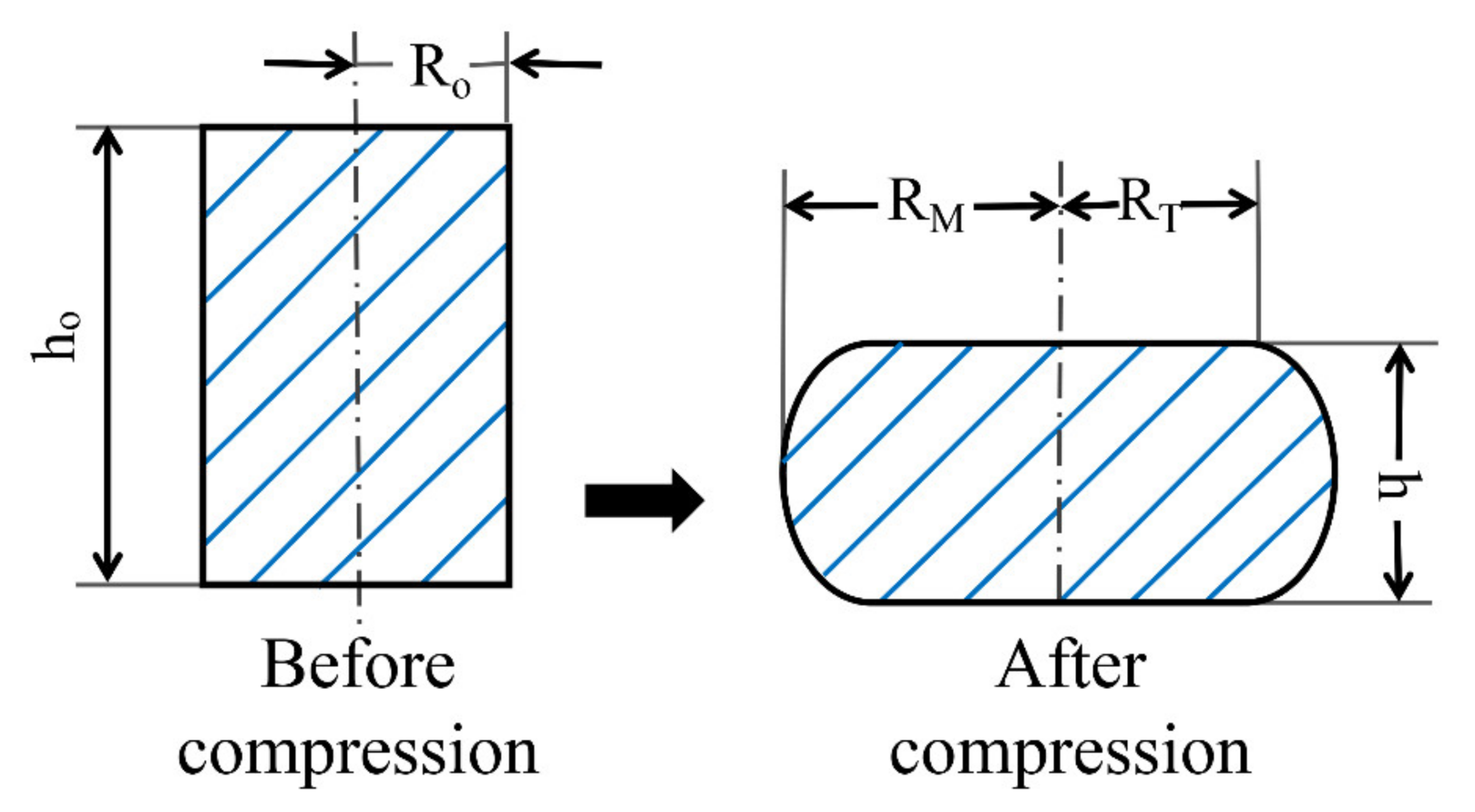
2. Experimental Details
3. Results and Discussion
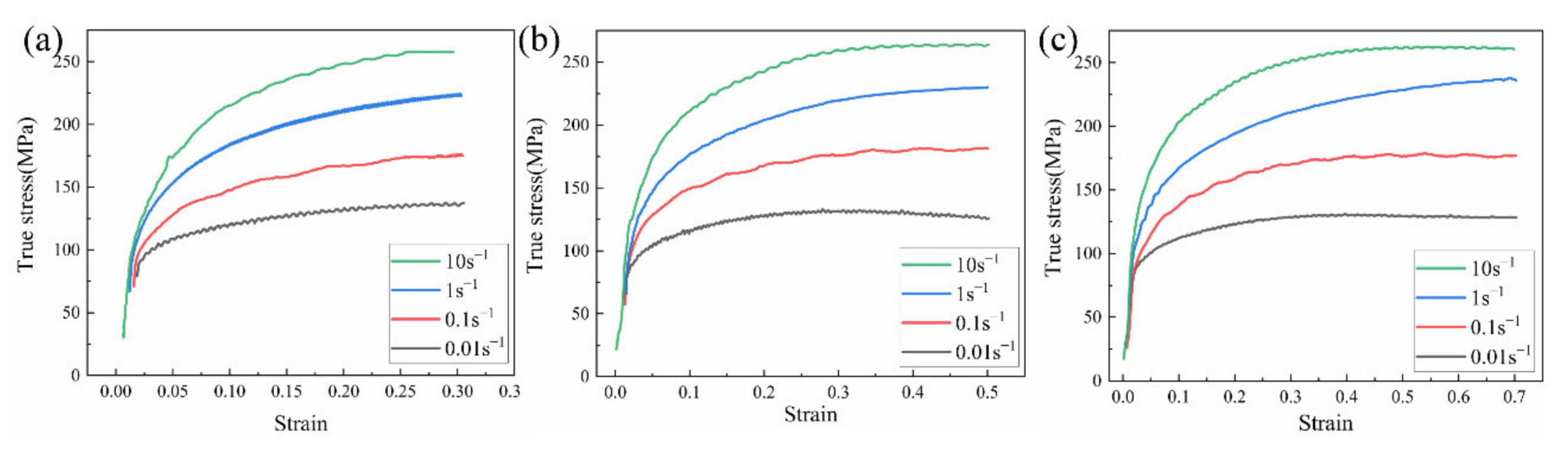
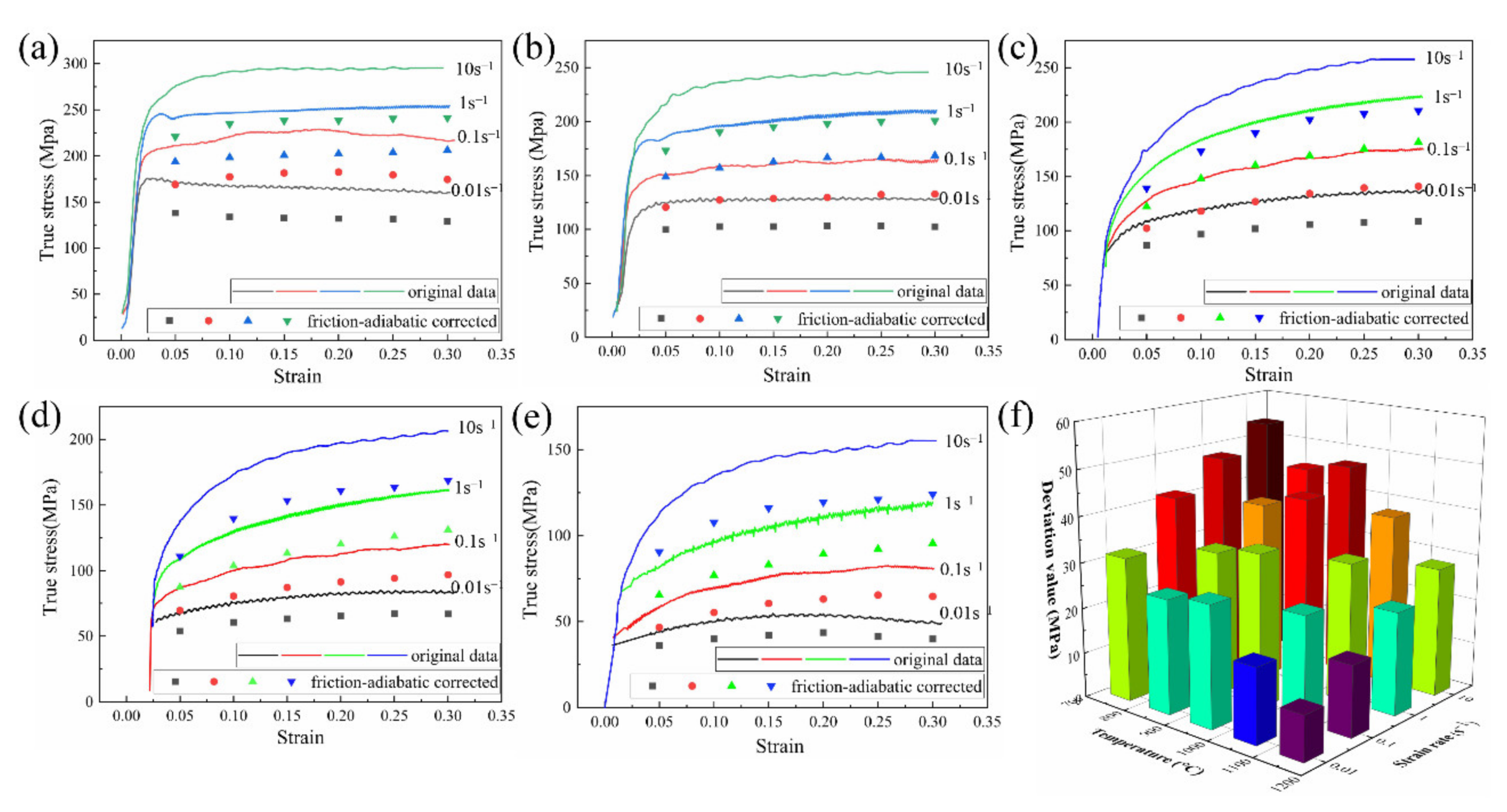
3.1. True Stress–Strain Curve
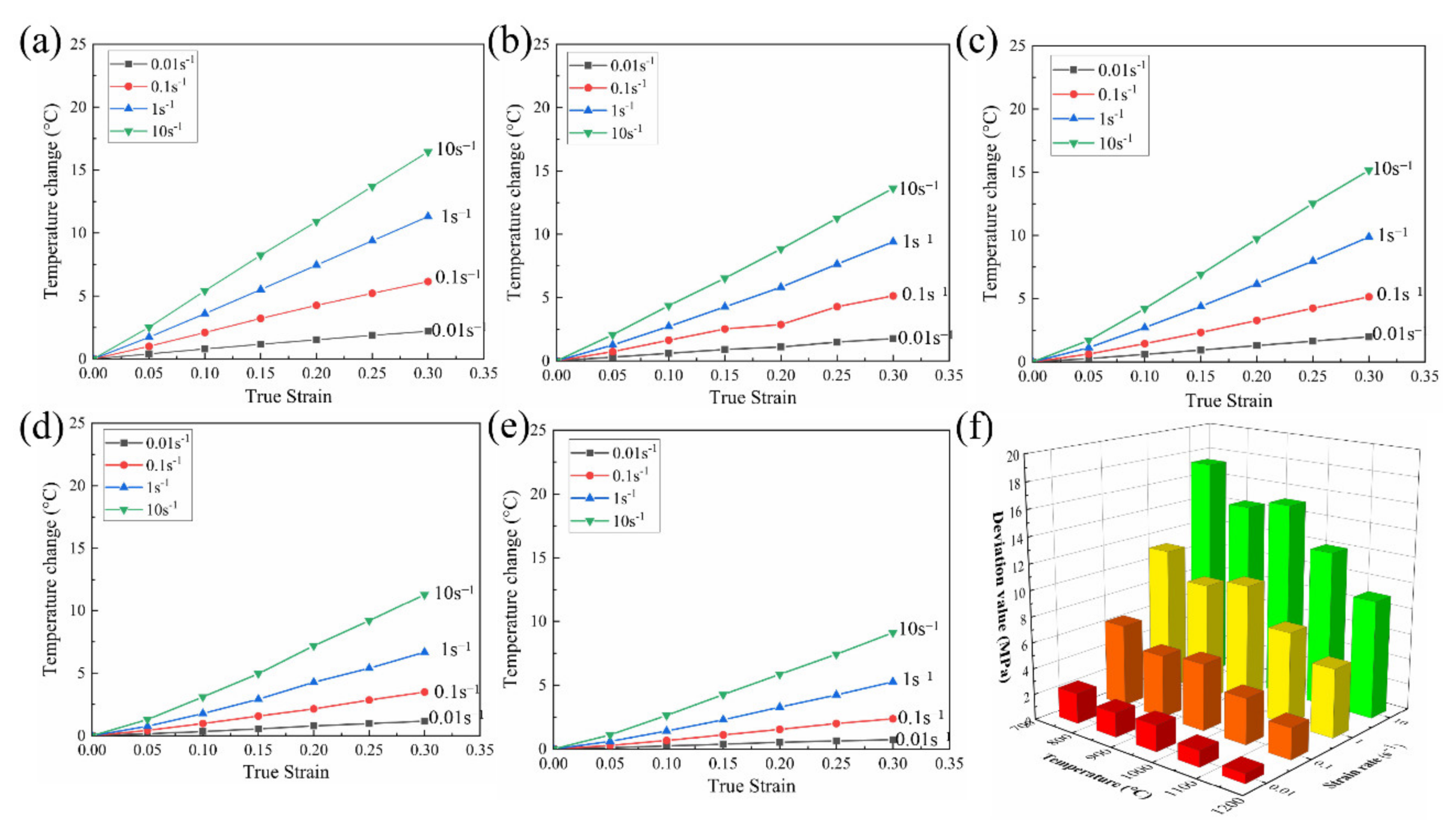
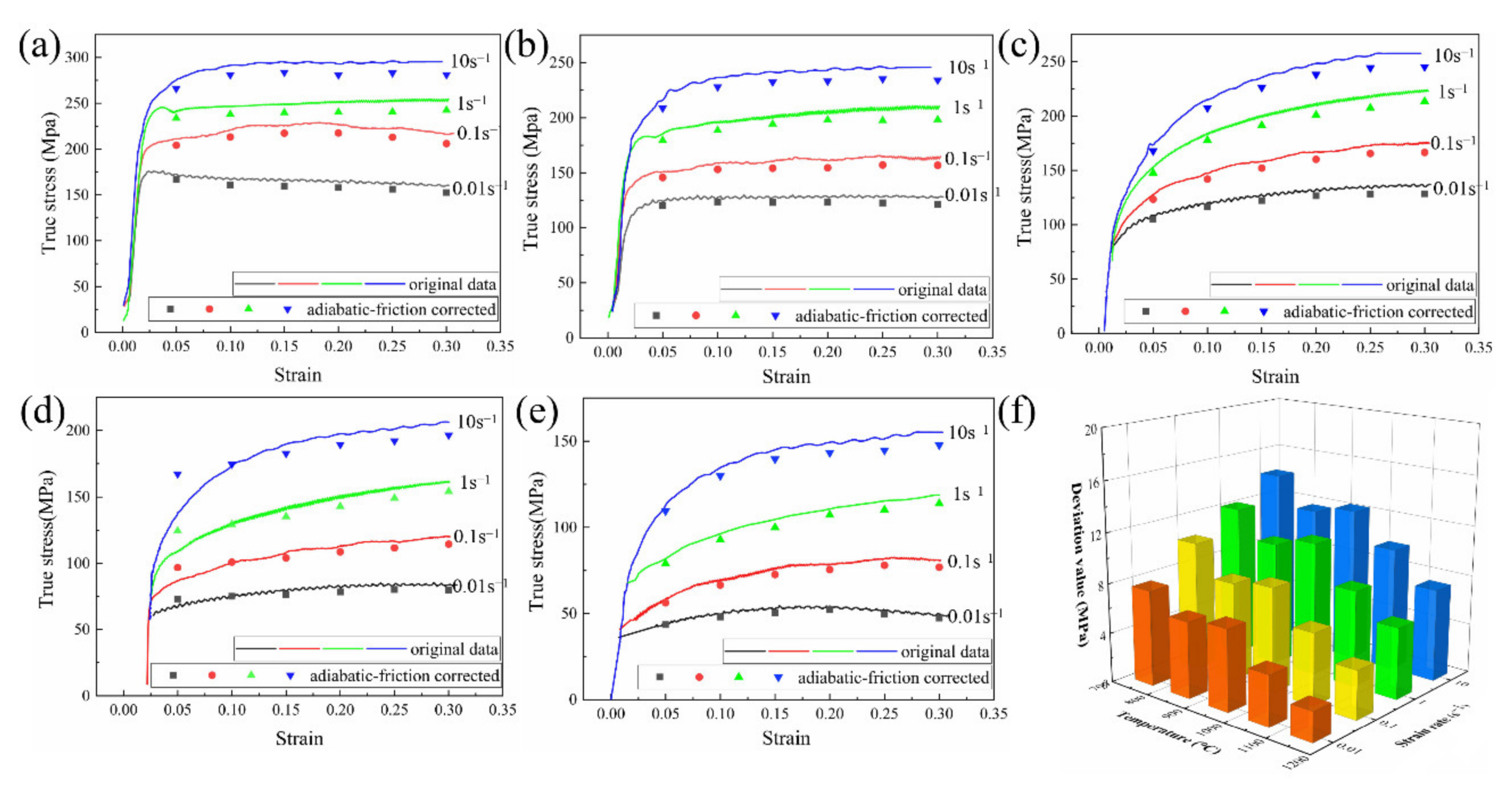
3.2. Stress Correction Model 1
3.3. Stress Correction Model 2
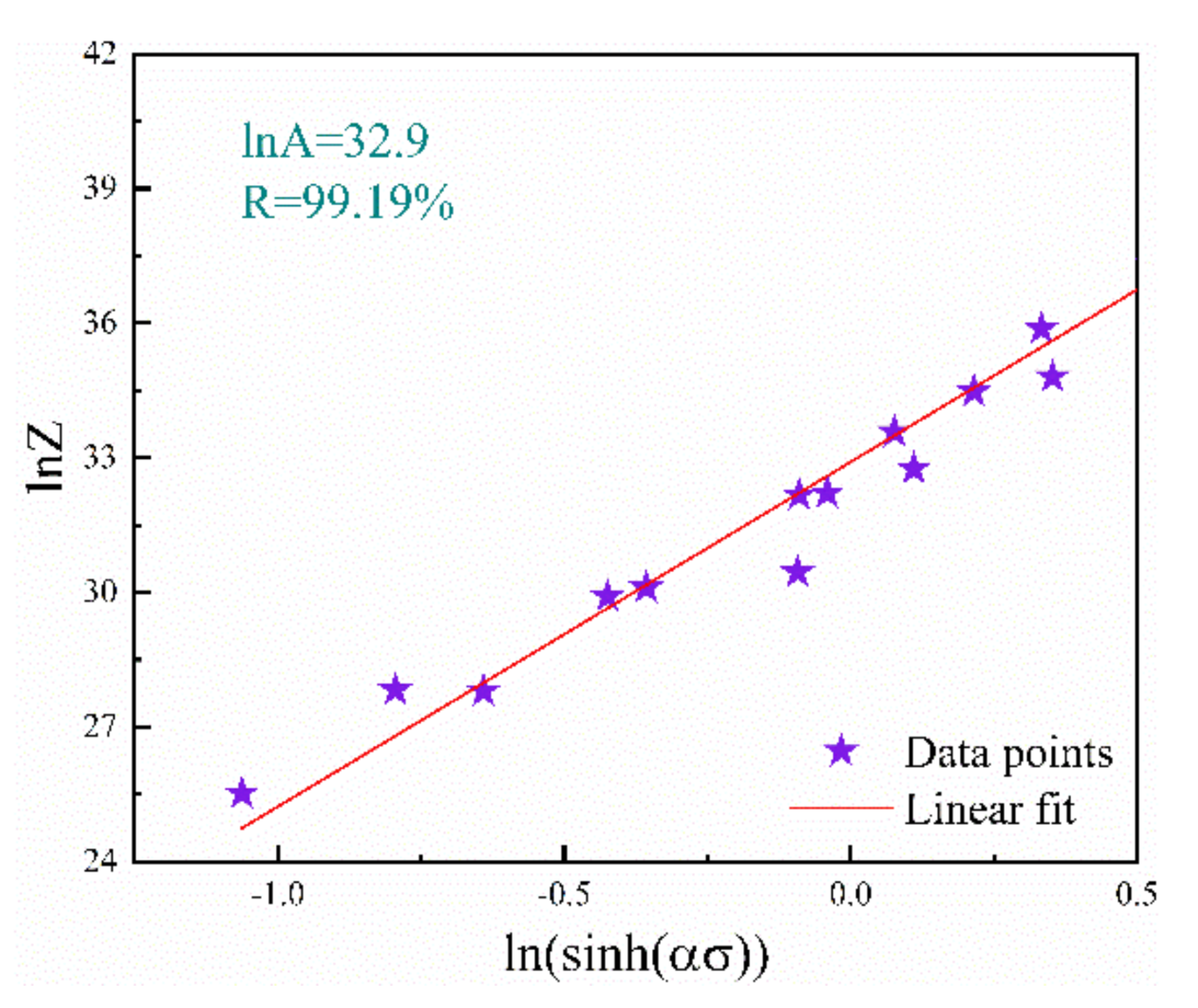
3.4. Arrhenius (AR) Model at Strain of 0.3
3.5. Microstructure Evolution
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, Z.; Zhang, X.; Song, X.; Ma, C.; Qi, Y.; Chen, X. Microstructure and properties of welded joint for T92 ferritic heat resistant steel. J. Alloys Compd. 2017, 140523. [Google Scholar] [CrossRef]
- Pandey, C.; Mahapatra, M.M.; Kumar, P.; Thakre, J.; Saini, N. Role of evolving microstructure on the mechanical behaviour of P92 steel welded joint in as-welded and post weld heat treated state. J. Mater. Process. Technol. 2019, 263, 241–255. [Google Scholar] [CrossRef]
- Yang, S.D. Research on the F91 valve body’s material welding process. Power Stn. Aux. Equip. 2015, 36, 41–45. [Google Scholar]
- Chen, Z.M. Heat treatment of F91 steel and A691gr.1-1/4crcl22 steel pipe welded joint. Welded Pipe Tube 2020, 43, 40–43+48. [Google Scholar]
- Paddea, S.; Francis, J.A.; Paradowaska, A.M.; Bouchard, P.; Shibli, I. Residual Stress Distribution in P91 Steel-Pipe Girth Weld Before and After Post-weld Heat Treatment. J. Mater. Sci. Eng. A 2012, 534, 663–672. [Google Scholar] [CrossRef]
- Ennis, P.J.; Czyrska-Filemonowicz, A. Recent advances in creep-resistant steels for power plant applications. Sadhana 2003, 28, 709–730. [Google Scholar] [CrossRef]
- Abson, D.J.; Rothwell, J.S. Review of type IV cracking of weldments in 9–12% Cr creep strength enhanced ferritic steels. Int. Mater. Rev. 2013, 58, 437–473. [Google Scholar] [CrossRef]
- Pandey, C.; Giri, A.; Mahapatra, M.M. Effect of normalizing temperature on microstructural stability and mechanical properties of creep strength enhanced ferritic P91 steel. Mater. Sci. Eng. A 2016, 657, 173–184. [Google Scholar] [CrossRef]
- Onoro, J. Martensite microstructure of 9–12% Cr steels weld metals. J. Mater. Process. Technol. 2006, 180, 137–142. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, C.X.; Qiao, B.W. Study on the deformation behavior and constitutive equation of 14Cr17Ni2 steel. Hot Work. Technol. 2018, 47, 38–43. [Google Scholar]
- Wang, M.H.; Chen, M.L.; Wang, R.; Wang, G.T. High-temperature flow stress model and hot working diagram of 2Cr12NiMo1W1V supercritical steel. J. Cent. South Univ. 2016, 47, 741–748. [Google Scholar]
- Ma, Y.F. Study on Hot Deformation Behavior of 17-4PH Stainless Steel; Jiangsu University: Zhenjiang, China, 2017. [Google Scholar]
- Pei, W.J.; Guo, X.Z.; Wang, W.T.; Tao, J. High-Temperature flow Behavior of 316L austenitic stainless steel. J. Plas. Eng. 2014, 21, 104–110. [Google Scholar]
- Roebuck, B.; Loveday, M.S.; Chastel, Y.; Fiorucci, G.; dal Negro, T. Measurement of flow stress at high temperature in solid torsion tests. Mater. High Temp. 2006, 23, 119–144. [Google Scholar] [CrossRef]
- Obiko, J. Friction correction of flow stress-strain curve in the upsetting process. IOP SciNotes 2021, 2, 014401. [Google Scholar] [CrossRef]
- Wan, Z.P.; Wang, T.; Li, Z.; Li, P.H.; Zhang, Y.; Sun, Y.; Hu, L.X. Effect of adiabatic heating and friction effect on flow stress of alloy during hot compression deformation. J. Plas. Eng. 2020, 27, 166–171. [Google Scholar]
- Xue, X.W.; Wang, C.X.; Li, Y.; Han, S.; Liu, S.Z.; Yuan, W.H. High temperature plastic deformation behavior of as-cast 300M steel based on friction correction. In Key Engineering Materials; Trans Tech Publications Ltd.: Bäch, Switzerland, 2019. [Google Scholar]
- Ebrahimi, R.; Najafizadeh, A. A new method for evaluation of friction in bulk metal forming. J. Mater. Process. Technol. 2004, 15, 136–143. [Google Scholar] [CrossRef]
- Cao, Y. Study on Microstructure Evolution and Mechanical Properties of Incoloy 800H Alloy during Hot Working; Northeast University: Boston, MA, USA, 2016. [Google Scholar]
- Churyumov, A.Y.; Khomutov, M.G.; Tsar’Kov, A.A.; Pozdnyakov, A.V.; Solonin, A.N.; Efimov, V.M.; Mukhanov, E.L. Study of the structure and mechanical properties of corrosion-resistant steel with a high concentration of boron at elevated temperatures. Phys. Met. Metallogr. 2014, 115, 809–813. [Google Scholar] [CrossRef]
- Evans, R.W.; Scharning, P.J. Axisymmetric compression test and hot working properties of alloys. Mater. Sci. Technol. 2001, 17, 995–1004. [Google Scholar] [CrossRef]
- Baktash, R.; Mirzadeh, H. A simple constitutive model for prediction of single-peak flow curves under hot working conditions. J. Eng. Mater. Technol. 2016, 138, 021004. [Google Scholar] [CrossRef]
- Chen, X.; Liao, Q.; Niu, Y.; Jia, W.; Le, Q.; Cheng, C.; Yu, F.; Cui, J. A constitutive relation of AZ80 magnesium alloy during hot deformation based on Arrhenius and Johnson–Cook model. J. Mater. Res. Technol. 2019, 8, 1859–1869. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A.K. Characterization of deformation instability in modified 9Cr–1Mo steel during thermo-mechanical processing. Mater. Des. 2011, 32, 716–722. [Google Scholar] [CrossRef]
- Rao, K.P.; Prasad, Y.V.; Suresh, K.; Hort, N.; Kainer, K.U. Hot deformation behavior of Mg–2Sn–2Ca alloy in as-cast condition and after homogenization. Mater. Sci. Eng. A 2012, 552, 444–450. [Google Scholar] [CrossRef]






| C | Si | Mn | P | S | V | Ni | Cr | Mo | Al | Cu | W | B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.12 | 0.3 | 0.44 | 0.01 | 0.002 | 0.23 | 0.14 | 8.65 | 0.46 | 0.007 | 0.082 | 1.78 | 0.003 |
| Symbol | Definition | Unit |
|---|---|---|
| Ro | radius before strain rate | mm |
| ho | height before strain rate | |
| h | height after strain rate | |
| RM | radius after strain rate |
| Strain Rate(s−1) | Deformation Temperature (°C) | ||||
|---|---|---|---|---|---|
| 250 | 300 | 350 | 400 | 450 | |
| 0.001 | 1.12 | 1.17 | 1.13 | 1.11 | 1.13 |
| 0.01 | 1.14 | 1.21 | 1.18 | 1.15 | 1.11 |
| 0.1 | 1.11 | 1.18 | 1.14 | 1.12 | 1.15 |
| 1 | 1.16 | 1.16 | 1.11 | 1.17 | 1.12 |
| 10 | 1.12 | 1.12 | 1.19 | 1.18 | 1.11 |
| Symbol | Definition | Unit | Numerical Value |
|---|---|---|---|
| Cp | specific heat capacity | J/(g*K) | 0.5 |
| ∫σdε | mechanical power | ||
| ∆ε | strain interval | 0.3/0.5/0.7 | |
| average stress | MPa | ||
| ρ | density of experimental materials | g/cm3 | 7.75 |
| ∆T | temperature rise | ||
| γ | adiabatic factor | 0 (0.001 s−1), 0.25 (0.01 s−1), 0.5 (0.1 s−1), 0.75 (1 s−1), 1(10 s−1) |
| Symbol | Definition | Unit | Numerical Value |
|---|---|---|---|
| σa | Adiabatic-corrected stress | Mpa | |
| σo | origin stress | Mpa | |
| Q’ | constant coefficient | J/mol | 23 |
| R | universal gas constant | J/(mol × K) | 8.5 |
| TD | deformation temperature | K | |
| TR | Thermocouple temperature | K | |
| f | friction coefficient | 0.25 | |
| ro | original radius | mm | 4 |
| ho | original height | mm | 12 |
| e | true deformation |
| Symbol | Definition | Unit |
|---|---|---|
| ε | strain rate | s−1 |
| σ | flow stress | MPa |
| Q | deformation activation energy | J/mol |
| T | absolute temperature | K |
| R | molar gas constant | 8.31 J/(mol*K) |
| A | structural factor | material constant |
| α | stress level parameters | |
| n | stress index |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yu, R.; Xu, G.; Chen, C.; Ha, Y.; Song, L.; Zhang, H. Research on Hot Deformation Behavior of F92 Steel Based on Stress Correction. Metals 2022, 12, 698. https://doi.org/10.3390/met12050698
Li J, Yu R, Xu G, Chen C, Ha Y, Song L, Zhang H. Research on Hot Deformation Behavior of F92 Steel Based on Stress Correction. Metals. 2022; 12(5):698. https://doi.org/10.3390/met12050698
Chicago/Turabian StyleLi, Jinghui, Renhai Yu, Gaoshan Xu, Changhua Chen, Yao Ha, Leijun Song, and Huiping Zhang. 2022. "Research on Hot Deformation Behavior of F92 Steel Based on Stress Correction" Metals 12, no. 5: 698. https://doi.org/10.3390/met12050698






