Hybrid Method for Endpoint Prediction in a Basic Oxygen Furnace
Abstract
:1. Introduction
2. Theory and Methodology
2.1. Nature of the Data
2.2. Formulation of Mass and Energy Balance
2.2.1. Mass Balance
2.2.2. Slag Chemistry Model
- Silicon from hot metal is completely oxidized.
- Weight percentage of CaO in slag is assumed to be the mean from the dataset, which is 51%.
- Coolant added is in the form of pure Fe2O3.
- Injected oxygen is completely consumed.
- All the lime added to the process goes into the slag.
2.2.3. Endpoint Carbon Theoretical Model
2.2.4. Heat Balance and Endpoint Temperature Theoretical Model
- Sulfur is not considered for heat balance.
- Weight percentages of iron and carbon in molten steel are assumed to be their respective medians from the dataset.
- Flux and scrap additions are assumed to be charged at room temperature (25 °C).
- Slag temperature is assumed to be 100 degrees Celsius higher than steel temperature [6].
- Off-gas temperature is assumed to be 1600 °C [6].
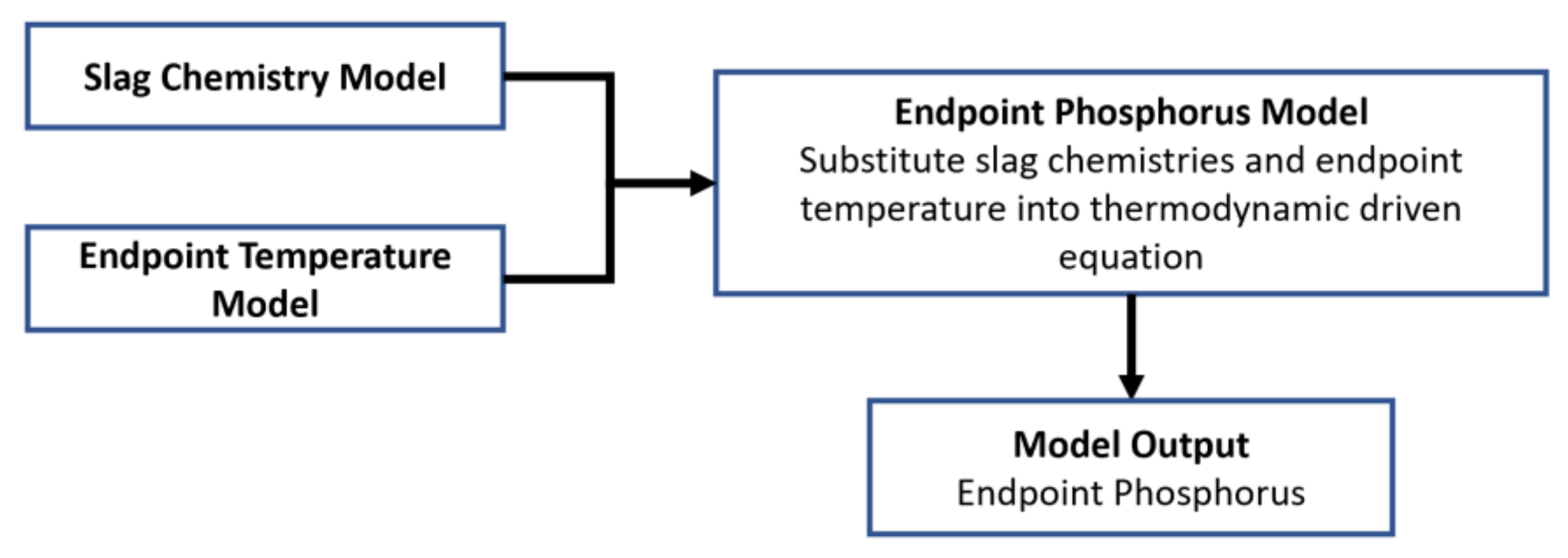
2.2.5. Endpoint Phosphorus Theoretical Model
2.3. Machine Learning Model Formulation
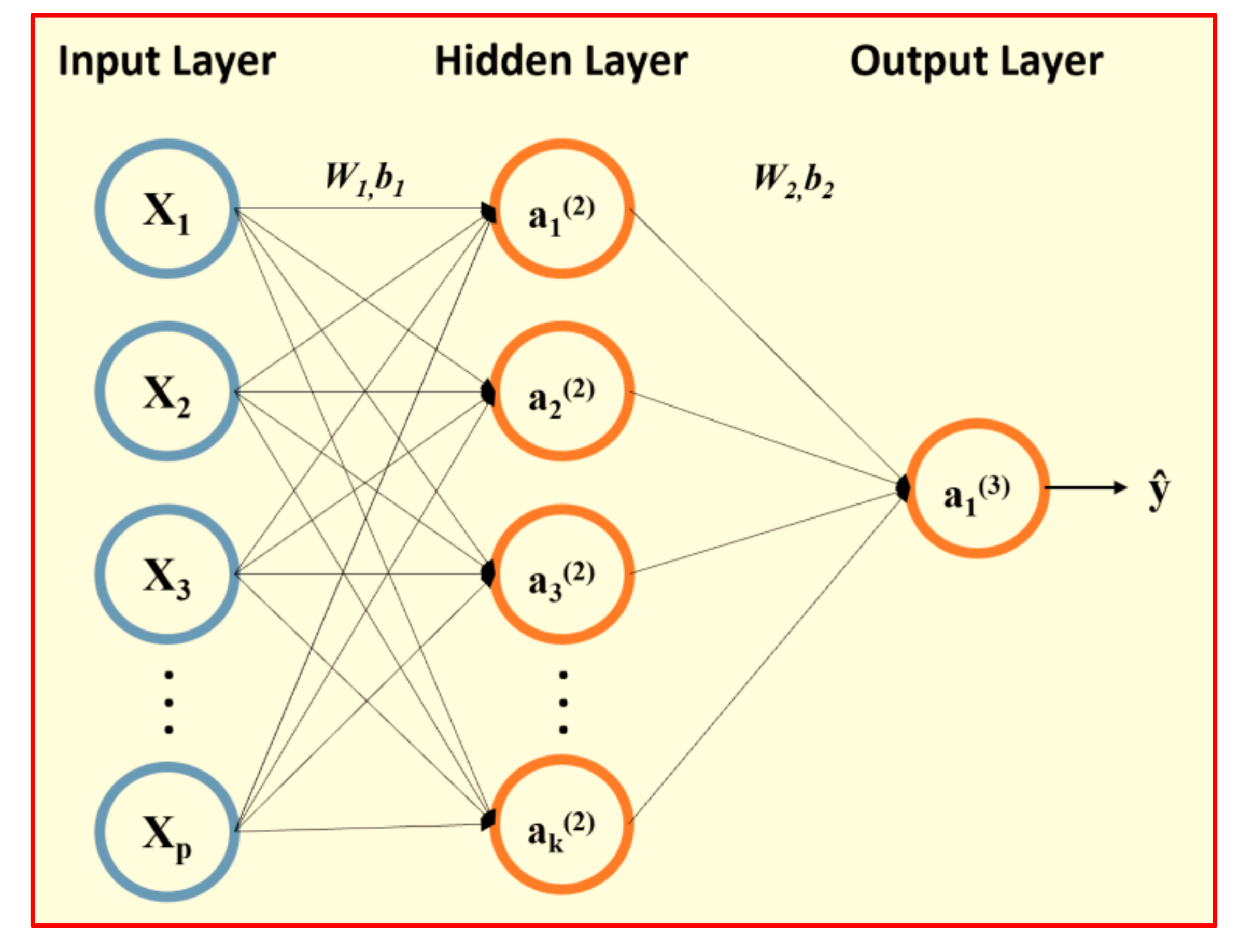
2.3.1. Neural Network
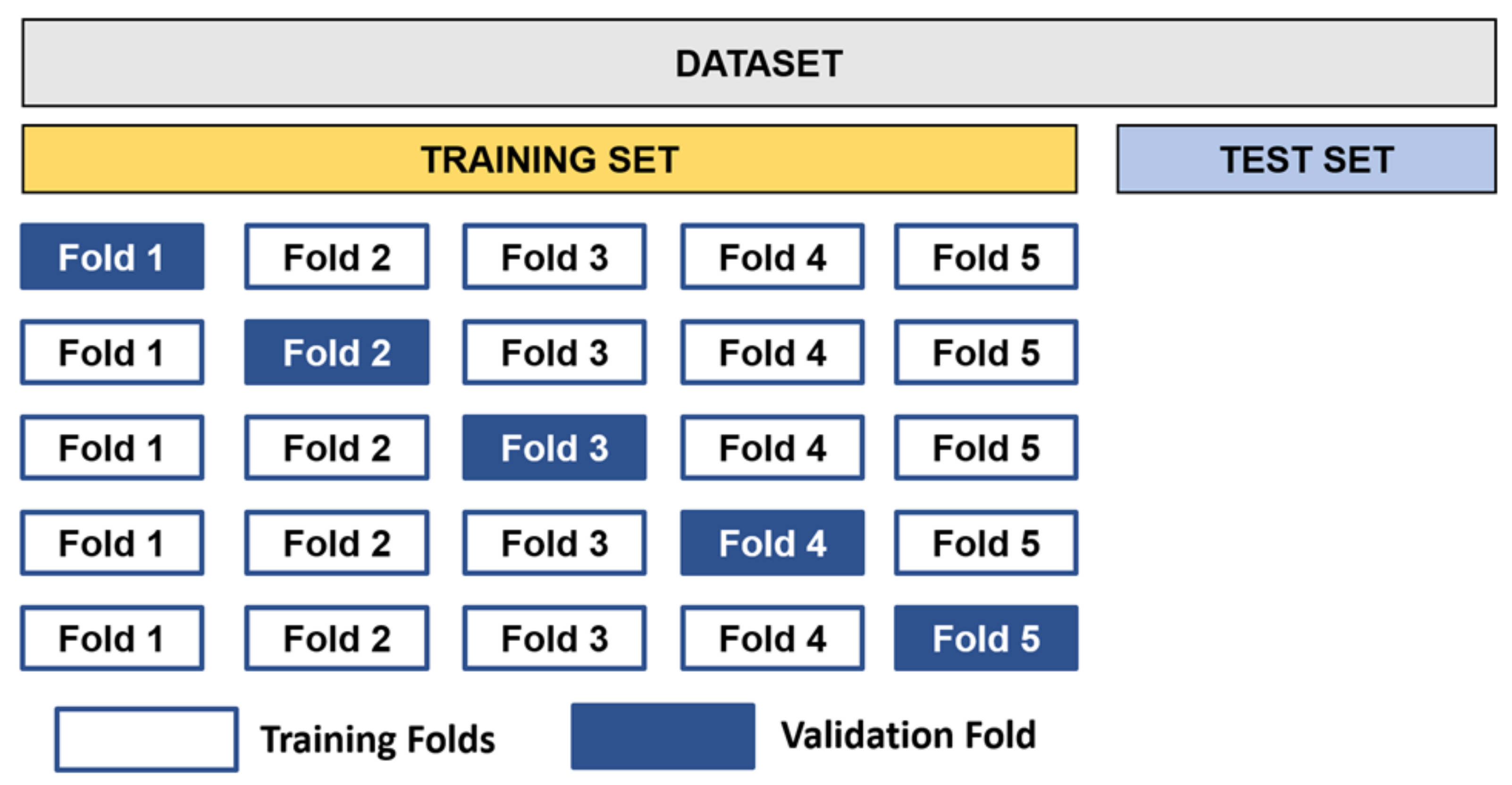
2.3.2. Model Adequacy
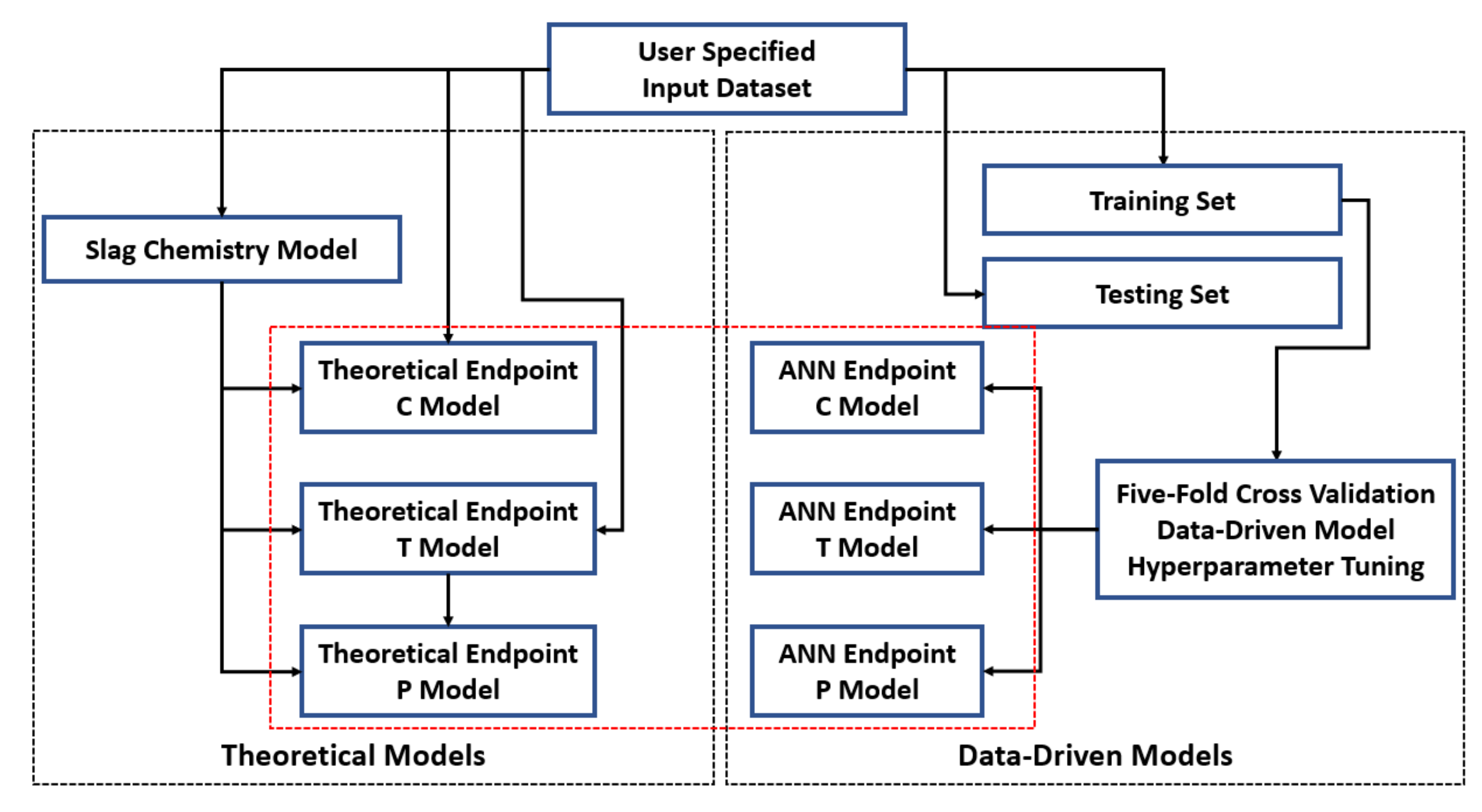
2.4. Hybrid Model Formulation
- User-specified inputs, such as hot metal chemistries, process parameters, and flux additions, were fed into the slag chemistry model. The results of “User Inputs” and “MM_S” corresponds to the input feature space that is used for model developments.
- Theoretical models for endpoint carbon and temperature (MM_C and MM_T) were established by formulating mass and energy balance based on the input features from step 1.
- Theoretical model for endpoint phosphorus (MM_P) was created based on slag chemistries from MM_S and endpoint temperature prediction from MM_T. Thermodynamic driven regression models [M1]–[M6] were tested against each other.
- Three ANN networks were established by using user inputs, and hyperparameter tuning was conducted with five-fold cross-validation.
- Endpoint carbon prediction from ANN_C was substituted as the endpoint carbon into MM_T to formulate mass balance. The assumption of using the median of endpoint carbon from dataset was discarded.
- Since endpoint phosphorus is heavily dependent on turndown temperature, endpoint temperature prediction from ANN_T was substituted into MM_P and ANN_P.
- Finally, endpoint phosphorus from ANN_P was substituted into MM_C and MM_T to complete the formulation of mass balance.

3. Results
3.1. Theoretical Phosphorus Model Validation
3.2. Theoretical Model Results
3.3. ANN Model Hyperparamter Selection
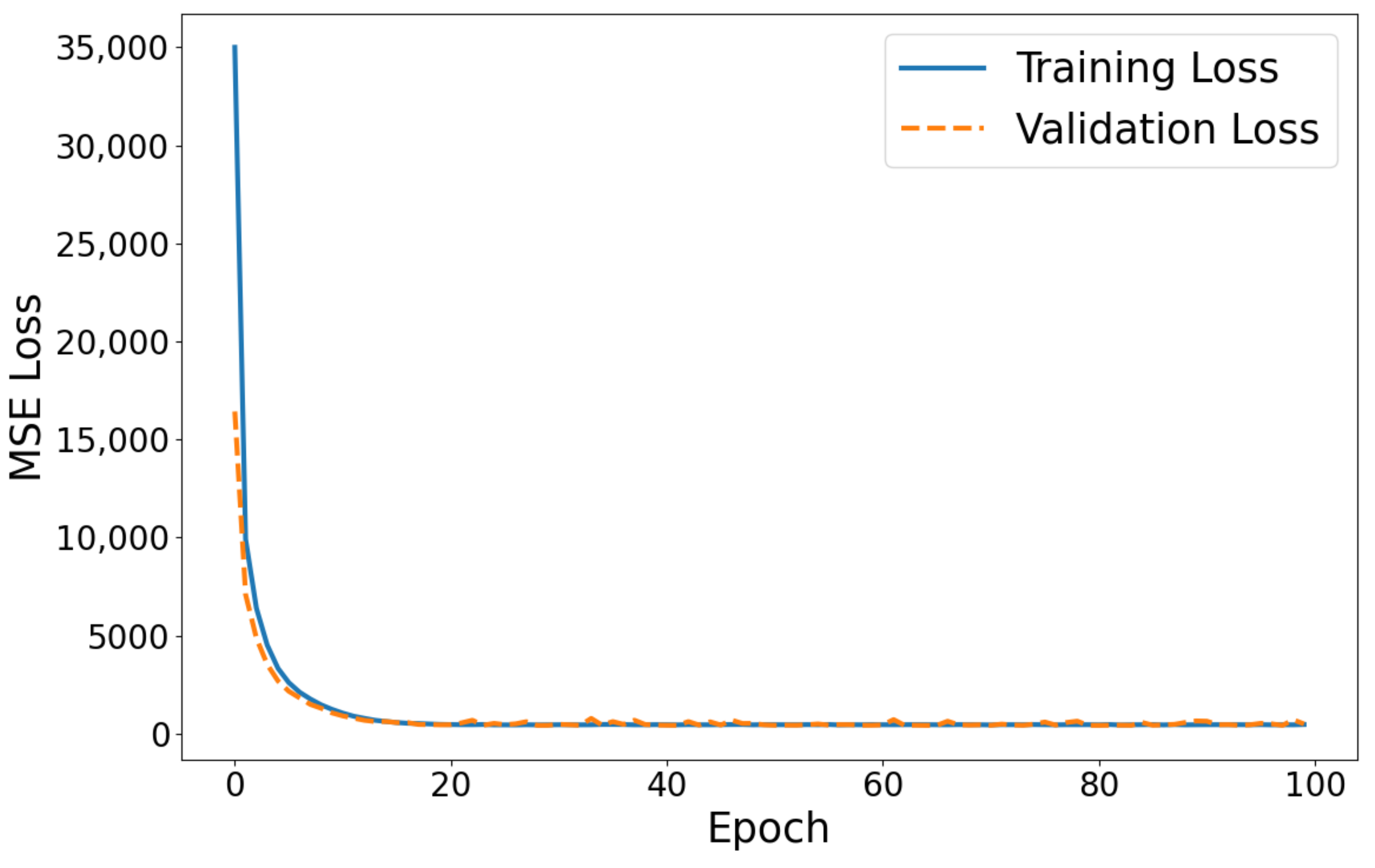
3.4. ANN Model Results
3.5. Hybrid Model Results
4. Discussion and Interpretation of Results
4.1. Hybrid Model Algorithm Performance and Comparison
4.2. Application of the Results and Models for Industry
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghosh, A.; Chatterjee, A. Ironmaking and Steelmaking: Theory and Practice; PHI Leanring Private Limited: New Delhi, India, 2008. [Google Scholar]
- Wang, X.; Han, M.; Wang, J. Applying input variables selection technique on input weighted support vector machine modeling for BOF endpoint prediction. Eng. Appl. Artif. Intell. 2010, 23, 1012–1018. [Google Scholar] [CrossRef]
- Iron Ore Monthly Price—US Dollars per Dry Metric Ton. Available online: https://www.indexmundi.com/commodities/?commodity=iron-ore (accessed on 15 November 2021).
- Bloom, T.A.; Fosnacht, D.R.; Haezebrouck, D.M. Influence of phosphorus on the properties of sheet steel products and methods used to control steel phosphorus levels in steel product Manufacturing. Part I. Iron Steelmak. 1990, 17, 35–41. [Google Scholar]
- Han, M.; Liu, C. Endpoint prediction model for basic oxygen furnace steel-making based on membrane algorithm evolving extreme learning machine. Appl. Soft Comput. J. 2014, 19, 430–437. [Google Scholar] [CrossRef]
- Xu, L.F.; Li, W.; Zhang, M.; Xu, S.X.; Li, J. A model of basic oxygen furnace (BOF) end-point prediction based on spectrum information of the furnace flame with support vector machine (SVM). Opt.-Int. J. Light Electron Opt. 2011, 122, 594–598. [Google Scholar] [CrossRef]
- Xu, L.; Li, W.; Xu, S.; Li, J.; Wang, Y. A new spectral analysis technique used in converter steelmaking BOF endpoint control. Adv. Mater. Res. 2010, 139–141, 689–692. [Google Scholar] [CrossRef]
- Iida, Y.; Emoto, K.; Ogawa, M.; Masuda, Y.; Onishi, M.; Yamada, H. Fully Automatic Blowing Technique for Basic Oxygen Steelmaking Furnace. Trans. Iron Steel Inst. Jpn. 1984, 24, 540–546. [Google Scholar] [CrossRef]
- Li, S.; Wei, X.; Yu, L. Numerical simulation of off-gas formation during top-blown oxygen converter steelmaking. Fuel 2011, 90, 1350–1360. [Google Scholar] [CrossRef] [Green Version]
- Cunha, A.P.; Pacianotto, T.A.; Frattini Fileti, A.M. Steelmaking process: Neural models improve end-point predictions. Comput. Aided Chem. Eng. 2004, 18, 631–636. [Google Scholar] [CrossRef]
- Philbrook, W.O. Thermochemistry of oxygen steel. JOM 1958, 10, 477–482. [Google Scholar] [CrossRef]
- Slatosky, W.J. End point temperature control in LD steelmaking. JOM 1960, 12, 226–230. [Google Scholar] [CrossRef]
- Meyer, H.W.; Dukelow, D.A.; Fischer, M.M. Static and dynamic control of the basic oxygen process. JOM 1964, 16, 501–507. [Google Scholar] [CrossRef]
- Neto, L.C. End-Blow Model for Control of LD Converters and Statistic Analysis of Its Performance. Master’s Thesis, Federal University of Minas Gerais, Belo Horizonte, Brazil, 1981. [Google Scholar]
- Fruehan, R.; Fortini, O.; Paxton, H. Theoretical Minimum Energies to Produce Steel for Selected Conditions; USDOE Office of Industrial Technologies: Washington, DC, USA, March 2000; Available online: http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:Theoretical+Minimum+Energies+To+Produce+Steel+for+Selected+Conditions#1 (accessed on 10 February 2022).
- Madhavan, N.; Brooks, G.A.; Rhamdhani, M.A.; Rout, B.K.; Overbosch, A. General heat balance for oxygen steelmaking. J. Iron Steel Res. Int. 2021, 28, 538–551. [Google Scholar] [CrossRef]
- Madhavan, N.; Brooks, G.A.; Rhamdhani, M.A.; Rout, B.K.; Overbosch, A. Application of mass and energy balance in oxygen steelmaking. Ironmak. Steelmak. 2021, 48, 995–1000. [Google Scholar] [CrossRef]
- Balajiva, K.; Quarrell, A.; Vajragupta, P. A laboratory investigation of the phosphorus reaction in the basic steelmaking process. J. Iron Steel Inst. 1946, 153, 115. [Google Scholar]
- Suito, H.; Inoue, R. Thermodynamic assesment of hot metal and steeel dephosphorization with MnO-containing BOF slags. ISIJ Int. 1995, 35, 258–265. [Google Scholar] [CrossRef] [Green Version]
- Healy, G. New look at phosphorus distribution. J. Iron Steel Inst. 1970, 208, 664–668. [Google Scholar]
- Ide, K.; Fruehan, R.J. Evaluation of phosphorus reaction equilibrium in steelmaking. Iron Steelmak. 2000, 27, 65–70. [Google Scholar]
- IKEDA, T.; MATSUO, T. The dephosphorization of hot metal outside the steelmaking furnace. Trans. Iron Steel Inst. Jpn. 1982, 22, 495–503. [Google Scholar] [CrossRef] [Green Version]
- Ito, Y.; Sato, S.; Kawachi, Y.; Tezuka, H. Dephosphorization in LD converter with low Si hot metal-develop of minimum slag practice. Tetsu-Hagane 1979, 63, S737. [Google Scholar]
- Kawai, Y.; Takahashi, I.; Miyashita, Y.; Tachibana, K. For dephosphorization equilibrium between slag and molten steel in the converter furnace. Tetsu-Hagane 1977, 63, S156. [Google Scholar]
- Sipos, K.; Alvez, E. Dephosphorization in BOF Steelmaking. In Proceedings of the Molten 2009: VIII International Conference on Molten Slags, Fluxes and Salts, Santiago, Chile, 18–21 January 2009; GECAMIN: Santiago, Chile, 2009; pp. 1023–1030. [Google Scholar]
- Lee, C.M.; Fruehan, R.J. Phosphorus equilibrium between hot metal and slag. Ironmak. Steelmak. 2005, 32, 503–508. [Google Scholar] [CrossRef]
- Ogawa, Y.; Yano, M.; Kitamura, S.; Hirata, H. Development of the continuous dephosphorization and decarburization process using BOF. Tetsu-Hagane 2001, 87, 21–28. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, R.; Gupta, P.; Basu, S.; Ballal, N.B. Dynamic Modeling of LD Converter Steelmaking: Reaction Modeling Using Gibbs’ Free Energy Minimization. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2015, 46, 961–976. [Google Scholar] [CrossRef]
- Biswas, J.; Ghosh, S.; Ballal, N.B.; Basu, S. A Dynamic Mixed-Control Model for BOF Metal–Slag–Gas Reactions. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2021, 52, 1309–1321. [Google Scholar] [CrossRef]
- Barui, S.; Mukherjee, S.; Srivastavs, A.; Chattopadhyay, K. Understanding dephosphorization in basic oxygen furnaces (BOFs) Using Data-driven Modeling Techniques. Metals 2019, 9, 955. [Google Scholar] [CrossRef] [Green Version]
- Phull, J.; Egas, J.; Barui, S.; Mukherjee, S.; Chattopadhyay, K. An application of decision tree-based twin support vector machines to classify dephosphorization in bof steelmaking. Metals 2020, 10, 25. [Google Scholar] [CrossRef] [Green Version]
- Li, J.N.; Li, Y.; Liu, F.; Bie, S.P.; Tang, C.C.; Zhang, X.L. Modeling of BOF steelmaking based on the data-driven approach. Adv. Mater. Res. 2013, 818, 92–97. [Google Scholar] [CrossRef]
- Wang, H.; Cai, J.; Feng, K. Predicting the Endpoint Phosphorus Content of Molten Steel in BOF by Two-stage Hybrid Method. J. Iron Steel Res. Int. 2014, 21, 65–69. [Google Scholar] [CrossRef]
- Feng, K.; Xu, A.J.; He, D.F.; Yang, L. Case-based reasoning method based on mechanistic model correction for predicting endpoint sulphur content of molten iron in KR desulphurization. Ironmak. Steelmak. 2020, 47, 799–806. [Google Scholar] [CrossRef]
- Hu, Y.; Zheng, Z.; Yang, J. Application of data mining in BOF steelmaking endpoint control. Adv. Mater. Res. 2012, 402, 96–99. [Google Scholar] [CrossRef]
- Han, M.; Jiang, L. Endpoint prediction model of basic Oxygen furnace steelmaking based on PSO-ICA and RBF neural network. In Proceedings of the 2010 International Conference on Intelligent Control and Information Processing, Dalian, China, 13–15 August 2010; pp. 388–393. [Google Scholar] [CrossRef]
- Laha, D.; Ren, Y.; Suganthan, P.N. Modeling of steelmaking process with effective machine learning techniques. Expert Syst. Appl. 2015, 42, 4687–4696. [Google Scholar] [CrossRef]
- Rahnama, A.; Li, Z.; Sridhar, S. Machine learning-based prediction of a BOS reactor performance from operating parameters. Processes 2020, 8, 371. [Google Scholar] [CrossRef] [Green Version]
- Cai, B.Y.; Zhao, H.; Yue, Y.J. Research on the BOF steelmaking endpoint temperature prediction. In Proceedings of the 2011 International Conference on Mechatronic Science, Electric Engineering and Computer (MEC), Jilin, China, 19–22 August 2011; pp. 2278–2281. [Google Scholar] [CrossRef]
- Fruehan, R.J.; Matway, R.J. Optimization of post combustion in steelmaking. In Office of Scientific & Tefchnical Information Technical Reports; American Iron and Steel Institute: Washington, DC, USA, 2004. [Google Scholar]
- Chen, E.; Coley, K.S. Kinetic study of droplet swelling in BOF steelmaking. Ironmak. Steelmak. 2010, 37, 541–545. [Google Scholar] [CrossRef]
- Selin, R. Studies on the MgO solubility in complex steelmaking slags in equilibrium with liquid iron and distribution of phosphorus and vanadium between slag and metal at MgO saturation. In Proceedings of the 3rd International Conference on Molten Slags and Fluxes, Glasgow, UK, 27–29 June 1988; pp. 317–322. [Google Scholar]
- Schurmann, E.; Fischer, H. Effect of composition and temperature of metal and slag on the dephosphorization with lime-saturated oxidizing slags at 1600 and 1700C. Steel Res. 1991, 62, 303–313. [Google Scholar]
- Bergman, A.; Gustafsson, A. Use of optical basicity to calculate phosphorus and oxygen contents in molten iron. In Proceedings of the 3rd International Conference on Molten Slags and Fluxes1, Glasgow, UK, 27–29 June 1988; pp. 150–153. [Google Scholar]





| Feature Category | Variable | Mean | Standard Deviation |
|---|---|---|---|
| Endpoints | Endpoint T | 1649.1 | 22.2 |
| Endpoint C | 0.044 | 0.013 | |
| Endpoint P | 0.0163 | 0.006 | |
| Hot Metal Chemistries | HM C | 4.556 | 0.066 |
| HM P | 0.176 | 0.015 | |
| HM S | 0.023 | 0.018 | |
| HM Mn | 0.043 | 0.006 | |
| HM Si | 0.641 | 0.162 | |
| HM Ti | 0.069 | 0.015 | |
| HM Cr | 0.009 | 0.005 | |
| Flux Additions | Lime | 8.507 | 1.345 |
| Dolomite | 3.656 | 0.698 | |
| Iron Ore | 6.596 | 2.004 | |
| Scrap | 10.606 | 6.616 | |
| Process Parameters | HM Weight | 163.9 | 7.0 |
| HM Temperature | 1362.1 | 31.8 | |
| Oxygen Volume | 7807.6 | 408.9 | |
| Blow Duration | 17.85 | 1.66 | |
| Blow End to Turndown Start Duration | 3.52 | 1.91 | |
| Blow End to Tapping Start Duration | 8.47 | 7.63 | |
| Tapping Duration | 5.5 | 1.99 |
| Feature Category | Variable |
|---|---|
| Hot Metal Chemistries | HM C |
| HM P | |
| HM S | |
| HM Mn | |
| HM Si | |
| Flux Additions | Lime |
| Dolomite | |
| Iron Ore | |
| Scrap |
| Model | Equation |
|---|---|
| M1 [41] | |
| M2 [30] | |
| M3 [42] | |
| M4 [43] | |
| M5 [4] | |
| M6 [44] |
| Feature Category | Feature Name |
|---|---|
| Hot Metal Chemistries | Hot Metal Carbon |
| Hot Metal Sulfur | |
| Hot Metal Silicon | |
| Hot Metal Manganese | |
| Hot Metal Phosphorus | |
| Hot Metal Chromium | |
| Hot Metal Titanium | |
| Process Parameters | Oxygen Blow Duration |
| Blow End to Turndown Start Duration | |
| Blow End to Tapping Start Duration | |
| Tapping Duration | |
| Blowing Strategy | |
| Injected Oxygen Volume | |
| Hot Metal Weight | |
| Hot Metal temperature | |
| Flux Additions | Limestone |
| Dolomite | |
| Iron Ore | |
| Scrap |
| Model Type | Predicted Endpoint | Abbreviation |
|---|---|---|
| Theoretical Models | Slag Chemistries | MM_S |
| Endpoint Temperature | MM_T | |
| Endpoint Carbon | MM_C | |
| Endpoint Phosphorus | MM_P | |
| Data-Driven Technique (ANN) | Endpoint Temperature | ANN_T |
| Endpoint Carbon | ANN_C | |
| Endpoint Phosphorus | ANN_P |
| Model Name | MM_T | MM_C | MM_P |
|---|---|---|---|
| RMSE | 53.58 | 0.0135 | 0.00695 |
| Range of Endpoint | 100 | 0.1 | 0.032 |
| Normalized RMSE | 0.536 | 0.135 | 0.217 |
| Hyperparameters | Starting Value | Increment | End Value | Selected Parameter | ||
|---|---|---|---|---|---|---|
| ANN_T | ANN_C | ANN_P | ||||
| Number of Neurons | 16 | 16 | 64 | 32 | 32 | 32 |
| Number of Layers | 1 | 1 | 3 | 2 | 2 | 2 |
| Batch Size | 16 | 16 | 64 | 32 | 64 | 32 |
| Learning Rate | 0.005 | 0.005 | 0.02 | 0.01 | 0.005 | 0.005 |
| Model Name | ANN_T | ANN_C | ANN_P |
|---|---|---|---|
| Training RMSE | 21.36 | 0.0127 | 0.00553 |
| Validation RMSE | 21.49 | 0.0129 | 0.00575 |
| Validation NRMSE | 0.215 | 0.129 | 0.1796 |
| Model Name | MM_T | MM_C | MM_P | ANN_P |
|---|---|---|---|---|
| RMSE | 53.07 | 0.0130 | 0.0063 | 0.005680 |
| NRMSE (With Hybrid) | 0.531 | 0.130 | 0.196 | 0.1775 |
| NRMSE (Without Hybrid) | 0.536 | 0.135 | 0.217 | 0.1796 |
| Improvement | 1.12% | 3.7% | 9.77% | 1.17% |
| Model Name | MM_T | MM_C | MM_P | ANN_P | ANN_T | ANN_C |
|---|---|---|---|---|---|---|
| NRMSE (With Hybrid) | 0.531 | 0.130 | 0.196 | 0.1775 | 0.215 | 0.129 |
| NRMSE (Without Hybrid) | 0.536 | 0.135 | 0.217 | 0.1796 | / | / |
| Improvement | 1.12% | 3.7% | 9.77% | 1.17% | / | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Mohanty, I.; Srivastava, A.; Roy, T.K.; Gupta, P.; Chattopadhyay, K. Hybrid Method for Endpoint Prediction in a Basic Oxygen Furnace. Metals 2022, 12, 801. https://doi.org/10.3390/met12050801
Wang R, Mohanty I, Srivastava A, Roy TK, Gupta P, Chattopadhyay K. Hybrid Method for Endpoint Prediction in a Basic Oxygen Furnace. Metals. 2022; 12(5):801. https://doi.org/10.3390/met12050801
Chicago/Turabian StyleWang, Ruibin, Itishree Mohanty, Amiy Srivastava, Tapas Kumar Roy, Prakash Gupta, and Kinnor Chattopadhyay. 2022. "Hybrid Method for Endpoint Prediction in a Basic Oxygen Furnace" Metals 12, no. 5: 801. https://doi.org/10.3390/met12050801
APA StyleWang, R., Mohanty, I., Srivastava, A., Roy, T. K., Gupta, P., & Chattopadhyay, K. (2022). Hybrid Method for Endpoint Prediction in a Basic Oxygen Furnace. Metals, 12(5), 801. https://doi.org/10.3390/met12050801






