Effect of Batch Dissimilarity on Permeability of Stacked Ceramic Foam Filters and Incompressible Fluid Flow: Experimental and Numerical Investigation
Abstract
1. Introduction
2. Materials and Method
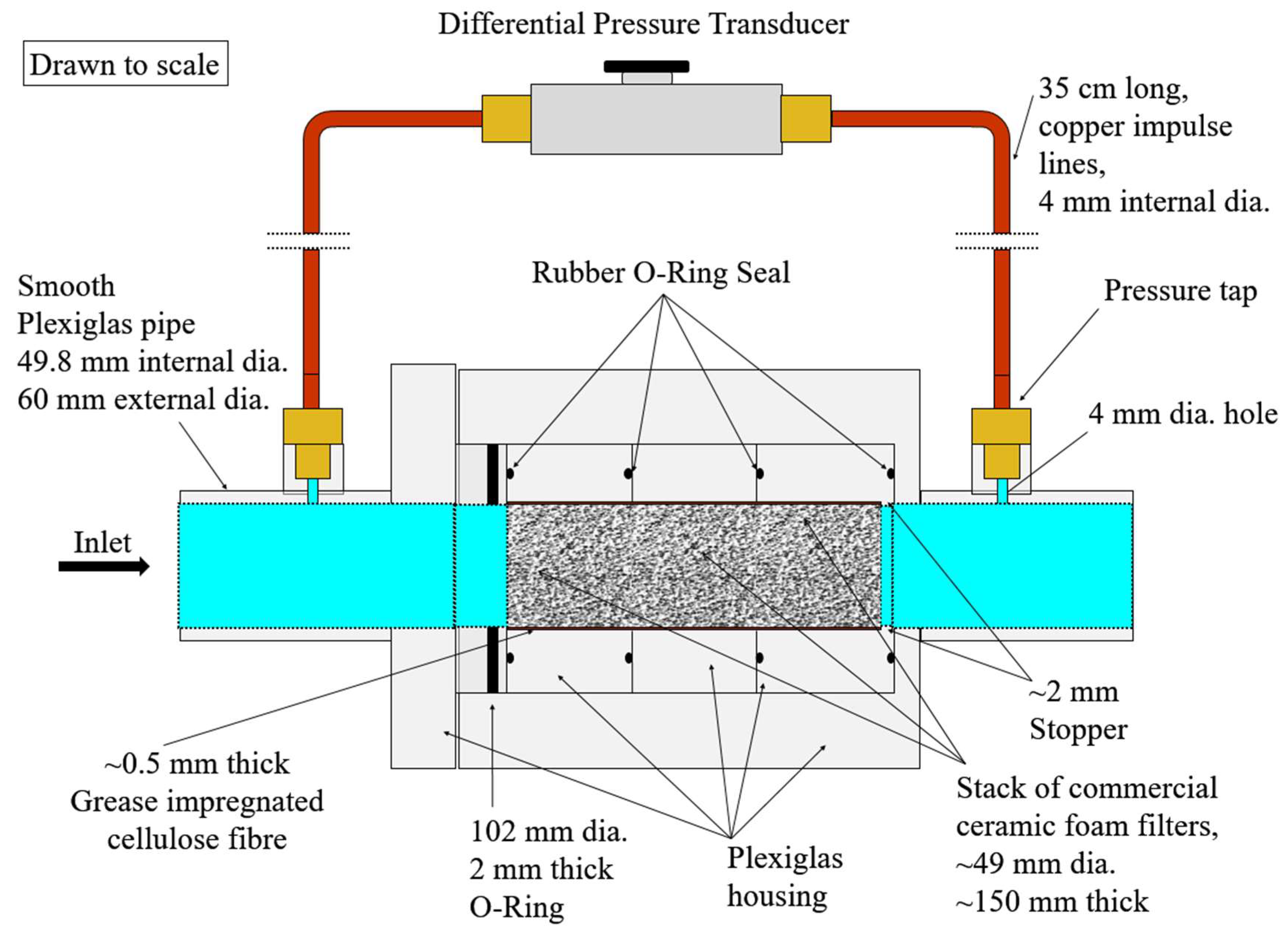
2.1. Liquid Permeability Experiments
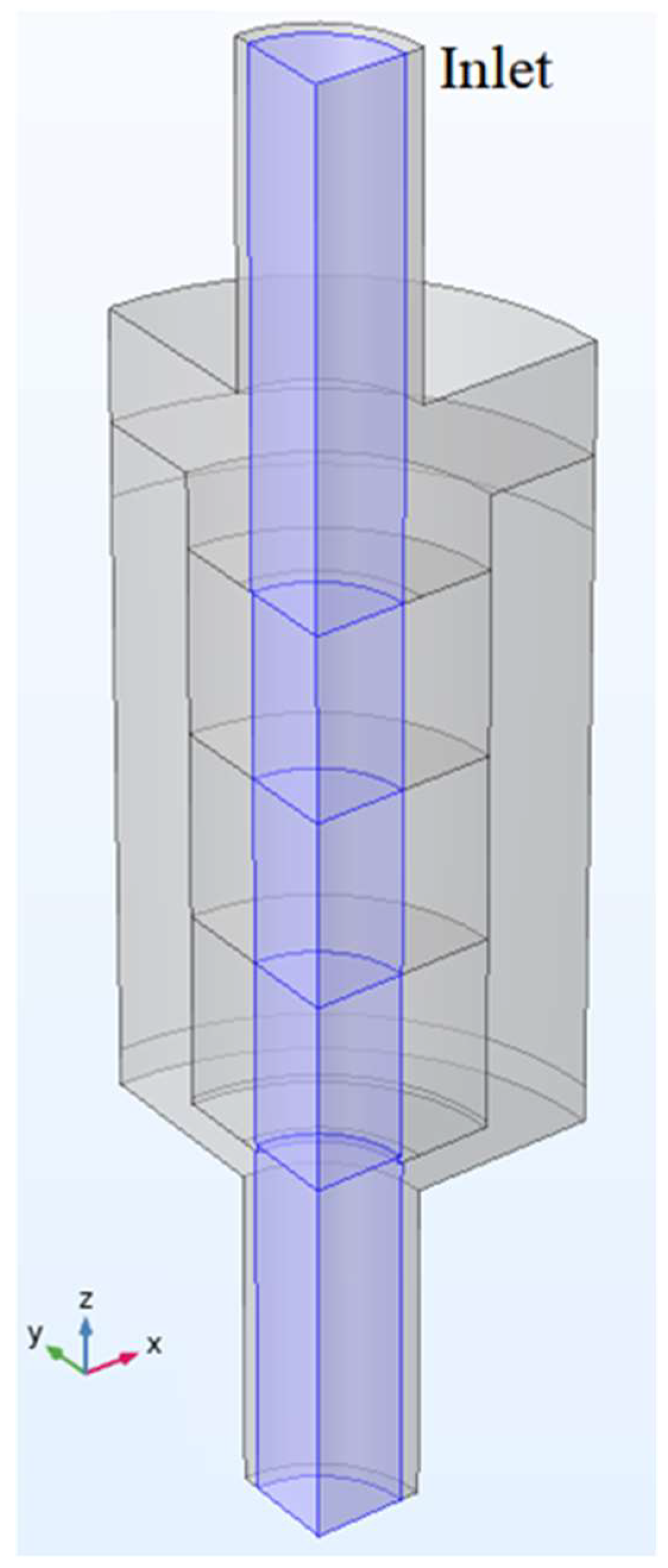
2.2. Numerical Modelling
2.2.1. Assumptions
- The solution is independent of time, i.e., a stationary solution with initialization was used;
- The solution is identical in all quarters of the model, i.e., the simulated experimental apparatus;
- The filters have perfectly cylindrical shapes;
- The fluid temperature, density and dynamic viscosity are constant;
- The pipe surface is smooth, which is expressed by using a no-slip boundary condition;
- Gravitational force is not considered (note that, in the experiment, the filters were positioned horizontally).
2.2.2. Transport Equations
- The Reynolds-averaged Navier–Stokes (RANS) equations for incompressible fluids, including the continuity and conservation of momentum equations;
- The Brinkman–Forchheimer equation, together with the continuity equation, for calculating the flow in the porous domains;
- An algebraic equation to model turbulence.
2.2.3. The Reynolds-Averaged Navier–Stokes (RANS) Equations
2.2.4. Brinkman–Forchheimer Equation
2.2.5. Boundary Conditions
3. Results
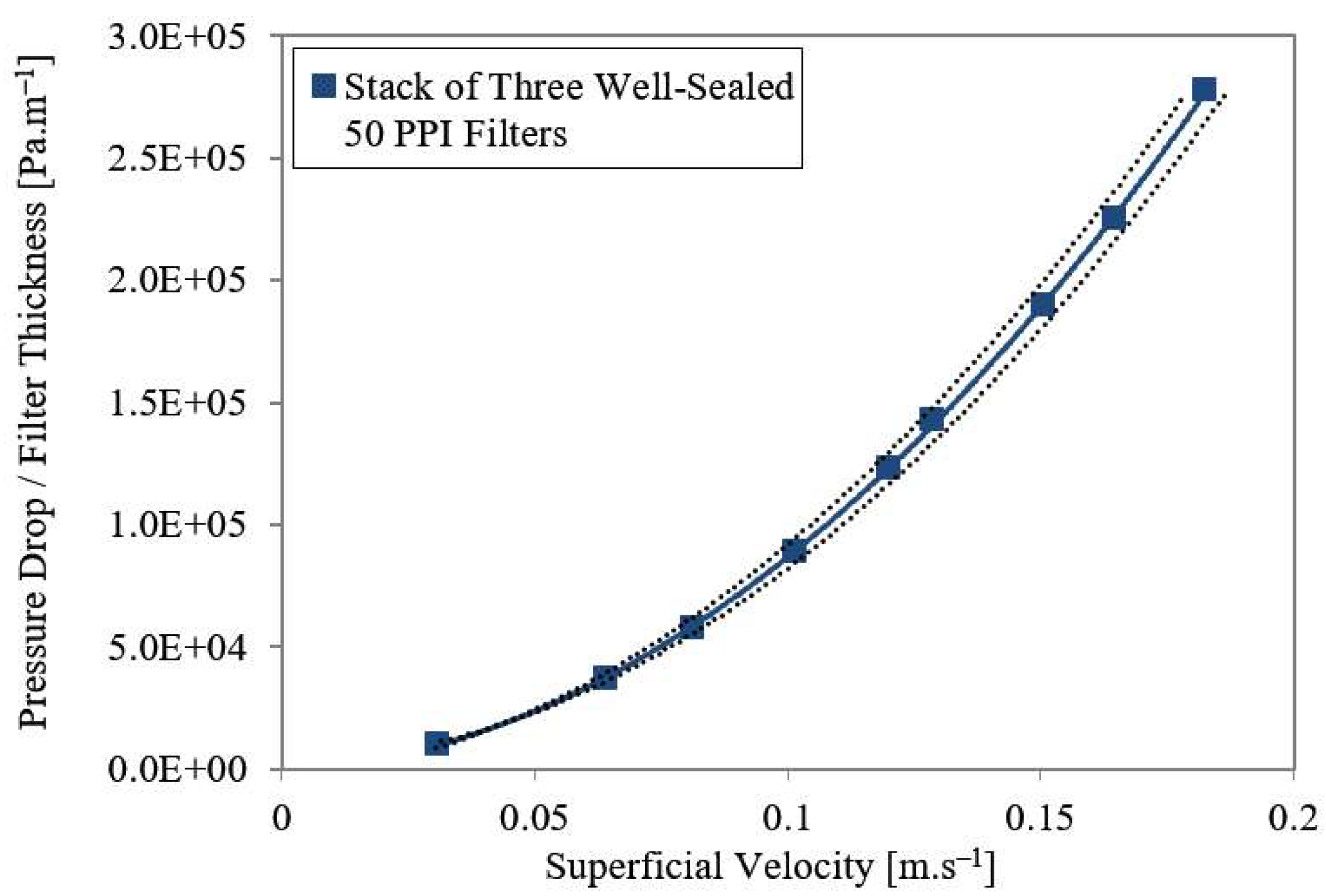
3.1. Liquid Permeability Experiments
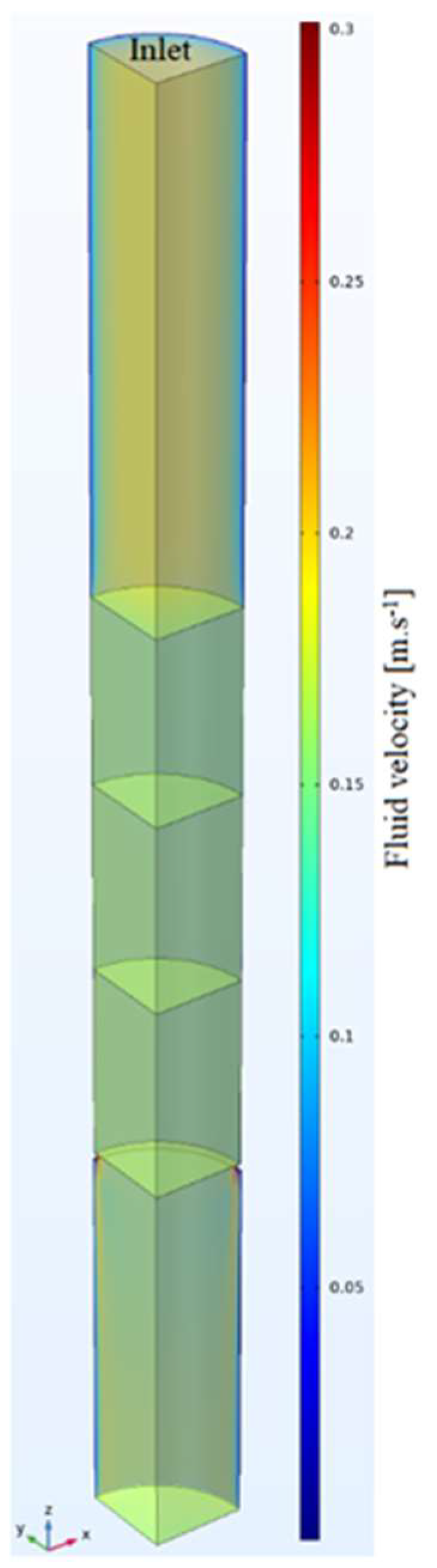
3.2. Numerical Modelling
4. Discussion
5. Conclusions
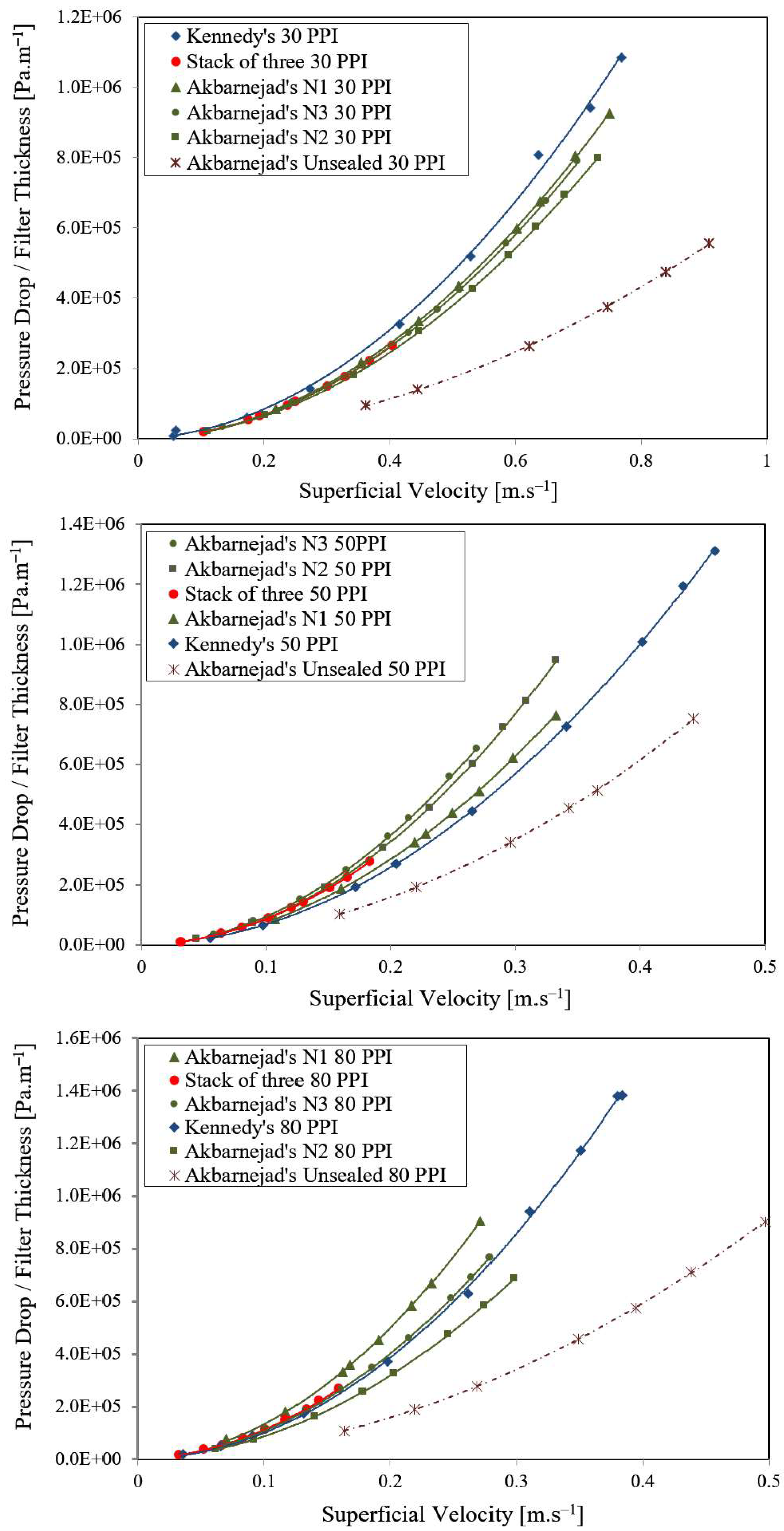
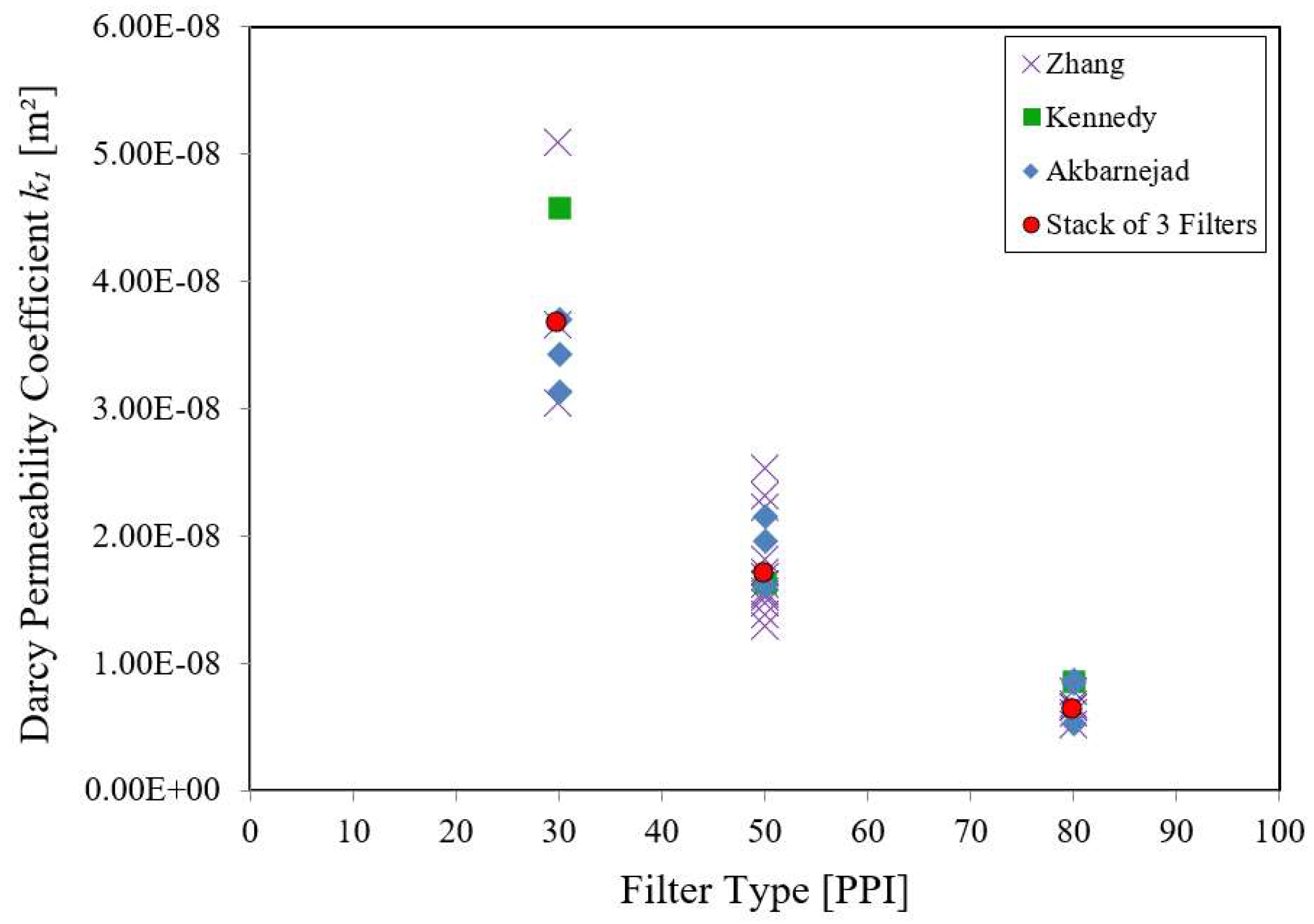
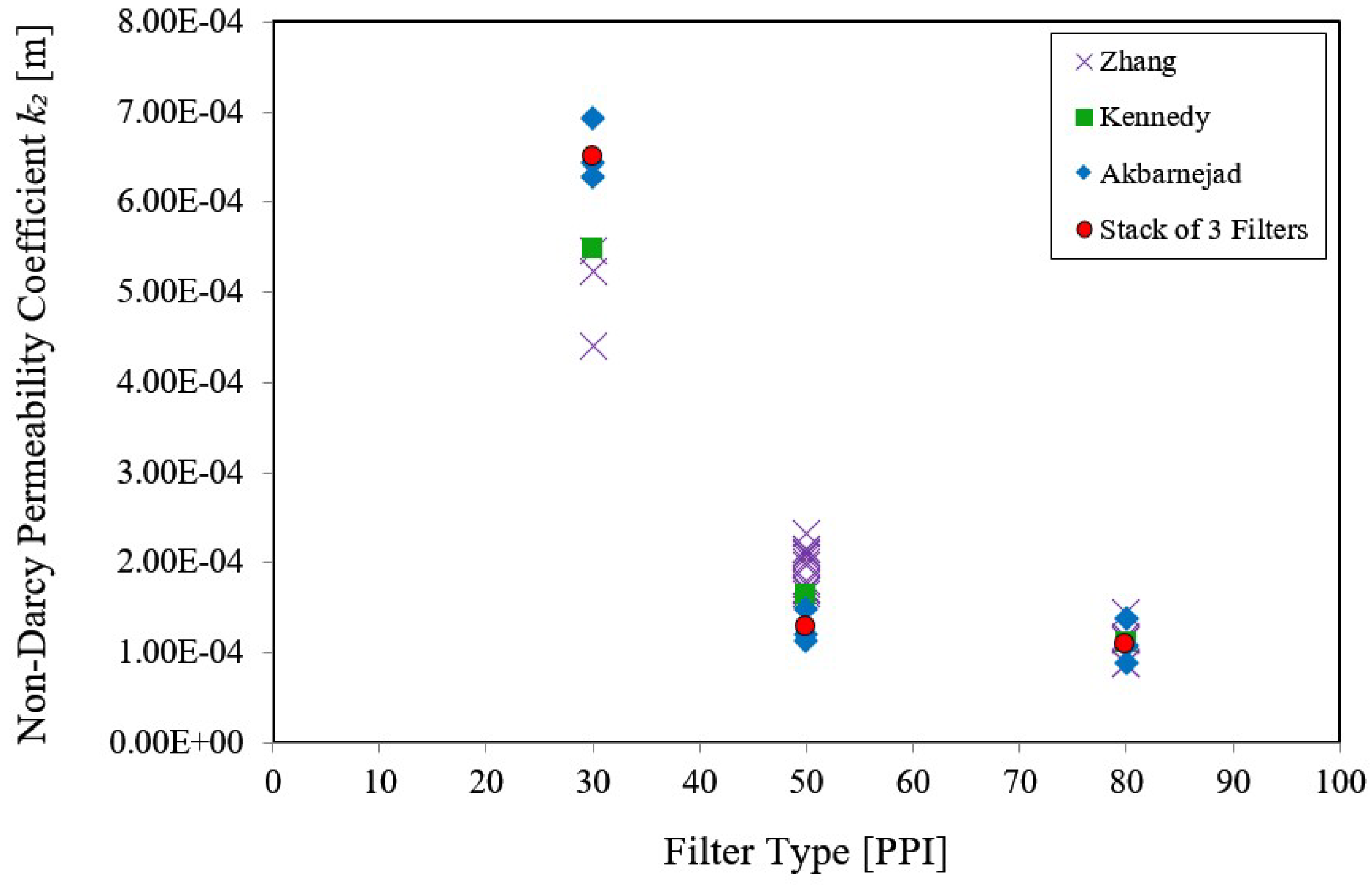
- Stacks of three identical filters from three different batches give substantially the same experimentally obtained pressure gradients as single filters. Therefore, nearly identical Darcy (k1) and non-Darcy (k2) coefficients for a single alumina ceramic foam filter can be empirically obtained;
- As expected, about three times greater pressure and/or pressure drop is required to make the fluid travel through the fully sealed stacked filters of the same PPI compared to an identical single filter;
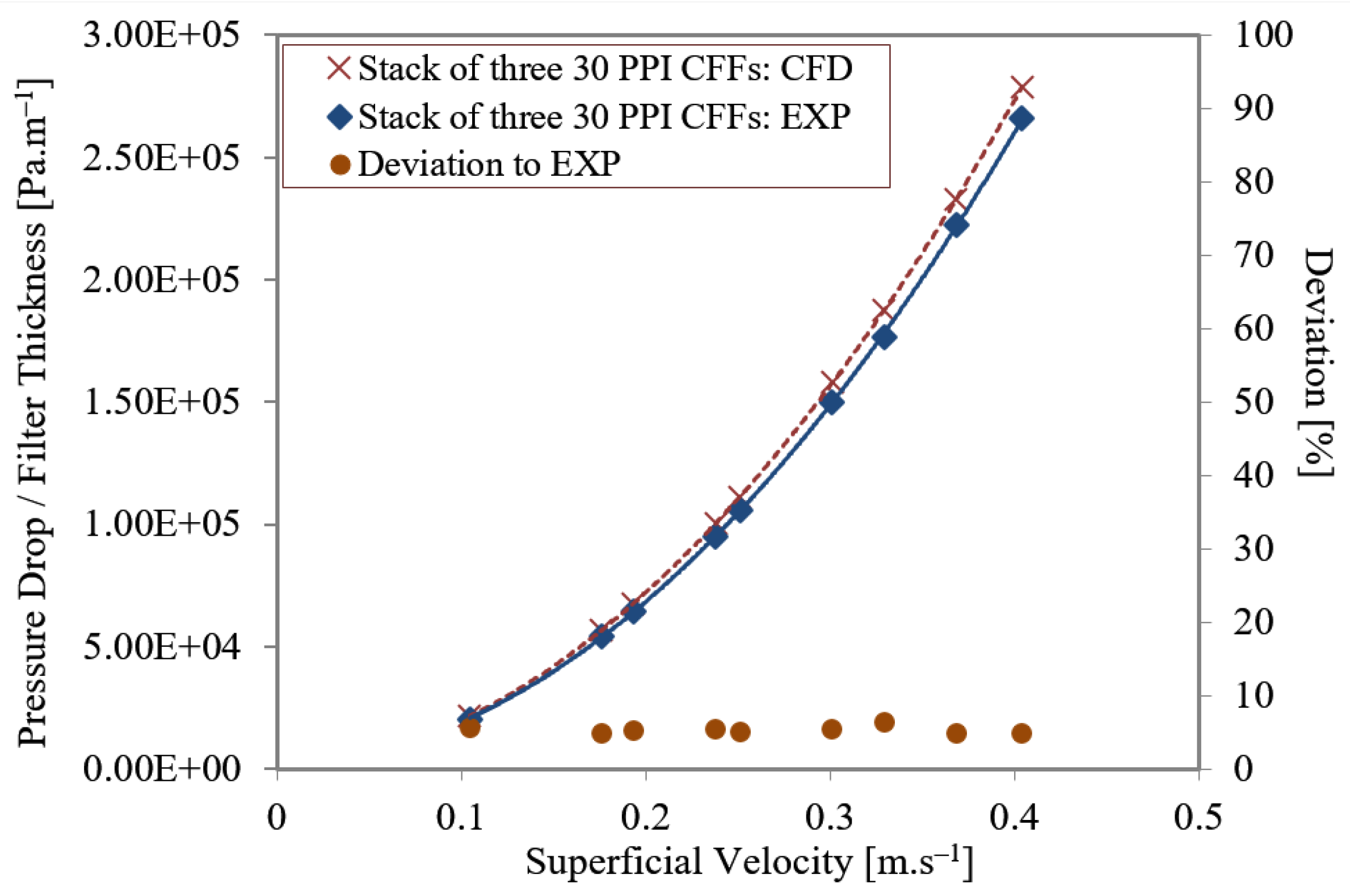
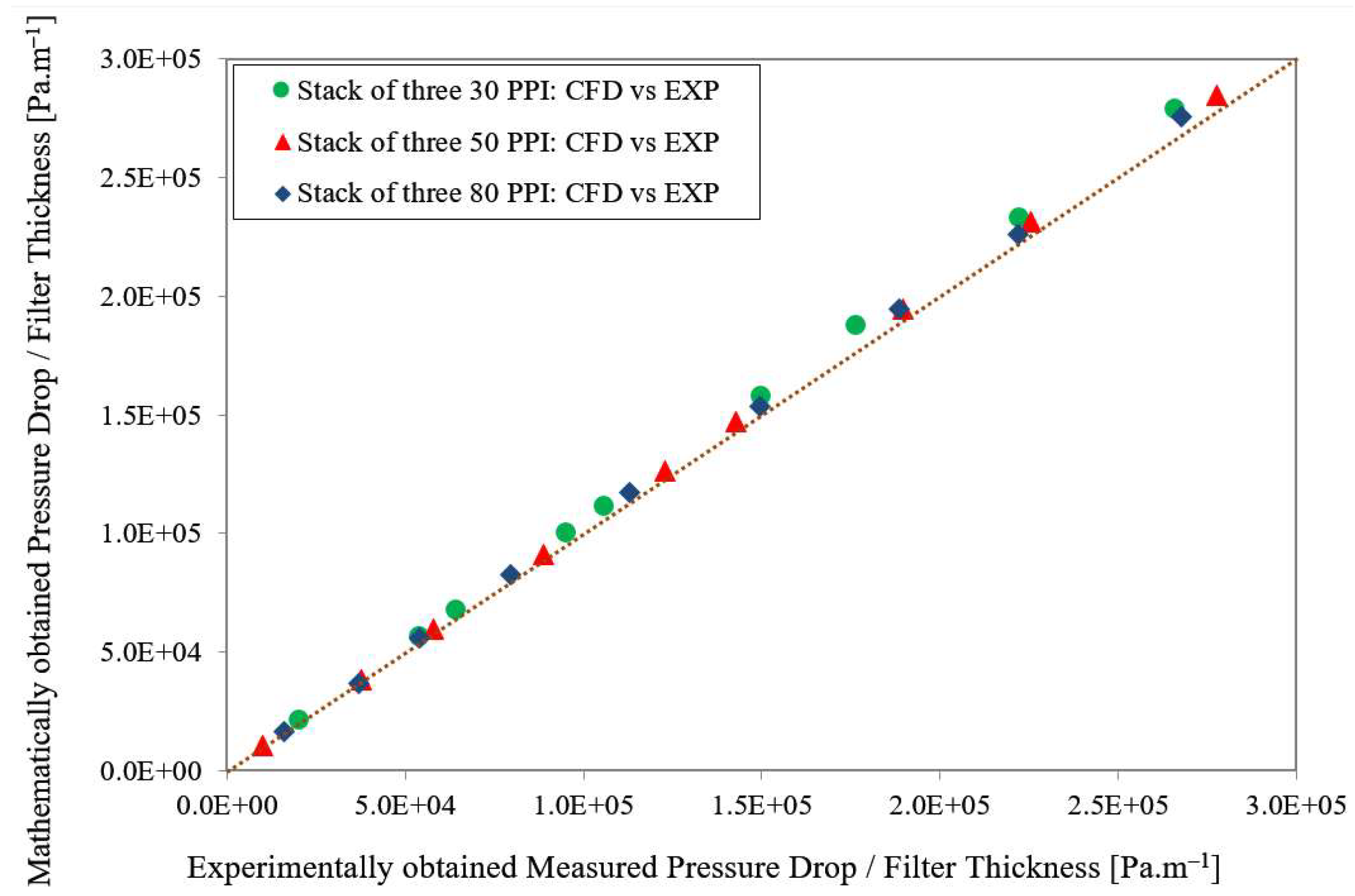
- The numerically obtained pressure gradients of the three identical filters are in good agreement with the experimental data, and the deviations are in the range of 0.4 to 6.3%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Große, J.; Dietrich, B.; Martin, H.; Kind, M.; Vicente, J.; Hardy, E.H. Volume Image Analysis of Ceramic Sponges. Chem. Eng. Technol. 2008, 31, 307–314. [Google Scholar] [CrossRef]
- Akbarnejad, S.; Saffari Pour, M.; Jonsson, L.T.I.; Jonsson, P.G. Effect of Fluid Bypassing on the Experimentally Obtained Darcy and Non-Darcy Permeability Parameters of Ceramic Foam Filters. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2017, 47, 197–207. [Google Scholar] [CrossRef]
- Grosse, J.; Dietrich, B.; Garrido, G.I.; Habisreuther, P.; Zarzalis, N.; Martin, H.; Kind, M.; Kraushaar-Czarnetzki, B. Morphological Characterization of Ceramic Sponges for Applications in Chemical Engineering. Ind. Eng. Chem. Res. 2009, 48, 10395–10401. [Google Scholar] [CrossRef]
- Inayat, A.; Freund, H.; Zeiser, T.; Schwieger, W. Determining the Specific Surface Area of Ceramic Foams: The Tetrakaidecahedra Model Revisited. Chem. Eng. Sci. 2011, 66, 1179–1188. [Google Scholar] [CrossRef]
- Innocentini, M.D.M.; Antunes, W.L.; Baumgartner, J.B.; Seville, J.P.K.; Coury, J.R. Permeability of Ceramic Membranes to Gas Flow. Mater. Sci. Forum 1999, 299–300, 19–28. [Google Scholar] [CrossRef]
- Moreira, E.A.; Innocentini, M.D.M.; Coury, J.R. Permeability of Ceramic Foams to Compressible and Incompressible Flow. J. Eur. Ceram. Soc. 2004, 24, 3209–3218. [Google Scholar] [CrossRef]
- Montanaro, L.; Jorand, Y.; Fantozzi, G.; Negro, A. Ceramic Foams by Powder Processing. J. Eur. Ceram. Soc. 1998, 18, 1339–1350. [Google Scholar] [CrossRef]
- Dietrich, B. Pressure Drop Correlation for Ceramic and Metal Sponges. Chem. Eng. Sci. 2012, 74, 192–199. [Google Scholar] [CrossRef]
- Twigg, M.V.; Richardson, J.T. Fundamentals and Applications of Structured Ceramic Foam Catalysts. Ind. Eng. Chem. Res. 2007, 46, 4166–4177. [Google Scholar] [CrossRef]
- Inayat, A.; Schwerdtfeger, J.; Freund, H.; Körner, C.; Singer, R.F.; Schwieger, W. Periodic Open-Cell Foams: Pressure Drop Measurements and Modeling of an Ideal Tetrakaidecahedra Packing. Chem. Eng. Sci. 2011, 66, 2758–2763. [Google Scholar] [CrossRef]
- Banhart, J. Manufacture, Characterisation and Application of Cellular Metals and Metal Foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Twigg, M.V.; Richardson, J.T. Theory and Applications of Ceramic Foam Catalysts. Chem. Eng. Res. Des. 2002, 80, 183–189. [Google Scholar] [CrossRef]
- Innocentini, M.D.M.; Salvini, V.R.; Pandolfelli, V.C.; Coury, J.R. The Permeability of Ceramic Foams. Am. Ceram. Soc. Bull. 1999, 78, 78–84. [Google Scholar]
- Scheffler, F.; Claus, P.; Schimpf, S.; Lucas, M.; Scheffler, M. Heterogeneously Catalyzed Processes with Porous Cellular Ceramic Monoliths. In Cellular Ceramics: Structure, Manufacturing, Properties and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; pp. 454–483. ISBN 3527313206. [Google Scholar]
- Olson, R.A.; Martins, L.C.B. Liquid Metal Filtration. In Cellular Ceramics: Structure, Manufacturing, Properties and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; pp. 403–415. ISBN 3527313206. [Google Scholar]
- Williams, E.J.A.E.; Evans, J.R.G. Expanded Ceramic Foam. J. Mater. Sci. 1996, 31, 559–563. [Google Scholar] [CrossRef]
- Keegan, N.; Schneider, W.; Krug, H. Evaluation of the Efficiency of Fine Pore Ceramic Foam Filters. Light Met. Warrendale 1999, 1031–1041. [Google Scholar]
- Bao, S.; Engh, T.A.; Syvertsen, M.; Kvithyld, A.; Tangstad, M. Inclusion (Particle) Removal by Interception and Gravity in Ceramic Foam Filters. J. Mater. Sci. 2012, 47, 7986–7998. [Google Scholar] [CrossRef]
- Kennedy, M.W.; Zhang, K.; Fritzsch, R.; Akhtar, S.; Bakken, J.A.; Aune, R.E. Characterization of Ceramic Foam Filters Used for Liquid Metal Filtration. Metall. Mater. Trans. B 2013, 44, 671–690. [Google Scholar] [CrossRef]
- Akbarnejad, S.; Kennedy, M.W.; Fritzsch, R.; Aune, R.E. An Investigation on Permeability of Ceramic Foam Filters (CFF). In Light Metals; Hyland, M., Ed.; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Fritzsch, R.; Kennedy, M.W.; Bakken, J.A.; Aune, R.E. Electromagnetic Priming of Ceramic Foam Filters (CFF) for Liquid Aluminum Filtration. In Proceedings of the Minerals, Metals & Materials Society; Springer: Cham, Switzerland, 2013; pp. 973–979. [Google Scholar]
- Kennedy, M.W.; Akhtar, S.; Bakken, J.A.; Aune, R.E. Electromagnetically Modified Filtration of Aluminum Melts—Part I: Electromagnetic Theory and 30 PPI Ceramic Foam Filter Experimental Results. Metall. Mater. Trans. B 2013, 44, 691–705. [Google Scholar] [CrossRef]
- Kennedy, M.W.; Akhtar, S.; Bakken, J.A.; Aune, R.E. Electromagnetically Enhanced Filtration of Aluminum Melts. In Light Metals; Springer: New York, NY, USA, 2011; pp. 763–768. [Google Scholar]
- Brockmeyer, J.W.; Aubrey, L.S. Application of Ceramic Foam Filters in Molten Metal Filtration. Ceram. Eng. Sci. Proc. 1987, 8, 63–74. [Google Scholar]
- De Génie, L.; Paris, É.C. Experimental and Numerical Study of Ceramic Foam Filtration. In Essential Readings in Light Metals; Grandfield, J.F., Eskin, D.G., Eds.; Springer: Cham, Switzerland, 2016; pp. 285–290. [Google Scholar] [CrossRef]
- Akbarnejad, S.; Jonsson, L.; Kennedy, M.W.; Aune, R.E.; Jönsson, P. Analysis on Experimental Investigation and Mathematical Modeling of Incompressible Flow through Ceramic Foam Filter. Metall. Mater. Trans. B 2016, 47, 2229–2243. [Google Scholar] [CrossRef]
- Kennedy, M.W.; Akhtar, S.; Fritzsch, R.; Bakken, J.A.; Aune, R.E. Apparatus and Method for Priming a Molten Metal Filter. U.S. Patent WO 2013/160754 A1, 28 March 2017. [Google Scholar]
- Fritzsch, R.; Akbarnejad, S.; Aune, R.E. Effect of Electromagnetic Fields on The Priming of High Grade Ceramic Foam Filters (Cff) with Liquid Aluminum. In Light Metals; Hyland, M., Ed.; Springer: Cham, Switzerland, 2015; pp. 929–935. [Google Scholar]
- Akbarnejad, S. Experimental and Mathematical Study of Incompressible Fluid Flow through Ceramic Foam Filters; KTH Royal Institute of Technology: Stockholm, Sweden, 2016. [Google Scholar]
- Kennedy, M.W. Removal of Inclusions from Liquid Aluminium Using Electromagnetically Modified Filtration; NTNU Norwegian University of Science and Technology: Trondheim, Norway, 2013. [Google Scholar]
- Innocentini, M.D.M.; Salvini, V.R.; Pandolfelli, V.C. Assessment of Forchheimer’s Equation to Predict the Permeability of Ceramic Foams. J. Am. Ceram. Soc. 1999, 82, 1945–1948. [Google Scholar] [CrossRef]
- Gupta, K.M. Permeameter. U.S. Patent No.4495795, 29 January 1985. [Google Scholar]
- Daniel, M.; Innocentini, D.M.; Sepulveda, P.; Ortega, S. Permeability in Cellular Ceramics: Structure, Manufacturing, Properties and Applications. In Cellular Ceramics: Structure, Manufacturing, Properties and Applications; Wiley: Hoboken, NJ, USA, 2005; pp. 313–341. ISBN 3527313206. [Google Scholar]
- Baril, E.; Mostafid, A.; Lefebvre, L.P.; Medraj, M. Experimental Demonstration of Entrance/Exit Effects on the Permeability Measurements of Porous Materials. Adv. Eng. Mater. 2008, 10, 889–894. [Google Scholar] [CrossRef]
- Dullien, F.A.L. Porous Media: Fluid Transport and Pore Structure; Academic Press, Inc.: San Diego, CA, USA, 1991; ISBN 9780323139335. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 4th ed.; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-5540-0. [Google Scholar]
- Neuman, S.P. Theoretical Derivation of Darcy’s Law. Acta Mech. 1977, 25, 153–170. [Google Scholar] [CrossRef]
- Lage, J.L. The Fundamental Theory of Flow through Permeable Media from Darcy to Turbulence; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1998. [Google Scholar]
- White, F.M. Fluid Mechanics, 7th ed.; Mc Graw Hill: New York, NY, USA, 2010; ISBN 978-0-07-352934-9. [Google Scholar]
- Darcy, H. Les Fontaines Publiques de La Ville de Dijon; National Library of France: Paris, France, 1856. [Google Scholar]
- Scheidegger, A.E. The Physics of Flow through Porous Media; University of Toronto Press: Toronto, ON, Canada, 1957. [Google Scholar]
- Forchheimer, P. Wasserbewegung Durch Boden. Z. Des Ver. Dtsch. Ing. 1901, 45, 1781–1788. [Google Scholar]
- Nield, D.A. The Limitations of the Brinkman-Forchheimer Equation in Modeling Flow in a Saturated Porous Medium and at an Interface. Int. J. Heat Fluid Flow 1991, 12, 269–272. [Google Scholar] [CrossRef]
- Kennedy, M.W.; Akhtar, S.; Bakken, J.A.; Aune, R.E. Empirical Verification of a Short-Coil Correction Factor. IEEE Trans. Ind. Electron. 2014, 61, 2573–2583. [Google Scholar] [CrossRef]
- Fritzsch, R. Electromagnetically Enhanced Priming of Ceramic Foam Filters; NTNU Norwegian University of Science and Technology: Trondheim, Norway, 2016. [Google Scholar]
- Vincent, M.; Bosworth, P.; Fritzsch, R. Filter Handling Tool. U.S. Patent WO 2018/191281 A2, 04 January 2018. [Google Scholar]
- Akbar Shakiba, S.; Ebrahimi, R.; Shams, M. Experimental Investigation of Pressure Drop Through Ceramic Foams: An Empirical Model for Hot and Cold Flow. J. Fluids Eng. 2011, 133, 111105. [Google Scholar] [CrossRef]
- Incera Garrido, G.; Patcas, F.C.; Lang, S.; Kraushaar-Czarnetzki, B. Mass Transfer and Pressure Drop in Ceramic Foams: A Description for Different Pore Sizes and Porosities. Chem. Eng. Sci. 2008, 63, 5202–5217. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Calmidi, V.V.; Mahajan, R.L. Thermophysical Properties of High Porosity Metal Foams. Int. J. Heat Mass Transf. 2002, 45, 1017–1031. [Google Scholar] [CrossRef]
- Calmidi, V.V.; Mahajan, R.L. Forced Convection in High Porosity Metal Foams. J. Heat Transf. 2000, 122, 557. [Google Scholar] [CrossRef]
- Paek, J.; Kang, B.; Kim, S.; Hyun, J. Effective Thermal Conductivity and Permeability of Aluminum Foam Materials. Int. J. Thermophys. 2000, 21, 453–464. [Google Scholar] [CrossRef]
- Lévêque, J.; Rouzineau, D.; Prévost, M.; Meyer, M. Hydrodynamic and Mass Transfer Efficiency of Ceramic Foam Packing Applied to Distillation. Chem. Eng. Sci. 2009, 64, 2607–2616. [Google Scholar] [CrossRef][Green Version]
- Banerjee, A.; Bala Chandran, R.; Davidson, J.H. Experimental Investigation of a Reticulated Porous Alumina Heat Exchanger for High Temperature Gas Heat Recovery. Appl. Therm. Eng. 2015, 75, 889–895. [Google Scholar] [CrossRef]
- Martin, J.L.; McCutcheon, S.C. Hydrodynamics and Transport for Water Quality Modeling; Lewis Publishers: Boca Raton, FL, USA, 1999; ISBN 0873716124. [Google Scholar]
- The International Association for the Properties of Water and Steam (IAPWS). Release on the IAPWS Formulation 2008 for the Viscosity of Ordinary Water Substance; IAPWS: Berlin, Germany, 2008. [Google Scholar]
- Huber, M.L.; Perkins, R.A.; Laesecke, A.; Friend, D.G.; Sengers, J.V.; Assael, M.J.; Metaxa, I.N.; Vogel, E.; Mareš, R.; Miyagawa, K. New International Formulation for the Viscosity of H2O. J. Phys. Chem. Ref. Data 2009, 38, 101–125. [Google Scholar] [CrossRef]
- Zhang, K. Liquid Permeability of Ceramic Foam Filters; Norwegian University of Science and Technology: Trondheim, Norway, 2012. [Google Scholar]
- Fox, R.W.; McDonald, A.T.; Pritchard, P.J. Introduction to Fluid Mechanics, 6th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; ISBN 0-471-20231-2. [Google Scholar]
- Reynolds, O. On the Dynamical Theory of Incompressible Viscous Fluids and the Determination of the Criterion. Philos. Trans. R. Soc. Lond. A 1895, 186, 123–164. [Google Scholar]
- CFD Module User’s Guide, Version 5.5; COMSOL Multiphysics: Stockholm, Sweden, 2019.
- Wilcox, D.C. Turbulence Modelling for CFD; DCW Industeries: Glendale, CA, USA, 1993. [Google Scholar]
- Antohe, B.V.; Lage, J.L. A General Two-Equation Macroscopic Turbulence Model for Incompressible Flow in Porous Media. Int. J. Heat Mass Transf. 1997, 40, 3013–3024. [Google Scholar] [CrossRef]
- Alfonsi, G. Reynolds-Averaged–Navier-Stokes Equations for Turbulence Modeling. Appl. Mech. Rev. 2009, 62, 040802. [Google Scholar] [CrossRef]
- Prinos, P.; Sofialidis, D.; Keramaris, E. Turbulent Flow Over and Within a Porous Bed. J. Hydraul. Eng. 2003, 129, 720–733. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Von Kármán, T. Mechanische Aenlichkeit Und Turbulenz; National Advisory Committee on Aeronautics: Washington, DC, USA, 1930; pp. 58–76.
- Prandtl, L. Über Die Ausgebildete Turbulenz. Z. Für Angew. Math. Und Mech. 1925, 5, 136–139. [Google Scholar] [CrossRef]
- Holton, J.R. An Introduction to Dynamic Meteorology, 4th ed.; Elsevier: Burlington, MA, USA, 2004; ISBN 0-12-354015-1. [Google Scholar]
- Getachew, D.; Minkowycz, W.J.; Lage, J.L. A Modified Form of the κ–ε Model for Turbulent Flows of an Incompressible Fluid in Porous Media. Int. J. Heat Mass Transf. 2000, 43, 2909–2915. [Google Scholar] [CrossRef]
- Hsu, C.T.; Cheng, P. Thermal Dispersion in a Porous Medium. Int. J. Heat Mass Transf. 1990, 33, 1587–1597. [Google Scholar] [CrossRef]
- Amiri, A.; Vafai, K. Transient Analysis of Incompressible Flow Through a Packed Bed. Int. J. Heat Mass Transf. 1998, 41, 4259–4279. [Google Scholar] [CrossRef]
- Amiri, A.; Vafai, K. Analysis of Dispersion Effects and Non-Thermal Equilibrium, Non-Darcian, Variable Porosity Incompressible Flow through Porous Media. Int. J. Heat Mass Transf. 1994, 37, 939–954. [Google Scholar] [CrossRef]
- Vafai, K.; Tien, C.L. Boundary and Inertia Effects on Flow and Heat Transfer in Porous Media. Int. J. Heat Mass Transf. 1981, 24, 195–203. [Google Scholar] [CrossRef]
- Hassanizadeh, S.; Gray, W. High Velocity Flow in Porous Media. Transp. Porous Media 1987, 2, 521–531. [Google Scholar] [CrossRef]
- Macdonald, I.F.; El-Sayed, M.S.; Mow, K.; Dullien, F.A.L. Flow through Porous Media-the Ergun Equation Revisited. Ind. Eng. Chem. Fundam. 1979, 18, 199–208. [Google Scholar] [CrossRef]
- Vafai, K. Convective Flow and Heat Transfer in Variable-Porosity Media. J. Fluid Mech. 1984, 147, 233–259. [Google Scholar] [CrossRef]
- Beavers, G.S.; Sparrow, E.M.; Rodenz, D.E. Influence of Bed Size on the Flow Characteristics and Porosity of Randomly Packed Beds of Spheres. J. Appl. Mech. Trans. ASME 1973, 40, 655–660. [Google Scholar] [CrossRef]
- Ward, J.C. Turbulent Flow in Porous Media. Hydraul. Div. 1964, 90, 1–12. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow through Packed Columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]




| Filter | Diameter (mm) | Thickness (mm) | Total Porosity (%) | Open Pore Porosity (%) | |
|---|---|---|---|---|---|
| No. | Type | ||||
| N1 | 30 PPI | 49.33 ± 0.30 | 50.42 ± 0.07 | 90.1 | 88.8 |
| N2 | 30 PPI | 49.00 ± 0.37 | 50.83 ± 0.04 | 90.8 | 90 |
| N3 | 30 PPI | 49.38 ± 0.14 | 50.76 ± 0.06 | 90.1 | 91.5 |
| N1 | 50 PPI | 49.58 ± 0.18 | 50.88 ± 0.05 | 85.8 | 83.5 |
| N2 | 50 PPI | 49.30 ± 0.17 | 49.98 ± 0.02 | 86.1 | 84.6 |
| N3 | 50 PPI | 49.68 ± 0.10 | 50.63 ± 0.06 | 85.9 | 82.6 |
| N1 | 80 PPI | 49.63 ± 0.15 | 49.79 ± 0.04 | 85.6 | 81.5 |
| N2 | 80 PPI | 49.38 ± 0.28 | 50.28 ± 0.03 | 86.4 | 85.8 |
| N3 | 80 PPI | 49.30 ± 0.15 | 50.96 ± 0.06 | 87.1 | 85.1 |
| Inlet | Outlet | Wall |
|---|---|---|
| Sample No. |
Water Temperature (K) |
Water Viscosity (Pa.s) |
Water Density (Kg.m−3) |
k1 (m2) |
k2 (m) |
|---|---|---|---|---|---|
| N1N2N3 30 | 283.7 | 1.28 × 10–3 | 999.7 | 3.67 × 10–8 | 6.51 × 10–4 |
| N1N2N3 50 | 283.6 | 1.29 × 10–3 | 999.7 | 1.70 × 10–8 | 1.28 × 10–4 |
| N1N2N3 80 | 284.2 | 1.27 × 10–3 | 999.6 | 6.42 × 10–9 | 1.08 × 10–4 |
| Mesh No. | Element Size in Domains (mm) | Element Size in Boundaries (mm) | Total Mesh Element (millions) | Calculation Time (minutes) | ||
|---|---|---|---|---|---|---|
| Min. | Max. | Min. | Max. | |||
| 1 | 3.2 | 10.4 | 1.6 | 5.36 | 0.13 | 3.2 |
| 2 | 2.4 | 8 | 0.8 | 4.24 | 0.24 | 5.3 |
| 3 | 1.6 | 5.36 | 0.32 | 2.96 | 0.79 | 18.5 |
| 4 | 0.8 | 4.24 | 0.12 | 1.84 | 2.3 | 63 |
| 5 | 0.32 | 2.96 | 0.12 | 1.84 | 2.9 | 63 |
| 6 | 0.12 | 1.84 | 0.12 | 1.84 | 4 | 95 |
| 7 | 0.1 | 1.5 | 0.1 | 1.5 | 1.3 | 29 |
| 8 | 0.08 | 1 | 0.08 | 1 | 3.9 | 103 |
| 9 | 0.06 | 0.8 | 0.06 | 0.8 | 7.2 | 210 |
| 10 | 0.04 | 0.6 | 0.04 | 0.6 | 16.8 | 580 |
| 11 | 0.04 | 0.4 | 0.04 | 0.4 | 27 | 1273 |
| 12 | 0.32 | 2.96 | 0.016 | 1.04 | 17.5 | 1095 |
| 13 | 0.12 | 1.84 | 0.016 | 1.04 | 21.4 | 1435 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbarnejad, S.; Tilliander, A.; Sheng, D.-Y.; Jönsson, P.G. Effect of Batch Dissimilarity on Permeability of Stacked Ceramic Foam Filters and Incompressible Fluid Flow: Experimental and Numerical Investigation. Metals 2022, 12, 1001. https://doi.org/10.3390/met12061001
Akbarnejad S, Tilliander A, Sheng D-Y, Jönsson PG. Effect of Batch Dissimilarity on Permeability of Stacked Ceramic Foam Filters and Incompressible Fluid Flow: Experimental and Numerical Investigation. Metals. 2022; 12(6):1001. https://doi.org/10.3390/met12061001
Chicago/Turabian StyleAkbarnejad, Shahin, Anders Tilliander, Dong-Yuan Sheng, and Pär Göran Jönsson. 2022. "Effect of Batch Dissimilarity on Permeability of Stacked Ceramic Foam Filters and Incompressible Fluid Flow: Experimental and Numerical Investigation" Metals 12, no. 6: 1001. https://doi.org/10.3390/met12061001
APA StyleAkbarnejad, S., Tilliander, A., Sheng, D.-Y., & Jönsson, P. G. (2022). Effect of Batch Dissimilarity on Permeability of Stacked Ceramic Foam Filters and Incompressible Fluid Flow: Experimental and Numerical Investigation. Metals, 12(6), 1001. https://doi.org/10.3390/met12061001






