Potentials for Describing Interatomic Interactions in γFe-Mn-C-N System
Abstract
:1. Introduction
2. Choice of Potential for Describing Interatomic Interactions in F.C.C. Iron
3. Fe-C, C-C, Fe-Mn, Mn-Mn, and Mn-C Bonds in the Crystal Lattice of F.C.C. Iron
4. Interatomic Potentials for Describing Nitrogen Impurity in Hadfield Steel
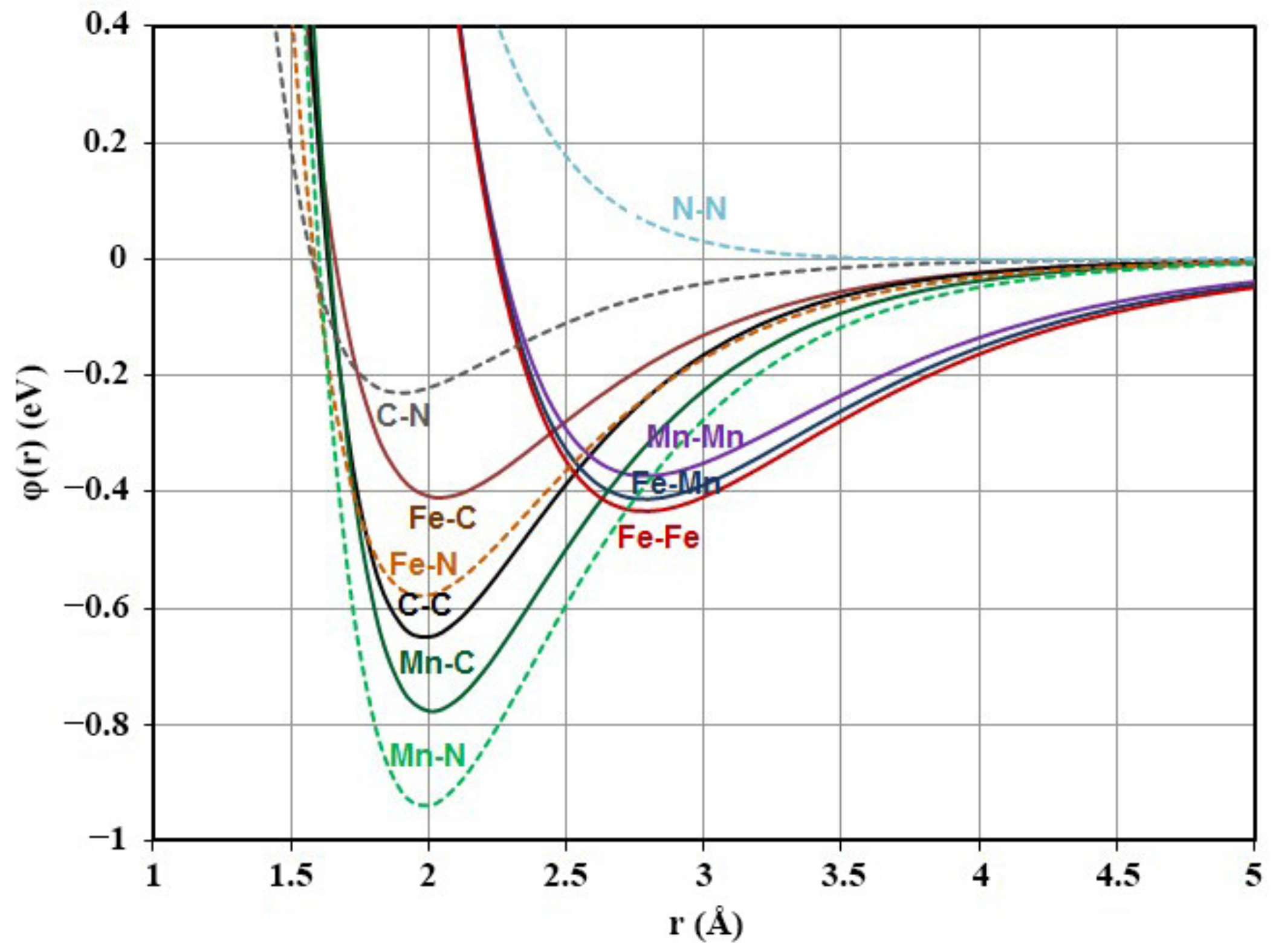
5. Potential Parameters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, C.; Zhang, F.; Wang, F.; Liu, H.; Yu, B. Effect of N+Cr alloying on the microstructures and tensile properties of Hadfield steel. Mater. Sci. Eng. A 2016, 679, 95–103. [Google Scholar] [CrossRef]
- Zhang, F.C.; Lv, B.; Wang, T.S.; Zheng, C.L.; Zhang, M.; Luo, H.H.; Liu, H.; Xu, A.Y. Explosion hardening of Hadfield steel crossing. Mater. Sci. Technol. 2010, 26, 223–229. [Google Scholar] [CrossRef]
- Chen, C.; Lv, B.; Ma, H.; Sun, D.; Zhang, F. Wear behavior and the corresponding work hardening characteristics of Hadfield steel. Tribol. Int. 2018, 121, 389–399. [Google Scholar] [CrossRef]
- Lee, B.J.; Baskes, M.I.; Kim, H.; Cho, Y.K. Second nearest-neighbor modified embedded atom method potentials for B.C.C. transition metals. Phys. Rev. B. 2001, 64, 184102. [Google Scholar] [CrossRef]
- Lee, B.-J.; Lee, J.W. A modified embedded atom method interatomic potential for carbon. Calphad 2005, 29, 7–16. [Google Scholar] [CrossRef]
- Lee, B.-J. A modified embedded-atom method interatomic potential for the Fe–C system. Acta Mater. 2006, 54, 701–711. [Google Scholar] [CrossRef]
- Kim, Y.-M.; Shin, Y.-H.; Lee, B.-J. Modified embedded-atom method interatomic potentials for pure Mn and the Fe–Mn system. Acta Mater. 2009, 57, 474–482. [Google Scholar] [CrossRef]
- Poletaev, G.M.; Starostenkov, M.D.; Zorya, I.V. Morse potentials for F.C.C. metals taking into account the interaction of the five coordination spheres. Fundam. Probl. Sovrem. Materialoved. 2017, 14, 70–75. [Google Scholar]
- Xie, J.-Y.; Chen, N.-X.; Shen, J.; Teng, L.; Seetharaman, S. Atomistic study on the structure and thermodynamic properties of Cr7C3, Mn7C3, Fe7C3. Acta Mater. 2005, 53, 2727–2732. [Google Scholar] [CrossRef]
- Numakura, H.; Yotsui, G.; Koiwa, M. Calculation of the strength of Snoek relaxation in dilute ternary B.C.C. alloys. Acta Met. Mater. 1995, 43, 705–714. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Ackland, G.J.; Mendelev, M.I.; Srolovitz, D.J.; Han, S.; Barashev, A.V. Development of an interatomic potential for phosphorus impurities in α-iron. J. Phys. Condens. Matter. 2004, 16, S2629. [Google Scholar] [CrossRef]
- Lau, T.T.; Först, C.J.; Lin, X.; Gale, J.D.; Yip, S.; van Vliet, K.J. Many-Body Potential for Point Defect Clusters in Fe-C Alloys. Phys. Rev. Lett. 2007, 98, 215501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rosato, V. Comparative behavior of carbon in B.C.C. and F.C.C. iron. Acta Met. 1989, 37, 2759–2763. [Google Scholar] [CrossRef]
- Oila, A.; Bull, S.J. Atomistic simulation of Fe-C austenite. Comp. Mater. Sci. 2009, 45, 235–239. [Google Scholar] [CrossRef]
- Ruda, M.; Farkas, D.; Abriata, J. Interatomic potentials for carbon interstitials in metals and intermetallics. Scr. Mater. 2002, 46, 349–355. [Google Scholar] [CrossRef]
- Vashishta, P.; Kalia, R.K.; Nakano, A.; Rino, J.P. Interaction potentials for alumina and molecular dynamics simulations of amorphous and liquid alumina. J. Appl. Phys. 2008, 103, 083504. [Google Scholar] [CrossRef]
- Liu, S.; Shi, S.; Huang, H.; Woo, C. Interatomic potentials and atomistic calculations of some metal hydride systems. J. Alloy. Compd. 2001, 330–332, 64–69. [Google Scholar] [CrossRef]
- San Miguel, M.A.; Sanz, J.F. Molecular-dynamics simulations of liquid aluminum oxide. Physical Review B. 1998, 58, 2369–2371. [Google Scholar] [CrossRef] [Green Version]
- Poletaev, G.M.; Zorya, I.V.; Rakitin, R.Y.; Iliina, M.A. Interatomic potentials for describing impurity atoms of light elements in F.C.C. metals. Mater. Phys. Mech. 2019, 42, 380–388. [Google Scholar]
- Poletaev, G.M.; Starostenkov, M.D.; Dmitriev, S.V. Interatomic potentials in the systems Pd-H and Ni-H. Mater. Phys. Mech. 2016, 27, 53–59. [Google Scholar]
- Poletaev, G.M.; Zorya, I.V. Effect of Light Element Impurities on the Edge Dislocation Glide in Nickel and Silver: Molecular Dynamics Simulation. J. Exp. Theor. Phys. 2020, 131, 432–436. [Google Scholar] [CrossRef]
- Poletaev, G.M.; Zorya, I.V. Influence of light impurities on the crystal-melt interface velocity in Ni and Ag. Molecular dy-namics simulation. Tech. Phys. Lett. 2020, 46, 575–578. [Google Scholar] [CrossRef]
- Ruda, M.; Farkas, D.; Garcia, G. Atomistic simulations in the Fe–C system. Comput. Mater. Sci. 2009, 45, 550–560. [Google Scholar] [CrossRef]
- Gustafson, P. A thermodynamic evaluation of the Fe-C System. Scand. J. Metall. 1985, 14, 259–267. [Google Scholar]
- Ridnyi, Y.M.; Mirzoev, A.A.; Mirzaev, D.A. Ab initio simulation of dissolution energy and carbon activity in F.C.C. Fe. Phys. Solid State 2017, 59, 1279–1284. [Google Scholar] [CrossRef]
- Jiang, D.E.; Carter, E.A. Carbon dissolution and diffusion in ferrite and austenite from first principles. Phys. Rev. B 2003, 67, 214103. [Google Scholar] [CrossRef] [Green Version]
- Askill, J. Tracer Diffusion Data for Metals, Alloys and Simple Oxides; Springer: Berlin/Heidelberg, Germany, 1970. [Google Scholar]
- Brandes, E.A.; Brook, G.B. Smithells Metals Reference Book; Butterworth-Heinemann: Oxford, UK, 1992. [Google Scholar]
- Slane, J.; Wolverton, C.; Gibala, R. Carbon–vacancy interactions in austenitic alloys. Mater. Sci. Eng. A 2003, 370, 67–72. [Google Scholar] [CrossRef]
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics (Internet Version 2005); CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Mirzoev, A.A.; Yalalov, M.M.; Mirzaev, D.A. Energy of mixing and magnetic state of components of Fe-Mn alloys: A first-principles calculation for the ground state. Phys. Met. Met. 2006, 101, 341–348. [Google Scholar] [CrossRef]
- Massardier, V.; Merlin, J.; Le Patézour, E.; Soler, M. Mn-C interaction in Fe-C-Mn steels: Study by thermoelectric power and internal friction. Met. Mater. Trans. A 2005, 36, 1745–1755. [Google Scholar] [CrossRef]
- Goldschmidt, H.J. Interstitial Alloys; Butterworths: London, UK, 1967. [Google Scholar]
- Mogutnov, B.M.; Tomilin, I.A.; Shvartsman, L.A. Thermodynamics of Iron Alloys; Metallurgiya: Moscow, Russia, 1984. (In Russian) [Google Scholar]
- Ridniy, Y.M.; Mirzoev, A.A.; Mirzaev, D.A. Ab initio modeling the energy of dissolution of nitrogen in F.C.C. lattice of iron. Vestn. SUSU. Seriya Metall. 2014, 14, 59–63. (In Russian) [Google Scholar]
- Frisk, K. A Thermodynamic evaluation of the Cr-N, Fe-N, Mo-N and Cr-Mo-N systems. CALPHAD 1991, 15, 79–106. [Google Scholar] [CrossRef]
- Rochana, P.; Lee, K.; Wilcox, J. Nitrogen adsorption, dissociation, and subsurface diffusion on the vanadium (110) surface: A DFT study for the nitrogen-selective catalytic membrane application. J. Phys. Chem. C. 2014, 118, 4238–4249. [Google Scholar] [CrossRef] [Green Version]
- Domain, C.; Becquart, C.S.; Foct, J. Ab initio study of foreign interstitial atom (C, N) interactions with intrinsic point defects in α-Fe. Phys. Rev. B. 2004, 69, 144112. [Google Scholar] [CrossRef]
- You, Z.; Paek, M.-K.; Jung, I.-H. Critical Evaluation and Optimization of the Fe-N, Mn-N and Fe-Mn-N Systems. J. Phase Equilibria Diffus. 2018, 39, 650–677. [Google Scholar] [CrossRef] [Green Version]
- Yin, X.; Opara, A.; Du, H.; Miller, J.D. Molecular dynamics simulations of metal-cyanide complexes: Fundamental considera-tions in gold hydrometallurgy. Hydrometallurgy 2011, 106, 64–70. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Weiser, V.G. Application of the Morse potential function to cubic metals. Phys. Rev. 1959, 114, 687–790. [Google Scholar] [CrossRef]

| Energy Characteristics | Our Model | Experiments or FP-Calc. | Potentials from [24] | Potentials from [13] |
|---|---|---|---|---|
| Esol (eV/atom) | 0.38 | 0.25–0.48 [25,26] (experiment, FP-calc.) | 1.01 | 0.78 |
| ΔEOT (eV) | 1.36 | 1.48 [27] (FP-calc.) | 1.03 | 1.12 |
| Em (eV) | 1.20 | 1.40–1.53 [4,28,29] (experiment) | 0.33 | 0.86 |
| Ebv (eV) | 0.41 | 0.37–0.41 [30] (experiment) | 0.50 | 0.54 |
| Energy Characteristics | Our Model | Experiment or FP-Calc. |
|---|---|---|
| Esol (eV/atom) | −0.13 | −0.13 [35] (experiment) −0.27 [36] (ab initio calculations) −0.53 [37] (thermodynamic evaluation) |
| Em (eV) | 1.29 | 1.29 [6,28,29,38,39] |
| Ebv (eV) | 0.45 | − |
| Bond | α (Å−1) | β | D (эB) |
|---|---|---|---|
| Fe-Fe | 1.285 | 35.878 | 0.433 |
| Fe-C | 1.82 | 41 | 0.41 |
| C-C | 1.97 | 50 | 0.65 |
| Mn-Mn | 1.321 | 39.792 | 0.373 |
| Mn-Fe | 1.306 | 38.030 | 0.413 |
| Mn-C | 1.87 | 43 | 0.777 |
| Fe-N | 1.788 | 34.046 | 0.579 |
| Mn-N | 1.812 | 36.482 | 0.940 |
| C-N | 2.140 | 58.323 | 0.230 |
| N-N | 1.556 | 700 | 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, B.; Chen, C.; Zhang, F.; Poletaev, G.M.; Rakitin, R.Y. Potentials for Describing Interatomic Interactions in γFe-Mn-C-N System. Metals 2022, 12, 982. https://doi.org/10.3390/met12060982
Lv B, Chen C, Zhang F, Poletaev GM, Rakitin RY. Potentials for Describing Interatomic Interactions in γFe-Mn-C-N System. Metals. 2022; 12(6):982. https://doi.org/10.3390/met12060982
Chicago/Turabian StyleLv, Bo, Chen Chen, Fucheng Zhang, Gennady M. Poletaev, and Roman Y. Rakitin. 2022. "Potentials for Describing Interatomic Interactions in γFe-Mn-C-N System" Metals 12, no. 6: 982. https://doi.org/10.3390/met12060982
APA StyleLv, B., Chen, C., Zhang, F., Poletaev, G. M., & Rakitin, R. Y. (2022). Potentials for Describing Interatomic Interactions in γFe-Mn-C-N System. Metals, 12(6), 982. https://doi.org/10.3390/met12060982







