A Study on the Thermo-Mechanical History, Residual Stress, and Dynamic Recrystallization Mechanisms in Additively Manufactured Austenitic Stainless Steels
Abstract
:1. Introduction
| Process Parameter | General Effect on RS | References |
|---|---|---|
| Laser power, P ※ | Higher power results in higher RS | [18,19,20,46] |
| Scan speed, v ※ | Higher speed results in lower RS | [18,21,46,47,48] |
| Layer thickness ※ | A thicker layer lowers the RS | [23,24] |
| Substrate heating | Higher temperatures result in lower RS | [29,47,48,49,50,51] |
| Scan orientation | Affects the RS distribution and the RS magnitude | [25,52,53,54] |
| Interlayer dwelling time | Material dependent. Affects the RS magnitude | [50,55] |
2. Materials and Methods
2.1. Materials and Processing Parameters
2.2. Experimental Procedures
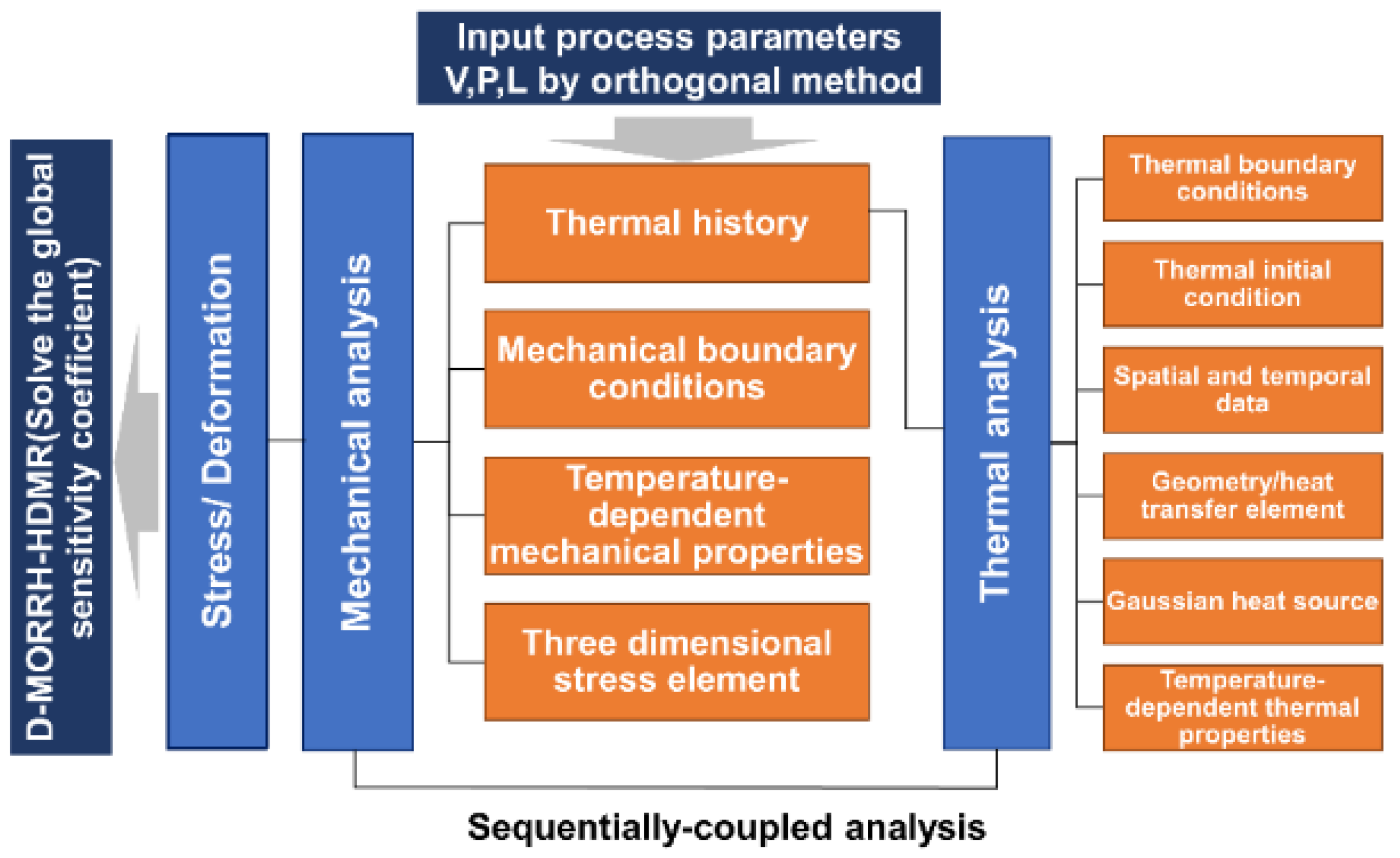
2.3. Thermo-mechanical Simulations
3. Results and Discussion
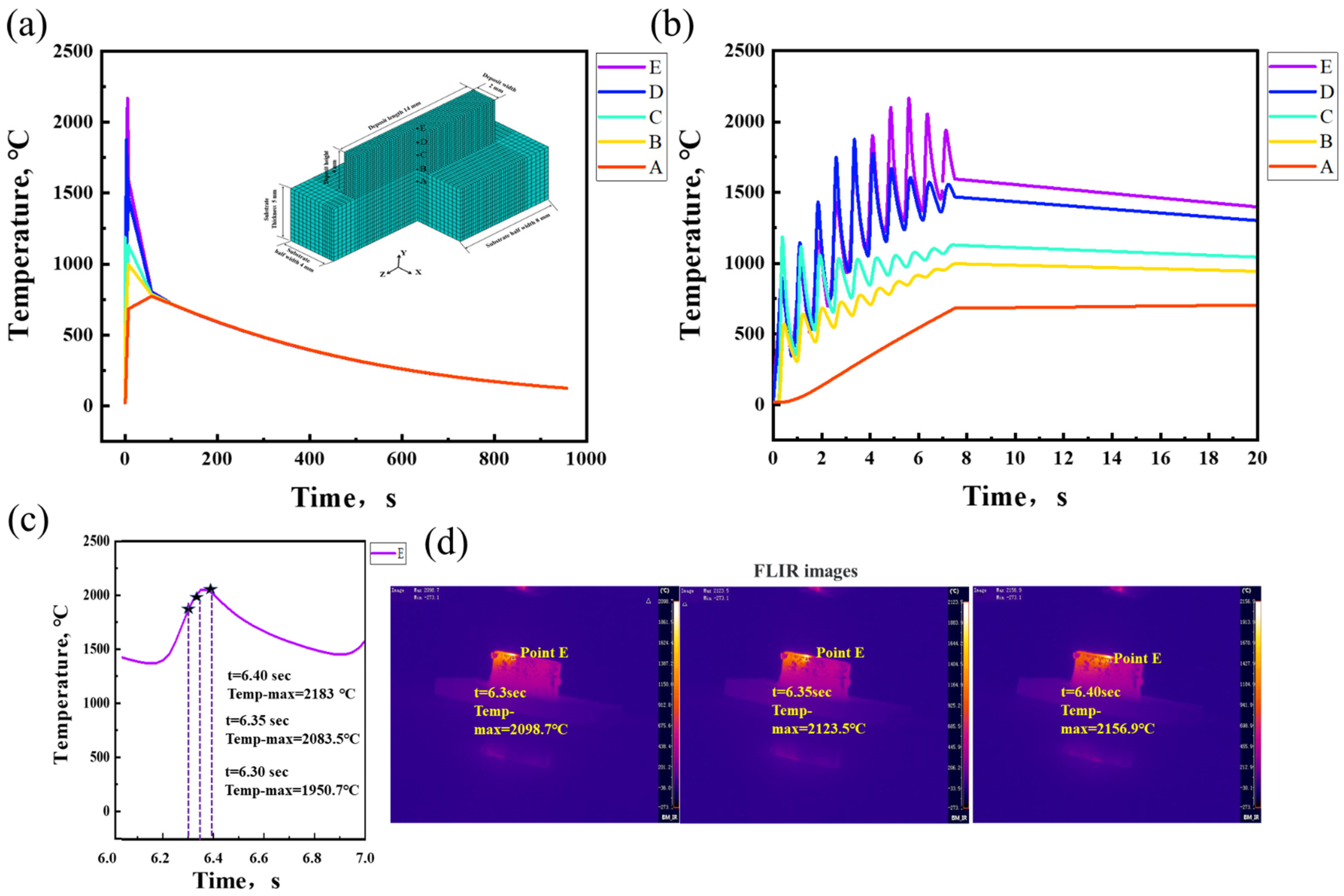
3.1. Thermo-Mechanical History
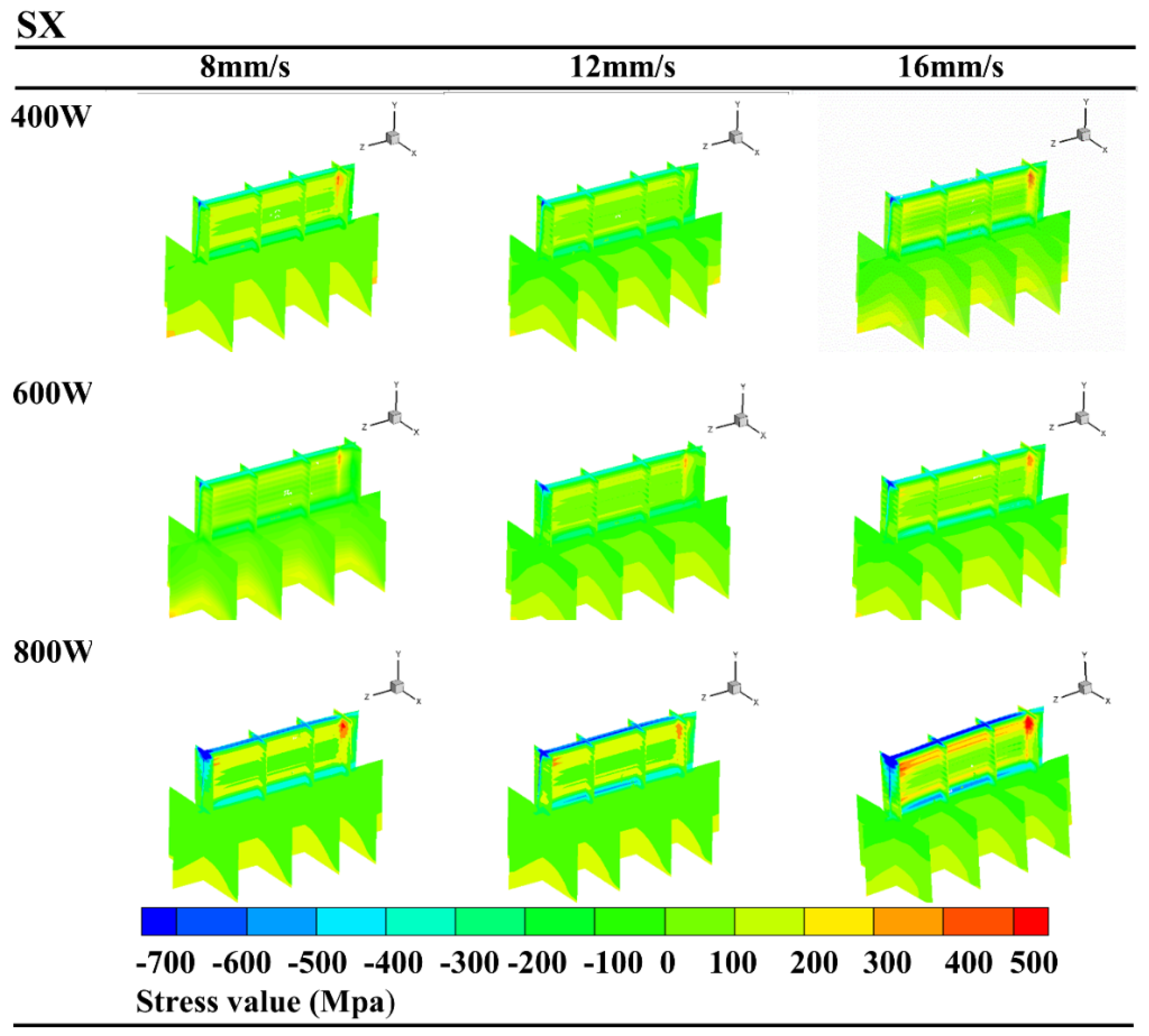
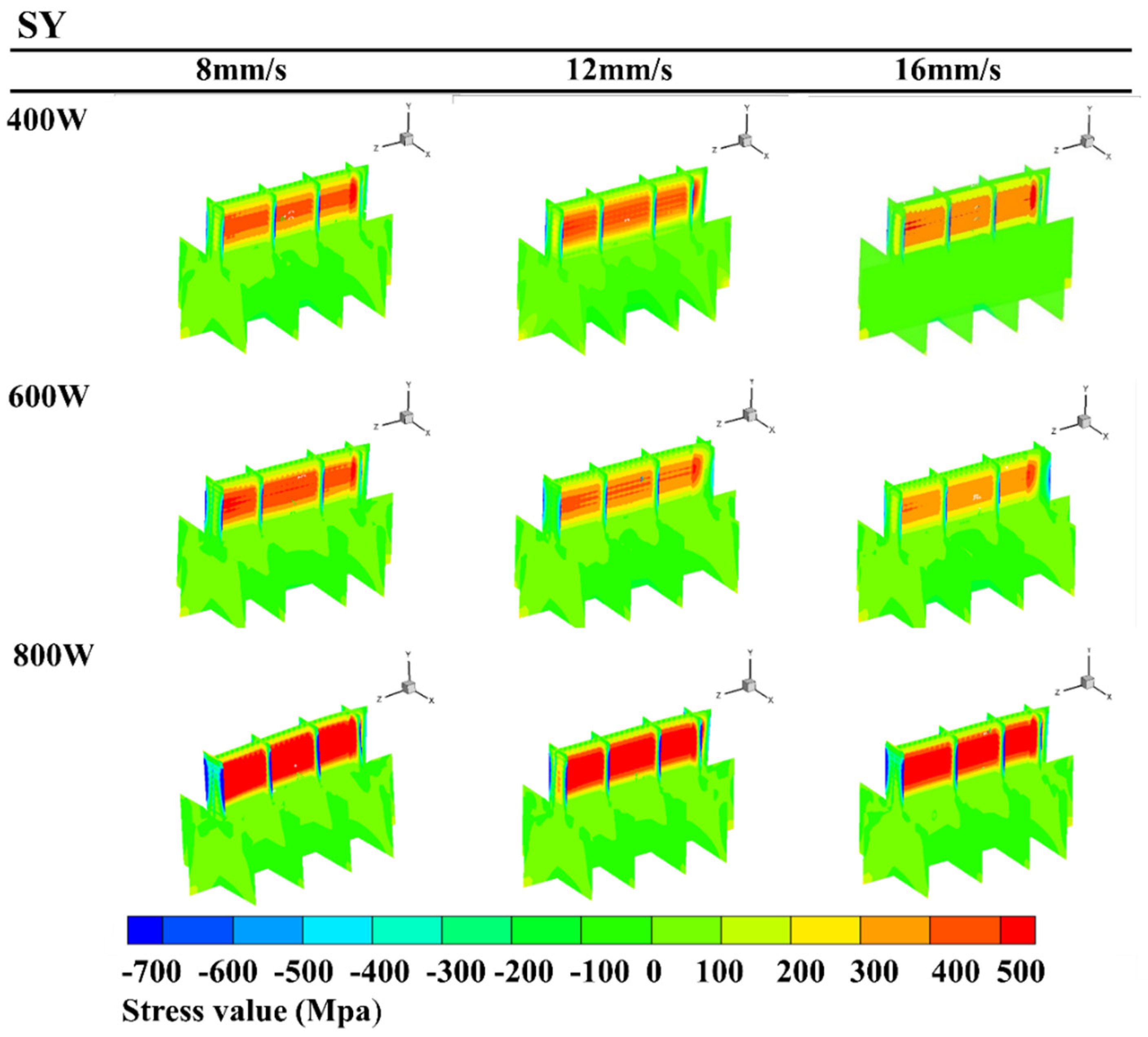
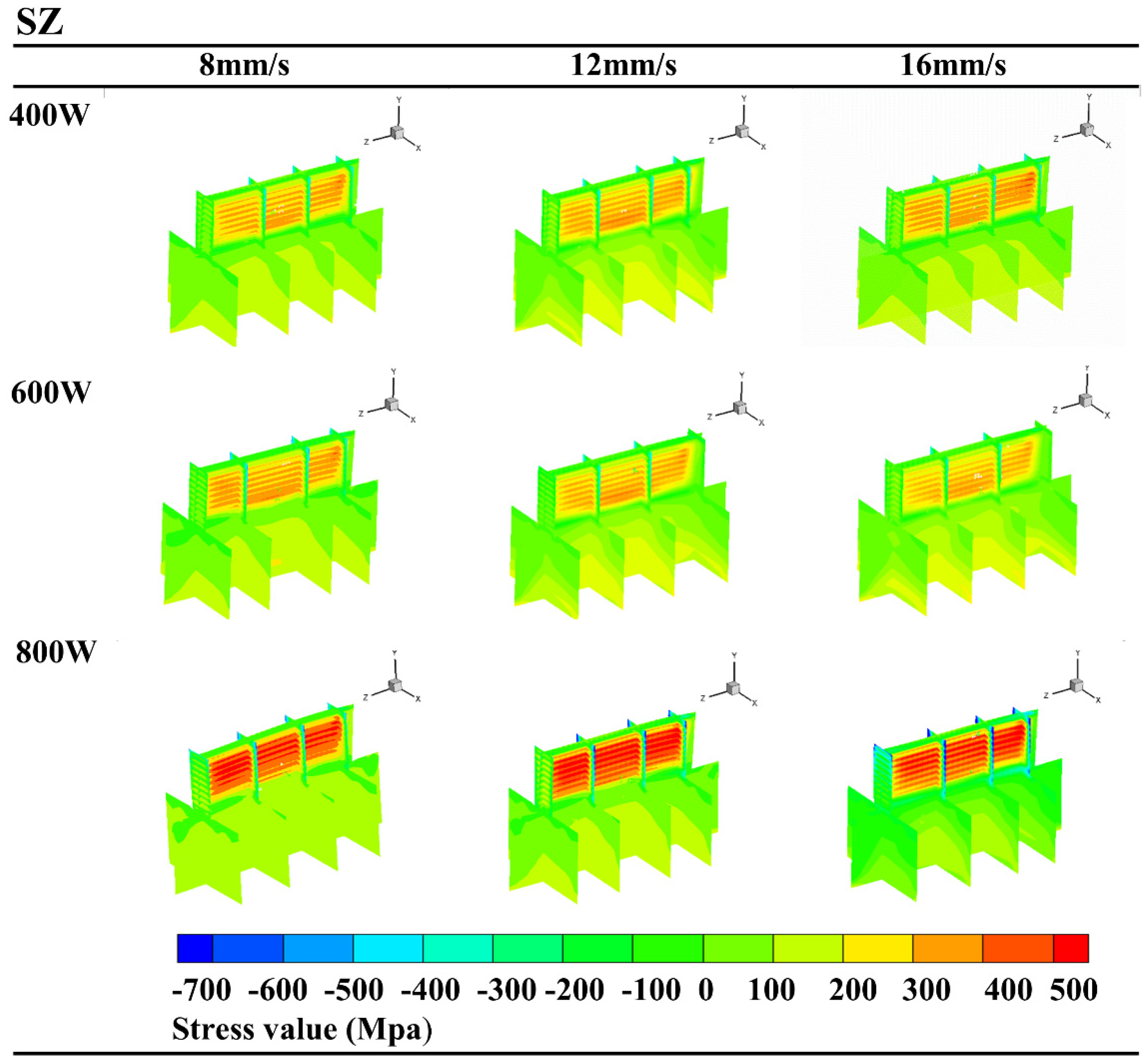
3.2. The Effect of Process Factors on Residual Stress
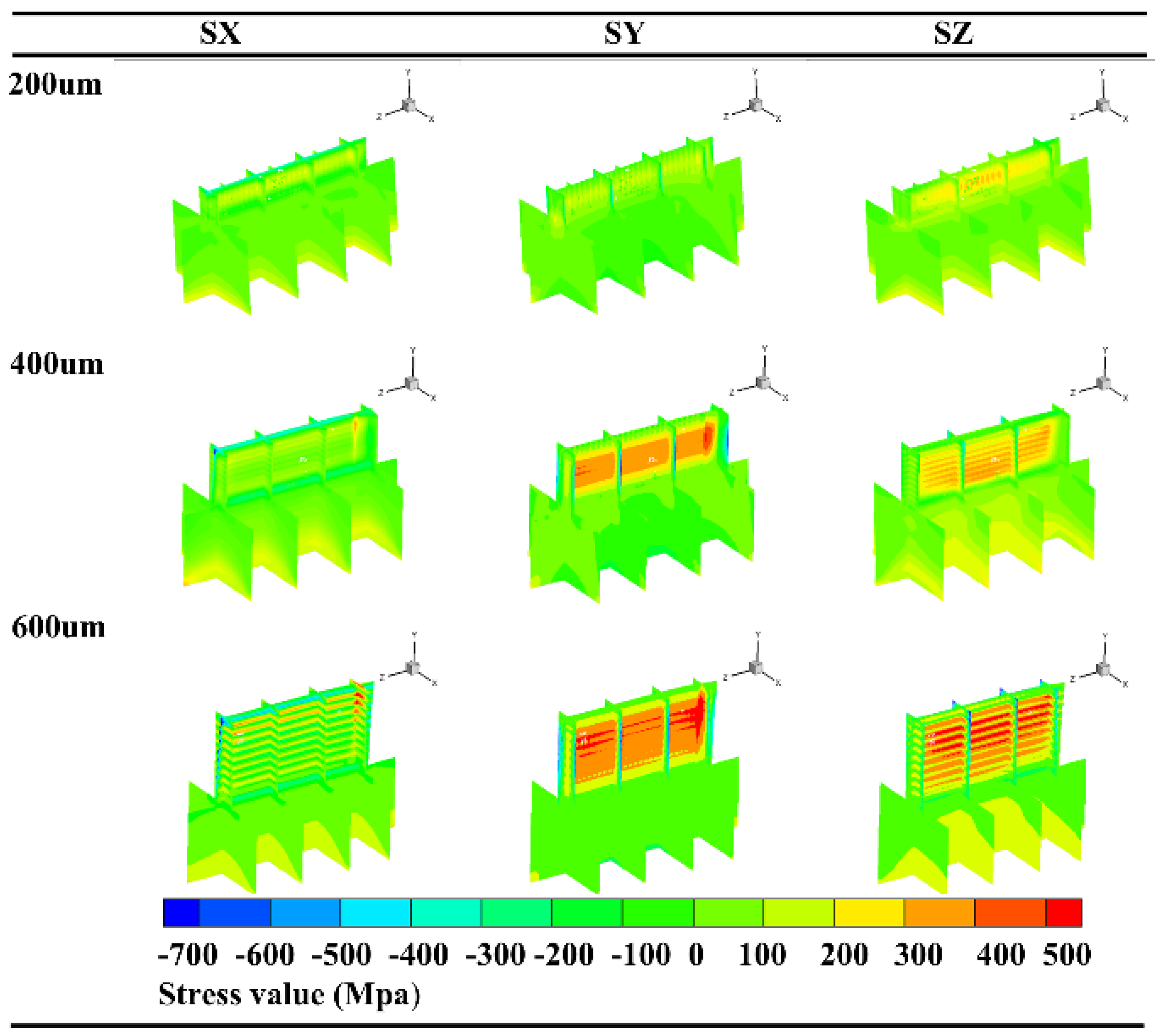
3.3. Reducing Residual Stress through Optimization
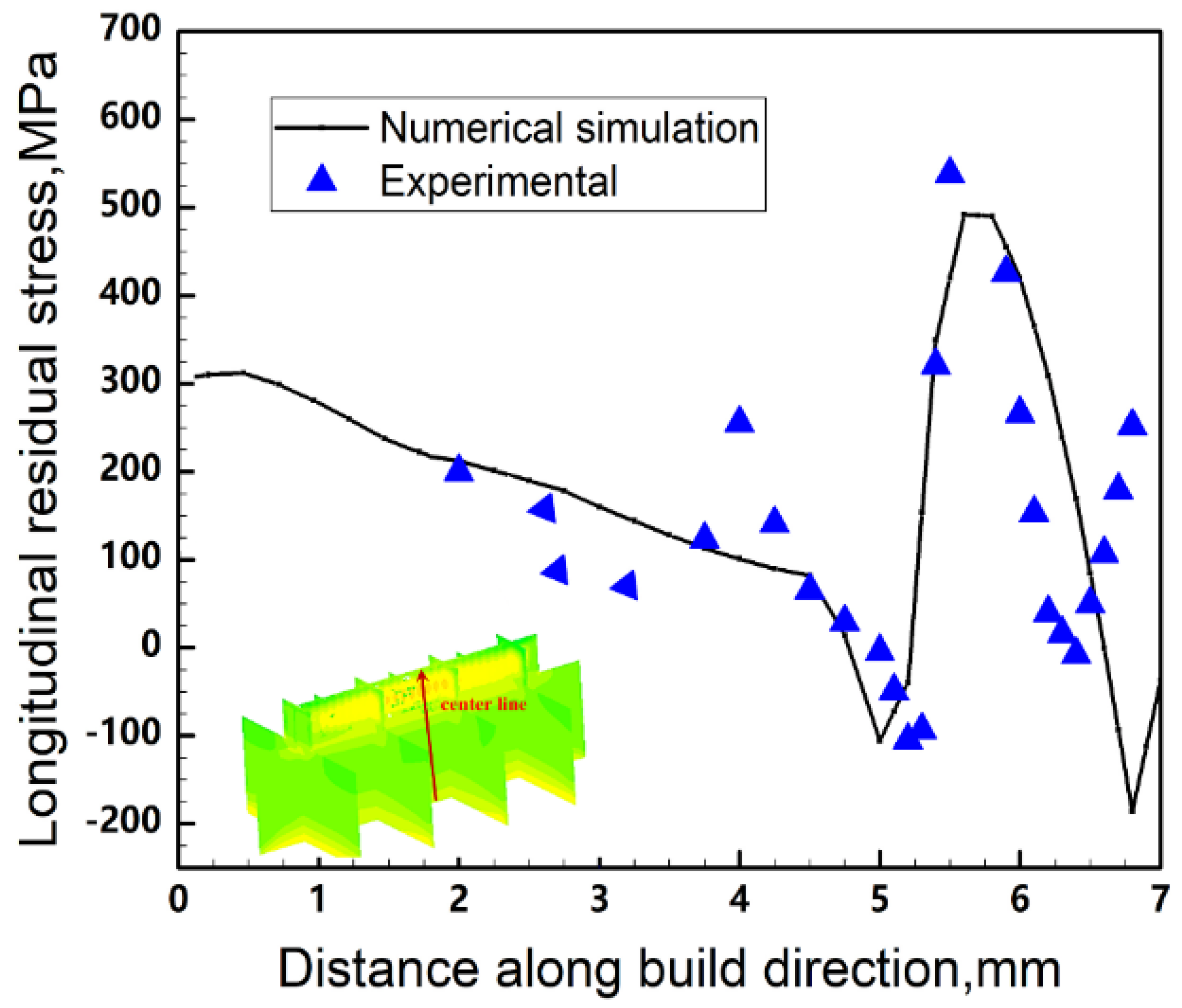
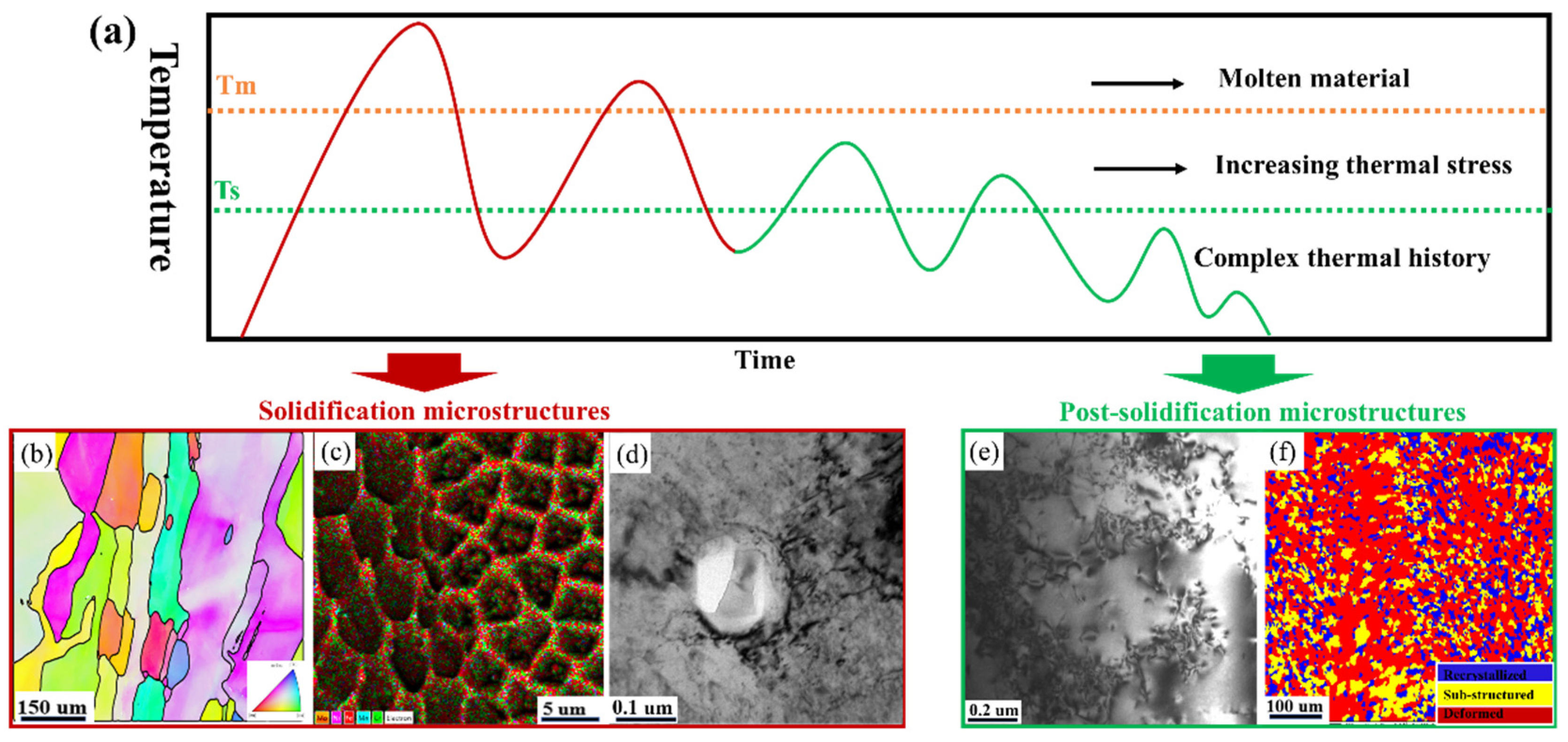
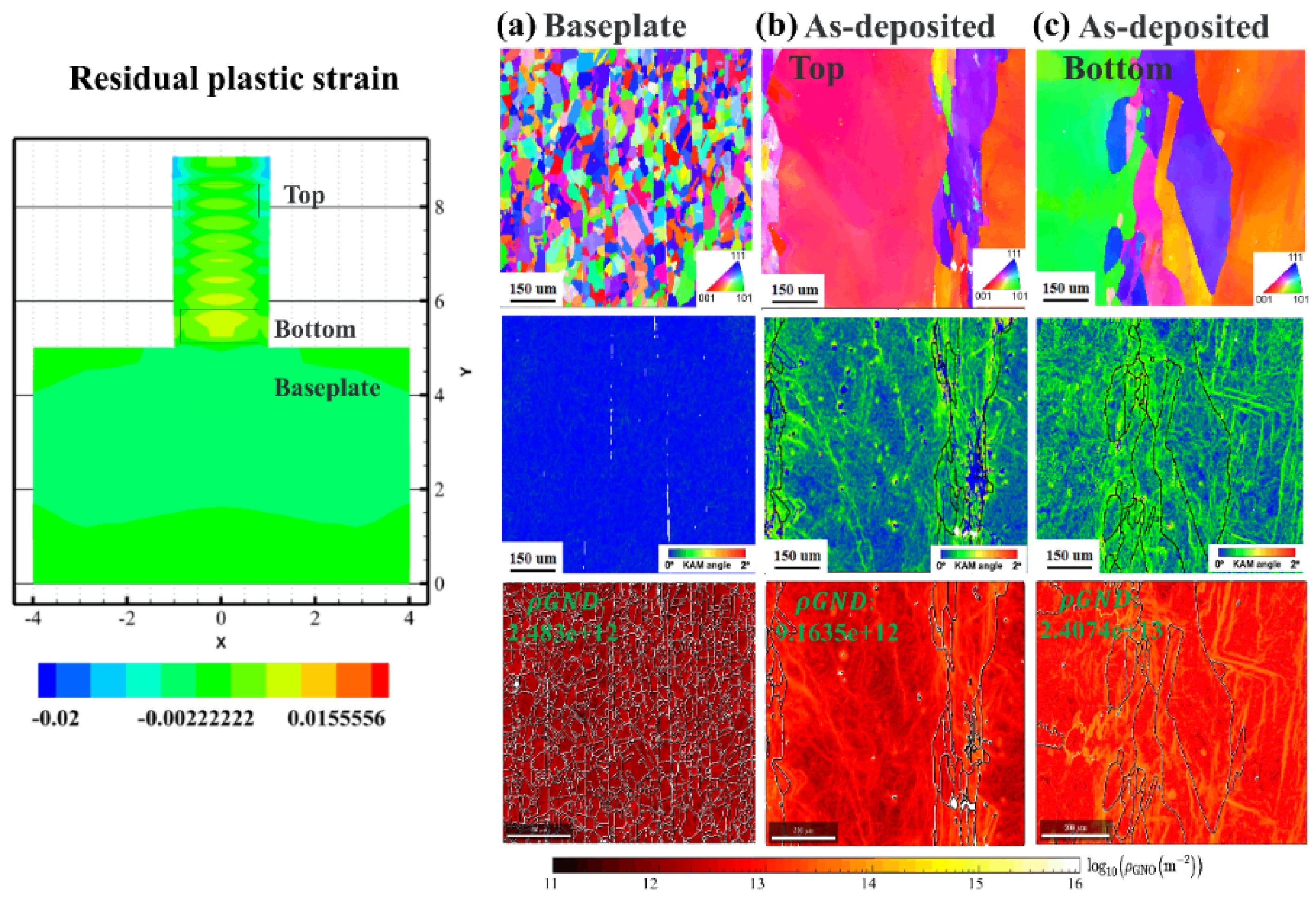
3.4. Structural Characterization of Post-Solidification-Related Stress
3.5. Dislocation Density
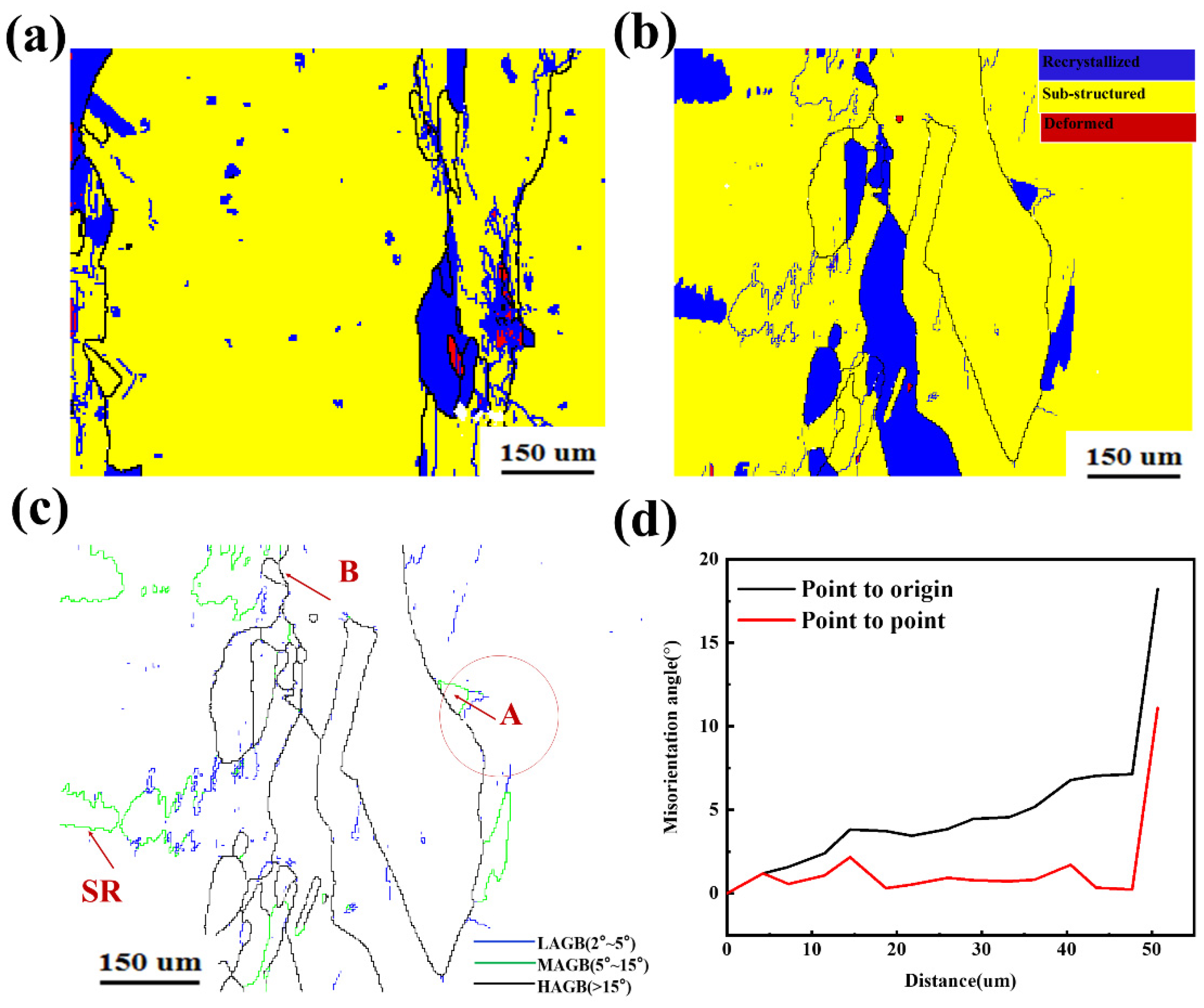
3.6. Dynamic Recrystallization Behavior
4. Conclusions
- The proposed modeling’s residual stress results are in good agreement with the experimental data, including the residual strain and GND distributions;
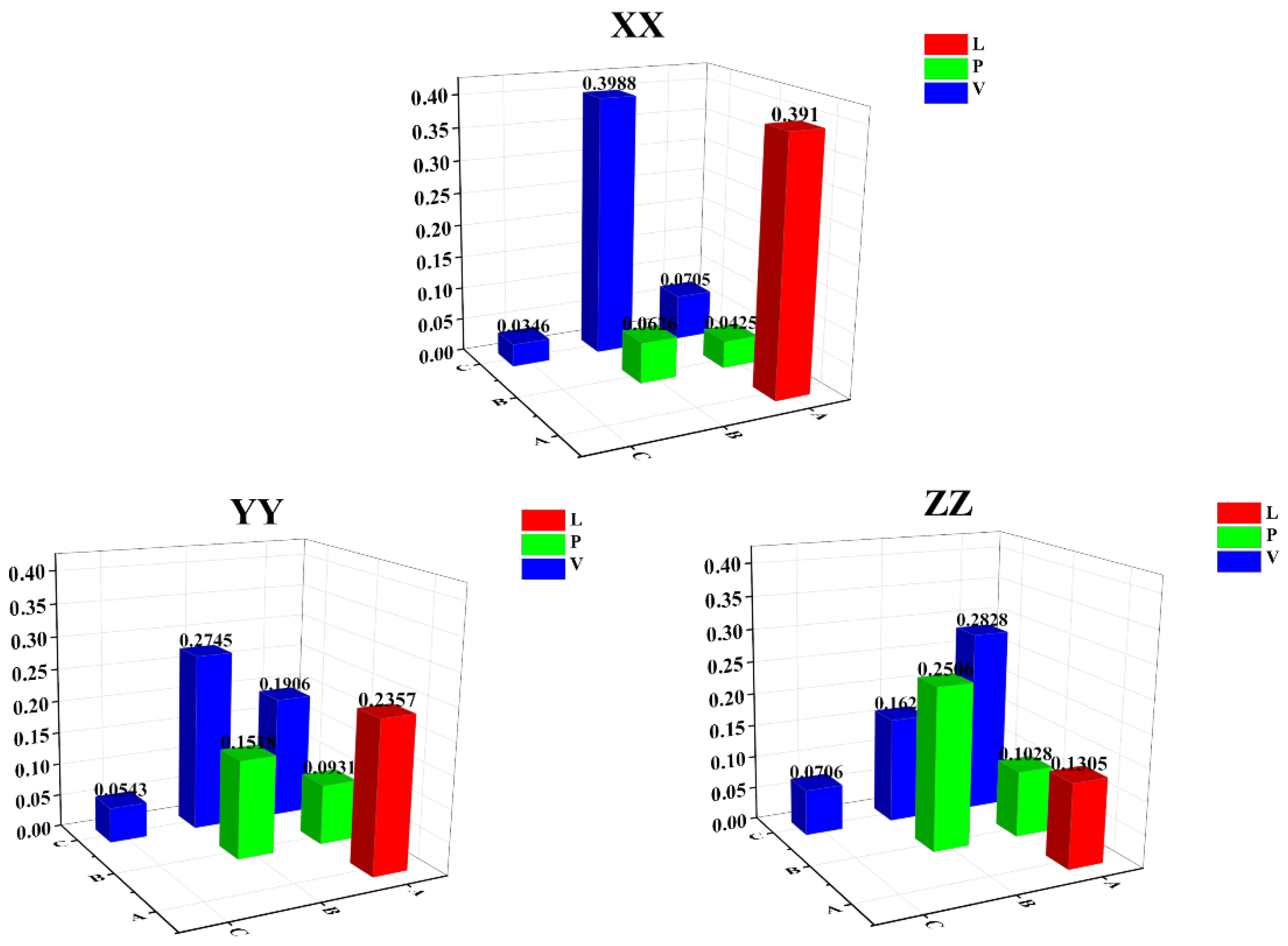
- Based on the analysis of the D-MORPH-HDMR influencing factor results, the degree of impact of process parameters on the RS for multilayer deposition was further quantified, taking into account the important role of the coupling of different parameters. The results of the research reveal that the amplified effect of the influence of the three input variables (layer thickness, L; laser power, P; and scanning speed, v) on the transverse stress and thickness-direction stress is L > P > v. In contrast, the influence of the three variables on the longitudinal stress is P > L > v;
- For DED of thin-walled parts formed from austenitic stainless steel, the selection of a lower deposition layer thickness L (200 μm), a moderate laser power P (600–800 W), and a higher scan rate v (12–16 mm/s) is of great significance to the reduction of residual stresses in the workpiece;
- The main mechanism for the formation of DDRX and CDRX is the expansion of pre-existing grains and the rotation of sub-grains, respectively. The sample bottom had more thermo-mechanical cycles than the top, resulting in a larger dislocation density and hence a higher likelihood of DDRX.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Clark, S.J.; Collins, D.M.; Marussi, S.; Hunt, S.A.; Fenech, D.M.; Connolley, T.; Atwood, R.C.; Magdysyuk, O.V.; Baxter, G.J. Correlative synchrotron X-ray imaging and diffraction of directed energy deposition additive manufacturing. Acta Mater. 2021, 209, 116777. [Google Scholar] [CrossRef]
- Bajaj, P.; Hariharan, A.; Kini, A.; Kürnsteiner, P.; Raabe, D.; Jägle, E.A. Steels in additive manufacturing: A review of their microstructure and properties. Mater. Sci. Eng. A 2019, 772, 138633. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Voisin, T.; Forien, J.-B.; Perron, A.; Aubry, S.; Bertin, N.; Samanta, A.; Baker, A.; Wang, Y.M. New insights on cellular structures strengthening mechanisms and thermal stability of an austenitic stainless steel fabricated by laser powder-bed-fusion. Acta Mater. 2021, 203, 116476. [Google Scholar] [CrossRef]
- Wang, Y.M.; Voisin, T.; McKeown, J.T.; Ye, J.; Calta, N.P.; Li, Z.; Zeng, Z.; Zhang, Y.; Chen, W.; Roehling, T.T. Additively manufactured hierarchical stainless steels with high strength and ductility. Nat. Mater. 2018, 17, 63–71. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Ding, Q.; Zhong, Y.; Zou, J.; Wu, J.; Chiu, Y.-L.; Li, J.; Zhang, Z.; Yu, Q.; Shen, Z. Dislocation network in additive manufactured steel breaks strength–ductility trade-off. Mater. Today 2018, 21, 354–361. [Google Scholar] [CrossRef] [Green Version]
- Yin, Y.; Sun, J.; Guo, J.; Kan, X.; Yang, D. Mechanism of high yield strength and yield ratio of 316 L stainless steel by additive manufacturing. Mater. Sci. Eng. A 2019, 744, 773–777. [Google Scholar] [CrossRef]
- Kong, D.; Dong, C.; Wei, S.; Ni, X.; Zhang, L.; Li, R.; Wang, L.; Man, C.; Li, X. About metastable cellular structure in additively manufactured austenitic stainless steels. Addit. Manuf. 2020, 38, 101804. [Google Scholar] [CrossRef]
- Xiao, H.; Li, S.M.; Xiao, W.J.; Li, Y.Q.; Cha, L.M.; Mazumder, J.; Song, L.J. Effects of laser modes on Nb segregation and Laves phase formation during laser additive manufacturing of nickel-based superalloy. Mater. Lett. 2017, 188, 260–262. [Google Scholar] [CrossRef]
- Xiao, W.; Li, S.; Wang, C.; Shi, Y.; Mazumder, J.; Xing, H.; Song, L. Multi-scale simulation of dendrite growth for direct energy deposition of nickel-based superalloys. Mater. Des. 2019, 164, 107553. [Google Scholar] [CrossRef]
- Zhang, S.; Lin, X.; Wang, L.; Yu, X.; Hu, Y.; Yang, H.; Lei, L.; Huang, W. Strengthening mechanisms in selective laser-melted Inconel718 superalloy. Mater. Sci. Eng. A 2021, 812, 141145. [Google Scholar] [CrossRef]
- Xiao, W.; Xu, Y.; Xiao, H.; Li, S.; Song, L. Investigation of the Nb element segregation for laser additive manufacturing of nickel-based superalloys. Int. J. Heat Mass Transf. 2021, 180, 121800. [Google Scholar] [CrossRef]
- Promoppatum, P.; Rollett, A.D. Influence of material constitutive models on thermomechanical behaviors in the laser powder bed fusion of Ti-6Al-4V. Addit. Manuf. 2021, 37, 101680. [Google Scholar] [CrossRef]
- Xiao, Z.; Chen, C.; Zhu, H.; Hu, Z.; Nagarajan, B.; Guo, L.; Zeng, X. Study of residual stress in selective laser melting of Ti6Al4V. Mater. Des. 2020, 193, 108846. [Google Scholar] [CrossRef]
- Tofail, S.A.M.; Koumoulos, E.P.; Bandyopadhyay, A.; Bose, S.; O’Donoghue, L.; Charitidis, C. Additive manufacturing: Scientific and technological challenges, market uptake and opportunities. Mater. Today 2018, 21, 22–37. [Google Scholar] [CrossRef]
- Bartlett, J.L.; Li, X. An overview of residual stresses in metal powder bed fusion. Addit. Manuf. 2019, 27, 131–149. [Google Scholar] [CrossRef]
- Yakout, M.; Elbestawi, M.; Veldhuis, S.C.; Nangle-Smith, S. Influence of thermal properties on residual stresses in SLM of aerospace alloys. Rapid Prototyp. J. 2020, 26, 213–222. [Google Scholar] [CrossRef]
- Mukherjee, T.; Manvatkar, V.; De, A.; DebRoy, T. Mitigation of thermal distortion during additive manufacturing. Scr. Mater. 2017, 127, 79–83. [Google Scholar] [CrossRef] [Green Version]
- Wu, A.S.; Brown, D.W.; Kumar, M.; Gallegos, G.F.; King, W.E. An experimental investigation into additive manufacturing-induced residual stresses in 316L stainless steel. Metall. Mater. Trans. A 2014, 45, 6260–6270. [Google Scholar] [CrossRef]
- Levkulich, N.; Semiatin, S.; Gockel, J.; Middendorf, J.; DeWald, A.; Klingbeil, N. The effect of process parameters on residual stress evolution and distortion in the laser powder bed fusion of Ti-6Al-4V. Addit. Manuf. 2019, 28, 475–484. [Google Scholar] [CrossRef]
- Brückner, F.; Lepski, D.; Beyer, E. Modeling the influence of process parameters and additional heat sources on residual stresses in laser cladding. J. Therm. Spray Technol. 2007, 16, 355–373. [Google Scholar] [CrossRef]
- Shiomi, M.; Osakada, K.; Nakamura, K.; Yamashita, T.; Abe, F. Residual stress within metallic model made by selective laser melting process. CIRP Ann. 2004, 53, 195–198. [Google Scholar] [CrossRef]
- Mukherjee, T.; Zhang, W.; DebRoy, T. An improved prediction of residual stresses and distortion in additive manufacturing. Comput. Mater. Sci. 2017, 126, 360–372. [Google Scholar] [CrossRef] [Green Version]
- Ghasri-Khouzani, M.; Peng, H.; Rogge, R.; Attardo, R.; Ostiguy, P.; Neidig, J.; Billo, R.; Hoelzle, D.; Shankar, M. Experimental measurement of residual stress and distortion in additively manufactured stainless steel components with various dimensions. Mater. Sci. Eng. A 2017, 707, 689–700. [Google Scholar] [CrossRef]
- Cheng, B.; Shrestha, S.; Chou, K. Stress and deformation evaluations of scanning strategy effect in selective laser melting. Addit. Manuf. 2016, 12, 240–251. [Google Scholar]
- Saboori, A.; Piscopo, G.; Lai, M.; Salmi, A.; Biamino, S. An investigation on the effect of deposition pattern on the microstructure, mechanical properties and residual stress of 316L produced by Directed Energy Deposition. Mater. Sci. Eng. A 2020, 780, 139179. [Google Scholar] [CrossRef]
- Yakout, M.; Elbestawi, M.A.; Veldhuis, S.C. Density and mechanical properties in selective laser melting of Invar 36 and stainless steel 316L. J. Mater. Process. Technol. 2019, 266, 397–420. [Google Scholar] [CrossRef]
- Zou, S.; Xiao, H.; Ye, F.; Li, Z.; Tang, W.; Zhu, F.; Chen, C.; Zhu, C. Numerical analysis of the effect of the scan strategy on the residual stress in the multi-laser selective laser melting. Results Phys. 2020, 16, 103005. [Google Scholar] [CrossRef]
- Sharma, R.; Kumar, A. Track-scale simulations of selective laser melting to investigate development and mitigation of thermal stresses. Lasers Manuf. Mater. Process. 2019, 6, 464–492. [Google Scholar] [CrossRef]
- Wang, H.; Chen, L.; Ye, F.; Chen, L. Global sensitivity analysis for fiber reinforced composite fiber path based on D-MORPH-HDMR algorithm. Struct. Multidiscip. Optim. 2017, 56, 697–712. [Google Scholar] [CrossRef]
- Smith, T.R.; Sugar, J.D.; San Marchi, C.; Schoenung, J.M. Microstructural development in DED stainless steels: Applying welding models to elucidate the impact of processing and alloy composition. J. Mater. Sci. 2020, 56, 762–780. [Google Scholar] [CrossRef]
- Banerjee, A.; Messina, S.; Begley, M.R.; Schwalbach, E.J.; Groeber, M.A.; Musinski, W.D.; Shade, P.A.; Cox, M.E.; Miller, J.D.; Hemker, K.J. The mechanical response of additively manufactured IN625 thin-walled structures. Scr. Mater. 2021, 205, 114188. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, D.; Wang, P.; Yan, M.; Yang, C.; Chen, Z.; Lu, J.; Lu, Z. Additive manufacturing of metals: Microstructure evolution and multistage control. J. Mater. Sci. Technol. 2022, 100, 224–236. [Google Scholar] [CrossRef]
- Li, H.; Huang, Y.; Sun, J.; Lu, Y. The relationship between thermo-mechanical history, microstructure and mechanical properties in additively manufactured CoCrFeMnNi high entropy alloy. J. Mater. Sci. Technol. 2021, 77, 187–195. [Google Scholar] [CrossRef]
- Fu, J.; Qu, S.; Ding, J.; Song, X.; Fu, M.W. Comparison of the microstructure, mechanical properties and distortion of stainless steel 316 L fabricated by micro and conventional laser powder bed fusion. Addit. Manuf. 2021, 44, 102067. [Google Scholar] [CrossRef]
- Gorsse, S.; Hutchinson, C.; Gouné, M.; Banerjee, R. Additive manufacturing of metals: A brief review of the characteristic microstructures and properties of steels, Ti-6Al-4V and high-entropy alloys. Sci. Technol. Adv. Mater. 2017, 18, 584–610. [Google Scholar] [CrossRef] [Green Version]
- Chew, Y.; Zhu, Z.; Weng, F.; Gao, S.; Ng, F.; Lee, B.; Bi, G. Microstructure and mechanical behavior of laser aided additive manufactured low carbon interstitial Fe49. 5Mn30Co10Cr10C0. 5 multicomponent alloy. J. Mater. Sci. Technol. 2021, 77, 38–46. [Google Scholar] [CrossRef]
- Smith, T.R.; Sugar, J.D.; San Marchi, C.; Schoenung, J.M. Strengthening mechanisms in directed energy deposited austenitic stainless steel. Acta Mater. 2019, 164, 728–740. [Google Scholar] [CrossRef]
- Yan, Z.; Zou, K.; Cheng, M.; Zhou, Z.; Song, L. Revealing relationships between heterogeneous microstructure and strengthening mechanism of austenitic stainless steels fabricated by directed energy deposition (DED). J. Mater. Res. Technol. 2021, 15, 582–594. [Google Scholar] [CrossRef]
- Wang, G.; Ouyang, H.; Fan, C.; Guo, Q.; Li, Z.; Yan, W.; Li, Z. The origin of high-density dislocations in additively manufactured metals. Mater. Res. Lett. 2020, 8, 283–290. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Z.; Chen, H.; Wang, A.; Liu, J.; Liu, H.; Zheng, R.; Nai, S.; Primig, S.; Babu, S. Effect of cyclic rapid thermal loadings on the microstructural evolution of a CrMnFeCoNi high-entropy alloy manufactured by selective laser melting. Acta Mater. 2020, 196, 609–625. [Google Scholar] [CrossRef]
- Bertsch, K.; de Bellefon, G.M.; Kuehl, B.; Thoma, D. Origin of dislocation structures in an additively manufactured austenitic stainless steel 316L. Acta Mater. 2020, 199, 19–33. [Google Scholar] [CrossRef]
- Barkia, B.; Aubry, P.; Haghi-Ashtiani, P.; Auger, T.; Gosmain, L.; Schuster, F.; Maskrot, H. On the origin of the high tensile strength and ductility of additively manufactured 316L stainless steel: Multiscale investigation. J. Mater. Sci. Technol. 2020, 41, 209–218. [Google Scholar] [CrossRef]
- Sabzi, H.E.; Aboulkhair, N.T.; Liang, X.; Li, X.-H.; Simonelli, M.; Fu, H.; Rivera-Díaz-del-Castillo, P.E. Grain refinement in laser powder bed fusion: The influence of dynamic recrystallization and recovery. Mater. Des. 2020, 196, 109181. [Google Scholar] [CrossRef]
- Hu, Y.; Lin, X.; Lu, X.; Zhang, S.; Yang, H.; Wei, L.; Huang, W. Evolution of solidification microstructure and dynamic recrystallisation of Inconel 625 during laser solid forming process. J. Mater. Sci. 2018, 53, 15650–15666. [Google Scholar] [CrossRef]
- Denlinger, E.R.; Jagdale, V.; Srinivasan, G.V.; El-Wardany, T.; Michaleris, P. Thermal modeling of Inconel 718 processed with powder bed fusion and experimental validation using in situ measurements. Addit. Manuf. 2016, 11, 7–15. [Google Scholar] [CrossRef]
- Vasinonta, A.; Beuth, J.L.; Griffith, M. Process maps for predicting residual stress and melt pool size in the laser-based fabrication of thin-walled structures. J. Manuf. Sci. Eng. 2007, 129, 101–109. [Google Scholar] [CrossRef]
- Vastola, G.; Zhang, G.; Pei, Q.X.; Zhang, Y.W. Controlling of residual stress in additive manufacturing of Ti6Al4V by finite element modeling. Addit. Manuf. 2016, 12, 231–239. [Google Scholar] [CrossRef]
- Lua, X.; Lin, X.; Chiumentic, M.; Cerverac, M.; Li, J.; Ma, L.; Wei, L.; Hu, Y.; Huang, W. Finite element analysis and experimental validation of the thermomechanical behavior in laser solid forming of Ti-6Al-4V. Addit. Manuf. 2018, 21, 30–40. [Google Scholar] [CrossRef]
- Wang, Z.; Denlinger, E.; Michaleris, P.; Stoica, A.D.; Ma, D.; Beese, A.M. Residual stress mapping in Inconel 625 fabricated through additive manufacturing: Method for neutron diffraction measurements to validate thermomechanical model predictions. Mater. Des. 2017, 113, 169–177. [Google Scholar] [CrossRef] [Green Version]
- Cao, J.; Gharghouri, M.A.; Nash, P. Finite-element analysis and experimental validation of thermal residual stress and distortion in electron beam additive manufactured Ti-6Al-4V build plates. J. Mater. Process. Technol. 2016, 237, 409–419. [Google Scholar] [CrossRef]
- Ali, H.; Ghadbeigi, H.; Mumtaz, K. Effect of scanning strategies on residual stress and mechanical properties of Selective Laser Melted Ti6Al4V. Mater. Sci. Eng. A 2018, 712, 175–187. [Google Scholar] [CrossRef]
- Yan, W.; Yue, Z.; Feng, J. Study on the role of deposition path in electron beam freeform fabrication process. Rapid Prototyp. J. 2017, 23, 1057–1068. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, S.; Gan, Y.; Huang, T.; Yang, C.; Junjie, L.; Lin, J. Study on the microstructure, mechanical property and residual stress of SLM Inconel-718 alloy manufactured by differing island scanning strategy. Opt. Laser Technol. 2015, 75, 197–206. [Google Scholar] [CrossRef]
- Denlinger, E.R.; Heigel, J.C.; Michaleris, P.; Palmer, T.A. Effect of inter-layer dwell time on distortion and residual stress in additive manufacturing of titanium and nickel alloys. J. Mater. Process. Technol. 2015, 215, 123–131. [Google Scholar] [CrossRef]
- DeWald, A.T.; Hill, M.R. Multi-Axial Contour Method for Mapping Residual Stresses in Continuously Processed Bodies. Exp. Mech. 2006, 46, 473. [Google Scholar] [CrossRef]
- Yan, Z.; Song, L.; Liu, W.; Zou, X.; Zhou, Z. Numerical analysis of thermal stress evolution of pulsed-wave laser direct energy deposition. Int. J. Adv. Manuf. Technol. 2021, 115, 1399–1410. [Google Scholar] [CrossRef]
- Gao, H.; Huang, Y. Geometrically necessary dislocation and size-dependent plasticity. Scr. Mater. 2003, 48, 113–118. [Google Scholar] [CrossRef]
- Hollomon, J.H. Tensile deformation. Aime Trans. 1945, 12, 1–22. [Google Scholar]
- Smith, T.R.; Sugar, J.D.; Schoenung, J.M.; San Marchi, C. Anomalous annealing response of directed energy deposited type 304L austenitic stainless steel. Jom 2018, 70, 358–363. [Google Scholar] [CrossRef]
- Wang, X.; Muñiz-Lerma, J.; Sanchez-Mata, O.; Shandiz, M.A.; Brodusch, N.; Gauvin, R.; Brochu, M. Characterization of single crystalline austenitic stainless steel thin struts processed by laser powder bed fusion. Scr. Mater. 2019, 163, 51–56. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, M.; Liu, Z.; Li, C.; Zhang, Y. Role of local recrystallization behavior on fatigue performance of SLMed 304L austenitic stainless steels. Mater. Charact. 2021, 177, 111159. [Google Scholar] [CrossRef]
- Gao, S.; Hu, Z.; Duchamp, M.; Krishnan, P.S.R.; Tekumalla, S.; Song, X.; Seita, M. Recrystallization-based grain boundary engineering of 316L stainless steel produced via selective laser melting. Acta Mater. 2020, 200, 366–377. [Google Scholar] [CrossRef]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef] [Green Version]
- Heidarzadeh, A.; Zavašnik, J.; Shabadi, R.; Mousavian, R.T. Dynamic recrystallization’s role in strength-ductility trade-off in polycrystalline Fe–Cr–Ni stainless steels produced by laser powder bed fusion. Mater. Sci. Eng. A 2021, 814, 141214. [Google Scholar] [CrossRef]




| Element | Cr | Ni | Mo | Si | Mn | C | S | P | O | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 16.9 | 11.6 | 2.25 | 0.59 | 0.54 | 0.013 | 0.005 | 0.011 | 0.011 | Bal. |
| Process Parameter | Value |
|---|---|
| Laser power, P (W) | 400, 600, 800 |
| Scanning speed, v (mm/s) | 8, 12, 16 |
| Powder layer thickness, L (μm) | 200, 400, 600 |
| Beam diameter, D (mm) | 1.2 |
| Interlayer powder laying time (s) | 0 |
| Trial No. | Factor A | Factor B | Factor C |
|---|---|---|---|
| Layer Thickness, L (μm) | Laser Power, P (W) | Scanning Speed, v (mm/s) | |
| 1 | 200 | 400 | 8 |
| 2 | 200 | 600 | 16 |
| 3 | 200 | 800 | 12 |
| 4 | 400 | 400 | 16 |
| 5 | 400 | 600 | 12 |
| 6 | 400 | 800 | 8 |
| 7 | 600 | 400 | 12 |
| 8 | 600 | 600 | 8 |
| 9 | 600 | 800 | 16 |
| Trial No. | XX-Stress | YY-Stress | ZZ-Stress |
|---|---|---|---|
| Mpa | Mpa | Mpa | |
| 1 | 525 | 463 | 488 |
| 2 | 392 | 299 | 274 |
| 3 | 412 | 358 | 385 |
| 4 | 442 | 666 | 473 |
| 5 | 368 | 548 | 390 |
| 6 | 712 | 790 | 992 |
| 7 | 841 | 871 | 489 |
| 8 | 1030 | 536 | 470 |
| 9 | 1303 | 1441 | 1483 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Zou, X.; Li, S.; Luo, G.; Song, L. A Study on the Thermo-Mechanical History, Residual Stress, and Dynamic Recrystallization Mechanisms in Additively Manufactured Austenitic Stainless Steels. Metals 2022, 12, 1109. https://doi.org/10.3390/met12071109
Yan Z, Zou X, Li S, Luo G, Song L. A Study on the Thermo-Mechanical History, Residual Stress, and Dynamic Recrystallization Mechanisms in Additively Manufactured Austenitic Stainless Steels. Metals. 2022; 12(7):1109. https://doi.org/10.3390/met12071109
Chicago/Turabian StyleYan, Zhou, Xi Zou, Simeng Li, Guoyun Luo, and Lijun Song. 2022. "A Study on the Thermo-Mechanical History, Residual Stress, and Dynamic Recrystallization Mechanisms in Additively Manufactured Austenitic Stainless Steels" Metals 12, no. 7: 1109. https://doi.org/10.3390/met12071109





