Next Article in Journal
Effect of Mn Element on the Structures and Properties of A2B7-Type La–Y–Ni-Based Hydrogen Storage Alloys
Previous Article in Journal
Why Color Matters—Proposing a Quantitative Stability Criterion for Laser Beam Processing of Metals Based on Their Fundamental Optical Properties
Previous Article in Special Issue
Analysis of Fatigue Strength of L-PBF AlSi10Mg with Different Surface Post-Processes: Effect of Residual Stresses
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 12
Issue 7
10.3390/met12071121
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Numerical Study into the Effect of Machining on the Interaction between Surface Roughness and Surface Breaking Defects on the Durability of WAAM Ti-6Al-4V Parts

by
Daren Peng
1,2,
Rhys Jones
1,2,*,
Andrew S. M. Ang
1,
Victor Champagne
3,
Aaron Birt
3 and
Alex Michelson
4
1
ARC Industrial Transformation Training Centre on Surface Engineering for Advanced Materials, School of Engineering, Swinburne University of Technology, John Street, Hawthorn, VIC 3122, Australia
2
Centre of Expertise for Structural Mechanics, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC 3800, Australia
3
US Army Research Laboratory, U.S. Army Combat Capabilities Development Command Weapons and Materials Research Directorate, Aberdeen Proving Ground, Aberdeen, MD 21005, USA
4
Solvus Global, 104 Prescott Street, Worcester, MA 01605, USA
*
Author to whom correspondence should be addressed.
Metals 2022, 12(7), 1121; https://doi.org/10.3390/met12071121
Submission received: 17 April 2022 / Revised: 25 June 2022 / Accepted: 27 June 2022 / Published: 29 June 2022
(This article belongs to the Special Issue Fatigue Behaviour of Additive Manufactured Metallic Materials)
Browse Figures
Versions Notes

Abstract

:
The airworthiness certification of military aircraft requires a durability analysis be performed using linear elastic fracture mechanics (LEFM). Furthermore, such analyses need to use a valid small crack growth equation. This paper focuses on the effect of rough surfaces and the effect of machining the surface on the durability of AM parts using LEFM and a valid small crack growth equation for the material. To this end, this paper analyses the effect of surface roughness on wire and arc additively manufactured (WAAM) Ti-6Al-4V titanium parts and the effect of machining on the durability of a part. The analysis reveals that the life of the component is a relatively strong function of the degree of surface roughness, and that the durability of a specimen is a strong function of the local radius of the curvature of the trough. It also appears that surfaces with tall narrow roughness will not overly benefit from partial machining of the surface.

1. Introduction

The 2019 memo by the Under Secretary, Acquisition and Sustainment [1] mandated the use of additive manufacturing (AM), and stated that AM parts could be used in both critical and non-critical applications. US Army Directive 2019-19 [2] subsequently stated that:
(i)
Advanced manufacturing can be used to address the readiness challenges posed by parts obsolescence, diminishing sources of supply, and sustained operations in austere environments.
(ii)
If employed to the maximum extent, advanced manufacturing could transform battlefield logistics through on-demand fabrication of parts close to the point of need, thus reducing the large number of parts stored and transported around the world.
The certification requirements for AM components are enunciated in United States Air Force (USAF) Structures Bulletin EZ-SB-19-01 [3], MIL-STD-1530D [4], and the United States (US) Joint Services Structural Guidelines JSSG2006 [5]. A proposed method for meeting the durability and damage tolerance (DADT) certification requirements is outlined in the recent keynote lecture at the 2021 EASA-FAA Industry Event [6]. This approach is built on the statement contained in MIL-STD-1530D [4] that analysis is the key to certification, and that the role of testing is merely to validate or correct the analysis.
In this context, is now well known that the fatigue life of additively manufactured (AM) parts can be a strong function of surface roughness [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Indeed, it has been suggested that the fatigue life of an AM part is driven by the size and nature of the defects at the root of the notches associated with the surface roughness [7,8,12,20,26,27,28,29,30,31].
When discussing the durability and damage tolerance (DADT) analyses needed to certify a part, MIL-STD-1530D states that the DADT analysis shall consider the disciplines of fracture mechanics as distinct from stress or strain life approaches. EZ-SB-19-01 [3] enunciates that both surface roughness and defect size be considered together. To this end, EZ-SB-19-01 requires the DADT analysis to utilize an “Equivalent Initial Damage Size (EIDS)” as per MIL-STD-1530D and JSSG2006. Here, EIDS is defined as per MIL-STD-1530D, viz: “an analytical characterization of the initial quality of the aircraft structure at the time of manufacture, modification or repair”. Examples of this approach applied to the analysis of rough surfaces on the fatigue life of AM parts are given in [21]. However, as highlighted in [21], this analysis used the long crack da/dN versus ΔK curve rather than the corresponding short crack curve. (The authors of [21] explained that this was performed in order to simplify the analysis.) In this context, it is important point to note that, as explained in [32,33,34], when performing a durability analysis the analysis tools needed to perform a durability analysis differ from those needed to perform a damage tolerance assessment. This was first documented in the USAF study into cracking in an operational F-15 aircraft [33], where it was shown that, when the small crack da/dN versus ΔK curve was not used, the EIDS values were dependent on the load spectrum; see [32,33] for more details. Consequently, the durability analysis of AM parts requires the use of the associated small crack da/dN versus ΔK curve. Furthermore, as illustrated in Figure 4 in NASA HDBK-5010 [35], the durability analysis requires the use of the worst possible (i.e., upper bound) da/dN versus ΔK curve.
Fortunately, as noted in [25] and in [6,24,28,30,32,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58], the growth of both long and small cracks in both conventionally manufactured and AM parts can be modelled using the Hartman–Schijve crack growth equation, viz
da/dN = D (Δκ)p
where Δκ is the Schwalbe crack driving force [52], viz:
Δκ = (ΔK − ΔKthr)/(1 − Kmax/A)1/2
Here, a is the crack length/depth, N is the number of cycles, D and p are material constants, K is the stress intensity factor, Kmax and Kmin are the maximum and minimum values of the stress intensity factor seen in the cycle, ∆K = (Kmax − Kmin) is the range of the stress intensity factor that is seen in a cycle, ΔKthr is the “effective fatigue threshold”, and A is the cyclic fracture toughness. A related formulation is given in [59], where it is shown to be able to represent the growth of cracks that nucleate from near surface porosity. As explained in [32], the terms ∆Kthr and A are best interpreted as parameters that are chosen so as to fit the measured da/dN versus ∆K data.
A feature of this formulation is that, as noted in [47], for AM Ti-6Al-4V, when allowance is made for the effect of the different build processes and post built processing on the terms ΔKthr and A, then each of the da/dN versus ∆κ curves in the 30 different tests analysed in [48], the 34 different tests in [49], and the 13 different tests in [50] all collapse onto the same master curve. As such, for both conventionally and AM Ti-6Al-4V the values of D (=2.79 × 10−10) and p (=2.12) are true materials constants, and remain the same for each of these seventy seven tests. The mean value of A given in [49] for as-built AM Ti-6Al-4V surfaces is 62 MPa √m.
Extensions of this observation, namely that when allowance is made for the effect of the different build processes and post built processing on the terms ΔKthr and A then the da/dN versus ∆κ curves collapse to a single curve, to a wide range of conventionally manufactured, AM and cold spray additively manufactured (CSAM) materials are given in [53,54].
An additional feature of this formulation is that it has also been shown [6,25,27,28,30,41,42,48,51,53] to account for:
(a)
The effect of different AM processes;
(b)
The effect of different build directions;
(c)
The residual stress fields induced by the different manufacturing process;
(d)
The variability in the crack growth rates associated with AM Ti-6Al-4V, thus enabling the worst case (mean-3σ, where σ is the variance) crack growth curve required in [35] for a durability analysis to be determined; see [48].
As such, the focus of the present paper is to present a numerical study which uses the small crack growth equation for T-6Al-4V, i.e., Equation (1) with the threshold term set to a small value, to investigate the effect of as-built (rough) surfaces on the durability of an as-built WAAM Ti-6Al-4V specimen. Noting that surface machining has been proposed [16,17,18,22] to improve durability, an investigation into the effect machining rough surfaces is also presented.
In this context, it should also be noted that, as shown in [30,48,50], this formulation is known to be able to accurately compute the interaction between rough surfaces on the growth of small naturally occurring material discontinuities in conventionally built materials.

2. Materials and Methods

The majority of references quoted in this paper are taken from peer-reviewed journals. The conference proceedings referenced are fully refereed and can be obtained from the web. Similarly, the referenced texts are available via Google searches. The journal papers referenced are in journals that are either listed in SCOPUS or in the World of Science (WOS). The book chapters referenced are listed in SCOPUS. Seven of the references are available on various US Department of Defense DTIC websites, and one reference is available on a NASA website. Keywords that were used in these searchers were additive manufacturing, aircraft certification, durability, damage tolerance, Hartman–Schijve crack growth equation, and small cracks.
This paper uses finite element analysis to assess the effect of surface roughness and partial machining of the surface on the stress distribution of a WAAM built specimen. The surface roughness analysed were based on measurements obtained on WAAM samples built at Solvus Global in the US. The effect of these rough surfaces and partial machining on durability of the specimens was computed using the Hartman–Schijve crack growth equation, which as discussed above has been shown to be able to characterise the growth of both long and small cracks in AM Ti-6Al-4V. A key feature of this analysis is that we study the effect of both different surface roughness heights and different distances between the peaks in the surface roughness using a validated small crack equation for this material. This enables us to comment on the effect of tall narrow surface roughness’s and hence make this paper potentially applicable to a greater range of WAAM built materials, i.e., WAAM built steels.

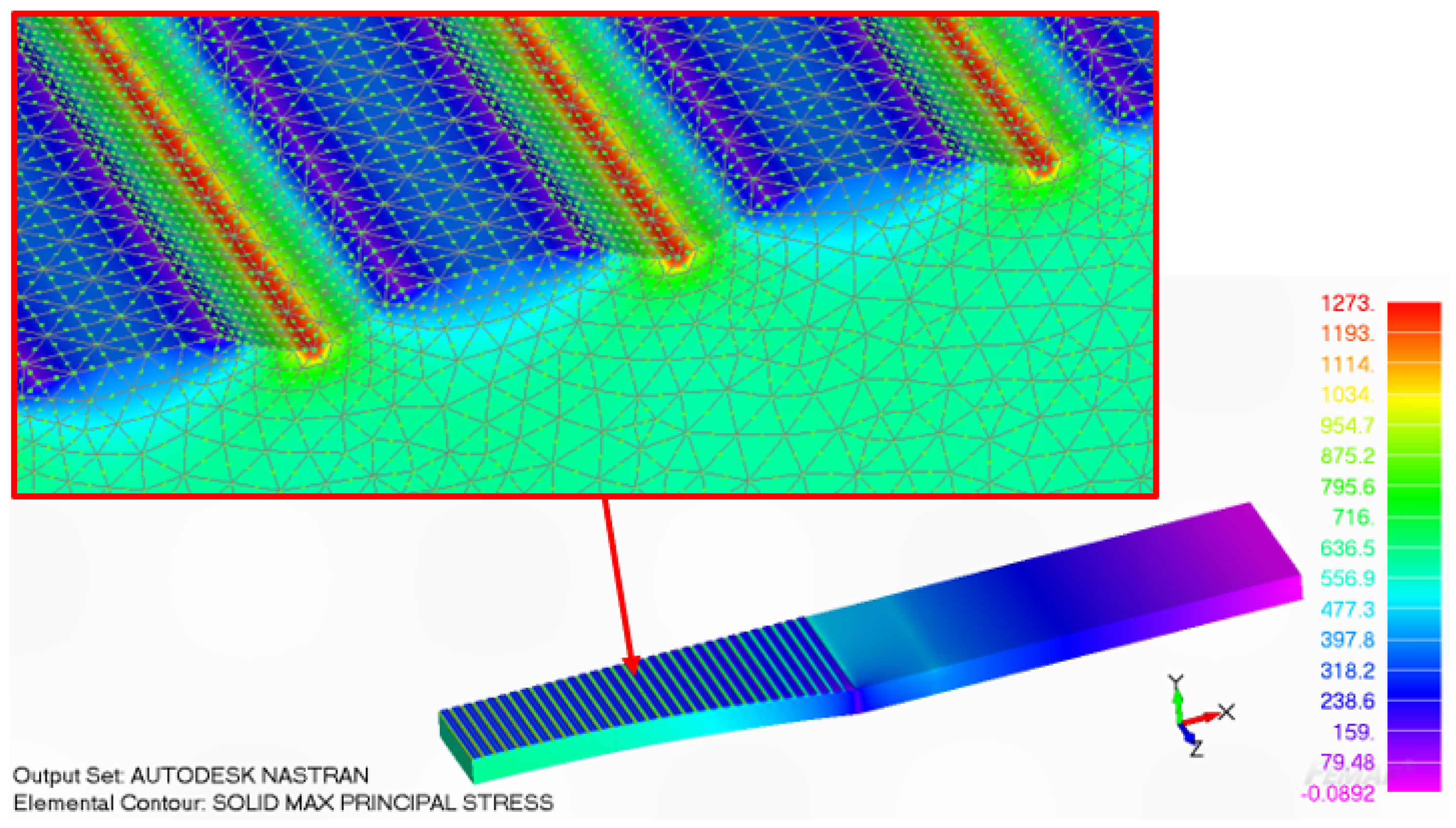
3. On the Interaction between Surface Roughness and Surface Breaking Defects on the Durability of WAAM Ti-6Al-4V Parts

The specimen geometry analysed in this study is the simple dogbone shape shown in Figure 1, where T is the height of the roughness and d is the separation between the peaks. The applied load is such that the working section sees a fatigue cycle with a (average section) maximum stress of 600 MPa and an R ratio of R = 0.1. (The R ratio in a fatigue test is defined as the minimum stress in a cycle divided by the maximum stress in the cycle.) In this preliminary study, specimens with both smooth (i.e., the baseline), and rough surfaces are analysed, as is the effect of machining the surface. The heights (T) of the surface roughness analysed were taken to be either 0.361, 0.142, or 0.071 mm; see Figure 2 and Figure 3. These values were taken from measurements on representative WAAM specimens.
The analysis associated with the “machined surfaces” assumed that half the height (T) had been removed by the machining process. Schematic diagrams showing the geometry of the baseline (smooth surface) specimen, the rough surface specimen and the machined surface specimen geometries are shown in Figure 1, Figure 2 and Figure 3. Nine different cases were analysed. These cases are outlined in Table 1 and Table 2.
A durability analysis was then performed using Equation (1) with D = 2.79 × 10−10, p = 2.12, and A = 62 MPa m . As noted above, this value of A represents the mean value given in [49] for as-built AM Ti-6Al-4V. The durability analysis requires the stress intensity factor solutions along the crack front to be determined as the crack grows. The approach adopted in this study to determine the stress intensity factor solutions is as outlined in [60]. This is a semi-analytical approach which has the advantage that it only uses the uncracked finite element model, and that the cracks are not explicitly modelled; see [60] for more details.
To be consistent with:
(i)
Appendix X3 of the fatigue test standard ASTM E647-15 [61], which questions the existence of a fatigue threshold for small (naturally occurring) cracks.
(ii)
The JSSG2006 [5] and NASA-HDBK-5010 [35] recommendations that the A-basis (mean-3σ) curves be used; see [48] for a more detailed discussion on this statement.
(iii)
The statement in the USAF Damage Tolerance Design Handbook [62] that the time to initiation is small.
(iv)
The methodology used in [45] to predict the crack growth history of cracks that nucleated near surface cracking from material discontinuities in AM Ti-6Al-4V, and, as per [37,41,42,43,48], to allow for the fastest possible growth the durability analyses used ΔKthr = 0.1 MPa m .
As noted above, the USAF Damage Tolerant Design Handbook [62] explains that more than 95% of the life of an airframe is consumed in crack growth so that the time consumed by crack initiation is minimal. Similar conclusions can be found in the USAF Durability Design Handbook [63], and the USAF approach to assessing the risk of failure [64]. These findings agree with those documented in [65], which discusses the Royal Australian Air Force (RAAF) experience with the RAAF F/A-18 fleet. Consequently, since it is accepted that AM material is generally more susceptible to cracking than conventionally manufactured aircraft quality materials and as explained above, the analysis performed in this section essentially enforces the requirement that time to crack initiation be minimal.
In this analysis, it was first assumed that the initial material discontinuity was either a small 0.03 mm deep surface breaking semi-circular crack, or a 0.03 mm quadrant crack located as per Figure 4. In each case, the crack is located at the notch root. The size of this initial defect was taken from [12,22]. The analysis was then repeat for the case when these initial discontinuities were 0.254 mm deep. In each case, for simplicity, the analyses assumed that the surface roughness was a simple wavy pattern; see Figure 3, Figure 4 and Figure 5. The dimensions of this idealized wavy were taken from a typical WAAM specimen built by Solvus Global, for which the build parameters were not recorded. The uncracked finite element models corresponding to Cases 6 and 9 are shown in Figure 6 and Figure 7. This analysis revealed that the stress concentration factors for Cases 6 and 9 were approximately 2.54 and 1.38, respectively.
The effect of these various surface roughness on the computed fatigue lives for the case of a 0.03 mm semi-circular initial crack are given in Table 1 and Figure 8 and Figure 9. (As shown in Table 1 and Table 2, the effect of surface roughness on the fatigue life of a specimen containing a corner crack is very similar to that of a semi-elliptical centrally located crack.) Here, we see that Case 7, which has a roughness that has the smallest height and the largest radius of curvature, is least effected by surface roughness, and that Case 6, which has the greatest height and the smallest radius of curvature is the most effected by surface roughness. Indeed, examining Table 1 and Table 2, and Figure 8 and Figure 9, it appears that the local radius of curvature (associated with the surface roughness) is a key driver in reducing the fatigue life of the specimen.

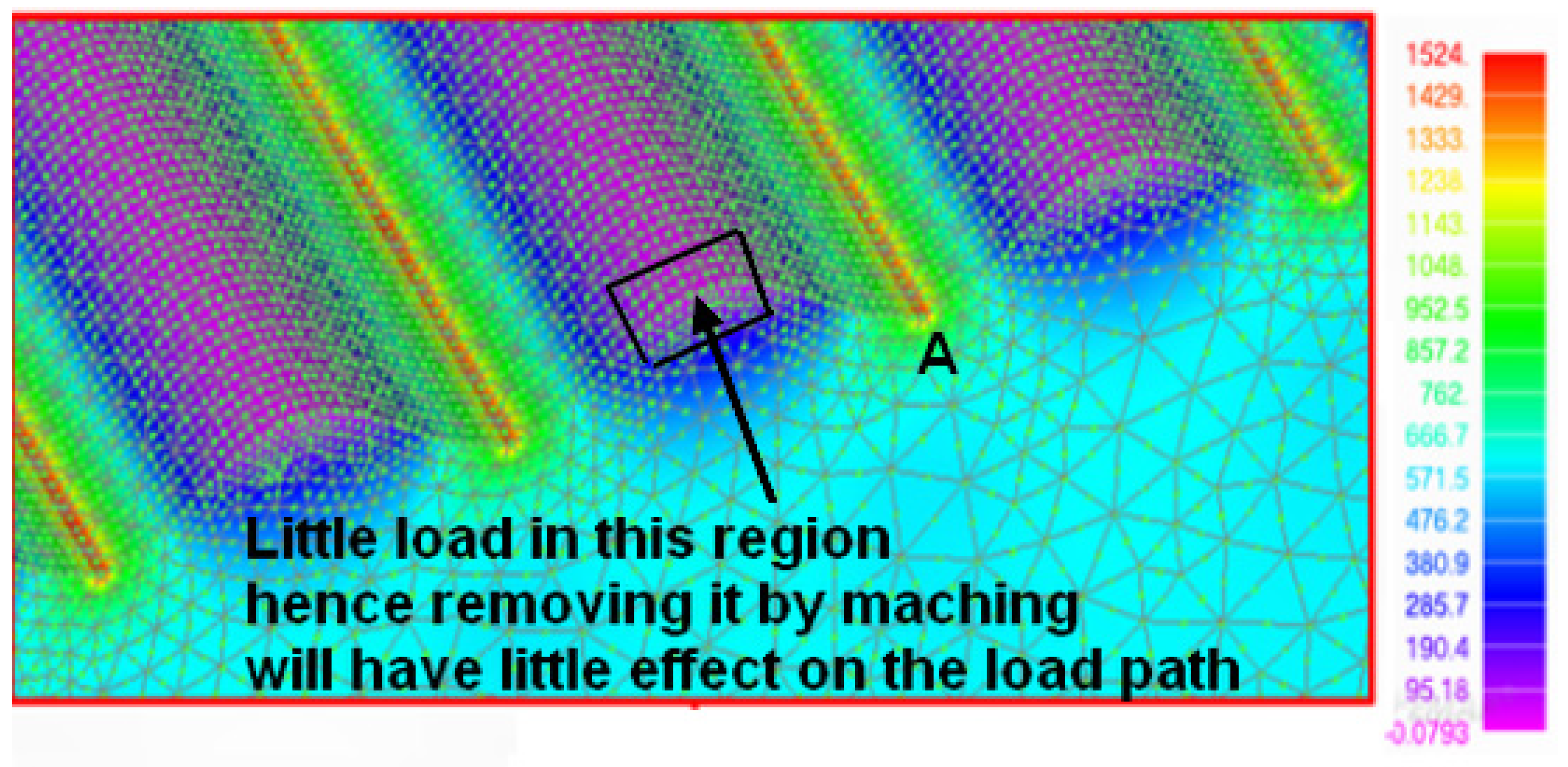
4. Effect of Machining the Rough Surfaces

The paper by Seungjong Lee et al. [22] studied the effect of machining rough surfaces in Ti-6Al-4V specimens fabricated by a laser beam powder bed fusion (LBPF). It concluded that the fatigue lives of as-built and polished specimens, where only half of the height of the surface roughness was removed, were similar. However, the degree of surface roughness in these specimen tests was low. The question thus arises: Is this generally true, or does the result depend on the nature and the height/depth of the surface roughness?
To investigate this question, we next studied the cases where the surfaces associated with the two prior studies were assumed to be machined such that ½ of the height was removed; see Figure 10 and Figure 11.
The effect of machining on the stress distributions associated with Cases 5 and 8, which are the machined versions of Cases 6 and 9, are shown in Figure 12 and Figure 13. Comparing Figure 6 and Figure 12, and Figure 7 and Figure 13, which compare the stress distribution in both un-machined and machined specimens, we see that whilst machining does indeed reduce the local stress concentration it does not remove it. The reason for this can be seen in Figure 14, which is associated with Case 6. Here, we see that the load path is such that very little load flows into the upper half (near peak) region that juts above the mean height of the surface. This phenomenon can be expected to occur whenever the height of the peak (T) divided by d, the separation between the peaks, is large.
Comparing Figure 7 and Figure 13, we see that the reduction in the stress field associated with Case 9 is very small. As shown in Table 1, this results in a small improvement in the fatigue life due to machining. On the other hand comparing Figure 6 and Figure 12 we see that (in this instance) machining results in a slightly greater reduction in the local stress concentration and hence a greater increase in the fatigue life. In other words, it appears that surfaces with tall narrow roughness exhibit the largest reductions in fatigue life and that these cases do not overly benefit from partial machining of the surface.
The results of the durability analysis associated with these machined surfaces are also shown in Figure 8 and Figure 9, and Table 1 and Table 2. Here, we see that, as first reported in [22], removal of a half of the height T does not appear to make a significant difference to the fatigue life. As such, this study, when taken in conjunction with the experimental results presented in [22], suggests that partial machining may only result in a relatively small improvement in durability.

5. Conclusions

MIL-STD-1530D and USAF Structures Bulletin require that any durability analysis be performed using linear elastic fracture mechanics (LEFM). Furthermore, such analyses need to use a valid small crack growth equation. To the best of the authors’ knowledge, this study is the first paper to numerically study the effect of rough surfaces and the effect of machining the surface on the durability of AM parts using LEFM and a valid small crack growth equation for the material. Indeed, a key feature of this analysis is that it uses the Hartman–Schijve crack growth equation, which has been shown to accurately model the growth of small cracks in both conventionally built and AM Ti-6Al-4V.
The primary conclusions that can be drawn from this preliminary analysis are:
  • Comparing the fatigue life-associated surfaces left in the unmachined state, the durability of an AM part appears to be a relatively strong function of the local radius of the curvature of the trough associated with the rough surfaces.
  • Surfaces with tall narrow roughness exhibit the largest reductions in fatigue life and these cases do not overly benefit from partial machining of the surface.
  • The size of the initial material discontinuities, porosity, lack of fusion, etc., associated with the AM process appears to strongly affect the fatigue life of the part.
It should be stressed that whilst this finding may be intuitively obvious, this is the first time that this observation has been supported by a detailed numerical study based on a crack growth equation that has been shown to hold for the growth of small naturally occurring cracks in AM Ti-6Al-4V.

Author Contributions

Problem definition, A.B.; initial draft, R.J.; numerical analysis, D.P.; creation of the uncracked computer models, A.S.M.A.; specimen fabrication and subsequent measurement of surface roughness, and review and editing of the initial draft, A.M.; funding and project overview, V.C. All authors have read and agreed to the published version of the manuscript.

Funding

R.J., A.S.M.A. and D.P. acknowledge funding provided by the US Army International Technology Center, Indo-Pacific (ITC-IPAC), Tokyo, Contract No. FA520921P0164.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The findings and conclusions or recommendations expressed in this paper are those of the authors and do not necessarily reflect the views of the ITC-IPAC.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Under Secretary. Acquisition and Sustainment, Directive-type Memorandum (DTM)-19-006-Interim Policy and Guidance for the Use of Additive Manufacturing (AM) in Support of Materiel Sustainment, Pentagon, Washington, DC, USA. 21 March 2019. Available online: https://www.esd.whs.mil/Portals/54/Documents/DD/issuances/dtm/DTM-19-006.pdf?ver=2019-03-21-075332-443 (accessed on 2 April 2022).
  2. US Army Directive 2019-29. Enabling Readiness and Modernization Through Advanced Manufacturing, Secretary of The Army, Pentagon, Washington, DC, USA. 18 September 2019. Available online: https://armypubs.army.mil/epubs/DR_pubs/DR_a/pdf/web/ARN19451_AD2019-29_Web_Final.pdf (accessed on 2 April 2022).
  3. Structures Bulletin EZ-SB-19-01. Durability and Damage Tolerance Certification for Additive Manufacturing of Aircraft Structural Metallic Parts, Wright Patterson Air Force Base, OH, USA. 10 June 2019. Available online: https://daytonaero.com/usaf-structures-bulletins-library/ (accessed on 2 July 2021).
  4. MIL-STD-1530D. Department Of Defense Standard Practice Aircraft Structural Integrity Program (ASIP). 13 October 2016. Available online: http://everyspec.com/MIL-STD/MIL-STD.../download.php?spec=MIL-STD-1530D (accessed on 2 April 2022).
  5. Department of Defense Joint Service Specification Guide. Aircraft Structures, JSSG-2006. October 1998. Available online: http://everyspec.com/USAF/USAF-General/JSSG-2006_10206/ (accessed on 2 April 2022).
  6. Molent, L. Thoughts on Fatigue Certification of Metal Additive Manufacturing for Aircraft Structures, Keynote Lecture. In EASA-FAA Industry-Regulator AM Event; EASA: Cologne, Germany, 2021; Available online: https://www.easa.europa.eu/newsroom-and-events/events/easa-faa-industry-regulator-am-event-0#group-easa-downloads (accessed on 2 April 2022).
  7. Cao, F.; Zhang, T.; Ryder, M.A.; Lados, D.A. A Review of the Fatigue Properties of Additively Manufactured Ti-6Al-4V. Jom 2018, 70, 349–357. [Google Scholar] [CrossRef]
  8. du Plessisa, A.; Beretta, S. Killer notches: The effect of as-built surface roughness on fatigue failure in AlSi10Mg produced by laser powder bed fusion. Addit. Manuf. 2020, 35, 101424. [Google Scholar] [CrossRef]
  9. Strano, G.; Hao, L.; Everson, R.M.; Evans, K.E. Surface roughness analysis, modelling and prediction in selective laser melting. J. Mater. Process. Technol. 2013, 213, 589–597. [Google Scholar] [CrossRef]
  10. Nicoletto, G.; Konecná, R.; Frkán, M.; Riva, E. Surface roughness and directional fatigue behavior of as-built EBM and DMLS Ti6Al4V. Int. J. Fatigue 2018, 116, 140–148. [Google Scholar] [CrossRef]
  11. Pegues, J.; Roach, M.; Williamson, R.S.; Shamsaei, N. Surface roughness effects on the fatigue strength of additively manufactured Ti-6Al-4V. Int. J. Fatigue 2018, 116, 543–552. [Google Scholar] [CrossRef]
  12. Zhang, J.; Fatemi, A. Surface roughness effect on multiaxial fatigue behavior of additive manufactured metals and its modelling. Theor. Appl. Fract. Mech. 2019, 103, 102260. [Google Scholar] [CrossRef]
  13. Solberg, K.; Berto, F. A diagram for capturing and predicting failure locations in notch geometries produced by additive manufacturing. Int. J. Fatigue 2020, 134, 105428. [Google Scholar] [CrossRef]
  14. Molaei, R.; Fatemi, A.; Sanaei, N.; Pegues, J.; Shamsaei, N.; Shao, S.; Lie, P.; Warner, D.H.; Phan, N. Fatigue of additive manufactured Ti-6Al-4V, Part II: The relationship between microstructure, material cyclic properties, and component performance. Int. J. Fatigue 2020, 132, 105363. [Google Scholar] [CrossRef]
  15. Fatemi, A.; Molaei, R.; Sharifimehr, S.; Phan, N.; Shamsaei, N. Multiaxial fatigue behavior of wrought and additive manufactured Ti-6Al-4V including surface finish effect. Int. J. Fatigue 2017, 100, 347–366. [Google Scholar] [CrossRef]
  16. Bagehorn, S.; Wehr, J.; Maier, H.J. Application of mechanical surface finishing processes for roughness reduction and fatigue improvement of additively manufactured Ti-6Al-4V parts. Int. J. Fatigue 2017, 102, 135–142. [Google Scholar] [CrossRef]
  17. Li, P.; Warner, D.H.; Fatemi, A.; Phan, N. Critical assessment of the fatigue performance of additively manufactured Ti-6Al-4V and perspective for future research. Int. J. Fatigue 2016, 85, 130–143. [Google Scholar] [CrossRef]
  18. Nezhadfar, P.D.; Shrestha, R.; Phan, N.; Shamsaei, N. Fatigue behavior of additively manufactured 17-4 pH stainless steel: Synergistic effects of surface roughness and heat treatment. Int. J. Fatigue 2019, 124, 188–204. [Google Scholar] [CrossRef]
  19. Chen, Z.; Cao, S.; Wu, X.; Davies, C.H.J. Chapter 13, Surface roughness and fatigue properties of selective laser melted Ti-6Al-4V alloy. In Additive Manufacturing for the Aerospace Industry; Froes, F., Boyer, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 283–299. ISBN 978-0-12-814062-8. [Google Scholar]
  20. Samadian, K.; De Waele, W. Fatigue Crack Growth Model Incorporating Surface Waviness For Wire+Arc Additively Manufactured Components. Procedia Struct. Integr. 2020, 28, 1846–1855. [Google Scholar] [CrossRef]
  21. Greitemeier, D.; Donne, C.D.; Syassen, F.; Eufinger, J.; Melz, T. Effect of surface roughness on fatigue performance of additive manufactured Ti-6Al-4V. Mater. Sci. Technol. 2016, 32, 629–634. [Google Scholar] [CrossRef]
  22. Seungjong, L.S.; Rasoolian, B.; Silva, D.F.; Pegues, J.W.; Shamsaei, N. Surface roughness parameter and modeling for fatigue behavior of additive manufactured parts: A non-destructive data-driven approach. Addit. Manuf. 2021, 46, 102094. [Google Scholar] [CrossRef]
  23. Molaei, R.; Fatemi, A.; Phan, N. Significance of hot isostatic pressing (HIP) on multiaxial deformation and fatigue behaviors of additive manufactured Ti-6Al-4V including build orientation and surface roughness effects. Int. J. Fatigue 2018, 117, 352–370. [Google Scholar] [CrossRef]
  24. Sanaei, N.; Fatemi, A. Defect-based fatigue life prediction of L-PBF additive manufactured metals. Eng. Fract. Mech. 2021, 244, 107541. [Google Scholar] [CrossRef]
  25. Sanaei, N.; Fatemi, A. Defects in additive manufactured metals and their effect on fatigue performance: A state-of-the-art review. Prog. Mater. Sci. 2021, 117, 100724. [Google Scholar] [CrossRef]
  26. Molaei, R.; Fatemi, A.; Phan, N. Multiaxial fatigue of LB-PBF additive manufactured 17-4 PH stainless steel including the effects of surface roughness and HIP treatment and comparisons with the wrought alloy. Int. J. Fatigue 2020, 137, 105646. [Google Scholar] [CrossRef]
  27. Sanaei, N.; Fatemi, A. Defect-based multiaxial fatigue life prediction of L-PBF additive manufactured metals. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 1897–1915. [Google Scholar] [CrossRef]
  28. Shamir, M.; Zhang, X.; Syed, A.K. Characterising and representing small crack growth in an additive manufactured titanium alloy. Eng. Fract. Mech. 2021, 253, 107876. [Google Scholar] [CrossRef]
  29. Benedetti, M.; Santus, C. Notch fatigue and crack growth resistance of Ti-6Al-4V ELI additively manufactured via selective laser melting: A critical distance approach to defect sensitivity. Int. J. Fatigue 2019, 121, 281–292. [Google Scholar] [CrossRef]
  30. Kundu, S.; Jones, R.; Peng, D.; Matthews, N.; Alankar, A.; Singh Raman, R.K.; Huang, P. Review of Requirements for the Durability and Damage Tolerance Certification of Additively Manufactured Aircraft Structural Parts and AM Repairs. Materials 2020, 13, 1341. [Google Scholar] [CrossRef] [Green Version]
  31. McMillan, A.; Jones, R. Combined effect of both surface finish and sub-surface porosity on component strength under repeated load conditions. Eng. Rep. 2020, 2, e12248. [Google Scholar] [CrossRef]
  32. Jones, R. Fatigue crack growth and damage tolerance. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 463–483. [Google Scholar] [CrossRef]
  33. Lincoln, J.W.; Melliere, R.A. Economic life determination for a military aircraft. J. Aircr. 1999, 36, 737–742. [Google Scholar] [CrossRef]
  34. Main, B.; Jones, M.; Barter, S. The practical need for short fatigue crack growth rate models. Int. J. Fatigue 2021, 142, 105980. [Google Scholar] [CrossRef]
  35. NASA-HDBK-5010. Fracture Control Handbook for Payloads, Experiments, and Similar Hardware, May 2005, Revalidated 2012. Available online: https://standards.nasa.gov/standard/nasa/nasa-hdbk-5010 (accessed on 2 April 2022).
  36. Lo, M.; Jones, R.; Bowler, A.; Dorman, M.; Edwards, D. Crack growth at fastener holes containing intergranular cracking. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1664–1675. [Google Scholar] [CrossRef]
  37. Main, B.; Evans, R.; Walker, K.; Yu, X.; Molent, L. Lessons from a Fatigue Prediction Challenge for an Aircraft Wing Shear Tie Post. Int. J. Fatigue 2019, 123, 53–65. [Google Scholar] [CrossRef]
  38. Tan, J.L.; Chen, B.K. Prediction of fatigue life in aluminum alloy (AA7050-T7451) structures in the presence of multiple artificial short cracks. Theor. Appl. Fract. Mech. 2015, 78, 1–7. [Google Scholar] [CrossRef]
  39. Godefroid, L.B.; Moreira, L.P.; Vilela, T.C.G.; Faria, G.L.; Candido, L.C.; Pinto, E.S. Effect of chemical composition and microstructure on the fatigue crack growth resistance of pearlitic steels for railroad application. Int. J. Fatigue 2019, 120, 241–253. [Google Scholar] [CrossRef]
  40. Zhang, Y.; Zheng, K.; Heng, J.; Zhu, J. Corrosion-Fatigue Evaluation of Uncoated Weathering Steel Bridges. Appl. Sci. 2019, 9, 3461. [Google Scholar] [CrossRef] [Green Version]
  41. Jones, R.; Molaei, R.; Fatemi, A.; Peng, D.; Phan, N. A note on computing the growth of small cracks in AM Ti-6Al-4V. Procedia Struct. Integr. 2020, 28, 364–369. [Google Scholar] [CrossRef]
  42. Jones, R.; Michopoulos, J.G.; Illiopoulos, A.P.; Raman, R.S.; Phan, N.; Nguyen, T. Representing crack growth in additively manufactured Ti-6Al-4V. Int. J. Fatigue 2018, 116, 610–622. [Google Scholar] [CrossRef]
  43. Jones, R.; Peng, D.; Singh Raman, R.K.; Huang, P. Computing the growth of small cracks in the assist round robin helicopter challenge. Metals 2020, 10, 944. [Google Scholar] [CrossRef]
  44. Tamboli, D.; Barter, S.; Jones, R. On the growth of cracks from etch pits and the scatter associated with them under a miniTWIST spectrum. Int. J. Fatigue 2017, 109, 10–16. [Google Scholar] [CrossRef]
  45. Jones, R.; Cizek, J.; Kovarik, O.; Ang, A.; Champagne, V. Observations on comparable aluminium alloy crack growth curves: Additively manufactured Scalmalloy® as an alternative to AA5754 and AA6061-T6 alloys? Addit. Manuf. Lett. 2022, 2, 100026. Available online: https://www.sciencedirect.com/science/article/pii/S2772369022000019 (accessed on 2 April 2022). [CrossRef]
  46. Jones, R.; Lang, J.; Papyan, V.; Peng, D.; Lua, J.; Ang, A. Characterising crack growth in commercially pure titanium. Eng. Fail. Anal. 2021, 122, 105287. [Google Scholar] [CrossRef]
  47. Jones, R.; Cizek, J.; Kovarik, O.; Lang, J.; Ang, A.; Michopoulos, J.G. Describing crack growth in additively manufactured Scalmalloy®. Addit. Manuf. Lett. 2021, 1, 100020. [Google Scholar] [CrossRef]
  48. Jones, R.; Rans, C.; IlIiopoulos, A.P.; Michopoulos, J.G.; Phan, N.; Peng, D. Modelling the Variability and the Anisotropic Behaviour of Crack Growth in SLM Ti-6Al-4V. Materials 2021, 14, 1400. [Google Scholar] [CrossRef]
  49. Jones, R.; Raman, R.K.S.; Iliopoulos, A.P.; Michopoulos, J.G.; Phan, N.; Peng, D. Additively manufactured Ti-6Al-4V replacement parts for military aircraft. Int. J. Fatigue 2019, 124, 227–235. [Google Scholar] [CrossRef]
  50. Iliopoulos, A.P.; Jones, R.; Michopoulos, J.G.; Phan, N.; Singh Raman, R.K. Crack growth in a range of additively manufactured aerospace structural materials. Aerospace 2018, 5, 118. [Google Scholar] [CrossRef] [Green Version]
  51. Illiopoulos, A.P.; Jones, R.; Michopoulos, J.G.; Phan, N.; Rans, C. Further Studies into Crack Growth in Additively Manufactured Materials. Materials 2020, 13, 2223. [Google Scholar] [CrossRef] [PubMed]
  52. Schwalbe, K.H. On the Beauty of Analytical Models for Fatigue Crack Propagation and Fracture-A Personal Historical Review. J. ASTM Intl. 2010, 7, 3–73. [Google Scholar] [CrossRef]
  53. Jones, R.; Kovarik, O.; Bagherifard, S.; Cizek, J.; Lang, J.; Papyan, V. Damage tolerance assessment of am 304L and cold spray fabricated 316L steels and its implications for attritable aircraft. Eng. Fract. Mech. 2021, 254, 107916. [Google Scholar] [CrossRef]
  54. Jones, R.; Kovarik, O.; Cizek, J.; Ang, A.; Lang, J. Crack growth in conventionally manufactured pure nickel, titanium and aluminium and the cold spray additively manufactured equivalents. Addit. Manuf. 2022, 3, 100043. [Google Scholar] [CrossRef]
  55. Ali, K.; Peng, D.; Jones, R.; Singh Raman, R.K.; Zhao, X.L.; McMillan, A.J.; Berto, F. Crack growth in a naturally corroded bridge steel. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1117–1127. [Google Scholar] [CrossRef]
  56. Nourian-Avval, A.; Fatemi, A. Fatigue life prediction of cast aluminum alloy based on porosity characteristics. Theor. Appl. Fract. 2020, 109, 102774. [Google Scholar] [CrossRef]
  57. Peng, D.; Tang, C.; Matthews, N.; Jones, R.; Kundu, S.; Singh Raman, R.K.; Alankar, A. Computing the Fatigue Life of Cold Spray Repairs to Simulated Corrosion Damage. Materials 2021, 14, 4451. [Google Scholar] [CrossRef]
  58. Jones, R.; Singh Raman, R.K.; McMillan, A.J. Crack growth: Does microstructure play a role? Eng. Fract. Mech. 2018, 187, 190–210. [Google Scholar] [CrossRef]
  59. Masuda, K.; Oguma, N.; Ishihara, S.; McEvily, A.J. Investigation of subsurface fatigue crack growth behavior of D2 tool steel (JIS SKD11) based on a novel measurement method. Int. J. Fatigue 2020, 133, 105395. [Google Scholar] [CrossRef]
  60. Peng, D.; Huang, P.; Jones, R. Chapter 4, Practical computational fracture mechanics for aircraft structural integrity. In Aircraft Sustainment and Repair; Jones, R., Matthews, N., Baker, A.A., Champagne, V., Jr., Eds.; Butterworth-Heinemann Press: Oxford, UK, 2018; ISBN 9780081005408. [Google Scholar]
  61. ASTM E647-13; Measurement of Fatigue Crack Growth Rates. ASTM: West Conshohocken, PA, USA, 2013.
  62. Gallagher, J.P.; Giessler, F.J.; Berens, A.P.; Engle, R.M., Jr.; Wood, H.A. USAF Damage Tolerant Design Handbook: Guidelines For The Analysis And Design Of Damage Tolerant Aircraft Structures, AFWAL-TR-82-3073. May 1984. Available online: https://apps.dtic.mil/sti/citations/ADA153161 (accessed on 2 April 2022).
  63. Manning, S.D.; Yang, Y.N. USAF Durability Design Handbook: Guidelines for the Analysis and Design of Durable Aircraft Structures, Air Force Wright Aeronautical Laboratories, Wright-Patterson Air Force Base, January 1984, AFWAL-TR-83-3027. Available online: https://apps.dtic.mil/sti/citations/ADA142424 (accessed on 2 April 2022).
  64. Berens, A.P.; Hovey, P.W.; Skinn, D.A. Risk analysis for aging aircraft fleets—Volume 1: Analysis, WL-TR-91-3066, Flight Dynamics Directorate, Wright Laboratory, Air Force Systems Command, Wright-Patterson Air Force Base. October 1991. Available online: https://apps.dtic.mil/sti/citations/ADA252000 (accessed on 2 April 2022).
  65. Main, B.; Molent, L.; Singh, R.; Barter, S. Fatigue crack growth lessons from thirty-five years of the Royal Australian Air Force F/A-18 A/B hornet aircraft structural integrity program. Int. J. Fatigue 2020, 133, 105426. [Google Scholar] [CrossRef]
Metals 12 01121 g001 550
Figure 1. A schematic diagram of the baseline model, smooth surface, dimensions are in mm.
Figure 1. A schematic diagram of the baseline model, smooth surface, dimensions are in mm.
Metals 12 01121 g001
Metals 12 01121 g002 550
Figure 2. A schematic diagram of the as-built specimen with a wavy surface, dimensions are in mm.
Figure 2. A schematic diagram of the as-built specimen with a wavy surface, dimensions are in mm.
Metals 12 01121 g002
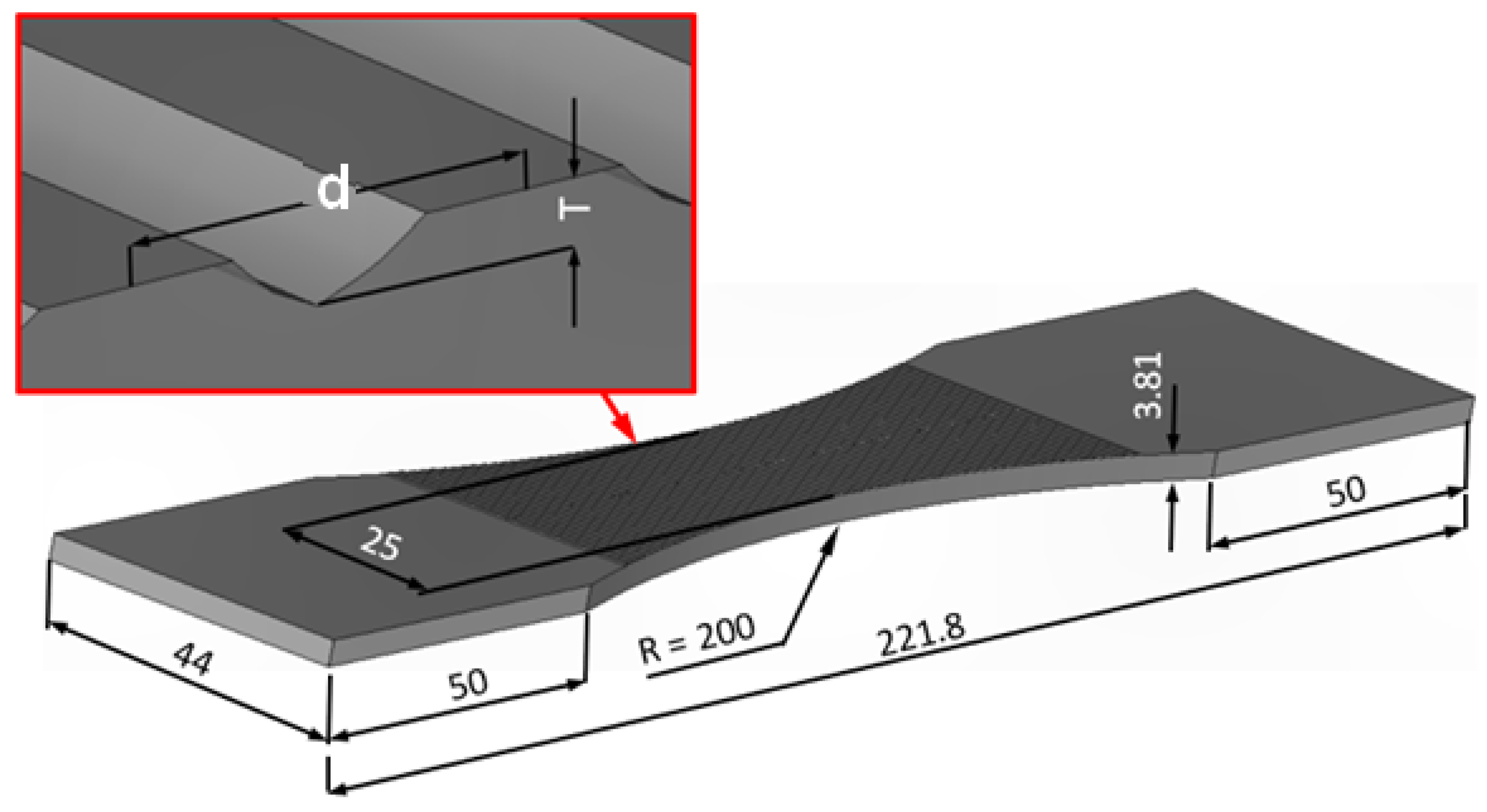
Metals 12 01121 g003 550
Figure 3. A schematic diagram of specimen with machined surfaces, dimensions are in mm.
Figure 3. A schematic diagram of specimen with machined surfaces, dimensions are in mm.
Metals 12 01121 g003
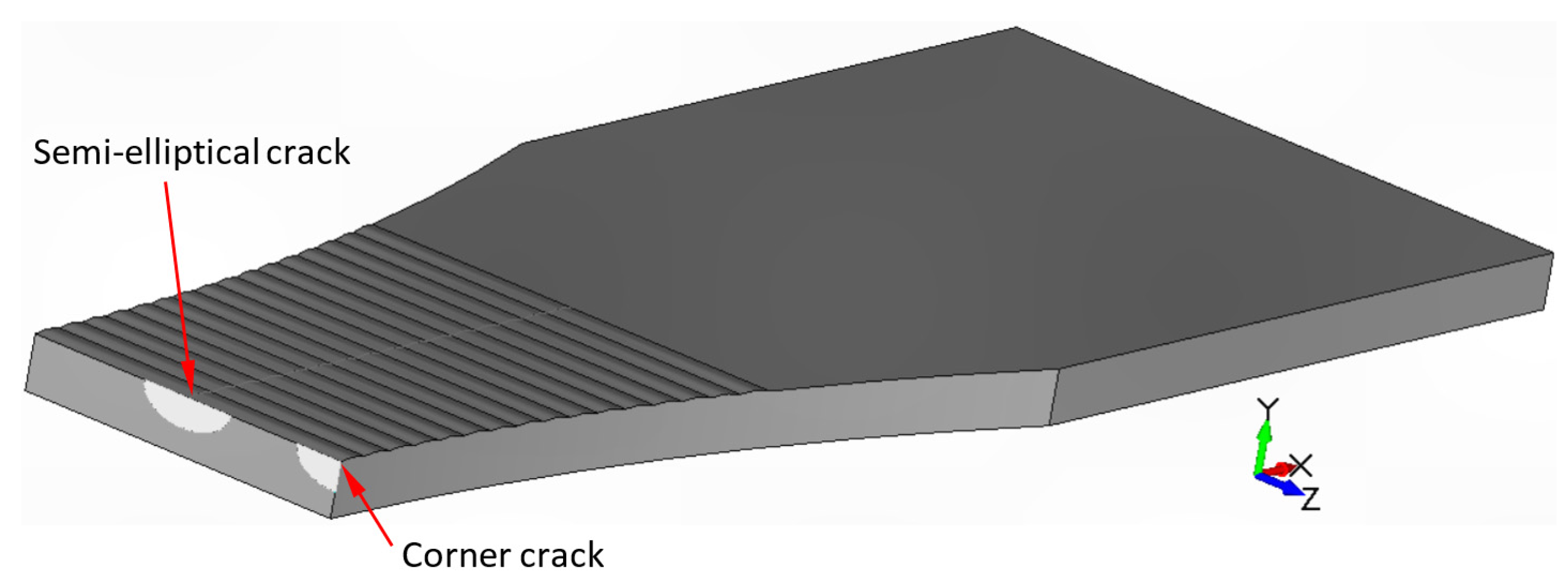
Metals 12 01121 g004 550
Figure 4. A schematic diagram showing the locations of the cracks analysed in this study.
Figure 4. A schematic diagram showing the locations of the cracks analysed in this study.
Metals 12 01121 g004
Metals 12 01121 g005 550
Figure 5. A photograph showing the “wavy” surface of a typical as-built billet.
Figure 5. A photograph showing the “wavy” surface of a typical as-built billet.
Metals 12 01121 g005
Metals 12 01121 g006 550
Figure 6. The local stress field associated with a rough surface, Case 6.
Figure 6. The local stress field associated with a rough surface, Case 6.
Metals 12 01121 g006
Metals 12 01121 g007 550
Figure 7. The local stress field associated with a rough surface Case 9.
Figure 7. The local stress field associated with a rough surface Case 9.
Metals 12 01121 g007
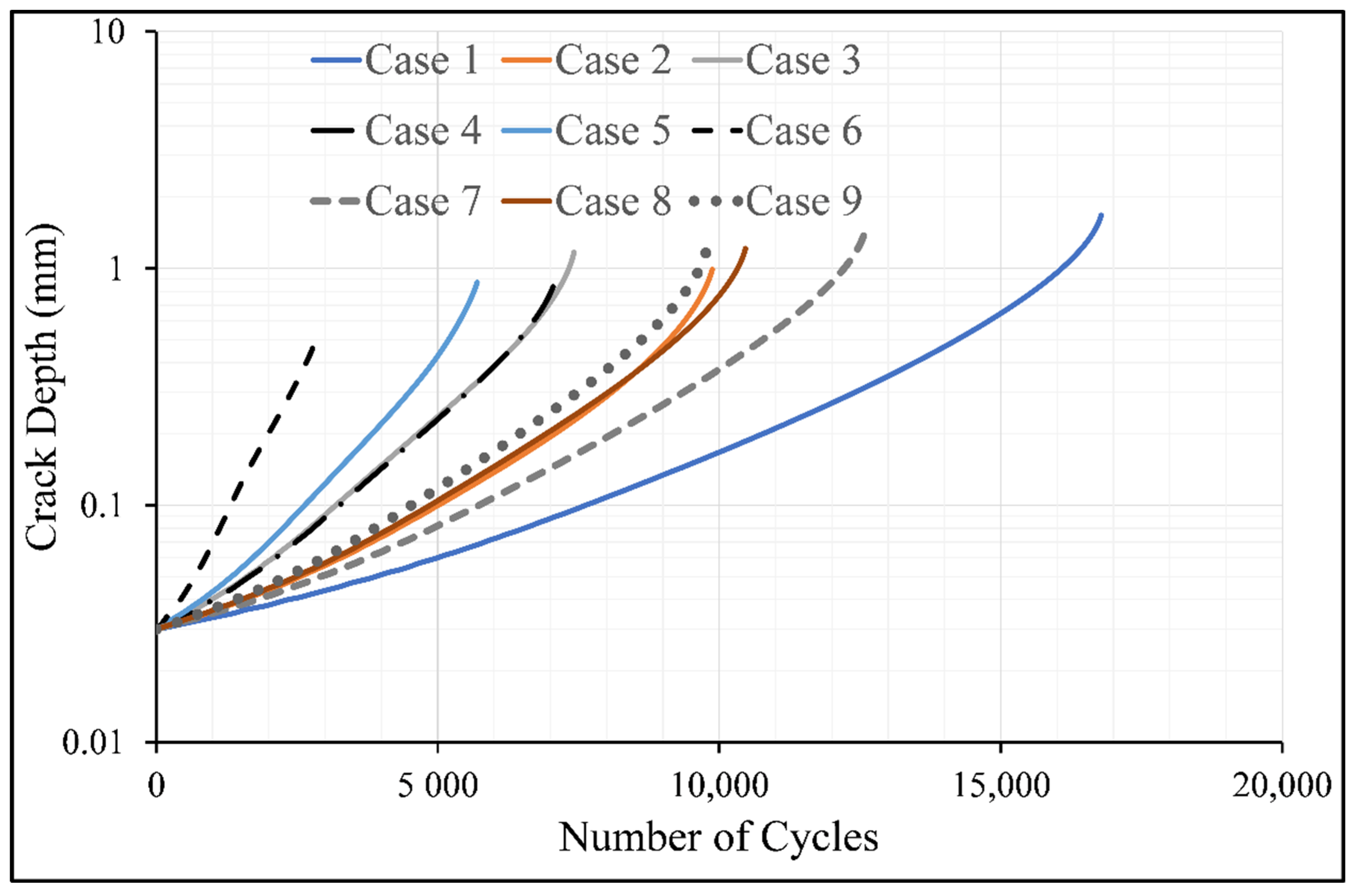
Metals 12 01121 g008 550
Figure 8. The effect of surface roughness on the fatigue life from an initial semi-elliptical defect size of 0.03 mm. Case 1 is the baseline specimen with no surface roughness.
Figure 8. The effect of surface roughness on the fatigue life from an initial semi-elliptical defect size of 0.03 mm. Case 1 is the baseline specimen with no surface roughness.
Metals 12 01121 g008
Metals 12 01121 g009 550
Figure 9. The effect of surface roughness on the fatigue life from an initial semi-elliptical defect size of 0.254 mm. Case 1 is the baseline specimen with no surface roughness.
Figure 9. The effect of surface roughness on the fatigue life from an initial semi-elliptical defect size of 0.254 mm. Case 1 is the baseline specimen with no surface roughness.
Metals 12 01121 g009
Metals 12 01121 g010 550
Figure 10. The assumed machined surface profile for case when the original peak to trough height was 0.363 mm.
Figure 10. The assumed machined surface profile for case when the original peak to trough height was 0.363 mm.
Metals 12 01121 g010
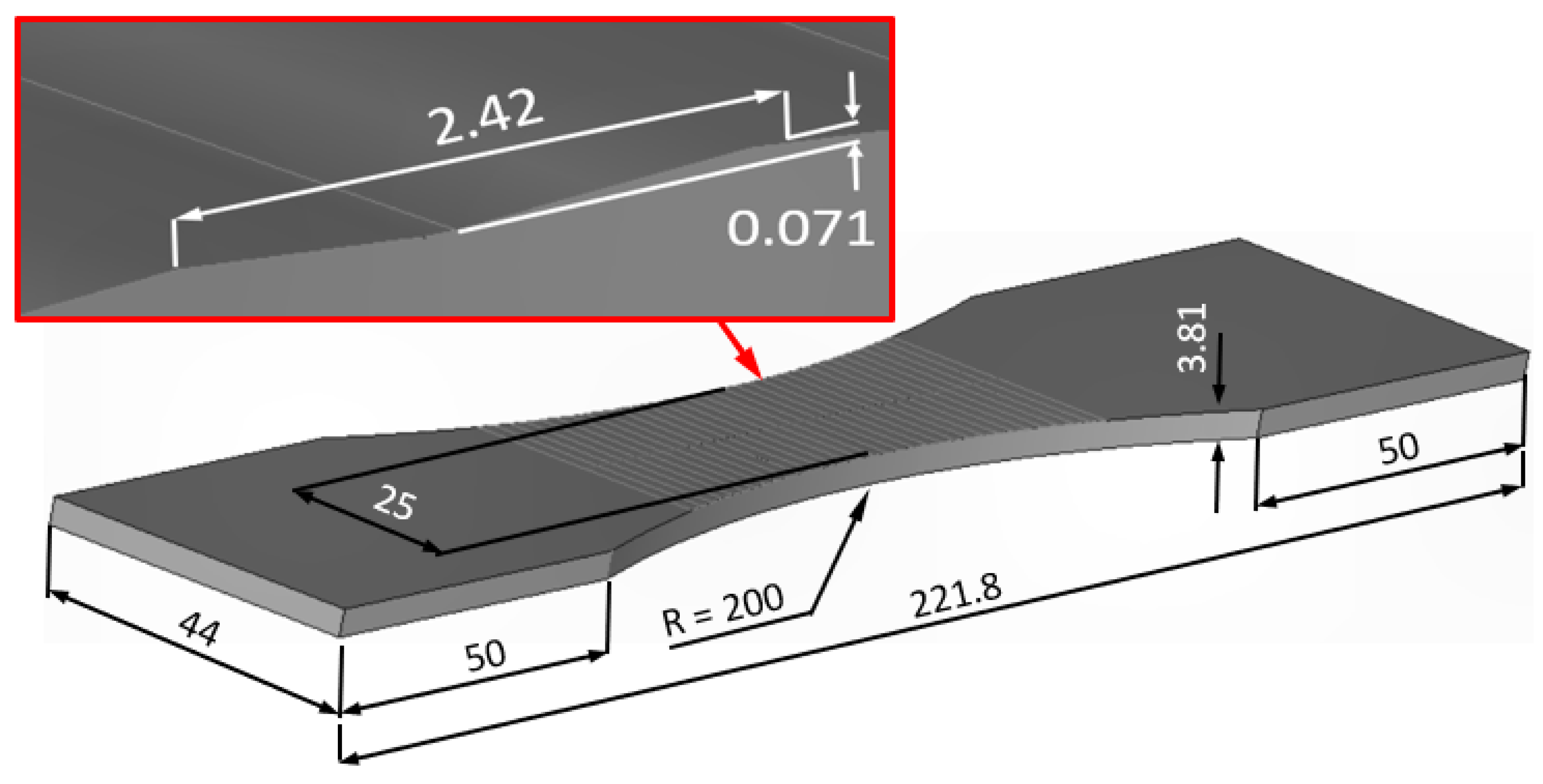
Metals 12 01121 g011 550
Figure 11. The assumed machined surface profile for case when the original peak to trough height was 0.141 mm.
Figure 11. The assumed machined surface profile for case when the original peak to trough height was 0.141 mm.
Metals 12 01121 g011
Metals 12 01121 g012 550
Figure 12. The local stress field associated with Case 5, which is the “machined” version of Case 6.
Figure 12. The local stress field associated with Case 5, which is the “machined” version of Case 6.
Metals 12 01121 g012
Metals 12 01121 g013 550
Figure 13. The local stress field associated with the Case 8, which is the “machined” version of Case 9.
Figure 13. The local stress field associated with the Case 8, which is the “machined” version of Case 9.
Metals 12 01121 g013
Metals 12 01121 g014 550
Figure 14. An expanded view of the stress field associated with Figure 6.
Figure 14. An expanded view of the stress field associated with Figure 6.
Metals 12 01121 g014
Table
Table 1. Summary of the fatigue life analyses for an initial crack depth of 0.03 mm.
Table 1. Summary of the fatigue life analyses for an initial crack depth of 0.03 mm.
d (mm)CaseSurface MachinedT (mm)Computed Life (Cycles)
Semi-Circular Surface CrackReduction * in Fatigue Life
(% diff)		Corner (Quadrant) CrackReduction * in Fatigue Life
(% diff)
1.571No016786Baseline16428Baseline
2Yes0.071987741.2961041.5
3No0.142741855.8801851.2
4No0.1815711257.6689658.0
5Yes0.1815569966.0616262.5
6No0.363288882.8497167.7
2.421No016786Baseline16428Baseline
7No0.0711258525.01327019.2
8Yes0.0711046437.71057835.5
9No0.142976541.81023537.7
* From the life of the baseline specimen.
Table
Table 2. Summary of the fatigue life analyses for an initial crack depth of 0.254 mm.
Table 2. Summary of the fatigue life analyses for an initial crack depth of 0.254 mm.
d (mm)CaseSurface MachinedT (mm)Computed Life (Cycles)
Semi-Circular Surface CrackReduction in Fatigue Life
(% diff) from the Baseline		Corner (Quadrant) CrackReduction in Fatigue Life (% diff) from the Baseline
1.571No05875Baseline5639Baseline
2Yes0.071327544.3340139.7
3No0.142274653.3305845.8
4No0.1815239959.2218661.2
5Yes0.1815218662.8246856.2
6No0.363113580.7192465.9
2.421No05875Baseline5639Baseline
7No0.071453622.8470116.6
8Yes0.071369337.1388331.1
9No0.142346341.1373033.9
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Peng, D.; Jones, R.; Ang, A.S.M.; Champagne, V.; Birt, A.; Michelson, A. A Numerical Study into the Effect of Machining on the Interaction between Surface Roughness and Surface Breaking Defects on the Durability of WAAM Ti-6Al-4V Parts. Metals 2022, 12, 1121. https://doi.org/10.3390/met12071121

AMA Style

Peng D, Jones R, Ang ASM, Champagne V, Birt A, Michelson A. A Numerical Study into the Effect of Machining on the Interaction between Surface Roughness and Surface Breaking Defects on the Durability of WAAM Ti-6Al-4V Parts. Metals. 2022; 12(7):1121. https://doi.org/10.3390/met12071121

Chicago/Turabian Style

Peng, Daren, Rhys Jones, Andrew S. M. Ang, Victor Champagne, Aaron Birt, and Alex Michelson. 2022. "A Numerical Study into the Effect of Machining on the Interaction between Surface Roughness and Surface Breaking Defects on the Durability of WAAM Ti-6Al-4V Parts" Metals 12, no. 7: 1121. https://doi.org/10.3390/met12071121

APA Style

Peng, D., Jones, R., Ang, A. S. M., Champagne, V., Birt, A., & Michelson, A. (2022). A Numerical Study into the Effect of Machining on the Interaction between Surface Roughness and Surface Breaking Defects on the Durability of WAAM Ti-6Al-4V Parts. Metals, 12(7), 1121. https://doi.org/10.3390/met12071121

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop