Effect of Cold Deformation on Microstructure and Mechanical Behavior of Commercially Pure Grade 4 Titanium Strip
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Mechanical Properties and Microstructure Analysis
3. Results and Discussion
3.1. Characteristics of the Original Microstructure
3.2. Microstructure of Cold Deformation
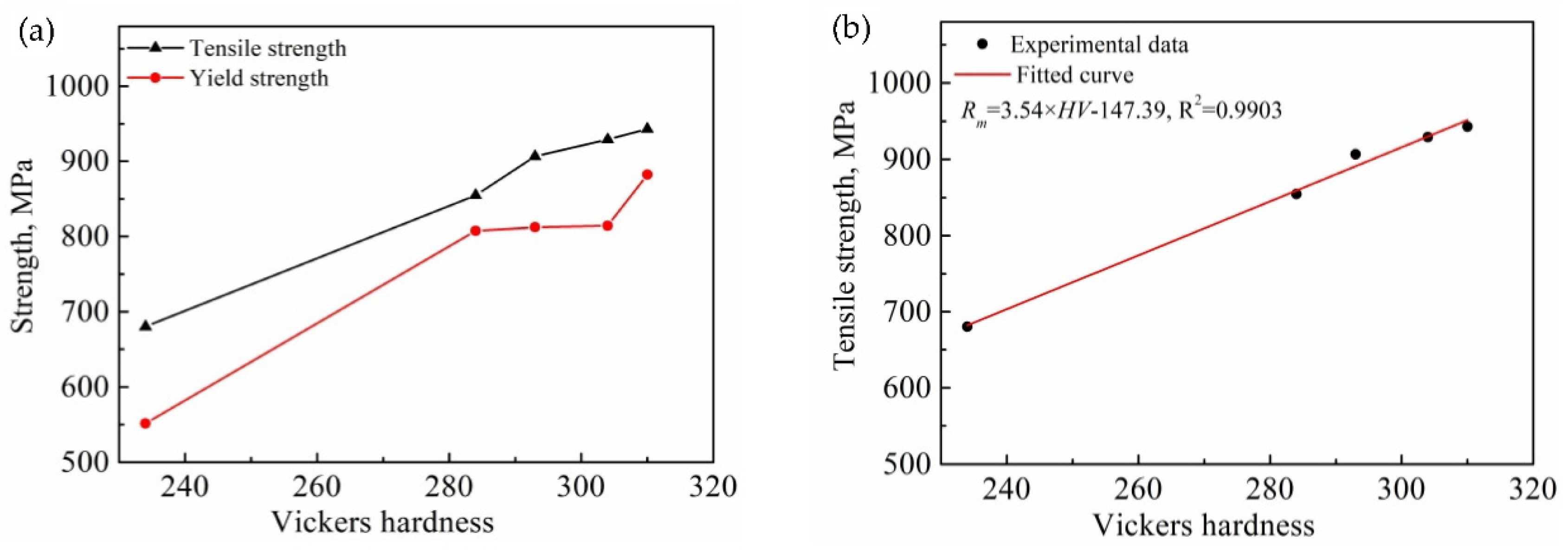
3.3. Mechanical Properties
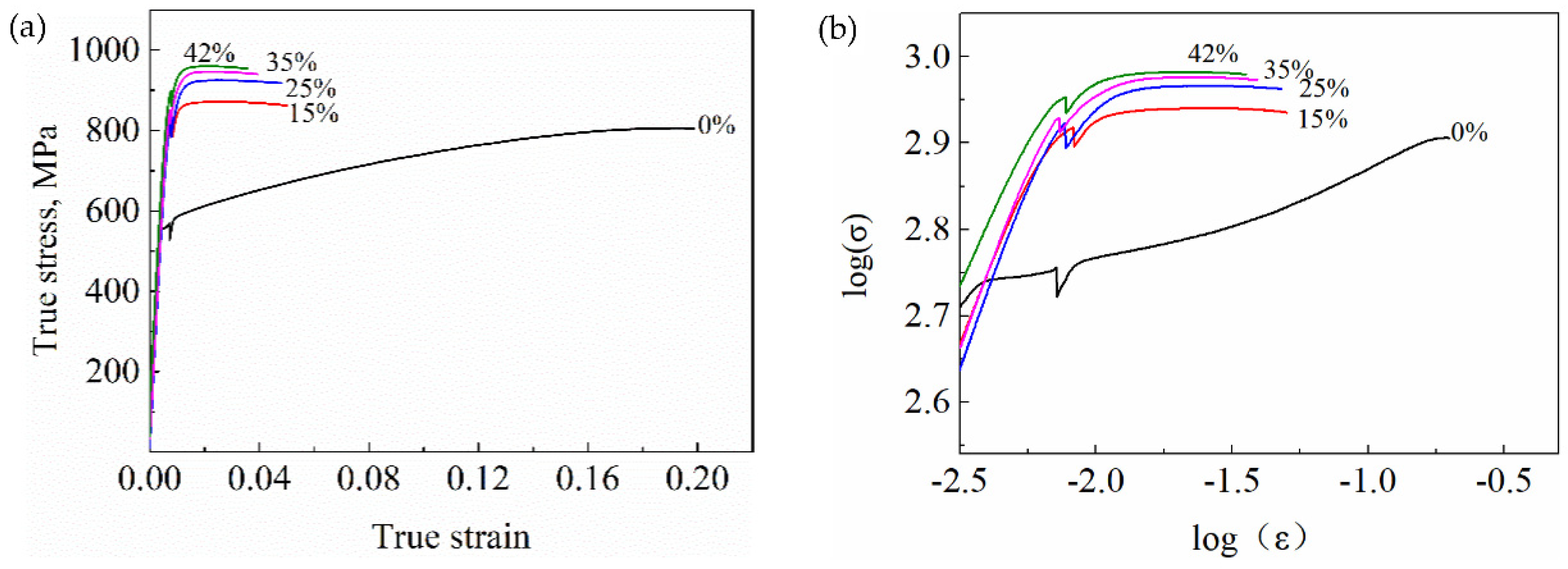
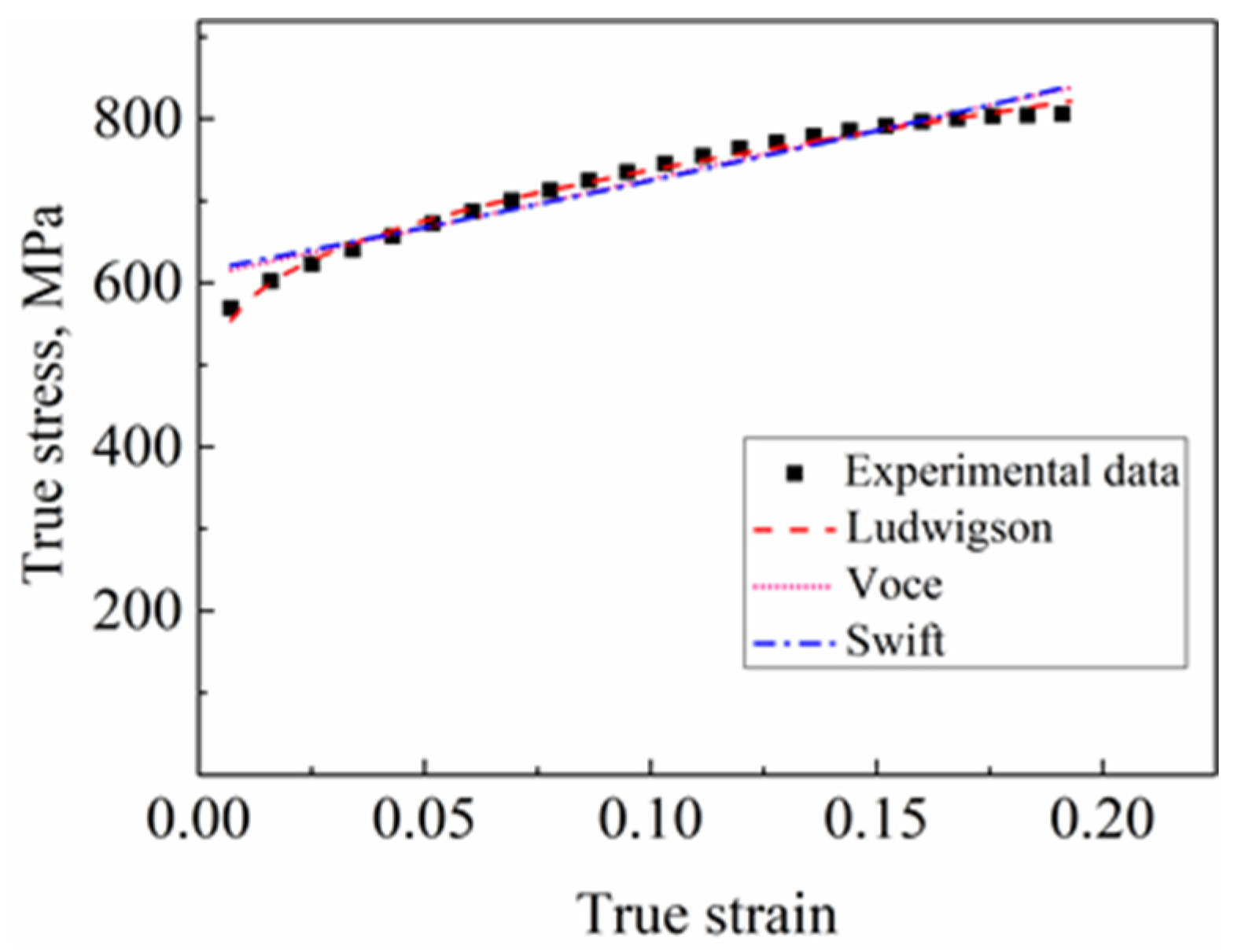
3.4. True-Stress–True-Strain Curve and Mathematical Description
3.5. Work Hardening
4. Conclusions
- (1)
- A Gr.4 strip has obvious work-hardening characteristics. After cold-rolling deformation, the strength, yield–strength ratio, and hardness of the material are greatly improved, while the plasticity decreases, and there is a significant linearity between the tensile strength and hardness relation.
- (2)
- With the increase in deformation, the work-hardening rate of a Gr.4 strip also decreased significantly. During the entire deformation stage, no twins were found in commercially pure titanium Gr.4, and the dominant deformation mechanism was the slipping mode, while the increase in dislocation density and dislocation entanglement resulted in the work-hardening behavior during cold deformation.
- (3)
- After fitting analysis, the Ludwigson, Voce, and Swift models are all suitable for regression analysis of the tensile true-stress–true-strain curve of the annealed Gr.4 strip, and the Ludwigson model has a higher fitting degree. However, the fitting results of the tensile true-stress–true-strain curve of the Gr.4 strip after cold-deformation hardening are unsatisfactory.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Langer, R.; Tirrell, D.A. Designing materials for biology and medicine. Nature 2004, 428, 487–492. [Google Scholar] [CrossRef] [PubMed]
- Roodposhti, P.S.; Farahbakhsh, N.; Sarkar, A.; Murty, K.L. Microstructural approach to equal channel angular processing of commercially pure titanium-A review. Trans. Nonferrous Met. Soc. China 2015, 25, 1353–1366. [Google Scholar] [CrossRef]
- Liu, N.; Wang, Y.; He, W.J.; Li, J.; Chapuis, A.; Luan, B.F.; Liu, Q. Microstructure and textural evolution during cold rolling and annealing of commercially pure titanium sheet. Trans. Nonferrous Met. Soc. China 2018, 28, 1123–1131. [Google Scholar] [CrossRef]
- Yang, H.; Li, H.; Sun, H.; Zhang, Y.H.; Liu, X.; Zhan, M.; Liu, Y.; Fu, M.W. Anisotropic plasticity and fracture of alpha titanium sheets from cryogenic to warm temperatures. Int. J. Plast. 2022, 156, 103348. [Google Scholar] [CrossRef]
- Claudio, B.; Gonzalo, P. Thermomechanical processing of alloys. case of study Ti Gr. 4. Procedia Mater. Sci. 2015, 8, 311–318. [Google Scholar]
- Fang, J.; Liu, F.; Di, W.Q.; Xu, G.L.; Cui, Q. Effect of cold-rolling process parameters on mechanical properties and corrosion properties of commercial pure titanium. J. Plast. Eng. 2019, 26, 98–105. [Google Scholar]
- Mertová, K.; Salvetr, P.; Duchek, M. Comparison of cryogenic and cold deformation of commercially pure titanium. Mater. Today Proc. 2020, 28, 916–919. [Google Scholar] [CrossRef]
- Su, Y.; Shang, Q.H.; Wu, H.; Yan, X.A.; Wu, G.W.; Xue, X.T.; Zhao, Y. Microstructure and mechanical properties of commercial pure titanium Gr4 strip. China Plant Eng. 2020, 16, 207–208. [Google Scholar]
- Islamgaliev, R.K.; Kazyhanov, V.U.; Shestakova, L.O.; Sharafutdinov, A.V.; Valiev, R.Z. Microstructure and mechanical properties of titanium (grade 4) processed by high-pressure torsion. Mater. Sci. Eng. A 2008, 493, 190–194. [Google Scholar] [CrossRef]
- Li, Y.; Ng, H.P.; Jung, H.D.; Kim, H.E.; Estrin, Y. Enhancement of mechanical properties of grade 4 titanium by equal channel angular pressing with billet encapsulation. Mater. Lett. 2014, 114, 144–147. [Google Scholar] [CrossRef]
- Dyakonov, G.S.; Mironov, S.; Enikeev, N.; Semenova, I.P.; Valiev, R.Z.; Semiatin, S.L. Annealing behavior of severely-deformed titanium grade 4. Mater. Sci. Eng. A 2019, 742, 89–101. [Google Scholar] [CrossRef]
- Masikane, A.M.; Johnson, O.T.; Ogunmuyiwa, E.N.; Sigalas, I. Densification and tensile properties of titanium grade 4 produced using different routes. Procedia Manuf. 2019, 35, 826–832. [Google Scholar] [CrossRef]
- Choi, S.W.; Jeong, J.S.; Won, J.W.; Hong, J.K.; Choi, Y.S. Grade-4 commercially pure titanium with ultrahigh strength achieved by twinning-induced grain refinement through cryogenic deformation. J. Mater. Sci. Technol. 2021, 66, 193–201. [Google Scholar] [CrossRef]
- Chausov, M.G.; Maruschak, P.O.; Hutsaylyuk, V.; Śnieżek, L.; Pylypenko, A.P. Effect of complex combined loading mode on the fracture toughness of titanium alloys. Vacuum 2018, 147, 51–57. [Google Scholar] [CrossRef]
- Tsukamoto, G.; Kunieda, T.; Yamasaki, S.; Mitsuhara, M.; Nakashima, H. Effects of temperature and grain size on active twinning systems in commercially pure titanium. J. Alloy. Compd. 2021, 884, 161154. [Google Scholar] [CrossRef]
- Wang, B.S.; Liu, H.M.; Zhang, Y.G.; Zhou, B.X.; Deng, L.P.; Wang, C.; Chen, J.F.; Zhang, Y.H. Effect of grain size on twinning behavior of pure titanium at room temperature. Mater. Sci. Eng. A 2021, 827, 142060. [Google Scholar] [CrossRef]
- Song, R.B.; Xiang, J.Y.; Hou, D.P. Microstructure characteristics and work-hardening mechanism and of 316L austenitic stainless steel during cold deformation. J. Univ. Sci. Technol. Beijing 2013, 35, 55–60. [Google Scholar]
- Agnew, S.R.; Capolungo, L.; Calhoun, C.A. Connections between the basal I1 “growth” fault and <c+a> dislocations. Acta Mater. 2015, 82, 255–265. [Google Scholar] [CrossRef]
- Sun, H.; Liang, Y.L.; Li, G.M.; Zhang, X.F.; Wang, S.; Huang, C.W. Dislocation hardening and phase transformation-induced high ductility in Ti-6Al-4V with a heterogeneous martensitic microstructure under tensile load. J. Alloy. Compd. 2021, 868, 159155. [Google Scholar] [CrossRef]
- Fan, J.H.; Chen, K.X.; Liang, J.P.; Li, Z.J.; Li, X.K. Effect of Cold deformation on microstructure and mechanical behavior of Ni-based high temperature alloy GH3535. Chin. J. Mater. Res. 2015, 29, 439–444. [Google Scholar]
- Deng, H.X.; Zheng, W.J.; Song, Z.G.; Cen, Q.H.; Feng, H. Effect of cold deformation on microstructure and mechanical behavior of 0Cr25Ni35AlTi. J. Iron Steel Res. 2015, 27, 67–72. [Google Scholar]
- Sun, S.C.; Sun, G.X.; Jiang, Z.H.; Ji, C.T.; Liu, J.A.; Lian, J.S. Effects of cold rolling deformation on microstructure, hardness, and creep behavior of high nitrogen austenitic stainless steel. Chin. Phys. B 2014, 23, 383–388. [Google Scholar] [CrossRef]
- Yasnii, P.V.; Marushchak, P.O.; Hlad’o, V.B.; Baran, D.Y. Correlation of the microdislocation parameters with the hardness of plastically deformed heat-resistant steels. Mater. Sci. 2008, 44, 194–200. [Google Scholar] [CrossRef]
- Zhang, S.C.; Zheng, W.J.; Song, Z.G.; Feng, H.; Sun, Y. Effect of cold deformation on structure and mechanical behavior of Inconel 690 alloy. J. Iron Steel Res. 2009, 21, 49–54. [Google Scholar]
- Cao, J.; Li, F.G.; Ma, X.K.; Sun, Z.K. Tensile stress-strain behavior of metallic alloys. Trans. Nonferrous Met. Soc. China 2017, 27, 2443–2453. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Monteiro, S.N.; Reed-Hill, R.E. An empirical analysis of titanium stress-strain curves. Metall. Trans. 1973, 4, 1011–1015. [Google Scholar] [CrossRef]
- Christopher, J.; Choudhary, B.K.; Samuel, E.I.; Mathew, M.D.; Jayakumar, T. Tensile stress-strain and work hardening behaviour of P9 steel for wrapper application in sodium cooled fast reactors. J. Nucl. Mater. 2012, 420, 583–590. [Google Scholar] [CrossRef]

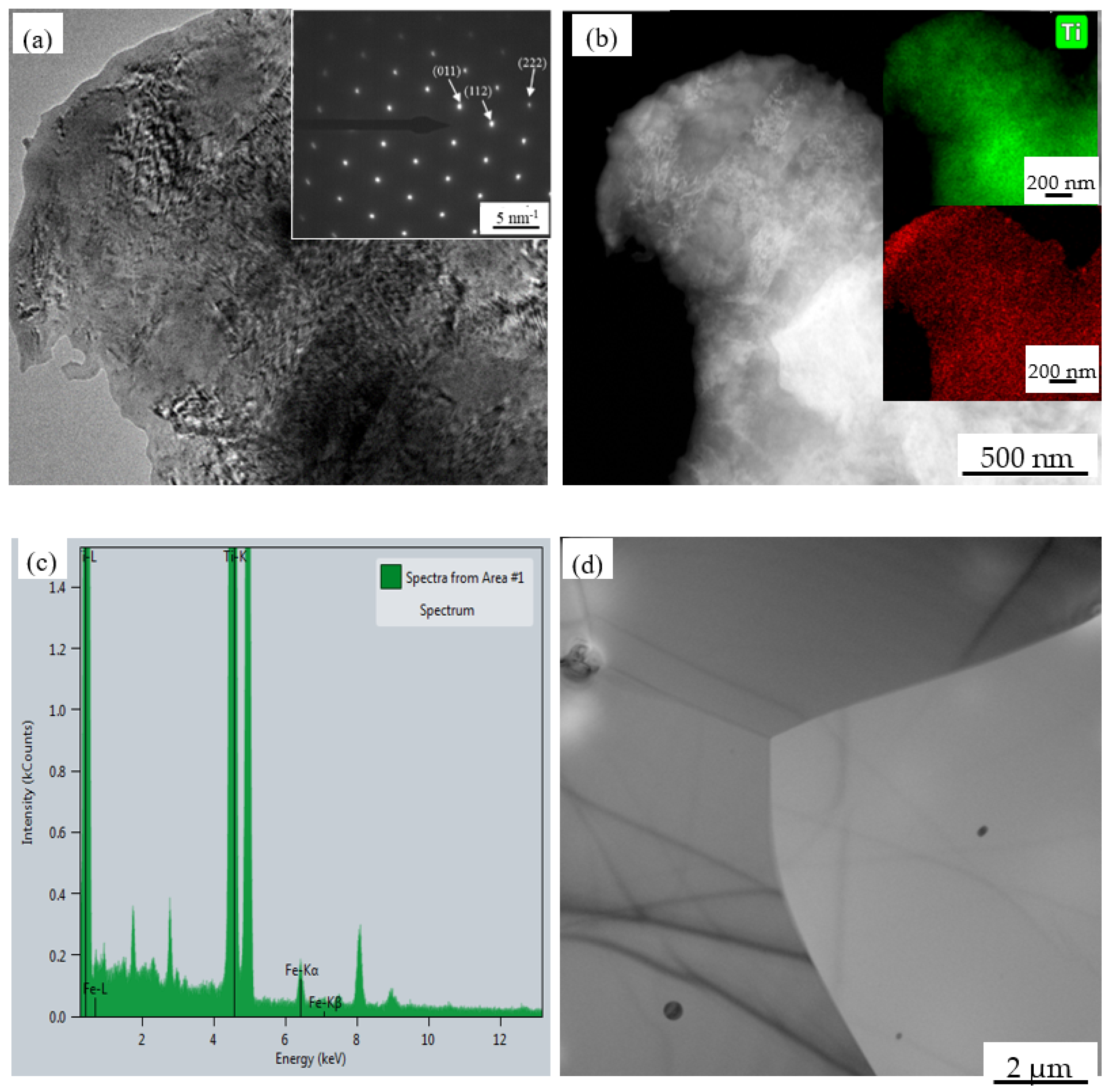




| C | N | H | O | Fe | Ti |
|---|---|---|---|---|---|
| 0.012 | <0.010 | 0.0012 | 0.30 | 0.35 | Bal. |
| Deformation, % | Ludwigson | Voce | Swift | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K1/MPa | n1 | K2 | n2 | R | σ0/MPa | σ0 × A | β | R | Ks/MPa | ns | ε0 | R | |
| 0 | 927.4 | 0.572 | 6.215 | −0.464 | 0.9971 | 1931.3 | 1329.3 | 1.0 | 0.9623 | 46.230 | 3.535 | 2.079 | 0.9401 |
| 15 | 1260.2 | 0.245 | 6.169 | −10.877 | 0.8393 | 867.5 | 329.7 | 5240.4 | −0.0060 | 5.525 | 1.817 | 16.138 | 0.0284 |
| 25 | 1380.2 | 0.245 | 6.147 | −10.239 | 0.7370 | 918.9 | −1.8 × 107 | 4.7 × 106 | −0.0063 | 29.054 | 2.303 | 4.453 | 0.1790 |
| 35 | 1502.3 | 0.245 | 6.092 | −11.135 | 0.7633 | 939.2 | −7.5 × 108 | 2.0 × 108 | −0.0076 | 156.725 | 2.118 | 2.305 | 0.2736 |
| 42 | 1412.8 | 0.246 | 6.244 | −10.838 | 0.8003 | 955.4 | −2.5 × 107 | 5.7 × 106 | −0.0087 | 12.968 | 2.621 | 5.135 | 0.2199 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, B.; Wu, X.; Wan, M.; Cui, X.; Li, H.; Li, X.; Shen, L. Effect of Cold Deformation on Microstructure and Mechanical Behavior of Commercially Pure Grade 4 Titanium Strip. Metals 2022, 12, 1166. https://doi.org/10.3390/met12071166
Zhu B, Wu X, Wan M, Cui X, Li H, Li X, Shen L. Effect of Cold Deformation on Microstructure and Mechanical Behavior of Commercially Pure Grade 4 Titanium Strip. Metals. 2022; 12(7):1166. https://doi.org/10.3390/met12071166
Chicago/Turabian StyleZhu, Baohui, Xiangdong Wu, Min Wan, Xuexi Cui, Heng Li, Xiaofei Li, and Lihua Shen. 2022. "Effect of Cold Deformation on Microstructure and Mechanical Behavior of Commercially Pure Grade 4 Titanium Strip" Metals 12, no. 7: 1166. https://doi.org/10.3390/met12071166
APA StyleZhu, B., Wu, X., Wan, M., Cui, X., Li, H., Li, X., & Shen, L. (2022). Effect of Cold Deformation on Microstructure and Mechanical Behavior of Commercially Pure Grade 4 Titanium Strip. Metals, 12(7), 1166. https://doi.org/10.3390/met12071166






