Crankshaft HCF Research Based on the Simulation of Electromagnetic Induction Quenching Approach and a New Fatigue Damage Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material and Research Objects
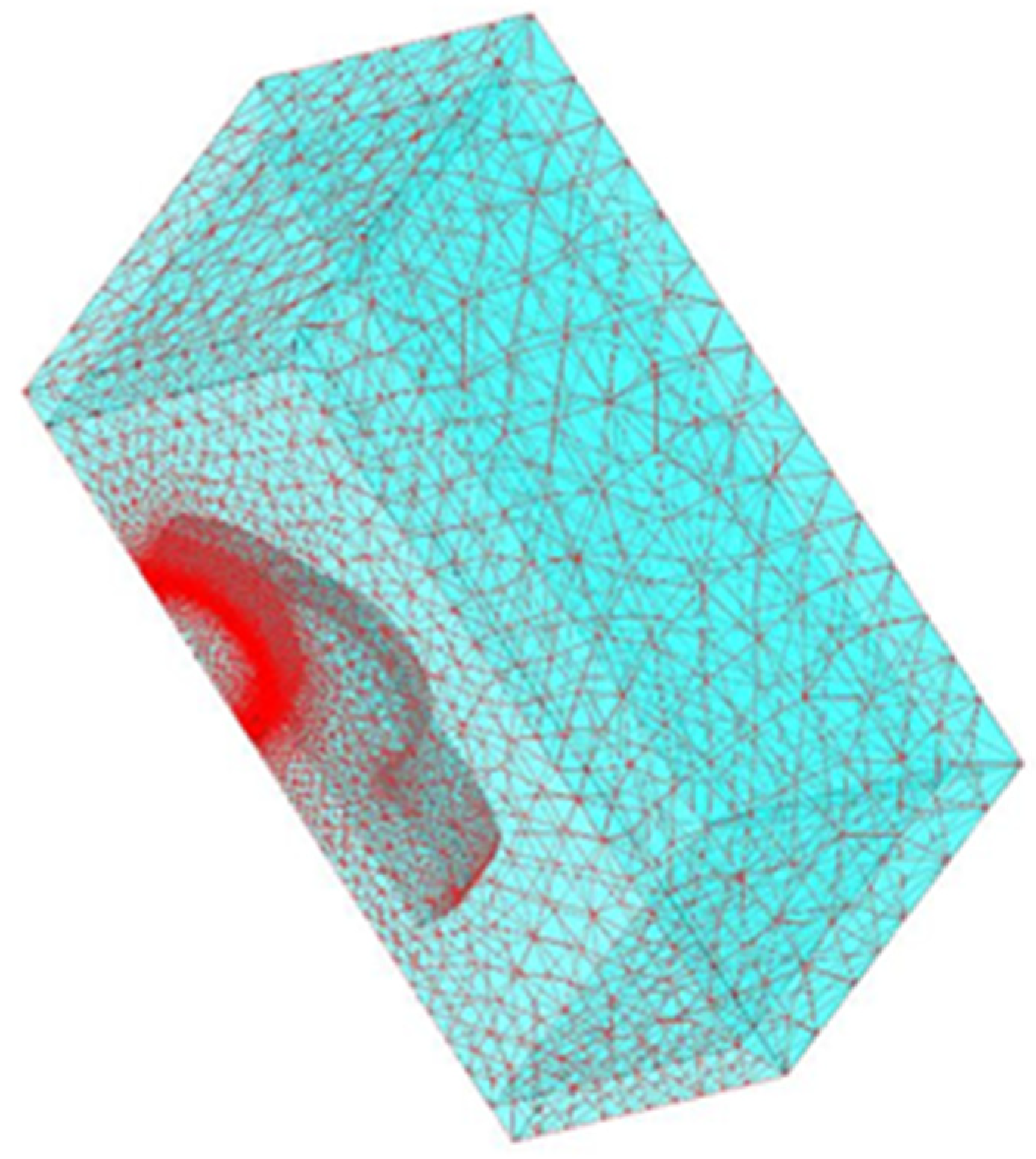
2.2. Prediction Method
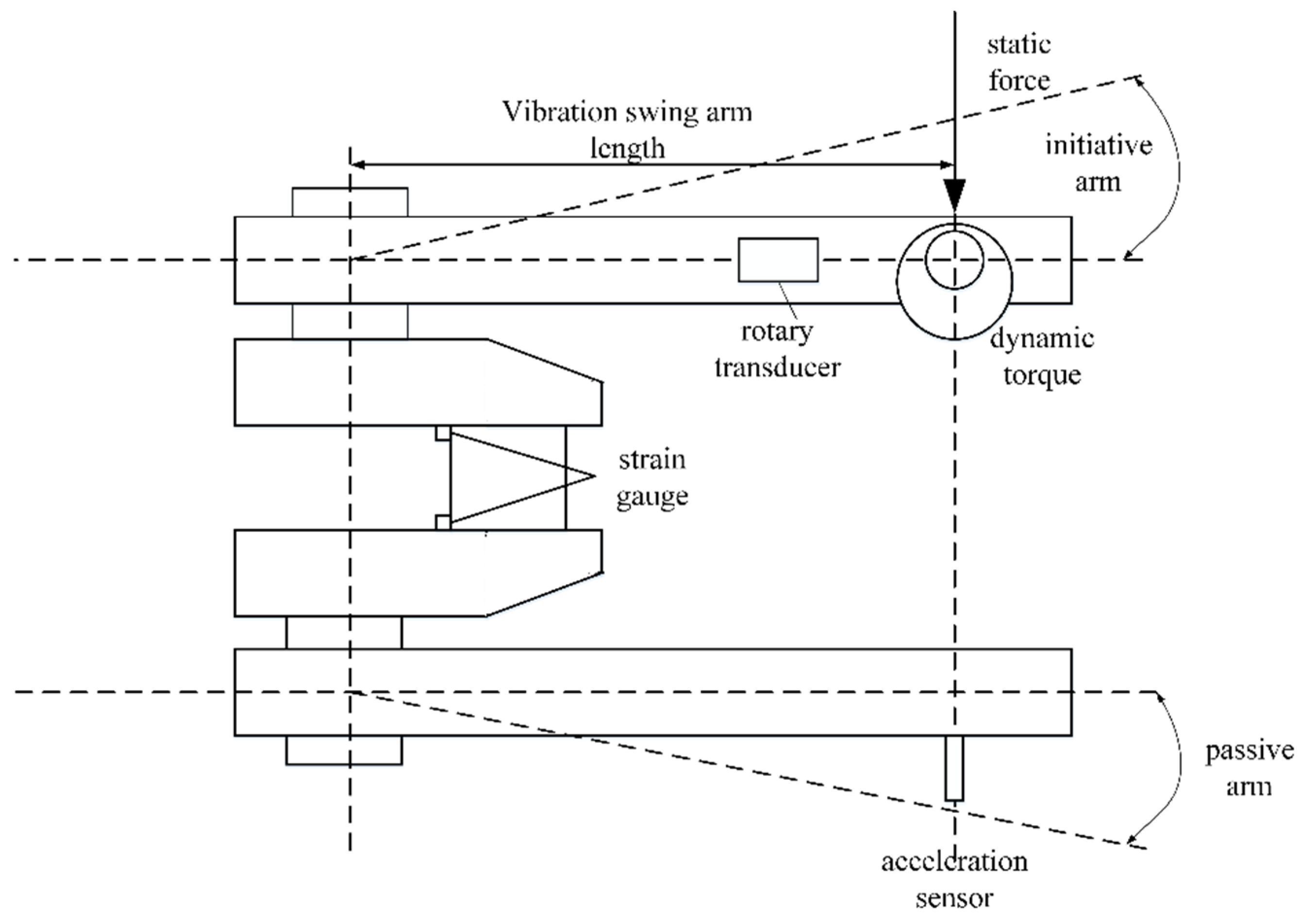
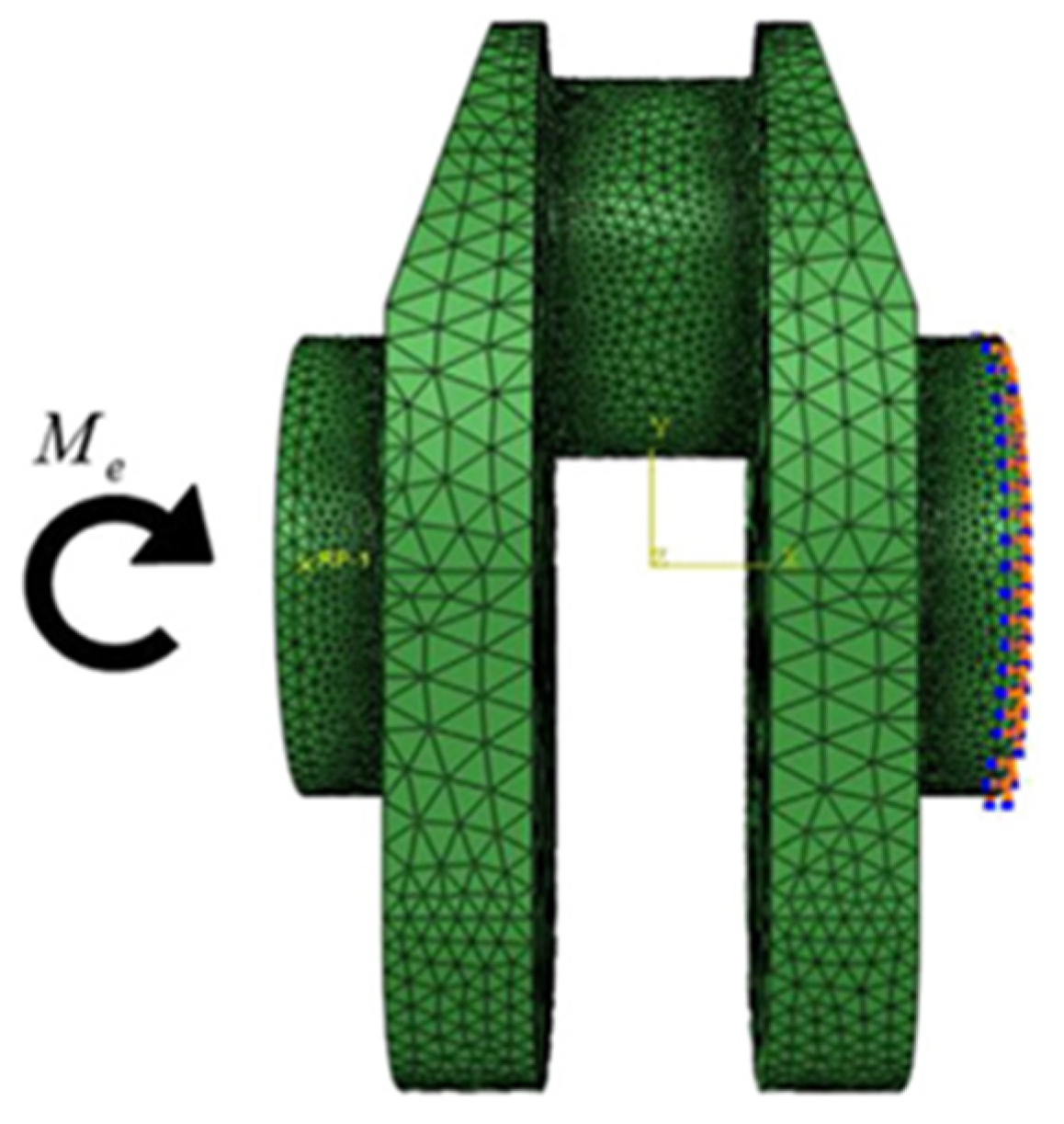
2.3. Experiment Verification Method
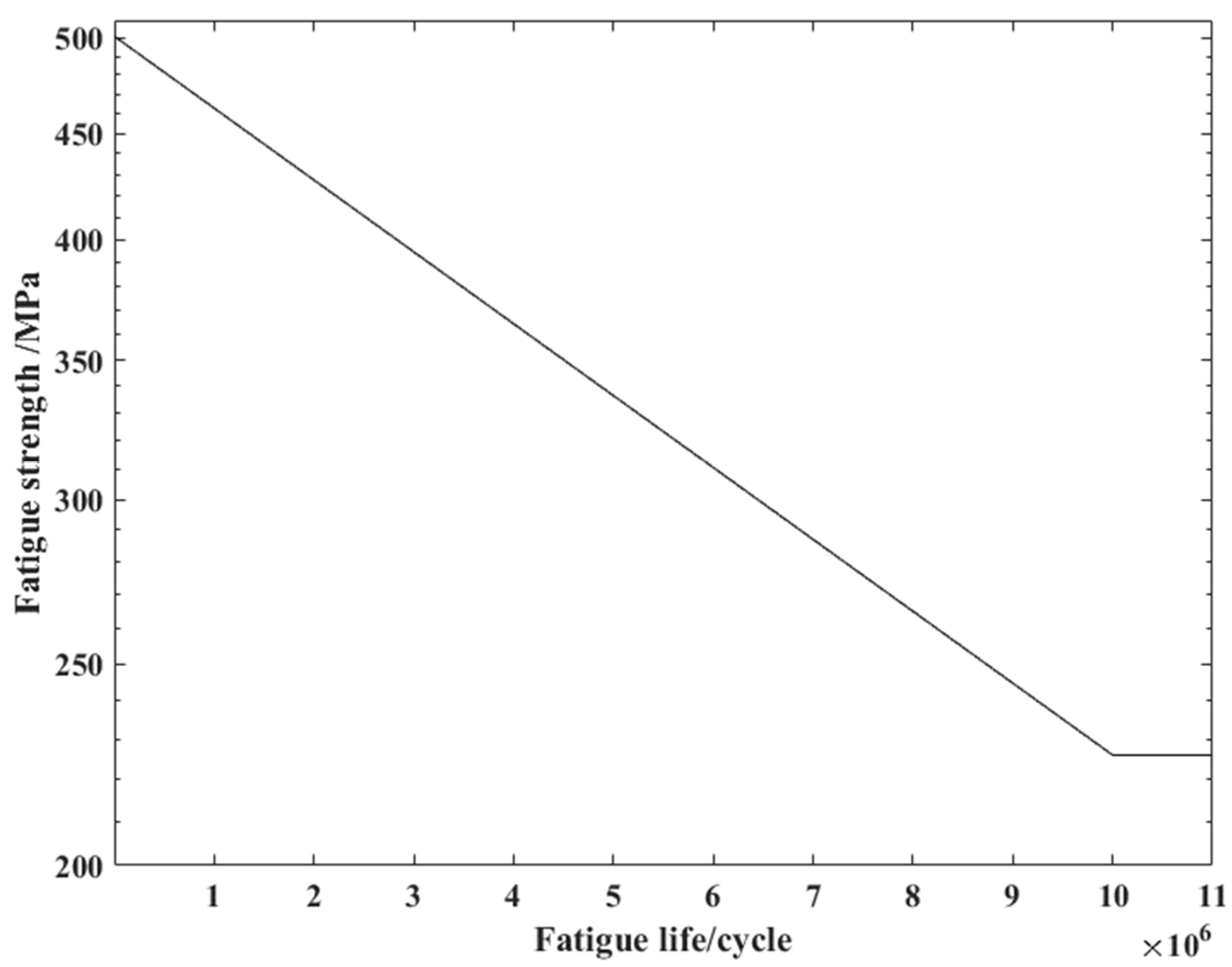
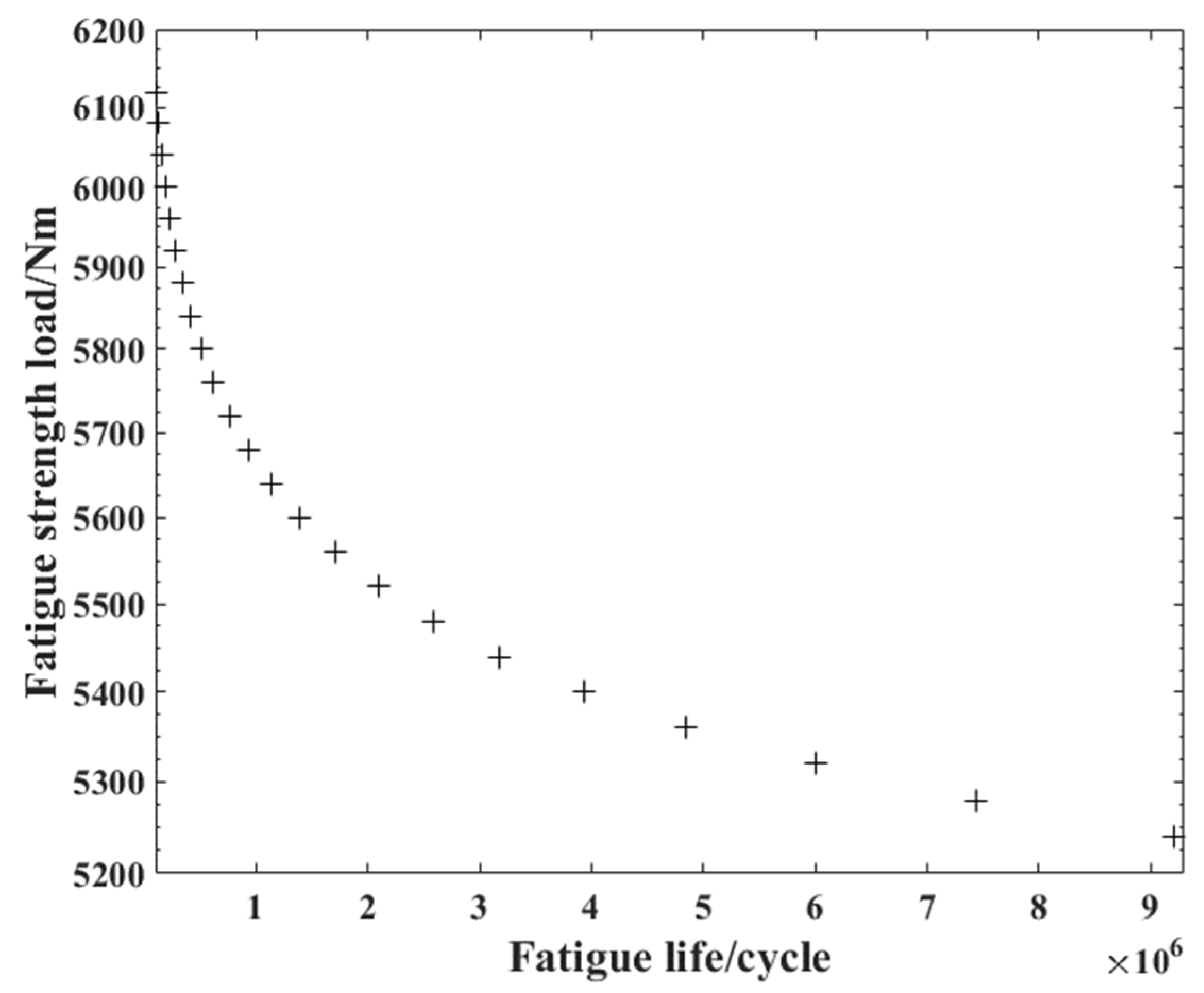
2.4. Fatigue Model Selection
3. Results
3.1. Prediction of Crankshaft N0
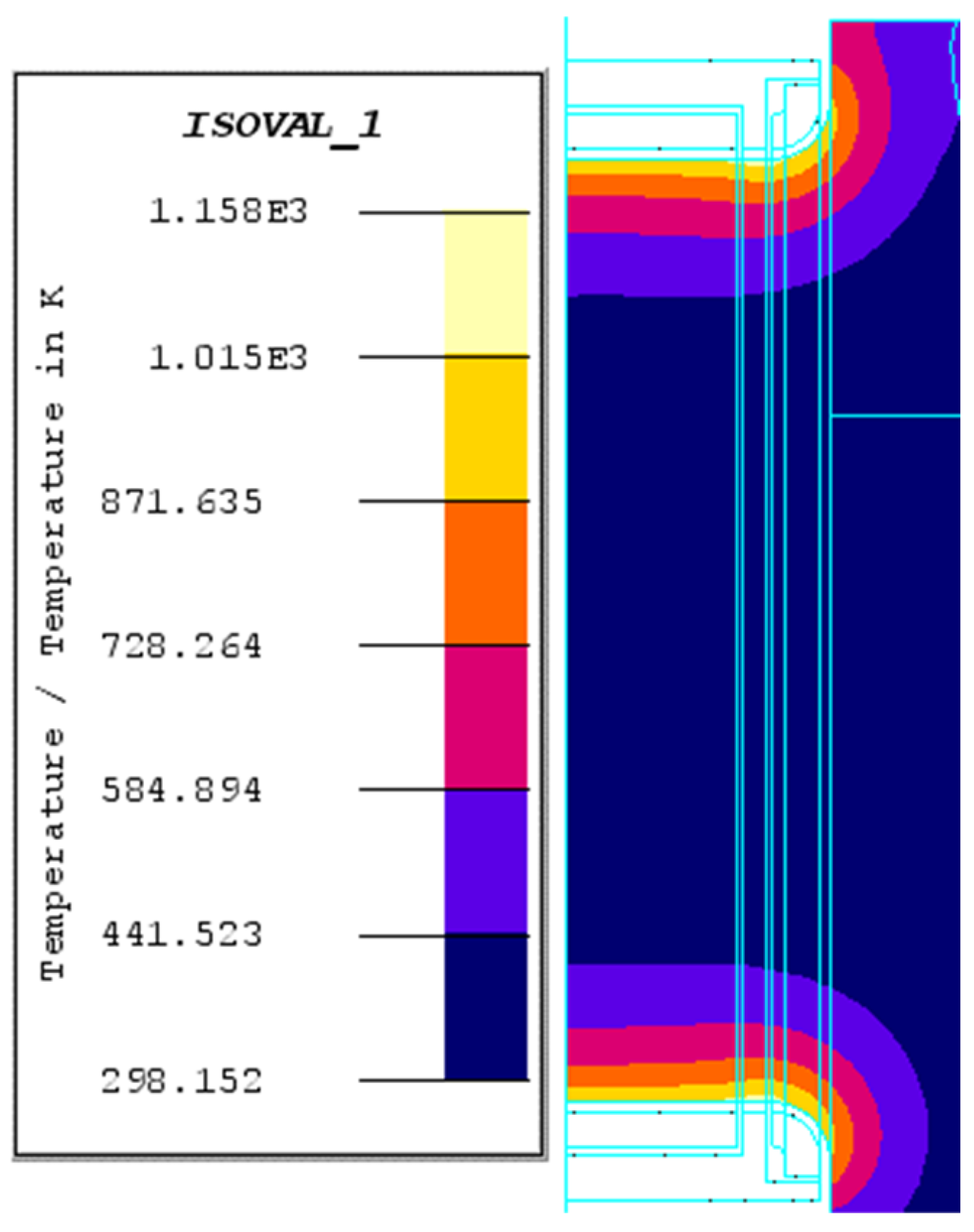
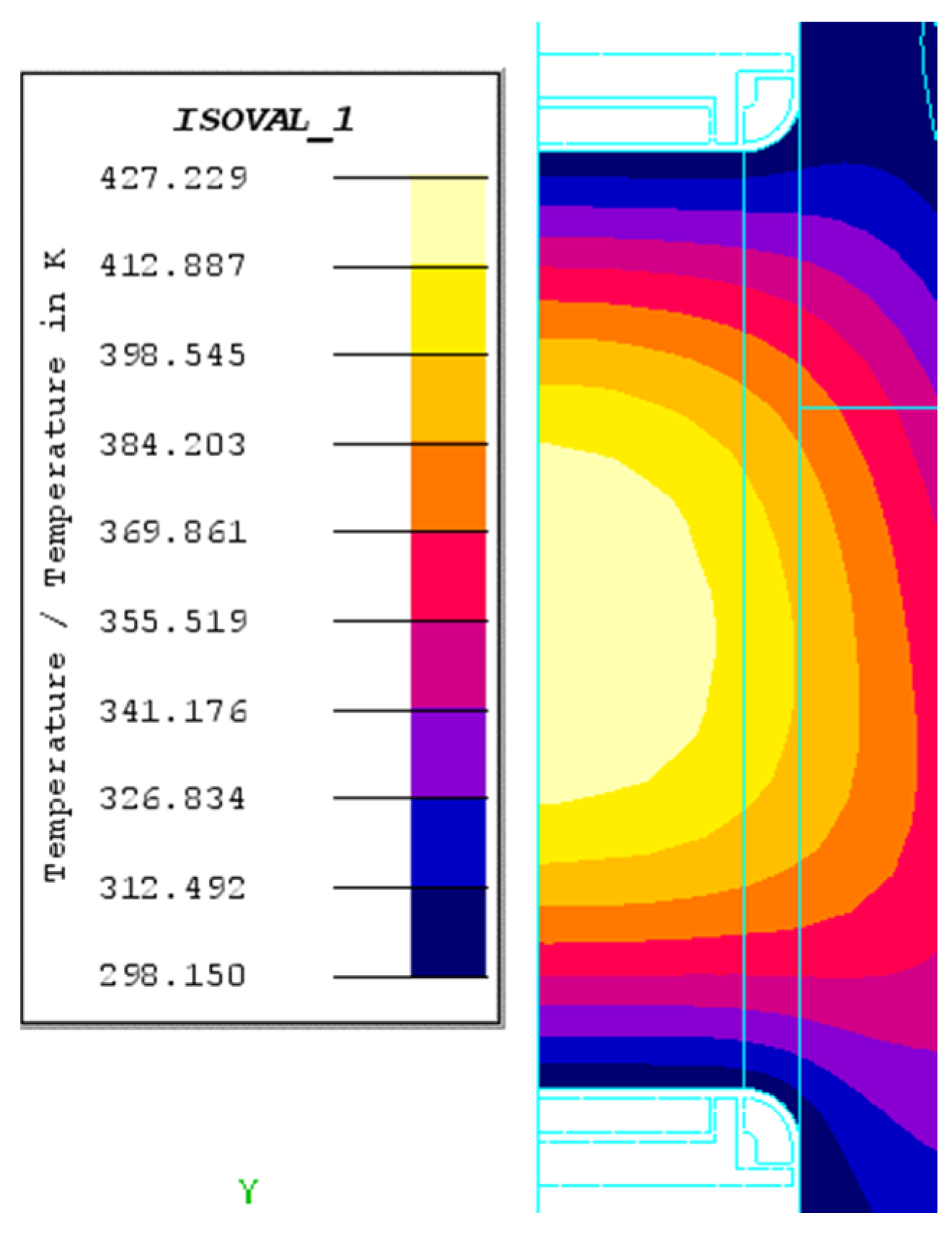
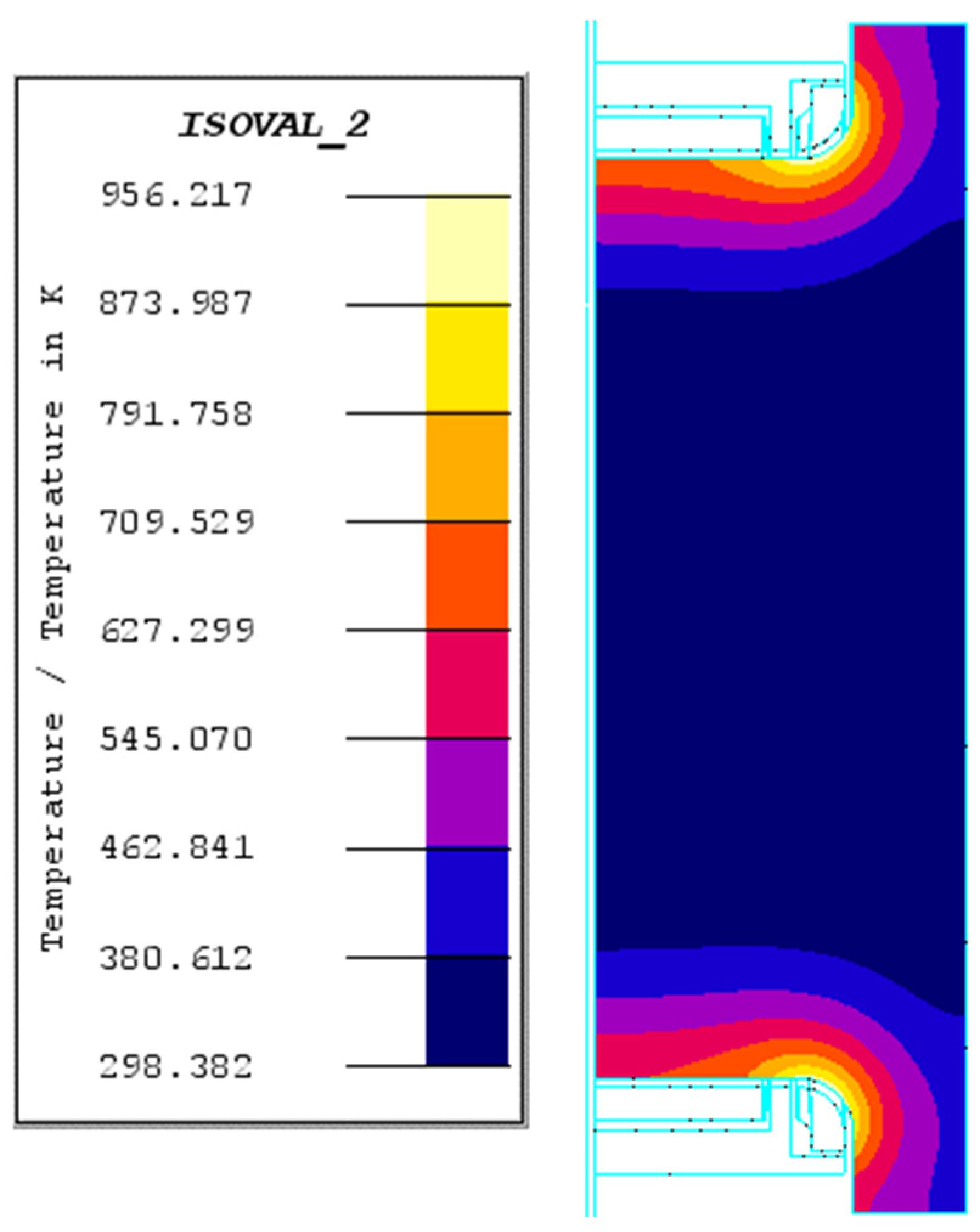
3.1.1. The Magnetic–Thermal Coupling Analysis
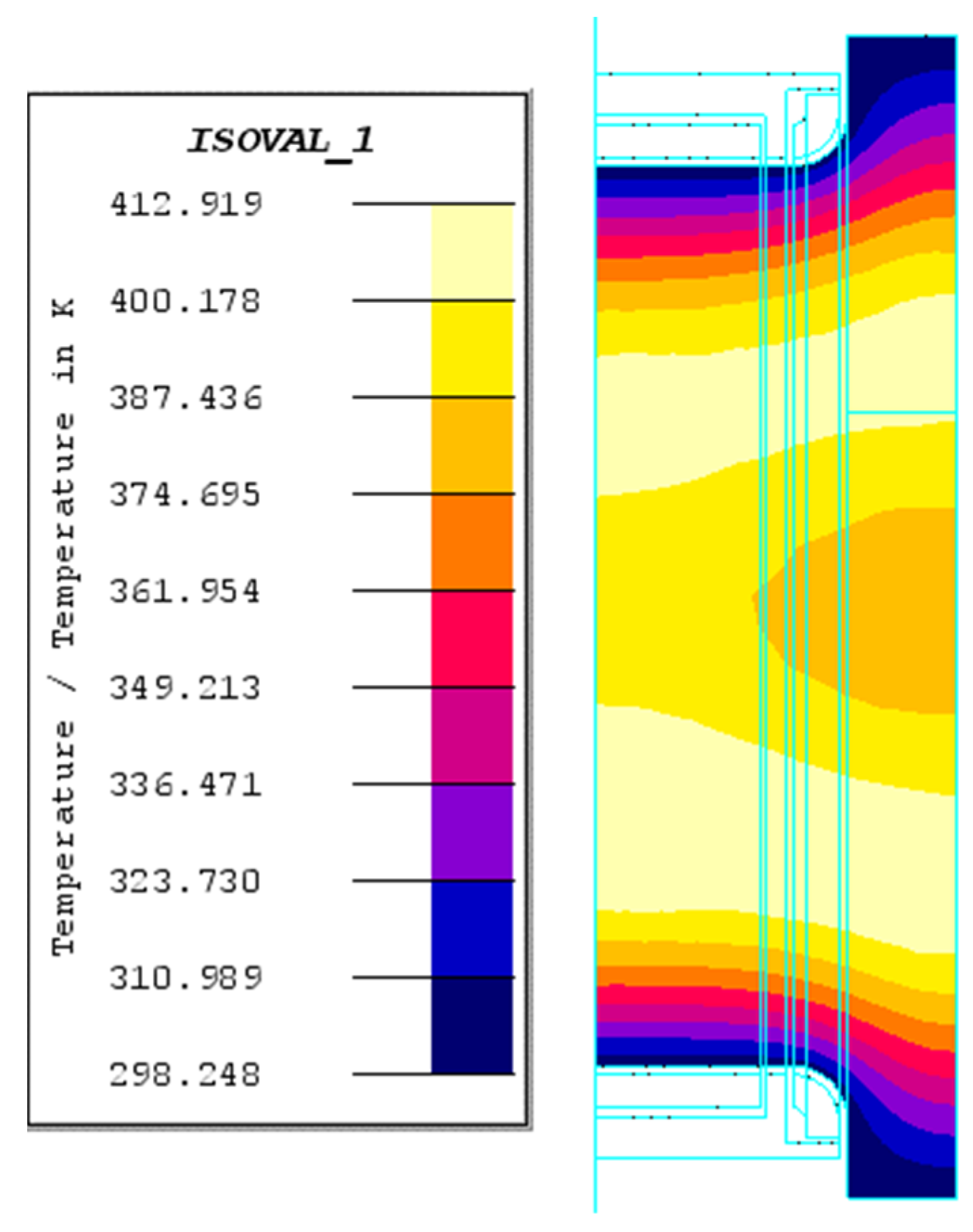
3.1.2. The Thermal-Mechanical Coupling Analysis
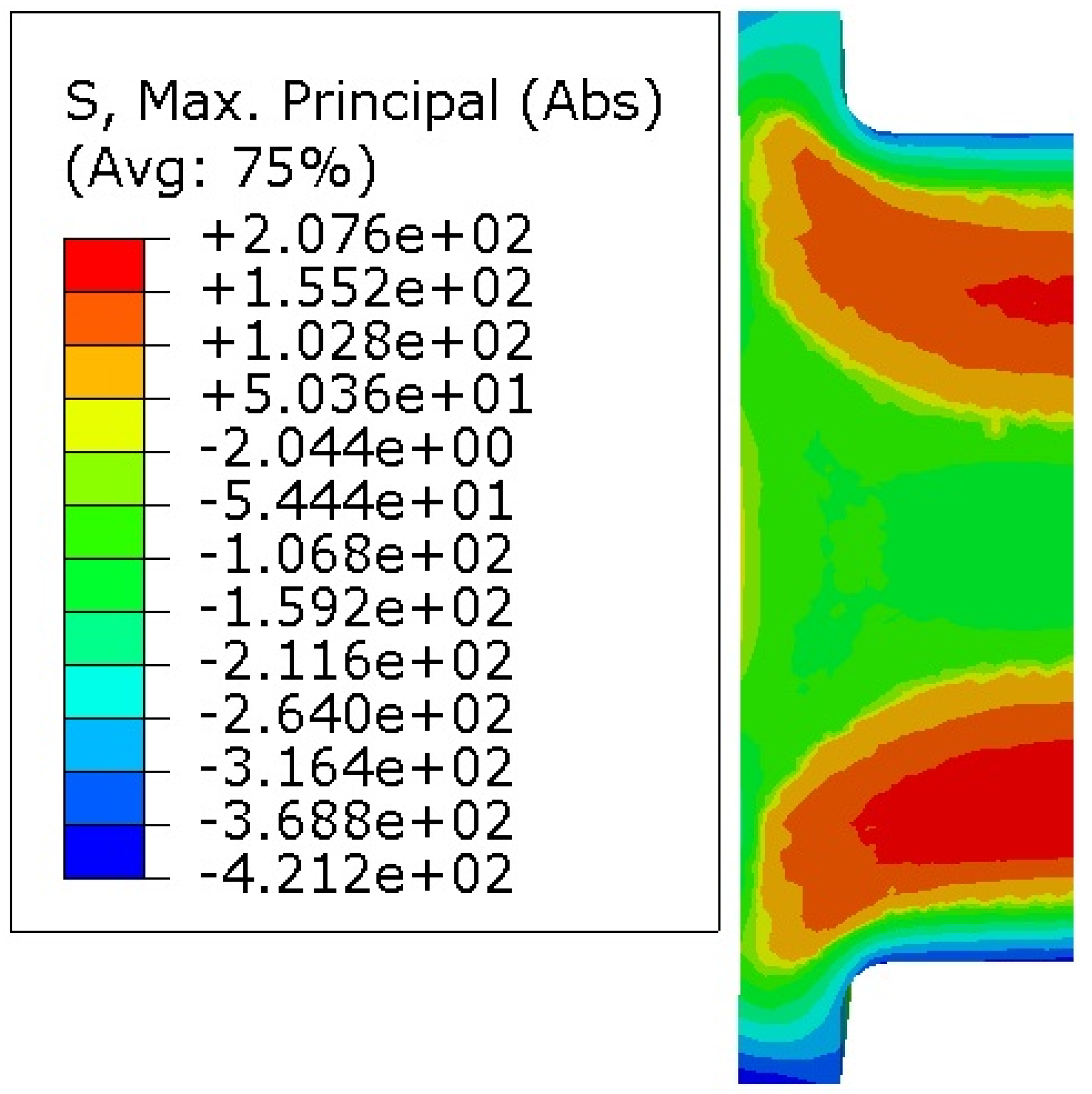
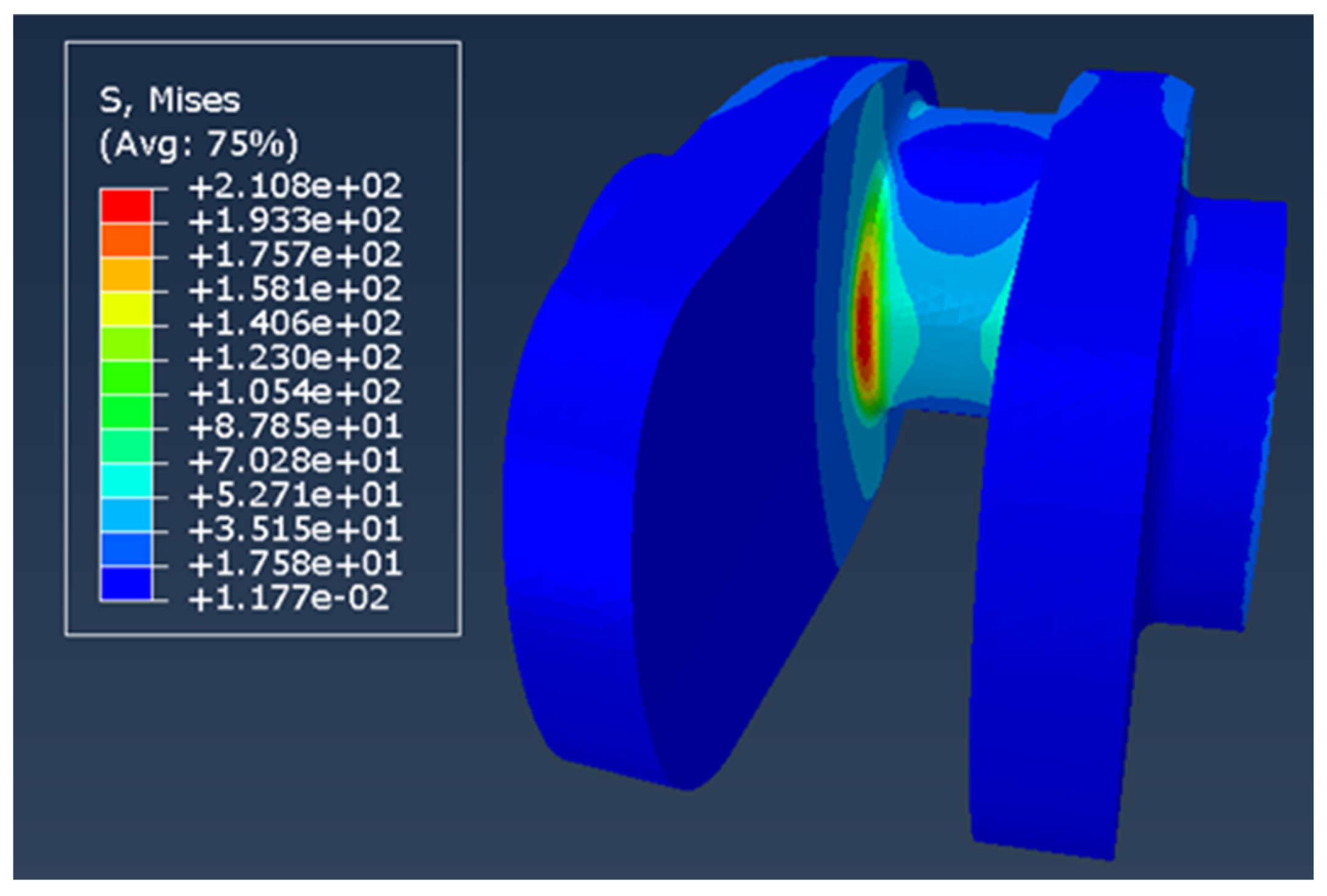
3.1.3. Equivalent Stress and Prediction Results
3.2. Prediction of Crankshaft N1
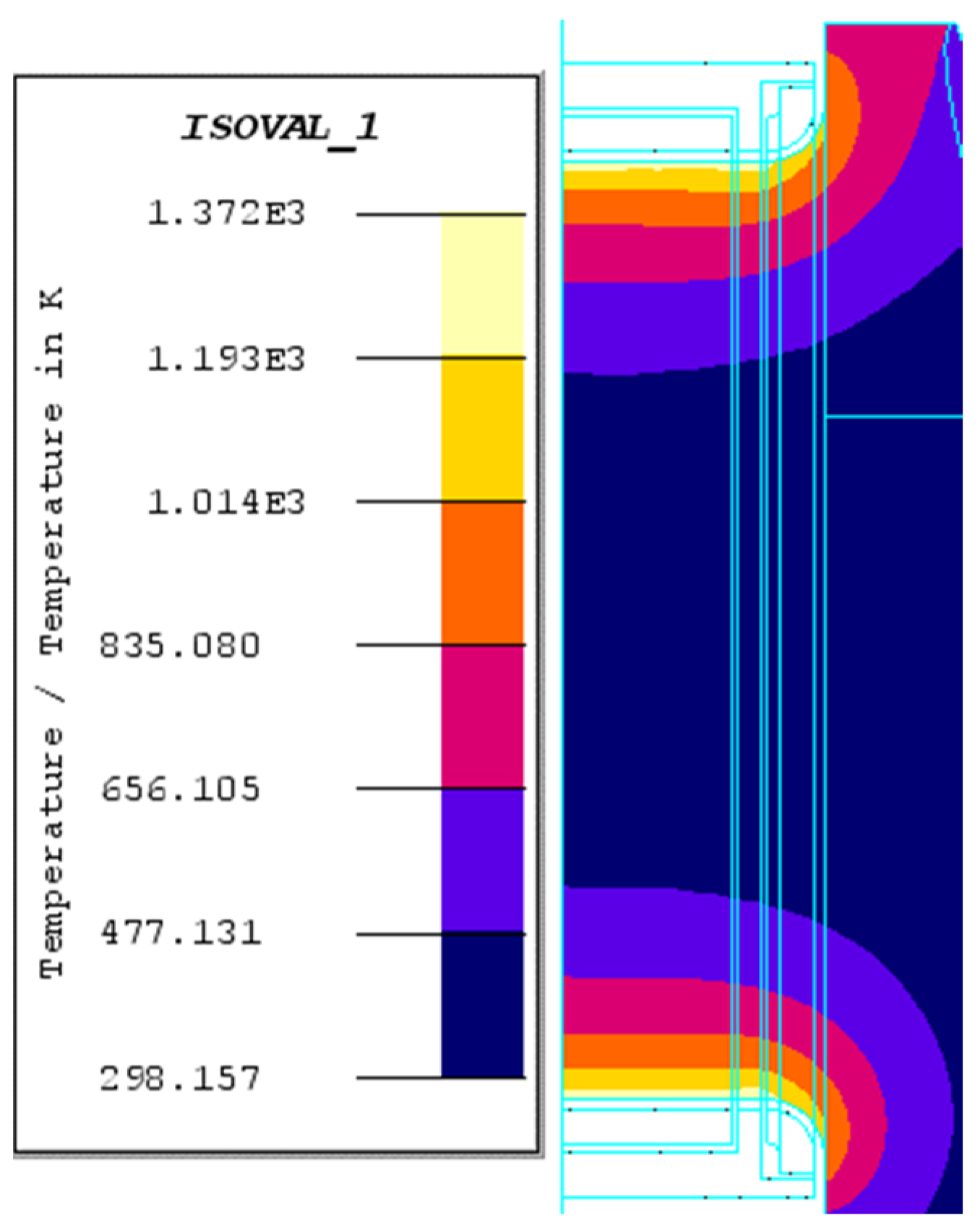
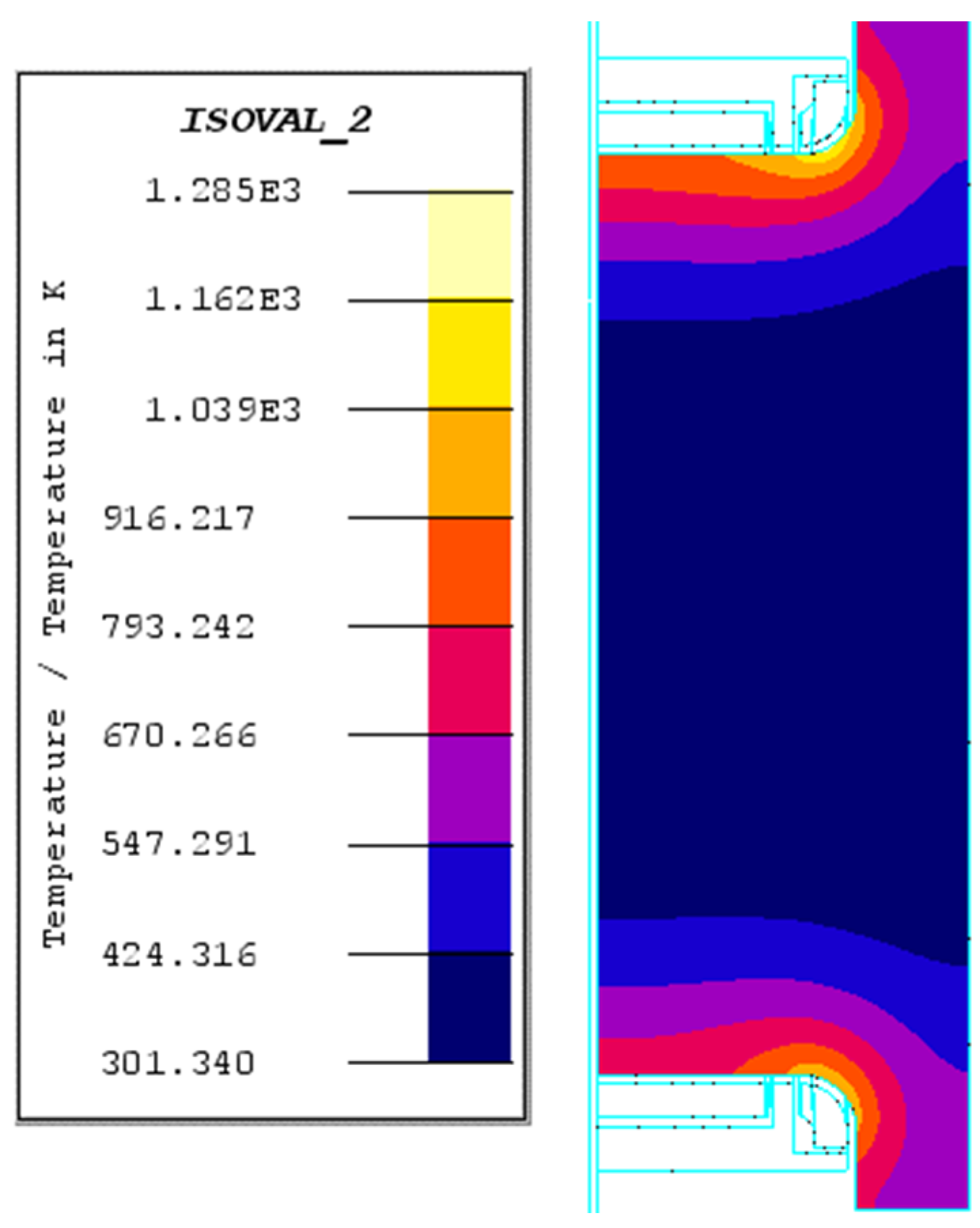
3.2.1. The Magnetic–Thermal Coupling Analysis
3.2.2. The Thermal-Mechanical Coupling Analysis
3.2.3. Equivalent Stress and Prediction Results
4. Experimental Verification and Discussion
5. Conclusions
- (1)
- For both crankshafts, during the heating up stage, the temperature at the fillet increased more quickly than that at the crankpin surface, which could be attributed to the longer effective heating time of the former. In addition, the uniform temperature fields at the surface of the crankpin area is useful to form the uniform layer.
- (2)
- After liquid cooling, the temperature of the surface dropped rapidly, and the internal body of the crankshaft began to rise. Additionally, the compressive residual stress was generated at the surface and the tensile residual stress was created within the central area.
- (3)
- The multi-axial fatigue damage model proposed in this paper can accurately predict the fatigue property of no less than one type of steel crankshaft, which makes it useful to be applied in guiding the design and manufacturing process of the part.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jie, T.; Tong, J.; Shi, L. Differential steering control of four-wheel independent-drive electric vehicles. Energies 2018, 11, 2892. [Google Scholar]
- Tian, J.; Wang, Q.; Ding, J.; Wang, Y.; Ma, Z. Integrated Control With DYC and DSS for 4WID Electric Vehicles. IEEE Access 2019, 7, 124077–124086. [Google Scholar] [CrossRef]
- Lin, Y.; Xiao, M.H.; Liu, H.J.; Li, Z.L.; Zhou, S.; Xu, X.M.; Wang, D.C. Gear fault diagnosis based on CS-improved variational mode decomposition and probabilistic neural network. Measurement 2022, 192, 110913. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, L.; Jiang, Y.; Chen, N. Active control on path following and lateral stability for truck–trailer com-binations. Arab. J. Sci. Eng. 2019, 44, 1365–1377. [Google Scholar] [CrossRef]
- Xu, X.; Lin, P. Parameter identification of sound absorption model of porous materials based on modified particle swarm optimization algorithm. PLoS ONE 2021, 16, e0250950. [Google Scholar] [CrossRef]
- Xu, X.; Chen, N.; Zhang, L.; Chen, N. Hopf Bifurcation Characteristics of the Vehicle with Rear Axle Compliance Steering. Shock Vib. 2019, 2019, 3402084. [Google Scholar] [CrossRef] [Green Version]
- Jiri, P.; Zdenek, P.; David, D. Service behavior of nitride layers of steels for military applications. Coating 2020, 10, 975. [Google Scholar]
- Sackl, S.; Leitner, H.; Zuber, M.; Clemens, H.; Primig, S. Induction Hardening vs Conventional Hardening of a Heat Treatable Steel. Met. Mater. Trans. A 2014, 45, 5657–5666. [Google Scholar] [CrossRef]
- Prisco, U. Case microstructure in induction surface hardening of steels: An overview. Int. J. Adv. Manuf. Technol. 2018, 98, 2619–2637. [Google Scholar] [CrossRef]
- Qi, P.; Sun, Q.; Zhong, J.; Wang, G.; Liu, X.; Liu, W. Effects of electromagnetic induction hardening on the microstructure and mechanical properties of B1500HS steel. IOP Conf. Ser. Mater. Sci. Eng. 2020, 892, 012017. [Google Scholar] [CrossRef]
- Barglik, J. Induction contour hardening of gear wheels made of steel 300M. IOP Conf. Ser. Mater. Sci. Eng. 2018, 424, 012062. [Google Scholar] [CrossRef]
- Barglik, J.; Smagór, A.; Smalcerz, A. Induction hardening of gear wheels of steel 41Cr4. Int. J. Appl. Electromagn. Mech. 2018, 57, 3–12. [Google Scholar] [CrossRef]
- Torres, H.; Pérez-González, F.A.; Zapata-Hernández, O.; Garza-Montes-deOca, N.F.; Ramírez-Ramírez, J.H.; Fried, Z.; Felde, I.; Réger, M.; Colás, R. Modeling the Induction Hardening of High-Carbon Saw Blades Reference. Mater. Perform. Charact. 2019, 8, 261–271. [Google Scholar]
- Baldan, M.; Stolte, M.H.; Nacke, B.; Nürnberger, F. Improving the Accuracy of FE Simulations of Induction Tempering Toward a Micro-structure-Dependent Electromagnetic Model. IEEE Trans. Magn. 2020, 56, 1–9. [Google Scholar] [CrossRef]
- Tong, D.; Gu, J.; Yang, F. Numerical simulation on induction heat treatment process of a shaft part: Involving induction hardening and tempering. J. Mater. Process. Technol. 2018, 262, 277–289. [Google Scholar] [CrossRef]
- Tong, D.; Gu, J.; Totten, G.E. Numerical investigation of asynchronous dual-frequency induction hardening of spur gear. Int. J. Mech. Sci. 2018, 142, 1–9. [Google Scholar] [CrossRef]
- Fisk, M.; Lindgren, L.E.; Datchary, W.; Deshmukh, V. Modelling of induction hardening in low alloy steels. Finite Elem. Anal. Des. 2018, 144, 61–75. [Google Scholar] [CrossRef]
- Wu, C.; Sun, S. Crankshaft High Cycle Bending Fatigue Research Based on a 2D Simplified Model and Different Mean Stress Models. J. Fail. Anal. Prev. 2021, 21, 1396–1402. [Google Scholar] [CrossRef]
- Sun, S.S.; Zhang, X.; Wu, C.; Wan, M.; Zhao, F. Crankshaft high cycle bending fatigue research based on the simulation of electromagnetic induction quenching and the mean stress effect. Engl. Fail. Anal. 2021, 122, 105214. [Google Scholar]
- Li, J. Numerical Studies on the Induction Quenching Process of Crankshaft; Beijing Institute of Technology: Beijing, China, 2015. [Google Scholar]
- Lim, B.K. Analysis of fatigue life of SPR (self-piercing riveting) jointed various specimens using FEM. In Proceedings of the International Welding/Joining Conference-Korea, IWJC-Korea 2007; Small Business Training Institute: Ansan, Korea, 2008. [Google Scholar]
- Hömberg, D.; Liu, Q.; Montalvo-Urquizo, J.; Nadolski, D.; Petzold, T.; Schmidt, A.; Schulz, A. Simulation of multi-frequency-induction-hardening including phase transitions and me-chanical effects. Finite Elem. Anal. Des. 2016, 121, 86–100. [Google Scholar] [CrossRef]
- Sun, S.S.; Yu, X.-L.; Li, J.F. A study on the equivalent fatigue of crankshaft structure based on the theory of multi-axial fatigue. Automot. Eng. 2016, 38, 1001–1005. [Google Scholar]
- Zhou, X.; Yu, X. Failure criterion in resonant bending fatigue test for crankshafts. Chin. Intern. Combust. Engine Eng. 2007, 28, 45–47. [Google Scholar]
- Zhou, X.; Yu, X. Error analysis and load calibration technique investigation of resonant loading fatigue test for crankshaft. Trans. Chin. Soc. Agric. Mach. 2007, 4, 35–38. [Google Scholar]
- Brown, M.W.; Miller, K.J. A theory for fatigue failure under multi-axial stress-strain conditions. Proc. Inst. Mech. Eng. 1973, 187, 1847–1982. [Google Scholar] [CrossRef]
- Sun, S.S.; Wan, M.S.; Wang, H. Crankshaft fatigue research based on modified multi-axial fatigue model. J. Mech. Electr. Engl. 2019, 36, 797–802. [Google Scholar]
- Sun, S.S.; Yu, X.L.; Chen, X.P.; Liu, Z.T. Component structural equivalent research based on different failure strength criterions and the theory of critical distance. Engl. Fail. Anal. 2016, 70, 31–43. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, A. Remaining Useful Life Prediction of Rolling Bearings Using Electrostatic Monitoring Based on Two-Stage Information Fusion Stochastic Filtering. Math. Probl. Engl. 2020, 2020, 2153235. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, Y.; Yu, Y. Joint Estimation of SOC of Lithium Battery Based on Dual Kalman Filter. Processes 2021, 9, 1412. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, Y.; Yu, Y. Lithium-Ion Battery SOC Estimation Based on Adaptive Forgetting Factor Least Squares Online Identification and Unscented Kalman Filter. Mathematics 2021, 9, 1733. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Pan, Z.; Lu, Q. Review on the Battery Model and SOC Estimation Method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- Chang, C.; Zheng, Y.; Sun, W.; Ma, Z. LPV Estimation of SOC Based on Electricity Conversion and Hysteresis Characteristic. J. Energy Engl. 2019, 145, 04019026. [Google Scholar] [CrossRef]
- Chang, C.; Zheng, Y.; Yu, Y. Estimation for Battery State of Charge Based on Temperature Effect and Fractional Extended Kalman Filter. Energies 2020, 13, 5947. [Google Scholar] [CrossRef]






| Composition | Percentage/% |
|---|---|
| C | 0.38–0.45 |
| Si | 0.17–0.37 |
| Mn | 0.50–0.80 |
| S | ≤0.035 |
| P | ≤0.035 |
| Cr | 0.9–1.2 |
| Ni | ≤0.3 |
| Cu | ≤0.3 |
| Mo | 0.15–0.25 |
| Serial Number | N1 | N0 |
|---|---|---|
| Crankpin diameter | 82 mm | 83 mm |
| Main journal diameter | 100 mm | 100 mm |
| Fillet radius | 5 mm | 5 mm |
| Overlap | 26 mm | 16 mm |
| Crank web width | 29 mm | 28 mm |
| Fillet heating time | 12 s | 9 s |
| Crankpin heating time | 4 s | 3 s |
| Current frequency | 8000 Hz | 8000 Hz |
| Crankpin current density | 6.5 × 107 A/m2 | 9.9 × 107 A/m2 |
| Fillet current density | 1 × 108 A/m2 | 1.15 × 108 A/m2 |
| Parameter | Residual Stress Field | Given Load |
|---|---|---|
| S11 | −72.5 MPa | 41.75 MPa |
| S22 | −75.1 MPa | 73 MPa |
| S33 | −323.8 MPa | 72.5 MPa |
| S12 | 75.4 MPa | −0.014 MPa |
| S13 | −1.6 MPa | 0.14 MPa |
| S23 | 2.03 MPa | 74.1 MPa |
| Shear stress | −24.4 MPa | 76.2 MPa |
| Normal stress | −157.3 MPa | 72.4 MPa |
| Parameter | Residual Stress Field | Given Load |
|---|---|---|
| S11 | −239.4 MPa | 35 MPa |
| S22 | −251.4 MPa | 62 MPa |
| S33 | −367.3 MPa | 62.5 MPa |
| S12 | 248.7 MPa | −0.08 MPa |
| S13 | 2 MPa | 0.128 MPa |
| S23 | 1.2 MPa | 64.2 MPa |
| Shear stress | −64.4 MPa | 64 MPa |
| Normal stress | −363.3 MPa | 62.4 MPa |
| Load Value/N·m | Load Cycle |
|---|---|
| 3335 | 6,711,179 |
| 3436 | 6,187,261 |
| 3881 | 4,502,460 |
| 3941 | 2,465,780 |
| 3941 | 273,493 |
| 3901 | 548,588 |
| 3416 | 6,142,771 |
| 3557 | 3,509,554 |
| Load Value/N·m | Load Cycle |
|---|---|
| 4909 | 496,300 |
| 4909 | 252,286 |
| 4664 | 868,306 |
| 4664 | 901,425 |
| 4764 | 687,944 |
| 4764 | 652,265 |
| 4541 | 1,435,103 |
| 4541 | 2,221,044 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Liu, W.; Zhang, X.; Wan, M. Crankshaft HCF Research Based on the Simulation of Electromagnetic Induction Quenching Approach and a New Fatigue Damage Model. Metals 2022, 12, 1296. https://doi.org/10.3390/met12081296
Sun S, Liu W, Zhang X, Wan M. Crankshaft HCF Research Based on the Simulation of Electromagnetic Induction Quenching Approach and a New Fatigue Damage Model. Metals. 2022; 12(8):1296. https://doi.org/10.3390/met12081296
Chicago/Turabian StyleSun, Songsong, Weiqiang Liu, Xingzhe Zhang, and Maosong Wan. 2022. "Crankshaft HCF Research Based on the Simulation of Electromagnetic Induction Quenching Approach and a New Fatigue Damage Model" Metals 12, no. 8: 1296. https://doi.org/10.3390/met12081296
APA StyleSun, S., Liu, W., Zhang, X., & Wan, M. (2022). Crankshaft HCF Research Based on the Simulation of Electromagnetic Induction Quenching Approach and a New Fatigue Damage Model. Metals, 12(8), 1296. https://doi.org/10.3390/met12081296






