Improved Compressive Properties of Lattice Structure Based on an Implicit Surface Hybrid Optimization Design Method via Selective Laser Melting

Abstract

In recent years, the lattice structure produced by additive manufacturing is a type of metal foam that has been increasingly investigated for its unique mechanical properties. However, the conventional Computer-Aided Design (CAD) is inefficient, the triply periodic minimal surfaces are rarely mixed, and the smooth transitions at the boundaries are not considered. In this study, a hybrid optimization design method based on implicit surfaces is proposed, which combines multiple implicit surfaces to achieve the continuous change in the curvature at the structure junctions and reduce the stress concentration. The hybrid lattice structures designed by this method were additively manufactured using 316L alloy via a selective laser melting. The results of the finite element analysis and mechanical compression test show that the hybrid lattice structures generated by this method exhibit a higher yield strength and energy absorption. These works can be used for other implicit surfaces, improve and enrich the types of implicit surfaces, and provide more good choices for practical applications.

1. Introduction

Additive manufacturing applied to metal foams provides a viable technical guarantee for the fabrication of complex lattice structures [1,2,3,4], making design concepts that once existed only on paper a reality.

As a unique implicit surface, a three-period minimal surface (TPMS) can quickly generate ideal cell structures in a three-dimensional space through mathematical expression modeling [5,6,7]. For example, the classical Gyroid [8,9,10], Diamond [11], Primitive [12], and I-WP [13] surfaces correspond to different implicit surface equations, and adjusting the coefficients and constant terms in the equations can easily control the shape and porosity of the cell, which is valuable and attractive for lightweight engineering design and medical application design [14,15,16,17].

A lot of research has been conducted on hybrid different materials [18,19], different structures [20,21,22,23], and different positions [24] for the purpose of improving the performance of porous structures. Novak et al. fabricated hybrid TPMS cellular lattices [25,26], hybrid structures with auxetic cellular and silicon filler [27], and sandwich composite panels with auxetic core [28,29], which improved the energy absorption capacity and the response to blast loading of the composite structure. Liu et al. proposed a hybrid lattice structure of a spherical ball and a body-centered cubic [30]. Zhao et al. used a novel parametric approach to generate the BCC lattice structures with taper struts [31]. In this way, they all reduced the stress concentration of the structure and improved the mechanical properties.

Although there are many ways to design hybrid lattice structures, many scholars have little research on the hybrid design of lattice structures with corresponding parameters directly generated by software between different implicit surfaces. To explore more topological geometries of lattice structures, a hybrid design method based on implicit surfaces is proposed in this paper, hoping to explore diverse geometries to obtain more excellent mechanical properties.

Compared with traditional Computer-Aided Design (CAD), this method can generate new implicit surface unitary structures that retain their respective morphological features, have smooth continuity in the structure junctions, and reduce the stress concentration so as to achieve a higher yield strength and energy absorption.

2. Materials and Methods

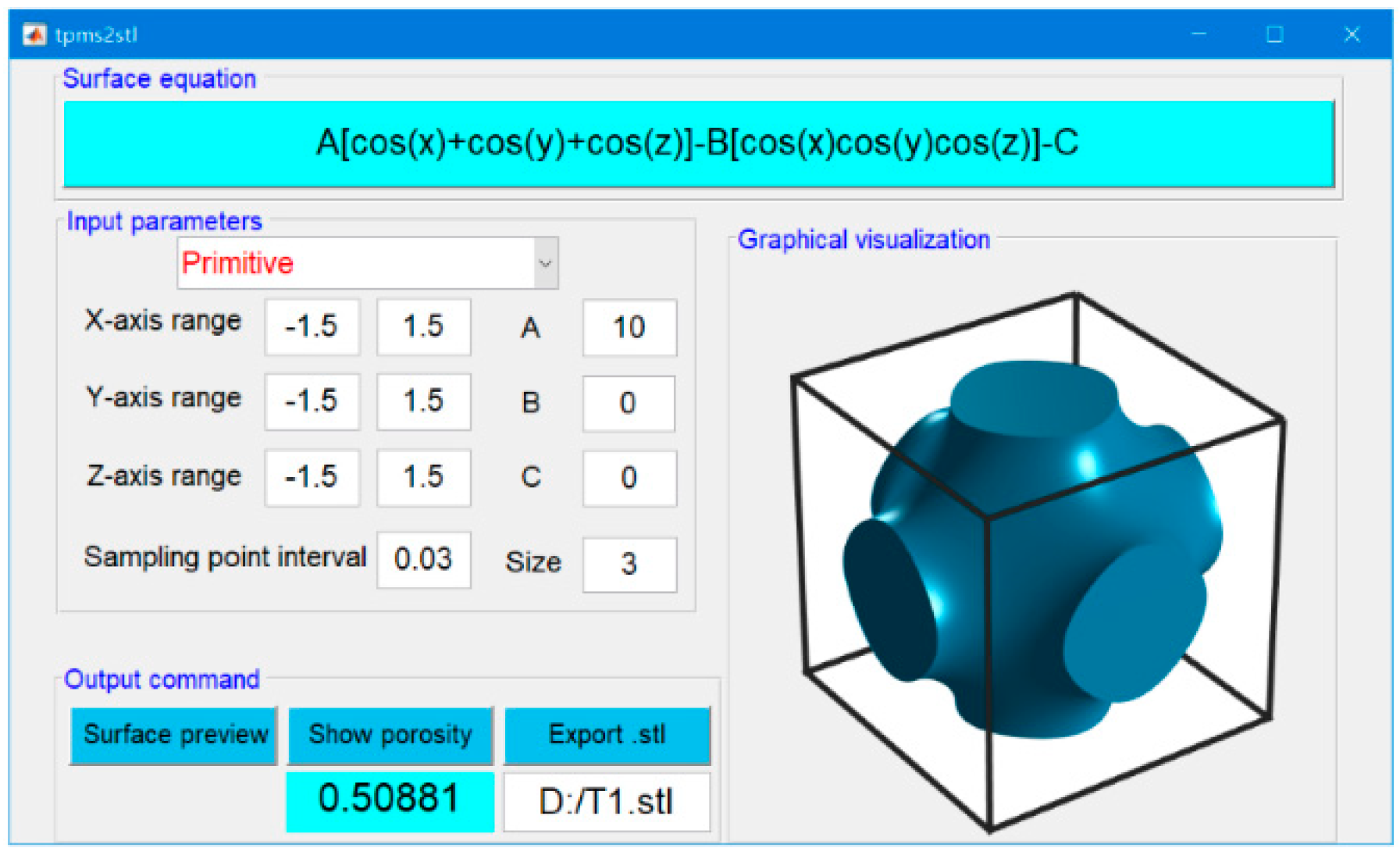
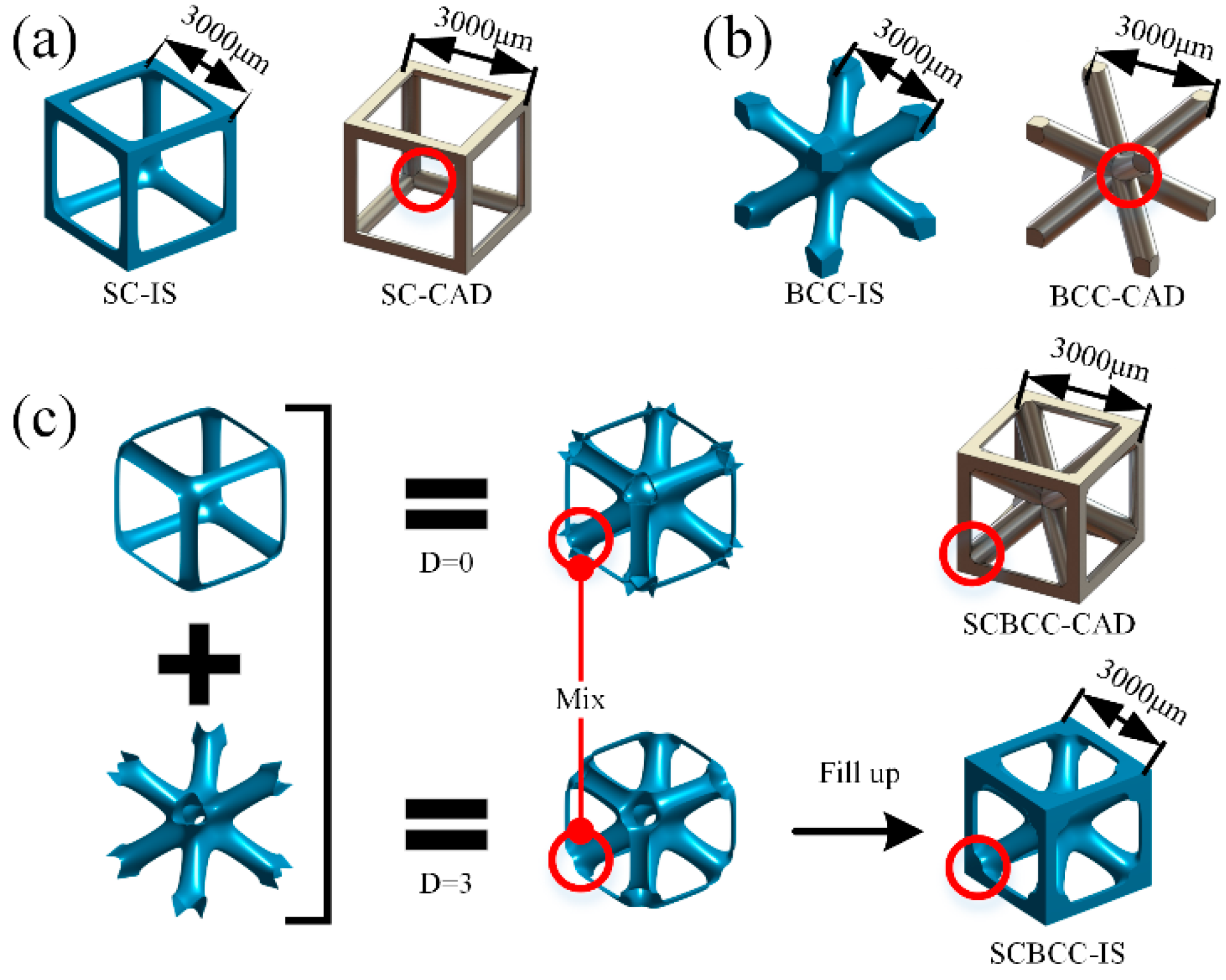
2.1. Structure Design

In this paper, a software named Tpms2stl (1.0, Matlab, Natick, MA, USA) was developed based on Matlab software, as shown in Figure 1. Tpms2stl can generate hybrid implicit surfaces (file format is .stl) directly based on different parameters. The hybrid implicit surface equation is as follows:

φ_mix(X,Y,Z) = φ₁(X,Y,Z) × φ₂(X,Y,Z)× ⋅⋅⋅ × φ_n(X,Y,Z) + D

(1)

where n is the number of implicit surfaces involved in the blend and D is the amount that controls the transition effect of the surface hybrid part.

As depicted in Figure 2a–c, six units with the same side length of 3000 μm were designed to construct the periodic lattice structures. The SC-CAD (simple cubic based on CAD) and BCC-CAD (body-centered cubic based on CAD) structures illustrated in Figure 2a were simple cubic and body-centered cubic structures designed by the CAD software, respectively. The SC-IS (simple cubic based on implicit surfaces) and BCC-IS (body-centered cubic based on implicit surfaces) structures illustrated in Figure 2b were generated by the Tpms2stl to have a more continuous curvature change at the strut boundaries and reduce the stress concentration. The SCBCC-CAD (a hybrid of simple cubic and body-centered cubic based on CAD) structure in Figure 2c was designed by mixing SC-CAD and BCC-CAD. The SCBCC-IS (a hybrid of simple cubic and body-centered cubic based on implicit surfaces) structure in Figure 2c, designed by mixing SC-IS and BCC-IS, was generated by Tpms2stl. When D = 0, two implicit surfaces of the mixture have a sudden change in shape at the boundaries.

When D = 3, two implicit surfaces are perfectly blended into one, and the transition is realized with a smooth and continuous surface at the blending part. The larger the D value is, the smoother the transition effect is.

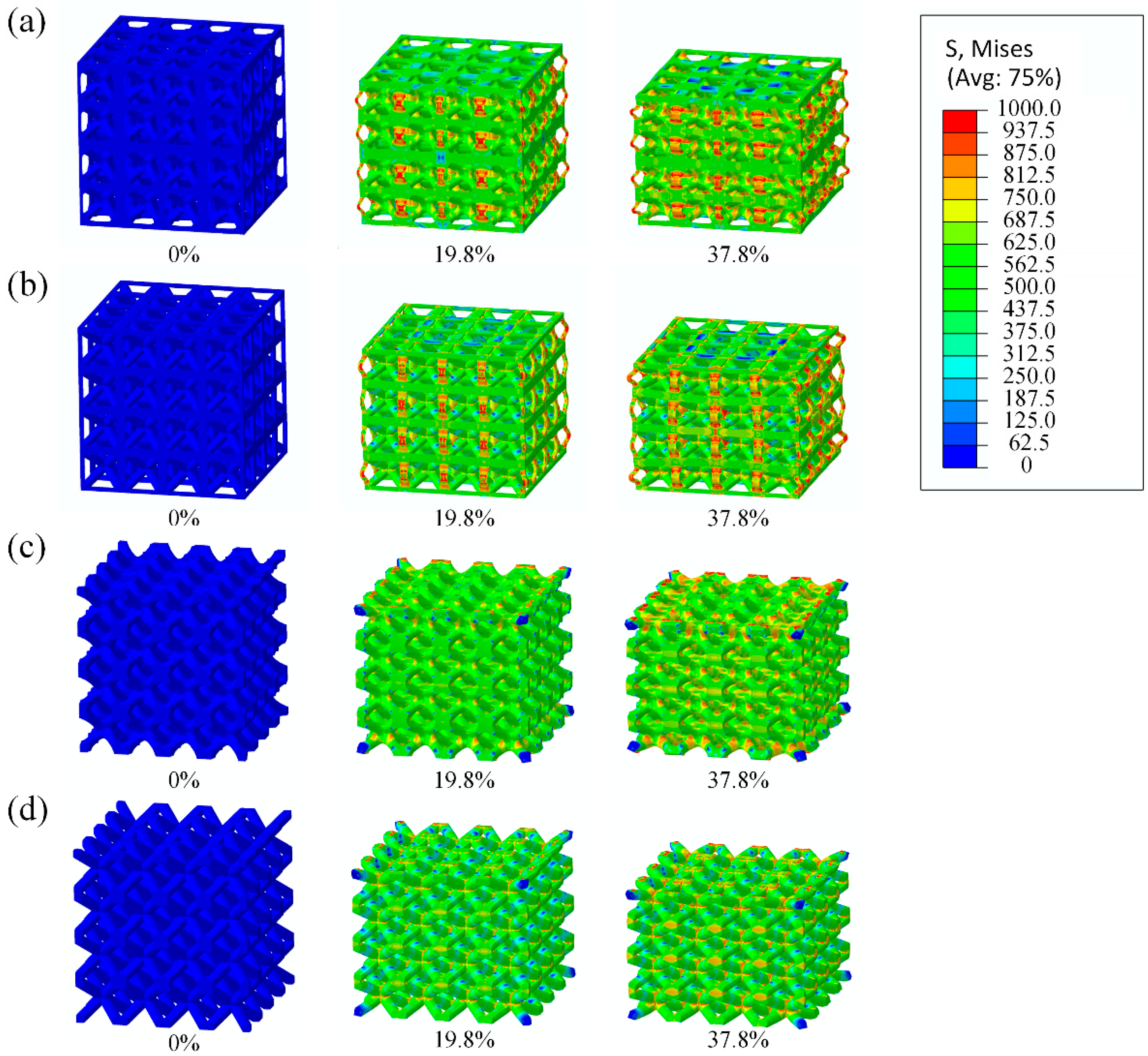
2.2. Finite Element Analysis

Quasi-static compression simulations were analyzed on 4 × 4 models by the finite element analysis (FEA) software (ABAQUS/explicit, Dassault Systems, Johnston, RI, USA), and the correlations between the optimized structure generated by tpms2stl and the mechanical loads were observed. The load direction, reference point, top rigid plate, model, and bottom rigid plate during the simulation are shown in Figure 3. Each model was placed between two parallel rigid plates and discretized with ten-node modified quadratic tetrahedron elements (C3D10M). The Young’s modulus and Poisson ratio of the material was assigned 196 MPa and 0.3. Stress distributions with a porosity of 73% from FEA under quasi-static compression are shown in Figure 4a–d.

Boundary conditions settings: The bottom rigid plate degrees of freedom were constrained, the top rigid plate was moved with a speed of 1 mm/min in the z-axis direction, and all other degrees of freedom constrained. Self-contact was set to general contact.

In the case of BCC-IS and BCC-CAD structures, the maximum equivalent stress values are mainly concentrated at the surface junctions of the oblique struts, and the free ends of the struts have to bear less stress because there are no external strut boundaries. The geometry of BCC-CAD has a more obvious abrupt change, so the stress concentration phenomenon is also more serious. The BCC-IS is a surface structure generated by independent functions through the tpms2stl software. The continuously changing curvature promotes the continuous distribution of stress along the oblique struts and finally uniformly converges on the main part where the struts intersect.

In the case of SCBCC-IS and SCBCC-CAD structures, the maximum equivalent stress values are concentrated at the surface junctions of the internal oblique struts. The main bearing area is vertical struts, which disperse most of the stress on the oblique struts, but the transverse struts do not distribute enough stress. The structure distributes the most stress at the vertical struts and the oblique struts junctions because the stress distribution of the porous structure is consistent with the direction of the force.

Compared with the porous structure designed by the CAD software, the structure directly generated by tpms2stl has a more uniform stress distribution, and the stress concentration effect is significantly improved.

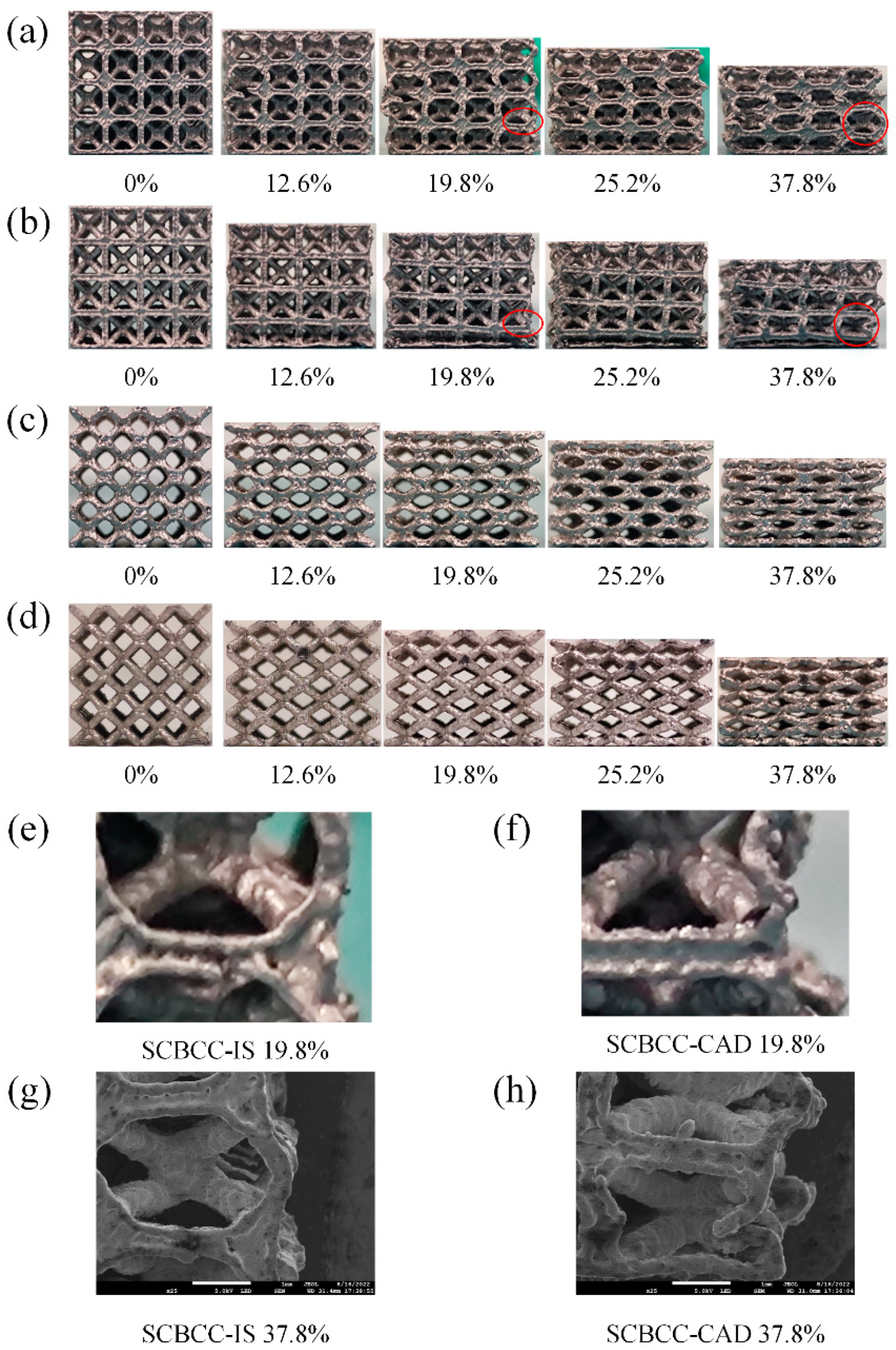
2.3. Specimen Fabrication

In this work, all structures were manufactured in a YLMs-1 selective laser melting machine (Jiangsu Yongnian Laser Forming Technology Co., Ltd., Kunshan, China) using SS316L powder with particle size of 15–50 μm. The processing parameters were: input energy of 170 W, laser scan speed of 900 mm/s, hatching spacing of 70 μm, and a layer thickness of 30 μm. The chemical composition of the SS316L powder was 2.79 wt.% C, 1.47 wt.% Mn, 0.03 wt.% P, 0.02 wt.% S, 0.72 wt.% Si, 16.72 wt.% Cr, 11.92 wt.% Ni, 2.13 wt.% Mo with balance Fe.

Yield strength and energy absorption capacity were tested by the compression test. The designed geometry of SCBCC-CAD, SCBCC-IS, BCC-CAD, and BCC-IS was cubes containing 4 × 4 × 4 unit cells and the compressed parts with a porosity of 73% were produced as shown in Figure 5. The dimension of each unit cell is 3 mm, and four quasi-static tests were carried out for all the compressed parts. All the compressed parts were cleaned by ultrasonic after being cut off with a wire cutting machine so as not to block the pores and affect the results of the experiment.

2.4. Mechanical Performance Test

Uniaxial compression tests were performed on an Instron-5869 universal testing machine. During compression, the samples were centrally located between two pressure plates, the top plate was moved with a speed of 1 mm/min, and the compression process was recorded with a high-speed camera. This test method has been used in many previous studies [1,2,6,8,13,14,17].

Yield strength was obtained from 5% strain to assess the strength of the lattice structures [32]. Energy absorption per unit volume can be calculated from:

$$\mathrm{W}={\int }_0^{{\epsilon }_0}\sigma \left(\epsilon \right)d\epsilon$$

(2)

where W is the energy absorption per unit volume, σ is the compressive stress, and ε₀ is the compressive strain. The end point of the energy absorption curves is obtained from the highest point of effective energy absorption.

2.5. Forming Quality

The microscopic morphologies of the SCBCC-CAD, SCBCC-IS, BCC-CAD, and BCC-IS structural local units were observed by a scanning electron microscope (SEM, JEOL JSM-7900F, Tokyo, Japan), as shown in Figure 6a–d. The local details of the four structures were relatively complete, and the performance was consistent with the geometry of the designed models, but the surface roughness was slightly lacking, the forming surface was uneven, and there were traces of laser spot sweeping and melting.

3. Results

3.1. Compressive Properties

The quasi-static compression stress–strain curves of the experimental and FEA results are shown in Figure 7a,c. It can be seen that the FEA and experimental curves have the same trend in the compression process. The stress–strain relationships show the stages as follows: elastic, yield, and densification, which are related to the excellent ductility and toughness of the 316L materials. The elastic stage was within a small strain of 5%, and the stress rose sharply with the change in strain, the bending phenomenon of the strut was not obvious, and the deformation was recoverable. After that, the stress in the yield plateau stage changed little, but the strain span was very long to 40%, and the upward trend of the curve was gentle. The oblique struts of all the structures gradually collapsed, the holes narrowed, and the vertical struts of the SCBCC-IS buckled at this stage. At the end of the yield plateau stage, the deformation was completely irrecoverable. Finally, there was an eventual sharp increase in the stress due to the more self-contacting surfaces and the final densification in the densification stage.

As shown in Figure 7a,c, the yield strength in the FEA increases from 38.39 MPa for the BCC-IS to 49.68 MPa for the SCBCC-IS, and in the experiment, it increases from 37.83 MPa for the BCC-IS to 44.84 MPa for the SCBCC-IS. This phenomenon is considered as a result of the vertical struts of the SCBCCZ-IS acting as the main load-bearing columns which resist most of the compressive stress, but in the BCC-IS, only the oblique struts are subjected to compressive stress. This result agrees with other lattice structures previously reported [33].

Figure 8a–d show the typical images captured by the camera during the compression testing. Figure 8e,f are enlarged views as pointed by the circles in Figure 8a,b, respectively. Figure 8g,h are enlarged views by SEM as pointed by the circles in Figure 8a,b, respectively. Due to the high stress concentrations at the boundaries between the vertical strut and the diagonal strut predicted by the FEA, the SCBCC-CAD structure fractured at the junctions in Figure 8f. It can be observed that a concentrated deformation zone appeared around the fracture position of the SCBCC-CAD, resulting in the local deformation of the bottom layer. In contrast, the smooth transition of the SCBCC-IS structure at the junctions dispersed the stress concentration and no fracture was observed. The SCBCC-IS structure deformation process was uniform, and no local deformation appeared. It can be seen from Figure 8g,h that the vertical strut of the SCBCC-IS deformed more uniformly at the end stage of the compression to the plateau region, while the vertical strut of the SCBCC-CAD was completely broken. Thus, it is verified that the hybrid optimization design method can significantly increase the yield strength from 39.11 MPa for the SCBCC-CAD to 44.84 MPa for the SCBCC-IS. This result agrees with the FEA results (increasing the yield strength from 43.14 MPa for the SCBCC-CAD to 49.68 MPa for the SCBCC-IS) and other optimization design methods previously reported [30].

3.2. Energy Absorption Properties

Based on the quasi-static compression stress–strain curves shown in Figure 7a,c, the energy absorption during the compression up to 50% was calculated to represent the energy absorption capacity of the four structures shown in Figure 7b,d. As seen from the curves, the structures absorbed little energy in the elastic stage but exhibited a steady and continuous energy absorption capacity during the long yield plateau stage until the final densification in the densification stage. With the increase in strain, the energy absorption of the same structure steadily increases. The energy absorption per unit volume in the FEA increased from 25.85 mJ/m³ for the SCBCC-CAD to 35.28 mJ/m³ for the SCBCC-IS, and in the experiment, it increased from 26.73 mJ/m³ for the SCBCC-CAD to 32.96 mJ/m³ for the SCBCC-IS, demonstrating the effectiveness of the hybrid optimization design method in increasing the energy absorption capacity.

It can also be seen from Figure 7b,d that the plateau region ended at 40%. Therefore, we added the calculation method of the energy absorption when the deformation reached 40%. The energy absorption per unit volume in the FEA increased from 19.46 mJ/m³ for the SCBCC-CAD to 25.13 mJ/m³ for the SCBCC-IS, and in the experiment, it increased from 18.99 mJ/m³ for the SCBCC-CAD to 22.71 mJ/m³ for the SCBCC-IS. The final results show that the conclusion drawn by using 40% as the end point of the energy absorption is consistent with 50%. We also use 40% energy absorption as a reference index in this paper.

4. Conclusions

In this study, we described an implicit surface hybrid design method that can directly generate hybrid lattice structures with continuously varying curvatures at the boundaries and reduced the stress concentration at the boundaries of the hybrid lattice structures. As a result, the yield strength and energy absorption were increased from 39.11 MPa and 26.73 mJ/m³ for the SCBCC-CAD designed by the CAD software to 44.84 MPa and 32.96 mJ/m³ for the SCBCC-IS generated by this method. It can be concluded that this implicit surface hybrid design method is an effective way to strengthen the lattice structure.