Finite Element Analysis of Restraint Intensities and Welding Residual Stresses in the Ti80 T-Joints
Abstract
:1. Introduction
2. FE Simulation and Verification
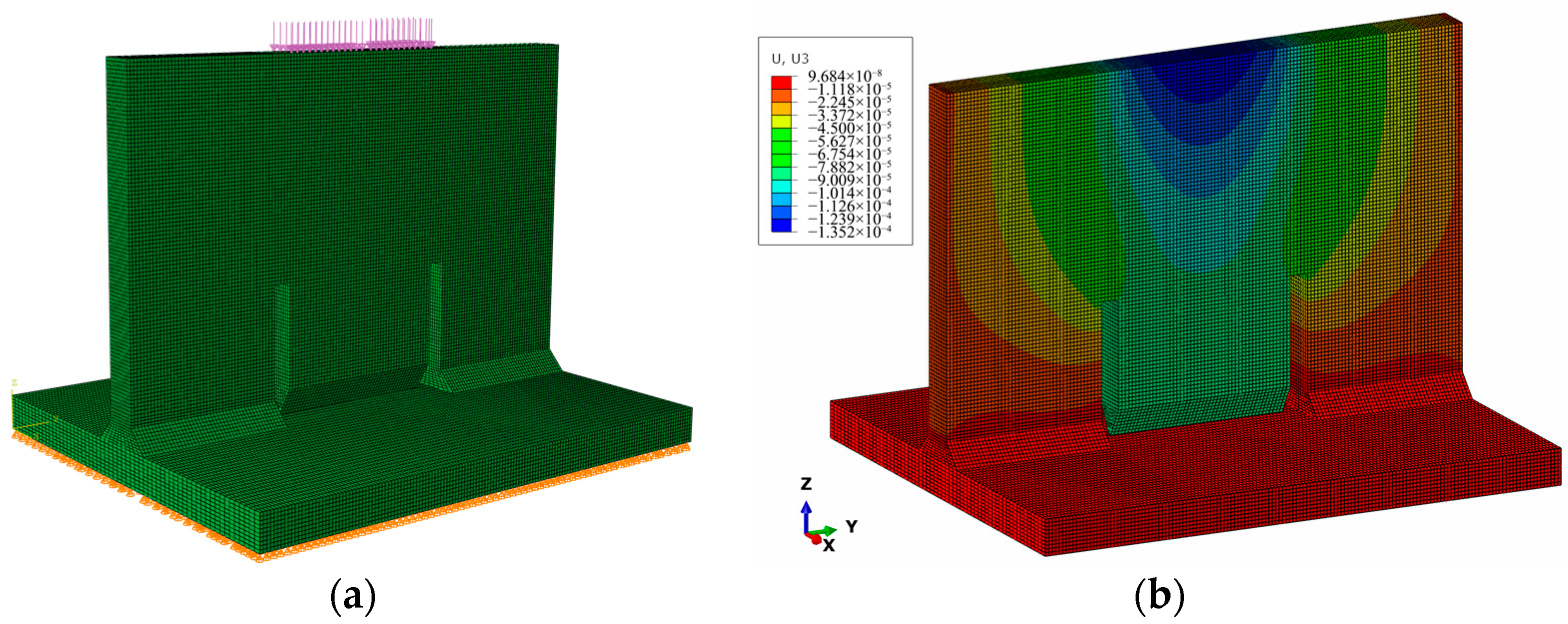
2.1. Fundamental Principles
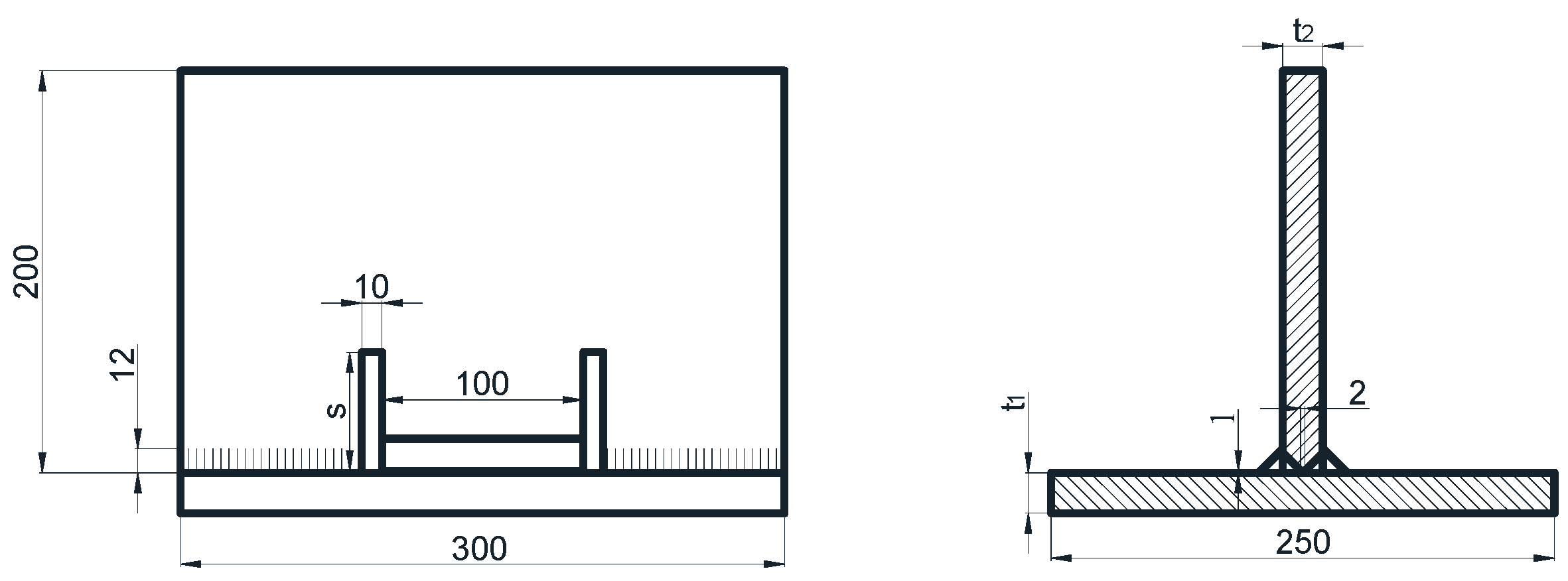
2.2. Dimensions
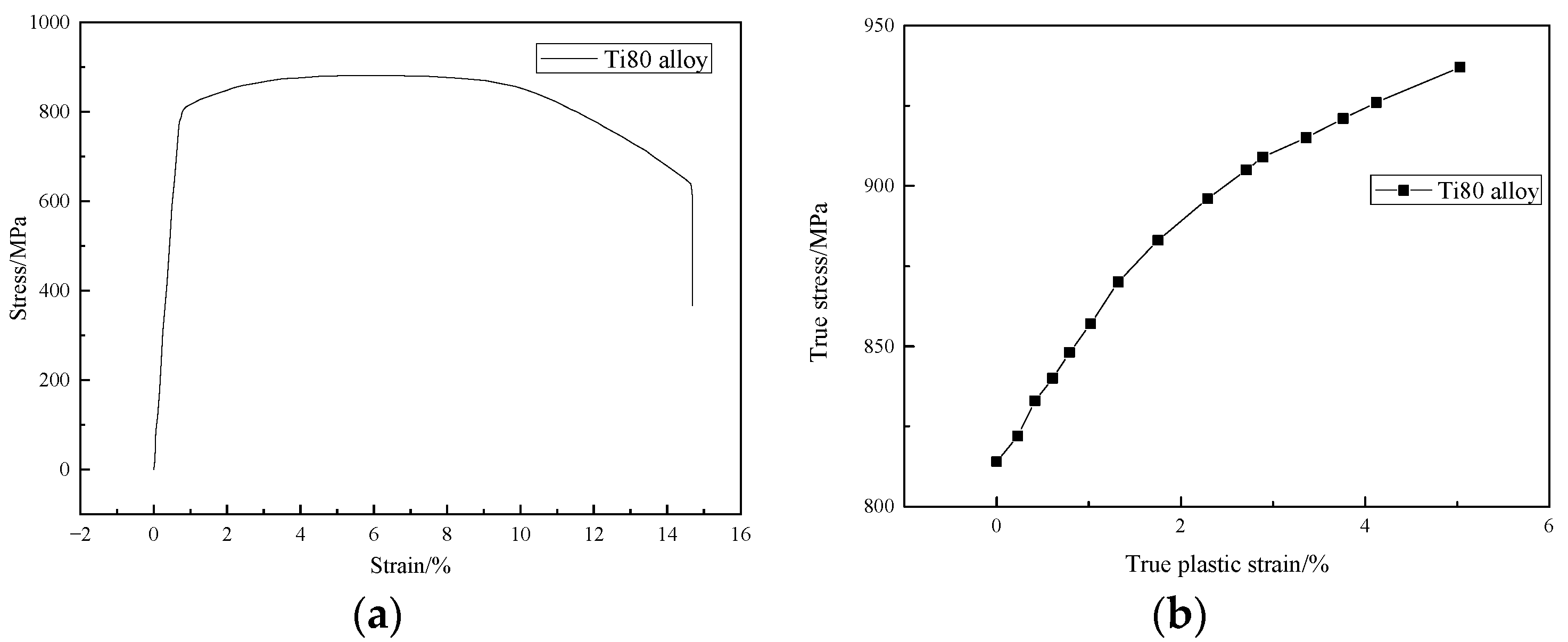
2.3. Mechanical Parameters
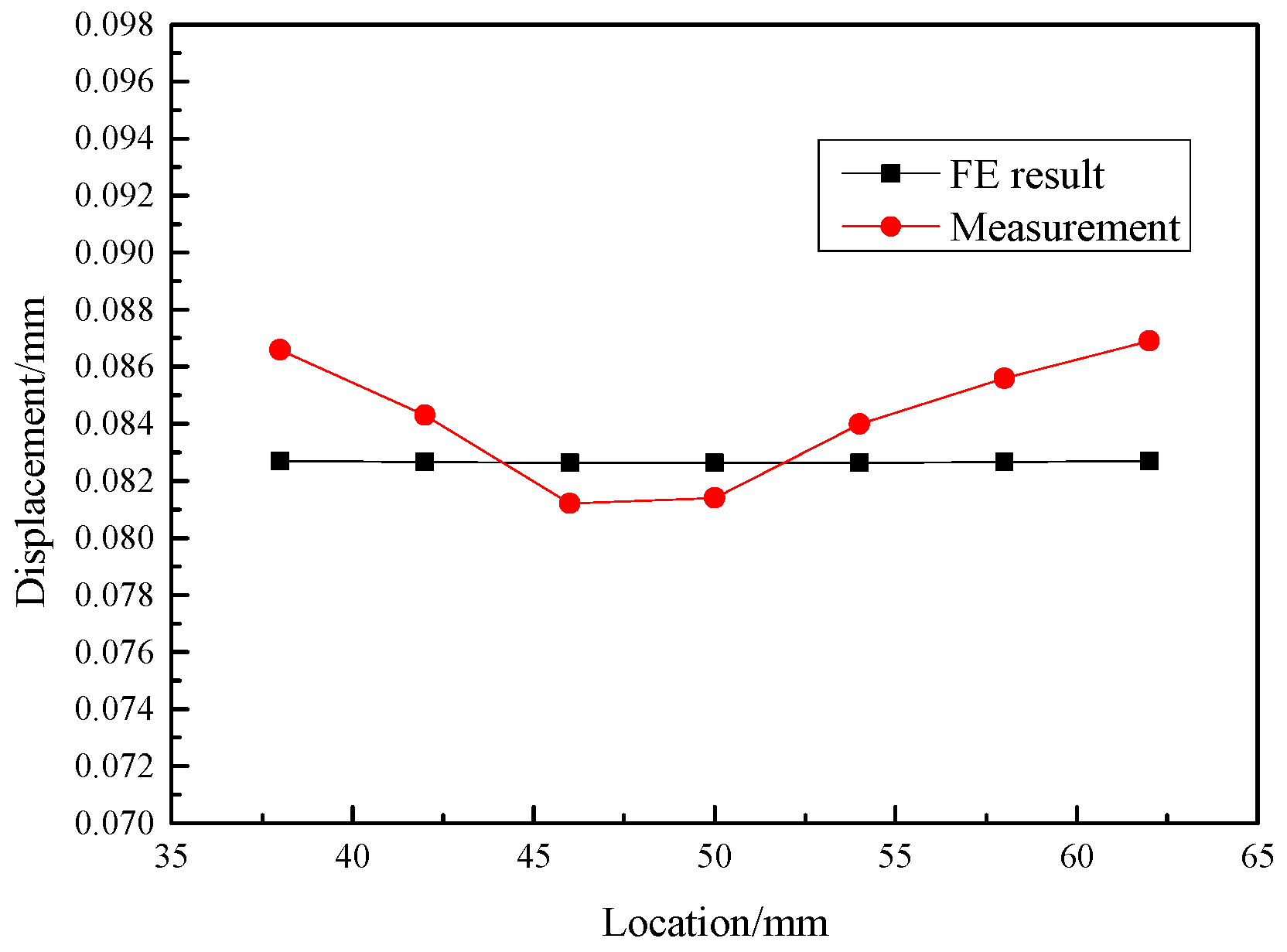
2.4. Experimental Validation
3. Results and Discussion
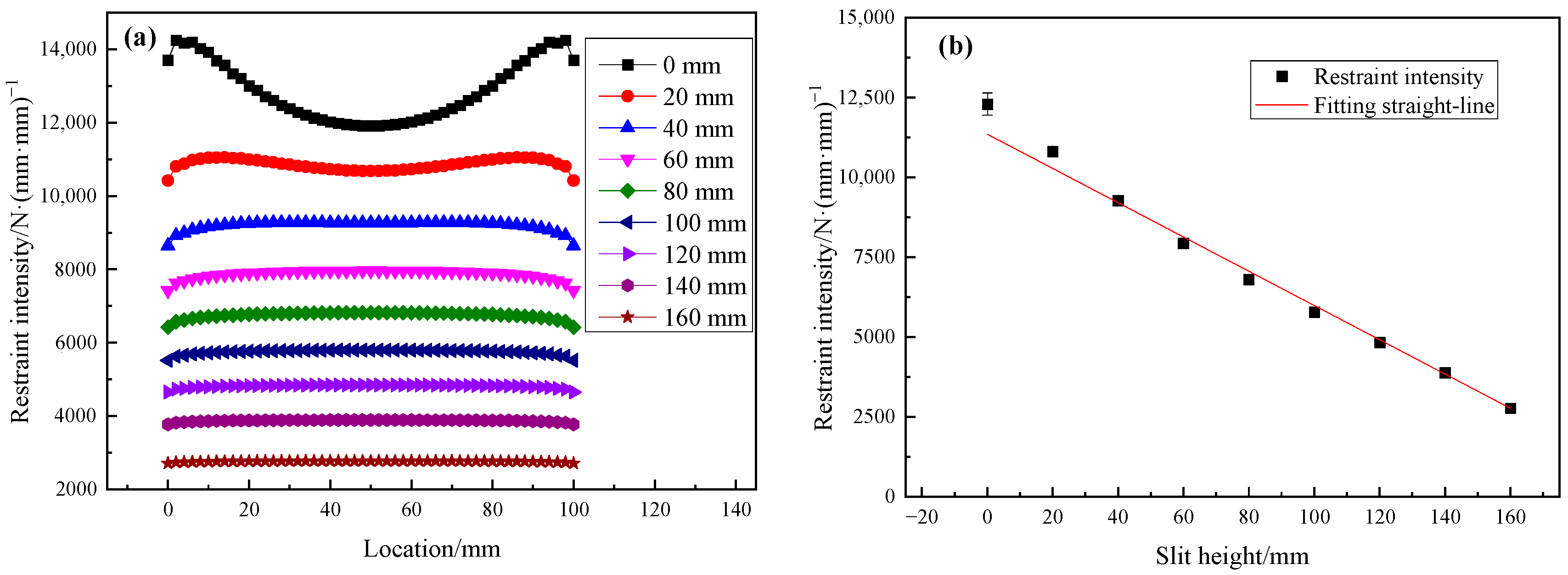
3.1. Effect of Slit Height on Restraint Intensity
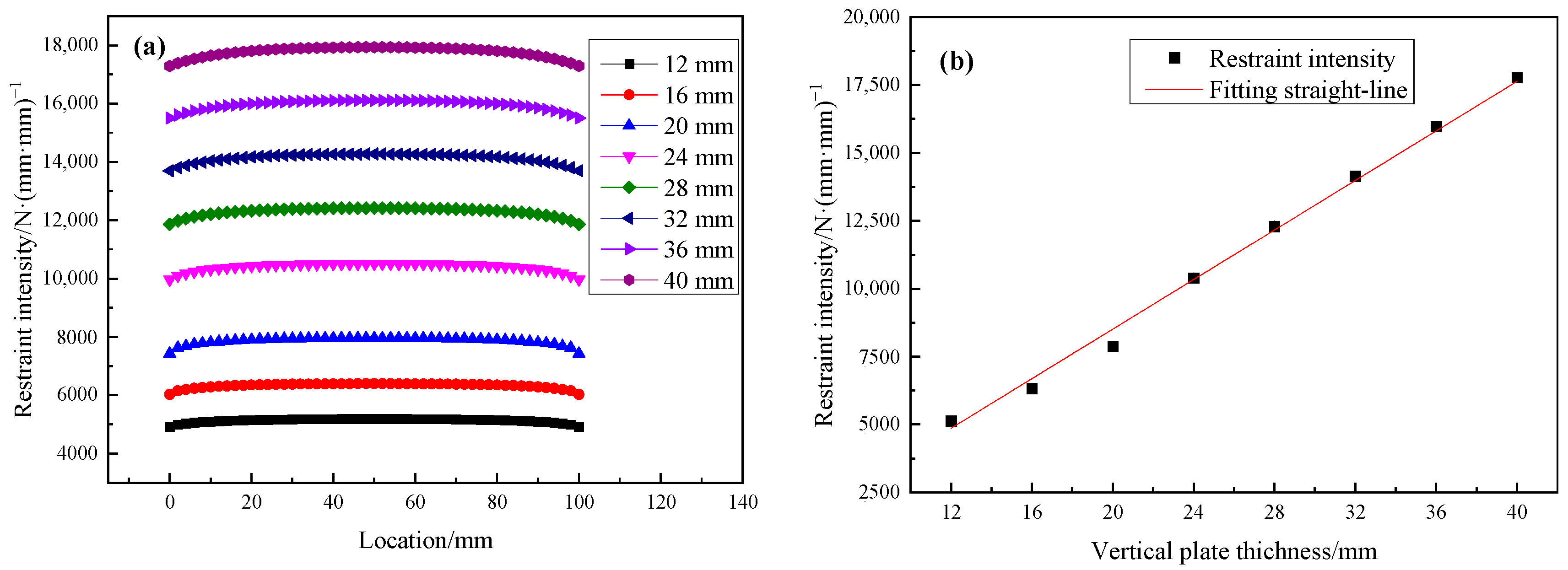
3.2. Effect of Vertical Plate Thickness on Restraint Intensity
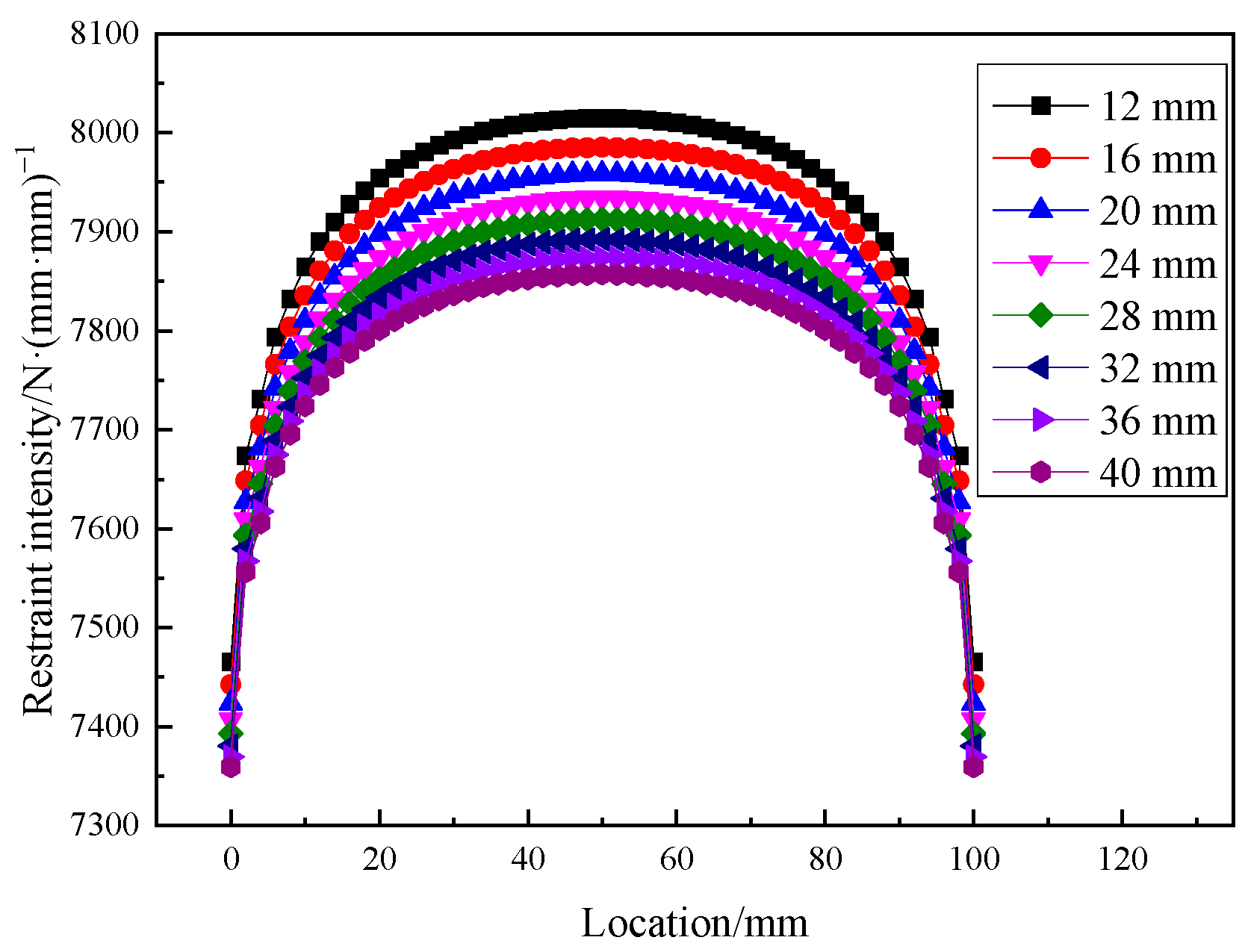
3.3. Effect of Base Plate Thickness on Restraint Intensity
3.4. Linear Regression Analysis
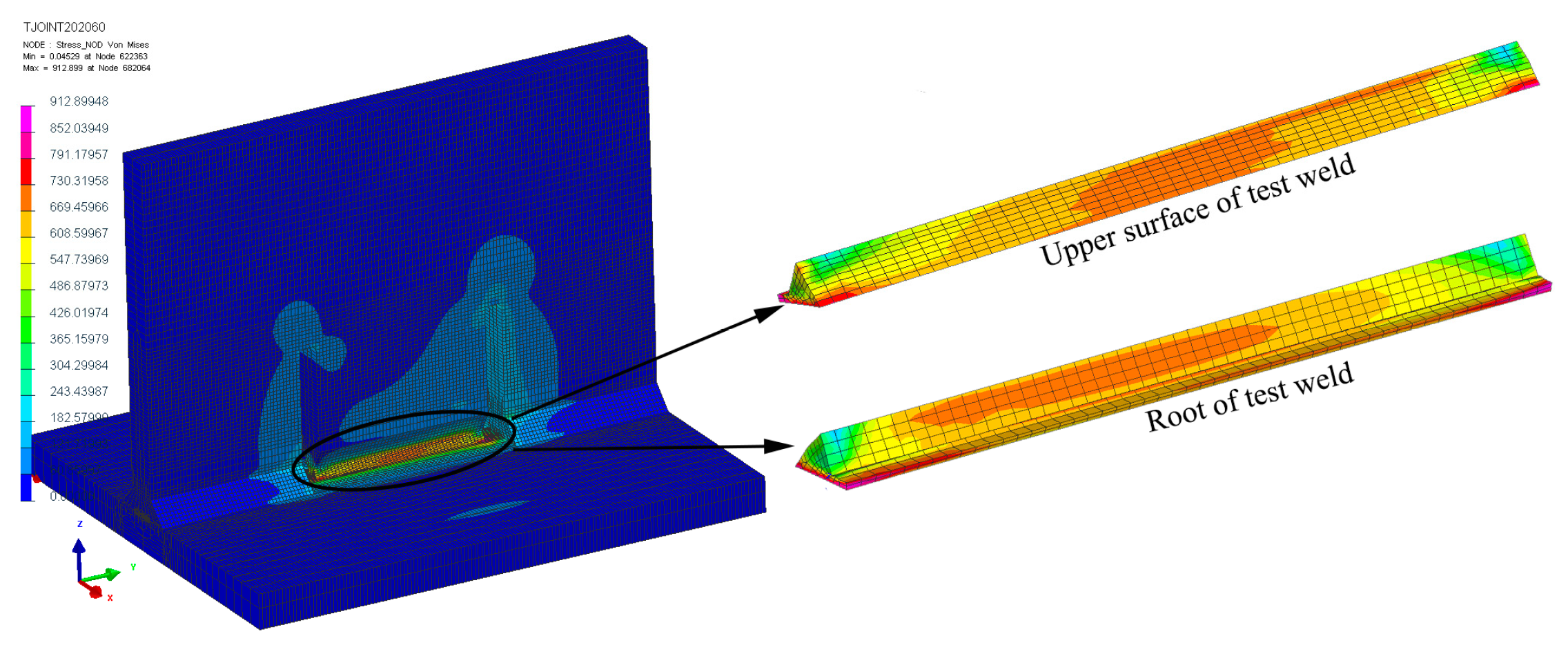
3.5. Effect of Restraint Intensity on Welding Residual Stress
4. Conclusions
- (1)
- The restraint intensity is significantly affected by the slit height. As the height increases, the restraint intensity decreases linearly. The reason for this is that with the height increase, the constraint effect of the anchor welds decreases and the deformation of the groove root is enhanced. The restraint intensity is not evenly distributed along the groove; when the slit heights are as small as 0 mm and 20 mm, the restraint intensity at the two ends is increased, which is mainly because the ends of the test welds are close to the anchor welds, and the deformation is significantly decreased. When the heights increase to more than 40 mm, the deformation at the ends of the test welds is enhanced due to the notch effect of the slits and the restraint intensity at the middle section is increased.
- (2)
- The vertical plate thickness has a significant impact on the restraint intensity. As the vertical plate thickness increases, the restraint intensity increases almost linearly. The distributions of the restraint intensity along the grooves fluctuate a little; the data points at both ends of the test welds are slightly reduced due to the notch effect of the slits.
- (3)
- The base plate thickness has little effect on the restraint intensity. As the thickness increases, the restraint intensity tends to decrease very slightly. This is likely caused by the reduced possibility of cooperative deformation in thicker base plates, i.e., deformation will be more likely to occur near the groove of the vertical plate.
- (4)
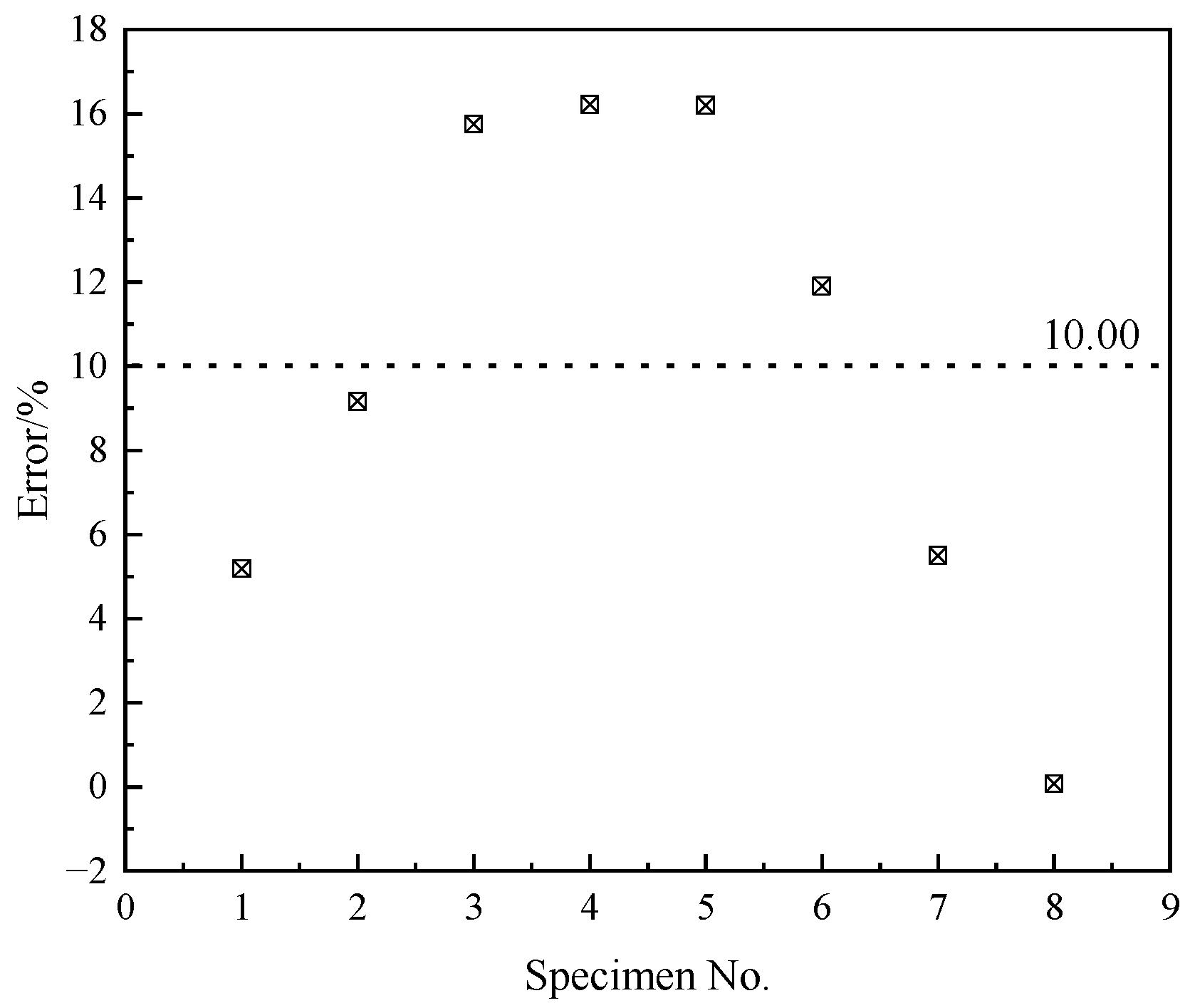
- A binary linear regression model of restraint intensity can be constructed as follows: where R is the restraint intensity, s is the slit height and t2 is the vertical plate thickness. Eight specimens with different dimensions were calculated by the formula, and the average error was 10%, indicating good accuracy for the prediction formula.
- (5)
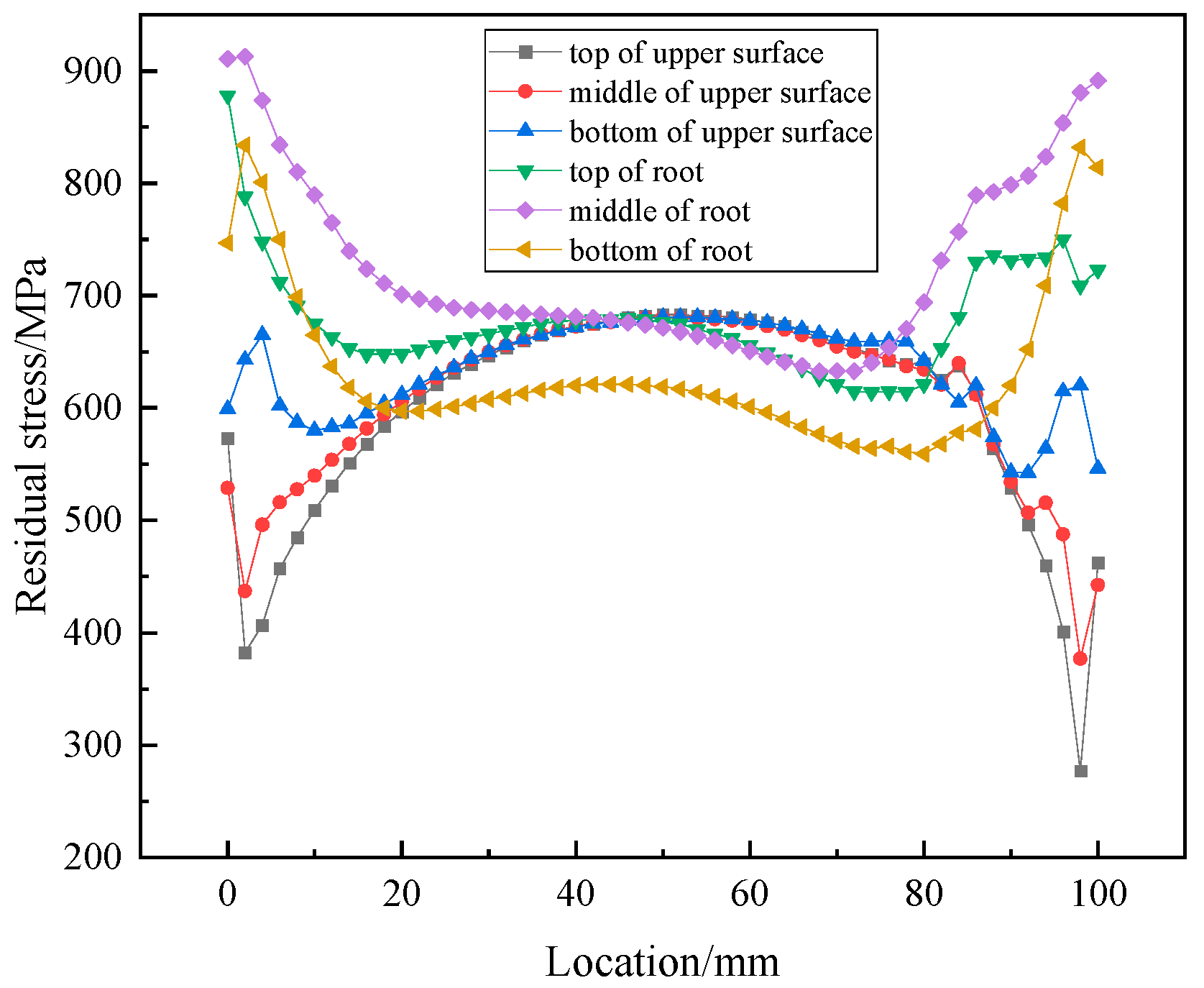
- The welding residual stresses on the backing weld surface are higher in the middle and lower at both ends, while the weld root shows opposite results. In general, stresses at the weld root are greater than those on the weld surface. The mean residual stress value at the weld root increases with the increase in the restraint intensity but not uniformly, i.e., it is slow at first and then increases rapidly. A prediction model of the residual stress was produced using cubic fitting as follows: where S is the welding residual stress and r is the logarithm of the restraint intensity. The errors between the finite element simulations and predictions were about 8%. Through the prediction model, the residual stress of actual Ti80 alloy workpieces can be estimated before welding, and a corresponding strategy for avoiding cracks can be generated.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Zhao, Y.Q.; Chang, H. Research and development of titanium alloy for shipbuilding in China. Mater. Rev. 2005, 6, 67–70. [Google Scholar]
- Zhao, Y.Q. The new main titanium alloys used for ship-building developed in China and their applications. Mater. China 2014, 33, 398–404. [Google Scholar]
- Sun, J.K.; Meng, X.J.; Chen, C.H. Research, application and development of shipbuilding titanium alloy in China. Acta Metall. Sin. 2004, 38, 33–36. [Google Scholar]
- Ruben, L.L.; Marina, C.B.; María, M.C. Residual stresses with time-independent cyclic plasticity in finite element analysis of welded joints. Metals 2017, 7, 136. [Google Scholar]
- Chen, C.; Wang, J.H.; Tang, Y.M. Constraint of welded joints in hull and its influence on cold cracks. Mar. Technol. 1981, 3, 7–14. [Google Scholar]
- Fukuda, K.; Tsuji, M. Japanese studies on structural restraint severity in relation to weld cracking. Weld. World 1977, 15, 155–189. [Google Scholar]
- Suzuki, H. Weldability of modern structural steels in Japan. Trans. Iron Steel Inst. Jpn. 1983, 23, 189–204. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.M.; Jonas, H.; Thomas, N.P. Influence of restraint conditions on welding residual stresses in H-type cracking test specimens. Materials 2019, 12, 2700. [Google Scholar] [CrossRef] [Green Version]
- Cross, C.E.; Boellinghaus, T. The effect of restraint on weld solidification cracking in aluminium. Weld. World 2006, 50, 51–54. [Google Scholar] [CrossRef]
- Qin, T.T.; Piao, X.H.; Jiang, Y.H. Analysis and prevention of forging stress cracks for sealing ring. Forg. Stamp. Technol. 2020, 45, 37–41. [Google Scholar]
- Thomas, K.; Thomas, B. Cold cracking tests-an overview of present technologies and applications. Weld. World 2013, 57, 3–37. [Google Scholar]
- Chen, C.; Wang, J.H.; Tang, Y.M. Study on the restraint intensity of welded joint. Weld. Joi. 1981, 6, 6–9. [Google Scholar]
- Liu, B.; Chen, M.M. Calculation of the restraint intensity of VRC test assemblies. J. Cent. Southwest Jiaotong Univ. 1993, 2, 31–36. [Google Scholar]
- Tao, S.S.; Zong, P.; Dong, J.Y. The calculation method for welding restraint intensity of fillet weld in ring stiffened cylinder. Trans. China Weld. Inst. 2013, 34, 97–100. [Google Scholar]
- Ramesh, B.; Elsheikh, A.H.; Satishkumar, S.; Shaik, A.M.; Djuansjah, J.; Ahmadein, M.; Moustafa, E.B.; Alsaleh, N.A. The Influence of boron carbide on the mechanical properties and bonding strength of B4C/Nickel 63 coatings of brake disc. Coatings 2022, 12, 663. [Google Scholar] [CrossRef]
- Ammar, H.E.; Guo, J.J.; Huang, Y.; Ji, J.J. Temperature field sensing of a thin-wall component during machining: Numerical and experimental investigations. Int. J. Heat Mass Transf. 2018, 126, 935–945. [Google Scholar]
- Abdallah, K.; Ezzat, S.; Ammar, E. Effect of single-period overload parameters on fatigue crack retardation for high-density polyethylene. Theor. Appl. Fract. Mec. 2022, 118, 103249. [Google Scholar]
- Jing, H.Y.; Xu, J.J.; Xu, L.Y. Finite element simulation of the restraint intensity of rigid butt-jointed cracking specimen and VRC specimen. Trans. China Weld. Inst. 2018, 39, 1–5. [Google Scholar]
- Alipooramirabad, H.; Paradowska, A.M.; Ghomashchi, R.; Kotousov, A.; Hoye, N. Prediction of welding stresses in WIC test and its application in pipelines. Mater. Sci. Technol. 2016, 32, 1462–1470. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Q.; Zhang, X.W.; He, W.X.; Li, X.X.; Gu, R.C. Finite element analysis on restraint intensity of Ti80 alloy specimen with Y-joint groove. Dev. Appl. Mater. 2020, 35, 37–41. [Google Scholar]
- Zhang, L.; Zhang, X.W.; Hu, Y.S.; Xu, J.X.; Geng, P.Z. Finite element analysis on restraint intensity of Ti80 alloy rigid restraint. Rare Met. 2021, 45, 1223–1229. [Google Scholar]
- Watanabe, M.; Satoh, K. Research on intensity of restraint and reaction stress in welded joints. J. Zosen Kiokai 1961, 1961, 349–358. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, M.; Takagi, O.; Satoh, K.; Aso, F. External constraint and shrinkage of butt-welded joints in the erection of assemblies on building way. J. Zosen Kiokai 1958, 1958, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; An, G.; Woo, W. The effect of initial stress induced during the steel manufacturing process on the welding residual stress in multi-pass butt welding. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 129–140. [Google Scholar] [CrossRef]
- Park, J.; An, G.; Kim, S. The effect of welding-pass grouping on the prediction accuracy of residual stress in multipass butt welding. Math. Probl. Eng. 2017, 2017, 7474020. [Google Scholar] [CrossRef] [Green Version]
- Satoh, K.; Ueda, Y.; Kihara, H. Recent trend of researches on restraint stresses and strains for weld cracking. Trans. JWRI 1972, 1, 53–68. [Google Scholar]
- Satoh, K. An analytical approach to the problem of restraint intensity in slit weld. Trans. JWRI 1972, 1, 69–76. [Google Scholar]
- Shin, S.B.; Lee, D.-J.; Park, D.-H. A study on the evaluation of transverse residual stress at the multi-pass FCA butt weldment using FEA. J. Weld. Join. 2010, 28, 26–32. [Google Scholar]
- Huang, X.M.; Sun, J.; Li, J.F. Finite element simulation and experimental investigation on the residual stress-related monolithic component deformation. Int. J. Adv. Manuf. Tech. 2015, 77, 1035–1041. [Google Scholar] [CrossRef]
- Tlili, I.; Baleanu, D.; Mohammad, S.S. Numerical and experimental analysis of temperature distribution and melt flow in fiber laser welding of Inconel 625. Int. J. Adv. Manuf. Tech. 2022, 121, 765–784. [Google Scholar] [CrossRef]
- Caruso, S.; Umbrello, D. Numerical and experimental validation of gas metal arc welding on AISI 441 ferritic stainless steel through mechanical and microstructural analysis. Int. J. Adv. Manuf. Tech. 2022, 120, 7433–7444. [Google Scholar] [CrossRef]
- Jia, Y.B.; Saadlaoui, Y.; Hamdi, H.; Sijobert, J.; Roux, J.C. An experimental and numerical case study of thermal and mechanical consequences induced by laser welding process. Case Stud. Therm. Eng. 2022, 35, 1–19. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wang, Q.; Chen, P.; Luo, B.; Zhu, Z.; Yang, X. Finite Element Analysis of Restraint Intensities and Welding Residual Stresses in the Ti80 T-Joints. Metals 2023, 13, 125. https://doi.org/10.3390/met13010125
Zhang L, Wang Q, Chen P, Luo B, Zhu Z, Yang X. Finite Element Analysis of Restraint Intensities and Welding Residual Stresses in the Ti80 T-Joints. Metals. 2023; 13(1):125. https://doi.org/10.3390/met13010125
Chicago/Turabian StyleZhang, Liang, Qi Wang, Pan Chen, Bingbing Luo, Ziling Zhu, and Xiaoyu Yang. 2023. "Finite Element Analysis of Restraint Intensities and Welding Residual Stresses in the Ti80 T-Joints" Metals 13, no. 1: 125. https://doi.org/10.3390/met13010125
APA StyleZhang, L., Wang, Q., Chen, P., Luo, B., Zhu, Z., & Yang, X. (2023). Finite Element Analysis of Restraint Intensities and Welding Residual Stresses in the Ti80 T-Joints. Metals, 13(1), 125. https://doi.org/10.3390/met13010125





