Stress-Invariants-Based Anisotropic Yield Functions and Its Application to Sheet Metal Plasticity
Abstract
:1. Introduction
2. Proposed Model
2.1. Proposed Anisotropic Yield Function
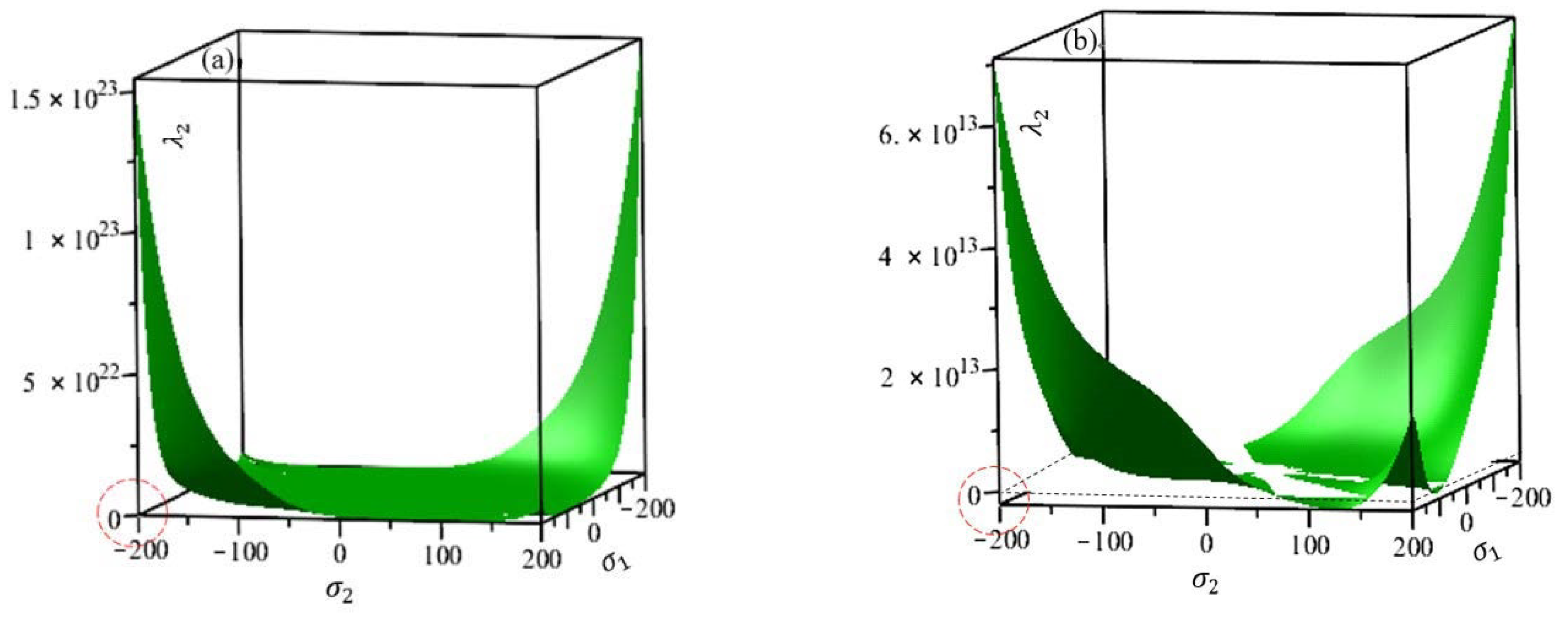
2.2. The Convexity Condition of the Yield Function
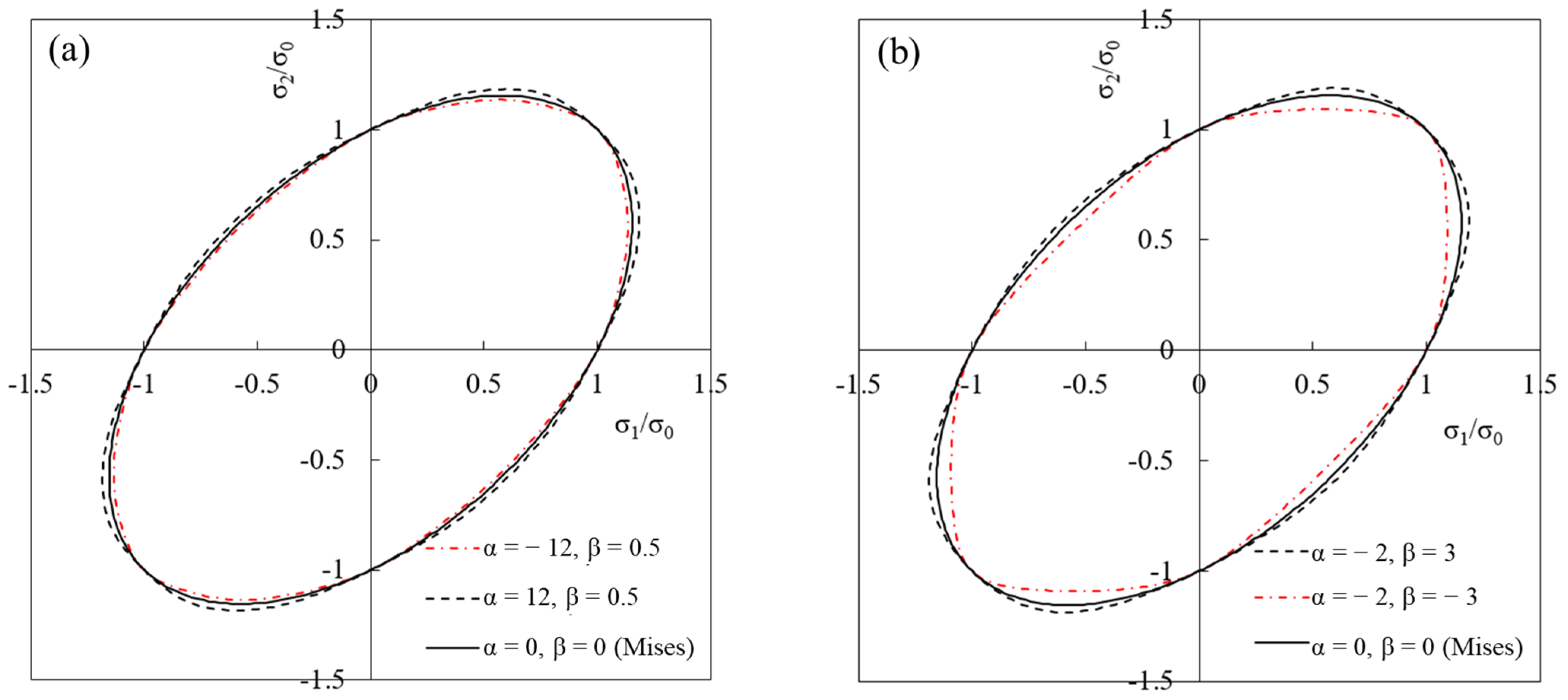
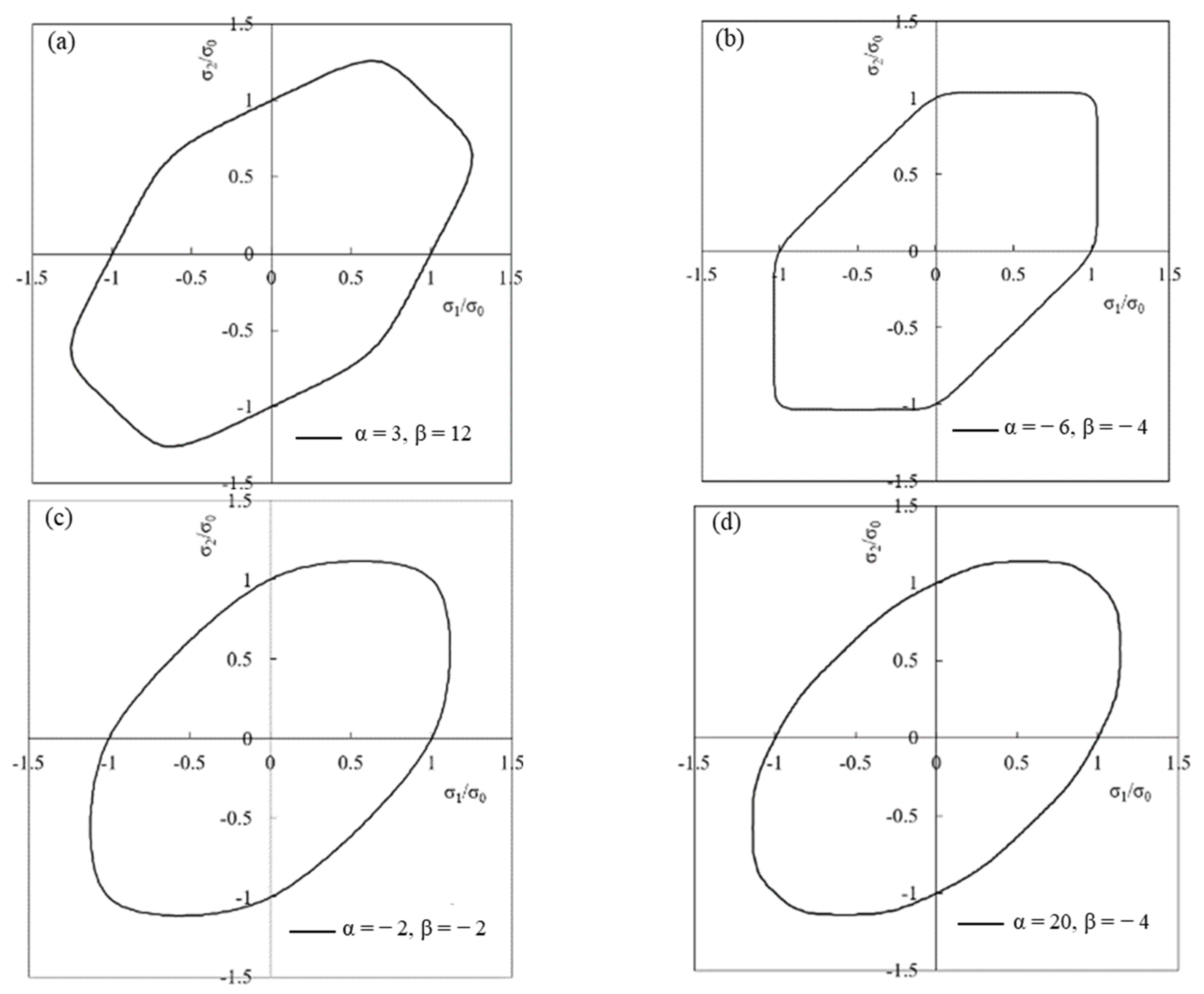
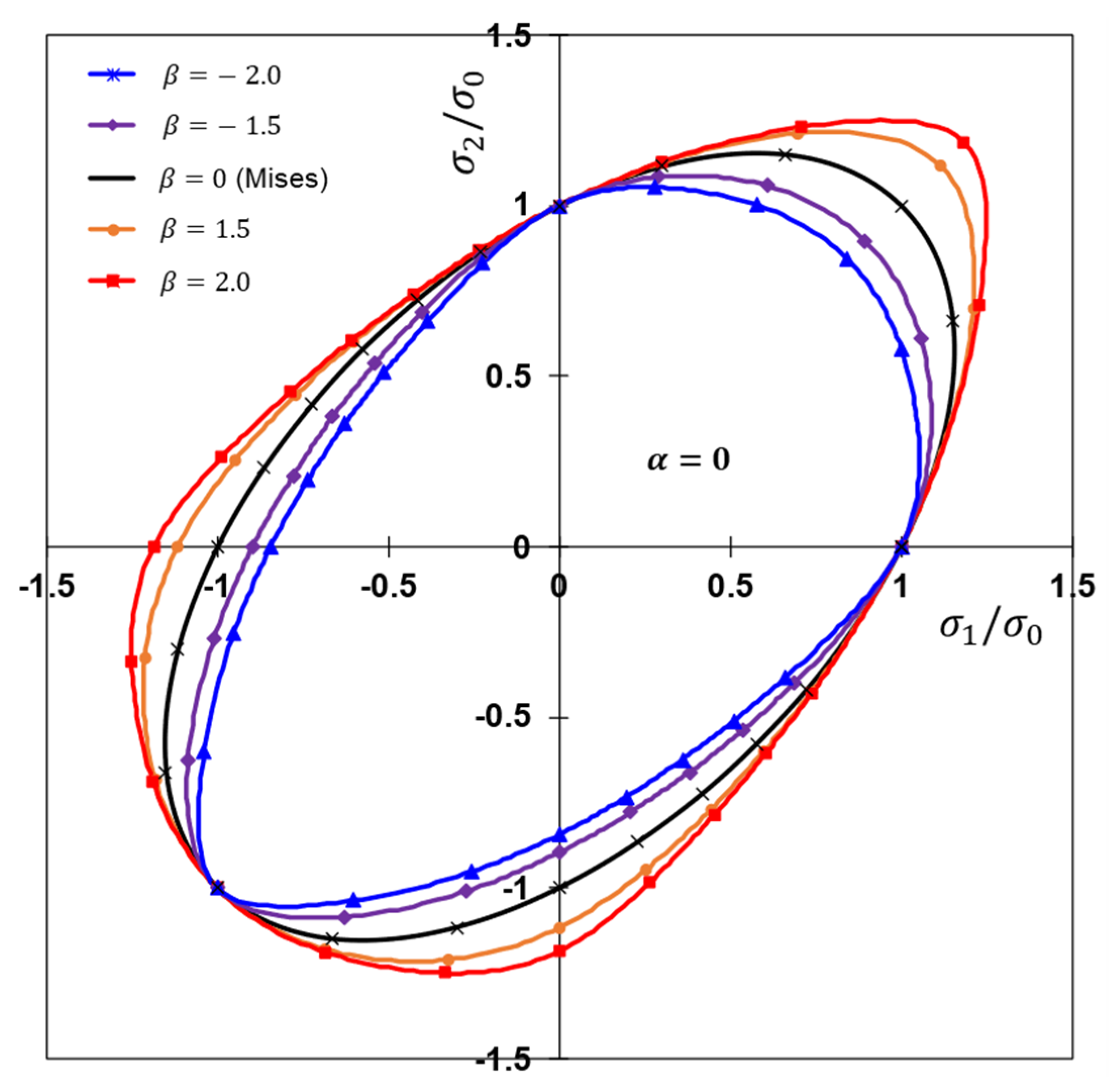
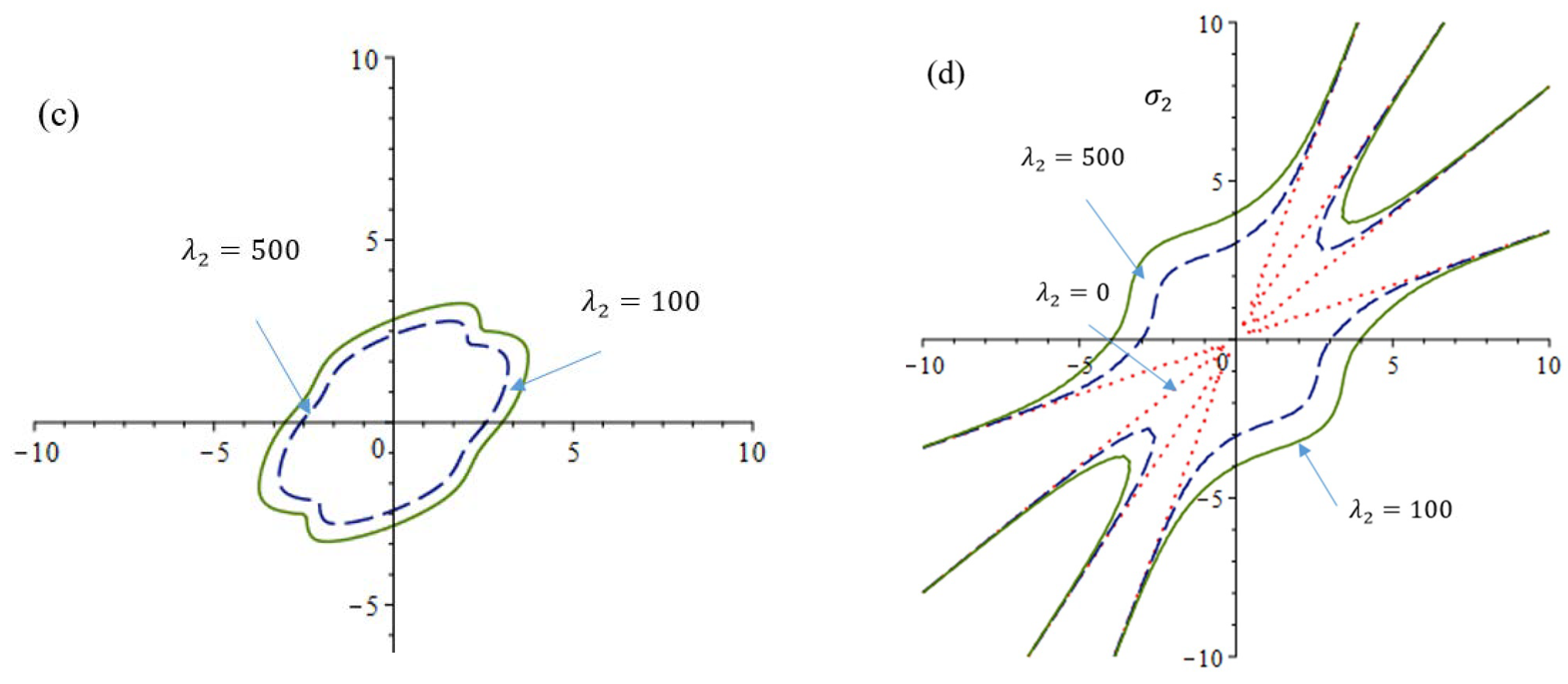
2.3. Effect of α and β on Yield Surface under Plane Stress
3. Application of the Proposed Yield Function Model
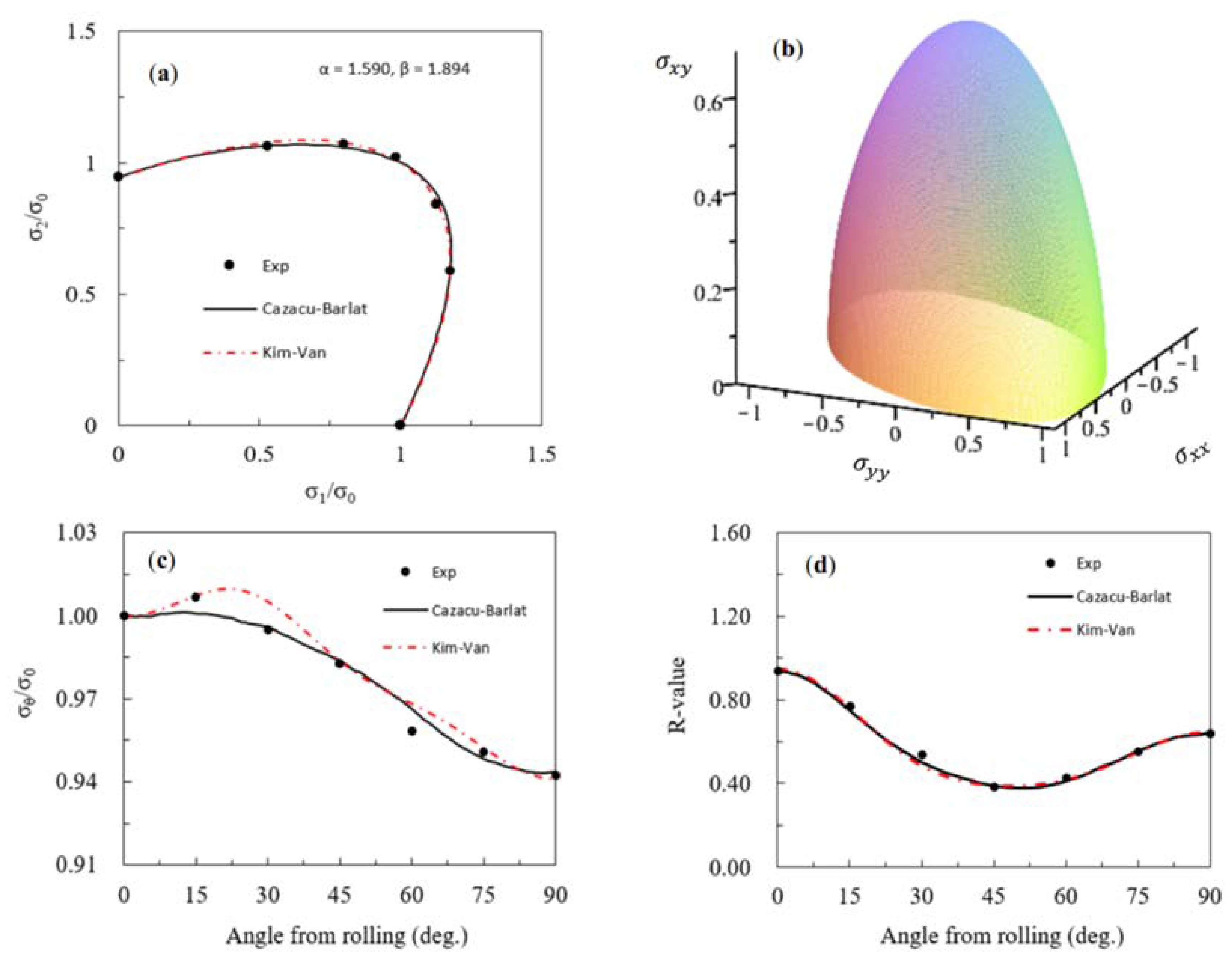
3.1. AA6016-T4 Sheet
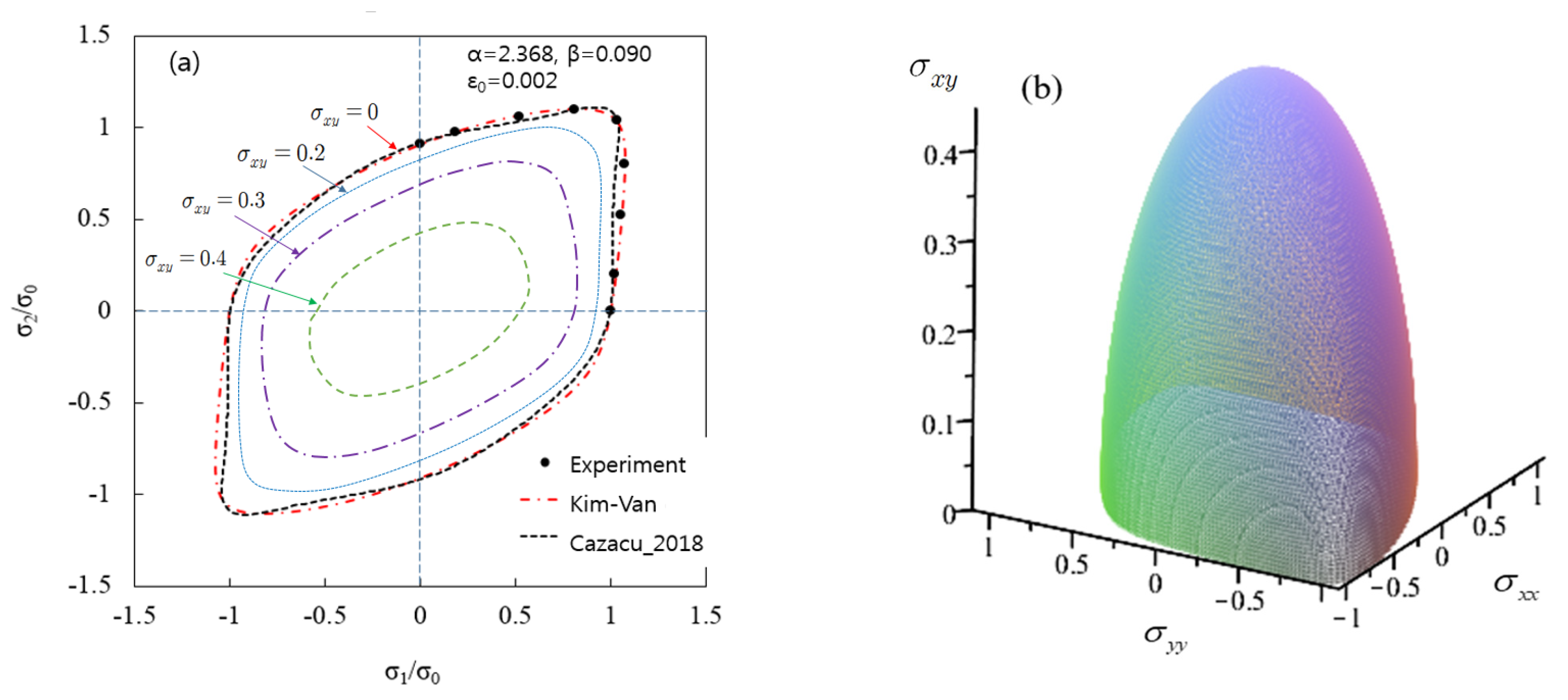
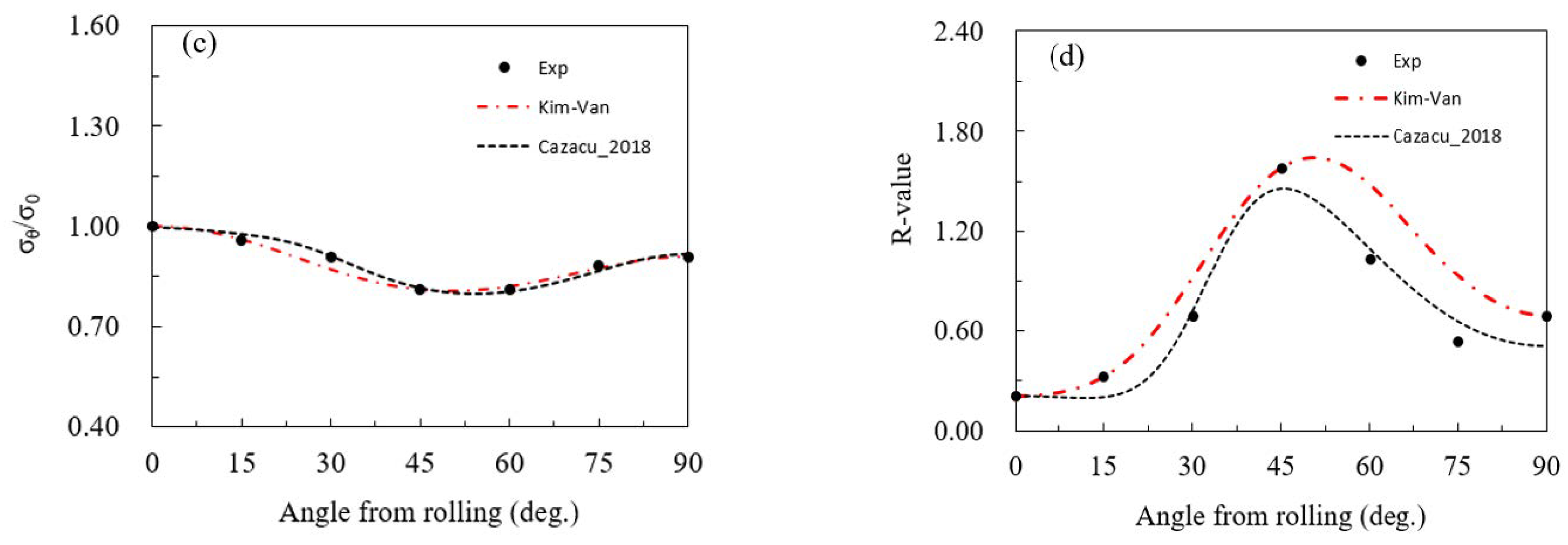
3.2. AA2090-Ts3 Sheet
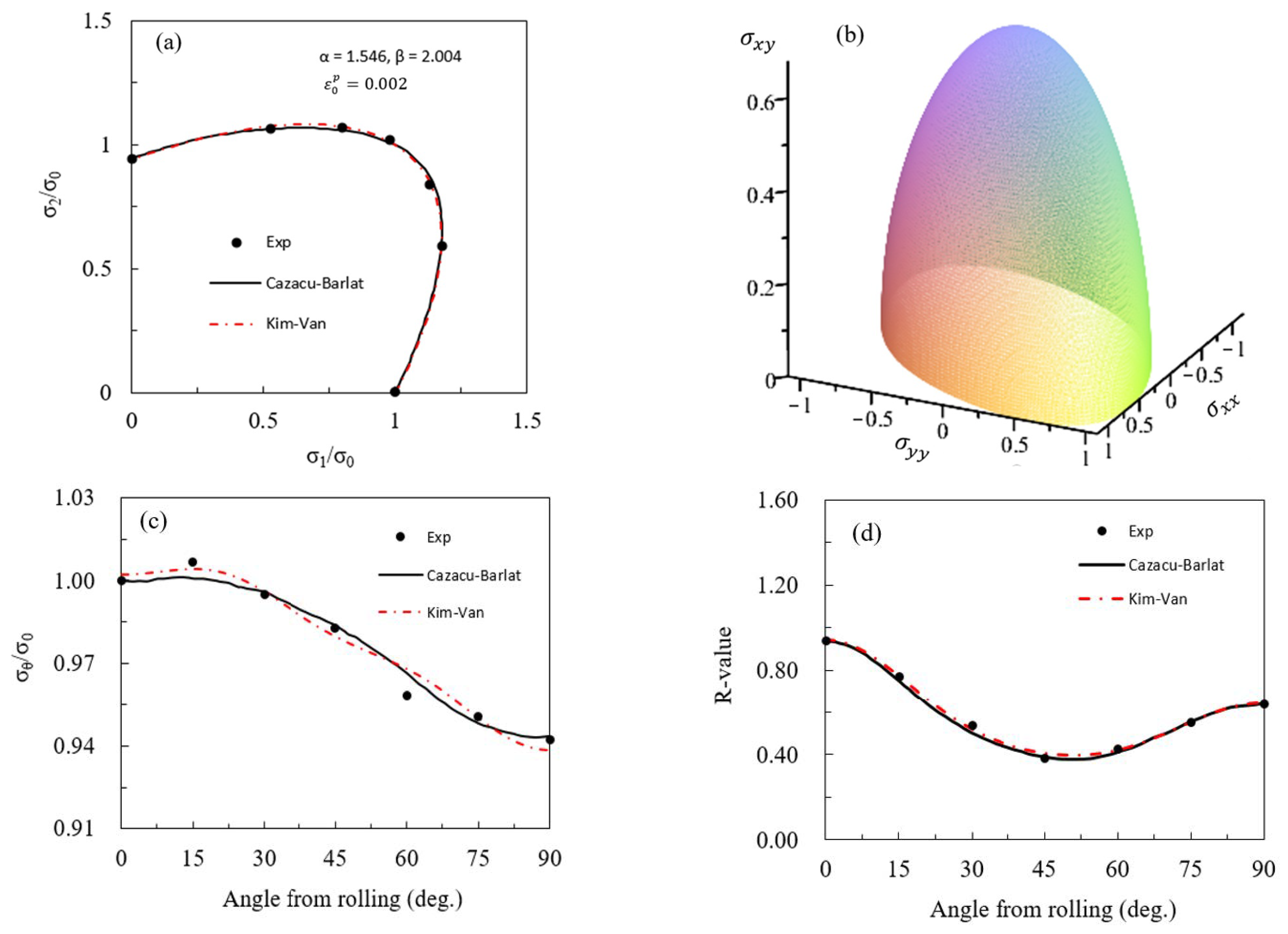
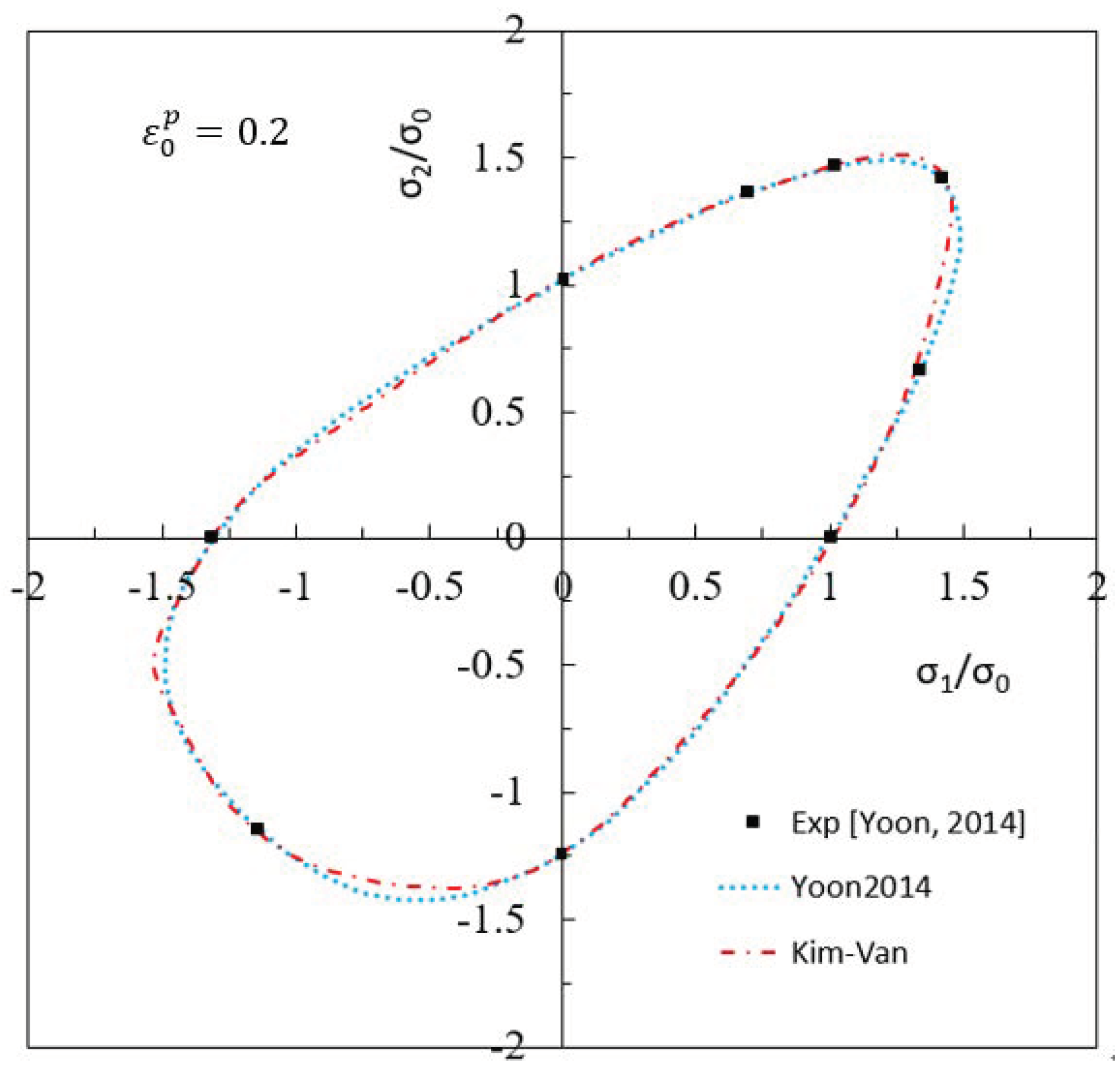
3.3. Pure Titanium Sheet
4. Conclusions
- (1)
- The KV’12S yield function results in the Von Mises yield function when the two parameters α and β are zero.
- (2)
- KV’12S can also well represent various types of yield curves including strongly anisotropic materials. It was shown that the proposed yield function can implement various types of yield surface shapes by combining the two parameters α and β.
- (3)
- To verify the flexibility of the proposed model, the convexity of the yield surface was checked and compared with the Cazacu 2018 yield function. The convexity of KV’12S was satisfied in most stress ranges, but the Cazacu 2018 yield function for the material covered in this study did not satisfy the convexity in some stress ranges.
- (4)
- As a result of applying the KV’12S yield function proposed in this study to the AA2090-T4 material, which exhibited very strong anisotropy, the results deviated from some experimental data. Attention should be paid to the selection of experimental data used for the parameter optimization of the yield function proposed in this study. In this case, twelve experimental data (e.g., ten experimental data from the uniaxial tensile test and two experimental data from the equi-biaxial tension test) are recommended.
- (5)
- The KV’21A yield function was used to predict the yield surface of a commercial pure titanium sheet that exhibited an asymmetrical yield surface shape, and it was compared with the Yoon 2014 yield function and experimental data. Both yield functions were in good agreement with the experiment overall.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhan, M.; Guo, K.; Yang, H. Advances and trends in plastic forming technologies for welded tubes. Chin. J. Aeronaut. 2016, 29, 305–315. [Google Scholar] [CrossRef] [Green Version]
- Meng, B.; Wan, M.; Wu, X.; Yuan, S.; Xu, X.; Liu, J. Inner wrinkling control in hydrodynamic deep drawing of an irregular surface part using drawbeads. Chin. J. Aeronaut. 2014, 27, 697–707. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Song, N.; Guo, G.; Sun, Z. Prediction of forming limit curve (FLC) for Al–Li alloy 2198-T3 sheet using different yield functions. Chin. J. Aeronaut. 2013, 26, 1317–1323. [Google Scholar] [CrossRef] [Green Version]
- Swift, H. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Voce, E. The relationship between stress and strain for homogeneous deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Pham, Q.T.; Oh, S.H.; Kim, Y.S. An efficient method to estimate the post-necking behavior of sheet metals. Int. J. Adv. Manuf. Technol. 2018, 98, 2563–2578. [Google Scholar] [CrossRef]
- Stoughton, T.B.; Yoon, J.W. On the existence of indeterminate solutions to the equations of motion under non-associated flow. Int. J. Plast. 2008, 24, 583–613. [Google Scholar] [CrossRef]
- Stoughton, T.B.; Yoon, J.W. Anisotropic hardening and non-associated flow in proportional loading of sheet metals. Int. J. Plast. 2009, 25, 1777–1817. [Google Scholar] [CrossRef]
- Ha, J.J.; Coppieters, S.; Korkolis, Y.P. On the expansion of a circular hole in an orthotropic elastoplastic thin sheet. Int. J. Mech. Sci. 2020, 182, 105706. [Google Scholar] [CrossRef]
- Pham, Q.T.; Kim, Y.S. Identification of the plastic deformation characteristics of AL5052-O sheet based on the non-associated flow rule. Met. Mater. Int. 2017, 23, 254–263. [Google Scholar] [CrossRef]
- Kim, J.J.; Pham, Q.T.; Kim, Y.S. Thinning prediction of hole-expansion test for DP980 sheet based on a non-associated flow rule. Int. J. Mech. Sci. 2021, 191, 106067. [Google Scholar] [CrossRef]
- Wu, B.; Ito, K.; Mori, N.; Oya, T.; Taylor, T.; Yanagimoto, J. Constitutive equations based on non-associated flow rule for the analysis of forming of anisotropic sheet metals. Int. J. Precis. Eng. Manuf. Green Technol. 2019, 7, 465–480. [Google Scholar] [CrossRef]
- Prager, W. Recent developments in the mathematical theory of plasticity. J. App. Phys. 1949, 20, 235–241. [Google Scholar] [CrossRef]
- Tresca, H. Mémoire sur l’écoulement des corps solides soumis à de fortes pressions. CR Acad. Sci. Paris 1864, 59, 754–758. [Google Scholar]
- Mises, V. Mechanics of solid bodies in the plastically-deformable state. Math. Phys. 1913, 4, 582–592. [Google Scholar]
- Drucker, D.C. Relations of experiments to mathematical theories of plasticity. J. Appl. Mech. 1949, 16, 349–357. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. A 1948, 193, 281–297. [Google Scholar]
- Hill, R. Theoretical plasticity of textured aggregates. Math. Proc. Camb. Phil. Soc. 1979, 85, 179–191. [Google Scholar] [CrossRef]
- Hosford, W.F. On yield loci of anisotropic cubic metals. In Proceedings of the 7th North American Metalworking Conference, SME, Dearborn, MI, USA, 13–16 May 1979; pp. 191–197. [Google Scholar]
- Barlat, F.; Brem, J.C.; Yoon, J.W.; Chung, K.; Dick, R.E.; Lege, D.J.; Pourboghrat, F.; Choi, S.-H.; Chu, E. Plane stress yield function for aluminum alloy sheets—Part 1: Theory. Int. J. Plast. 2003, 19, 1297–1319. [Google Scholar] [CrossRef]
- Cazacu, O.; Barlat, F. Generalization of Drucker’s yield criterion to orthotropy. Math. Mech. Solids 2001, 6, 613–630. [Google Scholar] [CrossRef]
- Barlat, F.; Aretz, H.; Yoon, J.W.; Karabin, M.E.; Brem, J.C.; Dick, R.E. Linear transformation based anisotropic yield function. Int. J. Plast. 2005, 21, 1009–1039. [Google Scholar] [CrossRef]
- Banabic, D. Sheet Metal Forming Processes: Constitutive Modelling and Numerical Simulation; Springer: Heidelberg, Germany; Dordrecht, The Netherlands; London, UK; New York, NY, USA, 2010. [Google Scholar]
- Banabic, D.; Barlat, F.; Cazacu, O.; Kuwabara, T. Advances in anisotropic behaviour and formability of sheet metals. Int. J. Mater. Form. 2020, 13, 749–787. [Google Scholar] [CrossRef]
- Yoshida, F.; Hamasaki, H.; Uemori, T. A user-friendly 3D yield function to describe anisotropy of steel sheet. Int. J. Plast. 2013, 45, 119–139. [Google Scholar] [CrossRef]
- Lou, Y.S.; Yoon, J.W. J2-J3 based anisotropic yield function under spatial loading. Procedia Eng. 2017, 207, 233–238. [Google Scholar] [CrossRef]
- Karafillis, A.P.; Boyce, M.C. A general anisotropic yield criterion using bounds and a transformation weighting tensor. J. Mech. Phys. Solids 1993, 41, 1859–1886. [Google Scholar] [CrossRef]
- Cazacu, O. New yield criteria for isotropic and textured metallic materials. Int. J. Solids Struct. 2018, 139–140, 200–210. [Google Scholar] [CrossRef]
- Kabirian, F.; Khan, A.S. Anisotropic yield criteria in σ-τ stress space for materials with yield asymmetry. Int. J. Solids Struct. 2015, 67, 116–126. [Google Scholar] [CrossRef]
- Koh, Y.; Kim, D.; Seok, D.Y.; Bak, J.; Kim, S.W.; Lee, Y.S.; Chung, K. Characterization of mechanical property of magnesium AZ31 alloy sheets for warm temperature forming. Int. J. Mech. Sci. 2015, 93, 204–217. [Google Scholar] [CrossRef]
- Chandola, N.; Lebensohn, R.A.; Cazacu, O.; Revil-Baudard, B.; Mishra, R.K.; Barlat, F. Combined effects of anisotropy and tension–compression asymmetry on the torsional response of AZ31 Mg. Int. J. Solids Struct. 2015, 58, 190–200. [Google Scholar] [CrossRef]
- Tari, G.; Worswick, M.J. Elevated temperature constitutive behavior and simulation of warm forming of AZ31BD. J. Mater. Process. Technol. 2015, 221, 40–55. [Google Scholar] [CrossRef]
- Tari, D.G.; Worswick, M.J.; Alia, U.; Gharghourib, M.A. Mechanical response of AZ31B magnesium alloy: Experimental characterization and material modeling considering proportional loading at room temperature. Int. J. Plast. 2014, 55, 247–267. [Google Scholar] [CrossRef]
- Muhammad, W.; Mohammadi, M.; Kang, J.; Mishra, R.K.; Inal, K. An elasto-plastic constitutive model for evolving asymmetric/anisotropic hardening behavior of AZ31B and ZEK100 magnesium alloy sheets considering monotonic and reverse loading paths. Int. J. Plast. 2015, 70, 30–59. [Google Scholar] [CrossRef]
- Khan, A.S.; Pandey, A.; Gnäupel-Herold, T.; Mishra, R.K. Mechanical response and texture evolution of AZ31 alloy at large strains for different strain rates and temperatures. Int. J. Plast. 2011, 27, 688–706. [Google Scholar] [CrossRef]
- Liu, C.; Huang, Y.; Stout, M.G. On the asymmetric yield surface of plastically orthotropic materials: A phenomenological study. Acta Mater. 1997, 45, 2397–2406. [Google Scholar] [CrossRef]
- Shimizu, I.; Tada, N. Plastic behavior of polycrystalline aluminum during biaxial compression with strain path change. Key Eng. Mater. 2007, 340, 883–888. [Google Scholar]
- Cazacu, O.; Barlat, F. A criterion for description of anisotropy and yield differential effects in pressure-insensitive metals. Int. J. Plast. 2004, 20, 2027–2045. [Google Scholar] [CrossRef]
- Cazacu, O.; Plunkett, B.; Barlat, F. Orthotropic yield criterion for hexagonal closed packed metals. Int. J. Plast. 2006, 22, 1171–1194. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, T.; Zhou, J.; Graham, S.M.; Hayden, M.; Roe, C. On stress-state dependent plasticity modeling: Significance of the hydrostatic stress, the third invariant of stress deviator and the non-associated flow rule. Int. J. Plast. 2011, 27, 217–231. [Google Scholar] [CrossRef]
- Khan, A.S.; Yu, S.; Liu, H. Deformation induced anisotropic responses of Ti–6Al–4V alloy Part II: A strain rate and temperature dependent anisotropic yield criterion. Int. J. Plast. 2012, 38, 14–26. [Google Scholar] [CrossRef]
- Yoon, J.W.; Lou, Y.; Yoon, J.; Glazoff, M.V. Asymmetric yield function based on the stress invariants for pressure sensitive metals. Int. J. Plast. 2014, 56, 184–202. [Google Scholar] [CrossRef]
- Cardoso, R.P.R.; Adetoro, O.B. A generalisation of the Hill’s quadratic yield function for planar plastic anisotropy to consider loading direction. Int. J. Mech. Sci. 2017, 128–129, 253–268. [Google Scholar] [CrossRef]
- Laydi, M.R.; Lexcellent, C. Yield criteria for shape memory materials: Convexity conditions and surface transport. Math. Mech. Solids 2010, 15, 165–208. [Google Scholar] [CrossRef]
- Zhang, S.; Leotoing, L.; Guines, D.; Thuillier, S.; Zang, S.L. Calibration of anisotropic yield criterion with conventional tests or biaxial test. Int. J. Mech. Sci. 2014, 85, 142–151. [Google Scholar] [CrossRef] [Green Version]
- Lăzărescu, L.; Nicodim, I.; Ciobanu, I.; Comşa, D.S.; Banabic, D. Determination of material parameters of sheet metals using the hydraulic bulge test. Acta Metall. Slovaca 2013, 19, 4–12. [Google Scholar] [CrossRef] [Green Version]
- Tamura, S.; Sumikawa, S.; Uemori, T.; Hamasaki, H.; Yoshida, F. Experimental observation of elasto-plasticity behavior of type 5000 and 6000 aluminum alloy sheets. Mater. Trans. 2011, 52, 868–875. [Google Scholar] [CrossRef]
- Sarraf, I.S.; Green, D.E. Prediction of DP600 and TRIP780 yield loci using Yoshida anisotropic yield function. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012089. [Google Scholar] [CrossRef] [Green Version]
- Habraken, A.M.; Aksen, T.A.; Alves, J.L.; Amaral, R.L.; Betaieb, E.; Chandola, N.; Corallo, L.; Cruz, D.J.; Duchêne, L.; Engel, B.; et al. Analysis of ESAFORM 2021 cup drawing benchmark of an Al alloy, critical factors for accuracy and efficiency of FE simulations. Int. J. Mater. Form. 2022, 15, 61. [Google Scholar] [CrossRef]
- Nomura, S.; Kuwabara, T. Material modeling of hot-rolled steel sheet considering differential hardening and hole expansion simulation. ISIJ Int. 2022, 62, 191–199. [Google Scholar] [CrossRef]
- Yoon, J.W.; Barlat, F.; Dick, R.E.; Karabin, M.E. Prediction of six or eight ears in a drawn cup based on a new anisotropic yield function. Int. J. Plast. 2006, 22, 174–193. [Google Scholar] [CrossRef]
- Tang, B.; Wang, Z.; Guo, N.; Wang, Q.; Liu, P. An Extended Drucker Yield Criterion to Consider Tension–Compression Asymmetry and Anisotropy on Metallic Materials: Modeling and Verification. Metals 2020, 10, 20. [Google Scholar] [CrossRef]
- Piehler, H.R. Crystal-plasticity fundamentals. ASM Handb. 2009, 22, 232. [Google Scholar]
| Parameters | a1 | a2 | a3 | a4 | b1 | b2 | b3 | b4 | b5 | b10 | α | β2 | c | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kim–Van | 1.039 | 1.018 | 0.729 | 0.720 | 0.722 | 2.006 | 2.825 | 0.251 | 1.574 | 1.633 | 1.546 | 2.004 | 0.0006 | |
| Cazacu–Barlat | 0.334 | 0.815 | 0.815 | 0.420 | 0.040 | −1.205 | −0.958 | 0.306 | 0.153 | −0.020 | 1.4 | 0.0007 |
| Parameters | a1 | a2 | a3 | a4 | b1 | b2 | b3 | b4 | b5 | b10 | α | β2 | c | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kim–Van | 1.020 | 1.035 | 0.787 | 0.685 | 0.747 | 1.871 | 2.744 | 0.296 | 1.720 | 1.656 | 1.590 | 1.894 | 0.0013 | |
| Cazacu–Barlat | 0.334 | 0.815 | 0.815 | 0.420 | 0.040 | −1.205 | −0.958 | 0.306 | 0.153 | −0.020 | 1.4 | 0.0007 |
| Parameters | a1 | a2 | a3 | a4 | b1 | b2 | b3 | b4 | b5 | b10 | α | β2 | c | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kim–Van | 0.989 | 1.430 | 0.252 | 1.663 | −0.544 | −3.571 | 0.065 | 0.337 | −2.049 | −2.148 | 2.368 | 0.090 | 0.0837 | 0.0013 |
| Cazacu–Barlat | 0.779 | 1.596 | 1.427 | 1.813 | 2.009 | 0.255 | −0.990 | 0.646 | 1.589 | 2.735 | 0.0007 |
| Parameters | a1 | a2 | a3 | a4 | b1 | b2 | b3 | b4 | b5 | b10 | α | β2 | c | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kim–Van | 1.014 | 0.673 | 0.660 | x | 1.159 | 1.765 | 1.063 | 1.089 | x | x | 1.124 | 1.654 | 0.0007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Nguyen, P.V.; Hong, J.G.; Kim, Y.S. Stress-Invariants-Based Anisotropic Yield Functions and Its Application to Sheet Metal Plasticity. Metals 2023, 13, 142. https://doi.org/10.3390/met13010142
Kim J, Nguyen PV, Hong JG, Kim YS. Stress-Invariants-Based Anisotropic Yield Functions and Its Application to Sheet Metal Plasticity. Metals. 2023; 13(1):142. https://doi.org/10.3390/met13010142
Chicago/Turabian StyleKim, Jinjae, Phu Van Nguyen, Jung Goo Hong, and Young Suk Kim. 2023. "Stress-Invariants-Based Anisotropic Yield Functions and Its Application to Sheet Metal Plasticity" Metals 13, no. 1: 142. https://doi.org/10.3390/met13010142
APA StyleKim, J., Nguyen, P. V., Hong, J. G., & Kim, Y. S. (2023). Stress-Invariants-Based Anisotropic Yield Functions and Its Application to Sheet Metal Plasticity. Metals, 13(1), 142. https://doi.org/10.3390/met13010142







