Bird’s Eye View on Lattice Structures: Design Issues and Applications for Best Practices in Mechanical Design
Abstract
:1. Introduction
2. Lattice Classification
- The unit cell’s characteristics, which include topology, cell’s element geometry, and cell’s size.
- The characteristics of the cell’s replication pattern.
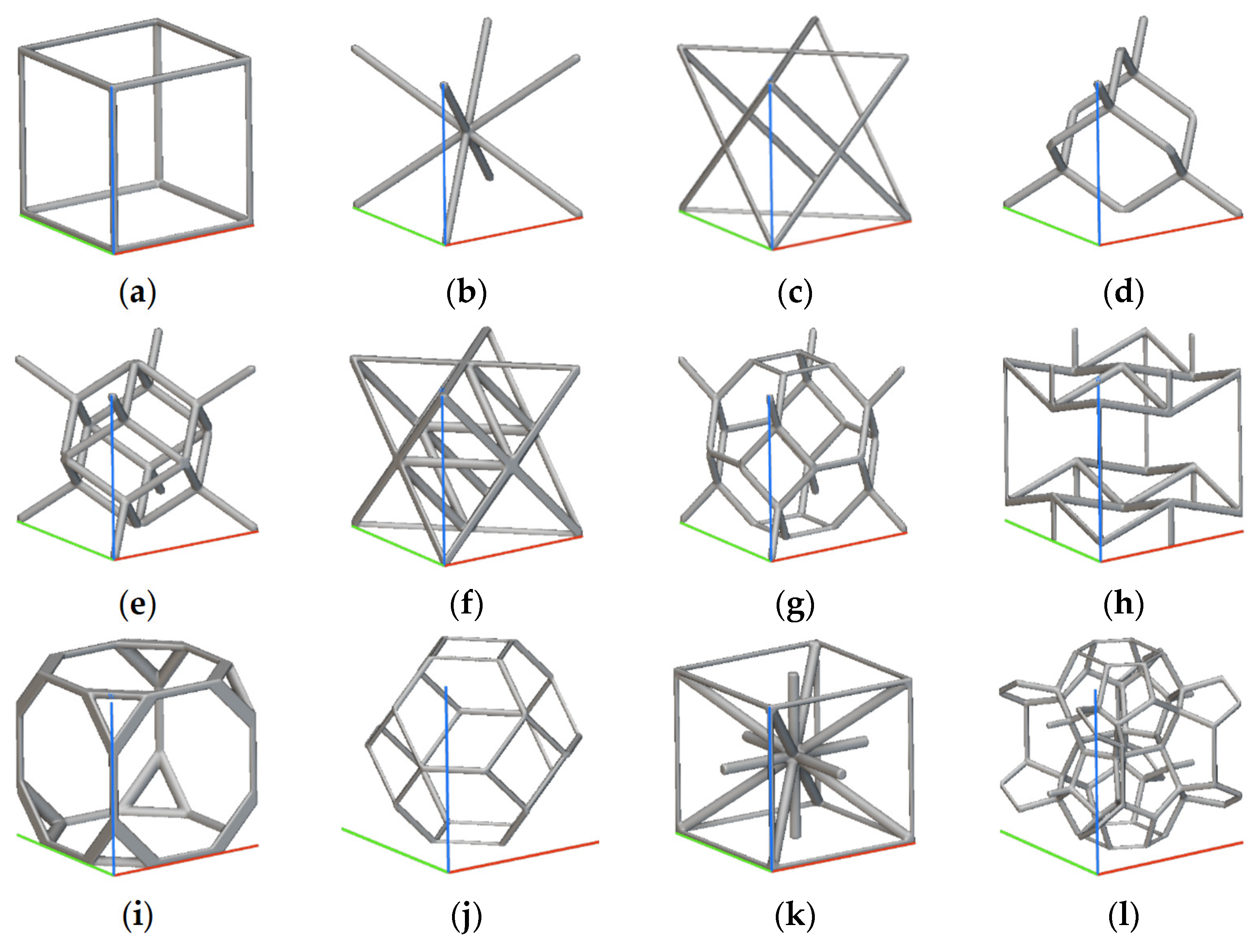
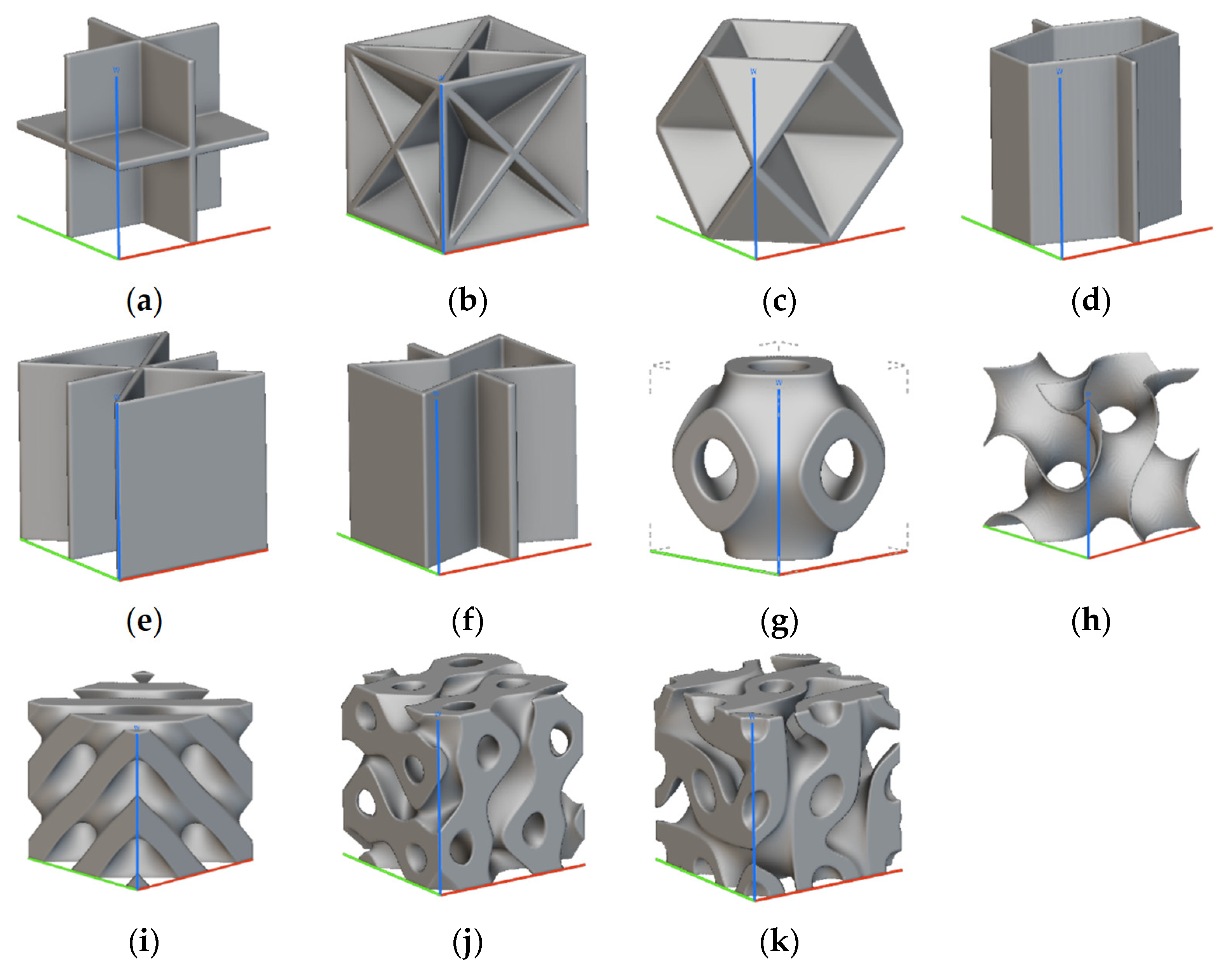
2.1. Unit Cell Characteristics
TPMS Formulation
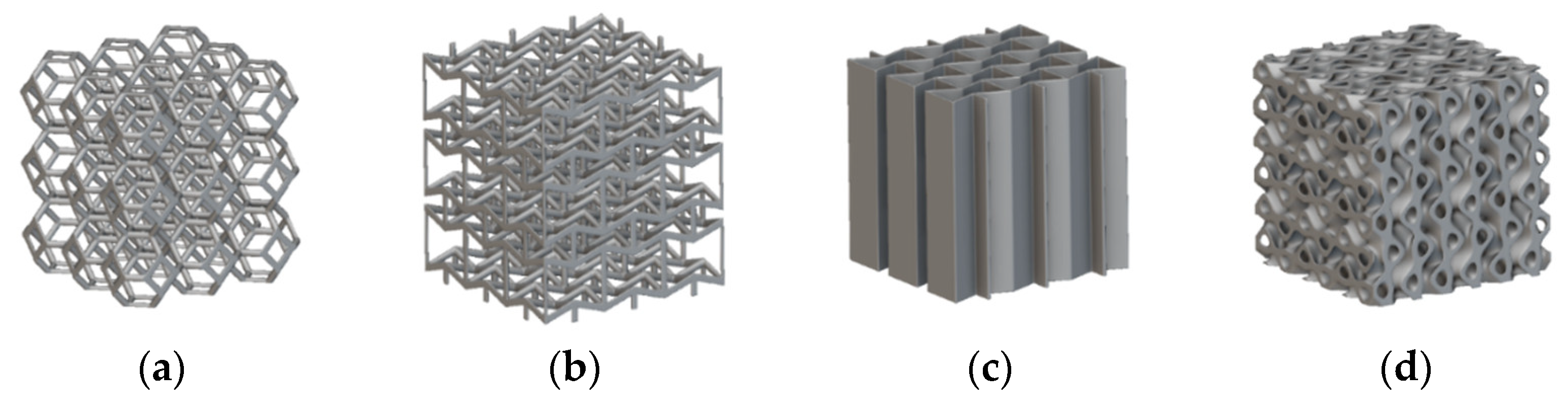
2.2. Characteristics of the Cell Replication Pattern
- Regular.
- Pseudo-regular.
- ○
- Hybrid,
- ○
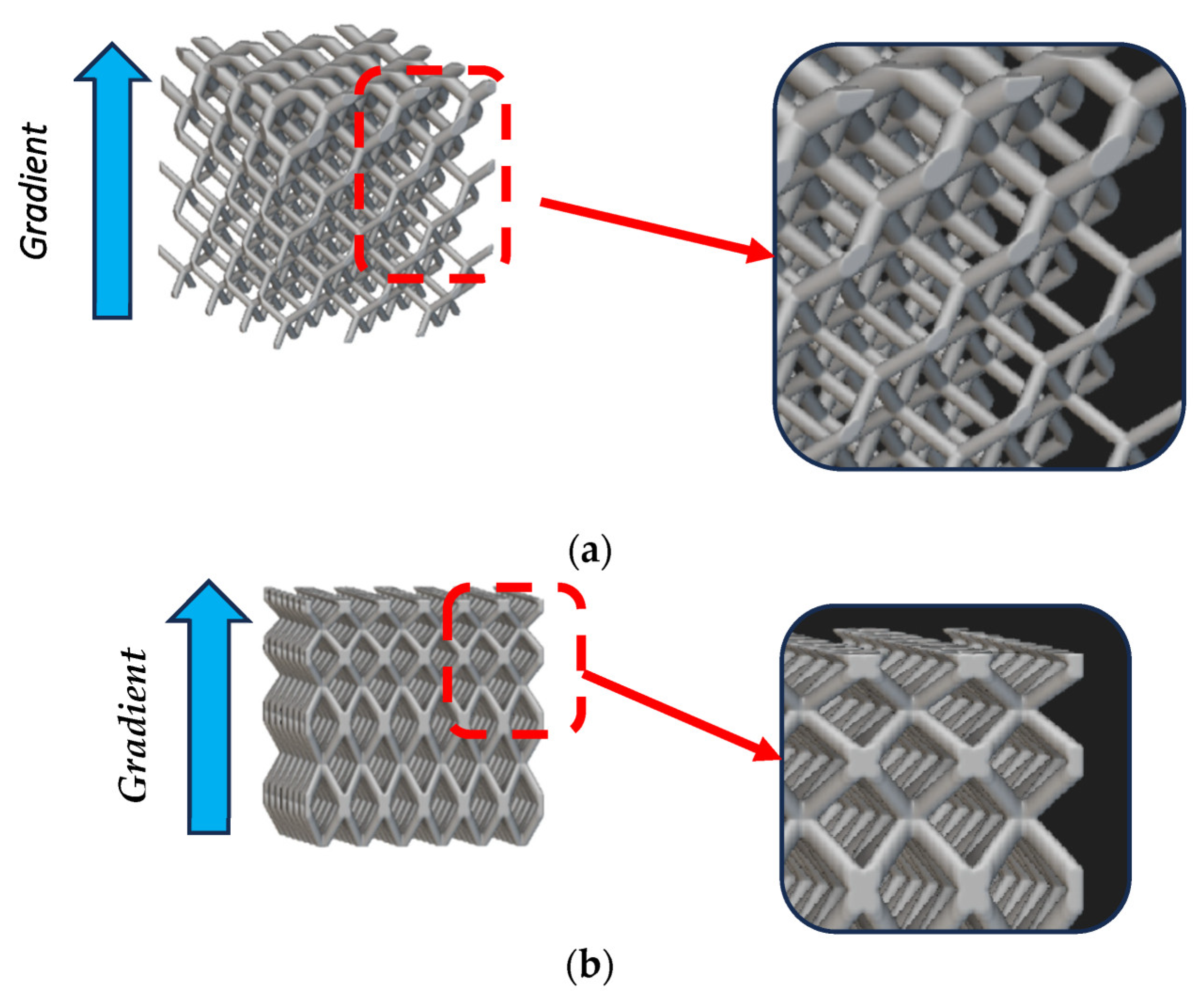
- Warped (or gradient) by cell size,Warped (or gradient) by thickness,
- ○
- Conformal.
- Stochastic.
- ○
- Random by cell size,
- ○
- Random also by thickness.
2.3. Mechanical Behavior
- Bending dominated.
- Stretch dominated.
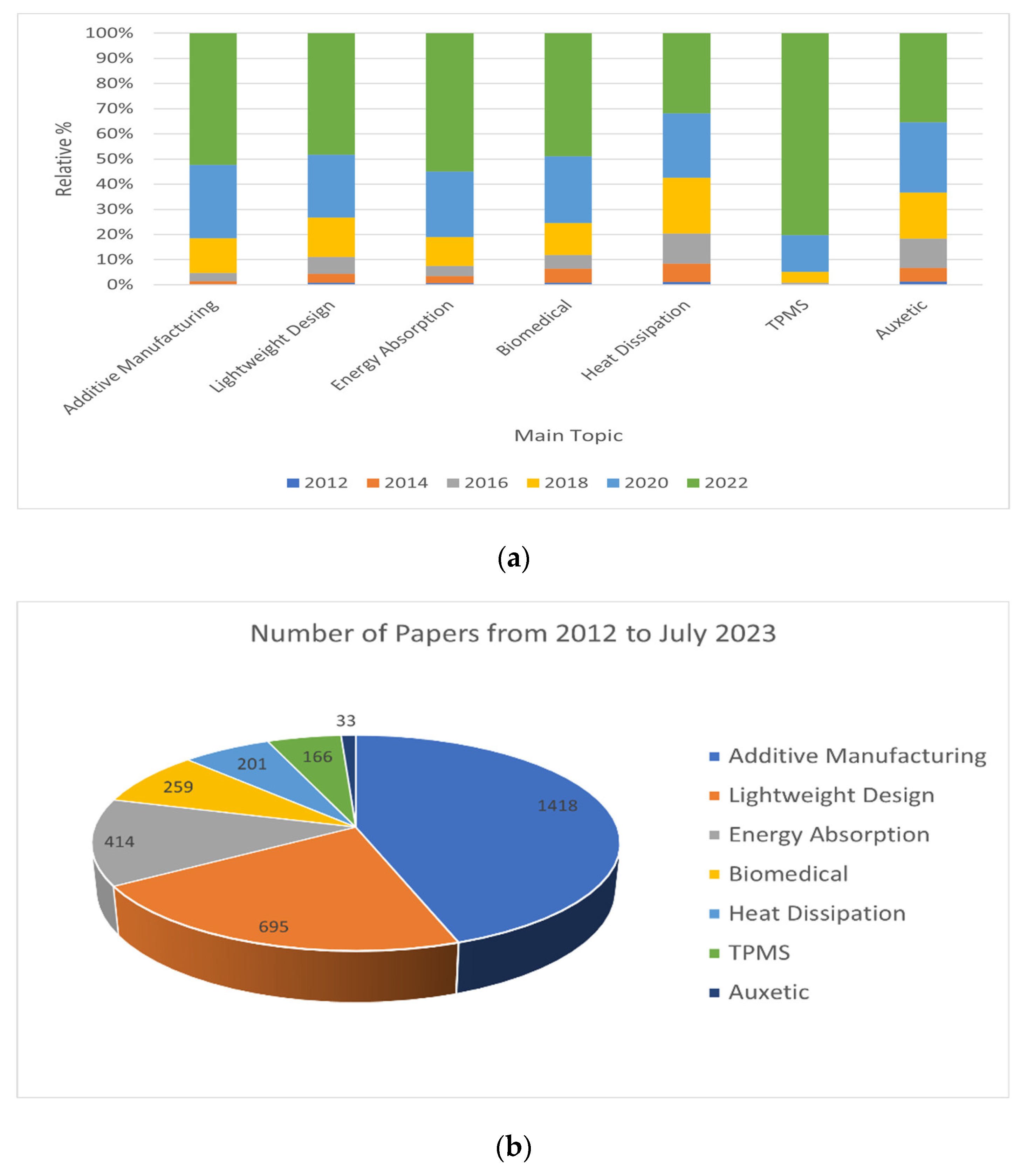
3. Applications
4. Design and Manufacturing Issues
- ○
- For AM: working volume, support and infill design, post processing.
- ○
- For traditional manufacturing processes: die design, extra and complex tooling/attachments, multiple machining/manufacturing processes, precise manufacturing process control, complex assembly/bonding process, post processing and/or set up by other design criteria such as aesthetics, assembly, etc.
5. Conclusions
- In order to investigate the mechanical properties of a structure derived from the multiscale properties of the component(s) and from mesoscale cell characteristics, proper functional behavior may be tailored. As such, a CAD-CAE approach may massively help this study by virtual testing.
- CAD-CAE approaches are also affected by the multiscale domains involved in the problem, with increasing computational costs. This provides impetus to adopt new modeling approaches, such as Implicit Geometric Modeling and/or homogenization techniques for CAE analyses.
- In the case of AM, the mechanical characteristics related to stress–strain curves must be investigated and validated to distinguish between the lattice structure properties and AM setup conditions.
- Metallic AM lattice structures suffer with fatigue loads due to the limited process conditions and/or setup. In addition, the post processing treatments may be infeasible due to the complexity of the structures. Therefore, a suitable workflow engulfing all of the design, manufacturing, and post processing requirements may be defined in order to minimize these concerns and facilitate the functional requirements of the lattice structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Symbols and Acronyms
| Basis Function of TPMS | Principal Curvature at a General Point ‘P’ | ||
| Unit Cell Size | Periodicities | ||
| Cell’s Repetition | Maxwell Number | ||
| Number of Struts | Number of Joints in the Unit Cell | ||
| Elastic Modulus of the Cellular Structure | Elastic Modulus of Equivalent Solid | ||
| Density of the Cellular Structure | Density of the Equivalent Solid | ||
| Gibson & Ashby Constant | Additive Manufacturing | ||
| Computer Aided Design | Computer Aided Engineering | ||
| Simple Cubic | Body-Centered | ||
| Body-Centered Cubic | Face-Centered Cubic | ||
| Octet Truss | Gibson–Ashby | ||
| Triply Periodic Minimal Surface | 3-Dimensional | ||
| Implicit CAD Modeling | Computer-Aided Engineering | ||
| Finite Element Analysis | Free Form Deformation | ||
| Twin Curve Division Method | Arc Division Method | ||
| Curvature Division Method | Non-Uniform Rational B-Splines | ||
| NURBS Free Form Deformation Method | B-Splines | Basis Splines |
References
- Gibson, L.J. Modelling the mechanical behavior of cellular materials. Mater. Sci. Eng. A 1989, 110, 1–36. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997; pp. 16–21. [Google Scholar] [CrossRef]
- Bhate, D. Four Questions in Cellular Material Design. Materials 2019, 12, 1060. [Google Scholar] [CrossRef]
- Tao, W.; Leu, M.C. Design of lattice structure for additive manufacturing. In Proceedings of the 2016 International Symposium on Flexible Automation Cleveland (ISFA 2016), Cleveland, OH, USA, 1–3 August 2016; pp. 326–332. [Google Scholar] [CrossRef]
- Mancini, E.; Campana, F.; Pilone, D.; Amodio, D.; Sasso, M. Definition of a unified material model for cellular materials with high morphological and topological dispersion: Application to an AA7075-T6 aluminium foam. Mater. Sci. Eng. A 2022, 833, 142346. [Google Scholar] [CrossRef]
- Pan, C.; Han, Y.; Lu, J. Design and optimization of lattice structures: A review. Appl. Sci. 2020, 10, 6374. [Google Scholar] [CrossRef]
- Suethao, S.; Shah, D.U.; Smitthipong, W. Recent progress in processing functionally graded polymer foams. Materials 2020, 13, 4060. [Google Scholar] [CrossRef] [PubMed]
- Bici, M.; Brischetto, S.; Campana, F.; Ferro, C.G.; Seclì, C.; Varetti, S.; Mazza, A. Development of a multifunctional panel for aerospace use through SLM additive manufacturing. Procedia CIRP 2018, 67, 215–220. [Google Scholar] [CrossRef]
- Ghouse, S.; Reznikov, N.; Boughton, O.R.; Babu, S.; Ng, K.G.; Blunn, G.; Jeffers, J.R. The design and in vivo testing of a locally stiffness-matched porous scaffold. Appl. Mater. Today 2019, 15, 377–388. [Google Scholar] [CrossRef] [PubMed]
- de Wild, M.; Schumacher, R.; Mayer, K.; Schkommodau, E.; Thoma, D.; Bredell, M.; Weber, F.E. Bone regeneration by the osteoconductivity of porous titanium implants manufactured by selective laser melting: A histological and micro computed tomography study in the rabbit. Tissue Eng. Part A 2013, 19, 2645–2654. [Google Scholar] [CrossRef] [PubMed]
- Saxena, K.K.; Das, R.; Calius, E.P. 3D printable multimaterial cellular auxetics with tunable stiffness. arXiv 2017, arXiv:1707.04486. [Google Scholar]
- Zhang, J.; Huang, H.; Liu, G.; Zong, H.; Zhang, C. Stiffness and energy absorption of additive manufactured hybrid lattice structures. Virtual Phys. Prototyp. 2021, 16, 428–443. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, W.; Zhu, L.; Meng, F.; Liu, J.; Wen, G. Review on lattice structures for energy absorption properties. Compos. Struct. 2022, 304, 116397. [Google Scholar] [CrossRef]
- Shan, S.; Kang, S.H.; Raney, J.R.; Wang, P.; Fang, L.; Candido, F.; Bertoldi, K. Multistable architected materials for trapping elastic strain energy. Adv. Mater. 2015, 27, 4296–4301. [Google Scholar] [CrossRef]
- Brennan-Craddock, J.; Brackett, D.; Wildman, R.; Hague, R. The design of impact absorbing structures for additive manufacture. J. Phys. Conf. Ser. 2012, 382, 012042. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Tyas, A.; Goodall, R.; Askes, H. Energy absorption in lattice structures in dynamics: Nonlinear FE simulations. Int. J. Impact Eng. 2017, 102, 1–15. [Google Scholar] [CrossRef]
- Habib, F.N.; Iovenitti, P.; Masood, S.H.; Nikzad, M. Fabrication of polymeric lattice structures for optimum energy absorption using Multi Jet Fusion technology. Mater. Des. 2018, 155, 86–98. [Google Scholar] [CrossRef]
- Maloney, K.J.; Fink, K.D.; Schaedler, T.A.; Kolodziejska, J.A.; Jacobsen, A.J.; Roper, C.S. Multifunctional heat exchangers derived from three-dimensional micro-lattice structures. Int. J. Heat Mass Transf. 2012, 55, 2486–2493. [Google Scholar] [CrossRef]
- Son, K.N.; Weibel, J.A.; Kumaresan, V.; Garimella, S.V. Design of multifunctional lattice-frame materials for compact heat exchangers. Int. J. Heat Mass Transf. 2017, 115, 619–629. [Google Scholar] [CrossRef]
- Chen, Y.; Li, T.; Scarpa, F.; Wang, L. Lattice metamaterials with mechanically tunable Poisson’s ratio for vibration control. Phys. Rev. Appl. 2017, 7, 024012. [Google Scholar] [CrossRef]
- Chen, D.; Zheng, X. Multi-material additive manufacturing of metamaterials with giant, tailorable negative Poisson’s ratios. Sci. Rep. 2018, 8, 9139. [Google Scholar] [CrossRef]
- Yuan, S.; Shen, F.; Bai, J.; Chua, C.K.; Wei, J.; Zhou, K. 3D soft auxetic lattice structures fabricated by selective laser sintering: TPU powder evaluation and process optimization. Mater. Des. 2017, 120, 317–327. [Google Scholar] [CrossRef]
- Savio, G.; Rosso, S.; Meneghello, R.; Concheri, G. Geometric modeling of cellular materials for additive manufacturing in biomedical field: A review. Appl. Bionics Biomech. 2018, 2018, 1654782. [Google Scholar] [CrossRef]
- Chan, Y.C.; Shintani, K.; Chen, W. Robust topology optimization of multi-material lattice structures under material and load uncertainties. Front. Mech. Eng. 2019, 14, 141–152. [Google Scholar] [CrossRef]
- Stanković, T.; Mueller, J.; Egan, P.; Shea, K. A generalized optimality criteria method for optimization of additively manufactured multimaterial lattice structures. J. Mech. Des. 2015, 137, 111405. [Google Scholar] [CrossRef]
- Ramirez-Chavez, I.E.; Anderson, D.; Sharma, R.; Lee, C.; Bhate, D. A classification of aperiodic architected cellular materials. Designs 2022, 6, 63. [Google Scholar] [CrossRef]
- Álvarez-Trejo, A.; Cuan-Urquizo, E.; Bhate, D.; Roman-Flores, A. Mechanical metamaterials with topologies based on curved elements: An overview of design, additive manufacturing and mechanical properties. Mater. Des. 2023, 233, 112190. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, X.; Li, P.; Huang, G.; Feng, S.; Shen, C.; Lu, T.J. Bioinspired engineering of honeycomb structure-Using nature to inspire human innovation. Prog. Mater. Sci. 2015, 74, 332–400. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Bubb, S.L.; Young, P.; Raymont, D. Evaluation of light-weight AlSi10Mg periodic cellular lattice structures fabricated via direct metal laser sintering. J. Mater. Process. Technol. 2014, 214, 856–864. [Google Scholar] [CrossRef]
- Hunt, C.J.; Morabito, F.; Grace, C.; Zhao, Y.; Woods, B.K. A review of composite lattice structures. Compos. Struct. 2022, 284, 115120. [Google Scholar] [CrossRef]
- Luxner, M.H.; Stampfl, J.; Pettermann, H.E. Finite element modeling concepts and linear analyses of 3D regular open cell structures. J. Mater. Sci. 2005, 40, 5859–5866. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Wang, F. Systematic design of 3D auxetic lattice materials with programmable Poisson’s ratio for finite strains. J. Mech. Phys. Solids 2018, 114, 303–318. [Google Scholar] [CrossRef]
- Kumar, S.; Vyavahare, S.; Teraiya, S.; Kootikuppala, J.; Bogala, H. A state of the art review of additively manufactured auxetic structures. In Recent Advances in Manufacturing Processes and Systems: Select Proceedings of RAM 2021; Springer: Singapore, 2022; pp. 69–84. [Google Scholar] [CrossRef]
- Xue, Y.; Gao, P.; Zhou, L.; Han, F. An enhanced three-dimensional auxetic lattice structure with improved property. Materials 2020, 13, 1008. [Google Scholar] [CrossRef]
- Berger, J.B.; Wadley, H.N.G.; McMeeking, R.M. Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness. Nature 2017, 543, 533–537. [Google Scholar] [CrossRef]
- Xue, R.; Cui, X.; Zhang, P.; Liu, K.; Li, Y.; Wu, W.; Liao, H. Mechanical design and energy absorption performances of novel dual scale hybrid plate-lattice mechanical metamaterials. Extrem. Mech. Lett. 2020, 40, 100918. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Abu Al-Rub, R.K. Multifunctional mechanical metamaterials based on triply periodic minimal surface lattices. Adv. Eng. Mater. 2019, 21, 1900524. [Google Scholar] [CrossRef]
- AlMahri, S.; Santiago, R.; Lee, D.W.; Ramos, H.; Alabdouli, H.; Alteneiji, M.; Alves, M. Evaluation of the dynamic response of triply periodic minimal surfaces subjected to high strain-rate compression. Addit. Manuf. 2021, 46, 102220. [Google Scholar] [CrossRef]
- Song, J.; Tang, Q.; Feng, Q.; Ma, S.; Guo, F.; Han, Q. Investigation on the modelling approach for variable-density lattice structures fabricated using selective laser melting. Mater. Des. 2021, 212, 110236. [Google Scholar] [CrossRef]
- Al Khalil, M.; Lebaal, N.; Demoly, F.; Roth, S. A design and optimization framework of variable-density lattice structures for additive manufacturing. Mech. Adv. Mater. Struct. 2022, 29, 4711–4725. [Google Scholar] [CrossRef]
- Sienkiewicz, J.; Płatek, P.; Jiang, F.; Sun, X.; Rusinek, A. Investigations on the mechanical response of gradient lattice structures manufactured via SLM. Metals 2020, 10, 213. [Google Scholar] [CrossRef]
- Seharing, A.; Azman, A.H.; Abdullah, S. A review on integration of lightweight gradient lattice structures in additive manufacturing parts. Adv. Mech. Eng. 2020, 12, 1687814020916951. [Google Scholar] [CrossRef]
- Li, D.; Liao, W.; Dai, N.; Xie, Y.M. Anisotropic design and optimization of conformal gradient lattice structures. Comput.-Aided Des. 2020, 119, 102787. [Google Scholar] [CrossRef]
- Seharing, A.; Azman, A.H.; Abdullah, S. Finite element analysis of gradient lattice structure patterns for bone implant design. Int. J. Struct. Integr. 2020, 11, 535–545. [Google Scholar] [CrossRef]
- Fabbro, P.D.; Rosso, S.; Ceruti, A.; Meneghello, R.; Concheri, G.; Savio, G. Conformal Lattice Structures: Modeling and Optimization. In Design Tools and Methods in Industrial Engineering II, Proceedings of the International Conference on Design, Simulation, Manufacturing: The Innovation Exchange, ADM 2021, Rome, Italy, 9–10 September 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 474–485. [Google Scholar] [CrossRef]
- Nguyen, J.; Park, S.I.; Rosen, D.W.; Folgar, L.; Williams, J. Conformal lattice structure design and fabrication. In Proceedings of the 2012 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 6–8 August 2012; University of Texas at Austin: Austin, TX, USA, 2012. [Google Scholar]
- D’Angelo, C.; Ortona, A.; Colombo, P. Influence of the loading direction on the mechanical behavior of ceramic foams and lattices under compression. Acta Mater. 2013, 61, 5525–5534. [Google Scholar] [CrossRef]
- Singamaneni, S.; Bertoldi, K.; Chang, S.; Jang, J.H.; Young, S.L.; Thomas, E.L.; Tsukruk, V.V. Bifurcated mechanical behavior of deformed periodic porous solids. Adv. Funct. Mater. 2009, 19, 1426–1436. [Google Scholar] [CrossRef]
- Ashby, M.F.; Gibson, L.J. Cellular Solids: Structure and Properties; Press Syndicate of the University of Cambridge: Cambridge, UK, 1997; pp. 175–231. [Google Scholar]
- Tumino, D.; Alaimo, A.; Orlando, C.; Valvano, S. A Preliminary Study on the Effect of Strut Waviness on the Mechanical Properties of BCC Lattice Unit Cells. In Design Tools and Methods in Industrial Engineering II, Proceedings of the International Conference on Design, Simulation, Manufacturing: The Innovation Exchange, ADM 2021, Rome, Italy, 9–10 September 2021; Springer: Cham, Switzerland, 2021; pp. 431–441. [Google Scholar] [CrossRef]
- Graziosi, S.; Ballo, F.M.; Libonati, F.; Senna, S. 3D printing of bending-dominated soft lattices: Numerical and experimental assessment. Rapid Prototyp. J. 2022, 28, 51–64. [Google Scholar]
- Wagner, M.A.; Lumpe, T.S.; Chen, T.; Shea, K. Programmable, active lattice structures: Unifying stretch-dominated and bending-dominated topologies. Extrem. Mech. Lett. 2019, 29, 100461. [Google Scholar] [CrossRef]
- Benedetti, M.; Du Plessis, A.; Ritchie, R.O.; Dallago, M.; Razavi, S.M.J.; Berto, F. Architected cellular materials: A review on their mechanical properties towards fatigue-tolerant design and fabrication. Mater. Sci. Eng. R Rep. 2021, 144, 100606. [Google Scholar] [CrossRef]
- Wei, K.; Yang, Q.; Ling, B.; Xie, H.; Qu, Z.; Fang, D. Mechanical responses of titanium 3D kagome lattice structure manufactured by selective laser melting. Extrem. Mech. Lett. 2018, 23, 41–48. [Google Scholar] [CrossRef]
- Elipe, J.C.Á.; Lantada, A.D. Comparative study of auxetic geometries by means of computer-aided design and engineering. Smart Mater. Struct. 2012, 21, 105004. [Google Scholar] [CrossRef]
- du Plessis, A.; Razavi, N.; Benedetti, M.; Murchio, S.; Leary, M.; Watson, M.; Berto, F. Properties and applications of additively manufactured metallic cellular materials: A review. Prog. Mater. Sci. 2022, 125, 100918. [Google Scholar] [CrossRef]
- Wu, G.; Cho, Y.; Choi, I.S.; Ge, D.; Li, J.; Han, H.N.; Yang, S. Directing the deformation paths of soft metamaterials with prescribed asymmetric units. Adv. Mater. 2015, 27, 2747–2752. [Google Scholar] [CrossRef] [PubMed]
- Niknam, H.; Akbarzadeh, A.H. Graded lattice structures: Simultaneous enhancement in stiffness and energy absorption. Mater. Des. 2020, 196, 109129. [Google Scholar] [CrossRef]
- Ji, J.C.; Luo, Q.; Ye, K. Vibration control based metamaterials and origami structures: A state-of-the-art review. Mech. Syst. Signal Process. 2021, 161, 107945. [Google Scholar] [CrossRef]
- Wei, Y.; Yu, B.; Yang, Q.; Gao, P.; Miao, Z.; Cheng, J.; Sun, X. Damping behaviors of steel-based Kelvin lattice structures fabricated by indirect additive manufacture combining investment casting. Smart Mater. Struct. 2020, 29, 055001. [Google Scholar] [CrossRef]
- Spadoni, A.; Ruzzene, M. Static aeroelastic response of chiral-core airfoils. J. Intell. Mater. Syst. Struct. 2007, 18, 1067–1075. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L. Auxetic materials. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2007, 221, 565–575. [Google Scholar] [CrossRef]
- Xia, Y.; Friswell, M.I.; Flores, E.S. Equivalent models of corrugated panels. Int. J. Solids Struct. 2012, 49, 1453–1462. [Google Scholar] [CrossRef]
- El-Sayed, M.A.; Essa, K.; Ghazy, M.; Hassanin, H. Design optimization of additively manufactured titanium lattice structures for biomedical implants. Int. J. Adv. Manuf. Technol. 2020, 110, 2257–2268. [Google Scholar] [CrossRef]
- Murr, L.E.; Gaytan, S.M.; Medina, F.; Lopez, H.; Martinez, E.; Machado, B.I.; Bracke, J. Next-generation biomedical implants using additive manufacturing of complex, cellular and functional mesh arrays. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 1999–2032. [Google Scholar] [CrossRef] [PubMed]
- Sajjad, U.; Rehman, T.U.; Ali, M.; Park, C.W.; Yan, W.M. Manufacturing and potential applications of lattice structures in thermal systems: A comprehensive review of recent advances. Int. J. Heat Mass Transf. 2022, 198, 123352. [Google Scholar] [CrossRef]
- Shabgard, H.; Allen, M.J.; Sharifi, N.; Benn, S.P.; Faghri, A.; Bergman, T.L. Heat pipe heat exchangers and heat sinks: Opportunities, challenges, applications, analysis, and state of the art. Int. J. Heat Mass Transf. 2015, 89, 138–158. [Google Scholar] [CrossRef]
- Moon, S.K.; Tan, Y.E.; Hwang, J.; Yoon, Y.J. Application of 3D printing technology for designing light-weight unmanned aerial vehicle wing structures. Int. J. Precis. Eng. Manuf.-Green Technol. 2014, 1, 223–228. [Google Scholar] [CrossRef]
- Magerramova, L.; Volkov, M.; Afonin, A.; Svinareva, M.; Kalinin, D. Application of light lattice structures for gas turbine engine fan blades. In Proceedings of the 31st Congress of the International Council of the Aeronautical Sciences, ICAS, Belo Horizonte, Brazil, 9–14 September 2018. [Google Scholar]
- Spadoni, A.; Ruzzene, M. Numerical and experimental analysis of the static compliance of chiral truss-core airfoils. J. Mech. Mater. Struct. 2007, 2, 965–981. [Google Scholar] [CrossRef]
- Aabid, A.; Parveez, B.; Parveen, N.; Khan, S.A.; Zayan, J.M.; Shabbir, O. Reviews on design and development of unmanned aerial vehicle (drone) for different applications. J. Mech. Eng. Res. Dev. 2022, 45, 53–69. [Google Scholar]
- Zhang, X.; Zhou, H.; Shi, W.; Zeng, F.; Zeng, H.; Chen, G. Vibration tests of 3D printed satellite structure made of lattice sandwich panels. AIAA J. 2018, 56, 4213–4217. [Google Scholar] [CrossRef]
- Vasiliev, V.V.; Barynin, V.A.; Razin, A.F. Anisogrid composite lattice structures-Development and aerospace applications. Compos. Struct. 2012, 94, 1117–1127. [Google Scholar] [CrossRef]
- Khorrami, M.R.; Humphreys, W.M.; Lockard, D.P. An assessment of flap and main landing gear noise abatement concepts. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015; p. 2987. [Google Scholar] [CrossRef]
- Jetté, B.; Brailovski, V.; Dumas, M.; Simoneau, C.; Terriault, P. Femoral stem incorporating a diamond cubic lattice structure: Design, manufacture and testing. J. Mech. Behav. Biomed. Mater. 2018, 77, 58–72. [Google Scholar] [CrossRef] [PubMed]
- Heinl, P.; Müller, L.; Körner, C.; Singer, R.F.; Müller, F.A. Cellular Ti-6Al-4V structures with interconnected macro porosity for bone implants fabricated by selective electron beam melting. Acta Biomater. 2008, 4, 1536–1544. [Google Scholar] [CrossRef]
- Challapalli, A.; Ju, J. Continuum model for effective properties of orthotropic octet-truss lattice materials. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 46583, p. V009T12A051. [Google Scholar] [CrossRef]
- Dumas, M.; Terriault, P.; Brailovski, V. Modelling and characterization of a porosity graded lattice structure for additively manufactured biomaterials. Mater. Des. 2017, 121, 383–392. [Google Scholar] [CrossRef]
- Stevenson, G.; Rehman, S.; Draper, E.; Hernández-Nava, E.; Hunt, J.; Haycock, J.W. Combining 3D human in vitro methods for a 3Rs evaluation of novel titanium surfaces in orthopaedic applications. Biotechnol. Bioeng. 2016, 113, 1586–1599. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.M.; Lee, S.J.; Lee, P.V.S. Failure analysis of an additive manufactured porous titanium structure for orthopedic implant applications. Mater. Sci. Forum 2016, 863, 45–49. [Google Scholar] [CrossRef]
- Gorguluarslan, R.M.; Choi, S.K.; Saldana, C.J. Uncertainty quantification and validation of 3D lattice scaffolds for computer-aided biomedical applications. J. Mech. Behav. Biomed. Mater. 2017, 71, 428–440. [Google Scholar] [CrossRef] [PubMed]
- Soro, N.; Attar, H.; Brodie, E.; Veidt, M.; Molotnikov, A.; Dargusch, M.S. Evaluation of the mechanical compatibility of additively manufactured porous Ti-25Ta alloy for load-bearing implant applications. J. Mech. Behav. Biomed. Mater. 2019, 97, 149–158. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, R.; Antonov, M.; Kollo, L.; Holovenko, Y.; Prashanth, K.G. Mechanical behavior of Ti6Al4V scaffolds filled with CaSiO3 for implant applications. Appl. Sci. 2019, 9, 3844. [Google Scholar] [CrossRef]
- Jia, D.; Li, F.; Zhang, C.; Liu, K.; Zhang, Y. Design and simulation analysis of Lattice bone plate based on finite element method. Mech. Adv. Mater. Struct. 2021, 28, 1311–1321. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Zhao, W.; Zou, S.; Zhou, G.; Wang, Y. Structure design and multi-objective optimization of a novel crash box based on biomimetic structure. Int. J. Mech. Sci. 2018, 138, 489–501. [Google Scholar] [CrossRef]
- Wang, C.; Wang, W.; Zhao, W.; Wang, Y.; Zhou, G. Structure design and multi-objective optimization of a novel NPR bumper system. Compos. Part B Eng. 2018, 153, 78–96. [Google Scholar] [CrossRef]
- Yin, S.; Chen, H.; Wu, Y.; Li, Y.; Xu, J. Introducing composite lattice core sandwich structure as an alternative proposal for engine hood. Compos. Struct. 2018, 201, 131–140. [Google Scholar] [CrossRef]
- Niutta, C.B.; Ciardiello, R.; Tridello, A. Experimental and Numerical Investigation of a Lattice Structure for Energy Absorption: Application to the Design of an Automotive Crash Absorber. Polymers 2022, 14, 1116. [Google Scholar] [CrossRef]
- Mantovani, S.; Campo, G.A.; Ferrari, A.; Cavazzuti, M. Optimization methodology for automotive chassis design by truss frame: A preliminary investigation using the lattice approach. In Transdisciplinary Engineering Methods for Social Innovation of Industry 4.0; IOS Press: Amsterdam, The Netherlands, 2018; pp. 984–992. [Google Scholar]
- Kumar, V.; Manogharan, G.; Cormier, D.R. Design of periodic cellular structures for heat exchanger applications. In 2009 International Solid Freeform Fabrication Symposium; University of Texas at Austin: Austin, TX, USA, 2009. [Google Scholar]
- Pannikottu, A.; Bandaru, S. Flexible Honeycomb Composite Vehicle Armor; SAE Technical Paper No. 2009-01-0601; SAE International: Warrendale, PA, USA, 2009. [Google Scholar] [CrossRef]
- Harris, J.A. Additively Manufactured Metallic Cellular Materials for Blast and Impact Mitigation. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2018. [Google Scholar]
- Acanfora, V.; Corvino, C.; Saputo, S.; Sellitto, A.; Riccio, A. Application of an additive manufactured hybrid metal/composite shock absorber panel to a military seat ejection system. Appl. Sci. 2021, 11, 6473. [Google Scholar] [CrossRef]
- Luo, J.W.; Chen, L.; Xia, Y.; Zheng, X.; Tao, W.Q. Topology optimization of natural convection using porous metal foam based on the adjoint lattice Boltzmann method and level set method. Comput. Fluids 2023, 265, 106007. [Google Scholar] [CrossRef]
- Baobaid, N.; Ali, M.I.; Khan, K.A.; Al-Rub, R.K.A. Fluid flow and heat transfer of porous TPMS architected heat sinks in free convection environment. Case Stud. Therm. Eng. 2022, 33, 101944. [Google Scholar] [CrossRef]
- Hussein, A.; Hao, L.; Yan, C.; Everson, R.; Young, P. Advanced lattice support structures for metal additive manufacturing. J. Mater. Process. Technol. 2013, 213, 1019–1026. [Google Scholar] [CrossRef]
- Vaissier, B.; Pernot, J.P.; Chougrani, L.; Véron, P. Genetic-algorithm based framework for lattice support structure optimization in additive manufacturing. Comput.-Aided Des. 2019, 110, 11–23. [Google Scholar] [CrossRef]
- Cheng, L.; Liang, X.; Bai, J.; Chen, Q.; Lemon, J.; To, A. On utilizing topology optimization to design support structure to prevent residual stress induced build failure in laser powder bed metal additive manufacturing. Addit. Manuf. 2019, 27, 290–304. [Google Scholar] [CrossRef]
- Alejandrino, J.D.; Concepcion, R.S., II; Lauguico, S.C.; Tobias, R.R.; Venancio, L.; Macasaet, D.; Dadios, E.P. A machine learning approach of lattice infill pattern for increasing material efficiency in additive manufacturing processes. Int. J. Mech. Eng. Robot. Res. 2020, 9, 1253–1263. [Google Scholar] [CrossRef]
- Ntintakis, I.; Stavroulakis, G.E. Infill Microstructures for Additive Manufacturing. Appl. Sci. 2022, 12, 7386. [Google Scholar] [CrossRef]
- Dong, G.; Tang, Y.; Li, D.; Zhao, Y.F. Design and optimization of solid lattice hybrid structures fabricated by additive manufacturing. Addit. Manuf. 2020, 33, 101116. [Google Scholar] [CrossRef]
- Ahmad, A.; Elamana, S.; Adam, K.; Bici, M.; Campana, F. Lightweight Horse Saddletree Through Reverse Engineering and Lattice Structure Design. Comput. Des. Appl. 2023, 20, 923–935. [Google Scholar] [CrossRef]
- Hanna, B.; Adams, R.; Townsend, S.; Robinson, M.; Soe, S.; Stewart, M.; Theobald, P. Auxetic metamaterial optimisation for head impact mitigation in American football. Int. J. Impact Eng. 2021, 157, 103991. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- ARUP. Canton Tower. Available online: https://www.arup.com/projects/guangzhou-tv-tower (accessed on 27 June 2023).
- ARUP. Beijing National Stadium (Bird’s Nest). Available online: https://www.arup.com/services/buildings/structural-engineering (accessed on 27 June 2023).
- Atomium. The Atomium (The Symbol of Brussels and Belgium). Available online: https://atomium.be/home/Index (accessed on 27 June 2023).
- Huang, R.; Ma, S.; Zhang, M.; Xu, J.; Wang, Z. Dynamic deformation and failure process of quasi-closed-cell aluminum foam manufactured by direct foaming technique. Mater. Sci. Eng. A 2019, 756, 302–311. [Google Scholar] [CrossRef]
- Luukkonen, T.; Yliniemi, J.; Sreenivasan, H.; Ohenoja, K.; Finnilä, M.; Franchin, G.; Colombo, P. Ag-or Cu-modified geopolymer filters for water treatment manufactured by 3D printing, direct foaming, or granulation. Sci. Rep. 2020, 10, 7233. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Singh, R. Precision investment casting: A state of art review and future trends. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 2143–2164. [Google Scholar] [CrossRef]
- Barnett, S.O. Investment Casting—The Multi-Process Technology. Foundry Trade J. Int. 1988, 11, 33. [Google Scholar]
- Jones, S.; Yuan, C. Advances in shell moulding for investment casting. J. Mater. Process. Technol. 2003, 135, 258–265. [Google Scholar] [CrossRef]
- Wadley, H.N. Multifunctional periodic cellular metals. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 31–68. [Google Scholar] [CrossRef] [PubMed]
- Ablat, M.A.; Qattawi, A. Investigating the design and process parameters of folded perforated sheet metal. Int. J. Adv. Manuf. Technol. 2019, 102, 615–633. [Google Scholar] [CrossRef]
- Cheung, K.C.; Gershenfeld, N. Reversibly assembled cellular composite materials. Science 2013, 341, 1219–1221. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Sun, F.; Zhang, X.; Fan, H. Interlocking orthogrid: An efficient way to construct lightweight lattice-core sandwich composite structure. Compos. Struct. 2017, 176, 55–71. [Google Scholar] [CrossRef]
- Cheung, K.C.W. Digital Cellular Solids: Reconfigurable Composite Materials. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2012. [Google Scholar]
- Queheillalt, D.T.; Murty, Y.; Wadley, H.N. Mechanical properties of an extruded pyramidal lattice truss sandwich structure. Scr. Mater. 2008, 58, 76–79. [Google Scholar] [CrossRef]
- Kang, K.J. Wire-woven cellular metals: The present and future. Prog. Mater. Sci. 2015, 69, 213–307. [Google Scholar] [CrossRef]
- Simovski, C.R.; Belov, P.A.; Atrashchenko, A.V.; Kivshar, Y.S. Wire metamaterials: Physics and applications. Adv. Mater. 2012, 24, 4229–4248. [Google Scholar] [CrossRef]
- Khoda, B.; Ahsan, A.N. A novel rapid manufacturing process for metal lattice structure. 3d Print. Addit. Manuf. 2021, 8, 111–125. [Google Scholar] [CrossRef]
- Li, M.; Du, W.; Elwany, A.; Pei, Z.; Ma, C. Metal binder jetting additive manufacturing: A literature review. J. Manuf. Sci. Eng. 2020, 142, 090801. [Google Scholar] [CrossRef]
- Du, W.; Ren, X.; Pei, Z.; Ma, C. Ceramic binder jetting additive manufacturing: A literature review on density. J. Manuf. Sci. Eng. 2020, 142, 040801. [Google Scholar] [CrossRef]
- Mirzababaei, S.; Pasebani, S. A review on binder jet additive manufacturing of 316L stainless steel. J. Manuf. Mater. Process. 2019, 3, 82. [Google Scholar] [CrossRef]
- Prashar, G.; Vasudev, H. A comprehensive review on sustainable cold spray additive manufacturing: State of the art, challenges and future challenges. J. Clean. Prod. 2021, 310, 127606. [Google Scholar] [CrossRef]
- Yin, S.; Cavaliere, P.; Aldwell, B.; Jenkins, R.; Liao, H.; Li, W.; Lupoi, R. Cold spray additive manufacturing and repair: Fundamentals and applications. Addit. Manuf. 2018, 21, 628–650. [Google Scholar] [CrossRef]
- Pathak, S.; Saha, G.C. Development of sustainable cold spray coatings and 3D additive manufacturing components for repair/manufacturing applications: A critical review. Coatings 2017, 7, 122. [Google Scholar] [CrossRef]
- Dass, A.; Moridi, A. State of the art in directed energy deposition: From additive manufacturing to materials design. Coatings 2019, 9, 418. [Google Scholar] [CrossRef]
- Yao, X.X.; Ge, P.; Li, J.Y.; Wang, Y.F.; Li, T.; Liu, W.W.; Zhang, Z. Controlling the solidification process parameters of direct energy deposition additive manufacturing considering laser and powder properties. Comput. Mater. Sci. 2020, 182, 109788. [Google Scholar] [CrossRef]
- Heigel, J.C.; Michaleris, P.; Reutzel, E.W. Thermo-mechanical model development and validation of directed energy deposition additive manufacturing of Ti-6Al-4V. Addit. Manuf. 2015, 5, 9–19. [Google Scholar] [CrossRef]
- Behera, D.; Cullinan, M. Current challenges and potential directions towards precision microscale additive manufacturing-Part I: Direct ink writing/jetting processes. Precis. Eng. 2021, 68, 326–337. [Google Scholar] [CrossRef]
- Costakis, W.J., Jr.; Rueschhoff, L.M.; Diaz-Cano, A.I.; Youngblood, J.P.; Trice, R.W. Additive manufacturing of boron carbide via continuous filament direct ink writing of aqueous ceramic suspensions. J. Eur. Ceram. Soc. 2016, 36, 3249–3256. [Google Scholar] [CrossRef]
- Tu, R.; Sodano, H.A. Additive manufacturing of high-performance vinyl ester resin via direct ink writing with UV-thermal dual curing. Addit. Manuf. 2021, 46, 102180. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Hu, Y.; Wang, H. Additive manufacturing of carbon fiber-reinforced plastic composites using fused deposition modeling: Effects of process parameters on tensile properties. J. Compos. Mater. 2017, 51, 451–462. [Google Scholar] [CrossRef]
- Singh, S.; Ramakrishna, S.; Singh, R. Material issues in additive manufacturing: A review. J. Manuf. Process. 2017, 25, 185–200. [Google Scholar] [CrossRef]
- Chacón, J.M.; Caminero, M.A.; García-Plaza, E.; Núnez, P.J. Additive manufacturing of PLA structures using fused deposition modelling: Effect of process parameters on mechanical properties and their optimal selection. Mater. Des. 2017, 124, 143–157. [Google Scholar] [CrossRef]
- Sukhotskiy, V.; Vishnoi, P.; Karampelas, I.H.; Vader, S.; Vader, Z.; Furlani, E.P. Magnetohydrodynamic drop-on-demand liquid metal additive manufacturing: System overview and modelling. In Proceedings of the 5th International Conference of Fluid Flow, Heat and Mass Transfer (FFHMT’18), Niagra Falls, ON, Canada, 7–9 June 2018. [Google Scholar] [CrossRef]
- Gan, Z.; Yu, G.; He, X.; Li, S. Surface-active element transport and its effect on liquid metal flow in laser-assisted additive manufacturing. Int. Commun. Heat Mass Transf. 2017, 86, 206–214. [Google Scholar] [CrossRef]
- Li, A.; Liu, X.; Wan, X.; Yang, Y. Thermal behaviors and fluid flow controlling the geometry of 7075 aluminum alloy single tracks during liquid metal flow rapid cooling additive manufacturing. Int. Commun. Heat Mass Transf. 2020, 116, 104664. [Google Scholar] [CrossRef]
- Dermeik, B.; Travitzky, N. Laminated object manufacturing of ceramic-based materials. Adv. Eng. Mater. 2020, 22, 2000256. [Google Scholar] [CrossRef]
- Tao, Y.; Yin, Q.; Li, P. An additive manufacturing method using large-scale wood inspired by laminated object manufacturing and plywood technology. Polymers 2020, 13, 144. [Google Scholar] [CrossRef] [PubMed]
- Luong, D.X.; Subramanian, A.K.; Silva, G.A.L.; Yoon, J.; Cofer, S.; Yang, K.; Tour, J.M. Laminated object manufacturing of 3D-printed laser-induced graphene foams. Adv. Mater. 2018, 30, 1707416. [Google Scholar] [CrossRef] [PubMed]
- King, W.E.; Anderson, A.T.; Ferencz, R.M.; Hodge, N.E.; Kamath, C.; Khairallah, S.A.; Rubenchik, A.M. Laser powder bed fusion additive manufacturing of metals; physics, computational, and materials challenges. Appl. Phys. Rev. 2015, 2, 041304. [Google Scholar] [CrossRef]
- Snow, Z.; Nassar, A.R.; Reutzel, E.W. Invited Review Article: Review of the formation and impact of flaws in powder bed fusion additive manufacturing. Addit. Manuf. 2020, 36, 101457. [Google Scholar] [CrossRef]
- Ladani, L.; Sadeghilaridjani, M. Review of powder bed fusion additive manufacturing for metals. Metals 2021, 11, 1391. [Google Scholar] [CrossRef]
- Cheng, L.; To, A. Part-scale build orientation optimization for minimizing residual stress and support volume for metal additive manufacturing: Theory and experimental validation. Comput.-Aided Des. 2019, 113, 1–23. [Google Scholar] [CrossRef]
- Zanini, F.; Sorgato, M.; Savio, E.; Carmignato, S. Uncertainty of CT dimensional measurements performed on metal additively manufactured lattice structures. In Proceedings of the 10th Conference on Industrial Computed Tomography, Wels, Austria, 4–7 February 2020. [Google Scholar] [CrossRef]
- Tamburrino, F.; Graziosi, S.; Bordegoni, M. The design process of additively manufactured mesoscale lattice structures: A review. J. Comput. Inf. Sci. Eng. 2018, 18, 040801. [Google Scholar] [CrossRef]
- Koch, P.; Korn, H.; Kordass, R.; Holtzhausen, S.; Schoene, C.; Mueller, B.; Stelzer, R. A CAD-based workflow and mechanical characterization for additive manufacturing of tailored lattice structures. In 2018 International Solid Freeform Fabrication Symposium; University of Texas at Austin: Austin, TX, USA, 2018. [Google Scholar]
- Daynes, S.; Feih, S.; Lu, W.F.; Wei, J. Design concepts for generating optimised lattice structures aligned with strain trajectories. Comput. Methods Appl. Mech. Eng. 2019, 354, 689–705. [Google Scholar] [CrossRef]
- Rosso, S.; Uriati, F.; Grigolato, L.; Meneghello, R.; Concheri, G.; Savio, G. An optimization workflow in design for additive manufacturing. Appl. Sci. 2021, 11, 2572. [Google Scholar] [CrossRef]
- Panagiotidou, V.; Koerner, A.; Cruz, M.; Parker, B.; Beyer, B.; Giannakopoulos, S. 3D extrusion of multi-biomaterial lattices using an environmentally informed workflow. Front. Archit. Res. 2022, 11, 691–708. [Google Scholar] [CrossRef]
- Hudak, Y.F.; Li, J.S.; Cullum, S.; Strzelecki, B.M.; Richburg, C.; Kaufman, G.E.; Aubin, P.M. A novel workflow to fabricate a patient-specific 3D printed accommodative foot orthosis with personalized latticed metamaterial. Med. Eng. Phys. 2022, 104, 103802. [Google Scholar] [CrossRef] [PubMed]
- Al-Tamimi, A.A.; Almeida, H.; Bartolo, P. Structural optimisation for medical implants through additive manufacturing. Prog. Addit. Manuf. 2020, 5, 95–110. [Google Scholar] [CrossRef]
- Nguyen, D.S.; Vignat, F. A method to generate lattice structure for additive manufacturing. In Proceedings of the 2016 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bali, Indonesia, 4–7 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 966–970. [Google Scholar] [CrossRef]
- Jafferson, J.M.; Sharma, H. Design of 3D printable airless tyres using NTopology. Mater. Today Proc. 2021, 46, 1147–1160. [Google Scholar] [CrossRef]
- Nguyen, D.S. Design of lattice structure for additive manufacturing in CAD environment. J. Adv. Mech. Des. Syst. Manuf. 2019, 13, JAMDSM0057. [Google Scholar] [CrossRef]
- Moreno Nieto, D.; Moreno Sánchez, D. Design for additive manufacturing: Tool review and a case study. Appl. Sci. 2021, 11, 1571. [Google Scholar] [CrossRef]
- Dragoni, E.; Ciace, V.A. Mechanical design and modelling of lightweight additively manufactured lattice structures evolved from regular three-dimensional tessellations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 1759–1773. [Google Scholar] [CrossRef]
- Abdulhadi, H.S.; Mian, A. Effect of strut length and orientation on elastic mechanical response of modified body-centered cubic lattice structures. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 2219–2233. [Google Scholar] [CrossRef]
- Al Rifaie, M.; Mian, A.; Srinivasan, R. Compression behavior of three-dimensional printed polymer lattice structures. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 1574–1584. [Google Scholar] [CrossRef]
- Lu, Y.; Birol, E.B.; Johnson, C.; Hernandez, C.; Sabin, J.E. A Method for Load-responsive Inhomogeneity and Anisotropy in 3D Lattice Generation Based on Ellipsoid Packing. In Proceedings of the 25th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA), Bangkok, Thailand, 5–8 August 2020; pp. 395–404. [Google Scholar] [CrossRef]
- Robles-Linares, J.A.; Ramírez-Cedillo, E.; Siller, H.R.; Rodríguez, C.A.; Martínez-López, J.I. Parametric modeling of biomimetic cortical bone microstructure for additive manufacturing. Materials 2019, 12, 913. [Google Scholar] [CrossRef] [PubMed]
- Fantini, M.; Curto, M. Interactive design and manufacturing of a Voronoi-based biomimetic bone scaffold for morphological characterization. Int. J. Interact. Des. Manuf. (IJIDeM) 2018, 12, 585–596. [Google Scholar] [CrossRef]
- Nazir, A.; Arshad, A.B.; Jeng, J.Y. Buckling and post-buckling behavior of uniform and variable-density lattice columns fabricated using additive manufacturing. Materials 2019, 12, 3539. [Google Scholar] [CrossRef]
- Jin, X.; Li, G.; Gong, J. Optimal design and modeling of 3D variable-density lattice structures. In Proceedings of the 2017 8th International Conference on Mechanical and Aerospace Engineering (ICMAE), Prague, Czech Republic, 22–25 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 320–325. [Google Scholar] [CrossRef]
- Fragassa, C. Electric city buses with modular platform: A design proposition for sustainable mobility. In Sustainable Design and Manufacturing 2017: Selected Papers on Sustainable Design and Manufacturing 4; Springer International Publishing: Cham, Switzerland, 2017; pp. 789–800. [Google Scholar] [CrossRef]
- Abate, K.M.; Nazir, A.; Yeh, Y.P.; Chen, J.E.; Jeng, J.Y. Design, optimization, and validation of mechanical properties of different cellular structures for biomedical application. Int. J. Adv. Manuf. Technol. 2020, 106, 1253–1265. [Google Scholar] [CrossRef]
- Dakshnamoorthy, V. Automated Lattice Optimization of Hinge Fitting with Displacement Constraint. Ph.D. Thesis, The University of Texas, Austin, TX, USA, 2016. [Google Scholar]
- He, Y.; Burkhalter, D.; Durocher, D.; Gilbert, J.M. Solid-lattice hip prosthesis design: Applying topology and lattice optimization to reduce stress shielding from hip implants. In Proceedings of the Frontiers in Biomedical Devices, 2018 Design of Medical Devices Conference, Minneapolis, MN, USA, 9–12 April 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 40789, p. V001T03A001. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Abu Al-Rub, R.K. MSLattice: A free software for generating uniform and graded lattices based on triply periodic minimal surfaces. Mater. Des. Process. Commun. 2021, 3, e205. [Google Scholar] [CrossRef]
- Maskery, I.; Parry, L.A.; Padrão, D.; Hague, R.J.M.; Ashcroft, I.A. FLatt Pack: A research-focussed lattice design program. Addit. Manuf. 2022, 49, 102510. [Google Scholar] [CrossRef]
- Li, Q.; Hong, Q.; Qi, Q.; Ma, X.; Han, X.; Tian, J. Towards additive manufacturing oriented geometric modeling using implicit functions. Vis. Comput. Ind. Biomed. Art 2018, 1, 9. [Google Scholar] [CrossRef]
- Tang, Y.; Dong, G.; Zhao, Y.F. A hybrid geometric modeling method for lattice structures fabricated by additive manufacturing. Int. J. Adv. Manuf. Technol. 2019, 102, 4011–4030. [Google Scholar] [CrossRef]
- Lei, H.Y.; Li, J.R.; Xu, Z.J.; Wang, Q.H. Parametric design of Voronoi-based lattice porous structures. Mater. Des. 2020, 191, 108607. [Google Scholar] [CrossRef]
- Bici, M.; Campana, F.; De Michelis, M. Mesoscale geometric modeling of cellular materials for finite element analysis. Comput.-Aided Des. Appl. 2017, 14, 760–769. [Google Scholar] [CrossRef]
- Dal Fabbro, P.; Rosso, S.; Ceruti, A.; Boscolo Bozza, D.; Meneghello, R.; Concheri, G.; Savio, G. Analysis of a Preliminary Design Approach for Conformal Lattice Structures. Appl. Sci. 2021, 11, 11449. [Google Scholar] [CrossRef]



| Sectors | Unit Cell/Replication Pattern | Applications | References |
|---|---|---|---|
| Aerospace Engineering |
|
| [18,70,71,72,73,74,75,76] |
| Biomedical Engineering |
|
| [77,78,79,80,81,82,83,84,85,86] |
| Mechanical Engineering: Automotive |
|
| [87,88,89,90,91,92] |
| Mechanical Engineering: Defense |
|
| [93,94,95] |
| Mechanical Engineering: Heat Exchanger |
|
| [96,97] |
| Mechanical Engineering |
|
| [98,99,100,101,102,103] |
| Product Design: Sports |
|
| [104,105,106] |
| Civil Engineering: Building Construction |
|
| [107,108,109] |
| Manufacturing Method | Base Material | Issues | References |
|---|---|---|---|
| Direct Foaming |
|
| [110,111] |
| Investment Casting |
|
| [112,113,114] |
| Stamping Forming |
|
| [115,116] |
| Interlocking Grid Assembly |
|
| [117,118,119] |
| Extrusion Wire Cutting |
|
| [120] |
| Lap Assembly |
|
| [115] |
| Wire-Woven Method |
|
| [121,122,123] |
| AM Method | Base Material | Issues | References |
|---|---|---|---|
| Binder jetting (BJ) |
|
| [124,125,126] |
| Cold Spray Additive Manufacturing (CSAM) |
|
| [127,128,129] |
| Direct Energy Deposition (DED) |
|
| [130,131,132] |
| Direct Ink Writing (DIW) |
|
| [133,134,135] |
| Fused Deposition Modeling (FDM) |
|
| [136,137,138] |
| Liquid Metal Additive Manufacturing |
|
| [139,140,141] |
| Laminated Object Manufacturing (LOM) |
|
| [142,143,144] |
| Powder Bed Fusion (PBF) |
|
| [145,146,147] |
| Design Tools | Software | Lattice Type | References |
|---|---|---|---|
| CAD Software/ Numerical Solvers |
|
| [152,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172] |
| Special Tools |
|
| [173,174] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, A.; Belluomo, L.; Bici, M.; Campana, F. Bird’s Eye View on Lattice Structures: Design Issues and Applications for Best Practices in Mechanical Design. Metals 2023, 13, 1666. https://doi.org/10.3390/met13101666
Ahmad A, Belluomo L, Bici M, Campana F. Bird’s Eye View on Lattice Structures: Design Issues and Applications for Best Practices in Mechanical Design. Metals. 2023; 13(10):1666. https://doi.org/10.3390/met13101666
Chicago/Turabian StyleAhmad, Abas, Luca Belluomo, Michele Bici, and Francesca Campana. 2023. "Bird’s Eye View on Lattice Structures: Design Issues and Applications for Best Practices in Mechanical Design" Metals 13, no. 10: 1666. https://doi.org/10.3390/met13101666
APA StyleAhmad, A., Belluomo, L., Bici, M., & Campana, F. (2023). Bird’s Eye View on Lattice Structures: Design Issues and Applications for Best Practices in Mechanical Design. Metals, 13(10), 1666. https://doi.org/10.3390/met13101666








