Inverse Identification of Drucker–Prager Cap Model for Ti-6Al-4V Powder Compaction Considering the Shear Stress State
Abstract
:1. Introduction
2. Experiment and Simulation of Hemispherical Punch Compaction
2.1. Material and Experiment
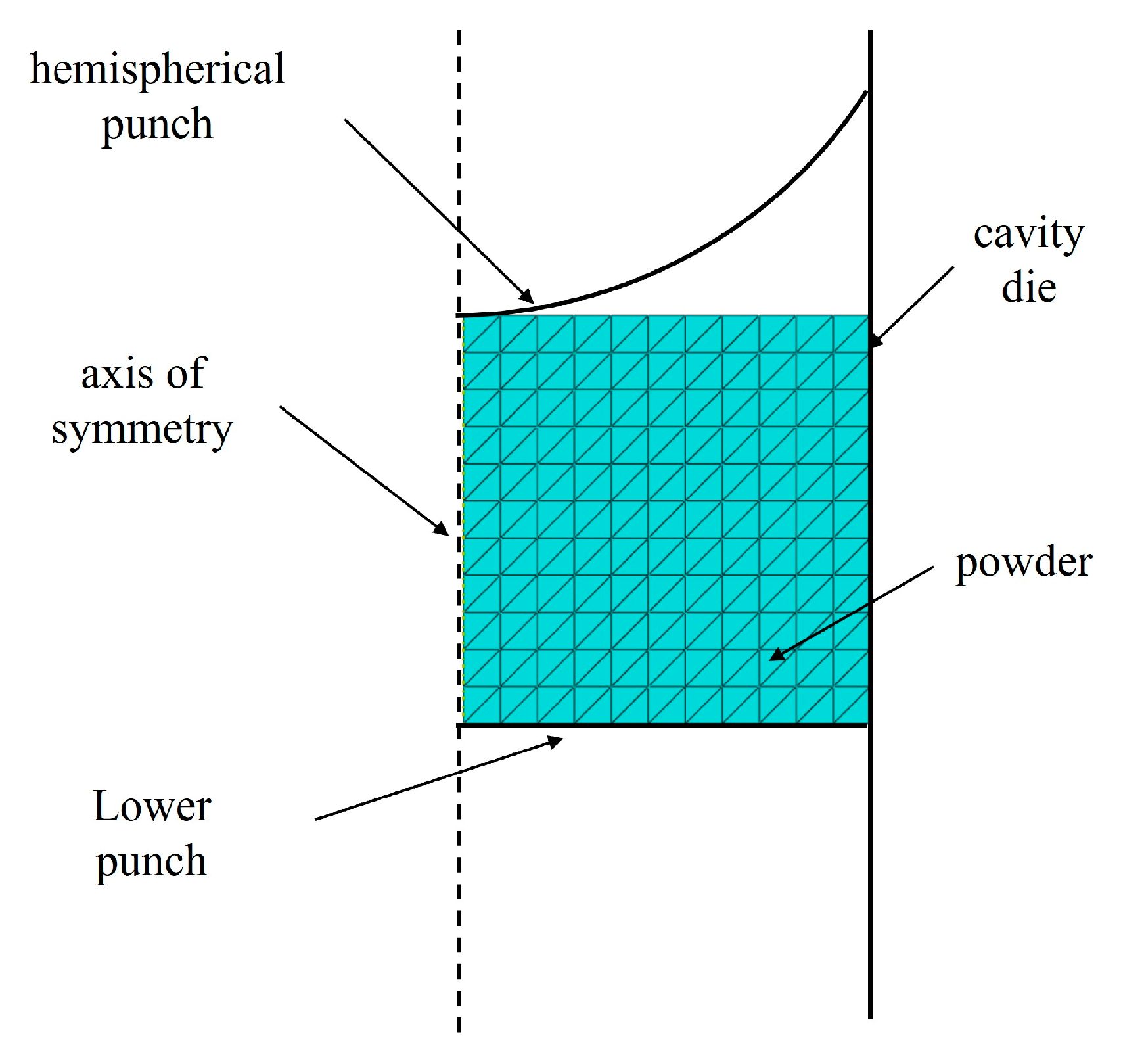
2.2. Numerical Simulation
3. Parameter Identification of the Drucker–Prager Cap Model
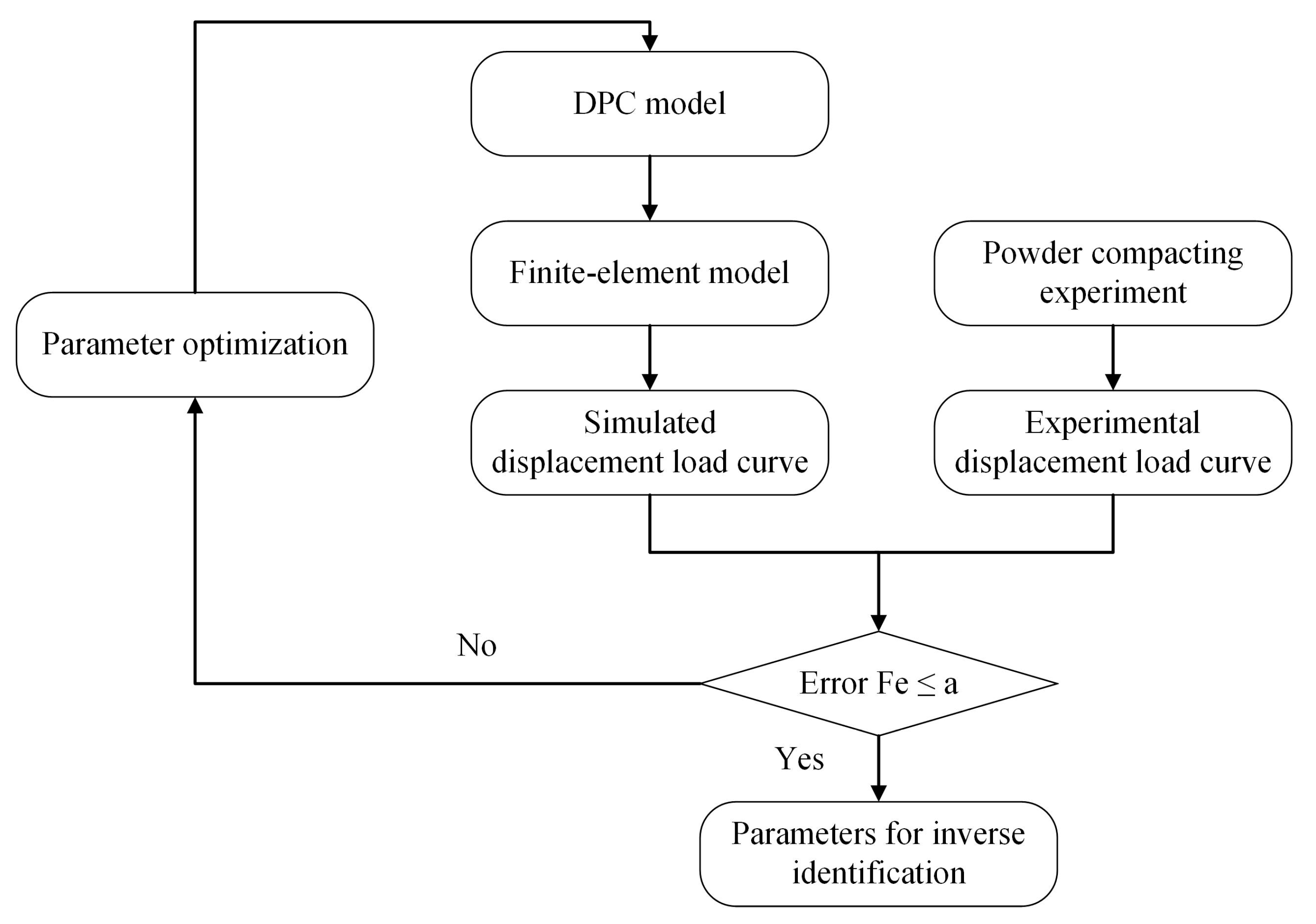
3.1. Inverse Identification
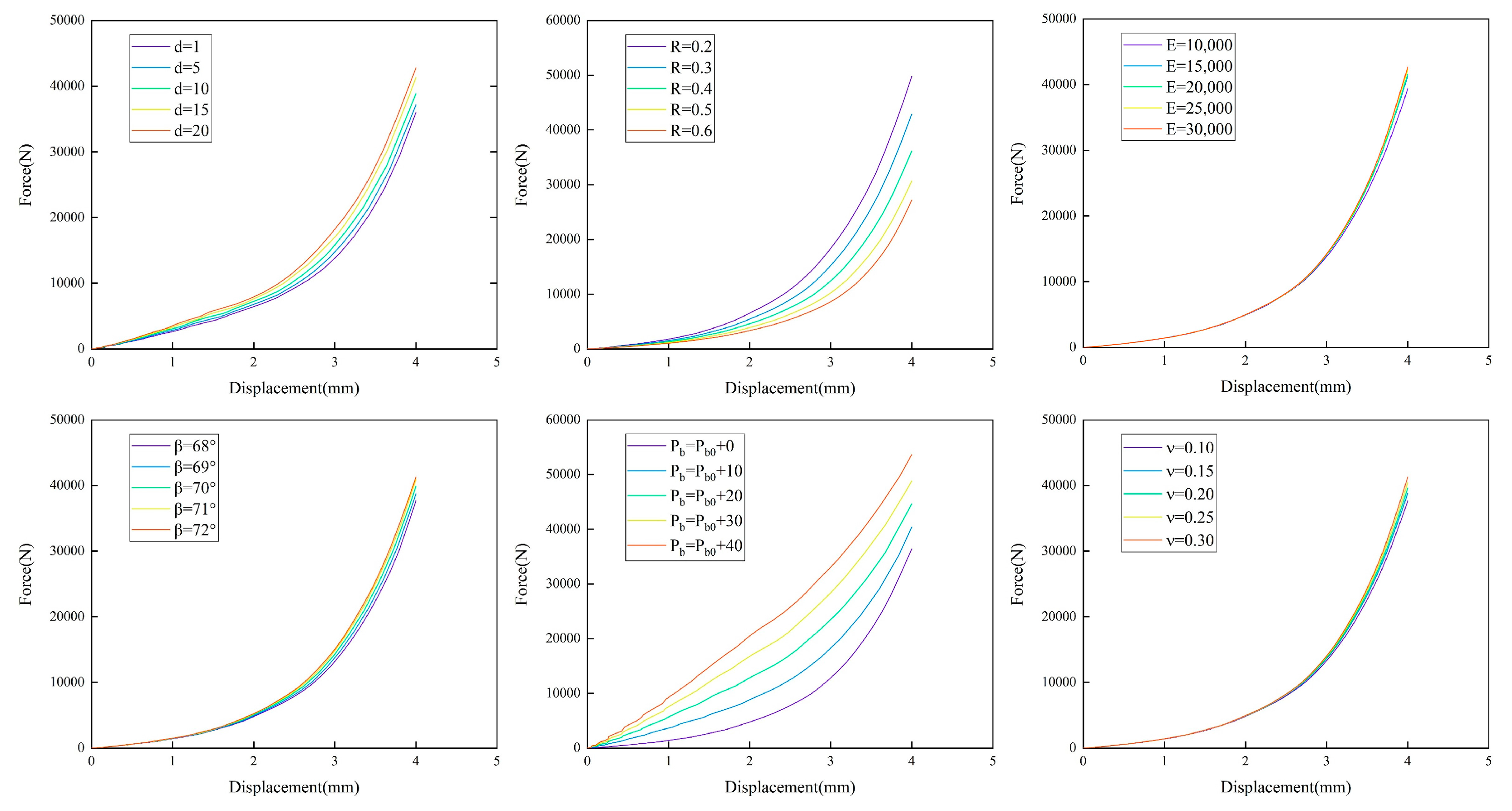
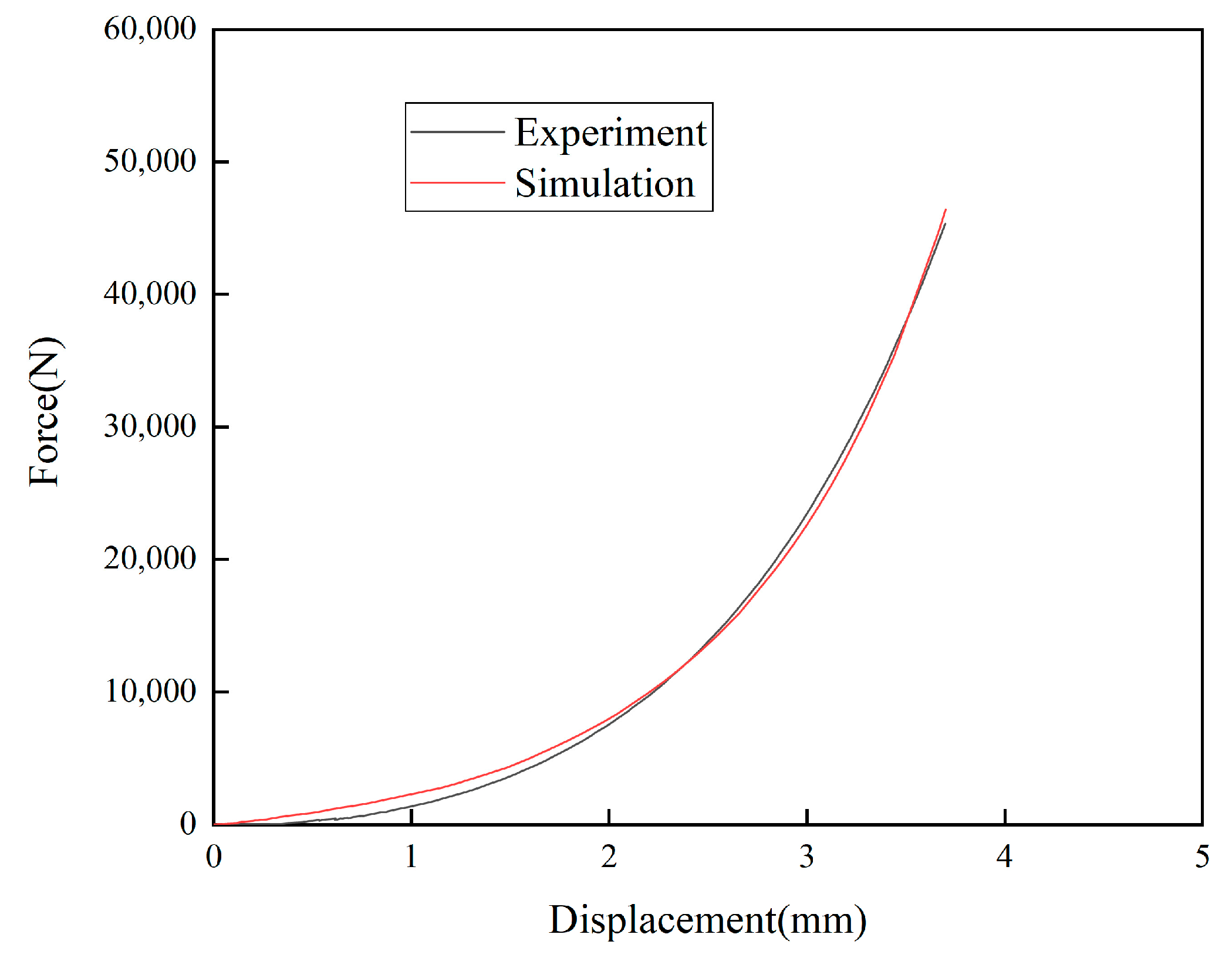
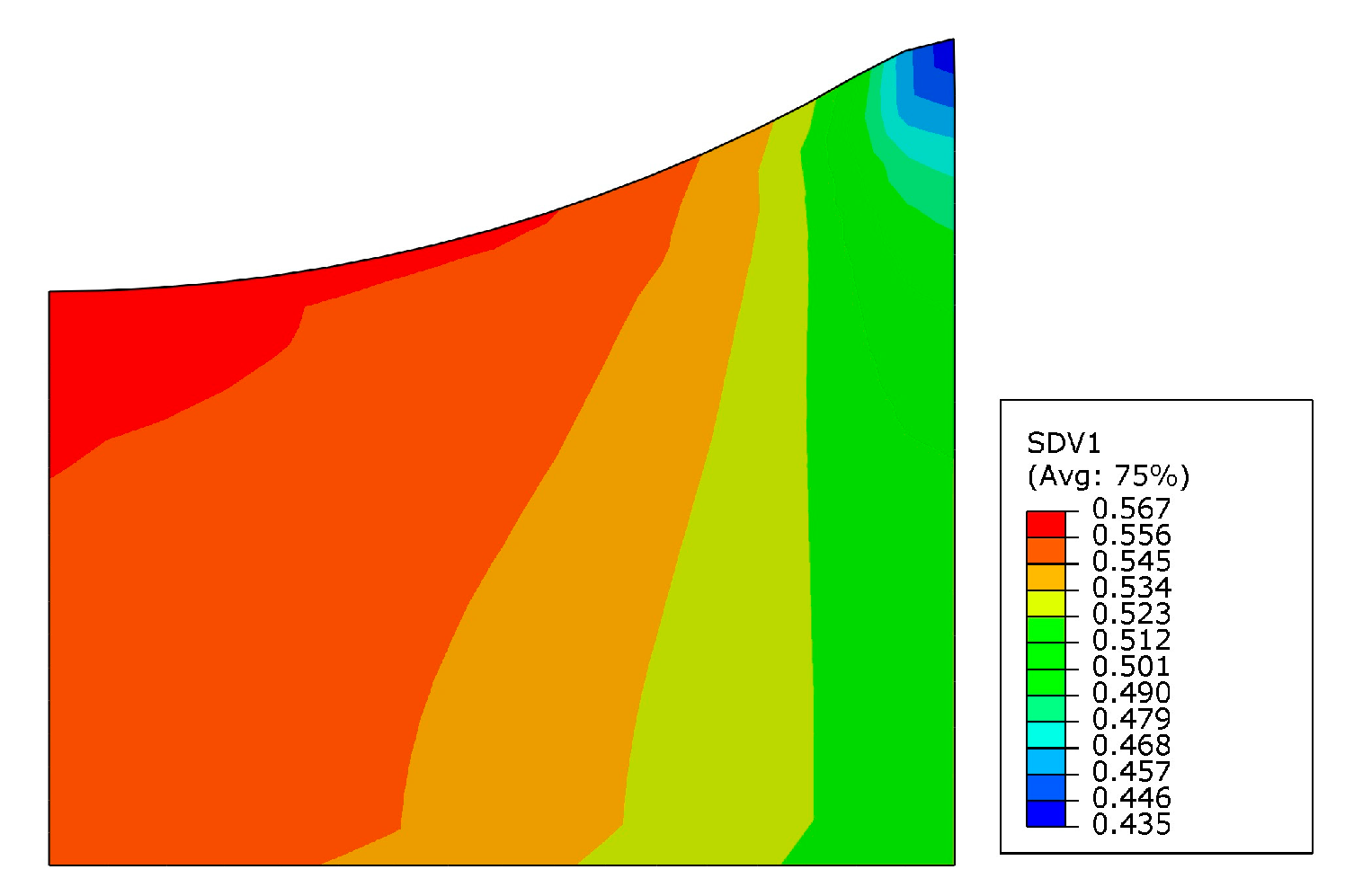
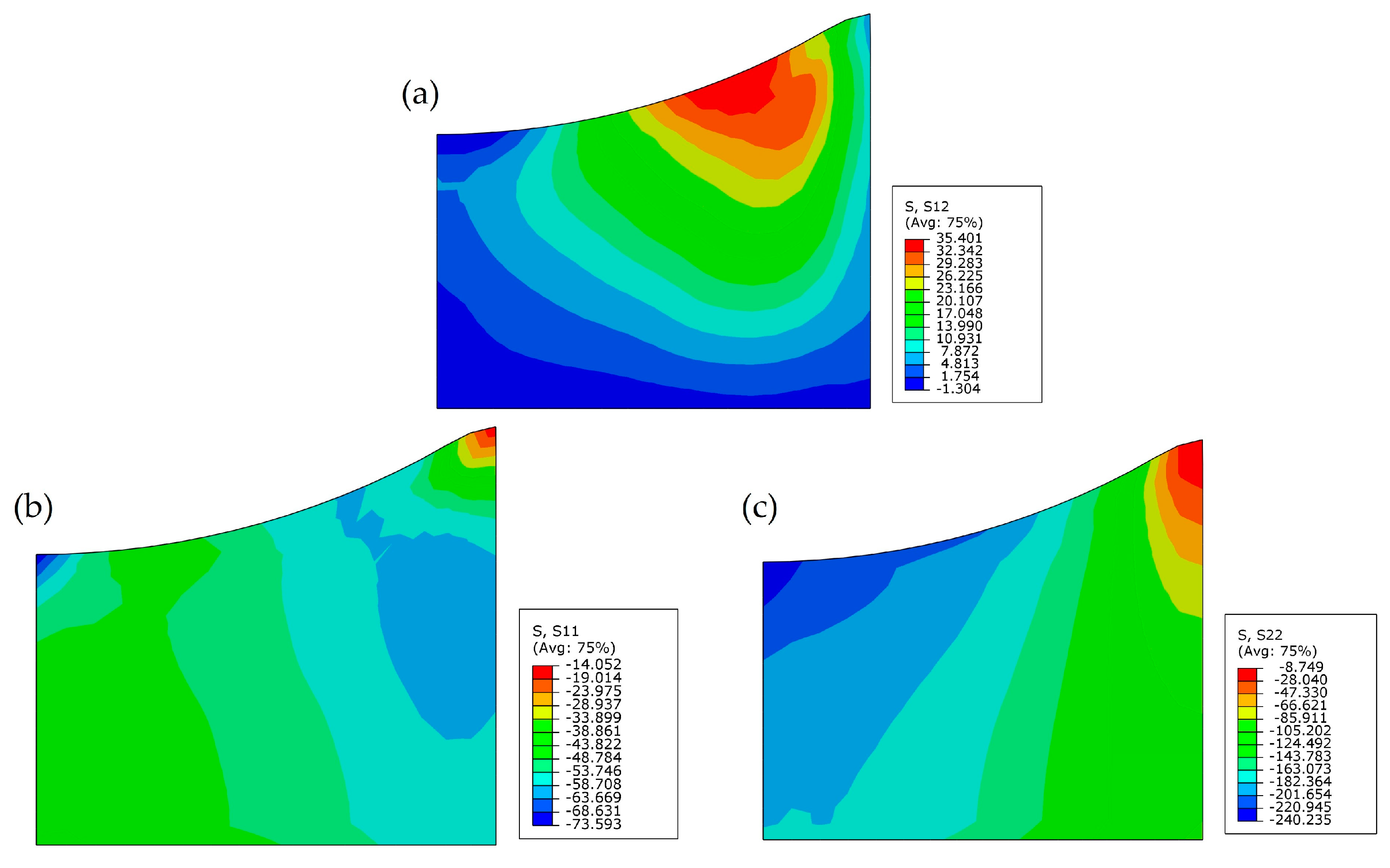
3.2. Numerical Results
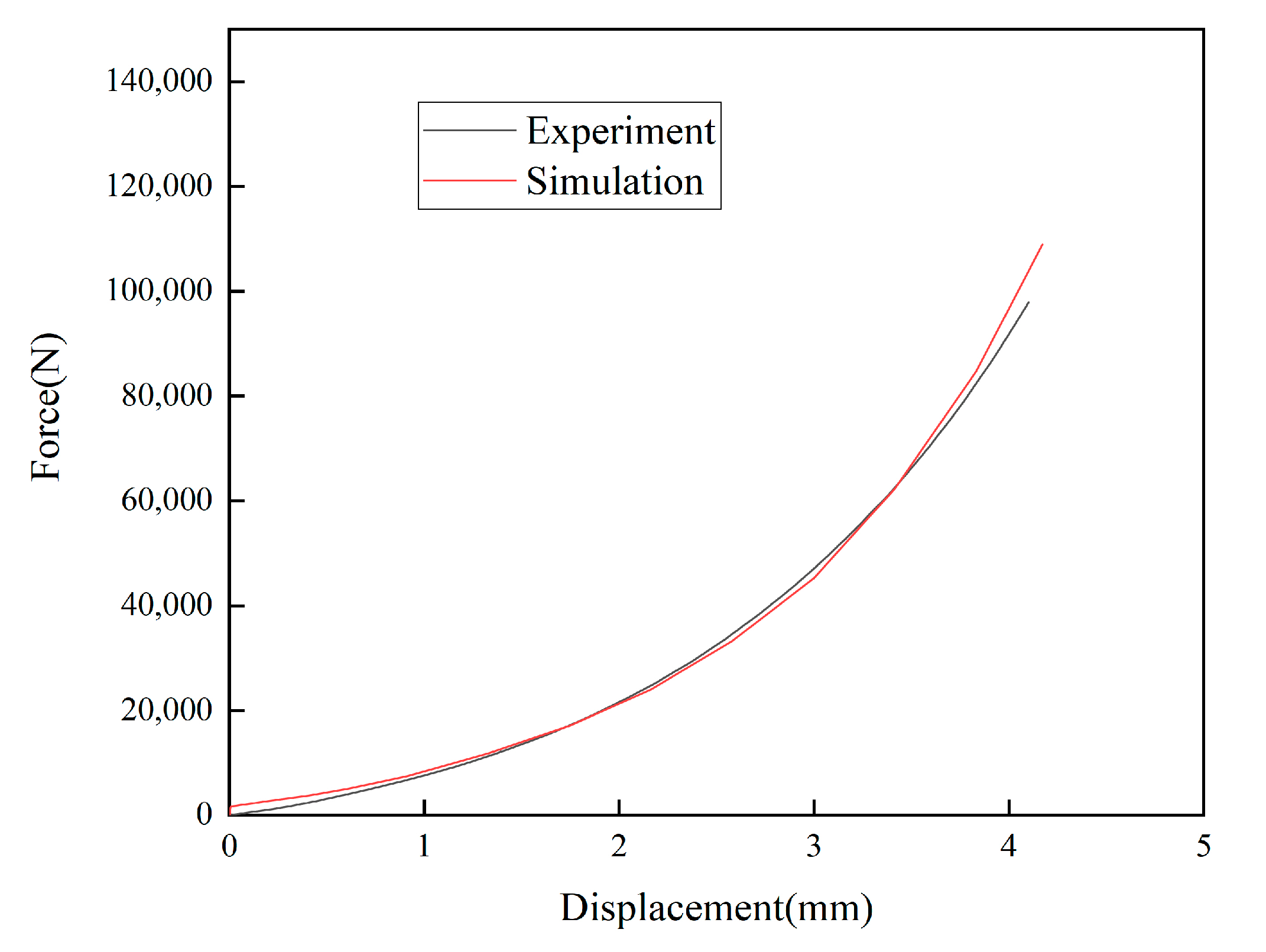
4. Experimental Validation by Flat-Punch Compaction
5. Conclusions
- (1)
- This paper proposed an inverse identification approach to quickly and efficiently determine the parameters of the Drucker–Prager cap constitutive model. The approach simply combines the displacement–load curve of the compacting experimental process, establishes the goal error function, and uses the simplex algorithm to compute. It is more convenient. At the same time, because the traditional parameter inverse identification makes it difficult to identify the shear surface parameters, the shape of the upper punch is creatively changed to a hemispherical punch. The parameters of the constitutive model are identified using the displacement–load curves obtained for powder compaction by a hemispherical punch. It makes the parameters obtained more comprehensive;
- (2)
- The parameters of the Drucker–Prager cap constitutive model for the Ti-6Al-4V powder material were identified inversely. The displacement–load curves obtained after the inverse identification were compared with the experimentally obtained displacement–load curves. It was found that the two curves were in good agreement. The error function value is 6.704%. At the same time, the relative density distributions were checked. It was found that the relative density distributions obtained from the parameter inverse identification were also more consistent with the actual situation. The feasibility and validity of this inverse identification process were further verified;
- (3)
- For the advanced powder metallurgy processes, such as hot pressing, hot isotropic pressing, spark plasma sintering, and so on, it is difficult to adopt the conventional semianalytical method for parameter identification of the material model. Therefore, the inverse identification methodology with a hemispherical punch shows great potential for numerical modeling.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yamanoglu, R.; Bahador, A.; Kondoh, K. Effect of Mo Addition on the Mechanical and Wear Behavior of Plasma Rotating Electrode Process Atomized Ti6Al4V Alloy. J. Mater. Eng. Perform. 2021, 30, 3203–3212. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, J.; Shi, Y.; Tang, J.; Huang, D.; Yan, M.; Dargusch, M.S. Surface modification of biomedical Ti and Ti alloys: A review on current advances. Materials 2022, 15, 1749. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Song, K.; Yu, X. A review on wire and arc additive manufacturing of titanium alloy. J. Manuf. Process. 2021, 70, 24–45. [Google Scholar] [CrossRef]
- Straumal, B.B.; Korneva, A.; Kuzmin, A.; Lopez, G.A.; Rabkin, E.; Straumal, A.B.; Gerstein, G.; Gornakova, A.S. The grain boundary wetting phenomena in the ti-containing high-entropy alloys: A review. Metals 2021, 11, 1881. [Google Scholar] [CrossRef]
- Kaushik, H.C.; Korayem, M.H.; Shaha, S.K.; Kacher, J.; Hadadzadeh, A. Achieving strength-ductility synergy in a laser-powder bed fused near-α titanium alloy through well-crafted heat treatments. J. Alloys Compd. 2023, 968, 171913. [Google Scholar] [CrossRef]
- Mukhopadhyay, M.; Kundu, P.K. Finding optimum cutting conditions for augmented grindability of Ti-6Al-4V. Mater. Manuf. Process. 2023, 38, 1561–1571. [Google Scholar] [CrossRef]
- Wu, S.; Zhou, C.; Shi, Y.; Hu, A.; Xiao, X. Plasticity, ductile fracture and ballistic impact behavior of Ti-6Al-4V Alloy. Int. J. Impact Eng. 2023, 174, 104493. [Google Scholar] [CrossRef]
- Gaillard, Q.; Boulnat, X.; Cazottes, S.; Dancette, S.; Desrayaud, C. Strength/ductility trade-off of Laser Powder Bed Fusion Ti-6Al-4V: Synergetic effect of alpha-case formation and microstructure evolution upon heat treatments. Addit. Manuf. 2023, 76, 103772. [Google Scholar] [CrossRef]
- Paul, M.; Alshammari, Y.; Yang, F.; Bolzoni, L. New ternary powder metallurgy Ti alloys via eutectoid and isomorphous beta stabilisers additions. Sci. Rep. 2023, 13, 1150. [Google Scholar] [CrossRef]
- Zyguła, K.; Wojtaszek, M. Processing and Characterization of β Titanium Alloy Composite Using Power Metallurgy Approach. Materials 2022, 15, 5800. [Google Scholar] [CrossRef]
- Attia, U.M. Cold-isostatic pressing of metal powders: A review of the technology and recent developments. Crit. Rev. Solid State Mater. Sci. 2021, 46, 587–610. [Google Scholar] [CrossRef]
- Yuan, W.; Yung, W.P.; Ju, H.Y.; Hung, Y.K.; Kuei, C.S.; Yi, C.C. Laser Doppler in Green Compact Density Inspection of Powder Metallurgy. Key Eng. Mater. 2023, 963, 215–222. [Google Scholar] [CrossRef]
- Zvinavashe, K.C.; Chikosha, S.; Madyira, D.M.; Maumela, M. The Effect of Cold Rolling Parameters on the Densification of Titanium Sintered Strips. Key Eng. Mater. 2022, 938, 31–39. [Google Scholar] [CrossRef]
- Sumalatha, C.; Rao, P.C.S.; Rao, V.S.; Deepak, M.S.K. Effect of grain refiner, modifier and graphene on the mechanical properties of hyper eutectic Al-Si alloys by experimental and numerical investigation. Mater. Today Proc. 2022, 62, 3891–3900. [Google Scholar] [CrossRef]
- Diarra, H.; Mazel, V.; Busignies, V.; Tchoreloff, P. Comparative study between Drucker-Prager/Cap and modified Cam-Clay models for the numerical simulation of die compaction of pharmaceutical powders. Powder Technol. 2017, 320, 530–539. [Google Scholar] [CrossRef]
- Audry, N.; Harthong, B.; Imbault, D. Comparison between periodic and non-periodic boundary conditions in the multi-particle finite element modelling of ductile powders. Powder Technol. 2023, 429, 118871. [Google Scholar] [CrossRef]
- Giannis, K.; Schilde, C.; Finke, J.H.; Kwade, A. Modeling of high-density compaction of pharmaceutical tablets using multi-contact discrete element method. Pharmaceutics 2021, 13, 2194. [Google Scholar] [CrossRef]
- Seyyedan, S.M.; Mirghasemi, A.A.; Mohammadi, S. Numerical simulation of direct shear test on granular materials composed of breakable angular particles: A DEM-XFEM approach. Powder Technol. 2021, 391, 450–466. [Google Scholar] [CrossRef]
- Zhang, C.; Jia, L.; Xie, H.; Niu, R.; Lu, Z.; Kondoh, K. Simulation on the Direct Powder Rolling Process of Cu Powder by Drucker–Prager/Cap Model and Its Experimental Verification. Metals 2022, 12, 1145. [Google Scholar] [CrossRef]
- Aruffo, G.A.; Michrafy, M.; Oulahna, D.; Michrafy, A. Modelling powder compaction with consideration of a deep grooved punch. Powder Technol. 2022, 395, 681–694. [Google Scholar] [CrossRef]
- Drucker, D.C.; Gibson, R.E.; Henkel, D.J. Soil mechanics and work-hardening theories of plasticity. Trans. Am. Soc. Civ. Eng. 1957, 122, 338–346. [Google Scholar] [CrossRef]
- Berezin, I.; Nesterenko, A.; Zalazinskii, A.; Kovacs, G. Influence of stress state conditions on densification behavior of titanium sponge. Acta Polytech. Hung. 2017, 14, 153–168. [Google Scholar] [CrossRef]
- Zhou, M.; Huang, S.; Hu, J.; Lei, Y.; Xiao, Y.; Li, B.; Yan, S.; Zou, F. A density-dependent modified Drucker-Prager Cap model for die compaction of Ag57. 6-Cu22. 4-Sn10-In10 mixed metal powders. Powder Technol. 2017, 305, 183–196. [Google Scholar] [CrossRef]
- Sinka, I.C.; Cunningham, J.C.; Zavaliangos, A. The effect of wall friction in the compaction of pharmaceutical tablets with curved faces: A validation study of the Drucker–Prager Cap model. Powder Technol. 2003, 133, 33–43. [Google Scholar] [CrossRef]
- Melo, C.C.; Moraes, A.L.I.; Rocco, F.O.; Montilha, F.S.; Canto, R.B. A validation procedure for numerical models of ceramic powder pressing. J. Eur. Ceram. Soc. 2018, 38, 2928–2936. [Google Scholar] [CrossRef]
- Staf, H.; Olsson, E.; Larsson, P.L. Mechanical characterization of powder materials: A general approach detailed for cemented carbides. Powder Technol. 2020, 364, 531–537. [Google Scholar] [CrossRef]
- Atrian, A.; Majzoobi, G.H.; Markert, B.; Nourbakhsh, S.H. A novel approach to calibrate the Drucker–Prager Cap model for Al7075 powder. Arch. Appl. Mech. 2018, 88, 1859–1876. [Google Scholar] [CrossRef]
- Morais, M.M.; de Melo, C.C.; Canto, R.B.; Fortulan, C.A. Calibration of powder constitutive model using digital image correlation validated for hollow hemisphere of lead zirconate titanate. Powder Technol. 2021, 392, 212–223. [Google Scholar] [CrossRef]
- Gan, Y.; Kamlah, M. Identification of material parameters of a thermo-mechanical model for pebble beds in fusion blankets. Fusion Eng. Des. 2007, 82, 189–206. [Google Scholar] [CrossRef]
- Diarra, H.; Mazel, V.; Busignies, V.; Tchoreloff, P. FEM simulation of the die compaction of pharmaceutical products: Influence of visco-elastic phenomena and comparison with experiments. Int. J. Pharm. 2013, 453, 389–394. [Google Scholar] [CrossRef]
- Sandler, I.S. Review of the development of cap models for geomaterials. Shock Vib. 2005, 12, 67–71. [Google Scholar] [CrossRef]
- Shang, C.; Sinka, I.C.; Pan, J. Constitutive model calibration for powder compaction using instrumented die testing. Exp. Mech. 2012, 52, 903–916. [Google Scholar] [CrossRef]
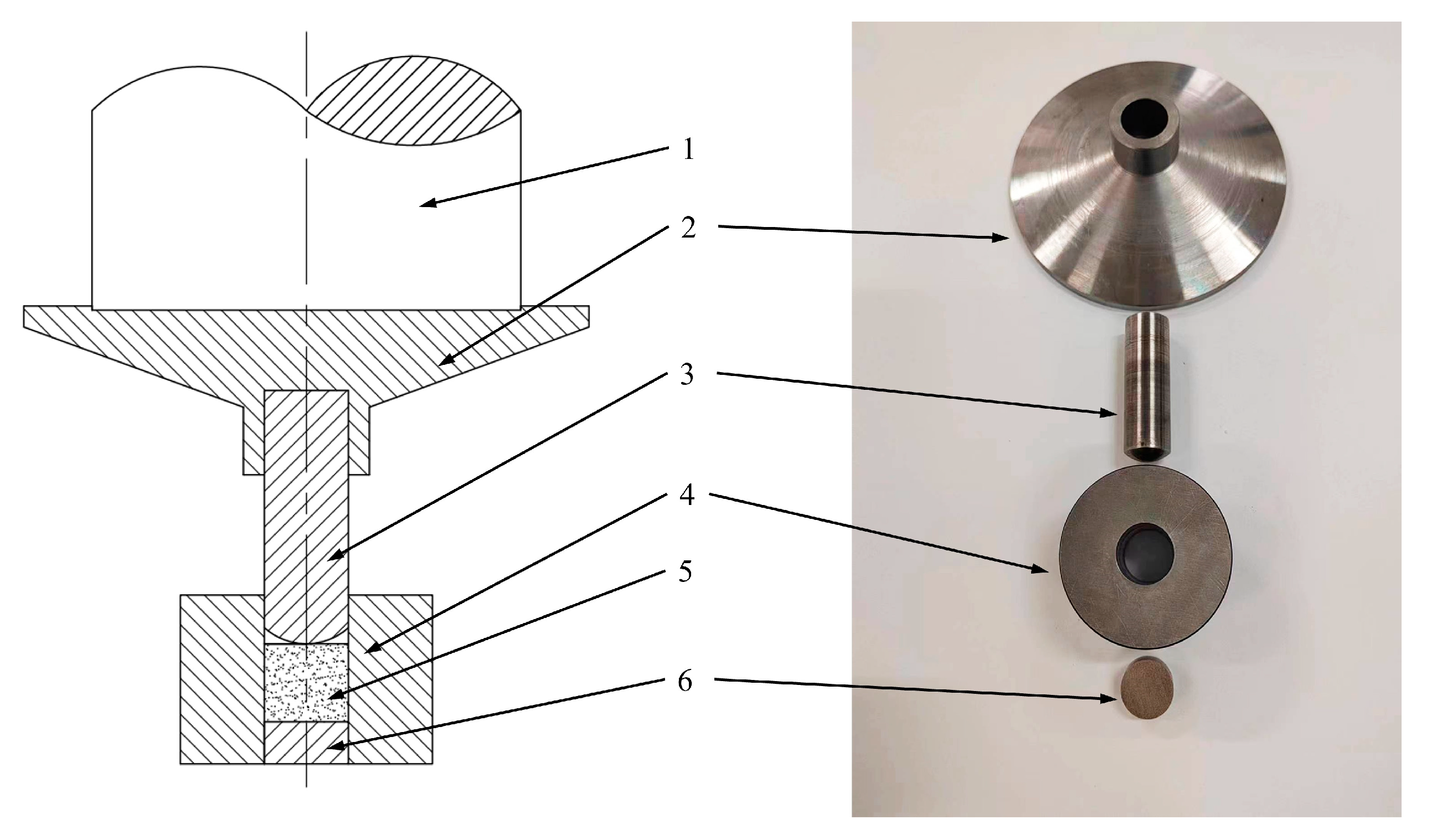



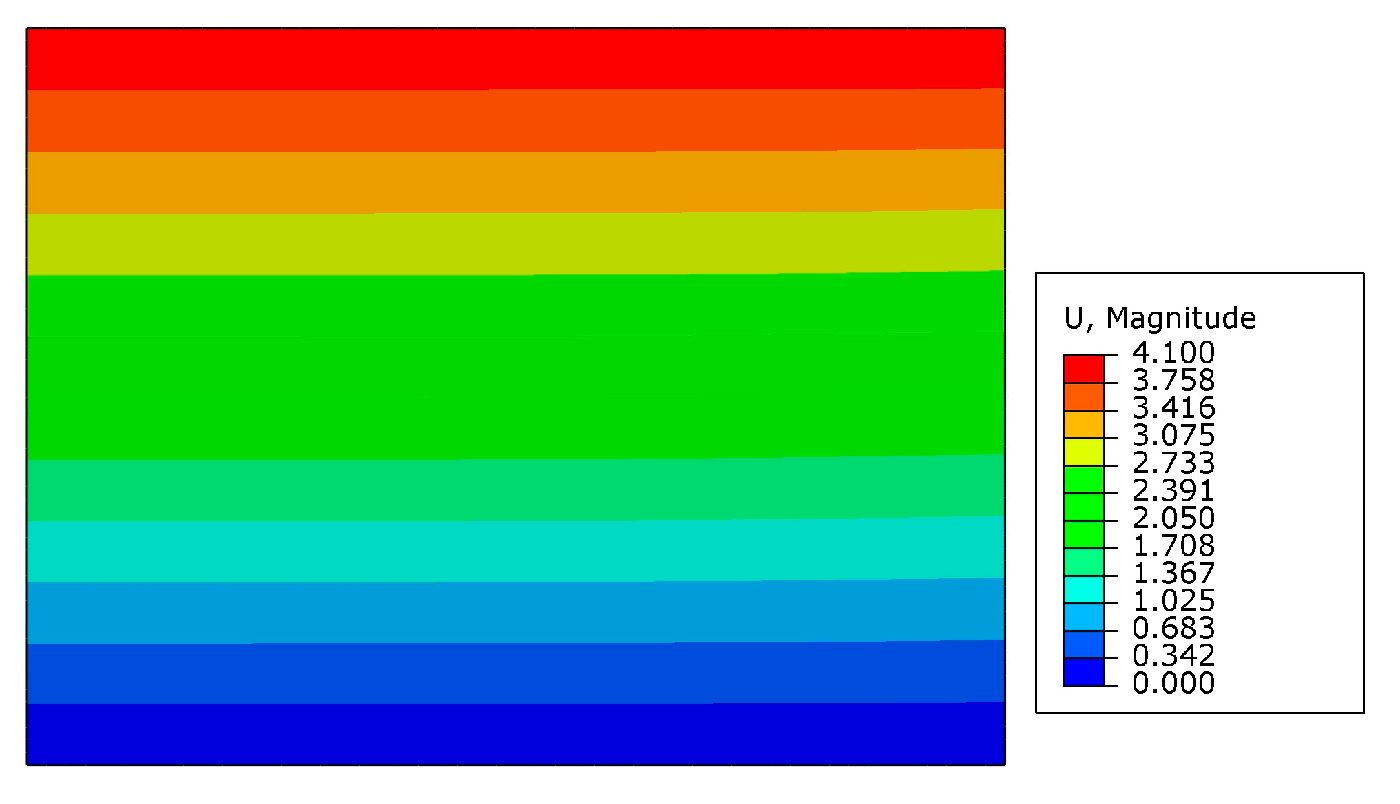
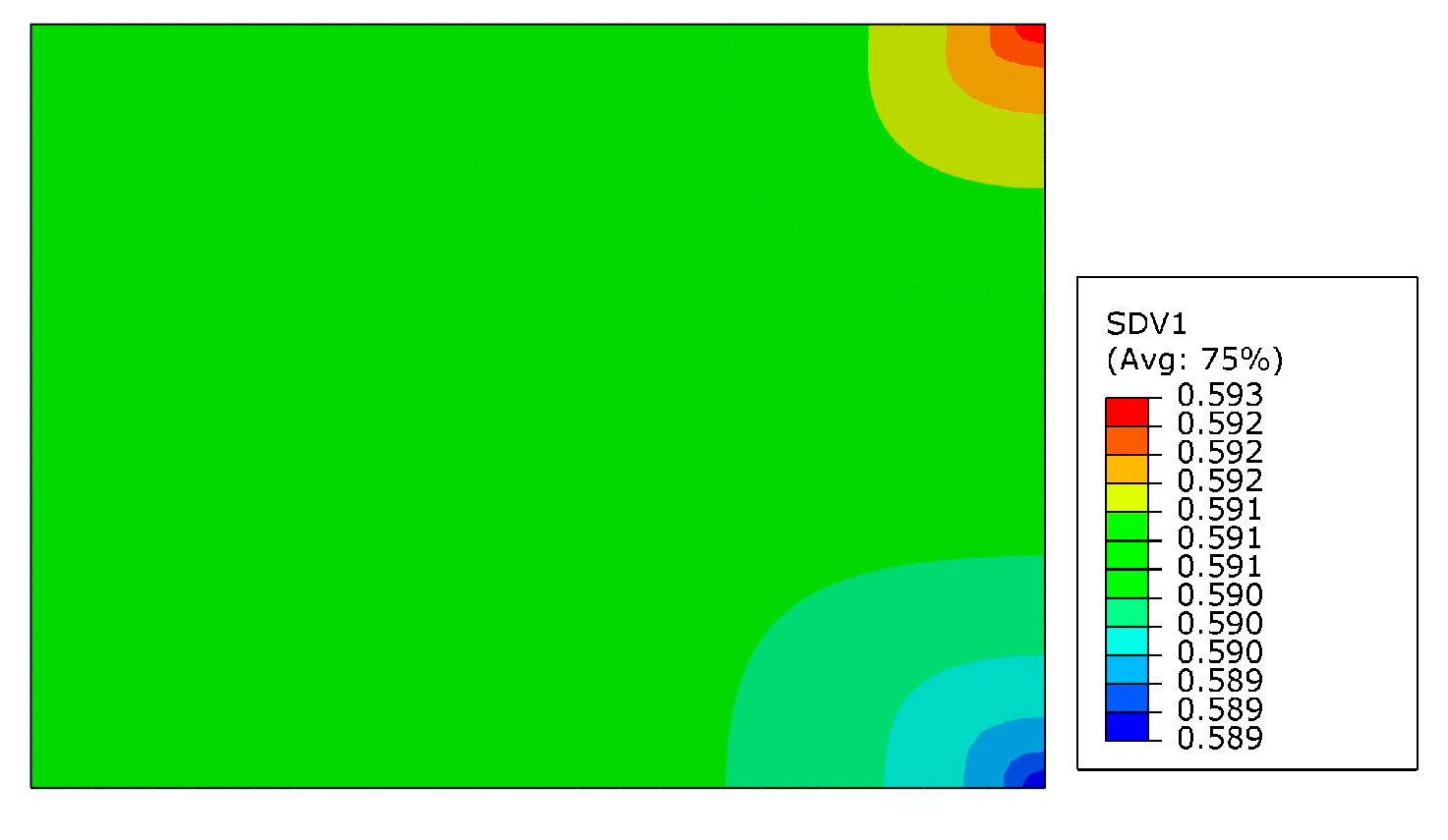
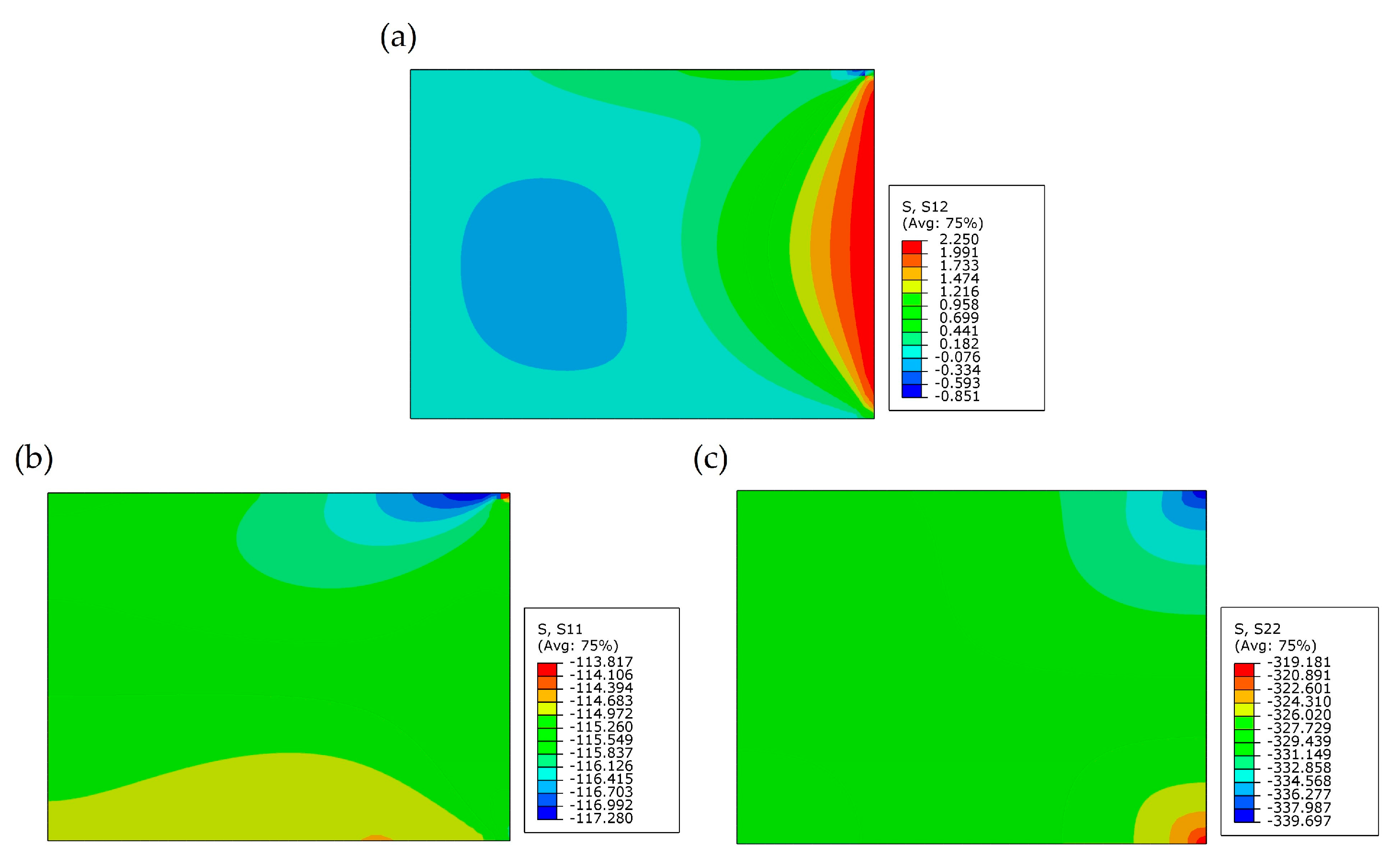
| Ti | Al | V | Fe | C | N | H | O |
|---|---|---|---|---|---|---|---|
| 89.611% | 6% | 3.9% | 0.05% | 0.02% | 0.18% | 0.039% | 0.20% |
| Model Parameter | Abstract Expression |
|---|---|
| d (material cohesion) | d = d1ed2ρ |
| β (angle of friction) | β = m1 + m2em3ρ |
| R (cap eccentricity) | R = r1 + er2ρ |
| Pb (material-hardening yield stress) | Pb = b1 + b2eb3ρ |
| E (modulus of elasticity) | E = e1 + e2ee3ρ |
| ν (Poisson’s ratio) | ν = ν1 + ν2eν3ρ |
| Input Variable | Lower Limit | Upper Limit | Reverse Identification Value |
|---|---|---|---|
| d1 | 5.0 × 10−5 | 1.0 × 10−4 | 7.8992 × 10−5 |
| d2 | 12 | 17 | 13.447 |
| m1 | 60 | 70 | 63.232 |
| m2 | 5.0 | 6.0 | 5.4107 |
| m3 | −0.3 | −0.1 | −0.11541 |
| r1 | 0.2 | 0.9 | 0.24013 |
| r2 | 0.9 | 1.3 | 1.1206 |
| b1 | −20 | −10 | −15.628 |
| b2 | 2.0 × 10−2 | 6.0 × 10−2 | 3.1592 × 10−2 |
| b3 | 16 | 20 | 16.689 |
| e1 | −3500 | −2500 | −2926.4 |
| e2 | 3000 | 4000 | 3874.4 |
| e3 | 2 | 4 | 2.2439 |
| v1 | −0.4 | −0.2 | −0.31622 |
| v2 | 0.4 | 0.8 | 0.51028 |
| v3 | 0.2 | 0.5 | 0.37028 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Liu, W.; Li, J.; Liu, J. Inverse Identification of Drucker–Prager Cap Model for Ti-6Al-4V Powder Compaction Considering the Shear Stress State. Metals 2023, 13, 1837. https://doi.org/10.3390/met13111837
Li R, Liu W, Li J, Liu J. Inverse Identification of Drucker–Prager Cap Model for Ti-6Al-4V Powder Compaction Considering the Shear Stress State. Metals. 2023; 13(11):1837. https://doi.org/10.3390/met13111837
Chicago/Turabian StyleLi, Runfeng, Wei Liu, Jiaqi Li, and Jili Liu. 2023. "Inverse Identification of Drucker–Prager Cap Model for Ti-6Al-4V Powder Compaction Considering the Shear Stress State" Metals 13, no. 11: 1837. https://doi.org/10.3390/met13111837






