Designing Quaternary and Quinary Refractory-Based High-Entropy Alloys: Statistical Analysis of Their Lattice Distortion, Mechanical, and Thermal Properties

Abstract

The rapid evolution in materials science has resulted in a significant interest in high-entropy alloys (HEAs) for their unique properties. This study focuses on understanding both quaternary and quinary body-centered cubic (BCC) of 12 refractory-based HEAs, and on analysis of their electronic structures, lattice distortions, mechanical, and thermal properties. A comprehensive assessment is undertaken by means of density functional theory (DFT)-based first principles calculations. It is well known that multiple constituents lead to notable lattice distortions, especially in quinary HEAs. This distortion, in turn, has significant implications on the electronic structure that ultimately affect mechanical and thermal behaviors of these alloys such as ductility, lattice thermal conductivity, and toughness. Our in-depth analysis of their electronic structures revealed the role of valence electron concentration and its correlation with bond order and mechanical properties. Local lattice distortion (LD) was investigated for these 12 HEA models. M1 (WTiVZrHf), M7 (TiZrHfW), and M12 (TiZrHfVNb) have the highest LD whereas the models M3 (MoTaTiV), M5 (WTaCrV), M6 (MoNbTaW), and M9 (NbTaTiV) have the less LD. Furthermore, we investigated the thermal properties focusing on Debye temperature (Θ_D), thermal conductivity (κ), Grüneisen parameter (γ_α), and dominant phonon wavelength (λ_dom). The NbTaTiV(M9) and TiVNbHf(M10) models have significantly reduced lattice thermal conductivities (κ_L). This reduction is due to the mass increase and strain fluctuations, which in turn signify lattice distortion. The findings not only provide an understanding of these promising materials but also offer guidance for the design of next-generation HEAs with properties tailored for potential specific applications.

1. Introduction

High-entropy alloys (HEAs) and high-entropy metal alloys (HEMAs) were explored for the first time in 2004 [1,2]. These materials have high configuration entropy (CE) gained by increasing the number of constituting elements (n) with n ≥ 5 [1]. Certain proportions of five or more principal elements (either equimolar or non-equimolar) are mixed to form a single-phase high-entropy alloy (HEA) solid solution. This solid solution is stabilized by a high CE of mixing [3]. The entropy of mixing (S) is expressed as: $S=-k_B\ln \omega =R\ln n$, where k_B is the Boltzmann constant, ω is the number of ways of mixing, R is the gas constant, and n is the number of elements within the HEA [4]. Materials are considered low-entropy when ΔS_mix is less than 0.69 R, medium-entropy when ΔS_mix is between 0.69 R and 1.59 R, and high-entropy when ΔS_mix is larger than 1.60 R [5]. HEAs come with very unique effects such as significant lattice distortion and the cocktail effect [6,7] which result in some unique properties such as high hardness, high resistance to corrosion, high thermoelectric (TE) performance [8,9], oxidation resistance [10], magnetic properties [11], and improved radiation performance [12,13,14,15]. The significant lattice distortion in HEAs results from the mismatch of mass, size, and bond state of different elements or ions in the structure of the HEA.

HEAs consisting of a high number of metallic elements (five or more) tend to form simple phases without complex intermetallic phases. In the early days of the HEAs, forming a single-phase solid solution was determined by empirical rules originating from Hume–Rothery rules. These rules rely on several factors, such as electronegativity, crystal structure of solutes, elemental atomic radii, and difference in valency [16]. Cantor et al. [2] found that forming a single-phase solid solution is controlled by CE. In Cantor’s work, the researchers equally distributed transitional metal elements of different lattices—Ni face-centered cubic (FCC), Fe body-centered cubic (BCC), Co hexagonal closed packed (HCP), Cr (BCC), and Mn (BCC)—in a single-phase solid solution. Other researchers [6,17] confirmed that forming a single-phase solid solution of FCC or BCC or HCP structures is controlled by a high CE. The microstructural properties of single-phase HEAs have been extensively studied to reach a clear understanding of these properties. A study [18] proposed that the phase of the solid solution could be determined by the following factors: mixing entropy, atomic sizes, and mixing enthalpy, which is given by $\mathsf{\Delta }{H}_{mix}=\sum _{i=1,i\ne j}^{n}4\mathsf{\Delta }{H}_{ij}^{mix}{c}_i{c}_j$, where $\mathsf{\Delta }{H}_{ij}^{mix}$, c denote the mixing enthalpy of a binary alloy consisting of the ith and jth elements and composition of the alloying element, respectively [19]. The valence electron count (VEC) could be the key factor to differentiate between the BCC and FCC phases in HEAs [20]. Another study showed that a FCC single phase of three (NiFeCo, NiCoCr, and NiCoMn), four (NiFeCoCr, NiFeCoMn, and NiCoCrMn), and five (NiFeCoCrMn and NiFeCoCrPd) alloys can be formed by adding the Pd element into Cantor alloys [21].

There has been extensive research on refractory-based HEAs in recent years. WTaMoNb and WTaMoNbV as refractory element-based alloys with single-phase BCC lattices were synthesized for the first time in 2010 by Senkov et al. [22]. Many experimental studies have been conducted since then, such as TiZrHfNbTa [23,24], NbZrTiCrMo_0.5Ta_0.5 [25], CrNbTiVZr [26,27], and TiZrNbMoV_x (x = 0–1.5) [28]. Ab initio molecular dynamics (AIMD) simulation was used to study the phase stability of HfNbTaTiZr HEA [29]. The ab initio method combined with virtual crystal approximation (VCA) was used to predict the tensile strength and shear strength of TiVNbMo HEA [30]. They found that alloying does not result in a remarkable change in tensile strength and shear strength of TiVNbMo. The microstructure and mechanical properties of TiZrHfNbV and TiZrHfNbCr HEAs were investigated using X-ray diffractometry and scanning electron microscopy (SEM) [31] The SEM study showed that strength and hardness were enhanced for these HEAs. The phase stability of MoNbTaW HEA was tested by using first principles calculations [32]. The distribution of interatomic distances and the lattice distortion (LD) in BCC MoNbTaVW HEA and its five sub-quaternary systems at different temperatures were studied by Toda et al. [33] Experimental (including X-ray diffraction and SEM) and computational study was carried out to investigate the microstructure and thermodynamic properties of BCC HfNbTaTiVZr HEA [34]. The effect of alloying on the elastic properties of ZrNbHf, ZrVTiNb, ZrVNbHf, and ZrVTiNbHf refractory-based HEAs was investigated via ab initio calculations by Li et al. [35]. A theoretical study was carried out to investigate the B2-ordering impacts on the thermodynamic properties of BCC NbMoTaW [36]. Elastic properties of TiZrVNb, TiZrNbMo, and TiZrVNbMo HEAs were investigated by using ab initio calculation combined with a special quasi-random structure (SQS) approach and coherent potential approximation (CPA) [37]. Hybrid Monte Carlo/molecular dynamics simulation was carried out to study the elastic properties and LD of NbTiVZr, CrMoNbV, HfNbTaZr, and MoNbTaW [38]. A theoretical study [39] showed that the effect of local lattice distortion is larger in refractory HEAs than in 3d transition metal HEAs. Another theoretical study [40] was carried out to investigate the elastic and thermal properties of single-phase ternary and quaternary Al-Ti-V-Cr-Nb-Mo refractory-based HEAs.

Thermoelectric (TE) devices can directly convert heat into electricity under a temperature gradient. One of the promising green solutions to mitigate the energy and environmental crisis is TE technology [41]. Figure of merit (ZT) determines the performance of TE devices. ZT is defined as ZT = S²σT/κ, where σ is the electrical conductivity, S is the Seebeck coefficient, T is the absolute temperature, and κ is the thermal conductivity. The considerable mass difference in HEAs causes chemical disorder, which results in significant phonon scattering and reduces κ. In addition, the distinct chemical environments in HEAs can produce force constant variations that modify the phonon spectral distribution, where the phonon dispersion can be expressed as [42]:

$$\omega =2\sqrt{\frac{F}{M}}\sin \left(\frac{\pi }{2}\frac{k}{k_c}\right)$$

(1)

where F, M, k, and k_c are the force constant, atomic mass, wave vector, and cut-off wave vector, respectively. The speed of phonons ($\omega$) can be changed by changes in these parameters. Large M and small F (weak chemical bonds) indicate low $\omega$ and low lattice thermal conductivity (κ_L). The variations in mass and force constant induce phonon-scattering processes, which are used to enhance the TE performance of HEAs. Thus, HEAs are good candidates for TE applications [43,44] and heat shield materials [45]. Studies on using chemical disorder to induce phonon scattering in HEAs are so far lacking. Some previous studies addressing phonon scattering in disordered alloys were limited to binaries [46,47,48,49,50,51]. The manipulation of mass and force constant in HEAs to induce phonon scattering and reduce κ_L is not yet fully explored.

Ab initio calculation is an effective tool that has been widely used in studying HEAs to understand and enrich their systems. Several random solid solution model (RSSM) approaches are used to simulate the solid solution phases [52], such as special quasi-random structure (SQS) [53], supercell (SC) method [54], coherent potential approximation (CPA) [55], and virtual crystal approximation (VCA) [56]. HEAs have very high chemical disorder, which requires using large supercells when using the SC method.

In most cases of HEAs, the theory of formation of HEAs is related to understanding the nature of metallic bonding. The metallic bonding nature of HEAs has not yet been fully investigated. Unlike covalent and ionic bonding, where the bond length (BL) can be explicitly defined as the separation distance between two atoms forming the bond, metallic bonding involves multiple atoms [57].

It is well known that for metallic glasses (MGs), all atoms with a certain distance of separation contribute to metallic bonding, which makes the expression of BL ambiguous. Consequently, multiple pairs of atoms may share the same separation distance for a specific bond strength or bond order (BO), and vice versa. However, our concept of total bond order density (TBOD) [58], a quantum mechanical metric, which takes into account the entire BO of the system, can avoid the usage of a pure geometric parameter describing the structure of HEAs.

In this work, we extensively study the effect of composition on the electronic structure, interatomic bonding, lattice distortion, micro-mechanical, and thermal properties of 12 BCC refractory-based HEAs, listed in

Table 1. The optimized structure parameters along with first and second nearest neighbors of the 12 BCC HEA models.

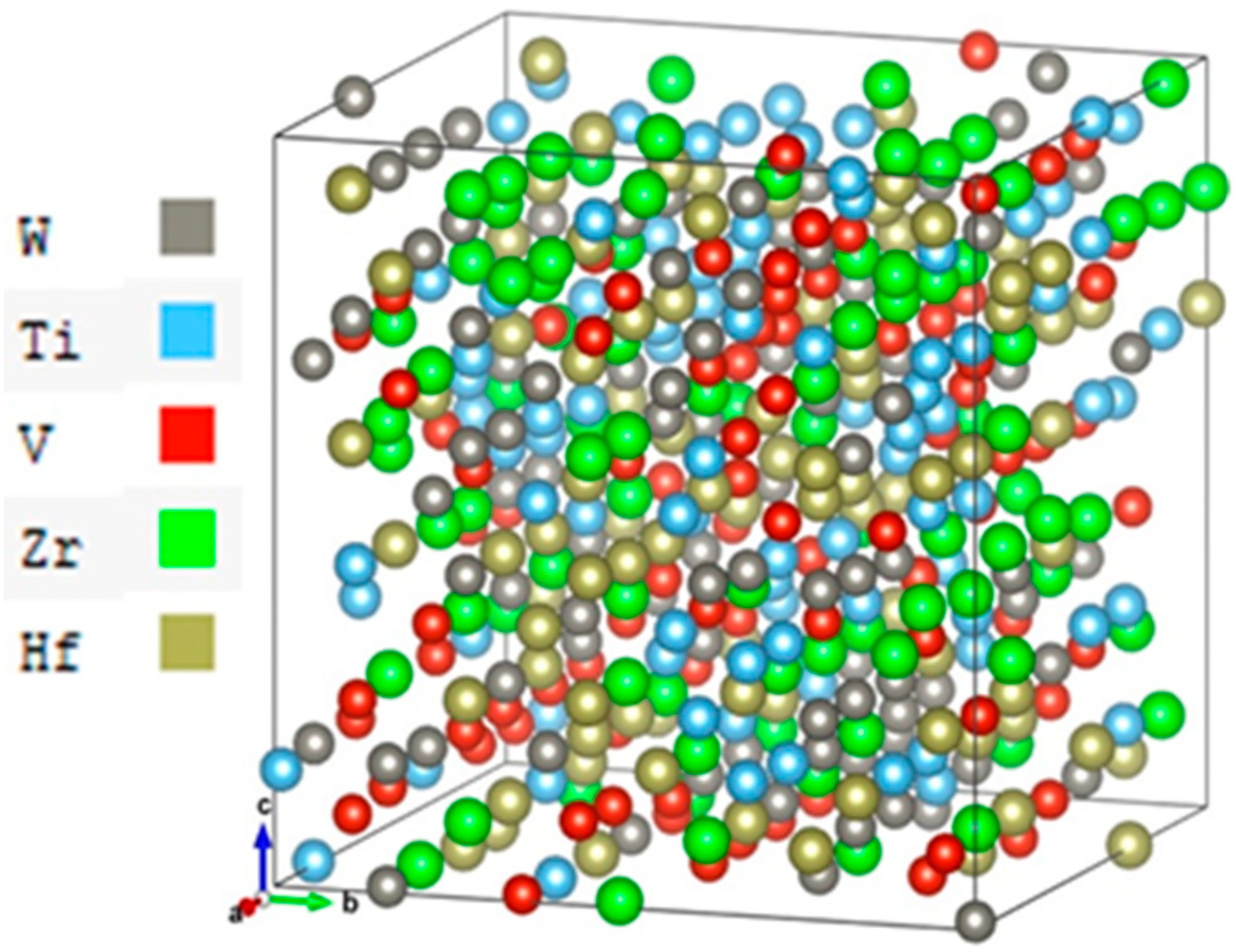
Models		a(Å)	b(Å)	c(Å)	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\gamma }$	Vol (Å3)	NN (Å)	SNN (Å)
M1	WTiVZrHf 1	19.871	19.915	19.794	90.327	90.329	89.885	7832.808	2.867	3.310
M2	HfMoTiWZr 1	19.91	19.987	19.889	90.174	90.232	89.945	7914.625	2.876	3.321
M3	MoTaTiV 2	19.015	19.015	18.988	89.928	90.14	90.056	6865.245	2.743	3.168
M4	MoTaTiVZr 1	19.589	19.507	19.487	90.164	90.355	89.943	7446.129	2.819	3.255
M5	WTaCrV 2	18.53	18.542	18.543	89.74	89.823	89.903	6370.888	2.676	3.09
M6	MoNbTaW 2	19.387	19.388	19.388	89.997	90.065	89.901	7287.275	2.742	3.878
M7	TiZrHfW 2	20.252	20.338	20.269	90.129	90.067	90.175	8348.226	2.928	3.381
M8	TiZrNbMoTa 1	19.844	19.857	19.875	89.903	89.918	90.103	7831.877	2.866	3.31
M9	NbTaTiV 2	19.288	19.325	19.290	90.060	90.058	90.16	7189.958	2.786	3.217
M10	TiVNbHf 2	19.711	19.72	19.628	89.843	89.583	90.268	7628.582	2.841	3.281
M11	Ti0.38V0.15Nb0.23Hf0.24 2	19.821	19.788	19.792	90.06	89.941	90.29	7762.676	2.858	3.300
M12	TiZrHfVNb 1	20.136	20.113	20.014	89.94	90.011	89.869	8105.873	2.899	3.348

¹ 5-component model; ² 4-component model. NN and SNN stand for average distances of nearest neighbors (NN) and second nearest neighbors (SNN).

with more information about their lattice parameters and their components. These 12 models mainly consist of refractory elements (Zr, Nb, Mo, Hf, Ta, W) with three 3d transition metals (Ti, V, Cr). Two DFT-based packages are used to perform the calculations. Due to the larger number of components and chemical disorder of the present refractory based HEAs, the supercell approach to model these systems becomes a very cumbersome but very efficient method. These 12 models are single-phase BCC supercells of 500 atoms each. The solvent and solute of these HEAs are indistinguishable, setting them apart from traditional solid solutions. The mechanical properties in the small deformation region described by the elastic constants and polycrystalline elastic moduli are discussed in detail. The effects of 3d transition metal alloying on the electronic structures and mechanical and thermal properties of the 12 BCC refractory-based HEAs are investigated. The correlation between total bond order density (TBOD), effective charge (Q^*) of every atom in each model, and the calculated mechanical parameters are discussed in detail. Moreover, interatomic bonding and local lattice distortion (LD) are discussed.

2. Computational Modeling and Method

This section delves into the modeling and computational packages employed in this study. Following that, the results and discussion section covers electronic structure, interatomic bonding, lattice distortion, mechanical properties, and thermal properties. This is subsequently followed by the conclusion.

2.1. Optimization and Mechanical Properties

The HEA structure was initially modeled using a Ni BCC unit cell with a space group number of 229. Subsequently, the HEA structure underwent random doping with transition elements (Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W), and our in-house Python code was employed to compute the lattice constants while considering the randomly doped atoms within their respective cell. To introduce a disordered local environment, 5 × 5 × 5 supercells of BCC were constructed, resulting in random solid solution HEAs with a total of 500 atoms, as shown in Figure 1. Each of these 12 HEA models was then optimized using Vienna ab initio simulation package (VASP) [59]. In VASP, we used projector augmented wave (PAW-PBE) including generalized gradient approximation (GGA) for exchange correlation potential. A kinetic energy cutoff of 500 eV was selected for plane wave expansion, with an electronic convergence criterion set at 1.0 × 10⁻⁵ eV, and the force convergence set at −1.0 × 10⁻³ eV/Å for ionic relaxation.

The VASP-relaxed structures were also used for elastic tensor calculations based on the stress–strain response scheme [60]. The elastic coefficient $C_{ij}$ matrix is calculated by solving the linear equation:

$${\sigma }_i=\sum _{j=1}{C}_{ij}{ϵ}_j$$

(2)

where $i$ and $j$ are 1, 2 … 6. ${\sigma }_i$ was obtained by applying a strain ${ϵ}_j$of +0.50% and −0.50% to the equilibrium large supercell. The bulk modulus (K), shear modulus (G), Young’s modulus (E), and Poisson’s ratio (η) were calculated based on the Voigt–Reuss–Hill (VRH) approximation for poly-crystals [61,62,63] from the calculated $C_{ij}$ values.

2.2. Electronic Structure

The orthogonalized linear combination of atomic orbital (OLCAO) method [64,65] was utilized for the electronic structure and bonding analysis, with the VASP optimized structure serving as the input. The OLCAO package is an all-electron method and employs Gaussian type orbitals to construct atomic orbitals within the basis expansion of the Bloch function. This approach is based on local density approximation within density functional theory. OLCAO calculates parameters of bond order (BO) and effective charge ($Q^{*}$) based on Mulliken’s scheme [66]. BO, synonymous with the strength of the bond, is the overlap population ${\rho }_{\alpha ,\beta }$between pairs of atoms ($\alpha , \beta$) separated by a distance—bond length.

$${\rho }_{\alpha \beta }=\sum _{n, occ}\sum _{i,j}{C}_{i\alpha }^{*n}{C}_{j\beta }^n{S}_{i\alpha , j\beta }$$

(3)

$$Q_{\alpha }^{*}=\sum _{i,j,\beta }\sum _{n,occ}{C}_{i\alpha }^{*n}{C}_{j\beta }^n{S}_{i\alpha ,j\beta }$$

(4)

where n, i, j, $C_{j\beta }^n$, and $S_{i\alpha , j\beta }$ are the band index, orbital quantum number, eigenvector coefficient, and overlap matrix, respectively. Following the effective charge, we also calculated the partial charge (PC) of each atom in all models. PC ($\mathsf{\Delta }{Q}^{*}$) is the deviation of $Q_{\alpha }^{*}$from their neutral charge $Q_{\alpha }^0$.

Summation of all BO in the model resulted in the total bond order (TBO). TBO, normalized by the volume of the model, resulted in total bond order density (TBOD). TBOD is the effective quantum mechanical metric that quantifies the cohesiveness of the alloy. OLCAO has been successful for DFT calculations of both crystalline [67,68,69] and non-crystalline materials [65,70], as well as complex bio-molecular systems [71,72].

3. Results and Discussion

3.1. Electronic Structure

The 12 BCC HEA models were created with an equal percentage of components that caused short-range order in the sites of the supercell. This causes deformation due to the new local chemical environment of the components. This deformation influences the properties of the material at the atomic level, including electronic structure and interatomic bonding. The optimized structure parameters along with first and second nearest neighbors are listed in Table 1. Although the 5d elements are heavier and contain more protons, which makes the atoms larger, it is hard to tell whether this makes the volume of the supercell larger, due to severe lattice distortion in BCC HEAs (see Section 3.2).

The stability of the material is explicitly associated with the electronic structure. The electronic structure contains density of states (DOS) and partial and effective charges. Figure 2 demonstrates the total density of states of the 12 BCC HEAs investigated. The DOS predominantly originated from the 3d orbitals in Ti, V, and Cr, the 4d orbitals in Zr, Nb, and Mo, and the 5d orbitals in Hf, Ta, and W. Figure 2 shows the DOS of the 12 BCC HEAs, in which M9 (M5) is the highest (lowest) at Fermi energy (E_F). None of the investigated DOS is minimum at E_F. By comparison, in the case of FCC, the minimum can be seen at E_F, which means that FCC HEAs are more stable and less deformed [73]. Detailed total and partial DOS of the 12 models are shown in Figure S1 in Supplementary Materials (SM). Notably, the 5d elements had lower DOS at E_F. For instance, M5, M6, and M7 are 4-component models, containing, e.g., W; and thus, this influences a lower total DOS for the models. Although M1 and M2 contain W and their total DOS are also low compared to the non-W models, it is not as low as M5 and M6 (see Figure S1). This is due to the higher number of components in their structure. Moreover, the partial DOS of elements contributing to the 12 models almost have same trend regardless of their different local chemical environments in the supercell. On the other hand, the partial DOS of 3d elements are usually higher, which is consistent with FCC HEAs such as the Cantor alloy [2,74].

Another essential factor of electronic structure is effective charge of the components in the HEAs. The quantum mechanical metric of effective charge $Q^{*}$ fulfills the inadequacy of valence election concentration (VEC) theory. VEC values are based on the pure, isolated environments of the components. The VEC of transition metals within a solid solution model often deviates from the number of electrons in the d orbital of HEAs due to the unique local environment of each component.

The calculated $Q^{*}$ of the HEAs are listed in

Table 2. List of partial charge (PC) and effective charge (Q*) for each atom in the 12 BCC HEA models.

Models		M1	M2	M3	M4	M5	M6	M7	M8	M9	M10	M11	M12	VEC
Ti	PC	−0.26	−0.16	0.07	−0.03	--	--	−0.32	−0.09	−0.12	−0.26	−0.24	−0.31	4
	Q*	4.26	4.16	3.93	4.03	--	--	4.32	4.09	4.12	4.26	4.24	4.31
V	PC	−0.24	--	0.01	−0.06	0.08	--	--	--	−0.12	−0.25	−0.23	−0.28	5
	Q*	5.24	--	4.99	5.06	4.92	--	--	--	5.12	5.25	5.23	5.28
Cr	PC	--	--	--	--	−0.71	--	--	--	--	--	--	--	6
	Q*	--	--	--	--	6.71	--	--	--	--	--	--	--
Zr	PC	0.24	0.31		0.38	--	--	0.19	0.32	--	--	--	0.18	4
	Q*	3.76	3.69		3.62	--	--	3.81	3.68	--	--	--	3.82
Nb	PC	--	--	--	--	--	0.32	--	0.21	0.22	0.09	0.09	0.02	5
	Q*	--	--	--	--	--	4.68	--	4.79	4.78	4.91	4.91	4.98
Mo	PC	--	−0.55	−0.31	−0.41		−0.43	--	−0.46	--	--	--	--	6
	Q*	--	6.55	6.31	6.41		6.43	--	6.46	--	--	--	--
Hf	PC	0.45	0.53	--	--	--	--	0.41	--	--	0.41	0.44	0.39	4
	Q*	3.55	3.47	--	--	--	--	3.59	--	--	3.59	3.56	3.61
Ta	PC	--	--	0.23	0.12	0.35	0.08	--	0.02	0.03	--	--	--	5
	Q*	--	--	4.77	4.88	4.65	4.92	--	4.98	4.97	--	--	--
W	PC	−0.2	−0.12	--	--	0.28	0.02	−0.28	--	--	--	--	--	6
	Q*	6.2	6.12	--	--	5.72	5.98	6.28	--	--	--	--	--
${\mathit{Q}}_{\mathit{a}\mathit{v}}^{\mathit{*}}$ or $\mathit{V}\mathit{E}{\mathit{C}}_{\mathit{a}\mathit{v}}$		4.6	4.8	5.0	4.8	5.5	5.5	4.5	4.8	4.75	4.5	4.5	4.4

. The average $Q^{*}$ of each HEA is obtained by using $Q_{av}^{*}=\sum c_i{Q}_i^{*}$, where $c_i$ is the composition of the components. Although the $Q^{*}$ differs from the VEC, their averages are the same (see Table 2). The highest $Q_{av}^{*}$ are in M5 and M6, and the lowest $Q_{av}^{*}$ is in M12. $Q_{av}^{*}$ is extremely important for designing HEAs because it is positively correlated with bulk modulus (K) and negatively correlated with total energy, as shown in Figure 3a,b, respectively.

In addition to effective charge, partial charge is equally important for transition metals in HEAs, which is the deviation of $Q^{*}$ from VEC. This difference creates a charge transfer between the neighboring atoms in the supercell. The value of PC reveals the electronic structure and interatomic bonding alteration. The calculated partial charge (PC) distribution for each of the 12 BCC HEA models is shown in Figure S2. PC values of the components in the 12 HEAs are listed in Table 2. From Figure 4 it can be seen that Zr, Nb, Hf and Ta are electropositive, whereas Cr and Mo are electronegative in all 12 BCC HEAs. It is well known that some transition metals can be both electropositive and electronegative, depending on the local chemical environment they are contributing to. Although Ti and V are electronegative in almost all cases, Ti (V) is electropositive in M3 (M3 and M5). This could be due to the electronegativity of Mo in M3, which is a 4d element with a larger number of atoms. Furthermore, in the case of M5, Cr exhibits the highest electronegative value. Additionally, the electronegativity (or electropositivity) of element W varies in M1, M2 and M7 (M5 and M6), depending on the other components present within the structure.

3.2. Interatomic Bonding and Lattice Distortion

Identifying the strength of a pair of atoms reveals better insight into the chemical properties of HEAs. Bonding in HEAs results from sharing the valence electrons in neighboring atoms, and the distance between atoms is the so-called interatomic distance. The bond order (BO) versus bond length (BL) for the 12 HEA models are shown in Figure S3 (M1–M12) with their discussion in the SM. Among the 12 HEAs, M9 and M10 exhibit greater dispersion (see Figure S3), while M5 and M6 display lower dispersion. The increased dispersion in M9 and M10 is indicative of more substantial lattice distortion. M5 and M6 notably exhibit a clear separation between two regions, corresponding to the first and second nearest neighbors (NN), which aligns with the expected behavior in a BCC structure. In general, the 1NN always dominates the contribution in bonding because it has a shorter interatomic distance (ID).

To attain deeper knowledge, we obtained the total bond order density (TBOD) as described in Section 2.2. TBOD can be further decomposed into partial BOD (PBOD), identifying the contributions from various types of bonds. Figure 5 shows the PBOD of the 12 BCC HEAs. More detailed pie charts for every HEA model are shown in Figure S4.

Among all 12 BCC models, Mo–Ta in M6 has the highest contributions of 15.9% as depicted in Figure S4, and bonds such as Hf–Hf and Zr–Zr have the lowest contributions. Bond pairs that consist of 5d elements exhibit higher PBOD, primarily attributed to the greater number of electrons in 5d orbitals compared to the 3d and 4d orbitals.

Another key point in HEAs is lattice distortion (LD), which can be obtained by interatomic bonding analysis. To investigate LD in HEAs, we employed atomic pair distribution analysis of interatomic distances (ID) utilizing a bimodal Gaussian distribution, as depicted in Figure 6. As is widely known, BCC structures consist of NN and SNN, as illustrated by the dual peaks in Figure 6. We calculated the averaged NN and SNN distances as shown in Table 1. To conduct a more detailed analysis of these two peaks, we determined their respective full width at half maximum (FWHM) values, as presented in Figure 6. The model with prominent peaks shows BCC structure integrity, whereas the pair distribution between the peaks denotes structural distortion or LD. Specifically, M1, M7, and M12 display a higher degree of LD. On the other hand, model M6 does not exhibit any LD, and models M3, M5, and M9 show lower LD.

3.3. Mechanical Properties

Since the discovery of HEAs, their elastic moduli have been the main focus in industries due to their superior properties. HEAs are very complex and expensive, and accurate computational study is needed to help researchers. We used the stress vs. strain approach [75] to find the elastic coefficients $C_{ij}$. The mechanical properties such as bulk modulus (K), shear modulus (G), and Young’s modulus (E) were derived from the $C_{ij}$.

Table 3. The calculated elastic coefficients (C11, C12, C44), Young’s modulus (E), bulk modulus (K), shear modulus (G), Vicker’s hardness (HV), Poisson’s ratio (η), Pugh’s ratio (G/K), Cauchy pressure (CP), total bond order density (TBOD), and Zener ratio (AZ) for the 12 BCC HEAs.

Model	C11	C12	C44	K	G	E	Hv	CP: C12–C44	η	G/K	TBOD	AZ
M1	170.71	107.04	37.11	128.24	34.86	95.88	2.59	69.93	0.375	0.272	0.041	1.166
M2	201.82	114.19	38.84	143.37	40.73	111.63	3.04	75.35	0.370	0.284	0.042	0.887
M3	258.38	139.11	31.43	178.46	40.72	113.51	2.37	107.67	0.394	0.228	0.055	0.527
M4	201.89	116.36	32.02	144.84	35.92	99.53	2.38	84.34	0.386	0.248	0.047	0.749
M5	376.99	159.09	48.63	230.47	67.53	184.57	4.50	110.47	0.367	0.293	0.057	0.446
M6	389.28	159.94	49.61	234.94	69.88	190.73	4.69	110.33	0.365	0.297	0.051	0.433
M7	164.35	102.72	44.12	123.22	38.20	103.88	3.20	58.60	0.360	0.310	0.038	1.432
M8	201.18	118.75	33.52	146.21	36.38	100.77	2.41	85.23	0.385	0.249	0.042	0.813
M9	200.66	136.46	24.30	157.83	27.15	77.03	1.29	112.16	0.419	0.172	0.048	0.757
M10	165.92	110.54	28.56	128.99	28.17	78.78	1.73	81.98	0.398	0.218	0.040	1.031
M11	159.86	105.79	32.62	123.81	30.24	83.89	2.07	73.17	0.387	0.244	0.040	1.207
M12	151.23	99.48	30.62	116.72	28.61	79.34	2.00	68.86	0.387	0.245	0.036	1.183

lists $C_{11}$, $C_{12}$ and $C_{44}$, and the calculated mechanical properties. The elastic constants C₁₁, C₂₂, and C₃₃ are strongly correlated with unidirectional compression along the principal x, y, and z directions [76] and have the same value in cubic structures. Synonymously, C₁₁, C₂₂, and C₃₃ can describe the resistance of a material against the deformation along the [100], [010], and [001] directions, respectively. C₄₄ measures the resistance against shear deformation in the (100) plane. A large value of C₁₁ indicates incompressibility under uniaxial stress along the x-axis. The C₁₁ of M5 and M6 are much larger than the C₁₁ of all remaining models, indicating that M5 and M6 are much less compressible under uniaxial stress along the x, y, and z directions. It also means that the bonding strength in M5 and M6 along the x, y, and z axes is much stronger than the bonding strength in all remaining models. The C₄₄ of M5 and M6 are larger than the C₄₄ of all remaining models. Larger C₁₁ and stronger bonding characteristics can result in higher values of K, G, and E. Larger C₁₁ and C₄₄ also indicate higher transverse (shear) velocity (v_s) and longitudinal sound velocity (v_l). The pure elements W and Ta have much larger densities and higher melting temperatures than the other elements in these 12 models. Thus, alloying with W and Ta in M5 and M6 results in harder materials for many mechanical applications. However, this also results in higher lattice thermal conductivity, which makes M5 and M6 much less applicable as TE materials. On the other hand, the pure elements Ti, V, and Zr have the lowest density among the studied elements. Thus, alloying with Ti and V in M10 and M11, and Ti, Vi, and Zr in M12, may result in softer materials with smaller C₁₁ and K for TE applications. A low value of C₄₄ indicates high shearability. Due to having the lowest C₄₄ value, M9 and M10 have the highest shearability among all solid solutions. The results in Figure 7a show the model M6 has the highest values for K, G, and E, while M9 exhibits the lowest values for both G and E. However, M12 has the lowest K value among the models. It should be noted that the G and E have the same trend from M6 (highest) to M9 (lowest). It can be observed that the model consisting of Ta has higher bulk modulus, especially the models with 4 components, because their number of atoms in the 4-element model is 125 atoms each. By contrast, models containing Hf possess lower bulk modulus. Vickers hardness (Hv) was calculated using the formula of Tian et al. [77]:

$$H_V=0.92{\left(\frac{G}{K}\right)}^{1.137}{G}^{0.708}$$

(5)

Among the 12 BCC models, M6 holds the highest $H_V$ followed by M5, while M9 exhibits the lowest $H_V$.

The ratio of shear modulus to bulk modulus (G/K) is called Pugh’s modulus ratio [78,79]. It is one of the useful parameters that determines the brittle and ductile behaviors of materials. The G/K ratios for the 12 BCC HEAs solid solution models are listed in Table 3. According to Pugh’s criterion, materials with G/K larger than 0.571 tend to be brittle and those less than 0.571 tend to be ductile [79,80]. All 12 BCC HEAs are ductile materials. The mechanical stability of a cubic structure involves the following criteria: C₄₄ > 0, C₁₁ > |C₁₂|, and C₁₁ + 2C₁₂ > 0 [81]. From Table 3, the calculated elastic constants satisfy these criteria, thus these alloys are expected to be mechanically stable. Frantsevich’s rule of Poisson’s ratio [82] is used to characterize material’s brittleness or ductility. It suggests that if Poisson’s ratio (η) is less than 0.26, the material tends to be brittle, otherwise it is ductile in nature. From Table 3, we notice that all refractory-based HEAs under study have an η much higher than 0.26. Hence, these HEAs are ductile and both Frantsevich’s rule and Pugh’s criterion are equivalent for these HEAs. Cauchy pressure (CP), which is given by: (C₁₂ − C₄₄) [83], can be used to characterize materials’ bonding nature. Generally speaking, a positive value of CP indicates metallic bonding dominating, while a negative value of CP suggests that the material is dominated by covalent bonding. The calculated positive values of CP in Table 3 show that these HEAs have a metallic character. M3, M5, M6, and M9 have the highest metallic bonding character, which may indicate that alloying with Ta increases the metallic character of the bonding. The Zener ratio (A_Z = 2C₄₄/(C₁₁ − C₁₂)) determines the elastic anisotropy of materials [40]. A_Z is a unity for isotropic materials. From Table 3, we notice that these refractory-based HEAs are elastically anisotropic. We can associate the electronic structure and chemical properties with the mechanical properties. For instance, the correlation between TBOD and bulk modulus (see Figure 7b) does not exhibit a perfect linear relationship but does display a closer-to-linear nature, with the exception of a few outliers (M5 and M6). This observation suggests the potential future prediction of bulk modulus based on TBOD. Another example is effective charge versus bulk modulus, with their coefficient of determination (R²) equaling 0.97, as shown in Figure 3a. The figure illustrates that an increase in $VE{C}_{av}$ within the model leads to an increase in the elastic moduli, particularly the bulk modulus. These insights offer valuable guidance for the design of HEAs.

3.4. Thermal Properties

The strength of bonding can be determined by the Debye temperature (Θ_D), which originates from the theory of thermal vibration of atoms. Θ_D is an important parameter for high temperature applications and correlates strongly to thermal conductivity (κ). Lower Θ_D indicates softer materials with lower melting temperatures (T_melt), while higher Θ_D indicates harder materials with stronger interatomic bonds and higher T_melt [84,85]. Θ_D is calculated here using Anderson’s method, shown in Equation (S1) in the SM. Average sound velocity (v_m), transverse (shear) velocity (v_s), and longitudinal sound velocity (v_l) are calculated using the equations shown in Equations (S2)–(S4) respectively. The calculated density(ρ), ν_s, ν_l, ν_m, and Θ_D for the 12 BCC HEAs are listed in

Table 4. The theoretical density (ρ), calculated sound velocity (longitudinal ν_l, transverse ν_s, and average ν_m), Debye temperature (Θ_D), and melting temperature (T_melt) of 12 BCC HEAs.

Model	ρ (Kg/m3)	νl (m/s)	νs (m/s)	νm (m/s)	ΘD (K)	Tmelt (K)
M1	11,709.54	3862.68	1725.29	1946.48	231.60	1561.88
M2	12,533.18	3971.51	1802.80	2032.49	241.00	1745.76
M3	11,358.89	4526.66	1893.26	2141.44	266.25	2080.01
M4	10,412.46	4302.30	1857.34	2098.35	253.92	1746.15
M5	15,238.36	4586.22	2105.19	2372.21	302.38	2781.03
M6	15,769.33	4561.45	2105.10	2371.51	289.05	2853.66
M7	12,466.75	3737.64	1750.56	1970.71	229.56	1524.32
M8	10,790.15	4247.93	1836.06	2074.22	246.82	1741.94
M9	10,758.12	4246.85	1588.55	1802.85	220.72	1738.88
M10	10,071.86	4066.47	1672.39	1892.72	227.19	1533.59
M11	9629.90	4128.41	1772.07	2002.46	238.98	1497.77
M12	9453.01	4047.57	1739.70	1965.78	231.23	1446.77

and plotted in Figure 8a–c. Figure 8a shows that M5 and M6 have the highest densities, while M12 has the lowest density. M1, M7, M9, M10, M11, and M12 have the lowest Θ_D and ν_s while M3, M5, and M6 have the highest Θ_D and ν_s. This indicates that alloying with Ti, V, and Hf may suppress transverse phonon velocity and Θ_D in HEAs, while alloying with W, Mo, Cr, and Ta may increase transverse phonon velocity and Θ_D. As individual elements, Ti, Hf, and Zr have the smallest lattice thermal conductivity(κ_L) [86], whereas W, Mo, and Ta, Nb, and Cr have the largest κ_L at room temperature [86], among the elements constituting these 12 HEAs. This indicates that the κ_L value of the individual elements constituting these 12 HEAs also counts in determining the value of κ_L for refractory-based HEA models. For example, M6 has the largest κ_L because it consists of W, Mo, Nb, and Ta, alongside M5, which contains the three elements W, Ta, and Cr. It is important to identify the thermal limits or melting temperature (T_melt) of a material. Low T_melt indicates lower Θ_D and higher thermal expansion. T_melt is calculated using Equation (S5). Models M1, M7, M9, M10, M11, and M12 also have the lowest T_melt, while M3, M5, and M6 have the highest T_melt among the models. This indicates that alloying with Ta increases T_melt and makes the alloys much harder. Significantly dampened transverse phonon modes (ν_s) would strengthen the scattering of phonons [87], which in turn results in reduced lattice thermal conductivity(κ_L).

The heat transfer performance at high temperatures can be measured by thermal conductivity (κ) [88]. Minimum thermal conductivity (κ_min) and lattice thermal conductivity (κ_L) at 300 K are estimated using Clarke’s model [89], Cahill’s model [90], Slack’s model, and mixed model [91]. κ_min and κ_L were calculated using Equations (S6)–(S8) and (S10) and are listed in

Table 5. Calculated minimum thermal conductivities (κ_min) (W⋅m⁻¹·K⁻¹) at 300 K, lattice thermal conductivities (κ_L) (W⋅m⁻¹·K⁻¹) at 300 K, and Grüneisen parameter (γ_a), thermal expansion coefficient (α), and dominant phonon wavelength (λ_dom) at 300 K for each model of the 12 BCC HEAs investigated.

Model	Clarke Model κmin (W·m−1·K−1)	Cahill Model κmin (W·m−1·K−1)	Slack Model κL (W·m−1·K−1)	Mixed Model κL (W·m−1·K−1)	γα	α (×10−5)	λdom (Å)
M1	0.54897	0.49659	0.69331	0.73710	2.361	4.59	0.815
M2	0.56862	0.50962	0.88163	0.91413	2.311	3.93	0.851
M3	0.66220	0.62294	0.76401	0.79356	2.556	3.93	0.897
M4	0.61351	0.56618	0.70941	0.75364	2.464	4.45	0.879
M5	0.76628	0.68246	1.75668	1.63648	2.276	2.37	0.994
M6	0.70012	0.62166	1.84346	1.76763	2.260	2.29	0.993
M7	0.53075	0.46744	0.87195	0.91217	2.213	4.19	0.825
M8	0.58636	0.54074	0.71212	0.76133	2.460	4.40	0.869
M9	0.54351	0.54905	0.34487	0.41132	2.860	5.89	0.755
M10	0.54606	0.51904	0.45064	0.51310	2.604	5.68	0.793
M11	0.56966	0.52752	0.56240	0.62115	2.481	5.29	0.839
M12	0.54328	0.50271	0.52396	0.58808	2.477	5.59	0.823

. κ_L for the 12 BCC HEAs is also shown in Figure 8d. M5 and M6 have the largest values of κ_L while M9 and M10 have the smallest κ_L. Phonon velocities or sound velocities and κ_L are correlated through Equation (6) [92]:

$${\kappa }_{ij}=\sum _{\alpha }{C}_{\alpha }{\tau }_{\alpha }{v}_i{v}_j$$

(6)

where $C_{\alpha }, {\tau }_{\alpha },$ and $\upsilon$ are the heat capacity, phonon scattering time or relaxation time, and phonon velocity, respectively. $i, j$ refer to the principal axes of the chosen coordinate system. Clearly, reducing κ_L requires suppressing sound velocity, particularly shear velocity (v_s). v_s and v_l are directly correlated to the shear elastic constant (C₄₄), C₁₁, and density (ρ) by Equations (7) and (8) below [93]:

$$v_s=\sqrt{\frac{C_{44}}{\rho } }$$

(7)

$$v_l=\sqrt{\frac{C_{11}}{\rho } }$$

(8)

In Table 3, it is evident that HEAs M9 and M10 exhibit the smallest C44 values, resulting in higher shear elastic strains. This observation clarifies their lower κ_L values when compared to other models.

The Grüneisen parameter (${\gamma }_{\alpha }$) [94] can offer a wealth of insights into the interatomic interactions and bond anharmonicity of materials. A large γ_α indicates strong anharmonic vibrations, which also indicate higher phonon scattering and thus low κ_L (depressed and temperature-independent lattice thermal conductivity). Element substitution in HEAs creates disorder, leading to weak displacements of the atoms and bonds resulting in higher bond anharmonicity and higher γ_α. Sound or phonon velocity and the strength of interatomic interactions are positively correlated. Weaker interatomic interactions between atoms indicate a lower sound velocity and thus larger γ_α [95]. In summary, alloying induces internal strain fields, which reduces the speed of sound.

In HEAs, the internal strains can change the speed of sound, which results in higher phonon scattering and lower κ_L. This can be fully understood by following formula [96], which correlates the phonon frequency (ω), Grüneisen parameter tensor (γ_ij), and strain tensor (ε_ij):

$$\omega ={\omega }_0\left(1-{\gamma }_{ij}{\epsilon }_{ij}\right)$$

(9)

where ${\omega }_0$ is the phonon frequency at zero strain. Increasing $\gamma$ or inducing high field strain (ε) reduces phonon frequency and increases phonon scattering, and thus reduces κ_L. In this study, γ_α is calculated using Equation (S11). The calculated γ_α for the 12 BCC HEA models are summarized in Table 5 and Figure 9. The four-component alloys M9 and M10 have the largest γ_α (weaker chemical bonds) and thus the lowest κ_L (see Figure 8d), which indicates strong anharmonic vibrations due to higher mass and force constant. The four-component alloys M5, M6, and M7 have the lowest γ_α and largest κ_L (see Figure 8d), which indicates weak anharmonic vibrations that result from the lower mass and force constant.

The tendency of material to change its shape, volume, and density in response to a change in temperature is described by the thermal expansion coefficient (α). The greater a material’s $\alpha$, the more it expands in response to heating. α is estimated from Equation (S12) in SM. The calculated α for the 12 refractory-based BCC HEAs is listed in Table 5, which shows that M5 and M6 have the highest α values, whereas M9 and M10 have the lowest α values. Lattice vibrations (phonons) in materials have a huge impact in several physical properties such as electrical conductivity, thermo-power, and thermal conductivity. To identify the maximum energy of phonons at a certain temperature, it is important to calculate the dominant phonon wavelength (λ_dom). λ_dom is defined as the wavelength at which the phonon energy distribution curve strikes its maximum value. λ_dom and mean free path (MFP) are positively correlated and both play a significant role in controlling κ_L. MFP is the average distance that a phonon travels between two successive inelastic collisions. Shortening MFP increases inelastic collisions between phonons, which means increasing the scattering of phonons and reducing κ_L [97]. This requires shifting the heat phonon spectra towards shorter wavelengths (smaller λ_dom). λ_dom can be roughly estimated at 300 K by using Equation (S13). The calculated λ_dom for the 12 BCC refractory-based HEAs are shown in Table S5. M5 and M6 have the largest λ_dom, whereas M9 and M10 have the smallest λ_dom among the HEAs.

4. Conclusions

The electronic structure, bonding, lattice distortion, elastic, and thermal properties of 12 BCC refractory-based HEAs—WTiVZrHf(M1), HfMoTiWZr(M2), MoTaTiV(M3), MoTaTiVZr(M4), WTaCrV(M5), MoNbTaW(M6), TiZrHfW(M7), TiZrNbMoTa(M8), NbTaTiV(M9), TiVNbHf(M10), Ti_0.38V_0.15Nb_0.23Hf_0.24(M11), and TiZrHfVNb(M12)—were investigated using first-principles calculations. The random solid solution model (RSSM) was used for alloying these solid solutions with large supercells of 500 atoms. We highlight the significance of TBOD as a valuable parameter in understanding the bonding of HEAs. Our calculations showed that TBOD is positively correlated with the mechanical properties, especially with bulk modulus. The average partial charge $Q_{av}^{*}$ is positively correlated with the bulk modulus, which is a new important finding from our current calculations. This feature of these refractory-based HEAs can be used to design new HEAs. Based on our calculations, all these 12 HEA models are mechanically stable. M3, M5 and M6 have the largest density and largest Young’s, bulk and shear moduli, while M9 and M10 have the lowest Young’s and shear moduli. Alloying with both W and Ta elements in M5 and M6 or both Mo and Ta in M3 results in very large elastic constants (C₁₁ and C₄₄) compared with other models, indicating higher hardness with higher fracture toughness and melting temperature. This feature can be useful for many mechanical and high temperature applications. Also, due to the high strength and ductility of M3, M5, and M6, they can be used as joint surrogate metals instead of the traditional stainless steels and titanium alloys, especially because they consist of refractory elements that are mostly non-toxic and hypoallergenic. However, this in turn results in high sound velocities or high phonon speeds, indicating larger lattice thermal conductivity. This feature makes the M5 and M6 models less applicable for TE applications. Considering that Ta has a higher density than Hf, and Mo has a higher density than V (see Figure 8a), replacing Hf in M10 with Ta in M9 and replacing V in M1 with Mo in M2 leads to a significant increase in the values of C₁₁ and bulk modulus. Compared to M1, a significant reduction in the values of C₁₁ and bulk modulus of M12 is observed when W is replaced with Nb, since W has a much higher density than Nb (see Figure 8a). M9 and M10 have the smallest v_s, v_m, Θ_D, and κ_L, whereas M5 and M6 have the largest v_s, v_m, Θ_D, and κ_L. M9 and M10 have the largest γ_α and thus the highest anharmonic vibrations. Thus, M9 and M10 are more suitable for TE applications. It is difficult to determine the main factor that caused the significant reduction in κ_L in M9 and M10. In general, the models from M9 to M12 have smaller κ_L than the other models. All these models (from M9 to M12) contain the elements Ti and V, which are the lightest of the remaining elements. This can cause a larger mismatch between size and mass, which may lead to larger lattice distortion in these models and thus smaller κ_L. These 12 HE models were investigated for their local lattice distortion (LD). M1, M7, and M12 have the highest LD while models M3, M5, M6, and M9 have the lowest LD. It is known that alloying with heavy elements, such as W and Ta in M5 and M6, may result in high LD. However, with the lower LD of M5 and M6, we conclude that heavy elements are not the only factor making the lattice more distorted. LD is correlated with lattice thermal conductivity (κ_L). A high LD indicates higher phonon scattering and thus low κ_L, while a small LD indicates higher κ_L. This correlation is revealed for most models, whereas it is not clear for the model M9. The higher LD and lower κ_L that some of these HE models have may not make them perfect for TE applications, since they are all metals with a zero energy band gap that indicates a very small Seebeck coefficient. Thus, more research work is required for enhancing the value of Seebeck coefficient and figure of merit. The promising current results encourage and inspire us to continue research in this direction for more complex and interesting high-entropy materials. Our DFT calculations could be improved by using better options, such as using either hybrid potential or Becke–Johnson potential. Overall, we believe our results can facilitate the design of new high-entropy materials with wider applications.