The Activation Energy of Viscous Flow and Liquid–Liquid Structure Transition in Co-B Alloys
Abstract
:1. Introduction
2. Materials and Methods
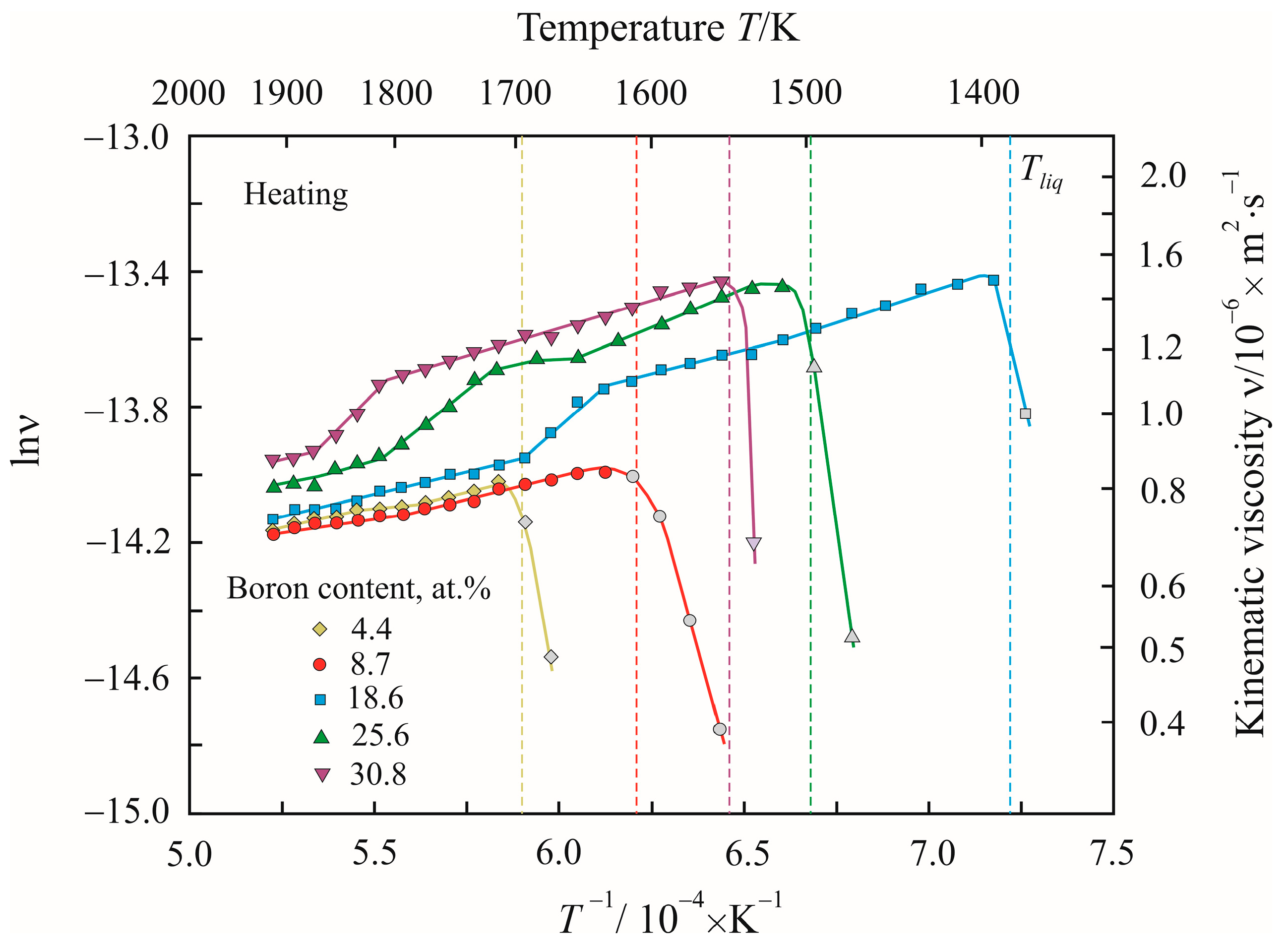
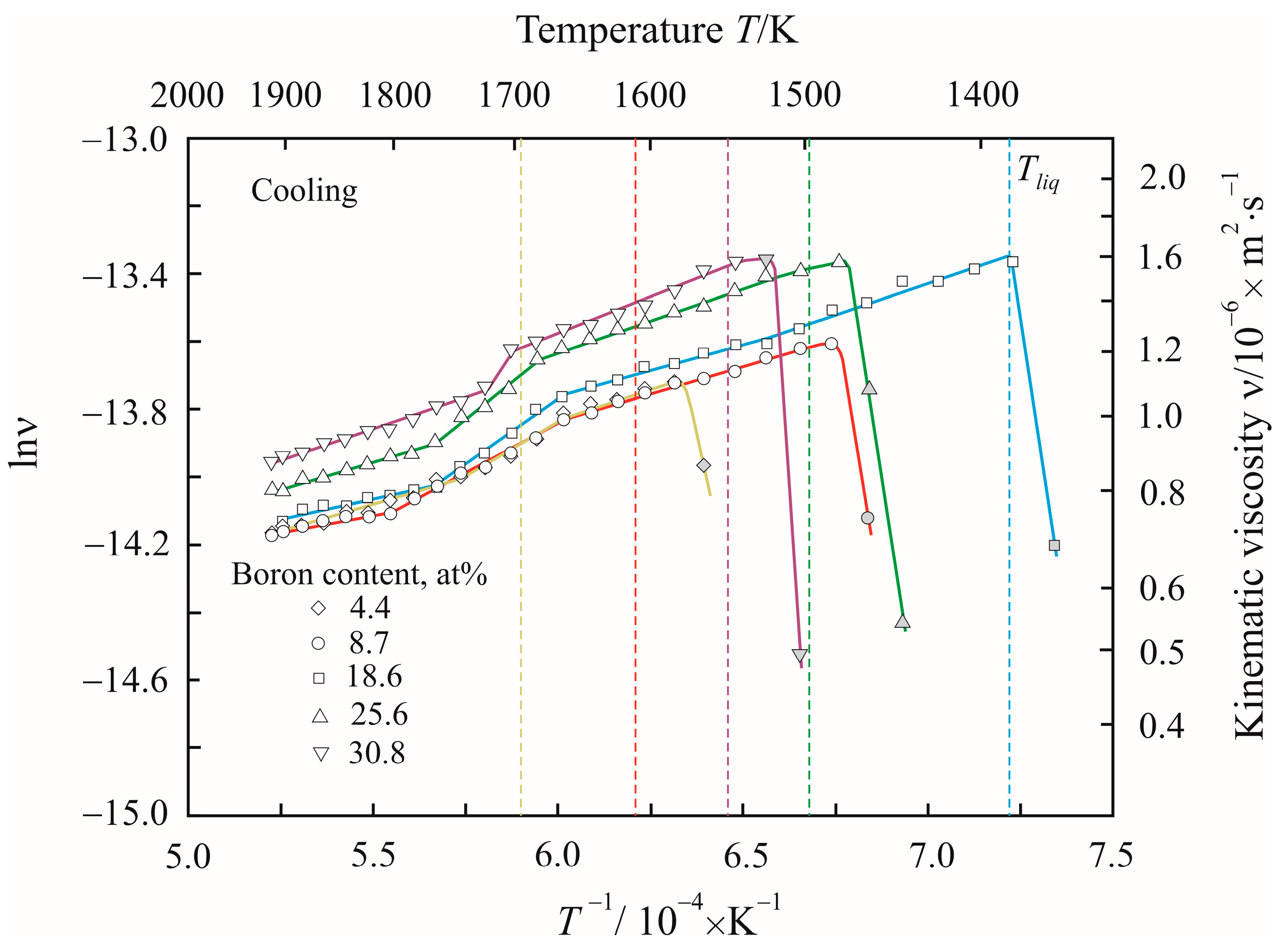
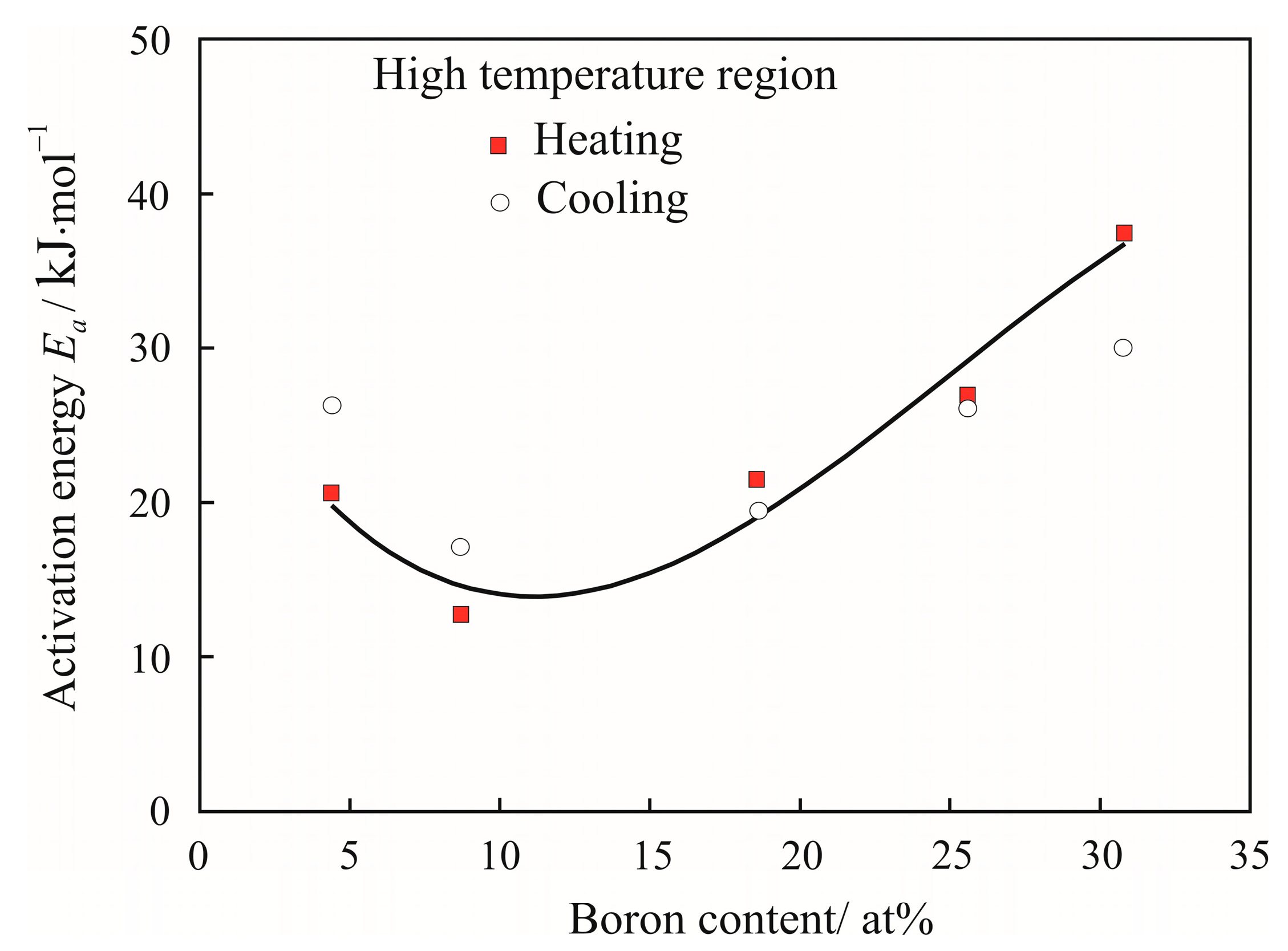
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Calvo-Dahlborg, M.; Popel, P.S.; Kramer, M.J.; Besser, M.; Morris, J.R.; Dahlborg, U. Superheat-dependent microstructure of molten Al-Si alloys of different compositions studied by small angle neutron scattering. J. Alloys Compd. 2013, 550, 9–22. [Google Scholar] [CrossRef]
- Tanaka, H. Liquid-liquid transition and polyamorphism. J. Chem. Phys. 2020, 153, 130901. [Google Scholar] [CrossRef]
- He, Y.-X.; Li, J.-S.; Wang, J.; Beaugnon, E. Liquid-liquid structure transition in metallic melt and its impact on solidification: A review. Trans. Nonferrous Met. Soc. China 2020, 30, 2293–2310. [Google Scholar] [CrossRef]
- Rusanov, B.A.; Sidorov, V.E.; Moroz, A.I.; Svec, P.; Janickovic, D. Density and electrical resistivity of Al-Ni-Co-Sm(Tb) alloys. Tech. Phys. Lett. 2021, 47, 770–772. [Google Scholar] [CrossRef]
- Starodubtsev, Y.N.; Tsepelev, V.S.; Tsepeleva, N.P. Kinematic viscosity of multicomponent FeCuNbSiB-based melts. Nanomaterials 2021, 11, 1042. [Google Scholar] [CrossRef] [PubMed]
- Tyagunov, A.; Tyagunov, G.; Milder, O.; Tarasov, D. Detection of the liquid-liquid transitions in superalloys melts upon overheating and relaxation by the electromagnetic method. J. Appl. Phys. 2021, 129, 015107. [Google Scholar] [CrossRef]
- Zu, F.Q.; Zhu, Z.G.; Gu, L.J.; Zhang, B.; Shui, J.P.; Liu, C.S. Liquid-liquid phase transition in Pb-Sn melts. Phys. Rev. B 2001, 64, 180203. [Google Scholar] [CrossRef]
- He, Y.; Li, J.; Li, L.; Wang, J.; Yildiz, E.; Beagnon, E. Composition dependent characteristic transition temperature of Co-B melts. J. Non-Cryst. Solids 2019, 522, 119583. [Google Scholar] [CrossRef]
- Dong, B.; Zhou, S.; Qin, J.; Li, Y.; Chen, H.; Wang, Y. The hidden disintegration of cluster heterogeneity in Fe-based glass-firming alloy melt. Prog. Nat. Sci. Mater. Intern. 2018, 28, 696–703. [Google Scholar] [CrossRef]
- Hou, J.X.; Zhan, C.W.; Tian, X.L.; Chen, X.C.; Kim, Y.-S.; Choe, H. Structure of Cu-Sn melt at high temperature. Metall. Mater. Trans. A 2012, 43, 4023–4027. [Google Scholar] [CrossRef]
- Tsepelev, V.; Starodubtsev, Y.; Zelenin, V.; Belozerov, V.; Konashkov, V. Temperature affecting the magnetic properties of the Co79−xFe3Cr3Si15Bx amorphous alloy. J. Alloys Compd. 2015, 643, S280–S282. [Google Scholar] [CrossRef]
- Baghbaderani, H.A.; Masud, A.; Alvarez, K.L.; Lordan, D.; Vancatesan, M.; Mathúna, C.Ó.; McCloskey, P.; Stamenov, P. Composition engineering of ultra-soft-magnetic Co-based alloys. J. Alloys Compd. 2022, 924, 166366. [Google Scholar] [CrossRef]
- Gao, P.; Yang, S.; Xue, G.; Liu, G.; Zhang, G.; Wang, L.; Li, G.; Sun, Y.; Chen, Y. High energy ball-milling preparation of Co-B amorphous alloy with high electrochemical hydrogen ability. J. Alloys Compd. 2012, 539, 90–96. [Google Scholar] [CrossRef]
- Jian, L.; Choi, G.M. Using amorphous Co-B alloy as transducer to detect acoustic propagation and heat transport at interface. Appl. Sci. 2021, 11, 5155. [Google Scholar] [CrossRef]
- Olyanina, N.V.; Bel’tyukov, A.L.; Lad’yanov, V.I. Viscosity of Co-B melts. Russ. Metall. Met. 2016, 2016, 150–155. [Google Scholar] [CrossRef]
- Du, Y.; Schuster, C.; Austin Chang, Y.; Jin, Z.; Huang, B. A thermodynamic description of the B-Co system: Modeling and experiment. Int. J. Mater. Res. 2002, 93, 1157–1163. [Google Scholar] [CrossRef]
- Wei, X.X.; Xu, W.; Kang, J.L.; Ferry, M.; Li, J.F. Metastable Co23B6 phase solidified from deeply undercooled Co79.3B20.7 alloy melt. J. Mater. Sci. 2016, 51, 6436–6443. [Google Scholar] [CrossRef]
- He, Y.; Li, J.; Wang, J.; Kou, H.; Beagunon, E. Liquid-liquid structure transition and nucleation in undercooled Co-B eutectic alloys. Appl. Phys. A 2017, 123, 391. [Google Scholar] [CrossRef]
- Liu, L.; Yang, L.; Li, J. Solidification pathways in highly undercooled Co79.3B20.7 alloy. Metall. Mater. Trans. A 2021, 52, 4324–4330. [Google Scholar] [CrossRef]
- He, Y.; Wu, Y.; Bu, F.; Zhang, Y.; Zhang, Y.; Hei, B.; Zhang, J. Re-examination of the microstructural evolution in undercooled Co-18.5at.%B eutectic alloy. Materials 2022, 15, 1315. [Google Scholar] [CrossRef]
- Konashkov, V.V.; Tsepelev, V.S.; V’yukhin, V.V.; Povadator, A.M.; Podoľskaya, A.I. A computer-aided plant for studying the kinamatic viscosity of high-temperature metallic melts. Instrum. Exp. Tech. 2011, 54, 284–285. [Google Scholar] [CrossRef]
- Glasstone, S.; Laidler, K.; Eyring, H. The Theory of Rate Processes: The Kinetics of Chemical Reactions, Viscosity, Diffusion and Electrochemical Phenomena; McGraw Hill: New York, NY, USA; London, UK, 1941; pp. 477–490. [Google Scholar]
- Coleman, P.G. Activation energies for vacancy migration, clustering and annealing in silicon. J. Phys. Conf. Ser. 2011, 265, 012001. [Google Scholar] [CrossRef]
- Welle, F. Diffusion coefficients and activation energies of diffusion of organic molecules in polystyrene below and above glass transition temperature. Polymers 2021, 13, 1317. [Google Scholar] [CrossRef]
- Batschinski, A.J. Untersuchungen über die innere Reibung der Flüssigkeiten. Z. Phys. Chem. 1913, 84, 643–706. [Google Scholar] [CrossRef]
- Tsepelev, V.; Starodubtsev, Y.; Konashkov, V.; Wu, K.; Wang, R. Melt viscosity of nanocrystalline alloys in the model of free volume. J. Alloys Comp. 2019, 790, 547–550. [Google Scholar] [CrossRef]
- Poole, C.P., Jr.; Owens, F.J. Introduction to Nanotechnology; John Wiley & Sons: Hoboken, NJ, USA, 2003; pp. 12–15. [Google Scholar]
- Starodubtsev, Y.N.; Tsepelev, V.S. Analysis of the kinematic viscosity and self-diffusion of liquid metals at the melting temperature. High Temp. 2021, 59, 306–311. [Google Scholar] [CrossRef]
- Koca, H.D.; Doganay, S.; Turgut, A.; Tavman, I.H.; Saidur, R.; Mahbubul, I.M. Effect of particles size on viscosity of nanofluids: A review. Renew. Sust. Energy Rev. 2018, 82, 1664–1674. [Google Scholar] [CrossRef]
- Filippov, G.G.; Gorbunov, A.I. Novel approach to selection of practical scale of electronegativity of atoms. Ross. Chim. Zh. 1995, 39, 39–43. [Google Scholar]
- The Materials Project. Available online: http://next-gent.materialsproject/materials (accessed on 20 June 2023).
- Faria, M.I.S.T.; Leonardi, T.; Coelho, G.C.; Nunes, C.A.; Avillez, R.R. Microstructural characterization of as-cast Co-B alloys. Mater. Charact. 2007, 58, 358–362. [Google Scholar] [CrossRef]
- Kelton, K.F.; Lee, G.W.; Gangopadhyay, A.K.; Hyers, R.W.; Rathz, T.J.; Rogers, J.R.; Robinson, M.B.; Robinson, D.S. First X-ray scattering studies on electrostatically levitated metallic liquids: Demonstrated influence of local icosahedral order on the nucleation barrier. Phys. Rev. Lett. 2003, 90, 195504. [Google Scholar] [CrossRef]
- Holland-Moritz, D.; Schenk, T.; Bellissent, R.; Simonet, V.; Funakoshi, K.; Merino, J.M.; Buslaps, T.; Reutzel, S. Short-range order in undercooled Co melts. J. Non-Cryst. Solids 2002, 312–314, 47–51. [Google Scholar] [CrossRef]
- Hirata, A.; Hirotsu, Y.; Amiya, K.; Nishiyama, N.; Inoue, A. Fe23B6-type quasicrystal-like structures without icosahedral atomic arrangement in an Fe-based metallic glass. Phys. Rev. B 2009, 80, 140201. [Google Scholar] [CrossRef]

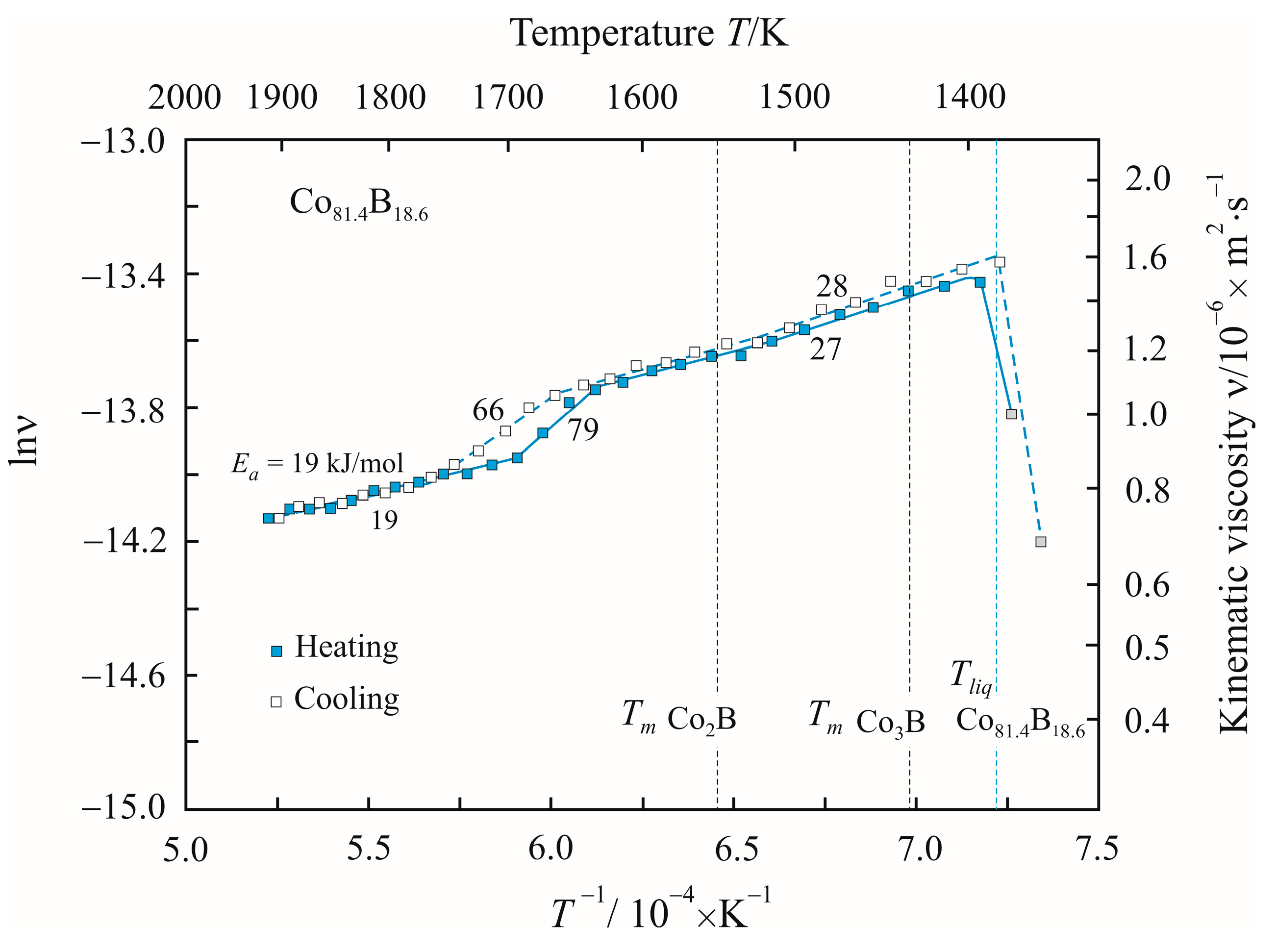
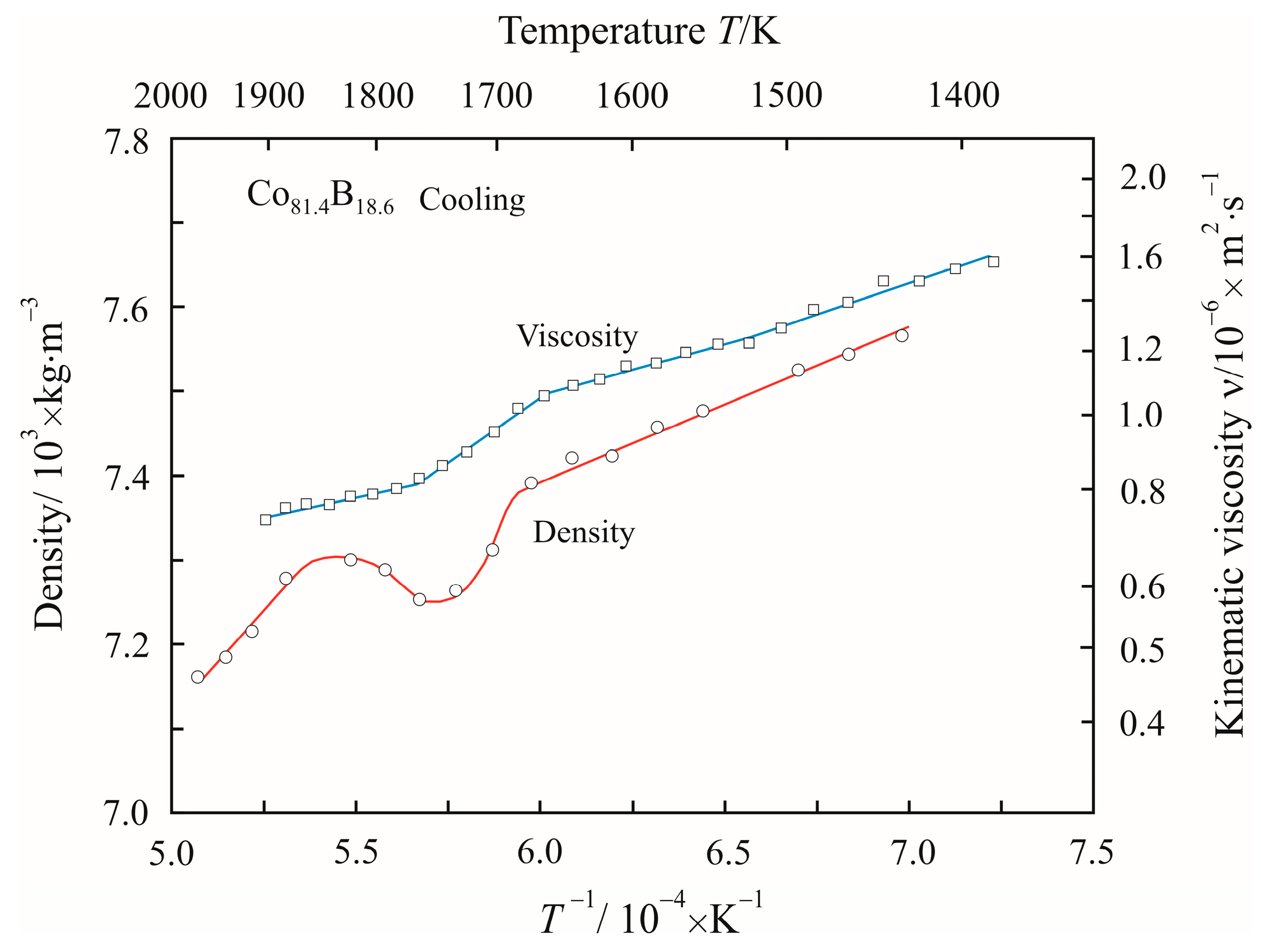
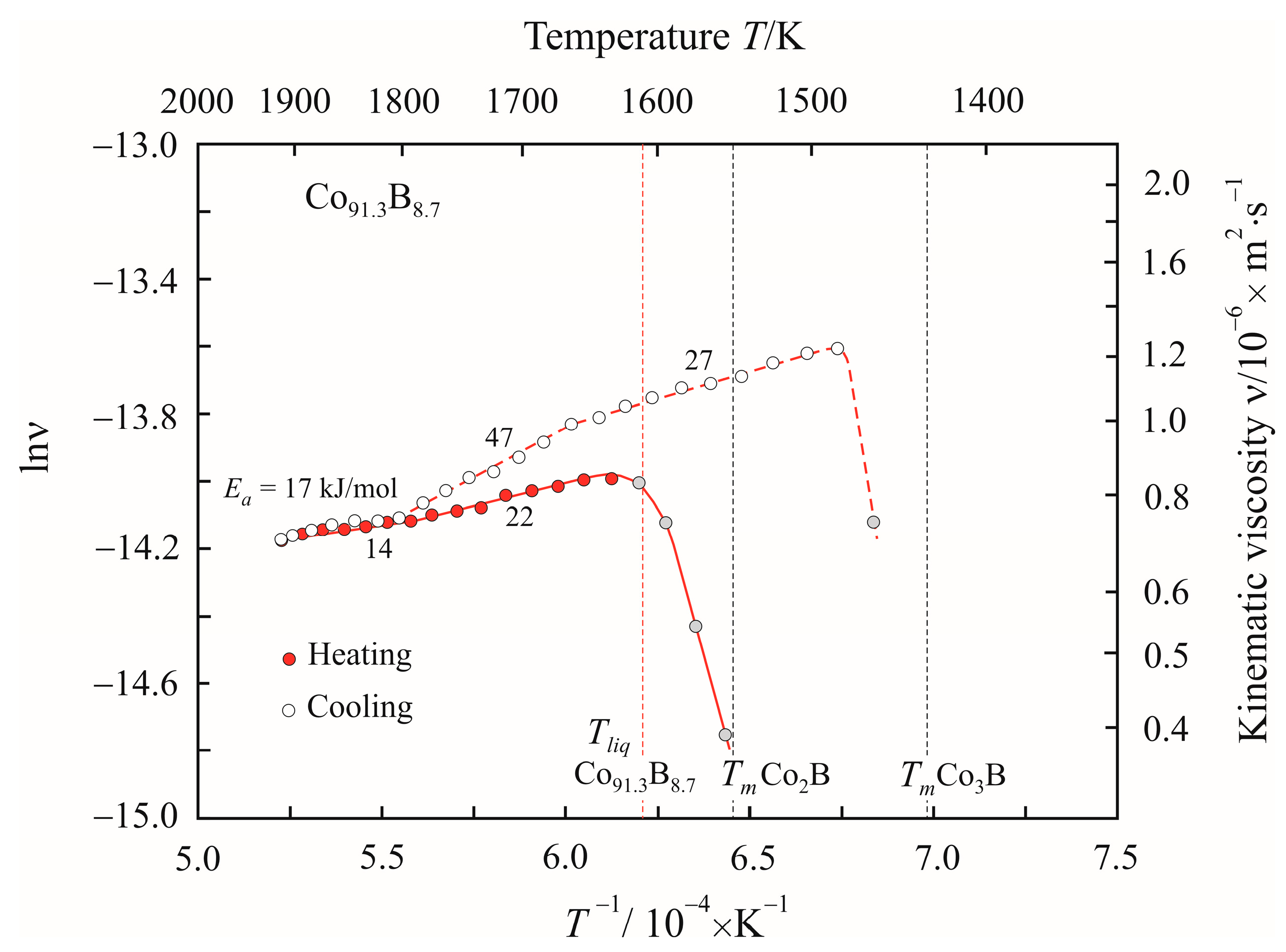
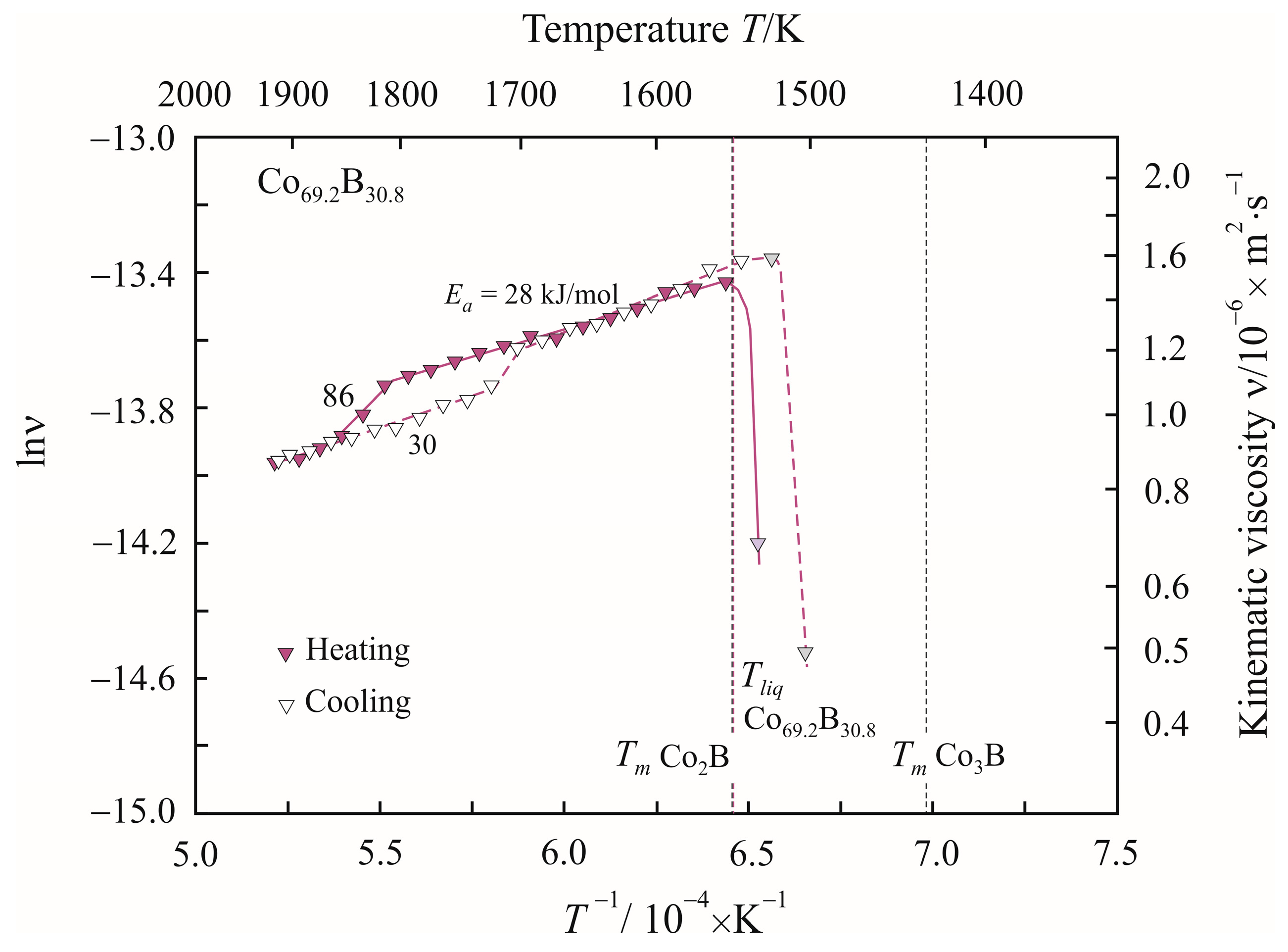
| Temperature T/K | Density ρ/kg·m−3 | Activation Energy Ea/kJ·mol−1 | Reduced Activation Energy Ea·(RT)−1 | Pre-Exponential Factor ν0/10−8·m2 s−1 | Relative Free Volume Vf/V | Cluster Size a/nm |
|---|---|---|---|---|---|---|
| 1500 | 7500 | 28 | 2.2 | 13 | 0.061 | 0.15 |
| 1720 | 7300 | 66 | 4.6 | 0.92 | 0.088 | 48 |
| 1850 | 7300 | 19 | 1.2 | 23 | 0.088 | 0.09 |
| Compound | Crystal System | Lattice Volume/nm3 [31] | Formation Energy/eV·atom−1 [31] | Mole Volume/10−6 m3·mole−1 | Liquidus Temperature Tliq/K |
|---|---|---|---|---|---|
| Co23B6 | Cubic | 1.116 | −0.089 | 5.795 | 1348 [18] |
| Co3B | Orthorhombic | 0.15028 | −0.133 | 5.658 | 1431 [16] |
| Co2B | Tetragonal | 0.10443 | −0.175 | 5.246 | 1544 [16] |
| CoB | Orthorhombic | 0.06052 | −0.298 | 4.558 | 1626 [16] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Starodubtsev, Y.N.; Tsepelev, V.S.; Konashkov, V.V.; Tsepeleva, N.P. The Activation Energy of Viscous Flow and Liquid–Liquid Structure Transition in Co-B Alloys. Metals 2023, 13, 1954. https://doi.org/10.3390/met13121954
Starodubtsev YN, Tsepelev VS, Konashkov VV, Tsepeleva NP. The Activation Energy of Viscous Flow and Liquid–Liquid Structure Transition in Co-B Alloys. Metals. 2023; 13(12):1954. https://doi.org/10.3390/met13121954
Chicago/Turabian StyleStarodubtsev, Yuri N., Vladimir S. Tsepelev, Viktor V. Konashkov, and Nadezhda P. Tsepeleva. 2023. "The Activation Energy of Viscous Flow and Liquid–Liquid Structure Transition in Co-B Alloys" Metals 13, no. 12: 1954. https://doi.org/10.3390/met13121954
APA StyleStarodubtsev, Y. N., Tsepelev, V. S., Konashkov, V. V., & Tsepeleva, N. P. (2023). The Activation Energy of Viscous Flow and Liquid–Liquid Structure Transition in Co-B Alloys. Metals, 13(12), 1954. https://doi.org/10.3390/met13121954







