Estimation of Activity and Molar Excess Gibbs Energy of Binary Liquid Alloys Al-Cu, Al-Ni, and Al-Fe from the Partial Radial Distribution Function Simulated by Ab Initio Molecular Dynamics
Abstract
:1. Introduction
2. Methods and Models
2.1. Obtaining the PRDF through AIMD Simulations
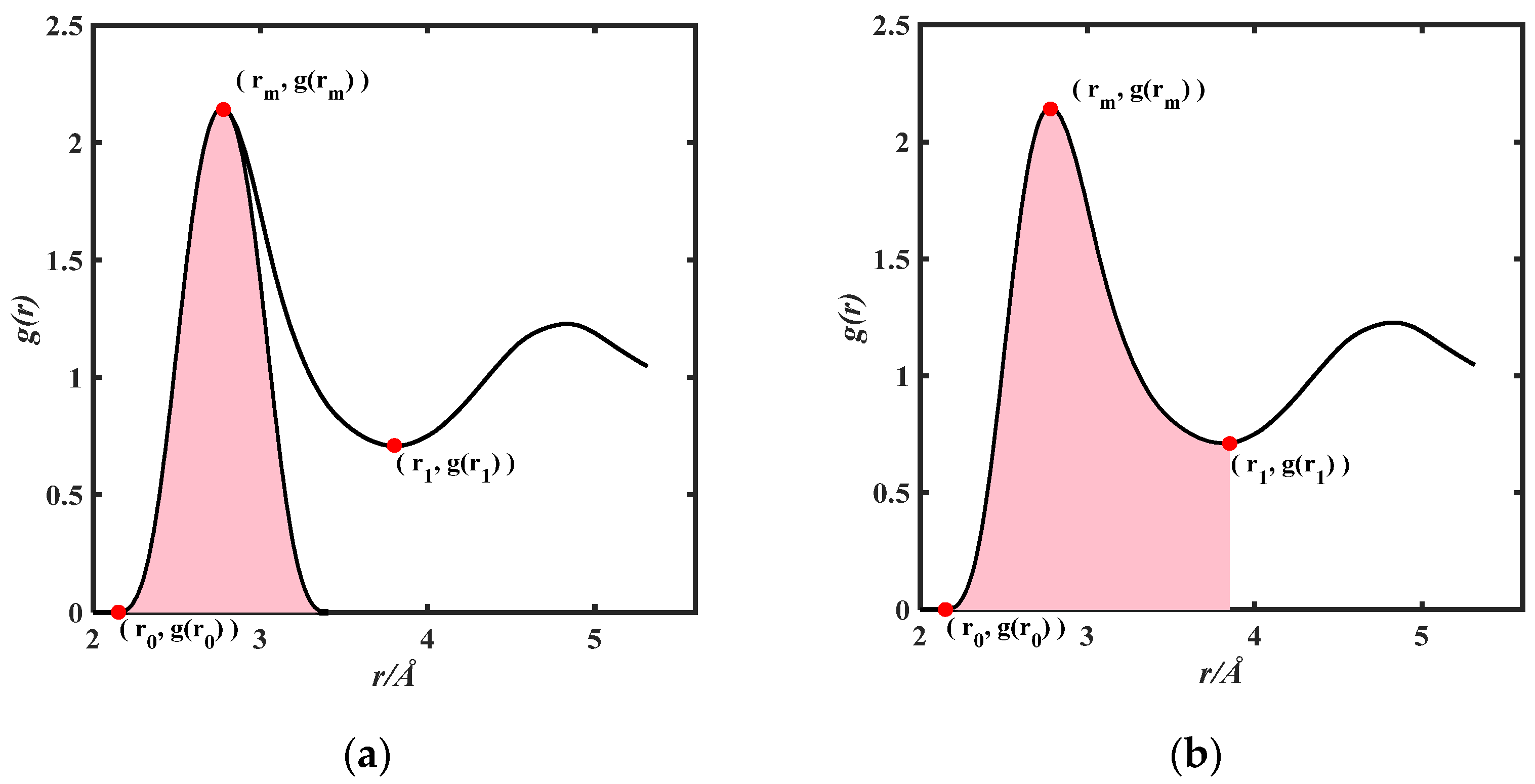
2.2. Symmetric and Non-Symmetric Methods
2.3. Thermodynamic Models
2.3.1. Molecular Interaction Volume Model (MIVM)
2.3.2. Regular Solution Model (RSM)
2.3.3. Wilson Model
2.3.4. Non-Random Two-Liquid Model (NRTL)
2.3.5. Miedema Model
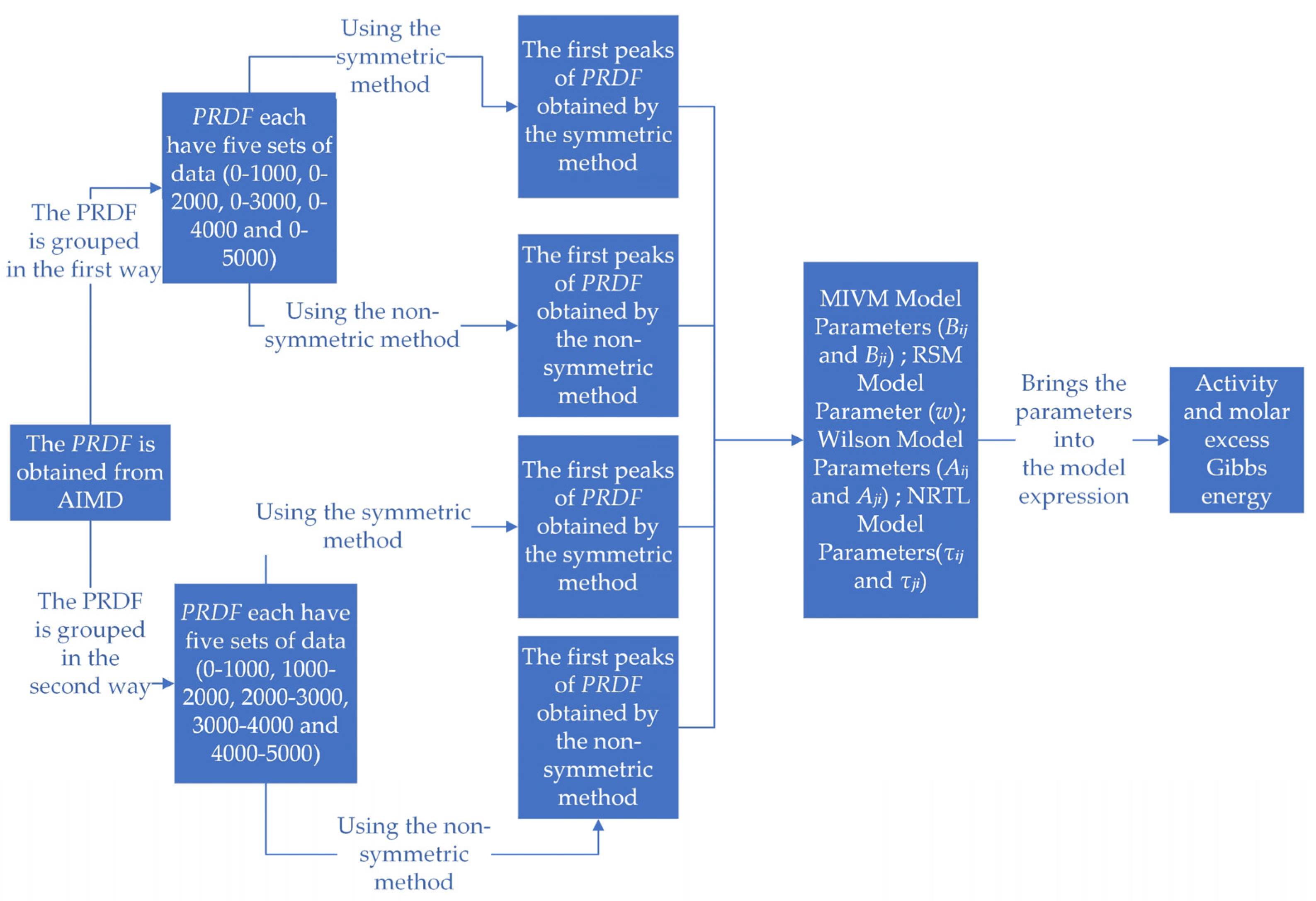
2.4. Calculation Process
3. Results and Discussion
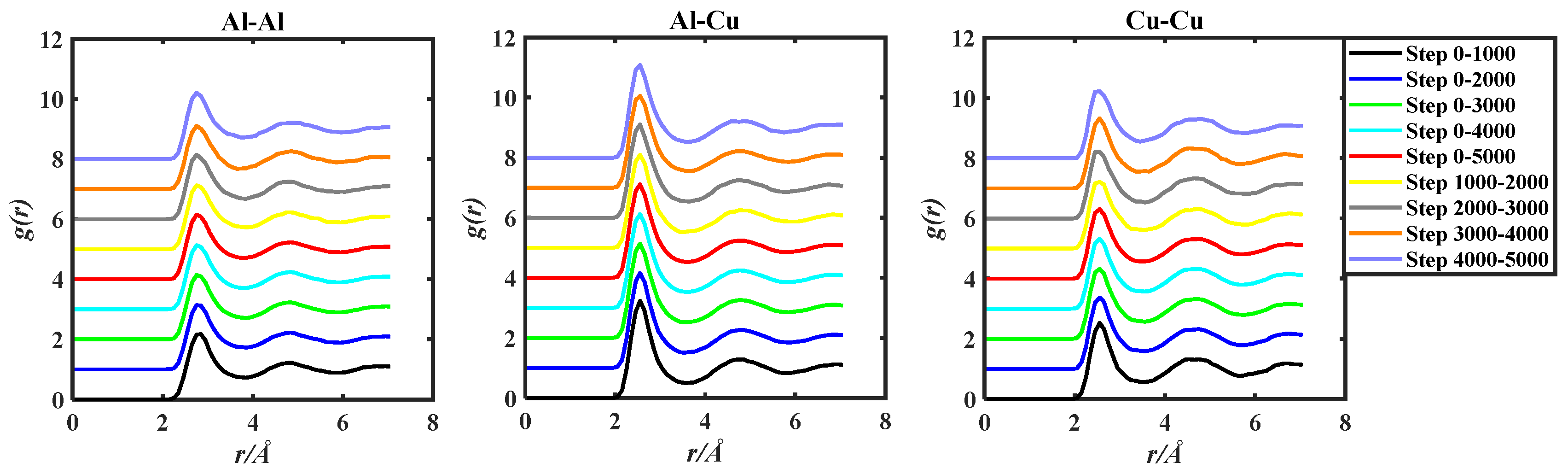
3.1. The g(r) Simulated by AIMD
3.2. Calculating Key Parameters of the Five Models
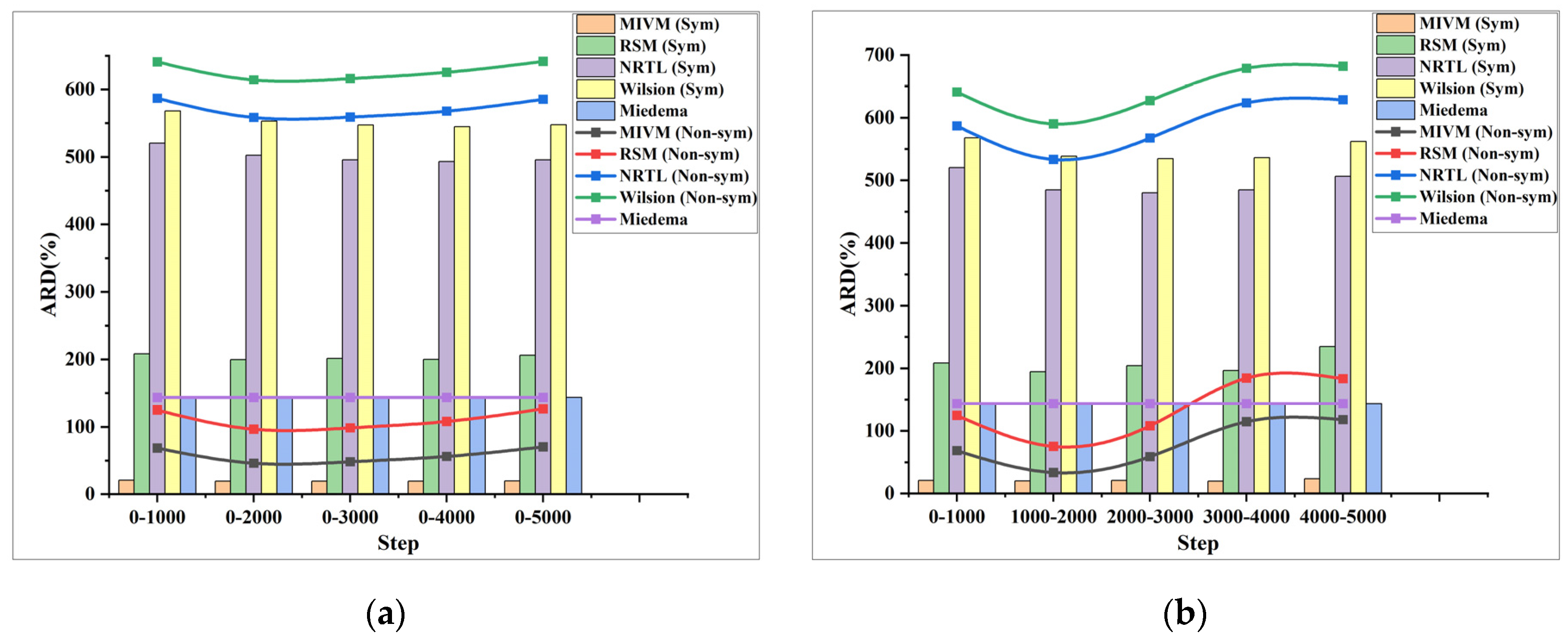
3.3. Estimating the Activity and Molar Excess Gibbs Energy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ajayi, A.A.; Oyeniyi, E.; Oshakuade, O.M. Bulk and surface properties of liquid Ag-Cu, Ag-Sb and Cu-Sb alloys. Pramana 2023, 97, 72. [Google Scholar] [CrossRef]
- Agbedor, S.O.; Yang, D.H.; Chen, J.Q.; Wang, L.; Wu, H. Low-Temperature Reactive Sintered Porous Mg-Al-Zn Alloy Foams. Metals 2022, 12, 692. [Google Scholar] [CrossRef]
- Zhou, C.; Jiang, L.; Gu, Z.; Wang, C.; He, L.; Huang, L.; Li, Z.; Li, K. Flexible core–shell structured Al-Cu alloy phase change materials for heat management. Chem. Eng. J. 2023, 471, 144610. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, X.; Chen, H.; Du, N.; Bao, K.; Tan, M. Mesoscale modeling on dynamic behavior of Al-Ni energetic structural materials under shock compression. Chin. J. Energ. Mater. 2020, 28, 984–994. [Google Scholar]
- Yao, Y.; Jing, L.; Wang, S.; Li, G.; Cui, J.; Tang, X.; Jiang, H. Mechanical properties and joining mechanisms of Al-Fe magnetic pulse welding by spot form for automotive application. J. Manuf. Process. 2022, 76, 504–517. [Google Scholar] [CrossRef]
- Shin, S.H.; Kim, S.J. Influence of slag composition on the distribution behavior of Cu between liquid sulfide and Cu-containing multicomponent slag via thermodynamic and kinetic assessment. Metals 2021, 11, 150. [Google Scholar] [CrossRef]
- Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985, 55, 2471. [Google Scholar] [CrossRef]
- Wei, H.Q.; Zhang, P.; Tang, Y.Y. Ab Initio Molecular Dynamics Study of the Structure and Properties of Nb-Doped Zr-Cu-Al Amorphous Alloys. Metals 2021, 11, 1821. [Google Scholar] [CrossRef]
- Louzguine-Luzgin, D.V.; Bazlov, A.I. Crystallization of FCC and BCC liquid metals studied by molecular dynamics simulation. Metals 2020, 10, 1532. [Google Scholar] [CrossRef]
- Han, C.; Zhou, Z.; Chen, X.; Xu, Y.; Jiang, W.; Yang, B.; Xu, B.; Liu, D. Structures and electronic properties of AlnVn (n = 2–12) clusters from ab initio calculations. Comput. Theor. Chem. 2020, 1176, 112746. [Google Scholar] [CrossRef]
- Xie, H.; Zhou, Z.; Xiong, H.; Chen, X.; Deng, P.; Wang, Y.; Yang, H.; Meng, C. Theoretical calculation and experimental study on the separation mechanism of PbS-Sb2S3. J. Mol. Struct. 2023, 1273, 134327. [Google Scholar] [CrossRef]
- Kurochkin, A.R.; Popee, P.S.; Yagodin, D.; Borisenko, A.V.; Okhapkin, A.V. Density of copper-aluminum alloys at temperatures up to 1400 °C determined by the gamma-ray technique. High Temp. 2013, 51, 197–205. [Google Scholar] [CrossRef]
- Plevachuk, Y.; Egry, I.; Brillo, J.; Holland-Moritz, D.; Kaban, I. Density and atomic volume in liquid Al-Fe and Al-Ni binary alloys. Int. J. Mater. Res. 2007, 98, 107–111. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1995, 47, 558–561. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Francis, G.P.; Payne, M.C. Finite basis set corrections to total energy pseudopotential calculations. J. Phys. Condens. Matter 1990, 2, 4395–4404. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 100, 191–198. [Google Scholar] [CrossRef]
- Guthrie, R.I.; Iida, T. The Physical Properties of Liquid Metals; Clarendon Press: Oxford, UK, 1988; pp. 71–72. [Google Scholar]
- Furukawa, K. The radial distribution curves of liquids by diffraction methods. Rep. Prog. Phys. 1962, 25, 395–440. [Google Scholar] [CrossRef]
- Tao, D. A new model of thermodynamics of liquid mixtures and its application to liquid alloys. Thermochim. Acta 2000, 363, 105–113. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; Tao, D. Estimation of Component Activities and Molar Excess Gibbs Energy of 19 Binary Liquid Alloys from Partial Pair Distribution Functions in Literature. Metals 2023, 13, 996. [Google Scholar] [CrossRef]
- Hill, T.L. Statistical Mechanics: Principles and Selected Applications; Courier Corporation: Chelmsford, MA, USA, 1957; p. 185. [Google Scholar]
- Hildebrande, J.H. The Regular Solution Model for Binary Alloy. Proc. Natl. Acad. Sci. USA 1927, 13, 267–272. [Google Scholar]
- Hildebrande, J.H. Solubility VIII Regular Solutions. Am. Chem. Soc. 1929, 51, 66–80. [Google Scholar] [CrossRef]
- Wilson, G.M. Vapor-Liquid Equilibrium. XI. A New Expression for the Excess Free Energy of Mixing. J. Am. Chem. Soc. 1964, 86, 127–130. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamics of high polymer solutions. J. Chem. Phys. 1941, 9, 660. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Miedema, A.R.; Châtel, P.F.; Boer, F.R. Cohesion in alloys-fundamentals of a semi-empirical model. Phys. B 1980, 100, 1–28. [Google Scholar] [CrossRef]
- Miedema, A.R. The electronegativity parameter for transition metals: Heat of formation and charge transfer in alloys. J. Less Common Met. 1973, 32, 117–136. [Google Scholar] [CrossRef]
- Tanaka, T.; Gokcen, N.A.; Spencer, P.J.; Morita, Z.; Tida, T. Evaluation of Interaction Parameters in Dilute Liquid Ternary Alloys by a Solution Model Based on the Free Volume Theory. Int. J. Mater. Res. 1993, 84, 100–105. [Google Scholar] [CrossRef]
- Ciobanu, B.C.; Pop, F.C.; Popescu, P.G. A fast way to compute definite integrals. Soft Comput. 2022, 26, 13485–13488. [Google Scholar] [CrossRef]
- Franke, P.; Neuschütz, D. Binary Systems. Part 1. Elements and Binary Systems from Ag-Al to Au-Tl. In Thermodynamic Properties of Inorganic Materials of Landolt-Börnstein-Group IV Physical Chemistry; Springer: Berlin/Heidelberg, Germany, 2002; Volume 19, p. 151. [Google Scholar]



| Parameters | Step of Al50Cu50 (1400 K) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0–1000 | 0–2000 | 0–3000 | 0–4000 | 0–5000 | 1000–2000 | 2000–3000 | 3000–4000 | 4000–5000 | ||
| r0/Å | i-i | 2.153 | 2.148 | 2.159 | 2.153 | 2.153 | 2.164 | 2.153 | 2.153 | 2.153 |
| i-j | 1.949 | 1.949 | 1.960 | 1.954 | 1.954 | 1.954 | 1.949 | 1.965 | 1.954 | |
| j-j | 1.954 | 1.954 | 1.954 | 1.954 | 1.954 | 1.954 | 1.949 | 1.954 | 1.965 | |
| rm/Å | i-i | 2.809 | 2.796 | 2.786 | 2.782 | 2.778 | 2.781 | 2.766 | 2.772 | 2.763 |
| i-j | 2.551 | 2.547 | 2.542 | 2.541 | 2.538 | 2.543 | 2.532 | 2.534 | 2.529 | |
| j-j | 2.557 | 2.551 | 2.544 | 2.545 | 2.542 | 2.540 | 2.525 | 2.548 | 2.526 | |
| g(rm) | i-i | 2.189 | 2.156 | 2.143 | 2.129 | 2.141 | 2.128 | 2.127 | 2.089 | 2.191 |
| i-j | 3.174 | 3.124 | 3.102 | 3.090 | 3.083 | 3.075 | 3.062 | 3.057 | 3.059 | |
| j-j | 2.495 | 2.369 | 2.327 | 2.320 | 2.305 | 2.246 | 2.251 | 2.298 | 2.253 | |
| r1/Å | i-i | 3.828 | 3.844 | 3.827 | 3.806 | 3.805 | 3.862 | 3.811 | 3.699 | 3.803 |
| i-j | 3.569 | 3.535 | 3.552 | 3.577 | 3.588 | 3.506 | 3.607 | 3.633 | 3.618 | |
| j-j | 3.543 | 3.536 | 3.543 | 3.539 | 3.506 | 3.531 | 3.554 | 3.416 | 3.452 | |
| g(r1) | i-i | 0.722 | 0.725 | 0.710 | 0.705 | 0.707 | 0.728 | 0.679 | 0.678 | 0.716 |
| i-j | 0.498 | 0.512 | 0.524 | 0.533 | 0.532 | 0.523 | 0.544 | 0.552 | 0.525 | |
| j-j | 0.564 | 0.591 | 0.574 | 0.571 | 0.571 | 0.617 | 0.539 | 0.556 | 0.559 | |
| Parameters | Step of Al50Ni50 (1923 K) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0–1000 | 0–2000 | 0–3000 | 0–4000 | 0–5000 | 1000–2000 | 2000–3000 | 3000–4000 | 4000–5000 | ||
| r0/Å | i-i | 2.153 | 2.153 | 2.159 | 2.159 | 2.153 | 2.159 | 2.153 | 2.159 | 2.153 |
| i-j | 1.858 | 1.858 | 1.858 | 1.863 | 1.858 | 1.858 | 1.858 | 1.868 | 1.954 | |
| j-j | 1.954 | 1.954 | 1.949 | 1.954 | 1.954 | 1.954 | 1.954 | 1.954 | 1.954 | |
| rm/Å | i-i | 2.877 | 2.858 | 2.846 | 2.838 | 2.837 | 2.833 | 2.817 | 2.816 | 2.836 |
| i-j | 2.459 | 2.456 | 2.454 | 2.452 | 2.451 | 2.452 | 2.449 | 2.447 | 2.444 | |
| j-j | 2.557 | 2.557 | 2.553 | 2.552 | 2.551 | 2.557 | 2.546 | 2.548 | 2.545 | |
| g(rm) | i-i | 1.811 | 1.795 | 1.783 | 1.779 | 1.780 | 1.785 | 1.766 | 1.771 | 1.784 |
| i-j | 3.351 | 3.268 | 3.238 | 3.241 | 3.234 | 3.186 | 3.180 | 3.250 | 3.207 | |
| j-j | 1.825 | 1.835 | 1.832 | 1.815 | 1.809 | 1.844 | 1.828 | 1.764 | 1.788 | |
| r1/Å | i-i | 3.916 | 3.823 | 3.841 | 3.785 | 3.777 | 3.666 | 3.847 | 3.684 | 3.703 |
| i-j | 3.565 | 3.534 | 3.563 | 3.575 | 3.587 | 3.515 | 3.595 | 3.598 | 3.611 | |
| j-j | 3.454 | 3.433 | 3.436 | 3.459 | 3.456 | 3.405 | 3.442 | 3.500 | 3.449 | |
| g(r1) | i-i | 0.863 | 0.868 | 0.852 | 0.856 | 0.861 | 0.849 | 0.821 | 0.853 | 0.879 |
| i-j | 0.483 | 0.496 | 0.500 | 0.494 | 0.491 | 0.507 | 0.508 | 0.474 | 0.479 | |
| j-j | 0.679 | 0.672 | 0.670 | 0.677 | 0.675 | 0.663 | 0.666 | 0.691 | 0.667 | |
| Parameters | Step of Al50Fe50 (1823 K) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0–1000 | 0–2000 | 0–3000 | 0–4000 | 0–5000 | 1000–2000 | 2000–3000 | 3000–4000 | 4000–5000 | ||
| r0/Å | i-i | 2.062 | 2.148 | 2.153 | 2.153 | 2.159 | 2.153 | 2.153 | 2.159 | 2.148 |
| i-j | 1.954 | 1.954 | 1.960 | 1.954 | 1.954 | 1.949 | 1.954 | 1.954 | 1.954 | |
| j-j | 1.734 | 1.750 | 1.750 | 1.755 | 1.750 | 1.750 | 1.761 | 1.745 | 1.755 | |
| rm/Å | i-i | 2.793 | 2.792 | 2.798 | 2.802 | 2.798 | 2.791 | 2.811 | 2.820 | 2.782 |
| i-j | 2.512 | 2.512 | 2.511 | 2.510 | 2.511 | 2.511 | 2.508 | 2.509 | 2.513 | |
| j-j | 2.310 | 2.304 | 2.308 | 2.304 | 2.311 | 2.296 | 2.316 | 2.293 | 2.342 | |
| g(rm) | i-i | 2.101 | 2.072 | 2.058 | 2.043 | 2.047 | 2.044 | 2.031 | 2.003 | 2.064 |
| i-j | 3.180 | 3.070 | 3.058 | 3.057 | 3.050 | 2.959 | 3.035 | 3.054 | 3.019 | |
| j-j | 2.208 | 2.179 | 2.169 | 2.151 | 2.143 | 2.152 | 2.150 | 2.099 | 2.125 | |
| r1/Å | i-i | 3.825 | 3.823 | 3.827 | 3.827 | 3.825 | 3.820 | 3.833 | 3.826 | 3.820 |
| i-j | 3.561 | 3.532 | 3.539 | 3.542 | 3.544 | 3.508 | 3.546 | 3.547 | 3.555 | |
| j-j | 3.385 | 3.377 | 3.380 | 3.374 | 3.367 | 3.370 | 3.384 | 3.308 | 3.251 | |
| g(r1) | i-i | 0.745 | 0.737 | 0.739 | 0.737 | 0.734 | 0.729 | 0.743 | 0.730 | 0.721 |
| i-j | 0.497 | 0.517 | 0.512 | 0.512 | 0.508 | 0.535 | 0.501 | 0.512 | 0.495 | |
| j-j | 0.515 | 0.528 | 0.524 | 0.522 | 0.523 | 0.541 | 0.517 | 0.510 | 0.510 | |
| System | Step | MIVM | RSM | Wilson | NRTL | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym | Non-Sym | Sym | Non-Sym | Sym | Non-Sym | Sym | Non-Sym | ||||||||
| Bij | Bji | Bij | Bji | w/kT | w/kT | Aij | Aji | Aij | Aji | τij | τji | τij | τji | ||
| Al-Cu (1400 K) | 0–1000 | 1.43 | 1.27 | 1.27 | 1.22 | −2.00 | −2.67 | 1.92 | 0.94 | 1.86 | 0.84 | −0.24 | −0.36 | −0.20 | −0.24 |
| 0–2000 | 1.44 | 1.31 | 1.30 | 1.27 | −2.05 | −2.99 | 1.99 | 0.95 | 1.92 | 0.85 | −0.27 | −0.36 | −0.24 | −0.26 | |
| 0–3000 | 1.43 | 1.33 | 1.28 | 1.27 | −2.04 | −2.96 | 2.01 | 0.95 | 1.93 | 0.85 | −0.28 | −0.36 | −0.24 | −0.25 | |
| 0–4000 | 1.44 | 1.33 | 1.27 | 1.27 | −2.05 | −2.85 | 2.02 | 0.95 | 1.92 | 0.83 | −0.28 | −0.36 | −0.24 | −0.24 | |
| 0–5000 | 1.43 | 1.33 | 1.25 | 1.24 | −2.01 | −2.65 | 2.02 | 0.94 | 1.87 | 0.83 | −0.29 | −0.36 | −0.21 | −0.23 | |
| 1000–2000 | 1.44 | 1.35 | 1.32 | 1.31 | −2.09 | −3.29 | 2.05 | 0.95 | 1.98 | 0.87 | −0.30 | −0.36 | −0.27 | −0.28 | |
| 2000–3000 | 1.43 | 1.37 | 1.25 | 1.28 | −2.02 | −2.85 | 2.08 | 0.94 | 1.94 | 0.82 | −0.31 | −0.36 | −0.24 | −0.22 | |
| 3000–4000 | 1.46 | 1.34 | 1.21 | 1.19 | −2.08 | −2.16 | 2.03 | 0.96 | 1.80 | 0.80 | −0.29 | −0.38 | −0.17 | −0.19 | |
| 4000–5000 | 1.38 | 1.34 | 1.22 | 1.18 | −1.84 | −2.17 | 2.03 | 0.91 | 1.78 | 0.80 | −0.29 | −0.32 | −0.16 | −0.20 | |
| Al-Ni (1923 K) | 0–1000 | 1.74 | 1.81 | 1.37 | 1.39 | −3.81 | −4.08 | 3.06 | 1.03 | 2.37 | 0.81 | −0.59 | −0.56 | −0.33 | −0.31 |
| 0–2000 | 1.74 | 1.75 | 1.36 | 1.41 | −3.62 | −3.98 | 2.98 | 1.02 | 2.39 | 0.80 | −0.56 | −0.55 | −0.34 | −0.31 | |
| 0–3000 | 1.74 | 1.74 | 1.35 | 1.39 | −3.54 | −3.91 | 2.96 | 1.03 | 2.36 | 0.79 | −0.56 | −0.55 | −0.33 | −0.30 | |
| 0–4000 | 1.71 | 1.77 | 1.33 | 1.41 | −3.58 | −3.85 | 3.00 | 1.01 | 2.39 | 0.78 | −0.57 | −0.54 | −0.34 | −0.28 | |
| 0–5000 | 1.76 | 1.76 | 1.32 | 1.40 | −3.56 | −3.78 | 2.99 | 1.04 | 2.37 | 0.78 | −0.57 | −0.57 | −0.34 | −0.28 | |
| 1000–2000 | 1.58 | 1.70 | 1.31 | 1.40 | −3.47 | −3.62 | 2.89 | 0.93 | 2.38 | 0.78 | −0.53 | −0.46 | −0.34 | −0.27 | |
| 2000–3000 | 1.76 | 1.72 | 1.33 | 1.38 | −3.39 | −3.84 | 2.93 | 1.03 | 2.35 | 0.79 | −0.55 | −0.56 | −0.32 | −0.29 | |
| 3000–4000 | 1.81 | 1.83 | 1.29 | 1.44 | −3.68 | −3.79 | 3.10 | 1.07 | 2.44 | 0.76 | −0.60 | −0.59 | −0.37 | −0.26 | |
| 4000–5000 | 1.78 | 1.77 | 1.29 | 1.38 | −3.53 | −3.52 | 3.00 | 1.05 | 2.34 | 0.76 | −0.57 | −0.58 | −0.32 | −0.25 | |
| Al-Fe (1823 K) | 0–1000 | 1.52 | 1.40 | 1.27 | 1.30 | −2.42 | −3.14 | 2.25 | 0.95 | 2.09 | 0.79 | −0.34 | −0.42 | −0.26 | −0.24 |
| 0–2000 | 1.47 | 1.38 | 1.27 | 1.31 | −2.23 | −3.15 | 2.21 | 0.91 | 2.10 | 0.79 | −0.32 | −0.39 | −0.27 | −0.24 | |
| 0–3000 | 1.47 | 1.38 | 1.26 | 1.31 | −2.25 | −3.18 | 2.22 | 0.91 | 2.12 | 0.78 | −0.32 | −0.38 | −0.27 | −0.23 | |
| 0–4000 | 1.47 | 1.39 | 1.26 | 1.32 | −2.27 | −3.21 | 2.24 | 0.91 | 2.12 | 0.78 | −0.33 | −0.38 | −0.28 | −0.23 | |
| 0–5000 | 1.47 | 1.39 | 1.26 | 1.32 | −2.27 | −3.19 | 2.24 | 0.91 | 2.12 | 0.78 | −0.33 | −0.38 | −0.27 | −0.23 | |
| 1000–2000 | 1.42 | 1.35 | 1.27 | 1.31 | −2.05 | −3.13 | 2.18 | 0.88 | 2.10 | 0.79 | −0.30 | −0.35 | −0.27 | −0.24 | |
| 2000–3000 | 1.46 | 1.39 | 1.26 | 1.34 | −2.28 | −3.29 | 2.24 | 0.91 | 2.16 | 0.78 | −0.33 | −0.38 | −0.29 | −0.23 | |
| 3000–4000 | 1.46 | 1.43 | 1.26 | 1.31 | −2.34 | −3.14 | 2.30 | 0.91 | 2.11 | 0.79 | −0.35 | −0.38 | −0.27 | −0.23 | |
| 4000–5000 | 1.46 | 1.38 | 1.26 | 1.24 | −2.24 | −2.81 | 2.23 | 0.91 | 2.00 | 0.79 | −0.33 | −0.38 | −0.22 | −0.23 | |
| System | nswi1/3 | nswj1/3 | Φi | Φj | Vi2/3 | Vj2/3 | ui | uj | p | r/p |
|---|---|---|---|---|---|---|---|---|---|---|
| Al-Cu (1400 K) | 1.39 | 1.47 | 4.2 | 4.55 | 4.6 | 3.7 | 0.07 | 0.04 | 12.3 | 0.57 |
| Al-Ni (1923 K) | 1.39 | 1.75 | 4.2 | 5.2 | 4.6 | 3.5 | 0.07 | 0.04 | 12.3 | 1.9 |
| Al-Fe (1823 K) | 1.39 | 1.77 | 4.2 | 4.93 | 4.6 | 3.7 | 0.07 | 0.04 | 12.3 | 1.9 |
| System | Step | MIVM | RSM | Wilson | NRTL | Miedema | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SD | ARD/% | SD | ARD/% | SD | ARD/% | SD | ARD/% | SD | ARD/% | ||
| Al-Cu (1400 K) | 0–1000 | 0.051 | 21 | 0.096 | 208 | 0.163 | 520 | 0.170 | 568 | 0.077 | 143 |
| 0–2000 | 0.053 | 19 | 0.094 | 200 | 0.160 | 502 | 0.167 | 553 | |||
| 0–3000 | 0.055 | 19 | 0.094 | 201 | 0.159 | 496 | 0.166 | 547 | |||
| 0–4000 | 0.054 | 19 | 0.094 | 200 | 0.158 | 493 | 0.166 | 545 | |||
| 0–5000 | 0.055 | 20 | 0.095 | 206 | 0.159 | 496 | 0.166 | 548 | |||
| Average | 0.054 | 20 | 0.095 | 203 | 0.160 | 501 | 0.167 | 552 | |||
| 0–1000 | 0.051 | 21 | 0.096 | 208 | 0.163 | 520 | 0.170 | 568 | |||
| 1000–2000 | 0.056 | 20 | 0.092 | 194 | 0.157 | 485 | 0.165 | 538 | |||
| 2000–3000 | 0.058 | 21 | 0.095 | 204 | 0.156 | 480 | 0.164 | 534 | |||
| 3000–4000 | 0.054 | 20 | 0.093 | 196 | 0.157 | 485 | 0.164 | 536 | |||
| 4000–5000 | 0.059 | 24 | 0.103 | 235 | 0.161 | 506 | 0.169 | 562 | |||
| Average | 0.056 | 21 | 0.096 | 208 | 0.159 | 495 | 0.166 | 548 | |||
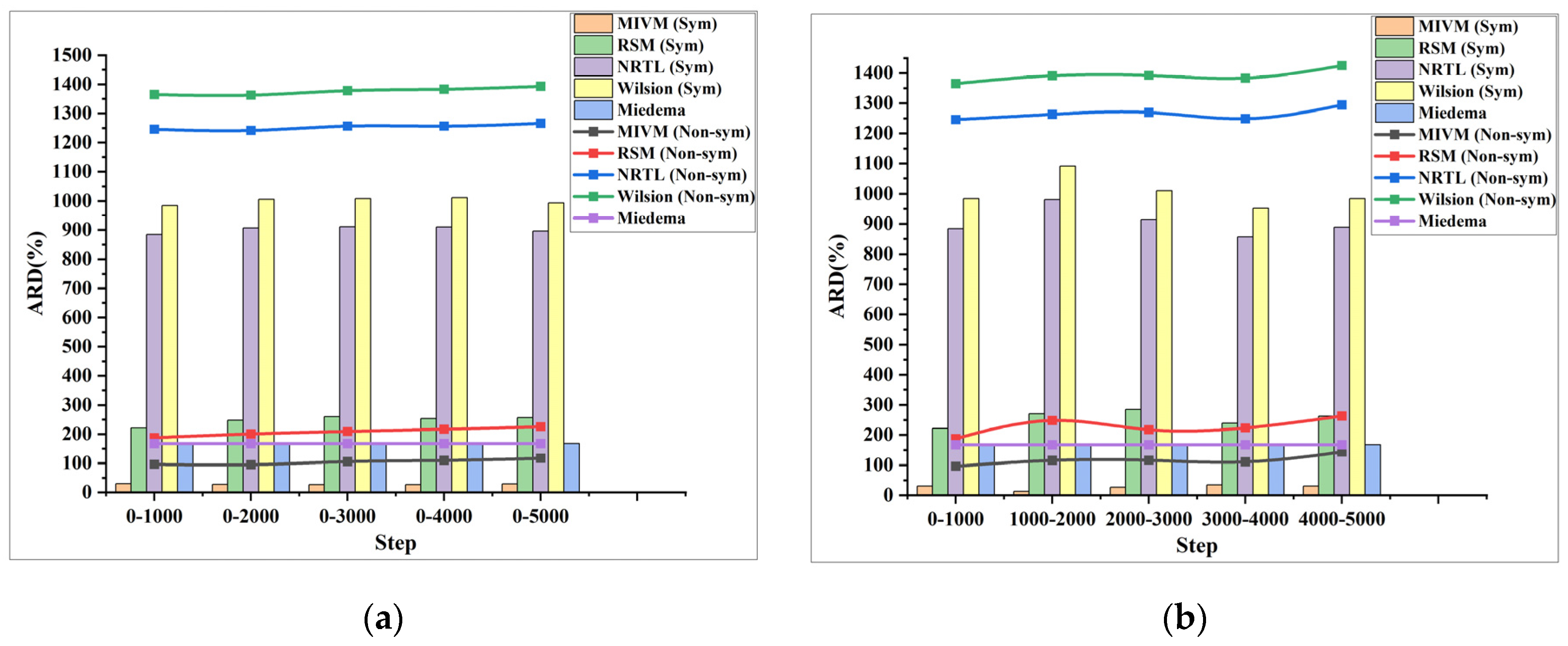
| Al-Ni (1923 K) | 0–1000 | 0.076 | 30 | 0.065 | 222 | 0.157 | 884 | 0.169 | 984 | 0.053 | 167 |
| 0–2000 | 0.071 | 28 | 0.071 | 248 | 0.160 | 907 | 0.171 | 1005 | |||
| 0–3000 | 0.070 | 27 | 0.073 | 260 | 0.160 | 911 | 0.171 | 1008 | |||
| 0–4000 | 0.069 | 27 | 0.072 | 254 | 0.160 | 911 | 0.172 | 1012 | |||
| 0–5000 | 0.074 | 29 | 0.072 | 257 | 0.159 | 896 | 0.170 | 993 | |||
| Average | 0.072 | 28 | 0.071 | 248 | 0.159 | 902 | 0.170 | 1001 | |||
| 0–1000 | 0.076 | 30 | 0.065 | 222 | 0.157 | 884 | 0.169 | 984 | |||
| 1000–2000 | 0.052 | 13 | 0.075 | 271 | 0.167 | 981 | 0.179 | 1091 | |||
| 2000–3000 | 0.070 | 27 | 0.078 | 285 | 0.161 | 914 | 0.171 | 1010 | |||
| 3000–4000 | 0.083 | 34 | 0.069 | 239 | 0.154 | 856 | 0.166 | 952 | |||
| 4000–5000 | 0.076 | 30 | 0.074 | 263 | 0.158 | 889 | 0.169 | 984 | |||
| Average | 0.071 | 27 | 0.072 | 256 | 0.160 | 905 | 0.171 | 1004 | |||
| Al-Fe (1823 K) | 0–1000 | 0.077 | 40 | 0.028 | 24 | 0.105 | 117 | 0.113 | 130 | 0.033 | 29 |
| 0–2000 | 0.066 | 36 | 0.036 | 31 | 0.109 | 123 | 0.117 | 136 | |||
| 0–3000 | 0.067 | 36 | 0.035 | 30 | 0.108 | 123 | 0.117 | 136 | |||
| 0–4000 | 0.068 | 36 | 0.034 | 30 | 0.108 | 122 | 0.116 | 135 | |||
| 0–5000 | 0.068 | 36 | 0.035 | 30 | 0.108 | 122 | 0.116 | 135 | |||
| Average | 0.069 | 37 | 0.034 | 29 | 0.108 | 121 | 0.116 | 135 | |||
| 0–1000 | 0.077 | 40 | 0.028 | 24 | 0.105 | 117 | 0.113 | 130 | |||
| 1000–2000 | 0.055 | 31 | 0.044 | 40 | 0.113 | 129 | 0.121 | 143 | |||
| 2000–3000 | 0.068 | 36 | 0.034 | 29 | 0.108 | 122 | 0.117 | 136 | |||
| 3000–4000 | 0.072 | 38 | 0.032 | 27 | 0.106 | 119 | 0.115 | 133 | |||
| 4000–5000 | 0.066 | 36 | 0.036 | 31 | 0.109 | 123 | 0.117 | 137 | |||
| Average | 0.067 | 36 | 0.035 | 30 | 0.108 | 122 | 0.117 | 136 | |||
| System | Step | MIVM | RSM | Wilson | NRTL | Miedema | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SD/J | ARD/% | SD/J | ARD/% | SD/J | ARD/% | SD/J | ARD/% | SD/J | ARD/% | ||
| Al-Cu (1400 K) | 0–1000 | 1077 | 11 | 5816 | 47 | 8360 | 69 | 8541 | 71 | 4933 | 39 |
| 0–2000 | 1158 | 12 | 5704 | 46 | 8269 | 69 | 8468 | 70 | |||
| 0–3000 | 1262 | 13 | 5727 | 46 | 8233 | 68 | 8441 | 70 | |||
| 0–4000 | 1312 | 13 | 5709 | 46 | 8220 | 68 | 8427 | 70 | |||
| 0–5000 | 1262 | 13 | 5789 | 46 | 8233 | 68 | 8443 | 70 | |||
| Average | 1214 | 12 | 5749 | 46 | 8263 | 69 | 8464 | 70 | |||
| 0–1000 | 1077 | 11 | 5816 | 47 | 8360 | 69 | 8541 | 71 | |||
| 1000–2000 | 1486 | 15 | 5635 | 45 | 8176 | 68 | 8395 | 69 | |||
| 2000–3000 | 1599 | 16 | 5765 | 46 | 8150 | 68 | 8376 | 69 | |||
| 3000–4000 | 1525 | 15 | 5660 | 45 | 8173 | 68 | 8382 | 69 | |||
| 4000–5000 | 1221 | 13 | 6133 | 49 | 8294 | 69 | 8516 | 71 | |||
| Average | 1382 | 14 | 5802 | 46 | 8231 | 68 | 8442 | 70 | |||
| Al-Ni (1923 K) | 0–1000 | 6729 | 29 | 10,611 | 40 | 17,138 | 65 | 17,745 | 68 | 9361 | 35 |
| 0–2000 | 5836 | 26 | 11,134 | 42 | 17,271 | 66 | 17,849 | 69 | |||
| 0–3000 | 5719 | 25 | 11,356 | 43 | 17,292 | 66 | 17,863 | 69 | |||
| 0–4000 | 5543 | 25 | 11,246 | 42 | 17,287 | 66 | 17,880 | 69 | |||
| 0–5000 | 6365 | 28 | 11,301 | 43 | 17,212 | 66 | 17,790 | 68 | |||
| Average | 6038 | 27 | 11,130 | 42 | 17,240 | 66 | 17,825 | 68 | |||
| 0–1000 | 6729 | 29 | 10,611 | 40 | 17,138 | 65 | 17,745 | 68 | |||
| 1000–2000 | 2359 | 11 | 11,550 | 44 | 17,659 | 68 | 18,248 | 70 | |||
| 2000–3000 | 5673 | 25 | 11,793 | 45 | 17,315 | 66 | 17,871 | 69 | |||
| 3000–4000 | 8190 | 35 | 10,965 | 41 | 16,978 | 65 | 17,584 | 67 | |||
| 4000–5000 | 6778 | 30 | 11,404 | 43 | 17,169 | 66 | 17,744 | 68 | |||
| Average | 5946 | 26 | 11,265 | 43 | 17,252 | 66 | 17,839 | 68 | |||
| Al-Fe (1823 K) | 0–1000 | 7016 | 67 | 2324 | 22 | 6241 | 59 | 6576 | 62 | 2647 | 25 |
| 0–2000 | 5775 | 55 | 2805 | 26 | 6397 | 60 | 6732 | 63 | |||
| 0–3000 | 5825 | 56 | 2759 | 26 | 6386 | 60 | 6726 | 63 | |||
| 0–4000 | 5973 | 57 | 2712 | 25 | 6360 | 60 | 6707 | 63 | |||
| 0–5000 | 5958 | 57 | 2717 | 25 | 6362 | 60 | 6709 | 63 | |||
| Average | 6110 | 58 | 2664 | 25 | 6349 | 60 | 6690 | 63 | |||
| 0–1000 | 7016 | 67 | 2324 | 22 | 6241 | 59 | 6576 | 62 | |||
| 1000–2000 | 4535 | 43 | 3298 | 31 | 6553 | 62 | 6890 | 65 | |||
| 2000–3000 | 5911 | 56 | 2674 | 25 | 6367 | 60 | 6715 | 63 | |||
| 3000–4000 | 6439 | 61 | 2538 | 24 | 6279 | 59 | 6648 | 63 | |||
| 4000–5000 | 5736 | 55 | 2777 | 26 | 6392 | 60 | 6737 | 63 | |||
| Average | 5927 | 57 | 2722 | 25 | 6366 | 60 | 6713 | 63 | |||
| System | Step | MIVM | RSM | Wilson | NRTL | Miedema | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SD | ARD/% | SD | ARD/% | SD | ARD/% | SD | ARD/% | SD | ARD/% | ||
| Al-Cu (1400 K) | 0–1000 | 0.062 | 69 | 0.076 | 125 | 0.174 | 587 | 0.182 | 641 | 0.077 | 143 |
| 0–2000 | 0.061 | 46 | 0.071 | 96 | 0.170 | 559 | 0.177 | 614 | |||
| 0–3000 | 0.062 | 48 | 0.071 | 98 | 0.170 | 559 | 0.178 | 616 | |||
| 0–4000 | 0.063 | 56 | 0.073 | 108 | 0.171 | 568 | 0.179 | 625 | |||
| 0–5000 | 0.063 | 70 | 0.076 | 127 | 0.174 | 585 | 0.182 | 641 | |||
| Average | 0.062 | 58 | 0.073 | 111 | 0.172 | 572 | 0.180 | 628 | |||
| 0–1000 | 0.062 | 69 | 0.076 | 125 | 0.174 | 587 | 0.182 | 641 | |||
| 1000–2000 | 0.061 | 34 | 0.069 | 75 | 0.166 | 533 | 0.174 | 590 | |||
| 2000–3000 | 0.065 | 59 | 0.073 | 108 | 0.171 | 567 | 0.180 | 627 | |||
| 3000–4000 | 0.071 | 115 | 0.090 | 184 | 0.180 | 624 | 0.188 | 679 | |||
| 4000–5000 | 0.071 | 118 | 0.090 | 183 | 0.181 | 629 | 0.188 | 682 | |||
| Average | 0.066 | 79 | 0.079 | 135 | 0.175 | 588 | 0.182 | 644 | |||
| Al-Ni (1923 K) | 0–1000 | 0.032 | 97 | 0.057 | 188 | 0.193 | 1246 | 0.204 | 1365 | 0.053 | 167 |
| 0–2000 | 0.032 | 95 | 0.060 | 201 | 0.193 | 1242 | 0.204 | 1362 | |||
| 0–3000 | 0.035 | 106 | 0.062 | 209 | 0.194 | 1256 | 0.205 | 1378 | |||
| 0–4000 | 0.036 | 110 | 0.064 | 217 | 0.194 | 1257 | 0.205 | 1383 | |||
| 0–5000 | 0.038 | 117 | 0.066 | 226 | 0.195 | 1266 | 0.206 | 1393 | |||
| Average | 0.034 | 105 | 0.062 | 208 | 0.194 | 1253 | 0.205 | 1376 | |||
| 0–1000 | 0.032 | 97 | 0.057 | 188 | 0.193 | 1246 | 0.204 | 1365 | |||
| 1000–2000 | 0.037 | 116 | 0.071 | 249 | 0.194 | 1263 | 0.206 | 1391 | |||
| 2000–3000 | 0.038 | 116 | 0.064 | 218 | 0.195 | 1270 | 0.206 | 1392 | |||
| 3000–4000 | 0.036 | 111 | 0.066 | 224 | 0.193 | 1249 | 0.205 | 1383 | |||
| 4000–5000 | 0.045 | 144 | 0.074 | 263 | 0.197 | 1294 | 0.209 | 1425 | |||
| Average | 0.038 | 117 | 0.066 | 228 | 0.195 | 1264 | 0.206 | 1391 | |||
| Al-Fe (1823 K) | 0–1000 | 0.020 | 13 | 0.010 | 4 | 0.123 | 146 | 0.133 | 163 | 0.033 | 29 |
| 0–2000 | 0.022 | 14 | 0.010 | 4 | 0.123 | 146 | 0.133 | 162 | |||
| 0–3000 | 0.023 | 15 | 0.010 | 3 | 0.123 | 145 | 0.132 | 162 | |||
| 0–4000 | 0.024 | 15 | 0.010 | 4 | 0.122 | 144 | 0.132 | 161 | |||
| 0–5000 | 0.023 | 15 | 0.010 | 3 | 0.122 | 145 | 0.132 | 162 | |||
| Average | 0.022 | 14 | 0.010 | 4 | 0.123 | 145 | 0.133 | 162 | |||
| 0–1000 | 0.020 | 13 | 0.010 | 4 | 0.123 | 146 | 0.133 | 163 | |||
| 1000–2000 | 0.022 | 14 | 0.010 | 4 | 0.123 | 145 | 0.133 | 162 | |||
| 2000–3000 | 0.027 | 17 | 0.010 | 4 | 0.121 | 142 | 0.131 | 160 | |||
| 3000–4000 | 0.022 | 14 | 0.010 | 4 | 0.123 | 145 | 0.133 | 162 | |||
| 4000–5000 | 0.008 | 5 | 0.014 | 10 | 0.128 | 154 | 0.137 | 169 | |||
| Average | 0.020 | 13 | 0.011 | 5 | 0.124 | 147 | 0.133 | 163 | |||
| System | Step | MIVM | RSM | Wilson | NRTL | Miedema | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SD/J | ARD/% | SD/J | ARD/% | SD/J | ARD/% | SD/J | ARD/% | SD/J | ARD/% | ||
| Al-Cu (1400 K) | 0–1000 | 3172 | 23 | 4510 | 35 | 8686 | 72 | 8881 | 74 | 4933 | 39 |
| 0–2000 | 2368 | 16 | 3892 | 29 | 8556 | 71 | 8763 | 73 | |||
| 0–3000 | 2451 | 17 | 3940 | 29 | 8559 | 71 | 8773 | 73 | |||
| 0–4000 | 2741 | 19 | 4161 | 32 | 8601 | 72 | 8815 | 73 | |||
| 0–5000 | 3215 | 23 | 4546 | 35 | 8681 | 72 | 8885 | 74 | |||
| Average | 2789 | 20 | 4210 | 32 | 8616 | 72 | 8823 | 73 | |||
| 0–1000 | 3172 | 23 | 4510 | 35 | 8686 | 72 | 8881 | 74 | |||
| 1000–2000 | 1704 | 13 | 3326 | 24 | 8433 | 70 | 8653 | 72 | |||
| 2000–3000 | 2821 | 19 | 4162 | 32 | 8600 | 72 | 8823 | 73 | |||
| 3000–4000 | 4340 | 34 | 5496 | 44 | 8849 | 74 | 9042 | 75 | |||
| 4000–5000 | 4420 | 34 | 5483 | 44 | 8869 | 74 | 9055 | 75 | |||
| Average | 3292 | 25 | 4595 | 35 | 8687 | 72 | 8891 | 74 | |||
| Al-Ni (1923 K) | 0–1000 | 6859 | 25 | 9853 | 37 | 18,861 | 72 | 19,332 | 74 | 9361 | 35 |
| 0–2000 | 6807 | 25 | 10,154 | 38 | 18,843 | 72 | 19,324 | 74 | |||
| 0–3000 | 7239 | 26 | 10,344 | 39 | 18,902 | 73 | 19,379 | 75 | |||
| 0–4000 | 7398 | 27 | 10,518 | 40 | 18,901 | 73 | 19,396 | 75 | |||
| 0–5000 | 7672 | 28 | 10,699 | 40 | 18,938 | 73 | 19,431 | 75 | |||
| Average | 7195 | 26 | 10,314 | 39 | 18,889 | 73 | 19,372 | 75 | |||
| 0–1000 | 6859 | 25 | 9853 | 37 | 18,861 | 72 | 19,332 | 74 | |||
| 1000–2000 | 7629 | 28 | 11,148 | 42 | 18,926 | 73 | 19,425 | 75 | |||
| 2000–3000 | 7643 | 28 | 10,534 | 40 | 18,953 | 73 | 19,429 | 75 | |||
| 3000–4000 | 7435 | 27 | 10,659 | 40 | 18,866 | 72 | 19,399 | 75 | |||
| 4000–5000 | 8566 | 32 | 11,415 | 43 | 19,047 | 73 | 19,543 | 75 | |||
| Average | 7626 | 28 | 10,722 | 40 | 18,930 | 73 | 19,425 | 75 | |||
| Al-Fe (1823 K) | 0–1000 | 1209 | 12 | 463 | 4 | 6968 | 66 | 7328 | 69 | 2647 | 25 |
| 0–2000 | 1324 | 13 | 436 | 4 | 6951 | 65 | 7312 | 69 | |||
| 0–3000 | 1409 | 14 | 370 | 3 | 6933 | 65 | 7302 | 69 | |||
| 0–4000 | 1485 | 14 | 326 | 3 | 6920 | 65 | 7292 | 69 | |||
| 0–5000 | 1424 | 14 | 363 | 3 | 6931 | 65 | 7300 | 69 | |||
| Average | 1370 | 13 | 392 | 3 | 6940 | 65 | 7307 | 69 | |||
| 0–1000 | 1209 | 12 | 463 | 4 | 6968 | 66 | 7328 | 69 | |||
| 1000–2000 | 1330 | 13 | 479 | 4 | 6949 | 65 | 7312 | 69 | |||
| 2000–3000 | 1746 | 17 | 236 | 3 | 6873 | 65 | 7258 | 68 | |||
| 3000–4000 | 1315 | 13 | 456 | 4 | 6950 | 65 | 7314 | 69 | |||
| 4000–5000 | 233 | 2 | 1305 | 12 | 7135 | 67 | 7459 | 70 | |||
| Average | 1166 | 11 | 588 | 5 | 6975 | 66 | 7334 | 69 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Chen, X.; Zhang, T.; Hang, J.; Tao, D. Estimation of Activity and Molar Excess Gibbs Energy of Binary Liquid Alloys Al-Cu, Al-Ni, and Al-Fe from the Partial Radial Distribution Function Simulated by Ab Initio Molecular Dynamics. Metals 2023, 13, 2011. https://doi.org/10.3390/met13122011
Lu Y, Chen X, Zhang T, Hang J, Tao D. Estimation of Activity and Molar Excess Gibbs Energy of Binary Liquid Alloys Al-Cu, Al-Ni, and Al-Fe from the Partial Radial Distribution Function Simulated by Ab Initio Molecular Dynamics. Metals. 2023; 13(12):2011. https://doi.org/10.3390/met13122011
Chicago/Turabian StyleLu, Yi, Xiumin Chen, Tianao Zhang, Jiulong Hang, and Dongping Tao. 2023. "Estimation of Activity and Molar Excess Gibbs Energy of Binary Liquid Alloys Al-Cu, Al-Ni, and Al-Fe from the Partial Radial Distribution Function Simulated by Ab Initio Molecular Dynamics" Metals 13, no. 12: 2011. https://doi.org/10.3390/met13122011
APA StyleLu, Y., Chen, X., Zhang, T., Hang, J., & Tao, D. (2023). Estimation of Activity and Molar Excess Gibbs Energy of Binary Liquid Alloys Al-Cu, Al-Ni, and Al-Fe from the Partial Radial Distribution Function Simulated by Ab Initio Molecular Dynamics. Metals, 13(12), 2011. https://doi.org/10.3390/met13122011





