Vacancy Formation Energy as an Effective Descriptor for the Catalytic Oxidation of CO by Au Nanoparticles
Abstract
:1. Introduction
2. Nanothermodynamic Model
2.1. The Relationship between the Vacancy Transfer Energy and Debye Temperature
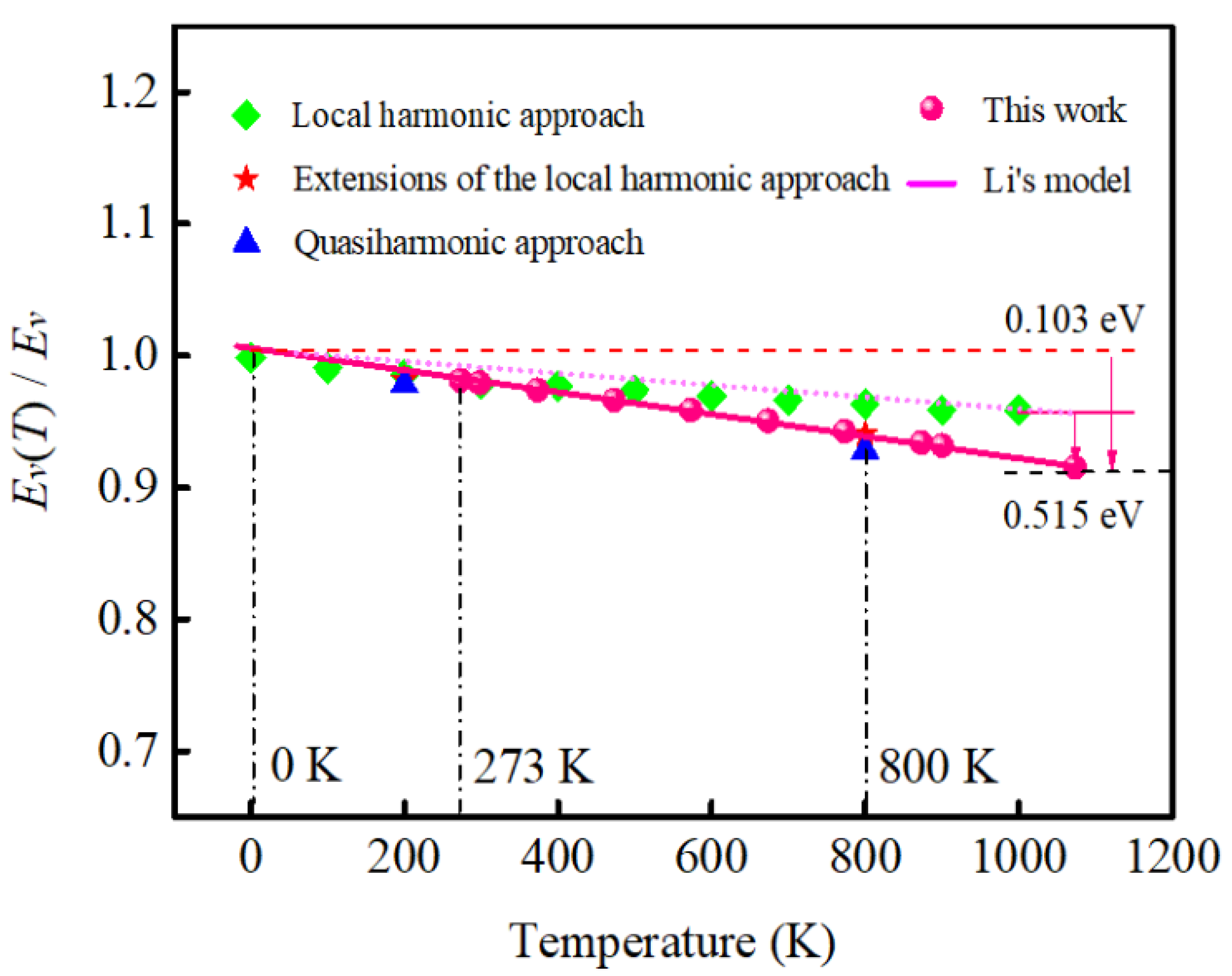
2.2. The Relationship between the Vacancy Formation Energy and Debye temperature
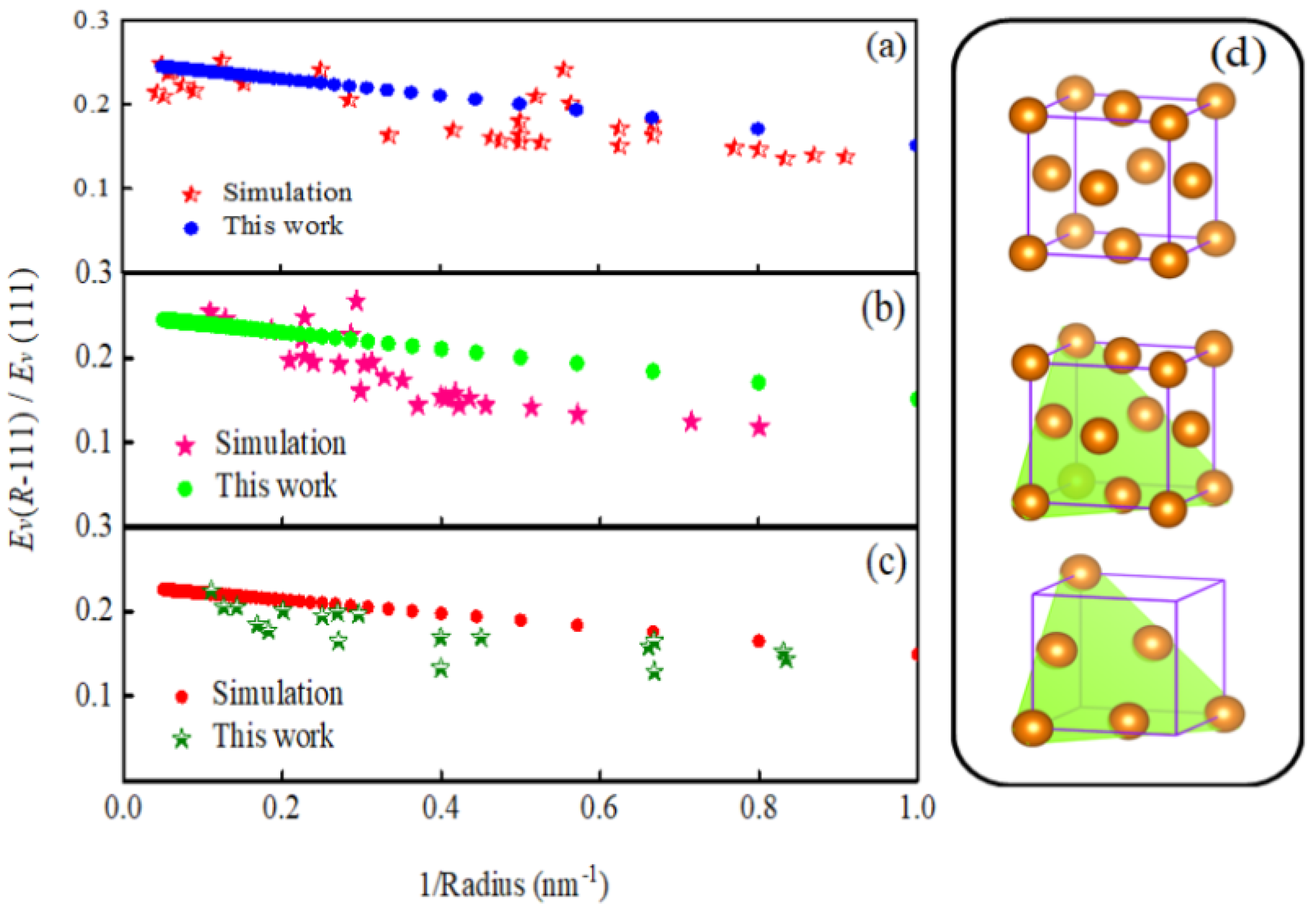
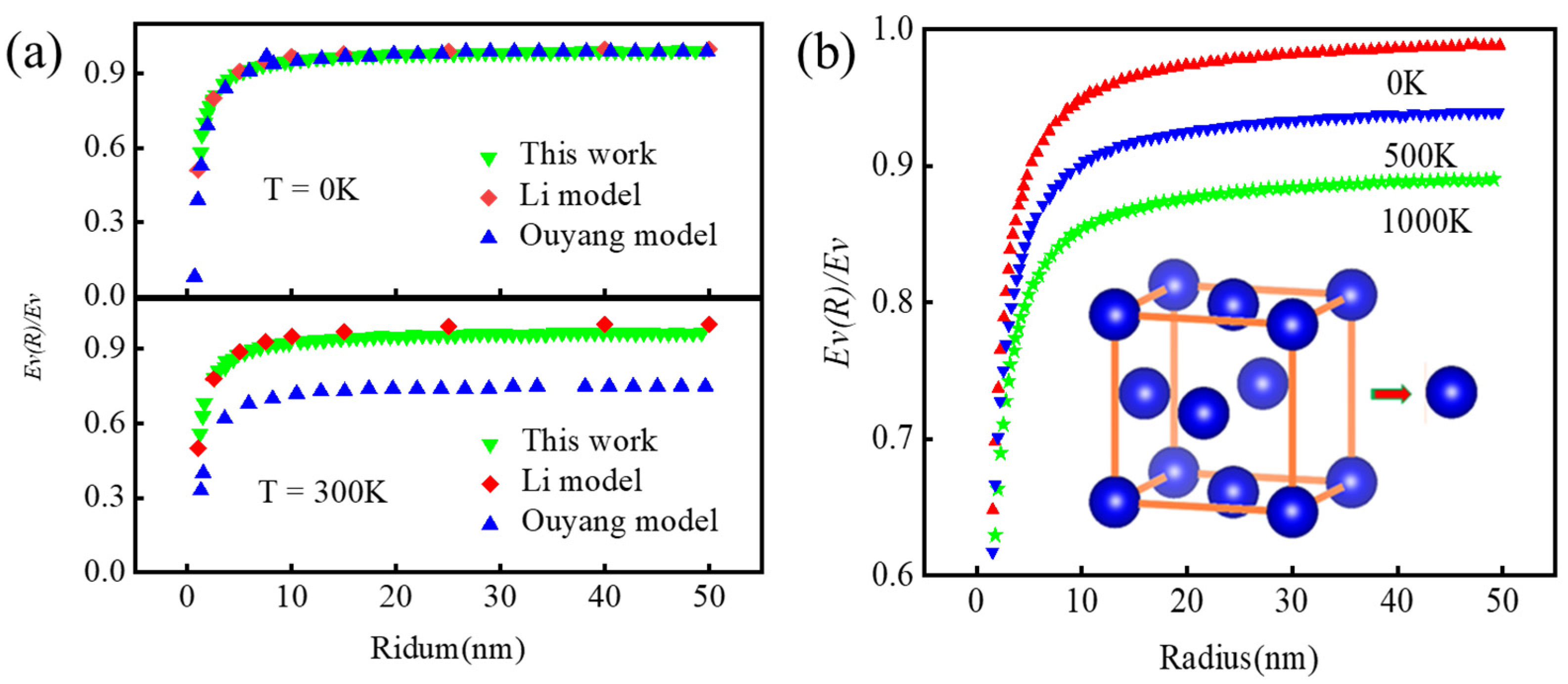
2.3. The Size Effect of the Debye Temperature
3. Results and Discussion
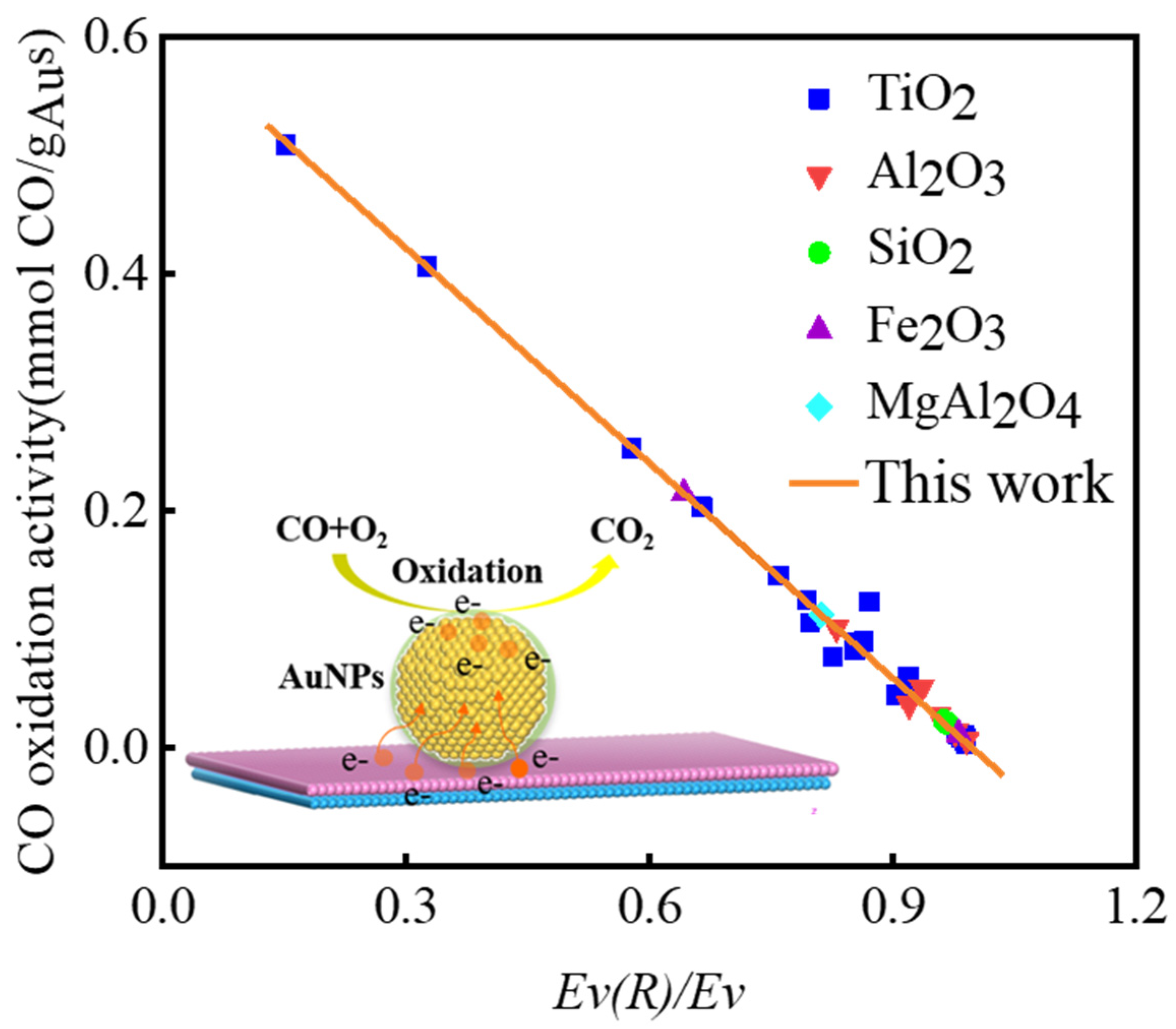
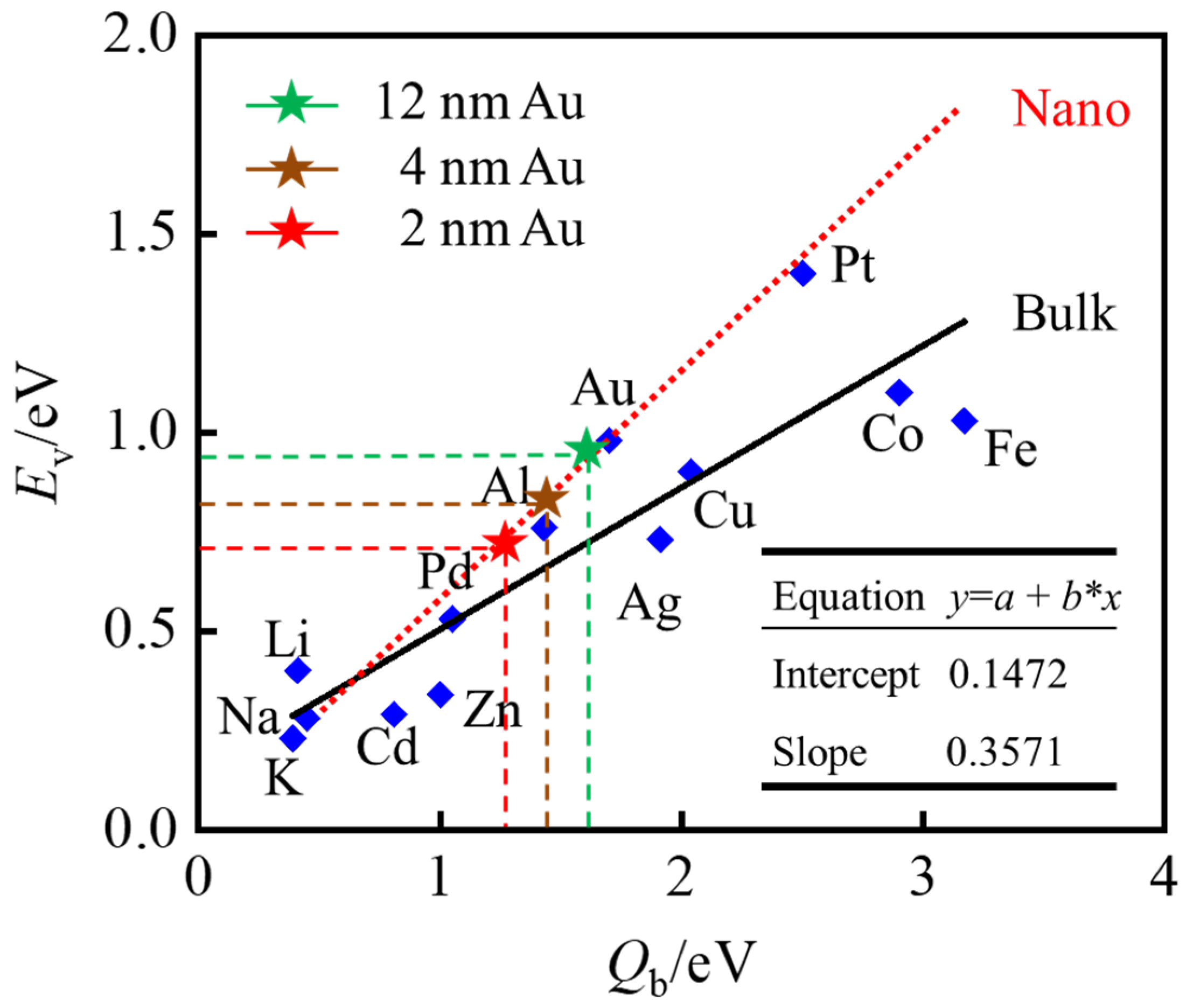
3.1. Relationship between Vacancy Formation Energy and Catalytic Activity
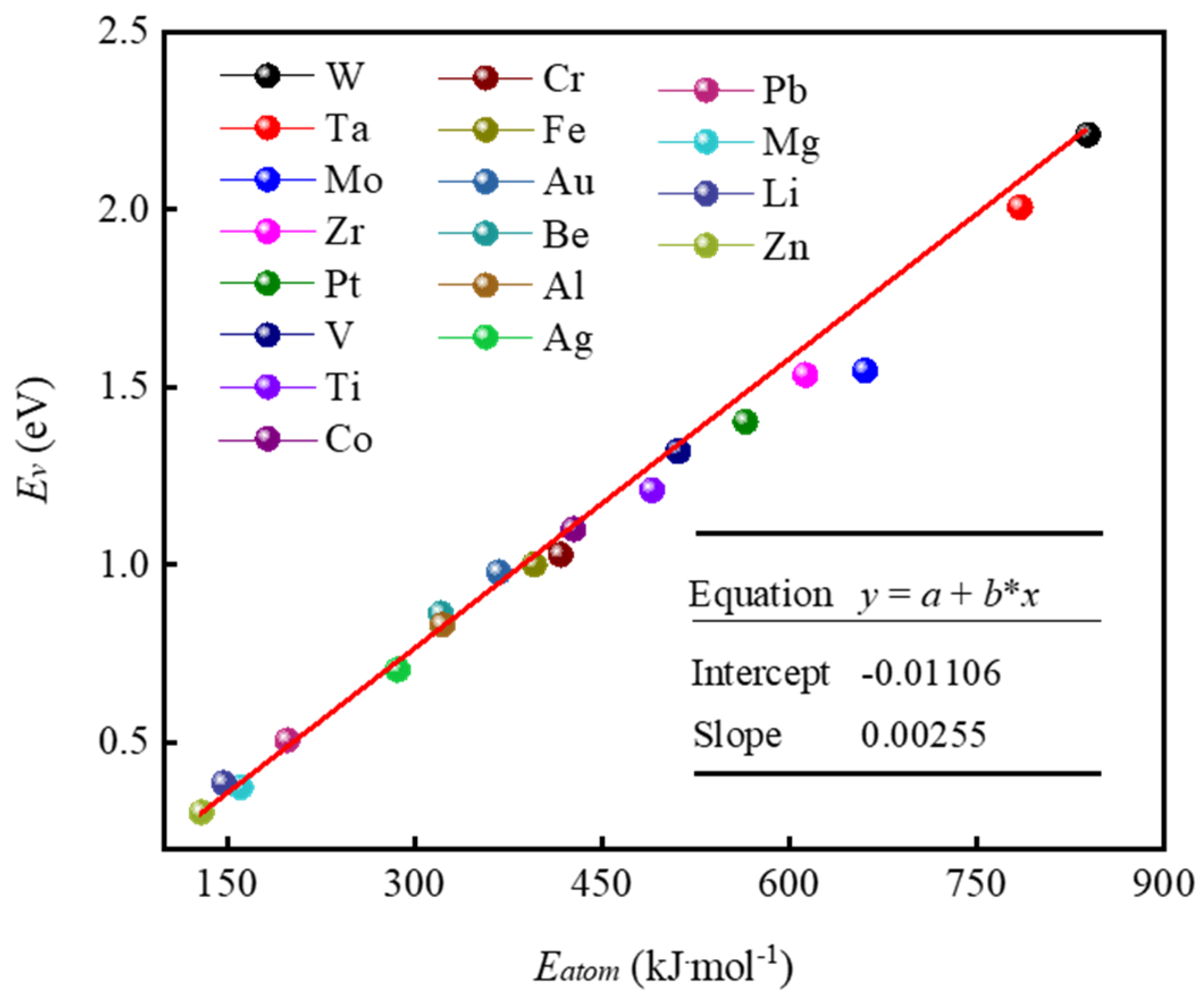
3.2. Vacancy Formation Energy Model
3.3. Essence of Vacancy Formation Energy
3.4. Relationships between Vacancy Formation Energy, Diffusion Activation Energy, and Adsorption Energy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hammer, B.; Norskov, J.K. Why gold is the noblest of all the metals. Nature 1995, 376, 238–240. [Google Scholar] [CrossRef]
- Palma, V.; Ruocco, C.; Cortese, M.; Renda, S.; Meloni, E.; Festa, G.; Martino, M. Platinum based catalysts in the water gas shift reaction: Recent advances. Metals 2020, 10, 866. [Google Scholar] [CrossRef]
- Knauss, S.J.; Guevara, L.N.; Atwater, M.A. Enhanced Performance of Bimetallic Co-Pd Catalysts Prepared by Mechanical Alloying. Metals 2019, 9, 335. [Google Scholar] [CrossRef]
- Manolis, S.; Hermenegildo, G. Catalysis by supported gold nanoparticles: Beyond aerobic oxidative processes. Chem. Rev. 2012, 112, 4469–4506. [Google Scholar]
- Thompson, D.T. Using gold nanoparticles for catalysis. Nano Today 2007, 2, 40–43. [Google Scholar] [CrossRef]
- Haruta, M. When gold is not noble: Catalysis by nanoparticles. Chem. Rec. 2003, 3, 75–87. [Google Scholar] [CrossRef]
- Tai, M.C.; Gentle, A.; De Silva, K.S.B.; Arnold, M.D.; Van der Lingen, E.; Cortie, M.B. Thermal stability of nanoporous Raney gold catalyst. Metals 2015, 5, 1197–1211. [Google Scholar] [CrossRef]
- Zhou, X.C.; Xu, W.L.; Liu, G.K.; Panda, D.; Chen, P. Size-dependent catalytic activity and dynamics of gold nanoparticles at the single-molecule level. J. Am. Chem. Soc. 2010, 132, 138–146. [Google Scholar] [CrossRef]
- Lin, C.H.; Compton, R.G. Size effects in nanoparticle catalysis at nanoparticle modified electrodes: The interplay of diffusion and chemical reactions. J. Phys. Chem. C 2017, 121, 2521–2528. [Google Scholar] [CrossRef]
- Guczi, L.; Beck, A.; Pászti, Z. Gold catalysis: Effect of particle size on reactivity towards various substrates. Catal. Today 2012, 181, 26–32. [Google Scholar] [CrossRef]
- Zhang, F.Z.; Zhao, X.F.; Feng, C.H.; Li, B.; Chen, T.; Lu, W.; Lei, X.D.; Xu, S.L. Crystal-face-selective supporting of gold nanoparticles on layered double hydroxide as efficient catalyst for epoxidation of styrene. ACS Catal. 2011, 1, 232–237. [Google Scholar] [CrossRef]
- Hvolbæk, B.; Janssens, T.V.W.; Clausen, B.S.; Falsig, H.; Christensen, C.H.; Nørskov, J.K. Catalytic activity of Au nanoparticles. Nano Today 2007, 2, 14–18. [Google Scholar] [CrossRef]
- Lin, C.; Tao, K.; Hua, D.Y.; Ma, Z.; Zhou, S.H. Size effect of gold nanoparticles in catalytic reduction of p-nitrophenol with NaBH4. Molecules 2013, 18, 12609–12620. [Google Scholar] [CrossRef] [PubMed]
- Laoufi, I.; Saint-Lager, M.C.; Lazzari, R.; Jupille, J.; Robach, O.; Garaudée, S.; Cabailh, G.; Dolle, P.; Cruguel, H.; Bailly, A. Size and catalytic activity of supported gold nanoparticles: An in operando study during CO oxidation. J. Phys. Chem. C 2011, 115, 4673–4679. [Google Scholar] [CrossRef]
- Valden, M.; Pak, S.; Lai, X.; Goodman, D.W. Structure sensitivity of CO oxidation over model Au/TiO2 catalysts. Catal. Lett. 1998, 56, 7–10. [Google Scholar] [CrossRef]
- Chiu, C.Y.; Chung, P.J.; Lao, K.U.; Liao, C.W.; Huang, M.H. Facet-dependent catalytic activity of gold nanocubes, octahedra, and rhombic dodecahedra toward 4-nitroaniline reduction. J. Phys. Chem. C 2012, 116, 23757–23763. [Google Scholar] [CrossRef]
- Lang, S.M.; Bernhardt, T.M.; Barnett, R.N.; Landman, U. Temperature-tunable selective methane catalysis on Au2+: From cryogenic partial oxidation yielding formaldehyde to cold ethylene production. J. Phys. Chem. C 2011, 115, 6788–6795. [Google Scholar] [CrossRef]
- Sun, J.T.; Metcalfe, I.S.; Sahibzada, M. Deactivation of Cu/ZnO/Al2O3 methanol synthesis catalyst by sintering. Ind. Eng. Chem. Res. 1999, 38, 3868–3872. [Google Scholar] [CrossRef]
- Liu, Y.L.; Yang, Z.; Zhang, X.Y.; He, Y.F.; Feng, J.T.; Li, D.Q. Shape/Crystal Facet of Ceria Induced Well-Dispersed and Stable Au Nanoparticles for the Selective Hydrogenation of Phenylacetylene. Catal. Lett. 2019, 149, 361–372. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.H.; Wu, J.X.; Wang, Z.P.; Dong, Y.P.; Wang, H.W.; Brash, J.L.; Yuan, L.; Chen, H. Gold nanoparticle–protein conjugate dually-responsive to pH and temperature for modulation of enzyme activity. J. Mater. Chem. B 2019, 7, 3260–3267. [Google Scholar] [CrossRef]
- Wang, H.W.; Gu, X.K.; Zhu, J.F.; Chen, S. Disentangling the size-dependent geometric and electronic effects of palladium nanocatalysts beyond selectivity. Sci. Adv. 2019, 5, eaat6413. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.F.; Wang, H. Facet-dependent catalytic activities of Au nanoparticles enclosed by high-index facets. ACS Catal. 2014, 4, 4027–4033. [Google Scholar] [CrossRef]
- Tang, F.W.; Song, X.Y.; Wang, H.B.; Liu, X.M.; Nie, Z.R. The thermal stability of the nanograin structure in a weak solute segregation system. Phys. Chem. Chem. Phys. 2017, 19, 4307–4316. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Li, W.G.; Deng, Y.; Shao, J.X.; Kou, H.B.; Ma, J.Z.; Zhang, X.H.; Li, Y. Theoretical analytical model of vacancy formation energy with simultaneous dependence on surface orientation, temperature, and material size. J. Phys. D 2018, 51, 075308. [Google Scholar] [CrossRef]
- Bedeaux, D.; Kjelstrup, S. Hill’s nano-thermodynamics is equivalent with Gibbs’ thermodynamics for surfaces of constant curvatures. Chem. Phys. Lett. 2018, 707, 40–43. [Google Scholar] [CrossRef]
- Jang, S.; Park, J.; Shin, S.; Yoon, C.; Choi, B.K.; Gong, M.S.; Joo, S.W. Adsorption of 4-biphenylmethanethiolate on different-sized gold nanoparticle surfaces. Langmuir 2004, 20, 1922–1927. [Google Scholar] [CrossRef]
- Tarasevich, Y.G. The dimensional dependence of the thermophysical properties of the nanoscale bodies in Hill’s nanothermodynamic representation. Prot. Met. Phys. Chem. Surf. 2016, 52, 607–611. [Google Scholar] [CrossRef]
- Cahn, R.W. Crystal defects and melting. Nature 1978, 273, 491–492. [Google Scholar] [CrossRef]
- Gorecki, T. Vacancies and changes of physical properties of metals at the melting point. Int. J. Mater. Res. 1974, 65, 426–431. [Google Scholar] [CrossRef]
- Glyde, H.R. Relation of vacancy formation and migration energies to the Debye temperature in solids. J. Phys. Chem. Solids 1967, 28, 2061–2065. [Google Scholar] [CrossRef]
- Yu, X.H.; Zhan, Z.L.; Rong, J.; Liu, Z.; Li, L.; Liu, J.X. Vacancy formation energy and size effects. Chem. Phys. Lett. 2014, 600, 43–45. [Google Scholar] [CrossRef]
- Yu, X.H.; Zhan, Z.L. The effects of the size of nanocrystalline materials on their thermodynamic and mechanical properties. Nanoscale Res. Lett. 2014, 3, 516–520. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.H.; Rong, J.; Zhan, Z.L.; Liu, Z.; Liu, J.X. Effects of grain size and thermodynamic energy on the lattice parameters of metallic nanomaterials. Mater. Des. 2015, 83, 159–163. [Google Scholar] [CrossRef]
- Hu, Z.T.; Yu, X.H. Controlling the chemical reactivity of nanostructured electrode materials by surface reactive sites. Mater. Res. Exp. 2019, 6, 095089. [Google Scholar] [CrossRef]
- Hu, Z.T.; Rong, J.; Zhan, Z.L.; Yu, X.H. Controlling microstructure and electrochemical performance of TiO2 film by defect engineering. Ceram. Int. 2020, 46, 5387–5393. [Google Scholar] [CrossRef]
- Fan, Y.C.; Kang, Q.; Zhang, K.; Rong, J.; Feng, J.; Yu, X.H. Design criterion based on the cohesive energy and defect patterns of VO2 thermally induced phase transition materials. Ceram. Int. 2020, 46, 13615–13621. [Google Scholar] [CrossRef]
- Yu, X.H.; Rong, J.; Zhan, Z.L.; Wang, Y. Thermodynamics of Nanocrystalline Materials; Science Press: Beijing, China, 2020; 145p. [Google Scholar]
- Gladkikh, N.T.; Kryshtal, O.P. On the size dependence of the vacancy formation energy. Funct. Mater. 1999, 6, 823–827. [Google Scholar]
- Yan, Z.; Chinta, S.; Mohamed, A.A.; Fackler, J.P., Jr.; Goodman, D.W. The Role of F-Centers in Catalysis by Au Supported on MgO. J. Am. Chem. Soc. 2005, 127, 1604–1606. [Google Scholar] [CrossRef]
- Yan, Z.; Chinta, S.; Mohamed, A.A.; Fackler, J.P., Jr.; Goodman, D.W. CO Oxidation over Au/TiO2. Cat. Lett. 2006, 111, 15–18. [Google Scholar] [CrossRef]
- Haruta, M. Size-and support-dependency in the catalysis of gold. Catal. Today 1997, 36, 153–166. [Google Scholar] [CrossRef]
- Schubert, M.M.; Hackenberg, S.; Van Veen, A.C.; Muhler, M.; Plzak, V.; Behm, R.J. CO oxidation over supported gold catalysts—“Inert” and “active” support materials and their role for the oxygen supply during reaction. J. Catal. 2001, 197, 113–122. [Google Scholar] [CrossRef]
- Lee, S.J.; Gavriilidis, A. Supported Au catalysts for low-temperature CO oxidation prepared by impregnation. J. Catal. 2002, 206, 305–313. [Google Scholar] [CrossRef]
- Lin, S.D.; Bollinger, M.; Vannice, M.A. Low temperature CO oxidation over Au/TiO2 and Au/SiO2 catalysts. Catal. Lett. 1993, 17, 245–262. [Google Scholar] [CrossRef]
- Okumura, M.; Nakamura, S.; Tsubota, S.; Nakamura, T.; Azuma, M.; Haruta, M. Chemical vapor deposition of gold on Al2O3, SiO2, and TiO2 for the oxidation of CO and of H2. Catal. Lett. 1998, 51, 53–58. [Google Scholar] [CrossRef]
- Schimpf, S.; Lucas, M.; Mohr, C.; Rodemerck, U.; Bruckner, A.; Radnik, J.; Hofmeister, H.; Claus, P. Supported gold nanoparticles: In-depth catalyst characterization and application in hydrogenation and oxidation reactions. Catal. Today 2002, 72, 63–78. [Google Scholar] [CrossRef]
- George, K. On the Size dependence of molar and specific properties of independent nano-phases and those in contact with other phases. J. Mater. Civ. Eng. 2017, 27, 2018–5023. [Google Scholar]
- Sun, C.Q. Size dependence of nanostructures: Impact of bond order deficiency. Prog. Solid State Chem. 2007, 35, 1–159. [Google Scholar] [CrossRef]
- Sun, K. Theoretical investigations on CO oxidation reaction catalyzed by gold nanoparticles. Chin. J. Catal. 2016, 37, 1608–1618. [Google Scholar] [CrossRef]
- Wu, D.Y.; Dong, C.K.; Zhan, H.B.; Du, X.W. Bond-energy-integrated descriptor for oxygen electrocatalysis of transition metal oxides. J. Phys. Chem. Lett. 2018, 9, 3387–3391. [Google Scholar] [CrossRef]
- Ouyang, G.; Zhu, W.G.; Yang, G.W.; Zhu, Z.M. Vacancy formation energy in metallic nanoparticles under high temperature and high pressure. J. Chem. Phys. C 2010, 144, 4929–4933. [Google Scholar] [CrossRef]
- Jiang, Q.; Lu, H.M. Size dependent interface energy and its applications. Surf. Sci. Rep. 2008, 63, 427–464. [Google Scholar] [CrossRef]
- Qi, W. Nanoscopic thermodynamics. Acc. Chem. Res. 2016, 49, 1587–1595. [Google Scholar] [CrossRef] [PubMed]
- Kleis, J.; Greeley, J.; Romero, N.A.; Morozov, V.A.; Falsig, H.; Larsen, A.H.; Lu, J.; Mortensen, J.J.; Dulak, M.; Thygesen, K.S.; et al. Finite size effects in chemical bonding: From small clusters to solids. Catal. Lett. 2011, 141, 1067–1071. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Meng, K.; Ou, P.; Wu, H.; Zhang, Y.; Yu, X. Vacancy Formation Energy as an Effective Descriptor for the Catalytic Oxidation of CO by Au Nanoparticles. Metals 2023, 13, 362. https://doi.org/10.3390/met13020362
Zhang Z, Meng K, Ou P, Wu H, Zhang Y, Yu X. Vacancy Formation Energy as an Effective Descriptor for the Catalytic Oxidation of CO by Au Nanoparticles. Metals. 2023; 13(2):362. https://doi.org/10.3390/met13020362
Chicago/Turabian StyleZhang, Zhiwei, Kun Meng, Peng Ou, Haijun Wu, Yannan Zhang, and Xiaohua Yu. 2023. "Vacancy Formation Energy as an Effective Descriptor for the Catalytic Oxidation of CO by Au Nanoparticles" Metals 13, no. 2: 362. https://doi.org/10.3390/met13020362
APA StyleZhang, Z., Meng, K., Ou, P., Wu, H., Zhang, Y., & Yu, X. (2023). Vacancy Formation Energy as an Effective Descriptor for the Catalytic Oxidation of CO by Au Nanoparticles. Metals, 13(2), 362. https://doi.org/10.3390/met13020362






