Effect of Graphite Morphology on the Thermomechanical Performance of Compacted Graphite Iron
Abstract
1. Introduction
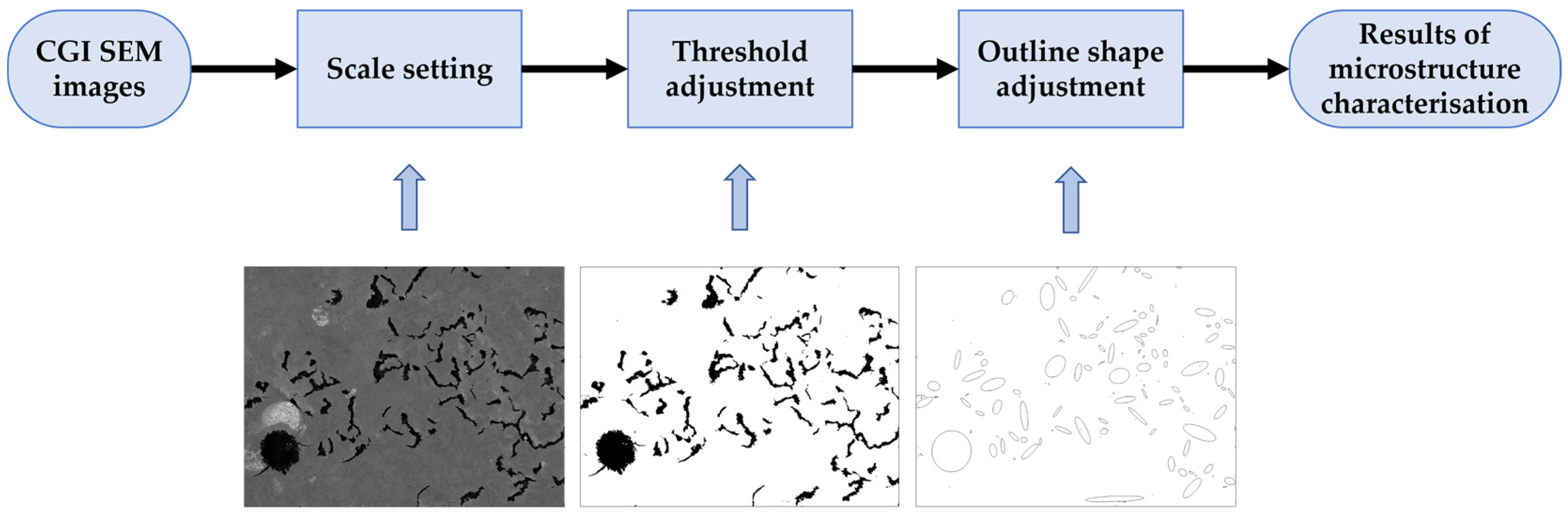
2. Microstructural Characterisation of CGI
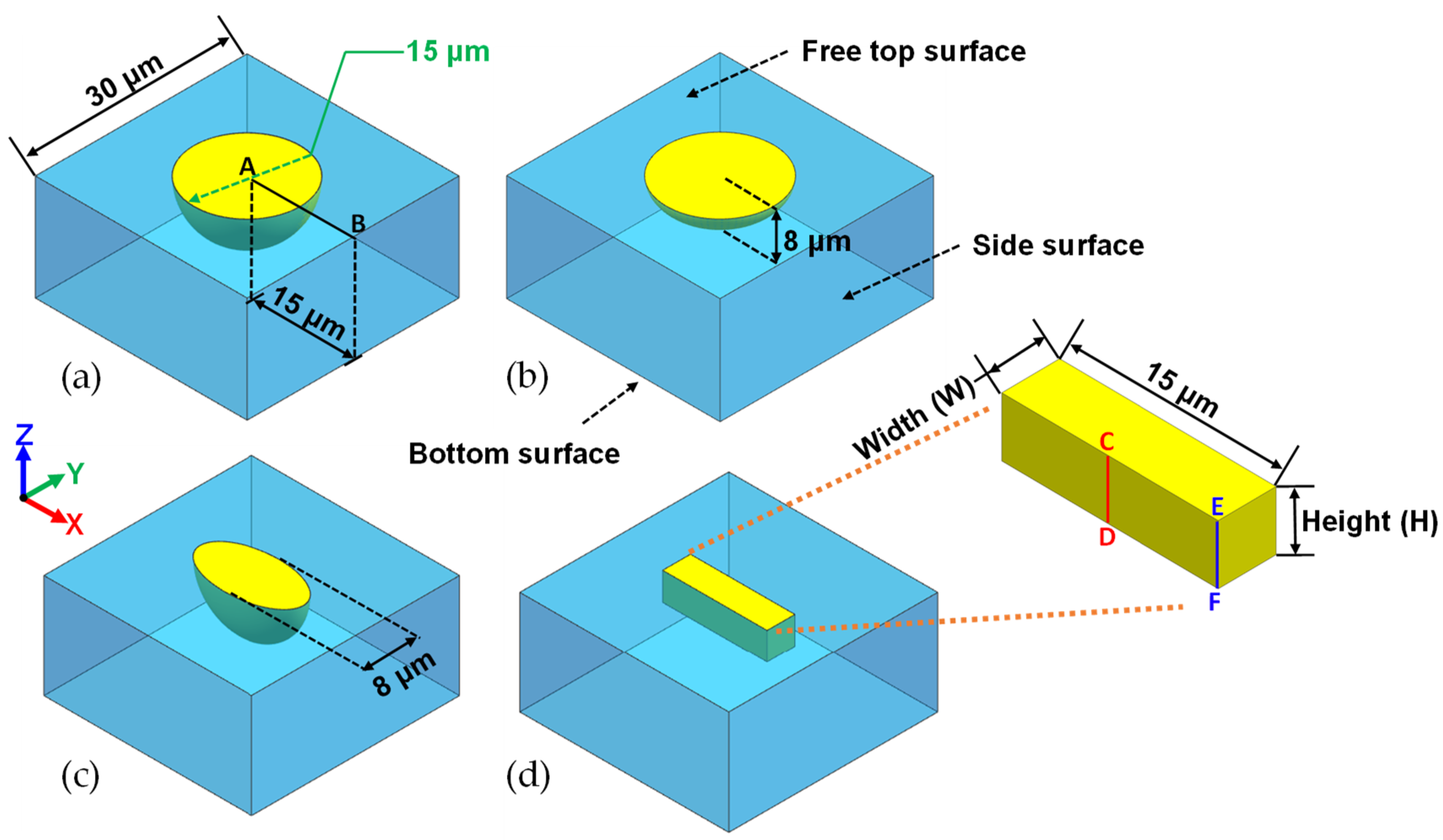
- Spherical (nodular) graphite in 2D was modelled as a sphere in 3D.
- Vermicular graphite inclusions in 2D were simulated as oblate spheroids in 3D.
- Flake graphite inclusions in 2D were considered as plates, becoming cuboid with increasing width and height in 3D.
- The length of the major axis in vermicular graphite and the length of flake graphite were assumed equal to the diameter of a spherical graphite.
- The rectangular matrix domain in 2D corresponded to a cuboid with equal length and width in 3D.
3. Thermal Experiments
4. Numerical Models
4.1. Geometry
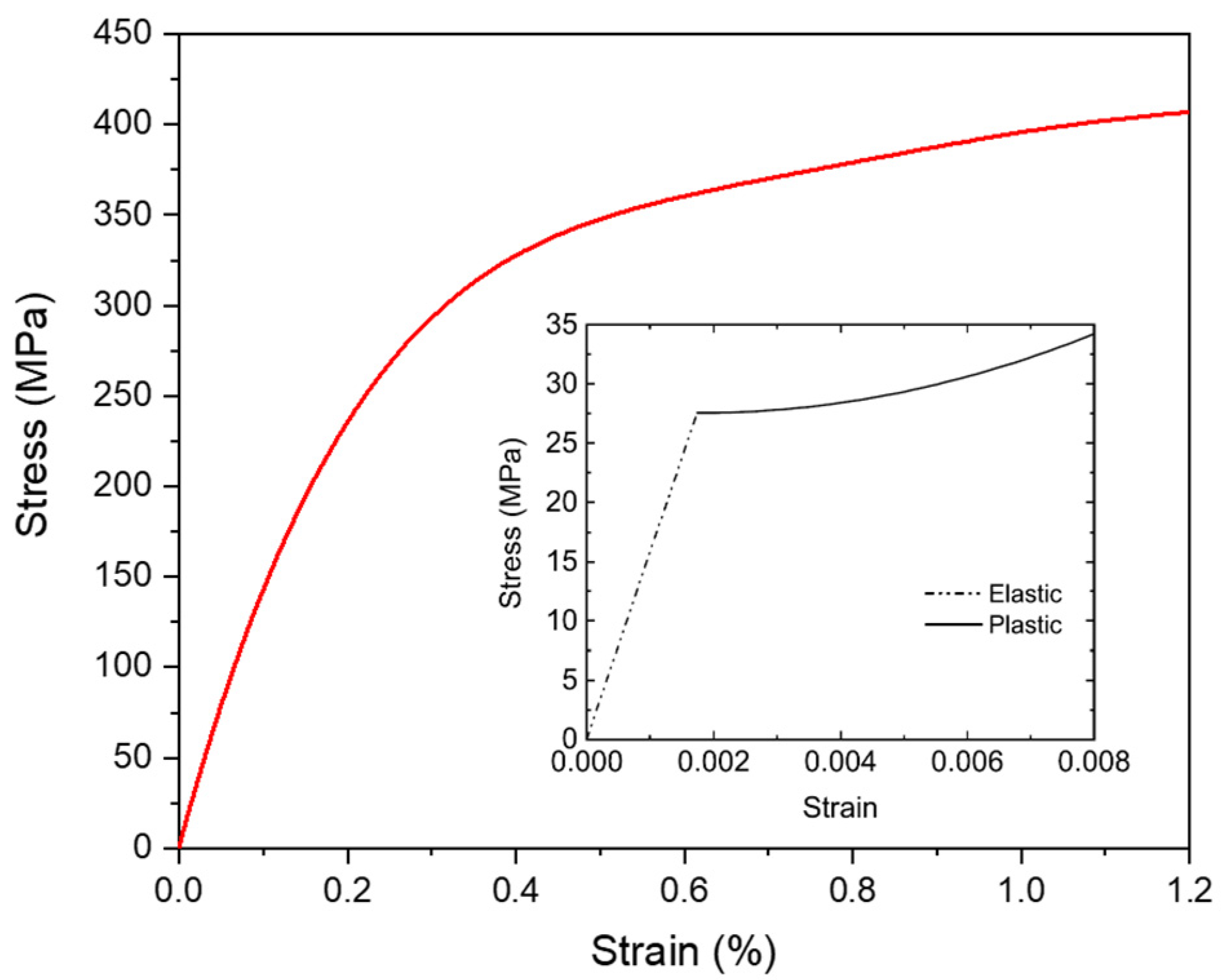
4.2. Constitutive Behaviour
4.3. Boundary and Loading Conditions
5. Results of Numerical Simulations
5.1. Height Profile of Graphite and Matrix in Numerical Simulations
5.2. Temperature of Damage Initiation
5.3. Damage Profile in Graphite at the Interface
5.4. Stress Distribution in Graphite and Matrix
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| area of graphite in 2D | |
| aspect ratio of vermicular graphite | |
| coefficient of thermal expansion | |
| diameter of spherical graphite | |
| fully fixed boundary condition | |
| length of flake graphite | |
| length of square matrix in 2D | |
| length of cubic matrix in 3D | |
| major axis of vermicular graphite | |
| minor axis of vermicular graphite | |
| periodic boundary condition | |
| pressure | |
| von Mises equivalent stress | |
| area of square matrix (2D) | |
| volume of cubic matrix in 3D | |
| volume fraction of graphite | |
| volume of spherical graphite in 3D | |
| plastic strain rate | |
| plastic strain at onset of damage | |
| stress triaxiality | |
| state variable |
References
- Nguyen, D.; Tooptong, S.; Park, K.-H.; Kwon, P. Formation Mechanism of Alumina Layer in Protecting Cubic Boron Nitride Inserts in Turning Cast Irons. Int. J. Mach. Tools Manuf. 2020, 153, 103539. [Google Scholar] [CrossRef]
- Dawson, S. Compacted Graphite Iron—A Material Solution for Modern Diesel Engine Cylinder Blocks and Heads. In Proceedings of the 68th WFC-World Foundry Congress, Chennai, India, 7–10 February 2008; pp. 93–99. [Google Scholar]
- Dawson, S.; Schroeder, T. Practical Applications for Compacted Graphite Iron. AFS Trans. 2004, 47, 1–9. [Google Scholar]
- Yang, W.; Pang, J.; Wang, L.; Wang, S.; Liu, Y.; Hui, L.; Li, S.; Zhang, Z. Tensile Properties and Damage Mechanisms of Compacted Graphite Iron Based on Microstructural Simulation. Mater. Sci. Eng. A 2021, 814, 141244. [Google Scholar] [CrossRef]
- Guesser, W.L.; Duran, P.V.; Krause, W. Compacted Graphite Iron for Diesel Engine Cylinder Blocks. In Proceedings of the Congrès Le Diesel Aujourd’hui Demain Ec. Cent., Lyon, France, 12–13 May 2004; pp. 1–11. [Google Scholar]
- Essam, M.A.; Shash, A.Y.; Megahed, H.; El-Kashif, E. Effect of Section Thickness on Microstructure and Mechanical Properties of Compacted Graphite Iron for Diesel Engine Applications. Heliyon 2021, 7, e05930. [Google Scholar] [CrossRef]
- Meng, F.; Zhang, Z.; Wu, B.; Hu, W.; Ai, X.; Meng, X.; Ding, Z.; Zhang, L. Turning Processes and Mechanism of Compacted Graphite Iron Used for High Performance Engine. J. Manuf. Process. 2021, 68, 951–960. [Google Scholar] [CrossRef]
- Chen, J.K.; Chen, S.F. Thermal Conductivity of an In-Situ Metal Matrix Composite—Cast Iron. In Metal, Ceramic and Polymeric Composites for Various Uses; Cuppoletti, J., Ed.; IntechOpen: Taiwan, 2011; pp. 211–224. ISBN 978-953-307-353-8. [Google Scholar]
- Fragassa, C.; Babic, M.; Bergmann, C.P.; Minak, G. Predicting the Tensile Behaviour of Cast Alloys by a Pattern Recognition Analysis on Experimental Data. Metals 2019, 9, 557. [Google Scholar] [CrossRef]
- Xu, B.; Rathod, D.; Yebi, A.; Filipi, Z.; Onori, S.; Hoffman, M. A Comprehensive Review of Organic Rankine Cycle Waste Heat Recovery Systems in Heavy-Duty Diesel Engine Applications. Renew. Sustain. Energy Rev. 2019, 107, 145–170. [Google Scholar] [CrossRef]
- Chen, Y.; Pang, J.C.; Li, S.X.; Zou, C.L.; Zhang, Z.F. Damage Mechanism and Fatigue Strength Prediction of Compacted Graphite Iron with Different Microstructures. Int. J. Fatigue 2022, 164, 107126. [Google Scholar] [CrossRef]
- Di Cocco, V.; Iacoviello, F.; Cavallini, M. Damaging Micromechanisms Characterization of a Ferritic Ductile Cast Iron. Eng. Fract. Mech. 2010, 77, 2016–2023. [Google Scholar] [CrossRef]
- Qiu, Y.; Pang, J.C.; Li, S.X.; Yang, E.N.; Fu, W.Q.; Liang, M.X.; Zhang, Z.F. Influence of Thermal Exposure on Microstructure Evolution and Tensile Fracture Behaviors of Compacted Graphite Iron. Mater. Sci. Eng. A 2016, 664, 75–85. [Google Scholar] [CrossRef]
- Di Cocco, V.; Iacoviello, F.; Rossi, A.; Iacoviello, D. Macro and Microscopical Approach to the Damaging Micromechanisms Analysis in a Ferritic Ductile Cast Iron. Theor. Appl. Fract. Mech. 2014, 69, 26–33. [Google Scholar] [CrossRef]
- Norman, V.; Calmunger, M. On the Micro- and Macroscopic Elastoplastic Deformation Behaviour of Cast Iron When Subjected to Cyclic Loading. Int. J. Plast. 2019, 115, 200–215. [Google Scholar] [CrossRef]
- Di Cocco, V.; Iacoviello, F.; Rossi, A.; Cavallini, M.; Natali, S. Graphite Nodules and Fatigue Crack Propagation Micromechanisms in a Ferritic Ductile Cast Iron. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 893–902. [Google Scholar] [CrossRef]
- Tang, C.; Liu, L.; Yang, Z.; Tao, D.; Li, J.; Guo, Q.; Zhen, J.; He, Y.; He, H. Surface Evolution of Vermicular Cast Iron in Ultra-High Temperature Combustion with Different Single-Pulsing Duration. Eng. Fail. Anal. 2022, 141, 106679. [Google Scholar] [CrossRef]
- Qiu, Y.; Pang, J.C.; Yang, E.N.; Li, S.X.; Zhang, Z.F. Transition of Tensile Strength and Damaging Mechanisms of Compacted Graphite Iron with Temperature. Mater. Sci. Eng. A 2016, 677, 290–301. [Google Scholar] [CrossRef]
- Wu, Y.; Li, J.; Yang, Z.; Guo, Y.; Ma, Z.; Liang, M.; Yang, T.; Tao, D. Thermal Conductivity Analysis of Compacted Graphite Cast Iron after a Creep Test. Metall. Mater. Trans. A 2019, 50, 3697–3704. [Google Scholar] [CrossRef]
- Selin, M. Tensile and Thermal Properties in Compacted Graphite Irons at Elevated Temperatures. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2010, 41, 3100–3109. [Google Scholar] [CrossRef]
- Rodriguez, F.J.; Boccardo, A.D.; Dardati, P.M.; Celentano, D.J.; Godoy, L.A. Thermal Expansion of a Spheroidal Graphite Iron: A Micromechanical Approach. Finite Elem. Anal. Des. 2018, 141, 26–36. [Google Scholar] [CrossRef]
- Maijer, D.; Cockcroft, S.; Jacot, A. Modeling of Microstructure and Residual Stress in Cast Iron Calender Rolls. Metall. Mater. Trans. A 2000, 31, 1201–1211. [Google Scholar] [CrossRef]
- Kim, D.-S.; Pyo, C.; Kim, J.; Kim, J.; Lee, H.-K. A Study on Cross-Shaped Structure of Invar Material Using Cold Wire Laser Fillet Welding (Part I: Feasibility Study for Weldability). Metals 2020, 10, 1385. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, X.; Li, B.; Yang, K.; Kong, Y.; Wang, Z. Microstructure and Thermal Expansion of Copper-Based Amorphous Alloys during Structural Relaxation. China Foundry 2020, 17, 8–14. [Google Scholar] [CrossRef]
- Yeon, J.; Yamamoto, M.; Ni, P.; Nakamoto, M.; Tanaka, T. Joining of Metal to Ceramic Plate Using Super-Spread Wetting. Metals 2020, 10, 1377. [Google Scholar] [CrossRef]
- Lin, H.-M.; Lui, T.-S.; Chen, L.-H. Effect of Maximum Temperature on the Cyclic-Heating-Induced Embrittlement of High-Silicon Ferritic Spheroidal-Graphite Cast Iron. Mater. Trans. 2004, 45, 569–576. [Google Scholar] [CrossRef]
- Zhang, Y.; Pang, J.C.; Shen, R.; Yu, Q.; Li, S.; Zhang, Z.Z. Investigation on Tensile Deformation Behavior of Compacted Graphite Iron Based on Cohesive Damage Model. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2018, 713, 260–268. [Google Scholar] [CrossRef]
- Salomonsson, K.; Jarfors, A.E.W. Three-Dimensional Microstructural Characterization of Cast Iron Alloys for Numerical Analyses. Mater. Sci. Forum 2018, 925, 427–435. [Google Scholar] [CrossRef]
- Zhan, Y.; Kaddouri, W.; Kanit, T.; Jiang, Q.; Liu, L.; Imad, A. From Unit Inclusion Cell to Large Representative Volume Element: Comparison of Effective Elastic Properties. Eur. J. Mech.-A/Solids 2022, 92, 104490. [Google Scholar] [CrossRef]
- Safaei, M.; Sheidaei, A.; Baniassadi, M.; Ahzi, S.; Mosavi Mashhadi, M.; Pourboghrat, F. An Interfacial Debonding-Induced Damage Model for Graphite Nanoplatelet Polymer Composites. Comput. Mater. Sci. 2015, 96, 191–199. [Google Scholar] [CrossRef]
- Kihlberg, E.; Norman, V.; Skoglund, P.; Schmidt, P.; Moverare, J. On the Correlation between Microstructural Parameters and the Thermo-Mechanical Fatigue Performance of Cast Iron. Int. J. Fatigue 2021, 145, 106112. [Google Scholar] [CrossRef]
- Anand, L. Elastic Moduli of Gray and Ductile Cast Irons. Scr. Metall. 1982, 16, 173–177. [Google Scholar] [CrossRef]
- Sjögren, T.; Svensson, I.L. Modelling the Effect of Graphite Morphology on the Modulus of Elasticity in Cast Irons. Int. J. Cast Met. Res. 2004, 17, 271–279. [Google Scholar] [CrossRef]
- Fragassa, C.; Radovic, N.; Pavlovic, A.; Minak, G. Comparison of Mechanical Properties in Compacted and Spheroidal Graphite Irons. Tribol. Ind. 2016, 38, 45–56. [Google Scholar]
- Liu, Y.; Li, Y.; Xing, J.; Wang, S.; Zheng, B.; Tao, D.; Li, W. Effect of Graphite Morphology on the Tensile Strength and Thermal Conductivity of Cast Iron. Mater. Charact. 2018, 144, 155–165. [Google Scholar] [CrossRef]
- Šamec, B.; Potrč, I.; Šraml, M. Low Cycle Fatigue of Nodular Cast Iron Used for Railway Brake Discs. Eng. Fail. Anal. 2011, 18, 1424–1434. [Google Scholar] [CrossRef]
- Stefanescu, D.M. The Meritocratic Ascendance of Cast Iron: From Magic to Virtual Cast Iron. Int. J. Met. 2019, 13, 726–752. [Google Scholar] [CrossRef]
- Frishmuth, R.E.; McLaughlin, P.V. Failure Analysis of Cast Irons under General Three-Dimensional Stress States. J. Eng. Mater. Technol. 1976, 98, 69–75. [Google Scholar] [CrossRef]
- Josefson, B.L.; Stigh, U.; Hjelm, H.E. A Nonlinear Kinematic Hardening Model for Elastoplastic Deformations in Grey Cast Iron. J. Eng. Mater. Technol. 1995, 117, 145–150. [Google Scholar] [CrossRef]
- Josefson, B.L.; Hjelm, H.E. Modelling Elastoplastic Deformations in Grey Cast Iron. In Low Cycle Fatigue and Elasto-Plastic Behaviour of Materials; Rie, K.-T., Grünling, H.W., König, G., Neumann, P., Nowack, H., Schwalbe, K.-H., Seeger, T., Eds.; Springer: Dordrecht, The Netherlands, 1992; pp. 465–472. ISBN 978-94-011-2860-5. [Google Scholar]
- Hjelm, H.E. Yield Surface for Grey Cast Iron under Biaxial Stress. J. Eng. Mater. Technol. 1994, 116, 148–154. [Google Scholar] [CrossRef]
- Altenbach, H.; Stoychev, G.B.; Tushtev, K.N. On Elastoplastic Deformation of Grey Cast Iron. Int. J. Plast. 2001, 17, 719–736. [Google Scholar] [CrossRef]
- Andriollo, T.; Zhang, Y.; Fæster, S.; Thorborg, J.; Hattel, J. Impact of Micro-Scale Residual Stress on in-Situ Tensile Testing of Ductile Cast Iron: Digital Volume Correlation vs. Model with Fully Resolved Microstructure vs. Periodic Unit Cell. J. Mech. Phys. Solids 2019, 125, 714–735. [Google Scholar] [CrossRef]
- Andriollo, T.; Thorborg, J.; Hattel, J. The Influence of the Graphite Mechanical Properties on the Constitutive Response of a Ferritic Ductile Cast Iron—A Micromechanical FE Analysis. In Proceedings of the COMPLAS XIII: Proceedings of the XIII International Conference on Computational Plasticity: Fundamentals and applications, Barcelona, Spain, 1–3 September 2015; pp. 632–641. [Google Scholar]
- Andriollo, T.; Thorborg, J.; Tiedje, N.; Hattel, J. A Micro-Mechanical Analysis of Thermo-Elastic Properties and Local Residual Stresses in Ductile Iron Based on a New Anisotropic Model for the Graphite Nodules. Model. Simul. Mater. Sci. Eng. 2016, 24, 55012. [Google Scholar] [CrossRef]
- Palkanoglou, E.N.; Baxevanakis, K.P.; Silberschmidt, V.V. Thermal Debonding of Inclusions in Compacted Graphite Iron: Effect of Matrix Phases. Eng. Fail. Anal. 2022, 139, 106476. [Google Scholar] [CrossRef]
- Seldin, E.J. Stress-Strain Properties of Polycrystalline Graphites in Tension and Compression at Room Temperature. Carbon N. Y. 1966, 4, 177–191. [Google Scholar] [CrossRef]
- Greenstreet, W.L.; Yahr, G.T.; Valachovic, R.S. The Behavior of Graphite under Biaxial Tension. Carbon N. Y. 1973, 11, 43–57. [Google Scholar] [CrossRef]
- Andriollo, T.; Thorborg, J.; Tiedje, N.S.; Hattel, J. Modeling of Damage in Ductile Cast Iron—The Effect of Including Plasticity in the Graphite Nodules. IOP Conf. Ser. Mater. Sci. Eng. 2015, 84, 12027. [Google Scholar] [CrossRef]
- Palkanoglou, E.N.; Cao, M.; Baxevanakis, K.P.; Silberschmidt, V.V. Effect of Graphite-Particle Morphology on Thermomechanical Performance of Compacted Graphite Iron: Numerical Modelling. In Proceedings of the 8th European Congress on Computational Methods in Applied Sciences and Engineering ECCOMAS Congress 2022, Oslo, Norway, 5–9 June 2022. [Google Scholar]
- Palkanoglou, E.N.; Baxevanakis, K.P.; Silberschmidt, V.V. Interfacial Debonding in Compacted Graphite Iron: Effect of Thermal Loading. Procedia Struct. Integr. 2020, 28, 1286–1294. [Google Scholar] [CrossRef]
- Hooputra, H.; Gese, H.; Dell, H.; Werner, H. A Comprehensive Failure Model for Crashworthiness Simulation of Aluminium Extrusions. Int. J. Crashworthiness 2004, 9, 449–464. [Google Scholar] [CrossRef]
- Garoz, D.; Gilabert, F.A.; Sevenois, R.D.B.; Spronk, S.W.F.; Van Paepegem, W. Consistent Application of Periodic Boundary Conditions in Implicit and Explicit Finite Element Simulations of Damage in Composites. Compos. Part B Eng. 2019, 168, 254–266. [Google Scholar] [CrossRef]
- Omairey, S.L.; Dunning, P.D.; Sriramula, S. Development of an ABAQUS Plugin Tool for Periodic RVE Homogenisation. Eng. Comput. 2019, 35, 567–577. [Google Scholar] [CrossRef]
- Drago, A.; Pindera, M.J. Micro-Macromechanical Analysis of Heterogeneous Materials: Macroscopically Homogeneous vs Periodic Microstructures. Compos. Sci. Technol. 2007, 67, 1243–1263. [Google Scholar] [CrossRef]

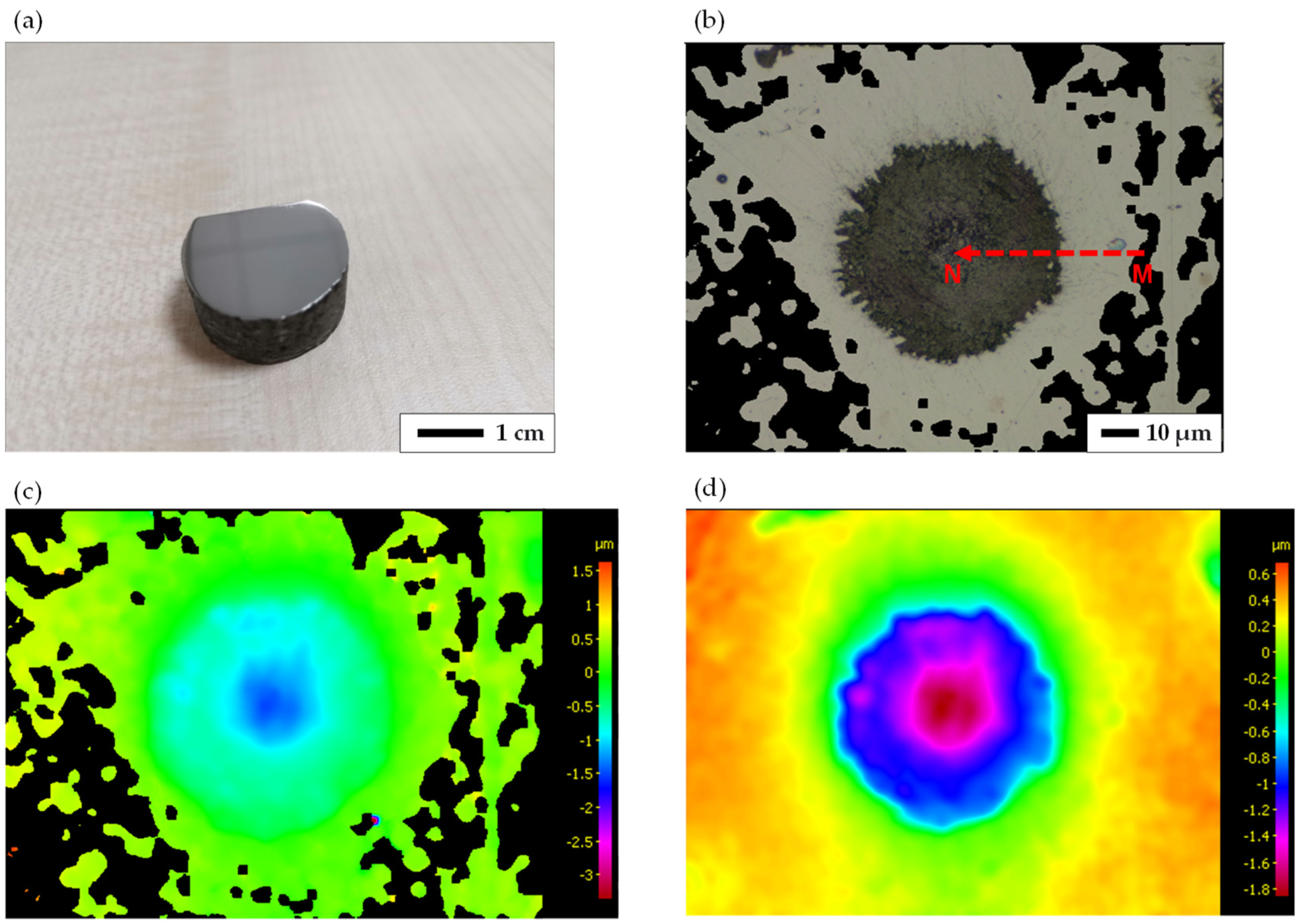

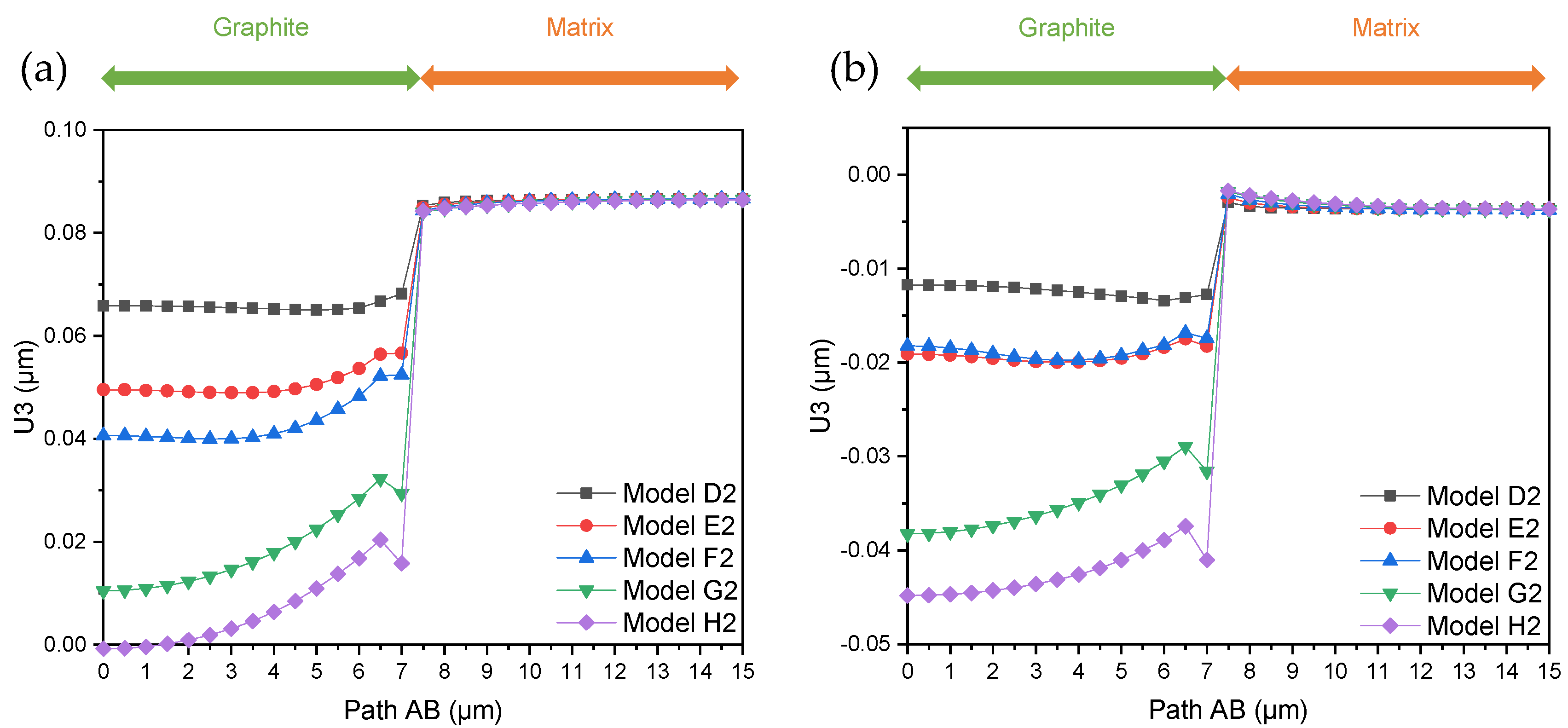
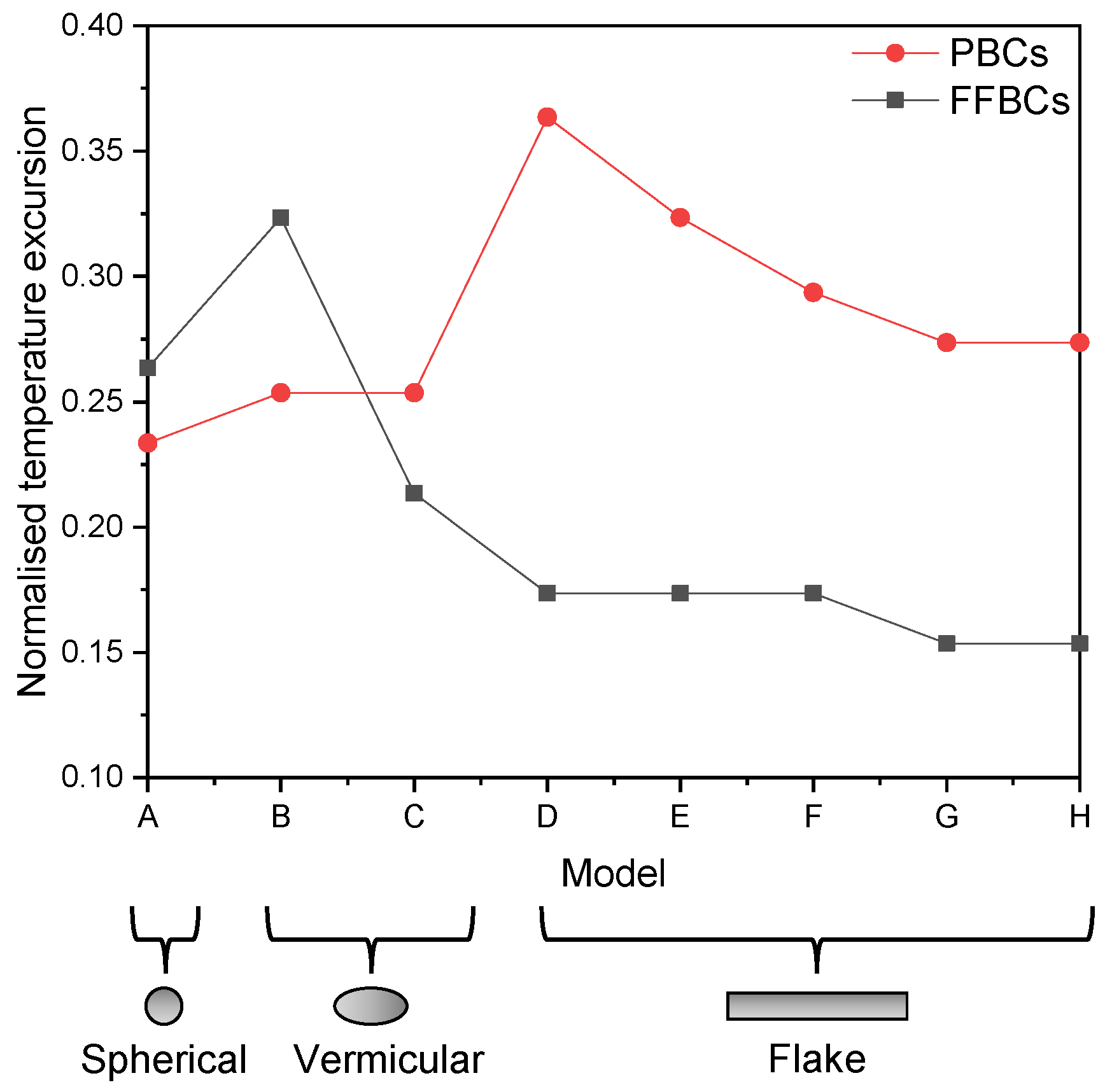

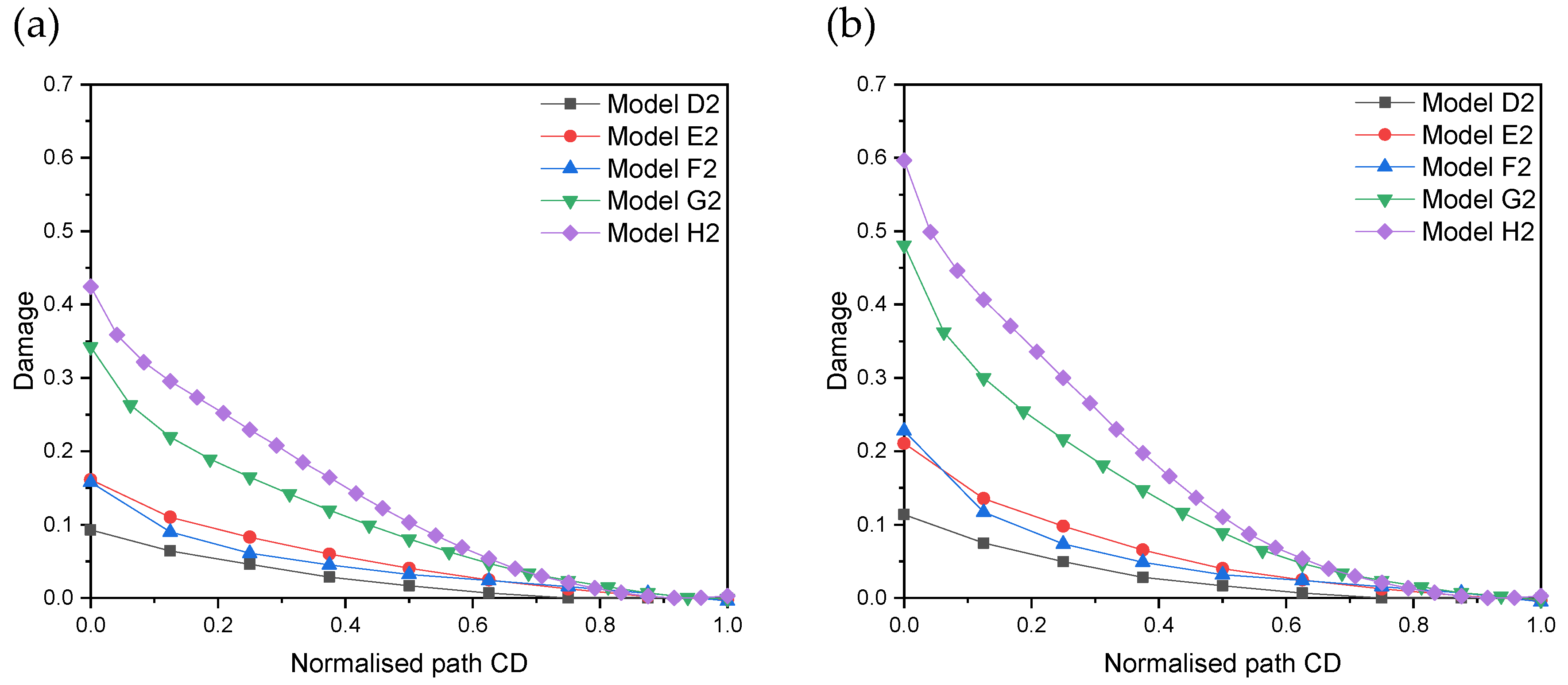
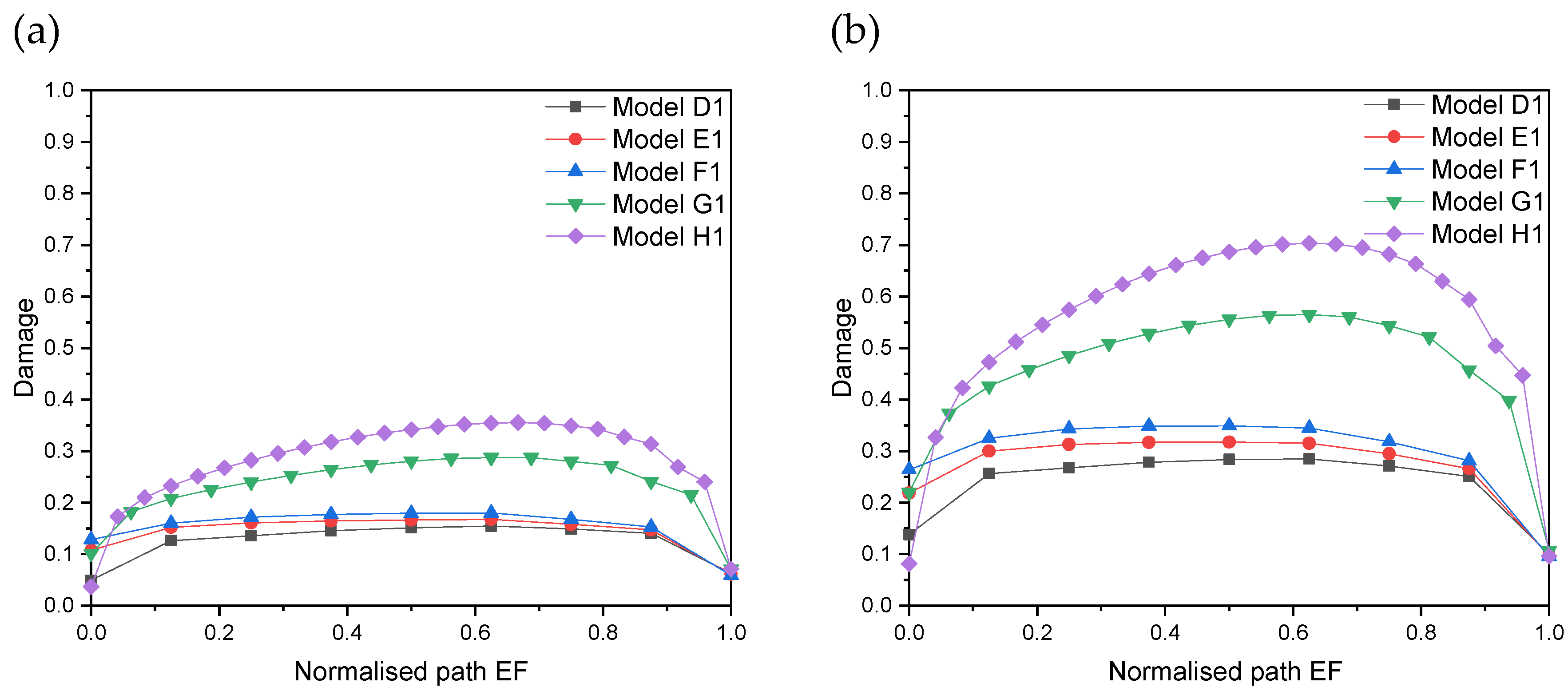

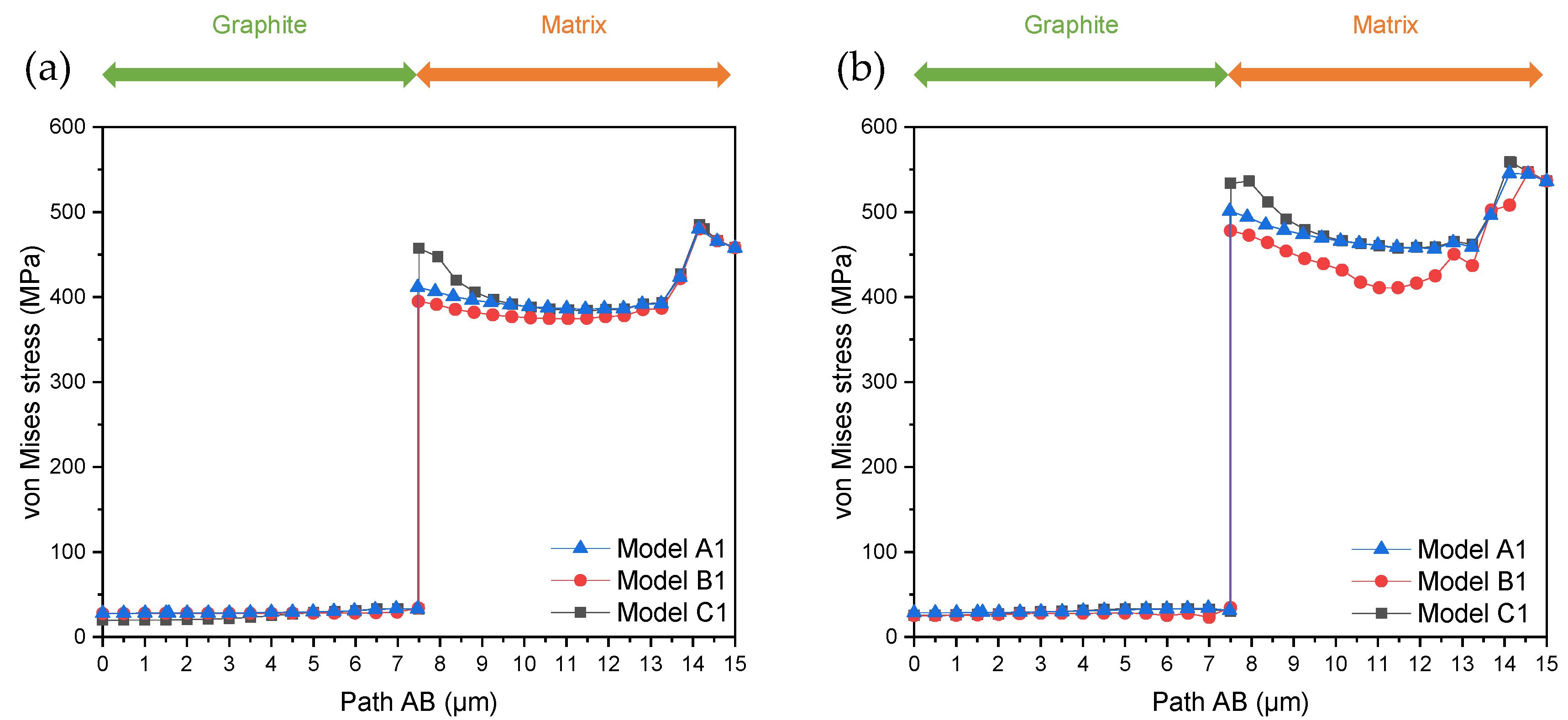
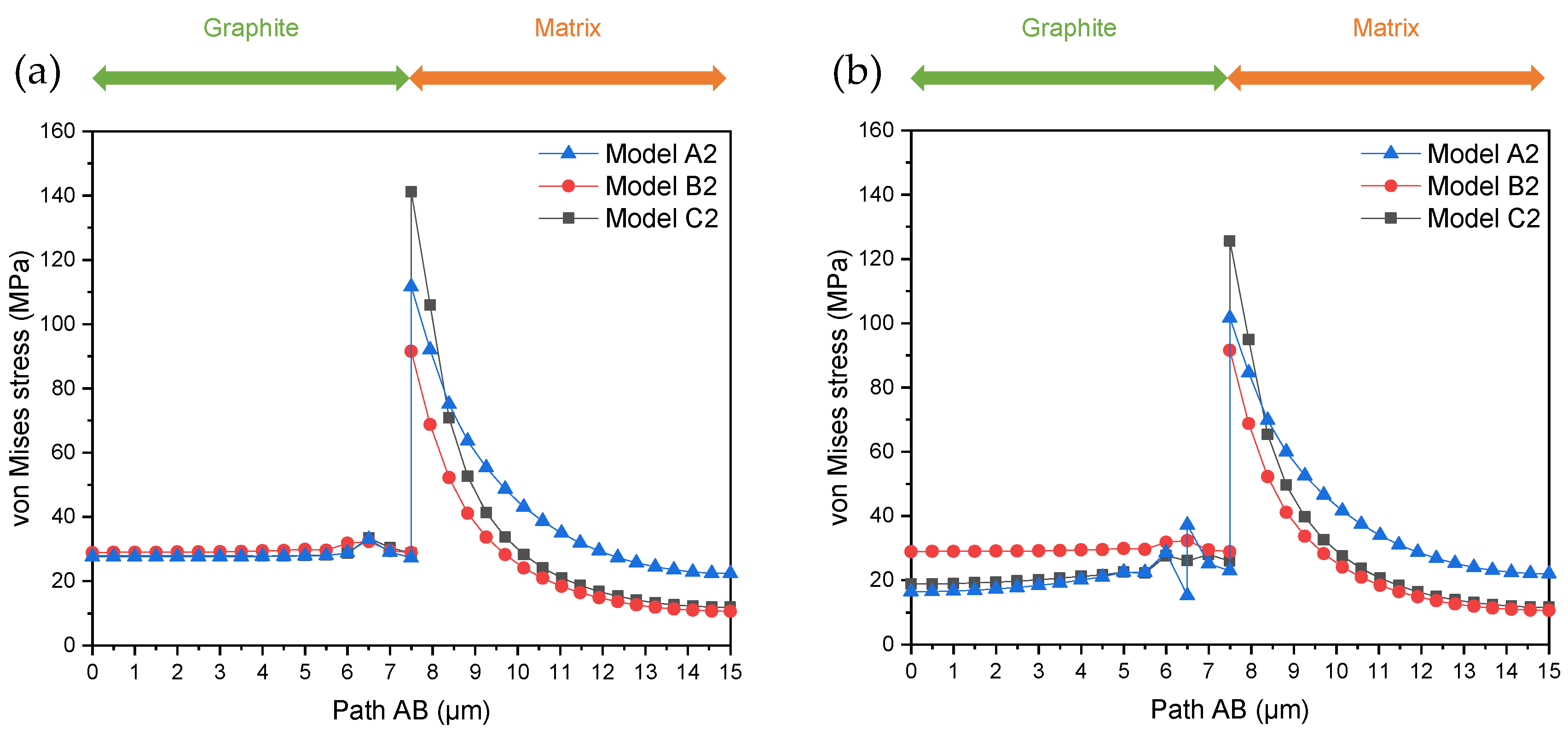
| Graphite Particle No. | Height Difference before Thermal Load (μm) | Height Difference after Thermal Load (μm) | Change of Height Difference (μm) |
|---|---|---|---|
| 1 | 0.598 | 0.720 | 0.122 |
| 2 | 0.603 | 0.813 | 0.210 |
| 3 | 0.327 | 0.539 | 0.212 |
| 4 | 0.288 | 0.485 | 0.197 |
| 5 | 0.382 | 0.447 | 0.065 |
| 6 | 0.365 | 0.502 | 0.137 |
| 7 | 0.117 | 0.252 | 0.135 |
| 8 | 1.769 | 1.962 | 0.193 |
| Model | Notation | Type of Graphite Inclusion | (µm) | W (µm) | H (µm) | Boundary Conditions | |
|---|---|---|---|---|---|---|---|
| A | A1 | Spherical | Spherical | 15 | - | - | FFBCs |
| A2 | PBCs | ||||||
| B | B1 | Ver_H4 | Vermicular | 8 | - | - | FFBCs |
| B2 | PBCs | ||||||
| C | C1 | Ver_H7.5 | Vermicular | 8 | - | - | FFBCs |
| C2 | PBCs | ||||||
| D | D1 | W2H4 | Flake | - | 2 | 4 | FFBCs |
| D2 | PBCs | ||||||
| E | E1 | W4H4 | Flake | - | 4 | 4 | FFBCs |
| E2 | PBCs | ||||||
| F | F1 | W8H4 | Flake | - | 8 | 4 | FFBCs |
| F2 | PBCs | ||||||
| G | G1 | W8H8 | Flake | - | 8 | 8 | FFBCs |
| G2 | PBCs | ||||||
| H | H1 | W8H12 | Flake | - | 8 | 12 | FFBCs |
| H2 | PBCs | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, M.; Baxevanakis, K.P.; Silberschmidt, V.V. Effect of Graphite Morphology on the Thermomechanical Performance of Compacted Graphite Iron. Metals 2023, 13, 473. https://doi.org/10.3390/met13030473
Cao M, Baxevanakis KP, Silberschmidt VV. Effect of Graphite Morphology on the Thermomechanical Performance of Compacted Graphite Iron. Metals. 2023; 13(3):473. https://doi.org/10.3390/met13030473
Chicago/Turabian StyleCao, Minghua, Konstantinos P. Baxevanakis, and Vadim V. Silberschmidt. 2023. "Effect of Graphite Morphology on the Thermomechanical Performance of Compacted Graphite Iron" Metals 13, no. 3: 473. https://doi.org/10.3390/met13030473
APA StyleCao, M., Baxevanakis, K. P., & Silberschmidt, V. V. (2023). Effect of Graphite Morphology on the Thermomechanical Performance of Compacted Graphite Iron. Metals, 13(3), 473. https://doi.org/10.3390/met13030473








