Deformation and Fracture Characterization of an Mg-Sn-Ca Alloy Using 3D Processing Maps
Abstract
:1. Introduction
2. Experimental
2.1. Experiment Materials
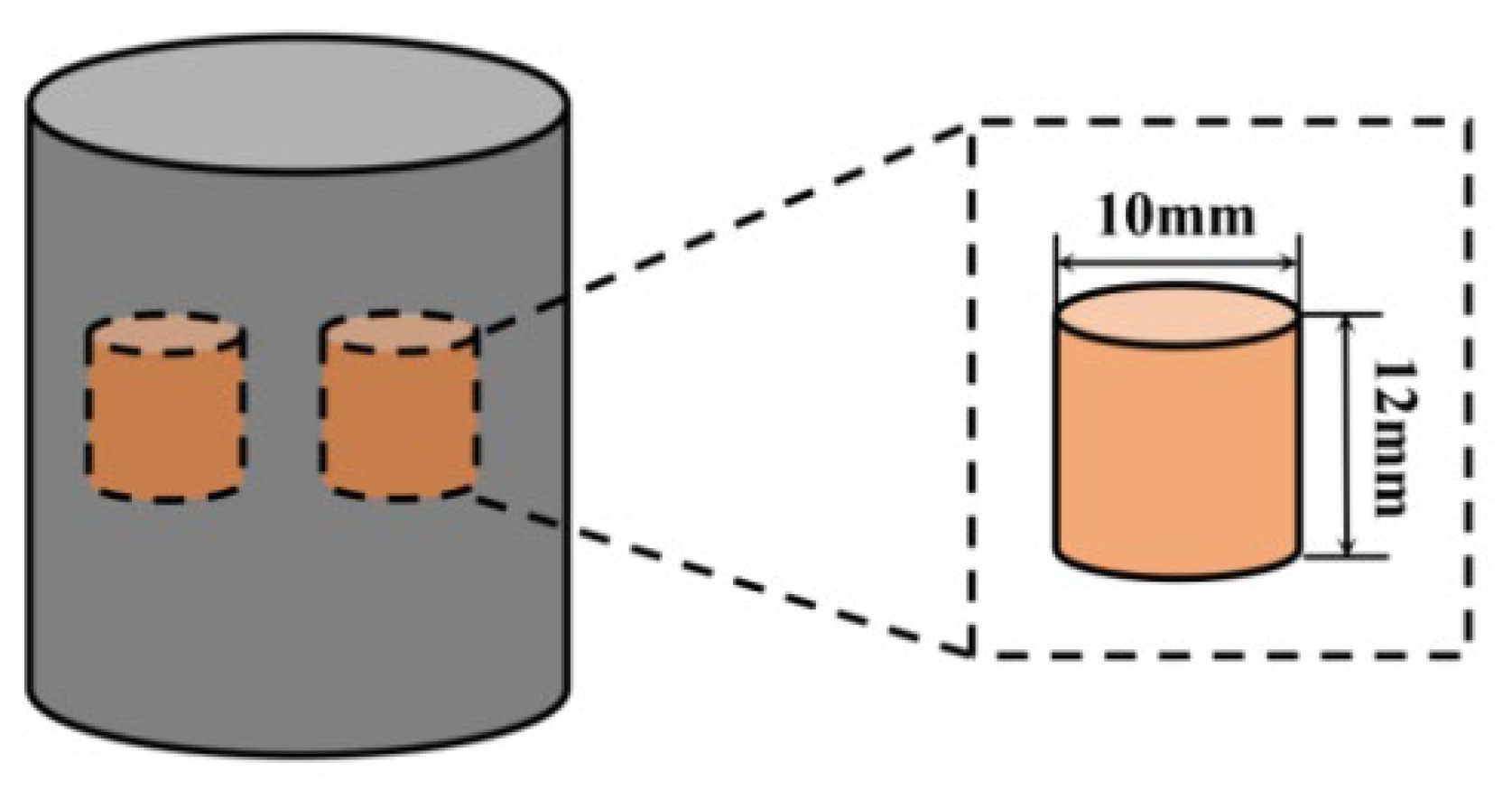
2.2. Experiment Methods
3. Results and Discussion
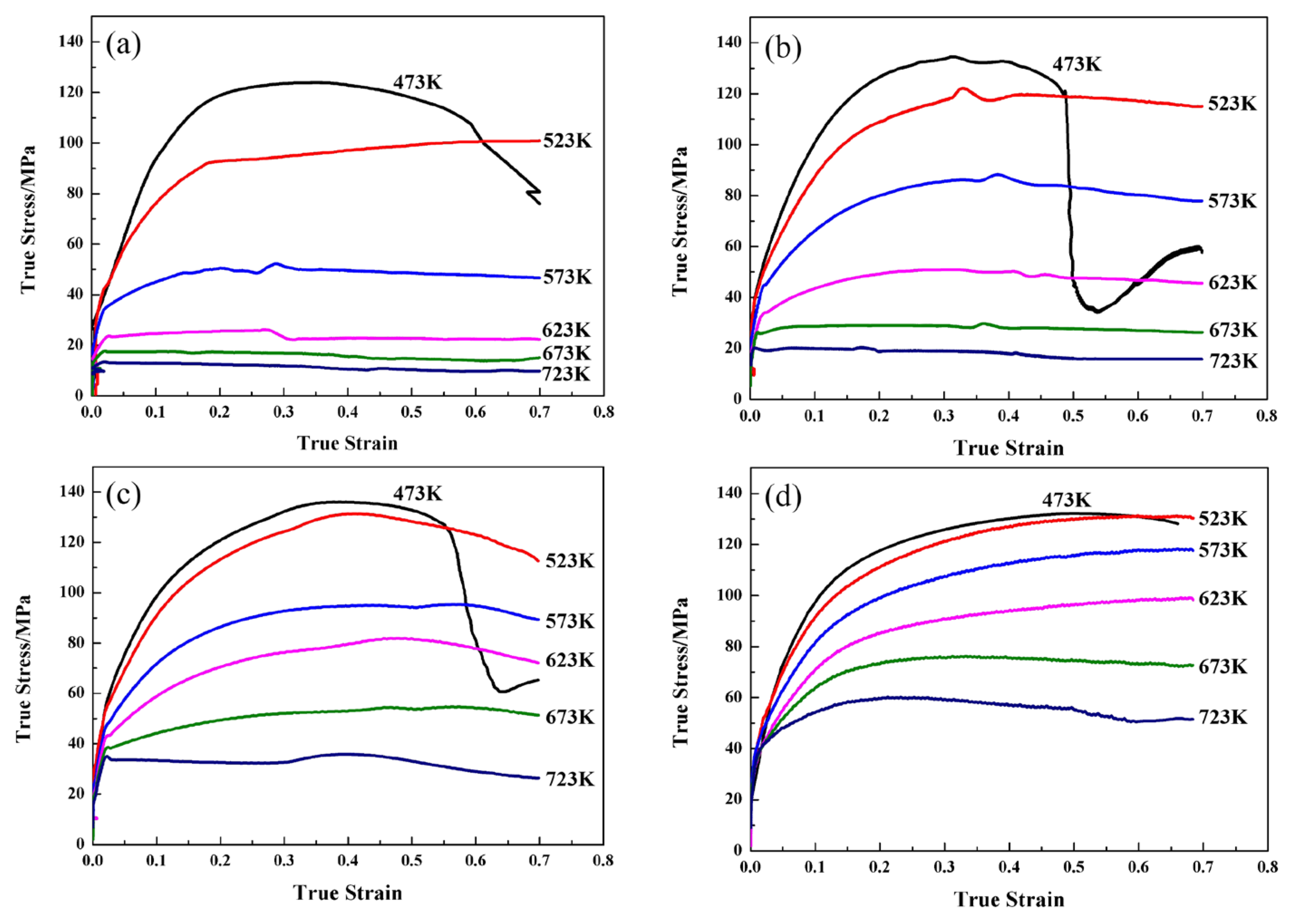
3.1. Flow Curves and Softening Analyses
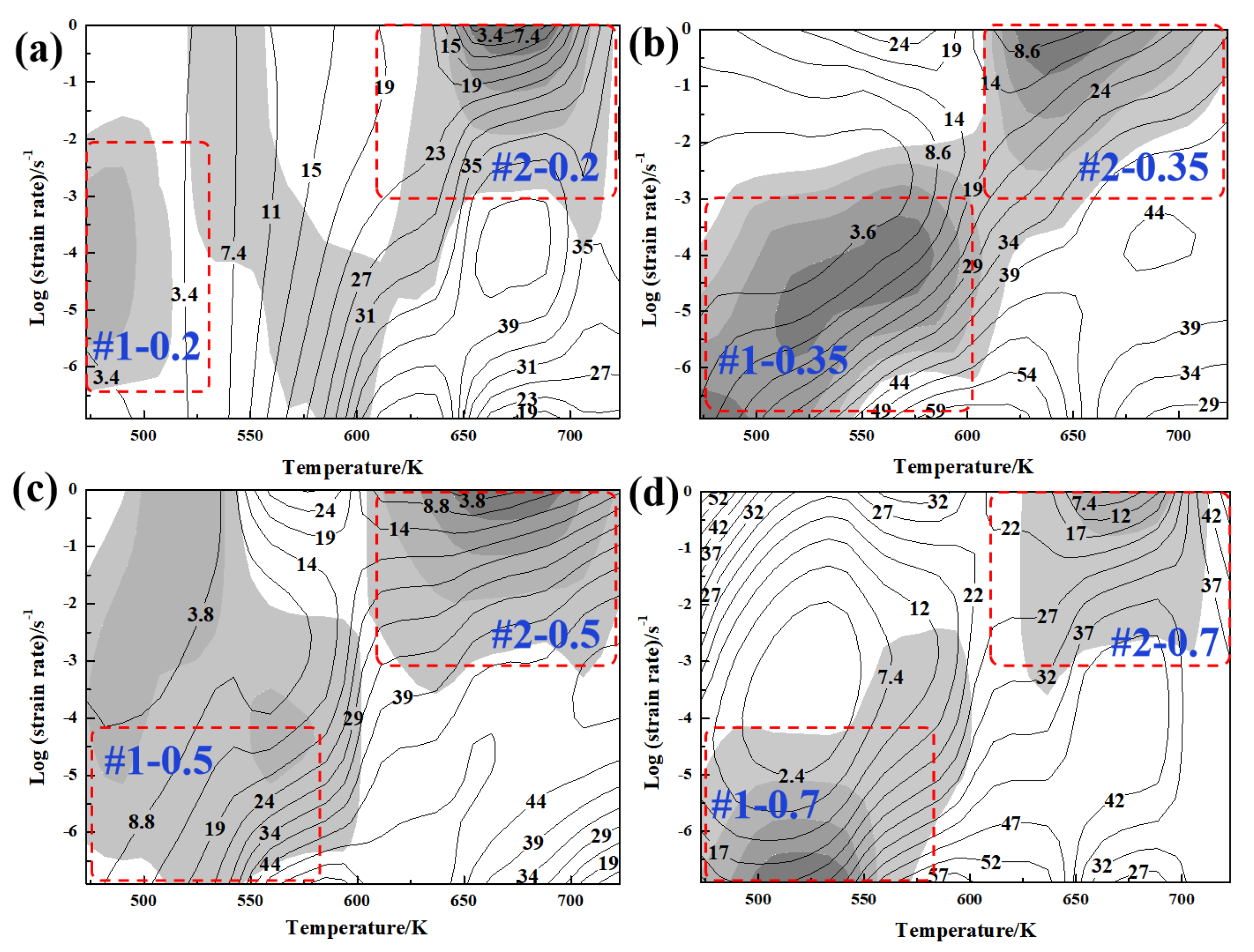
3.2. Establishment of the Processing Map
3.2.1. The Principle of the Processing Map
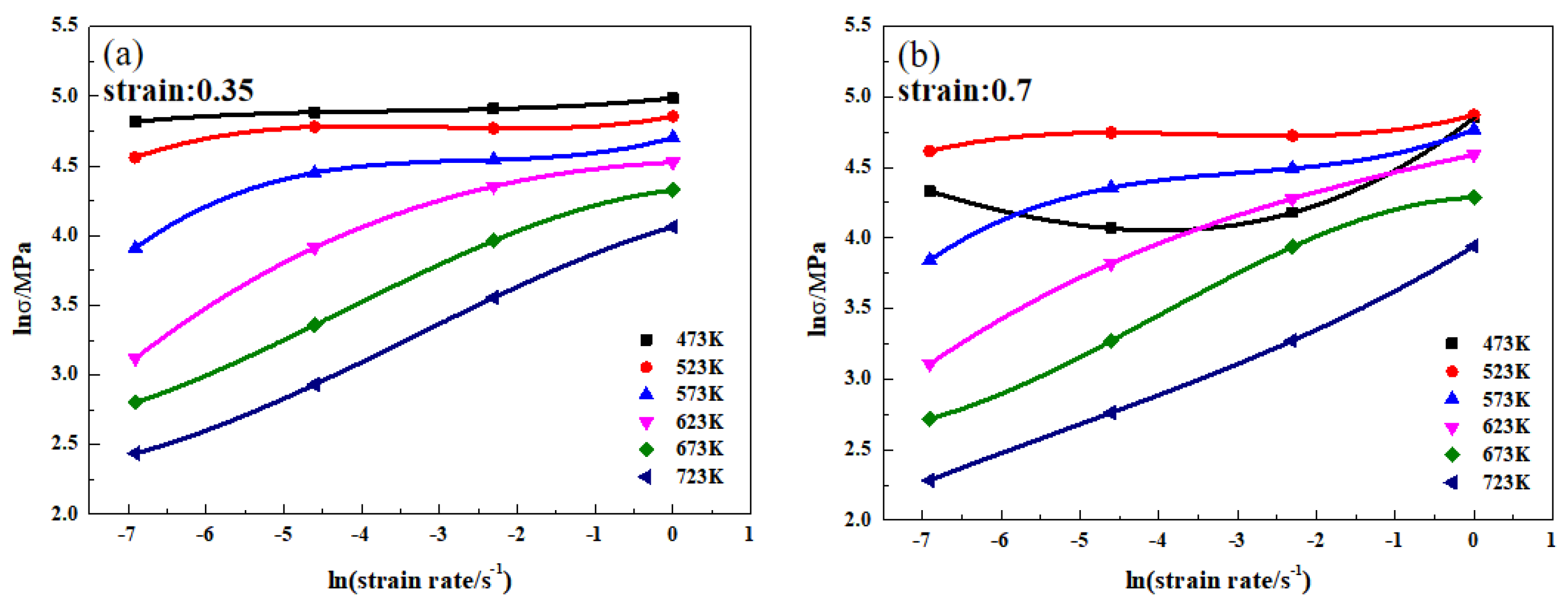
3.2.2. Values of the Power Dissipation (η%) under Different Parameters
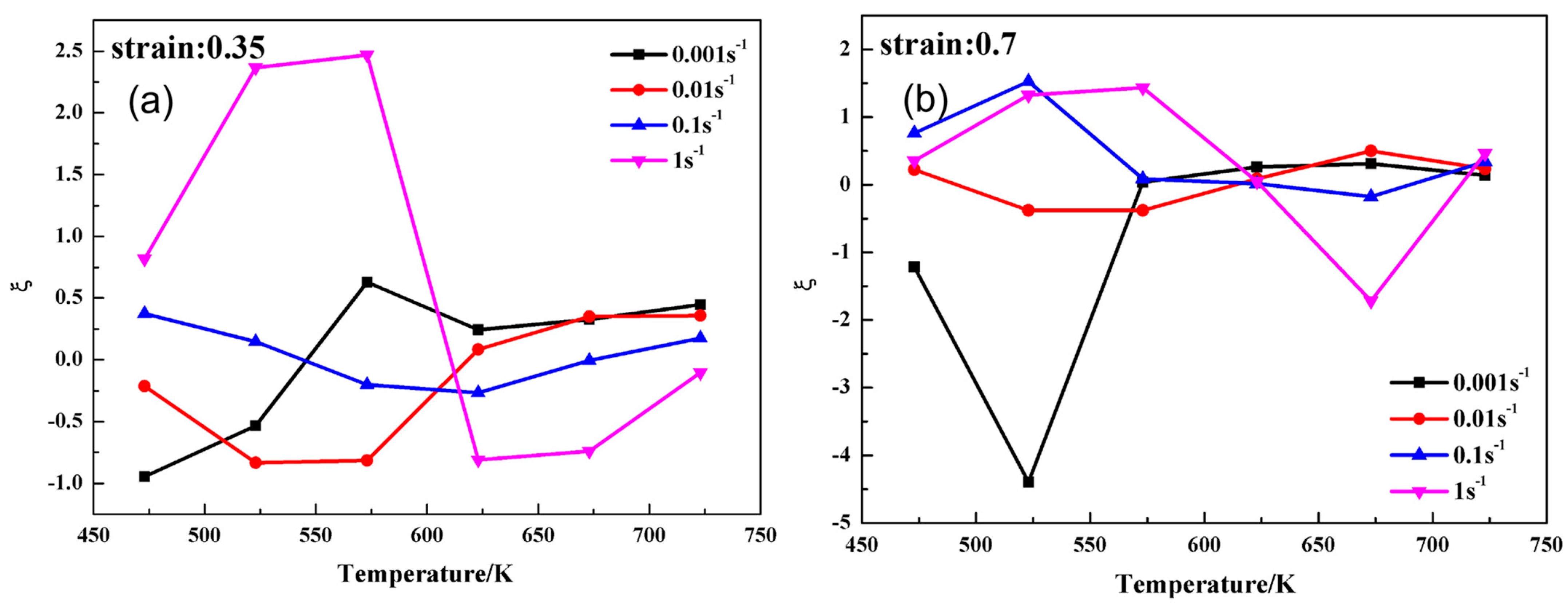
3.2.3. Values of the Instability Parameter (ξ) under Different Parameters
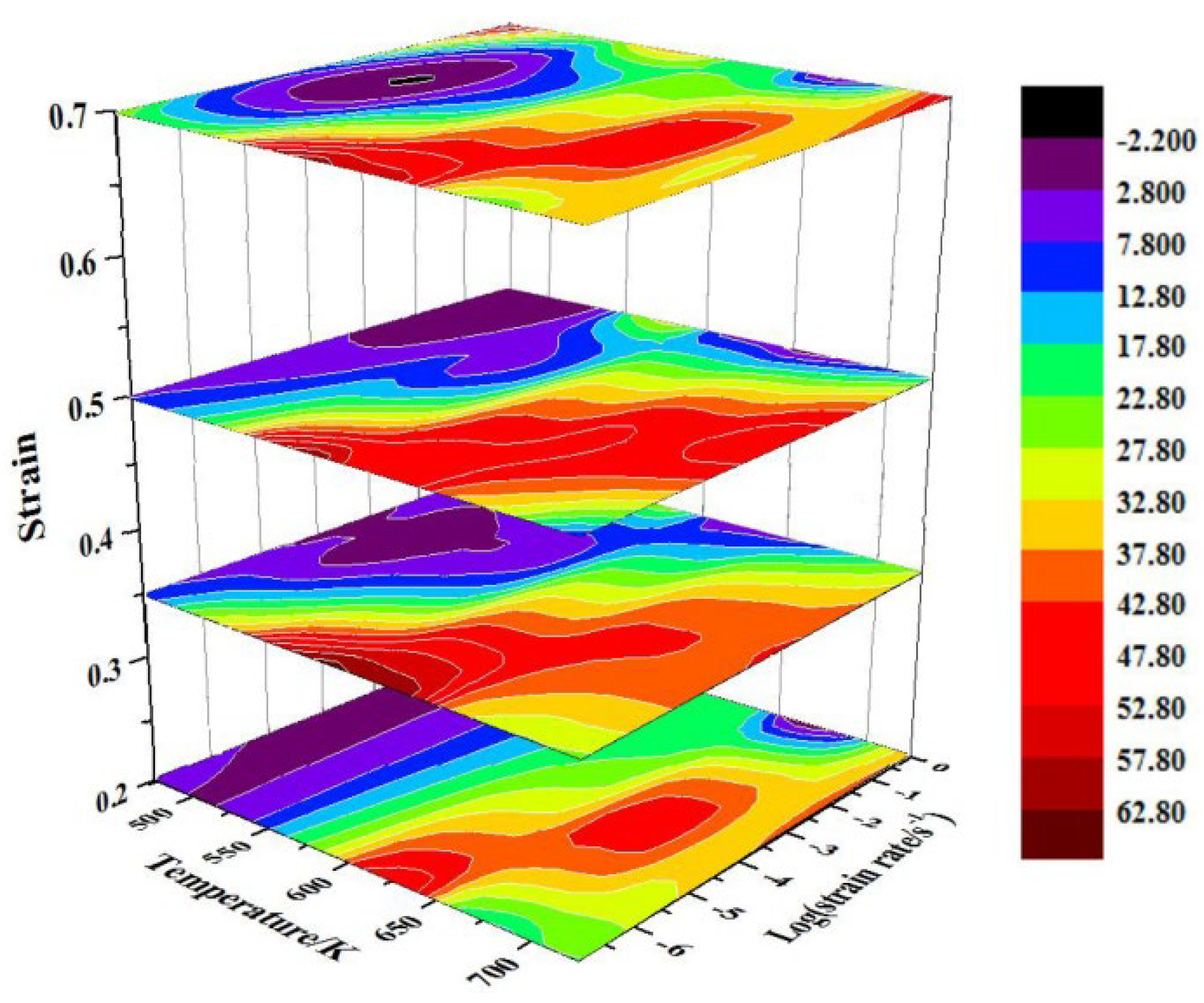
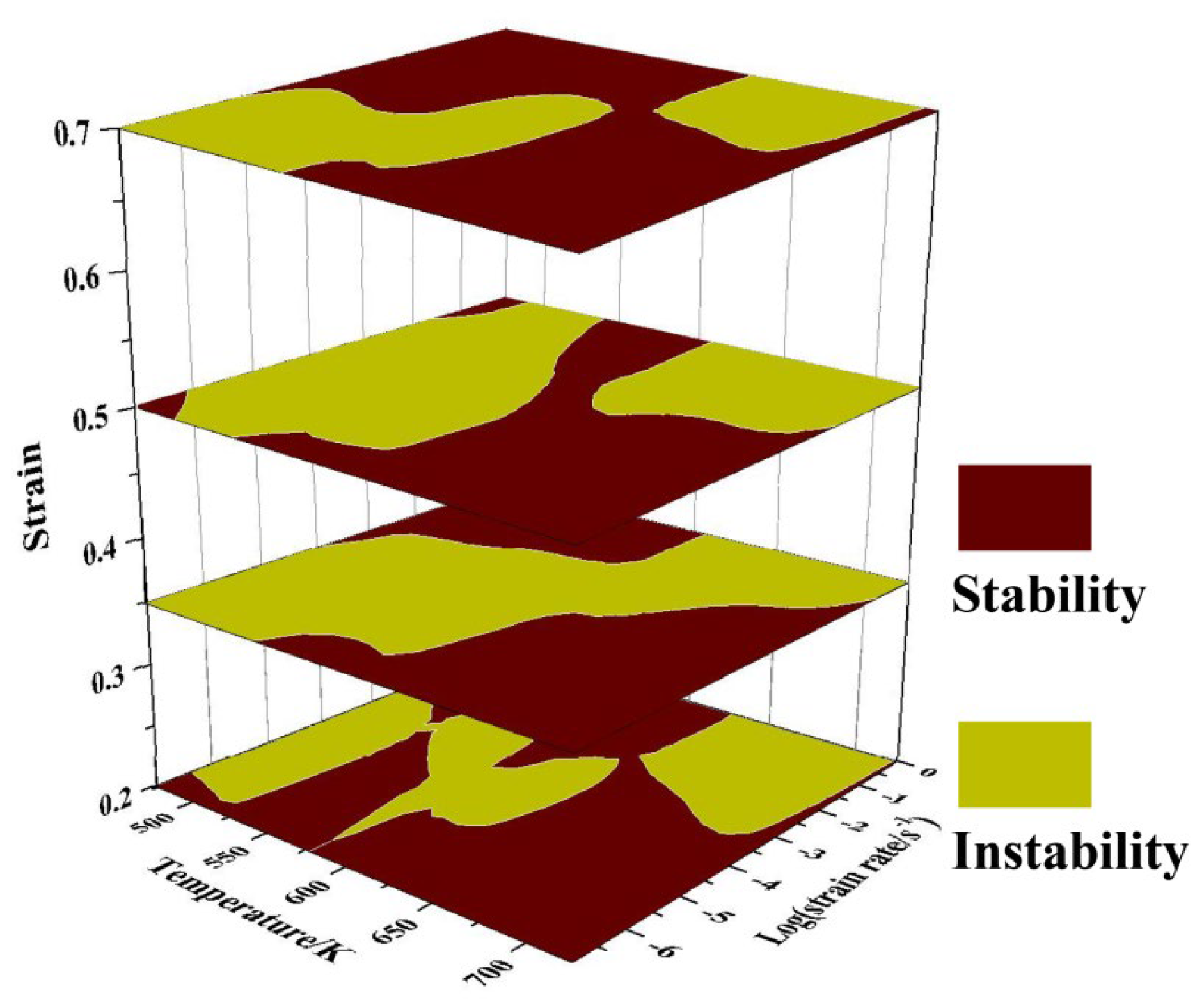
3.2.4. The 3D Processing Map Development
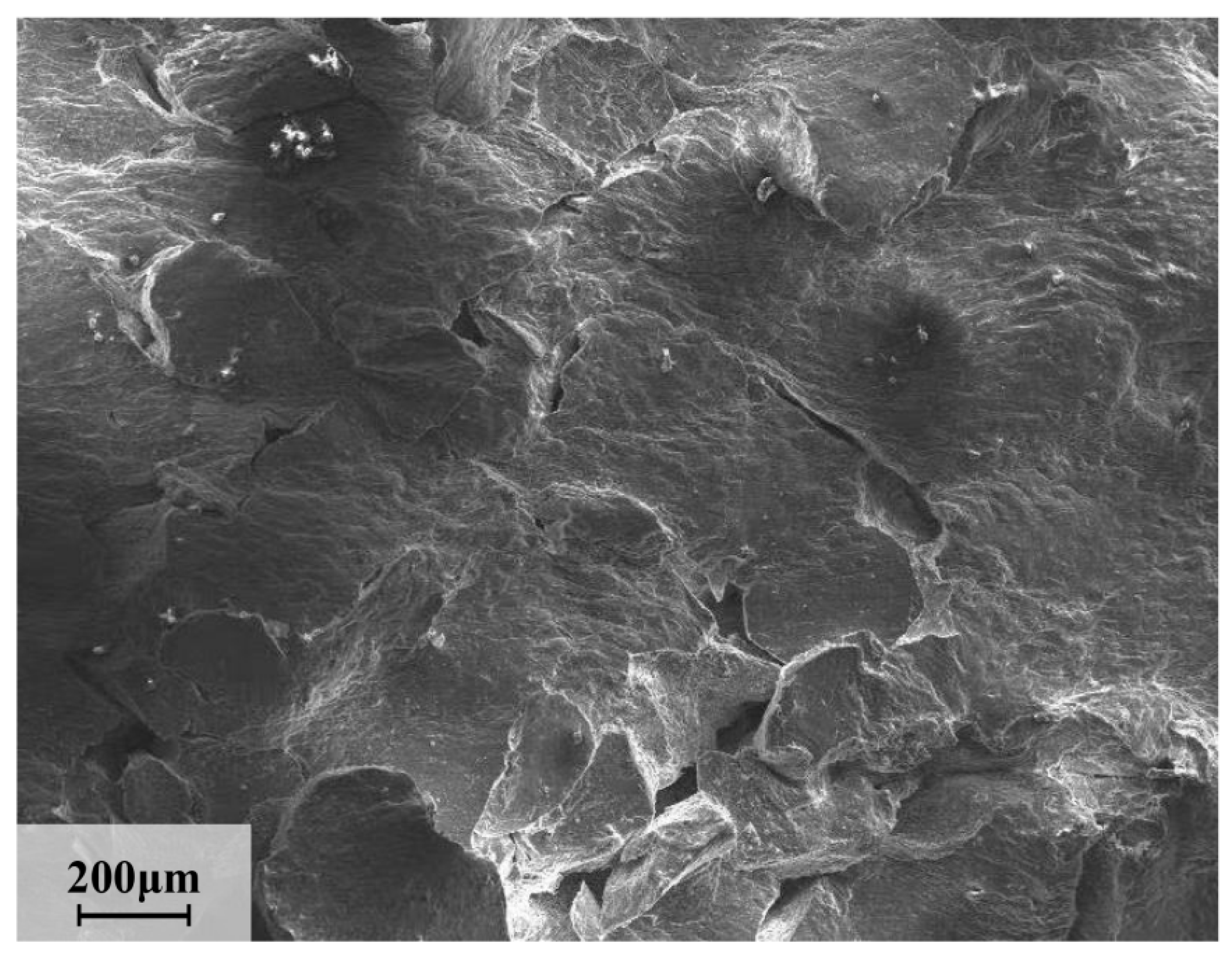
4. Fracture Behavior
5. Conclusions
- (1)
- The hot processing parameters of the Mg−2Sn−1Ca alloy exert a great impact on the isothermal deformation feature parameters, such as strain rate sensitivity (m), the efficiency of power dissipation (η) and instability parameters (ξ) for the establishment of the processing map.
- (2)
- Combined with the 3D processing diagram, the instability region of the Mg−2Sn−1Ca alloy could be divided into two regions: region 1 is within the range of 450–600 K/0.001–0.1 s−1; region 2 is within the range of 600–723 K/0.1–1 s−1. The processing conditions are within the temperature range of 630–723 K and within the safe processing area, which can effectively promote the occurrence of DRX.
- (3)
- Because of the poor forming performance of a magnesium alloy under low temperatures, specimens show unidirectional cracks under 473 K. The propagation of cracks decreased with an increase in temperature under a high strain rate. The area of 623–723 K/0.001–0.1 s−1 can be considered the optimum hot working parameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Mao, P.; Zhou, L.; Wang, X.; Wang, Z.; Wang, F.; Wei, Z.; Liu, Z. Effect of Grain Size on Dynamic Compression Behavior and Deformation Mechanism of ZK60 Magnesium Alloy. Metals 2023, 13, 314. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Zhi, C.C.; Ma, L.F.; Zheng, Z.B.; Zhu, Y.C.; Jia, W.T. Effect of initial temperature on the microstructure and properties of cryogenic rolled AZ31 magnesium alloy. Mater. Tehnol. 2022, 56, 571–577. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Pan, F.S.; Pan, H.C. Microstructure, mechanical and bio-corrosion properties of as-extruded Mg–Sn–Ca alloys. Trans. Nonferrous Met. Soc. China 2016, 26, 1574–1582. [Google Scholar] [CrossRef]
- Zeng, Z.R.; Bian, M.Z.; Xu, S.W.; Davies, C.; Nie, J.F. Texture evolution during cold rolling of dilute Mg alloys. Scr. Mater. 2015, 108, 6–10. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, L.; Zhou, H.; Wang, J.; Zeng, X. Improving ductility of a Mg alloy via non-basal slip induced by Ca addition. Int. J. Plast. 2019, 120, 164–179. [Google Scholar] [CrossRef]
- Pan, H.; Huang, Q.; Qin, G.; Fu, H.; Xu, M.; Ren, Y.; She, J.; Song, B.; Li, B. Activations of stacking faults in the calcium-containing magnesium alloys under compression. J. Alloys Compd. Interdiscip. J. Mater. Sci. Solid State Chem. Phys. 2017, 692, 898–902. [Google Scholar] [CrossRef]
- Pan, H.; Qin, G.; Ren, Y.; Wang, L.; Sun, S.; Meng, X. Achieving high strength in indirectly-extruded binary Mg–Ca alloy containing Guinier–Preston zones. J. Alloys Compd. 2015, 630, 272–276. [Google Scholar] [CrossRef]
- Bowles, A.L.; Dieringa, H.; Blawert, C.; Hort, N.; Kainer, K.U. Investigations in the Magnesium-Tin System. Mater. Sci. Forum 2005, 488–489, 135–138. [Google Scholar] [CrossRef]
- Jia, W.; Tang, Y.; Le, Q.; Cui, J. Air-cooling analysis of AZ31B magnesium alloy plate: Experimental verification, numerical simulation and mathematical modeling. J. Alloys Compd. 2017, 695, 1838–1853. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, Z.; Ning, Y.; Yang, N.; Guo, H.; Qin, C.; Shi, Z. The flow behavior and constitutive equation in isothermal compression of FGH4096-GH4133B dual alloy. Mater. Des. 2014, 63, 829–837. [Google Scholar] [CrossRef]
- Liao, S.L.; Zhang, L.W.; Yue, C.X.; Pei, J.B.; Gao, H.J. Hot deformation behaviors and flow stress model of GCr15 bearing steel. J. Cent. South Univ. Technol. 2008, 15, 575–580. [Google Scholar] [CrossRef]
- Prasad, Y. Recent advances in the science of mechanical processing. Indian J. Technol. 1990, 28, 435–451. [Google Scholar]
- Ebrahimpourghandi, B.; Mahmudi, R. Hot deformation constitutive analysis and processing maps of the as-cast and wrought Mg–2.5Gd–0.5Zr alloy. J. Alloys Compd. 2023, 942, 169132. [Google Scholar] [CrossRef]
- Zhang, L.; Yuan, S.; Wang, J.; Chen, L.; Jin, P. Hot deformation behavior, processing map, microstructure evolution and dynamic recrystallization mechanism of Mg-5Al-0.6Sc alloy. J. Alloys Compd. 2022, 922, 166244. [Google Scholar] [CrossRef]
- Nayyeri, G.; Mahmudi, R.; Salehi, F. The microstructure, creep resistance, and high-temperature mechanical properties of Mg-5Sn alloy with Ca and Sb additions, and aging treatment. Mater. Sci. Eng. A 2010, 527, 5353–5359. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, R.; Ren, J.; Peng, C.; Feng, Y. Hot deformation behavior of Mg-8Li-3Al-2Zn-0.2Zr alloy based on constitutive analysis, dynamic recrystallization kinetics, and processing map. Mech. Mater. 2019, 131, 158–168. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Gegel, H.L.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, K.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. A 1984, 15, 1883–1892. [Google Scholar] [CrossRef]
- Liu, J.; Cui, Z.; Li, C. Analysis of metal workability by integration of FEM and 3-D processing maps. J. Mater. Process. Technol. 2008, 205, 497–505. [Google Scholar] [CrossRef]
- Kwak, T.Y.; Kim, W.J. Effect of refinement of grains and icosahedral phase on hot compressive deformation and processing maps of mg-zn-y magnesium alloys with different volume fractions of icosahedral phase. J. Mater. Sci. Technol. 2019, 35, 11. [Google Scholar] [CrossRef]
- Bk, A.; Lya, B.; Jta, B.; Yong, Z.A.; Sla, B.; Hl, C.; Yu, D.A.; Xl, A. Hot deformation behavior and 3D processing maps of AA7020 aluminum alloy. J. Alloys Compd. 2020, 845, 156113. [Google Scholar]
- Sun, Y.; Cao, Z.; Wan, Z.; Hu, L.; Ye, W.; Li, N.; Fan, C. 3D processing map and hot deformation behavior of 6A02 aluminum alloy. J. Alloys Compd. 2018, 742, 356–368. [Google Scholar] [CrossRef]
- Wang, Q.; Ma, L.; Wang, Q.; Lin, J.; Ren, W. In-Situ Study on Deformation Behavior of ZK60 Alloy Processed by Cyclic Extrusion and Compression. Mater. Trans. 2014, 55, 1180–1183. [Google Scholar]
- Zhi, C.; Ma, L.; Jia, W.; Huo, X.; Lin, J. Dependence of deformation behaviors on temperature for twin-roll casted AZ31 alloy by processing maps. J. Mater. Res. Technol. 2019, 8, 5217–5232. [Google Scholar] [CrossRef]
- Bajargan, G.; Singh, G.; Sivakumar, D.; Ramamurty, U. Effect of temperature and strain rate on the deformation behavior and microstructure of a homogenized AZ31 magnesium alloy. Mater. Sci. Eng. A 2013, 579, 26–34. [Google Scholar] [CrossRef]
- Saxena, K.K.; Yadav, S.D.; Sonkar, S.; Pancholi, V.; Chaudhari, G.P.; Srivastava, D.; Dey, G.K.; Jha, S.K.; Saibaba, N. Effect of Temperature and Strain Rate on Deformation Behavior of Zirconium Alloy: Zr-2.5Nb. Procedia Mater. Sci. 2014, 6, 278–283. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhi, C.; Wu, Z.; Lei, J.; Huang, Z.; Xv, H.; Zhu, Y.; Jia, W.; Liu, P.; Ma, L. Deformation and Fracture Characterization of an Mg-Sn-Ca Alloy Using 3D Processing Maps. Metals 2023, 13, 645. https://doi.org/10.3390/met13040645
Zhi C, Wu Z, Lei J, Huang Z, Xv H, Zhu Y, Jia W, Liu P, Ma L. Deformation and Fracture Characterization of an Mg-Sn-Ca Alloy Using 3D Processing Maps. Metals. 2023; 13(4):645. https://doi.org/10.3390/met13040645
Chicago/Turabian StyleZhi, Chenchen, Zhenyu Wu, Junyi Lei, Zhiquan Huang, Haijie Xv, Yanchun Zhu, Weitao Jia, Pengtao Liu, and Lifeng Ma. 2023. "Deformation and Fracture Characterization of an Mg-Sn-Ca Alloy Using 3D Processing Maps" Metals 13, no. 4: 645. https://doi.org/10.3390/met13040645
APA StyleZhi, C., Wu, Z., Lei, J., Huang, Z., Xv, H., Zhu, Y., Jia, W., Liu, P., & Ma, L. (2023). Deformation and Fracture Characterization of an Mg-Sn-Ca Alloy Using 3D Processing Maps. Metals, 13(4), 645. https://doi.org/10.3390/met13040645






