Prediction of Recrystallization Structure of 2A12 Aluminum Alloy Pipe Extrusion Process Based on BP Neural Network
Abstract
1. Introduction
2. Constitutive Equation and Recrystallization Process Analysis of 2A12 Aluminum Alloy
2.1. Material Constitutive Model
2.2. Material Recrystallization Modeling
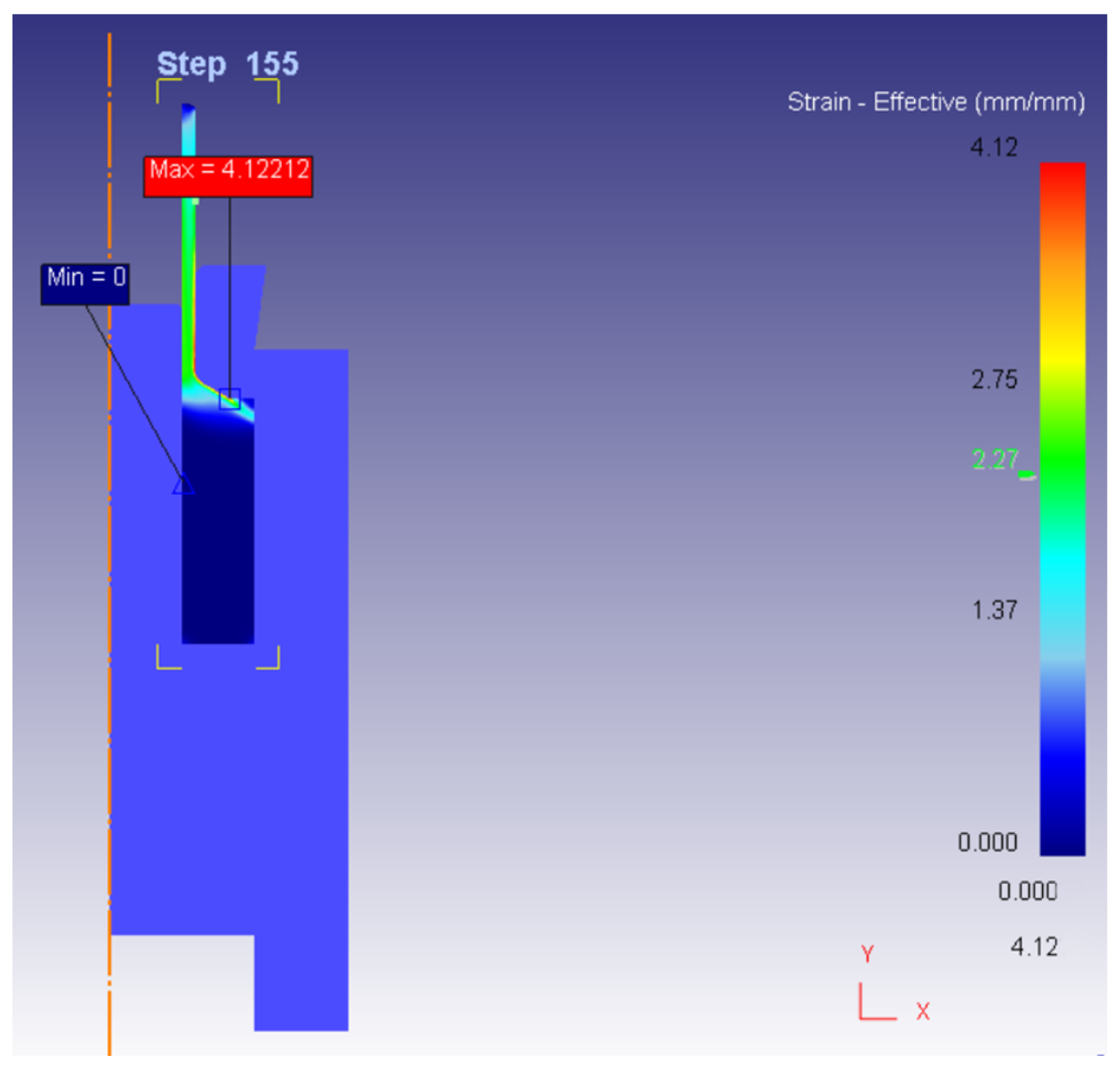
3. FEM Analysis of Extrusion Process
4. BP Neural Network Prediction Model
5. Experimental Verification
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, S.X.; Zhu, Y.P.; Cai, G.Y. Effects of Deformation Ratio above Recrystallizaton Temperature on Microstructure and Properties of 2A12 Aluminum Alloy. Appl. Mech. Mater. 2012, 217–219, 279–282. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, G.; Gong, J.; Chen, X.; Chen, M. Hot Deformation Behaviors and Processing Maps of 2024 Aluminum Alloy in As-cast and Homogenized States. J. Mater. Eng. Perform. 2015, 24, 5002–5012. [Google Scholar] [CrossRef]
- Chandla, N.K.; Kant, S.; Goud, M.M. A review on mechanical properties of stir cast Al-2024 metal matrix composites. Adv. Mater. Process. Technol. 2022, 8, 1–22. [Google Scholar] [CrossRef]
- Wang, H.; Peng, E. Effect of extrusion temperature on microstructure and properties of 2A12 aluminium alloy. Heat Treat. Met. 2020, 45, 138–140. [Google Scholar]
- Fan, X.; He, Z.; Zheng, K.; Yuan, S. Strengthening behavior of Al–Cu–Mg alloy sheet in hot forming–quenching integrated process with cold–hot dies. Mater. Des. 2015, 83, 557–565. [Google Scholar] [CrossRef]
- Xie, J. Current Situation and Development Trends of Metals Extrusion Technology. Mater. China 2013, 32, 257–263. [Google Scholar]
- Görzen, D.; Schäfke, F.P.; Blinn, B.; Klose, C.; Maier, H.J.; Beck, T. Investigating the Influence of Process Parameters on the Mechanical Properties of Extruded Aluminum Tubes by Cyclic Indentation Tests. Metals 2021, 11, 744. [Google Scholar] [CrossRef]
- Ku, M.-H.; Hung, F.-Y.; Lui, T.-S.; Lai, J.-J. Enhanced Formability and Accelerated Precipitation Behavior of 7075 Al Alloy Extruded Rod by High Temperature Aging. Metals 2018, 8, 648. [Google Scholar] [CrossRef]
- Negendank, M.; Taparli, U.A.; Gall, S.; Müller, S.; Reimers, W. Microstructural evolution of indirectly extruded seamless 6xxx aluminum tubes with axial variable wall thickness. J. Mater. Process. Technol. 2016, 230, 187–197. [Google Scholar] [CrossRef]
- Lucignano, C.; Montanari, R.; Tagliaferri, V.; Ucciardello, N. Artificial neural networks to optimize the extrusion of an aluminium alloy. J. Intell. Manuf. 2010, 21, 569–574. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Z.; Xu, B. Prediction of Spherical Sheet Springback Based on a Sparrow-Search-Algorithm-Optimized BP Neural Network. Metals 2022, 12, 1377. [Google Scholar] [CrossRef]
- Yu, F.; Zhao, Y.; Lin, Z.; Miao, Y.; Zhao, F.; Xie, Y. Prediction of Mechanical Properties and Optimization of Friction Stir Welded 2195 Aluminum Alloy Based on BP Neural Network. Metals 2023, 13, 267. [Google Scholar] [CrossRef]
- Choi, W.; Won, S.; Kim, G.-S.; Kang, N. Artificial Neural Network Modelling of the Effect of Vanadium Addition on the Tensile Properties and Microstructure of High-Strength Tempcore Rebars. Metals 2022, 15, 3781. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Hao, K.; Luo, Z.; Fan, Z. Plastic Deformation Behavior of Metal Materials: A Review of Constitutive Models. Metals 2022, 12, 2077. [Google Scholar] [CrossRef]
- Shen, Z.; Wu, R.; Yuan, C.; Jiao, W. Comparative study of metamodeling methods for modeling the constitutive relationships of the TC6 titanium alloy. J. Mater. Res. Technol. 2021, 10, 188–204. [Google Scholar] [CrossRef]
- Abdul Jawwad, A.K.; Barghash, M.A. Evaluating the effects of process parameters on maximum extrusion pressure using a new artificial neural network-based (ANN-based) partial-modeling technique. Int. J. Adv. Manuf. Technol. 2013, 68, 2547–2564. [Google Scholar] [CrossRef]
- Wei, W.; Yuan, C.; Wu, R.; Jiao, W. Prediction of breakthrough extruding force in large-scale extrusion process using artificial neural networks. Sci. Prog. 2021, 104, 0036850421992609. [Google Scholar] [CrossRef] [PubMed]
- Churyumov, A.; Kazakova, A.; Churyumova, T. Modelling of the Steel High-Temperature Deformation Behaviour Using Artificial Neural Network. Metals 2022, 12, 447. [Google Scholar] [CrossRef]
- Shan, D.; Yi, X.; Yan, L. Three-dimensional rigid-plastic finite-element analysis of the isothermal precision forging of a cylindrical housing. J. Mater. Process. Technol. 2000, 102, 188–192. [Google Scholar] [CrossRef]
- Doherty, R.D.; Hughes, D.A.; Humphreys, F.J.; Jonas, J.J.; Jensen, D.J.; Kassner, M.E.; King, W.E.; McNelley, T.R.; McQueen, H.J.; Rollett, A.D. Current issues in recrystallization: A review. Mater. Sci. Eng. A 1997, 238, 219–274. [Google Scholar] [CrossRef]
- Beltran, O.; Huang, K.; Loge, R.E. A mean field model of dynamic and post-dynamic recrystallization predicting kinetics, grain size and flow stress. Comput. Mater. Sci. 2015, 102, 293–303. [Google Scholar] [CrossRef]
- Hallberg, H. Approaches to Modeling of Recrystallization. Metals 2011, 1, 16–48. [Google Scholar] [CrossRef]
- Huang, K.; Logé, R.E. A review of dynamic recrystallization phenomena in metallic materials. Mater. Des. 2016, 111, 548–574. [Google Scholar] [CrossRef]
- Sun, C.Y.; Liu, D.; Fu, M.W.; Yang, J. Investigation of extrusion limit of Incoloy028 alloy tube by combining numerical and analytical methods. Int. J. Adv. Manuf. Technol. 2016, 83, 177–185. [Google Scholar] [CrossRef]
- Dang, L.; Yang, H.; Guo, L.G.; da Zeng, W.; Zhang, J. Study on exit temperature evolution during extrusion for large-scale thick-walled Inconel 625 pipe by FE simulation. Int. J. Adv. Manuf. Technol. 2015, 76, 1421–1435. [Google Scholar] [CrossRef]
- Sun, C.; Xiang, Y.; Liu, G.; Zuo, X.; Wang, M.; Zhang, Q. Extrusion limit diagram of IN 690 super-alloy tube based on hot processing map. Int. J. Adv. Manuf. Technol. 2017, 89, 3419–3428. [Google Scholar] [CrossRef]
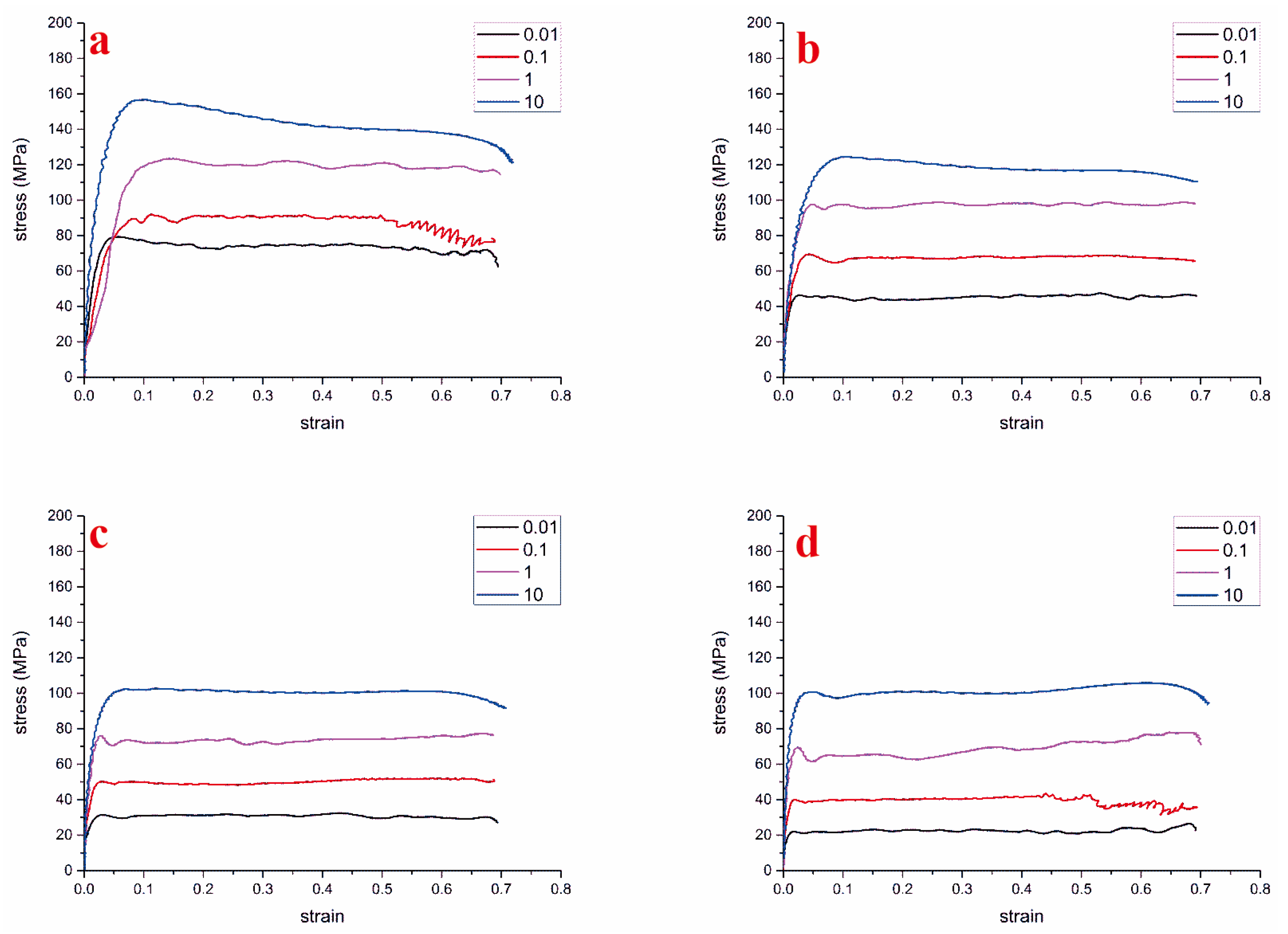





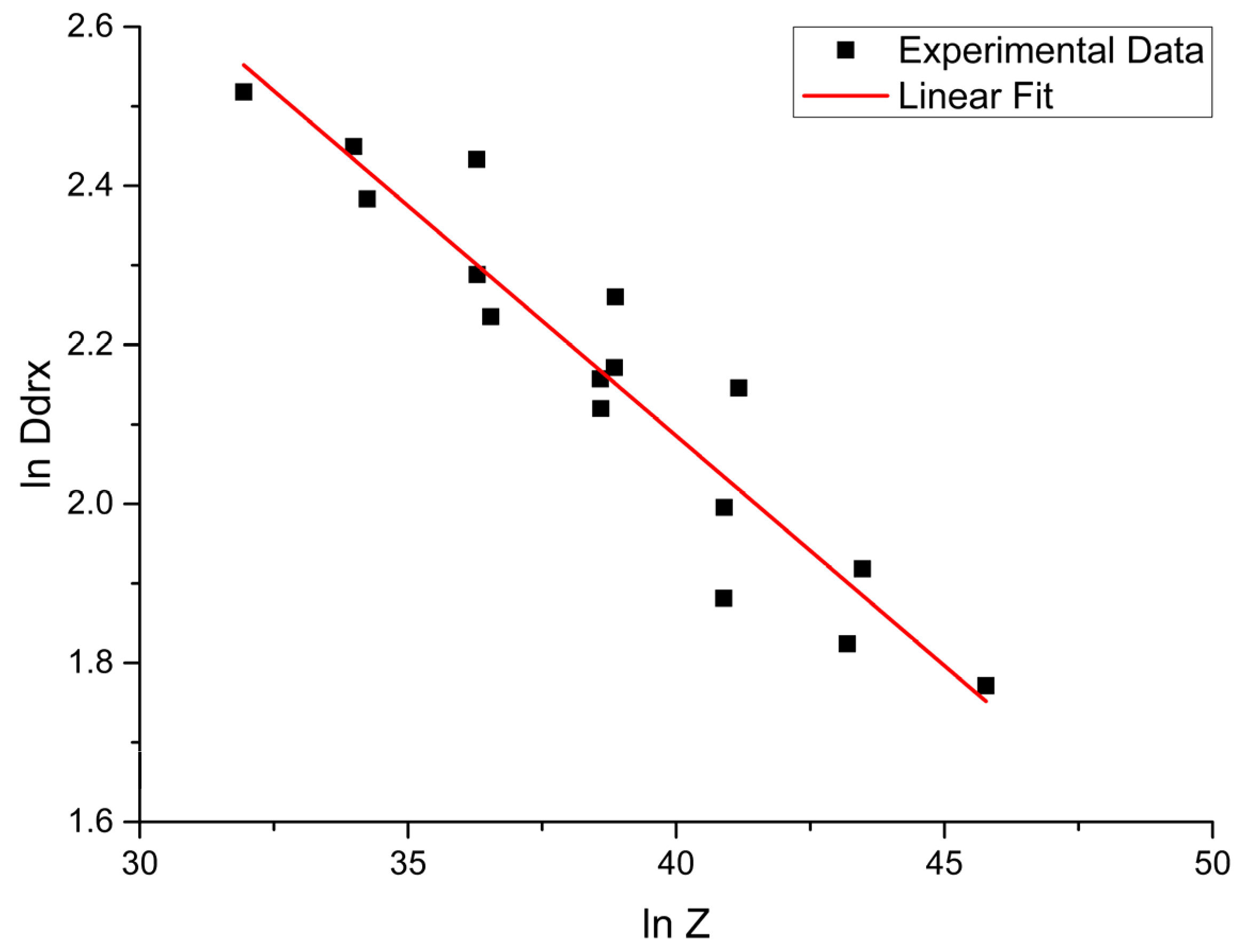
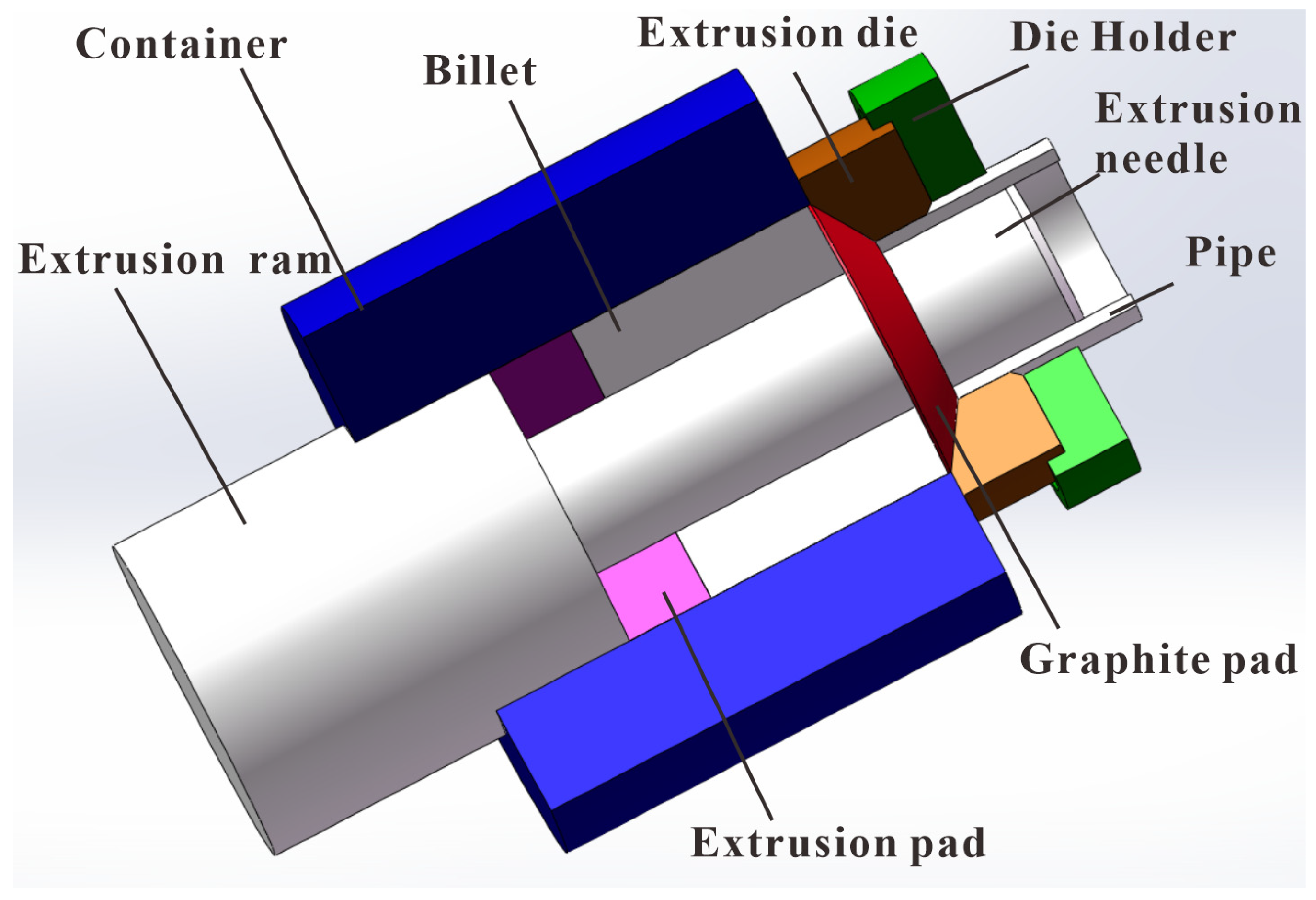


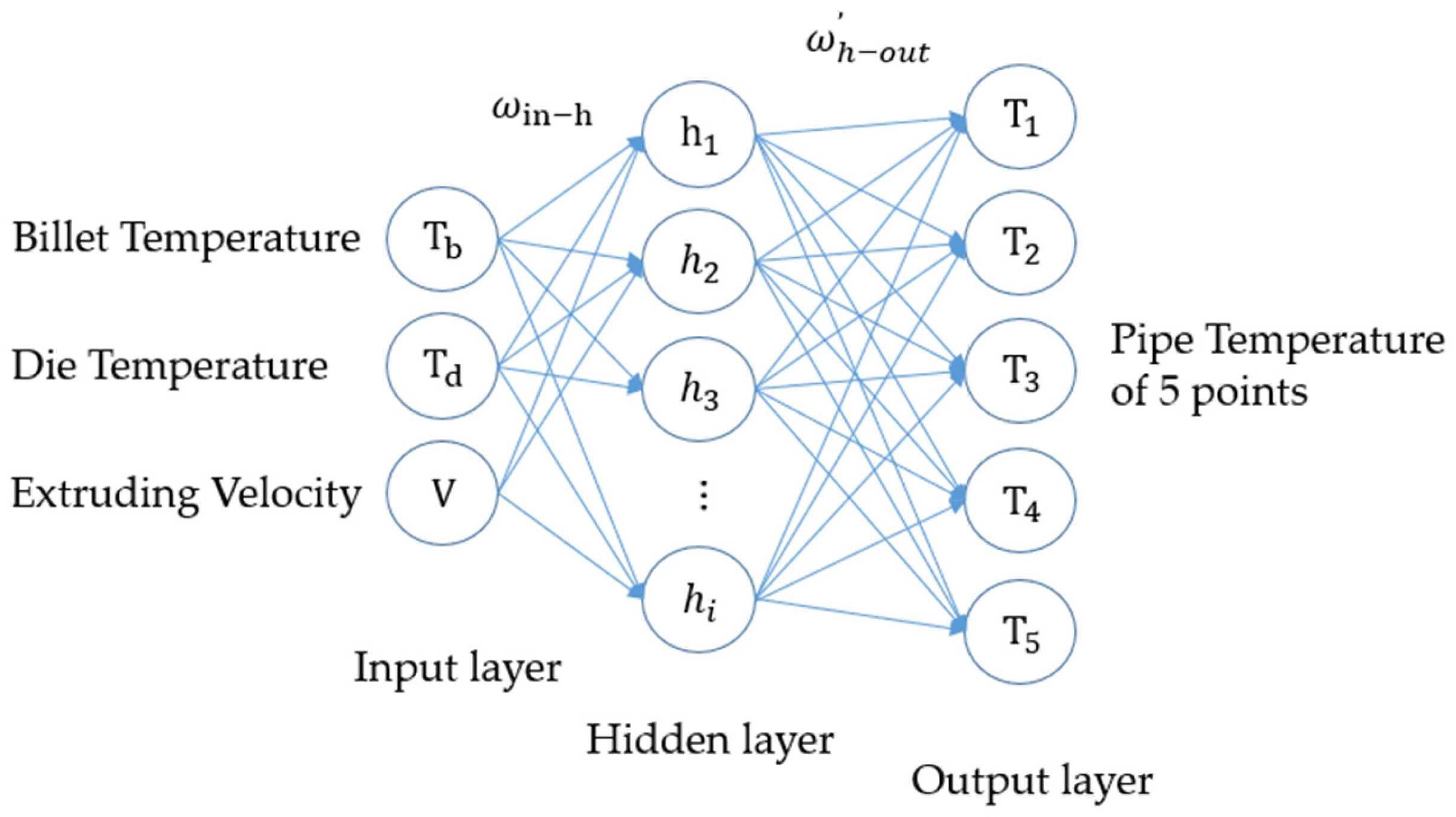


| Cu | Mg | Si | Zn | Mn | Fe | Ti | Al |
|---|---|---|---|---|---|---|---|
| 4.42 | 1.51 | 0.21 | 0.07 | 0.67 | 0.23 | 0.04 | Bal. |
| Temperature (°C) | ||||
|---|---|---|---|---|
| 360 | 0.01 | 0.1 | 1 | 10 |
| 400 | 0.01 | 0.1 | 1 | 10 |
| 440 | 0.01 | 0.1 | 1 | 10 |
| 480 | 0.01 | 0.1 | 1 | 10 |
| Drawing Number | Deformation Temperature (°C) | Recrystallization Grain Diameter (μm) | |
|---|---|---|---|
| 5-a | 360 | 0.01 | 9.59 |
| 5-b | 360 | 0.1 | 8.55 |
| 5-c | 360 | 1 | 6.81 |
| 5-d | 360 | 10 | 5.88 |
| 5-e | 400 | 0.01 | 11.40 |
| 5-f | 400 | 0.1 | 8.65 |
| 5-g | 400 | 1 | 6.56 |
| 5-h | 400 | 10 | 6.20 |
| 6-a | 440 | 0.01 | 11.58 |
| 6-b | 440 | 0.1 | 9.86 |
| 6-c | 440 | 1 | 8.33 |
| 6-d | 440 | 10 | 7.36 |
| 6-e | 480 | 0.01 | 12.40 |
| 6-f | 480 | 0.1 | 10.84 |
| 6-g | 480 | 1 | 9.35 |
| 6-h | 480 | 10 | 8.77 |
| Deformation Temperature (°C) | Messured Grain Diameter (μm) | Calculated Grain Diameter (μm) | Error (μm) | Relative Error | |
|---|---|---|---|---|---|
| 360 | 0.01 | 9.59 | 8.6 | 0.99 | 10.32% |
| 360 | 0.1 | 8.55 | 7.51 | 1.04 | 12.16% |
| 360 | 1 | 6.81 | 6.59 | 0.22 | 3.23% |
| 360 | 10 | 5.88 | 5.77 | 0.11 | 1.87% |
| 400 | 0.01 | 11.40 | 10.04 | 1.36 | 11.93% |
| 400 | 0.1 | 8.65 | 8.74 | 0.09 | 1.04% |
| 400 | 1 | 6.56 | 7.12 | 0.56 | 8.54% |
| 400 | 10 | 6.20 | 6.69 | 0.49 | 7.90% |
| 440 | 0.01 | 11.58 | 11.4 | 0.18 | 1.55% |
| 440 | 0.1 | 9.86 | 9.97 | 0.11 | 1.12% |
| 440 | 1 | 8.33 | 8.73 | 0.4 | 4.80% |
| 440 | 10 | 7.36 | 7.64 | 0.28 | 3.80% |
| 480 | 0.01 | 12.40 | 12.83 | 0.43 | 3.47% |
| 480 | 0.1 | 10.84 | 11.23 | 0.39 | 3.60% |
| 480 | 1 | 9.35 | 9.83 | 0.48 | 5.13% |
| 480 | 10 | 8.77 | 8.61 | 0.16 | 1.82% |
| RSME | 0.58 |
| Input Parameters | Parameter Value |
|---|---|
| Environment Temperature | 20 °C |
| Thermal Convection Coefficient (with air) | 0.1 N/s/mm/c |
| Thermal Conductivity | 11 N/s/mm/c |
| Friction Coefficient | 0.3 |
| Die Material | H13 steel |
| Young’s Modulus (2A12) | 68,900 |
| Poisson’s Ratio (2A12) | 0.33 |
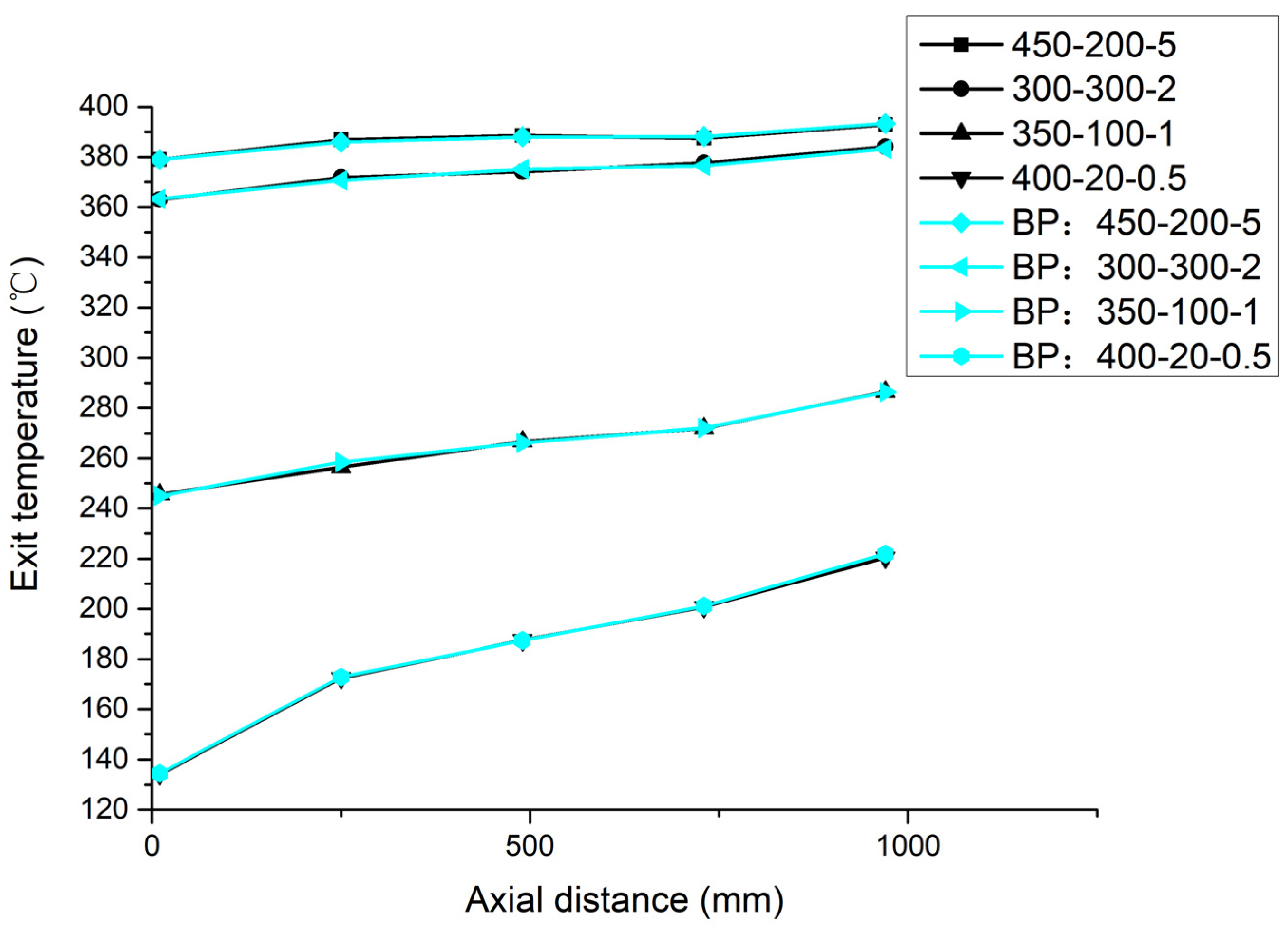
| Experimental Parameters | Classification of Experimental and Prediction Value | 1-Point Temperature | 2-Point Temperature | 3-Point Temperature | 4-Point Temperature | 5-Point Temperature |
|---|---|---|---|---|---|---|
| 450–200–5 | Experimental value (°C) | 379.0 | 386.8 | 388.5 | 387.5 | 392.8 |
| BP prediction value (°C) | 378.9 | 385.9 | 388.0 | 388.2 | 393.3 | |
| 300–300–2 | Experimental value (°C) | 362.9 | 371.8 | 374.1 | 377.6 | 384.1 |
| BP prediction value (°C) | 363.2 | 370.6 | 375.1 | 376.4 | 383.2 | |
| 350–100–1 | Experimental value (°C) | 245.5 | 256.4 | 266.7 | 271.9 | 286.5 |
| BP prediction value (°C) | 245.0 | 258.5 | 266.1 | 272.0 | 286.3 | |
| 400–20–0.5 | Experimental value (°C) | 134.1 | 172.4 | 187.5 | 200.6 | 220.4 |
| BP prediction value (°C) | 134.5 | 172.9 | 187.4 | 201.1 | 221.9 | |
| Data Analysis | Max. error (°C) | 2.1 | Relative Max Error | 0.82% | RMSE | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Wu, R.; Yuan, C.; Jiao, W.; Chen, L.; Zhou, X. Prediction of Recrystallization Structure of 2A12 Aluminum Alloy Pipe Extrusion Process Based on BP Neural Network. Metals 2023, 13, 664. https://doi.org/10.3390/met13040664
Jiang H, Wu R, Yuan C, Jiao W, Chen L, Zhou X. Prediction of Recrystallization Structure of 2A12 Aluminum Alloy Pipe Extrusion Process Based on BP Neural Network. Metals. 2023; 13(4):664. https://doi.org/10.3390/met13040664
Chicago/Turabian StyleJiang, Haishun, Rendong Wu, Chaolong Yuan, Wei Jiao, Lingling Chen, and Xingyou Zhou. 2023. "Prediction of Recrystallization Structure of 2A12 Aluminum Alloy Pipe Extrusion Process Based on BP Neural Network" Metals 13, no. 4: 664. https://doi.org/10.3390/met13040664
APA StyleJiang, H., Wu, R., Yuan, C., Jiao, W., Chen, L., & Zhou, X. (2023). Prediction of Recrystallization Structure of 2A12 Aluminum Alloy Pipe Extrusion Process Based on BP Neural Network. Metals, 13(4), 664. https://doi.org/10.3390/met13040664





