Q&P Response of a Medium Carbon Low Alloy Steel
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Critical Temperatures and Q&T/Q&P Route
3.2. Microstructure
3.2.1. Q&T
3.2.2. Q&P
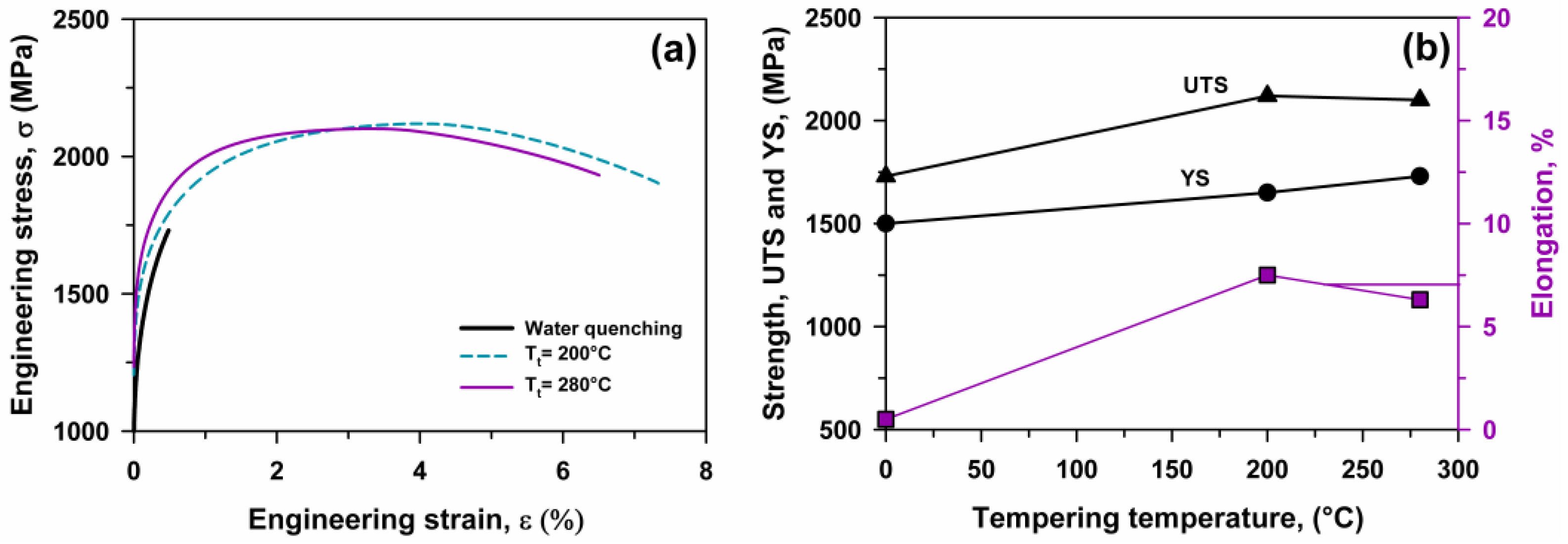
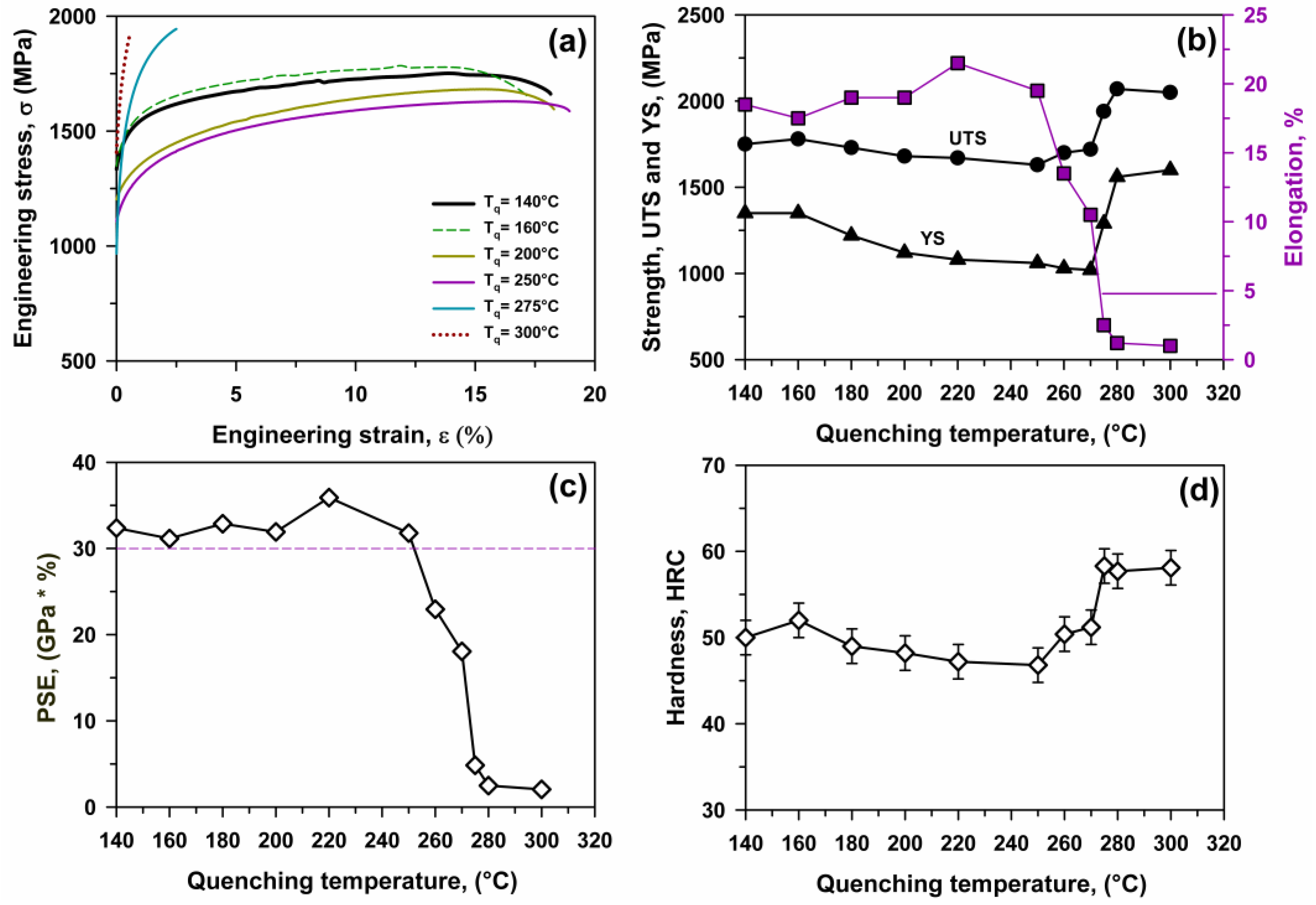
3.3. Mechanical Properties
3.3.1. Q&T
3.3.2. Q&P
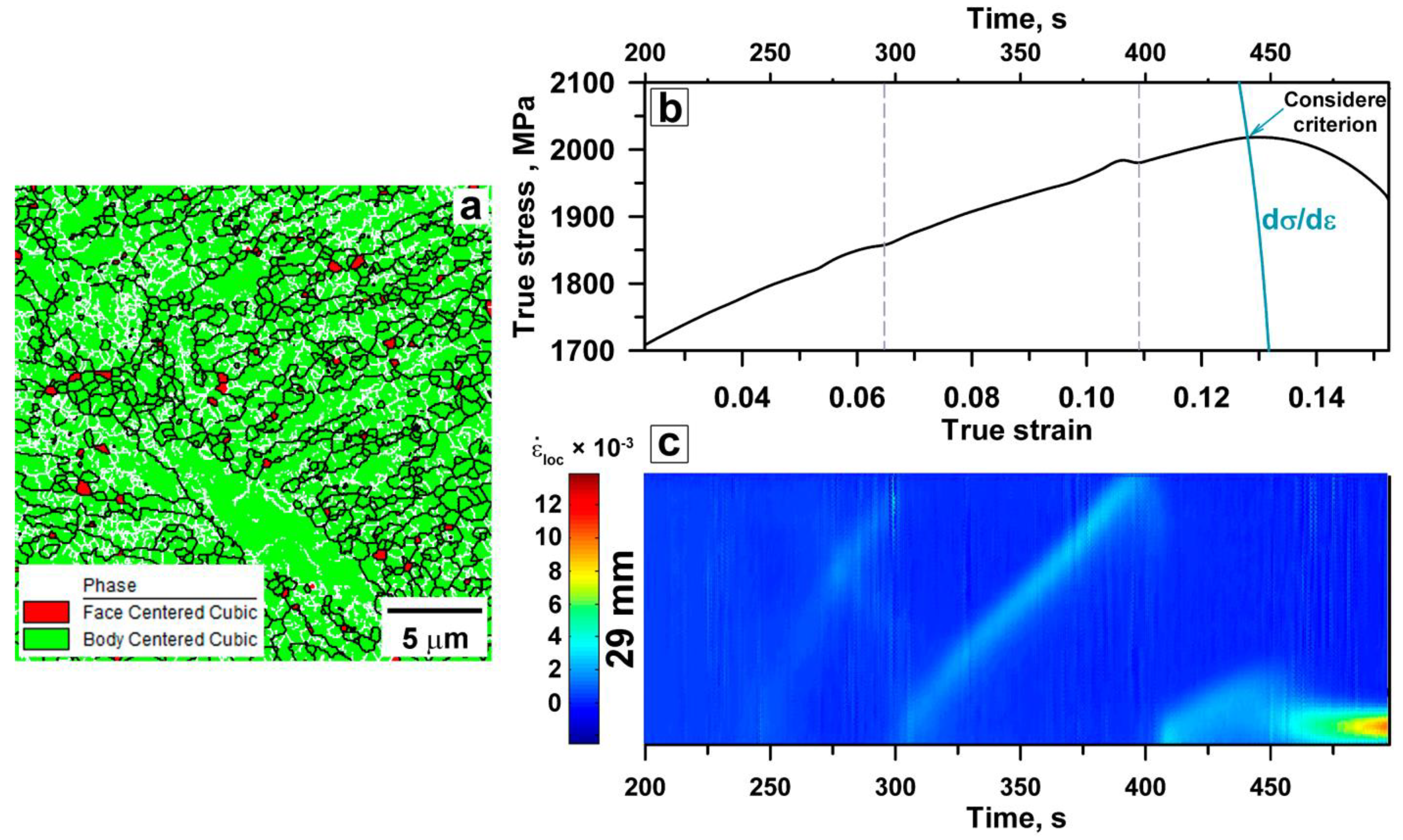
3.4. PLC Band Behavior
4. Discussion
| Tq, °C | CRA | ρKAM, ×1014 m−2 | σSS | σHP | σdisl | σ0.2 of RA , MPa | YS, MPa | ΔYS, MPa |
|---|---|---|---|---|---|---|---|---|
| 140 | 1.315 | 5.81 | 575.8 | 118.0 | 331.9 | 1025.7 | 1350 | 324.3 |
| 160 | 1.313 | 6.18 | 575.1 | 104.4 | 342.3 | 1021.8 | 1350 | 328.2 |
| 180 | 1.4 | 6.30 | 606.1 | 103.3 | 345.7 | 1055.1 | 1220 | 164.9 |
| 200 | 1.383 | 6.22 | 600.0 | 98.3 | 343.4 | 1041.7 | 1120 | 78.3 |
| 220 | 1.393 | 6.26 | 603.6 | 103.3 | 344.5 | 1051.4 | 1080 | 28.6 |
| 250 | 1.572 | 6.15 | 667.4 | 104.2 | 341.4 | 1113 | 1060 | −53 |
| Tq, °C | Volume Fraction of M1, % | Volume Fraction of RA, % | Volume Fraction of M2, % | Contribution of M1 to YS, 1730·fM1 (MPa) | Contribution of M2 to YS, 1500·fM2 (MPa) | Contribution of RA to YS, | YS Calculated by Equation (1) |
|---|---|---|---|---|---|---|---|
| 140 | 77 | 17 | 6 | 1332 | 90 | 174 | 1596 |
| 160 | 72 | 17 | 11 | 1246 | 165 | 172 | 1583 |
| 180 | 65 | 22 | 13 | 1125 | 195 | 232 | 1552 |
| 200 | 56 | 23 | 21 | 969 | 315 | 239 | 1523 |
| 220 | 45 | 24 | 31 | 778 | 465 | 252 | 1495 |
| 250 | 24 | 25 | 51 | 415 | 765 | 278 | 1458 |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fonstein, N. Advanced High Strength Sheet Steels; Springer International Publishing: Cham, Switzerland, 2015; ISBN 978-3-319-19164-5. [Google Scholar]
- Zhang, K.; Liu, P.; Li, W.; Guo, Z.; Rong, Y. Ultrahigh Strength-Ductility Steel Treated by a Novel Quenching–Partitioning–Tempering Process. Mater. Sci. Eng. A 2014, 619, 205–211. [Google Scholar] [CrossRef]
- An, B.; Zhang, C.; Gao, G.; Gui, X.; Tan, Z.; Misra, R.D.K.; Yang, Z. Experimental and Theoretical Analysis of Multiphase Microstructure in a Newly Designed MnSiCrC Quenched and Partitioned Steel to Promote Bainitic Transformation: The Significant Impact on Mechanical Properties. Mater. Sci. Eng. A 2019, 757, 117–123. [Google Scholar] [CrossRef]
- Zurnadzhy, V.I.; Efremenko, V.G.; Wu, K.M.; Petryshynets, I.; Shimizu, K.; Zusin, A.M.; Brykov, M.N.; Andilakhai, V.A. Tailoring Strength/Ductility Combination in 2.5 Wt% Si-Alloyed Middle Carbon Steel Produced by the Two-Step Q-P Treatment with a Prolonged Partitioning Stage. Mater. Sci. Eng. A 2020, 791, 139721. [Google Scholar] [CrossRef]
- Chen, K.; Jiang, Z.; Liu, F.; Li, H.; Kang, C.; Zhang, W.; Wang, A. Achievement of High Ductility and Ultra-High Strength of V-Nb Microalloyed Spring Steel by Austempered Multiphase Microstructure. Metall. Mater. Trans. A 2020, 51, 3565–3575. [Google Scholar] [CrossRef]
- Dong, X.X.; Shen, Y.F.; Jia, N.; Zhu, Y.T. Improving Mechanical Properties and Retained-Austenite Stability of a Medium Carbon Q&P Steel by Adjusting Phase Ratio. Mater. Sci. Eng. A 2022, 833, 142580. [Google Scholar] [CrossRef]
- Kusakin, P.S.; Kaibyshev, R.O. High-Mn twinning-induced plasticity steels: Microstructure and mechanical properties. Rev. Adv. Mater. Sci. 2016, 44, 326–360. [Google Scholar]
- De Cooman, B.C.; Estrin, Y.; Kim, S.K. Twinning-Induced Plasticity (TWIP) Steels. Acta Mater. 2018, 142, 283–362. [Google Scholar] [CrossRef]
- Dai, Z.; Chen, H.; Ding, R.; Lu, Q.; Zhang, C.; Yang, Z.; Zwaag, S. Fundamentals and Application of Solid-State Phase Transformations for Advanced High Strength Steels Containing Metastable Retained Austenite. Mater. Sci. Eng. R 2021, 143, 100590. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, Z. Thermomechanical Processing of Advanced High Strength Steels. Prog. Mater. Sci. 2018, 94, 174–242. [Google Scholar] [CrossRef]
- Bouquerel, J.; Verbeken, K.; Cooman, B.C.D. Microstructure-Based Model for the Static Mechanical Behaviour of Multiphase Steels. Acta Mater. 2006, 54, 1443–1456. [Google Scholar] [CrossRef]
- Seo, E.J.; Cho, L.; Estrin, Y.; De Cooman, B.C. Microstructure-Mechanical Properties Relationships for Quenching and Partitioning (Q&P) Processed Steel. Acta Mater. 2016, 113, 124–139. [Google Scholar] [CrossRef]
- Speer, J.; Matlock, D.K.; De Cooman, B.C.; Schroth, J.G. Carbon Partitioning into Austenite after Martensite Transformation. Acta Mater. 2003, 51, 2611–2622. [Google Scholar] [CrossRef]
- Speer, J.G. Phase Transformations in Quenched and Partitioned Steels in Diffusionless Transformation, High Strength Steels, Modeling and Advanced Analytical Techniques; Pereloma, E., Edmonds, D.V., Eds.; Woodhead Publishing Ltd.: Cambridge, UK, 2012; Volume 2, pp. 247–270. [Google Scholar]
- Moor, E.D.; Speer, J.G.; Matlock, D.K.; Kwak, J.-H.; Lee, S.-B. Effect of Carbon and Manganese on the Quenching and Partitioning Response of CMnSi Steels. ISIJ Int. 2011, 51, 137–144. [Google Scholar] [CrossRef] [Green Version]
- Xiong, X.C.; Chen, B.; Huang, M.X.; Wanga, J.F.; Wang, L. The Effect of Morphology on the Stability of Retained Austenite in a Quenched and Partitioned Steel. Scr. Mater. 2013, 68, 321–324. [Google Scholar] [CrossRef]
- Shen, Y.F.; Qiu, L.N.; Sun, X.; Zuo, L.; Liaw, P.K.; Raabe, D. Effects of Retained Austenite Volume Fraction, Morphology, and Carbon Content on Strength and Ductility of Nanostructured TRIP-Assisted Steels. Mater. Sci. Eng. A 2015, 636, 551–564. [Google Scholar] [CrossRef] [Green Version]
- Soleimani, M.; Kalhor, A.; Mirzadeh, H. Transformation-Induced Plasticity (TRIP) in Advanced Steels: A Review. Mater. Sci. Eng. A 2020, 795, 140023. [Google Scholar] [CrossRef]
- Yan, S.; Liu, X.; Liu, W.J.; Liang, T.; Zhang, B.; Liu, L.; Zhao, Y. Comparative Study on Microstructure and Mechanical Properties of a C-Mn-Si Steel Treated by Quenching and Partitioning (Q&P) Processes after a Full and Intercritical Austenitization. Mater. Sci. Eng. A 2017, 684, 261–269. [Google Scholar] [CrossRef]
- Liu, L.; Li, H.; Xu, H.; Dai, X.; Tian, Y.; Chen, L. The Effect of Partitioning Temperature on Residual Austenite and Mechanical Properties of Q&P High Strength Steel during the Continuous Annealing Process. Metals 2022, 12, 2165. [Google Scholar] [CrossRef]
- Nakada, N.; Ishibashi, Y.; Tsuchiyama, T.; Takaki, S. Self-Stabilization of Untransformed Austenite by Hydrostatic Pressure via Martensitic Transformation. Acta Mater. 2016, 110, 95–102. [Google Scholar] [CrossRef]
- Gao, G.; Gao, B.; Gui, X.; Hu, J.; He, J.; Tan, Z.; Bai, B. Correlation between Microstructure and Yield Strength of As-Quenched and Q&P Steels with Different Carbon Content (0.06–0.42 Wt%C). Mater. Sci. Eng. A 2019, 753, 1–10. [Google Scholar] [CrossRef]
- HajyAkbary, F.; Sietsma, J.; Miyamoto, G.; Kamikawa, N.; Petrov, R.H.; Furuhara, T.; Santofimia, M.J. Analysis of the Mechanical Behavior of a 0.3C-1.6Si-3.5Mn(Wt%) Quenching and Partitioning Steel. Mater. Sci. Eng. A 2016, 677, 505–514. [Google Scholar] [CrossRef]
- Lebedkina, T.A.; Lebyodkin, M.A.; Chateau, J.-P.; Jacques, A.; Allain, S. On the Mechanism of Unstable Plastic Flow in an Austenitic FeMnC TWIP Steel. Mater. Sci. Eng. A 2009, 519, 147–154. [Google Scholar] [CrossRef]
- Hirsh, P.B.; Howie, A.; Nicholson, R.B.; Pashley, D.W.; Whelan, M.J. Electron Microscopy of Thin Crystals; Butterworths: London, UK, 1965. [Google Scholar]
- Zhilyaev, A.; Shakhova, I.; Belyakov, A.; Kaibyshev, R.; Langdon, T.G. Wear Resistance and Electroconductivity in Copper Processed by Severe Plastic Deformation. Wear 2013, 305, 89–99. [Google Scholar] [CrossRef]
- Niessen, F.; Nyyssönen, T.; Gazder, A.A.; Hielscher, R. Parent Grain Reconstruction from Partially or Fully Transformed Microstructures in MTEX. J. Appl. Crystallogr. 2022, 55, 180–194. [Google Scholar] [CrossRef] [PubMed]
- Miyamoto, G.; Iwata, N.; Takayama, N.; Furuhara, T. Mapping the Parent Austenite Orientation Reconstructed from the Orientation of Martensite by EBSD and Its Application to Ausformed Martensite. Acta Mater. 2010, 58, 6393–6403. [Google Scholar] [CrossRef]
- Cullity, B.D. Elements of X-Ray Diffraction. In Addison-Wesley Series in Metallurgy and Materials, 2nd ed.; Addison-Wesley Pub. Co.: Boston, MA, USA, 1978; ISBN 978-0-201-01174-6. [Google Scholar]
- Vandijk, N.; Butt, A.; Zhao, L.; Sietsma, J.; Offerman, S.; Wright, J.; Vanderzwaag, S. Thermal Stability of Retained Austenite in TRIP Steels Studied by Synchrotron X-Ray Diffraction during Cooling. Acta Mater. 2005, 53, 5439–5447. [Google Scholar] [CrossRef]
- Ranjan, R.; Beladi, H.; Hodgson, P.D.; Singh, S.B. The Mechanical Properties of Low Alloy TRIP-Aided Steel: The Role of Retained Austenite. Met. Mater. Trans. A 2021, 52, 4649–4663. [Google Scholar] [CrossRef]
- Tkachev, E.; Borisov, S.; Belyakov, A.; Kniaziuk, T.; Vagina, O.; Gaidar, S.; Kaibyshev, R. Effect of Quenching and Tempering on Structure and Mechanical Properties of a Low-Alloy 0.25C Steel. Mater. Sci. Eng. A 2023, 868, 144757. [Google Scholar] [CrossRef]
- Hidalgo, J.; Celada-Casero, C.; Santofimia, M.J. Fracture Mechanisms and Microstructure in a Medium Mn Quenching and Partitioning Steel Exhibiting Macrosegregation. Mater. Sci. Eng. A 2019, 754, 766–777. [Google Scholar] [CrossRef]
- Carpio, M.; Calvo, J.; García, O.; Pedraza, J.P.; Cabrera, J.M. Heat Treatment Design for a QP Steel: Effect of Partitioning Temperature. Metals 2021, 11, 1136. [Google Scholar] [CrossRef]
- Bagliani, E.P.; Santofimia, M.J.; Zhao, L.; Sietsma, J.; Anelli, E. Microstructure, Tensile and Toughness Properties after Quenching and Partitioning Treatments of a Medium-Carbon Steel. Mater. Sci. Eng. A 2013, 559, 486–495. [Google Scholar] [CrossRef]
- Huyghe, P.; Malet, L.; Caruso, M.; Georges, C.; Godet, S. On the Relationship between the Multiphase Microstructure and the Mechanical Properties of a 0.2C Quenched and Partitioned Steel. Mater. Sci. Eng. A 2017, 701, 254–263. [Google Scholar] [CrossRef]
- Peng, F.; Xu, Y.; Gu, X.; Wang, Y.; Liu, X.; Li, J. The Relationships of Microstructure-Mechanical Properties in Quenching and Partitioning (Q&P) Steel Accompanied with Microalloyed Carbide Precipitation. Mater. Sci. Eng. A 2018, 723, 247–258. [Google Scholar] [CrossRef]
- Pashangeh, S.; Somani, M.C.; Banadkouki, S.S.G.; Zarchi, H.R.K.; Kaikkonen, P.; Porter, D.A. On the decomposition of austenite in a high-silicon medium-carbon steel during quenching and isothermal holding above and below the Ms temperature. Mater. Charact. 2020, 162, 110224. [Google Scholar] [CrossRef]
- Kitahara, H.; Ueji, R.; Tsuji, N.; Minamino, Y. Crystallographic Features of Lath Martensite in Low-Carbon Steel. Acta Mater. 2006, 54, 1279–1288. [Google Scholar] [CrossRef]
- Koistinen, D.P.; Marburger, R.E. A General Equation Prescribing the Extent of the Austenite-Martensite Transformation in Pure Iron-Carbon Alloys and Plain Carbon Steels. Acta Metall. 1959, 7, 59–60. [Google Scholar] [CrossRef]
- Yuzbekova, D.; Mogucheva, A.; Zhemchuzhnikova, D.; Lebedkina, T.; Lebyodkin, M.; Kaibyshev, R. Effect of Microstructure on Continuous Propagation of the Portevin–Le Chatelier Deformation Bands. Int. J. Plast. 2017, 96, 210–226. [Google Scholar] [CrossRef]
- Choi, J.H.; Jo, M.C.; Lee, H.; Zargaran, A.; Song, T.; Sohn, S.S.; Kim, N.J.; Lee, S. Cu Addition Effects on TRIP to TWIP Transition and Tensile Property Improvement of Ultra-High-Strength Austenitic High-Mn Steels. Acta Mater. 2019, 166, 246–260. [Google Scholar] [CrossRef]
- Li, Z.C.; Ding, H.; Misra, R.D.K.; Cai, Z.H. Deformation Behavior in Cold-Rolled Medium-Manganese TRIP Steel and Effect of Pre-Strain on the Lüders Bands. Mater. Sci. Eng. A 2017, 679, 230–239. [Google Scholar] [CrossRef] [Green Version]
- Torganchuk, V.; Belyakov, A.; Kaibyshev, R. On the Transformation-Induced Plasticity of a Medium-Manganese Steel. Mater. Lett. 2021, 304, 130599. [Google Scholar] [CrossRef]
- Baker, T.N. Yield, Flow and Fracture of Polycrystals; Applied Science Publishers: London, UK, 1983. [Google Scholar]
- Gavriljuk, V.G.; Berns, H. High Nitrogen Steels: Structure, Properties, Manufacture, Applications; Springer: Berlin/Heidelberg, Germany, 1999; ISBN 978-3-642-08567-3. [Google Scholar]
- Hall, E.O. The Deformation and Ageing of Mild Steel: III Discussion of Results. Proc. Phys. Society. Sect. B 1951, 64, 747–753. [Google Scholar] [CrossRef]
- Petch, N.J. The Cleavage Strength of Polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Odnobokova, M.; Belyakov, A.; Enikeev, N.; Kaibyshev, R.; Valiev, R.Z. Microstructural Changes and Strengthening of Austenitic Stainless Steels during Rolling at 473 K. Metals 2020, 10, 1614. [Google Scholar] [CrossRef]
- Malopheyev, S.; Kulitskiy, V.; Kaibyshev, R. Deformation Structures and Strengthening Mechanisms in an Al Mg Sc Zr Alloy. J. Alloy. Compd. 2017, 698, 957–966. [Google Scholar] [CrossRef]
- Odnobokova, M.V.; Belyakov, A.N.; Dolzhenko, P.D.; Kostina, M.V.; Kaibyshev, R.O. On the Strengthening Mechanisms of High Nitrogen Austenitic Stainless Steels. Mater. Lett. 2023, 331, 133502. [Google Scholar] [CrossRef]
- Kusakin, P.; Belyakov, A.; Haase, C.; Kaibyshev, R.; Molodov, D. Microstructure Evolution and Strengthening Mechanisms of Fe–23Mn–0.3C–1.5Al TWIP Steel during Cold Rolling. Mater. Sci. Eng. A 2014, 617, 52–60. [Google Scholar] [CrossRef]
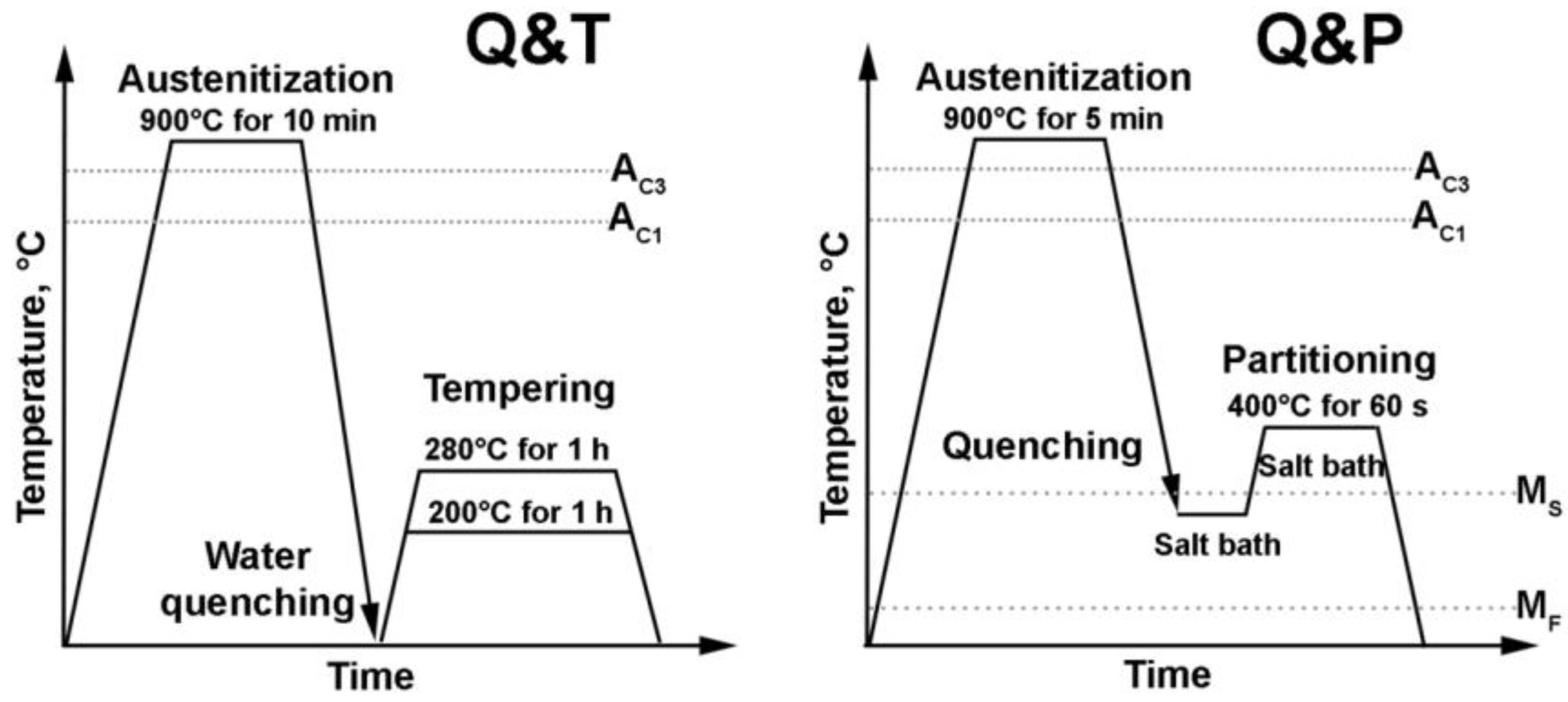
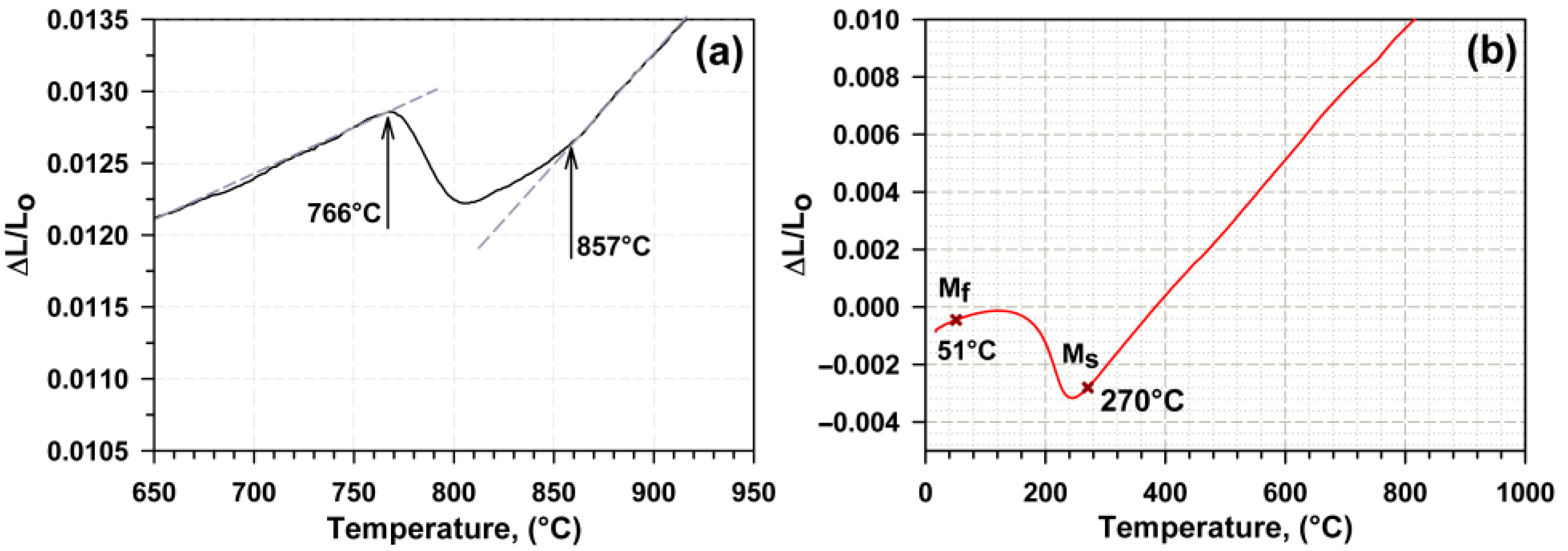
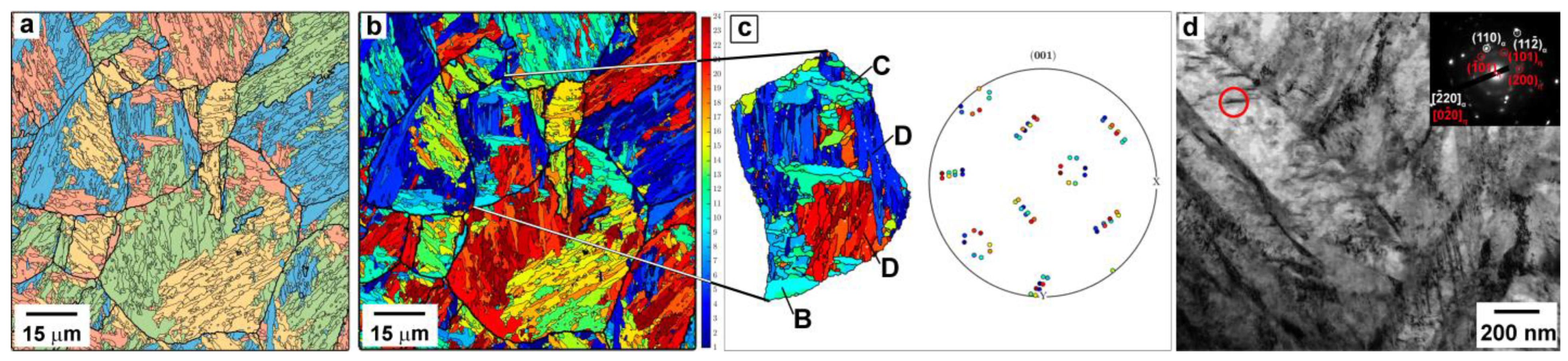





| Method | Ac1, °C | Ac3, °C | MS, °C | MF, °C |
|---|---|---|---|---|
| Thermo-Calc | 729 | 798 | – | – |
| Dilatometry curve | 760 | 857 | 270 | 51 |
| Tq, °C | KAM Value of RA, ° | KAM Value of Martensite, ° | Average Grain Size of RA, μm |
|---|---|---|---|
| 140 | 0.56 | 0.53 | 1.84 |
| 160 | 0.59 | 0.52 | 2.35 |
| 180 | 0.60 | 0.51 | 2.4 |
| 200 | 0.59 | 0.57 | 2.65 |
| 220 | 0.6 | 0.59 | 2.4 |
| 250 | 0.59 | 0.57 | 2.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishnev, R.; Borisova, Y.; Gaidar, S.; Kniaziuk, T.; Vagina, O.; Kaibyshev, R. Q&P Response of a Medium Carbon Low Alloy Steel. Metals 2023, 13, 689. https://doi.org/10.3390/met13040689
Mishnev R, Borisova Y, Gaidar S, Kniaziuk T, Vagina O, Kaibyshev R. Q&P Response of a Medium Carbon Low Alloy Steel. Metals. 2023; 13(4):689. https://doi.org/10.3390/met13040689
Chicago/Turabian StyleMishnev, Roman, Yuliya Borisova, Sergey Gaidar, Tatiana Kniaziuk, Olga Vagina, and Rustam Kaibyshev. 2023. "Q&P Response of a Medium Carbon Low Alloy Steel" Metals 13, no. 4: 689. https://doi.org/10.3390/met13040689
APA StyleMishnev, R., Borisova, Y., Gaidar, S., Kniaziuk, T., Vagina, O., & Kaibyshev, R. (2023). Q&P Response of a Medium Carbon Low Alloy Steel. Metals, 13(4), 689. https://doi.org/10.3390/met13040689







