Study on the Behavior of Assembled T-Shaped Aluminum Alloy Specimens under Axial Compression
Abstract
:1. Introduction
2. Experimental Studies
2.1. Specimen Design
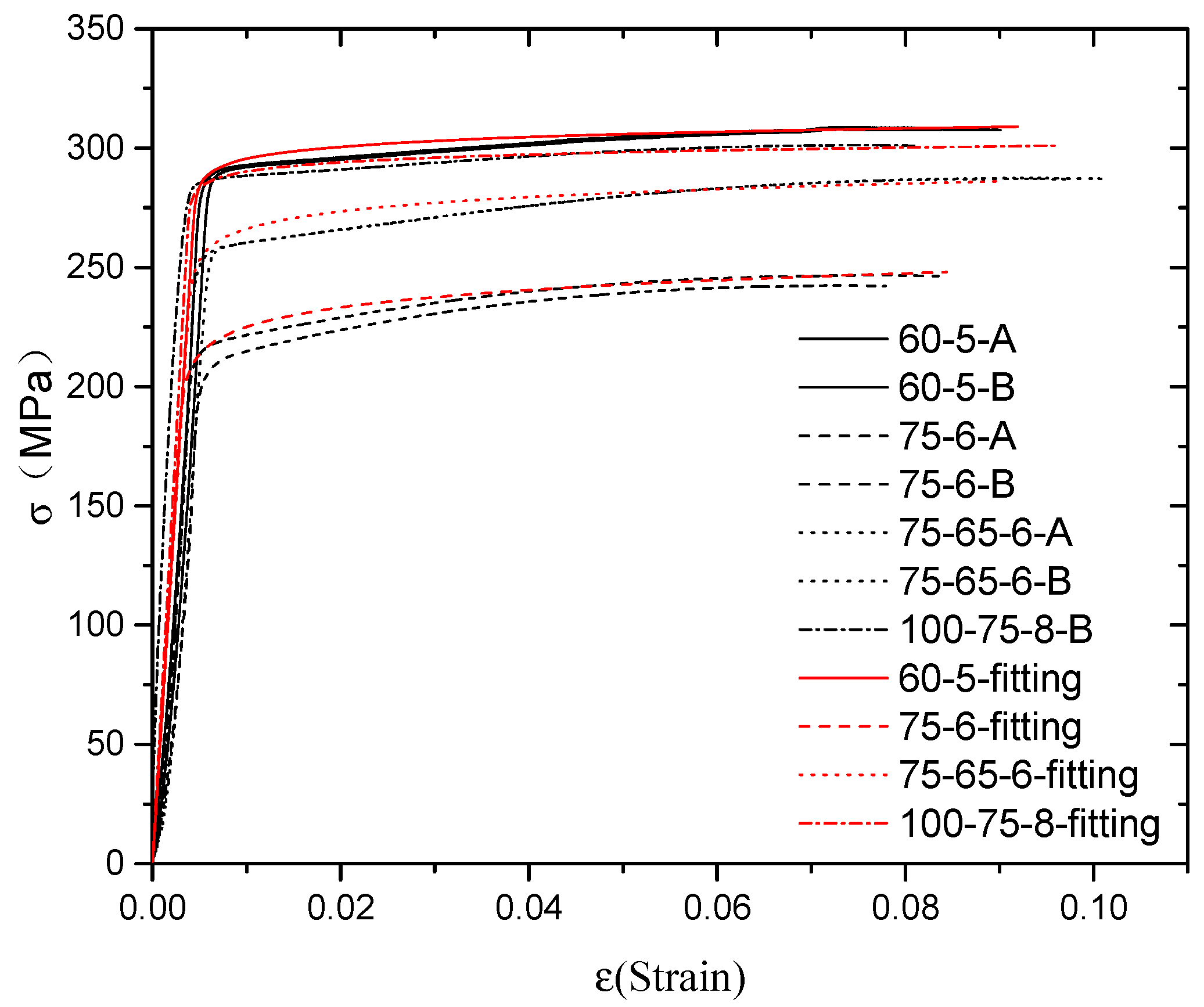
2.2. Material Properties
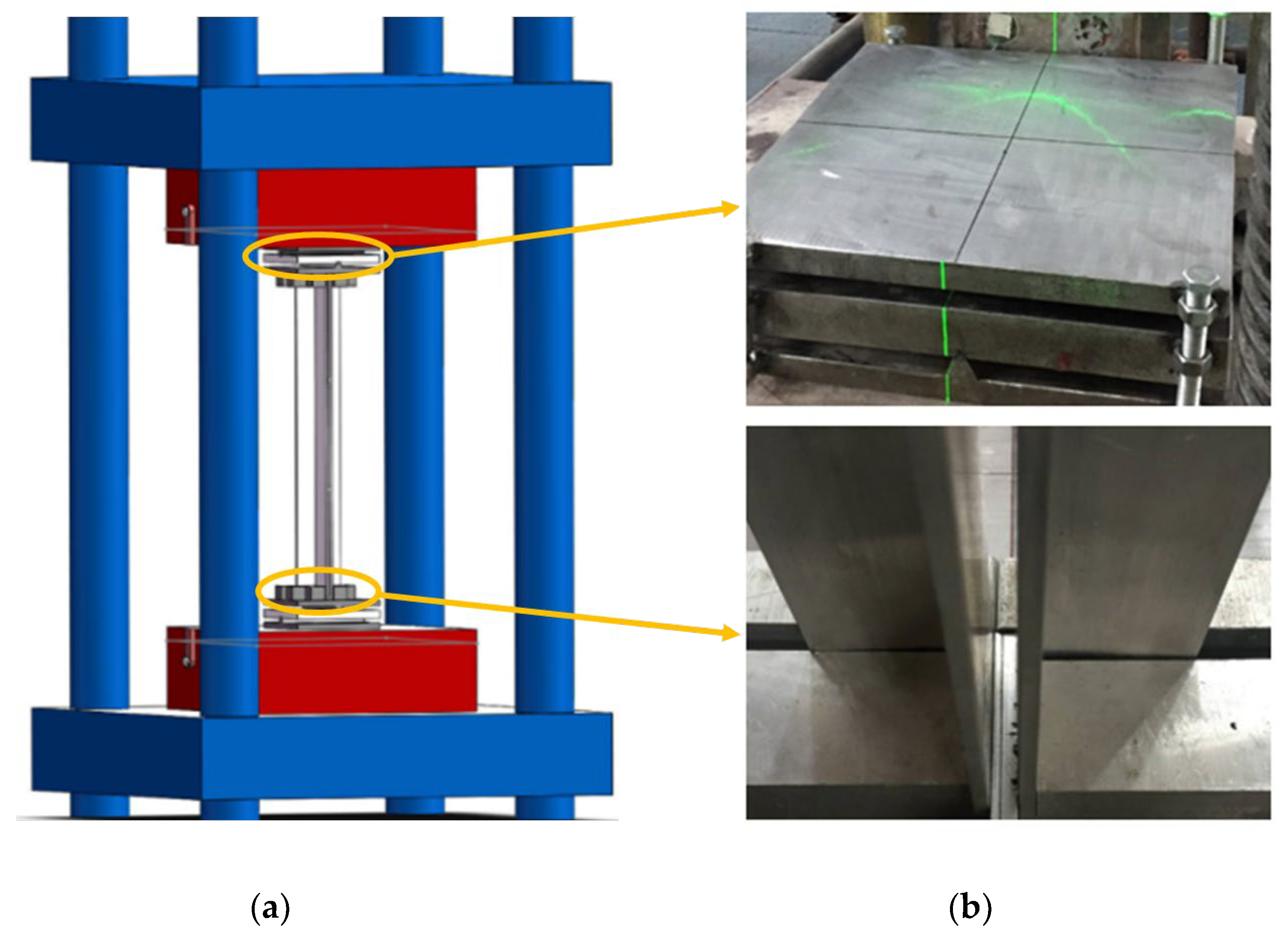
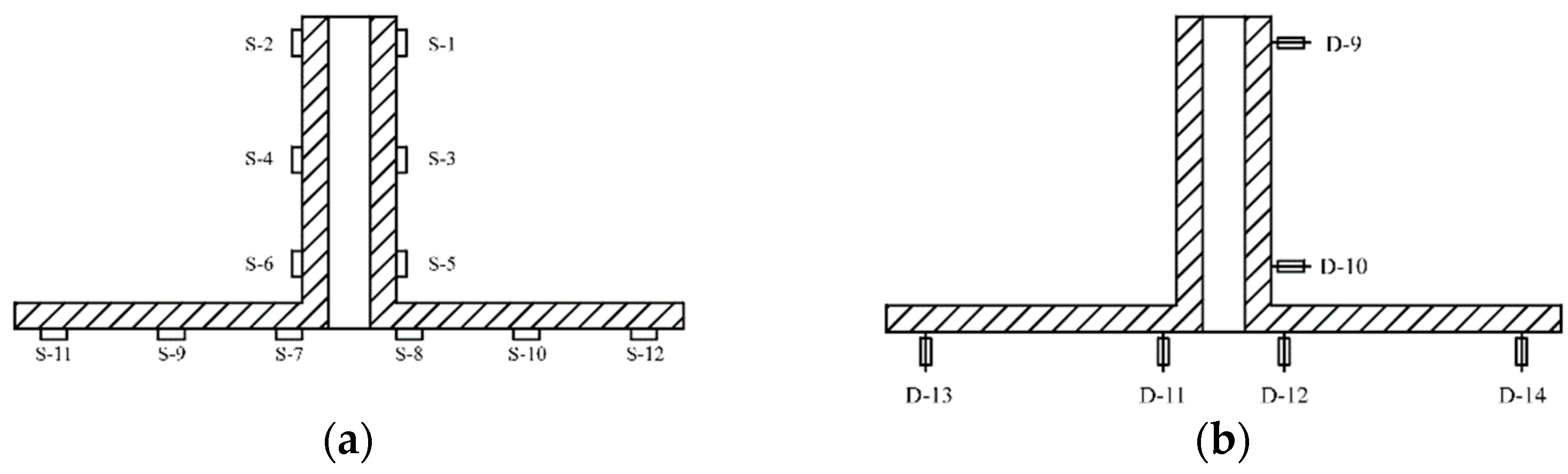
2.3. Loading Scheme and Measurement Point Arrangement
3. Experimental Results and Design
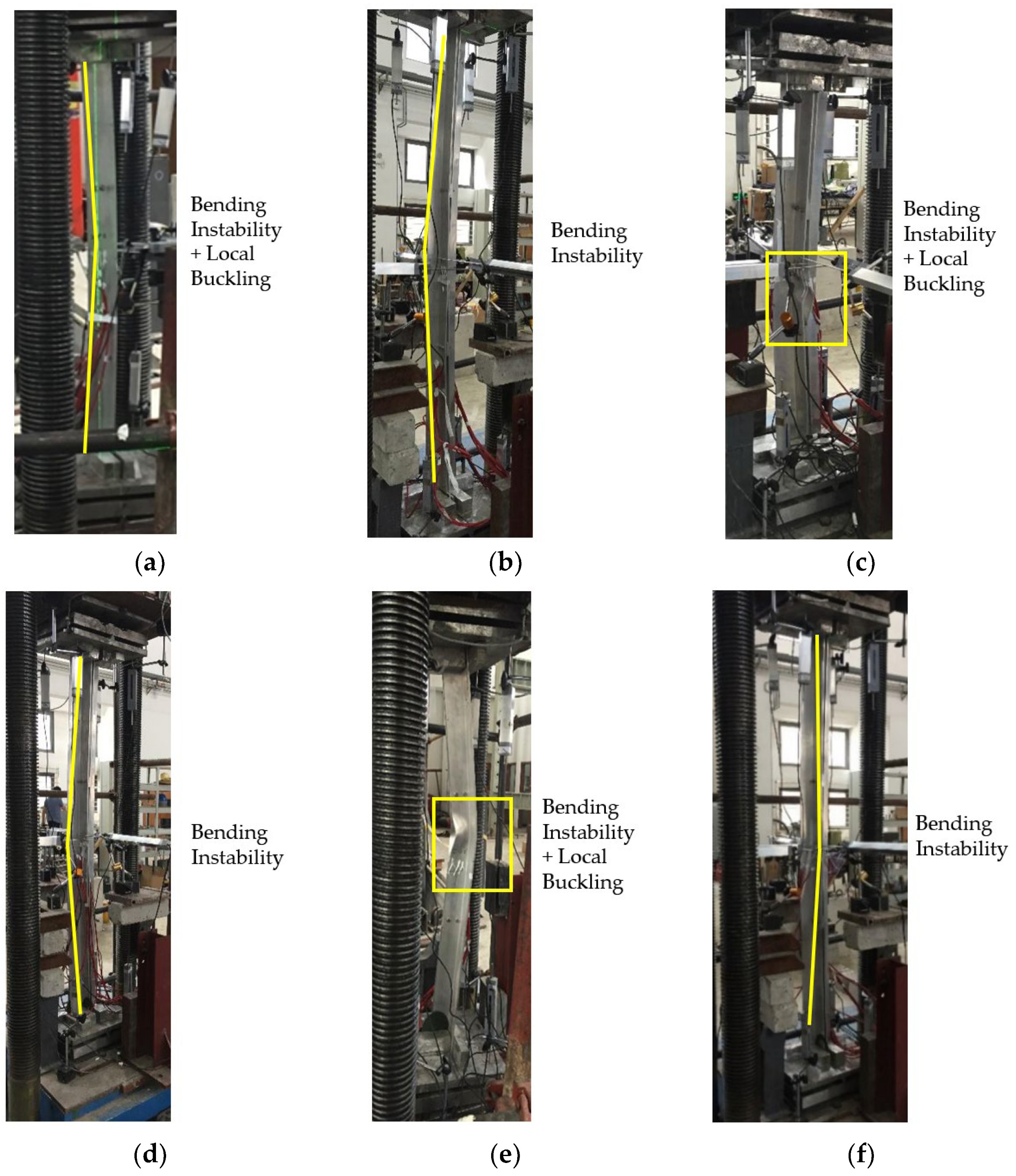
3.1. Specimen Phenomena and Damage Patterns
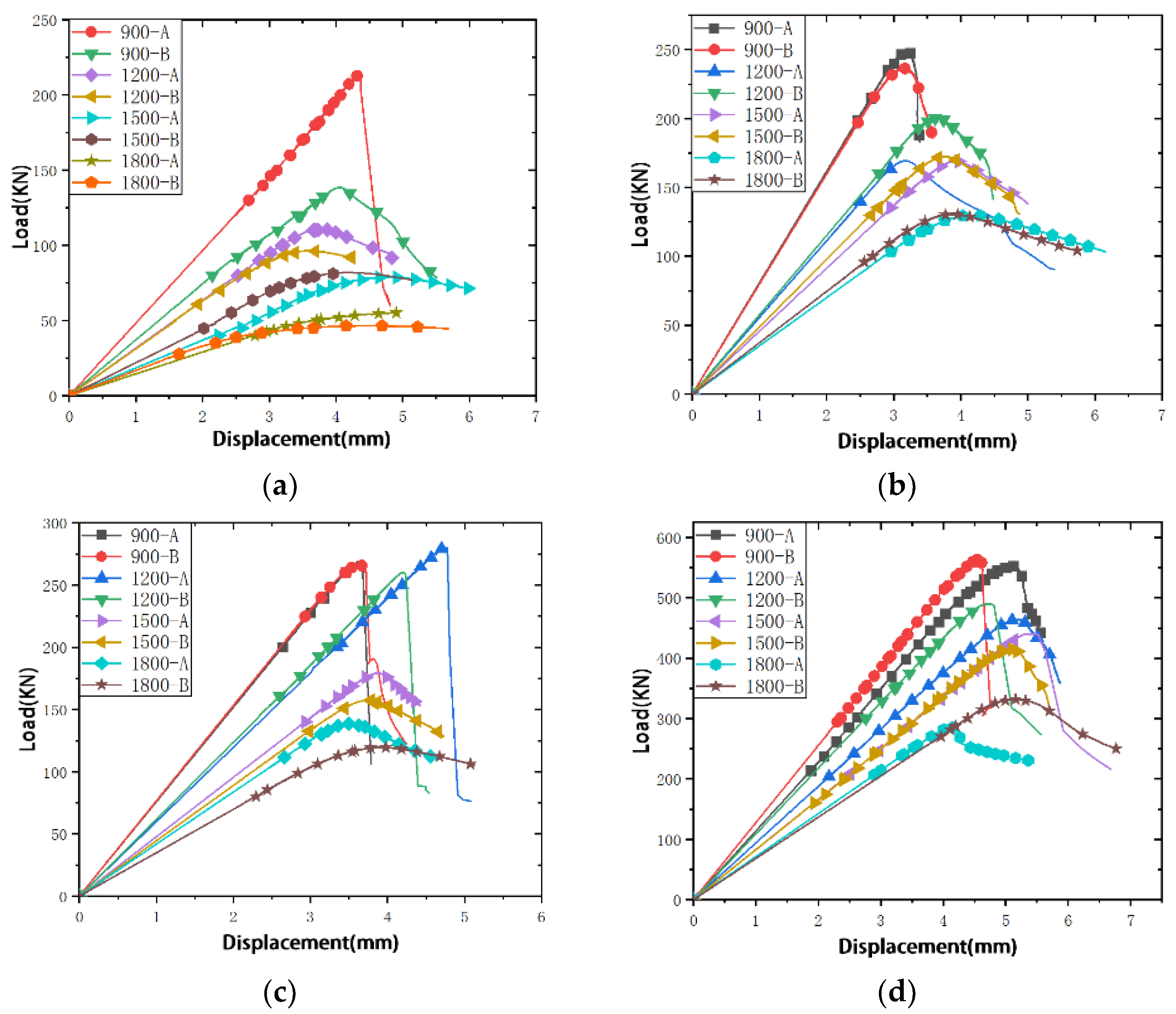
3.2. Load-Axial Displacement Curve
4. Finite Element Analysis
4.1. Finite Element Modeling
4.2. Verification of the Reasonableness of the Simplified Model for the Axial Compression Test of Assembled T-Shaped Aluminum Alloy Specimens
4.3. Parameter Analysis
- (1)
- Initial bending
- (2)
- Section size
- (3)
- Thickness of infill plate
5. Design Method for Assembled T-Shaped Aluminum Alloy Axial Compression Specimens
5.1. Load-Carrying Capacity Formula for Assembled T-Shaped Axially Compressed Specimens
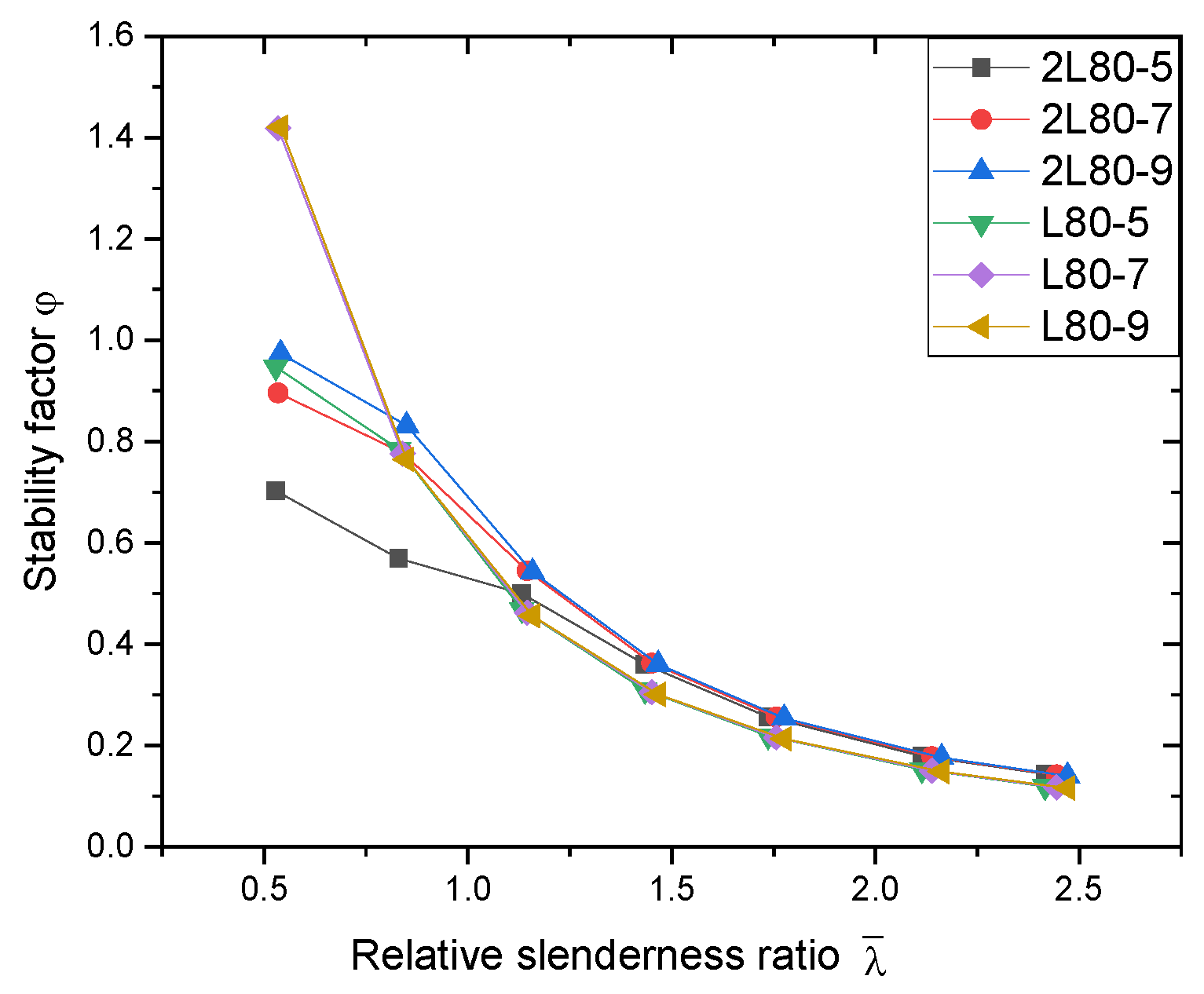
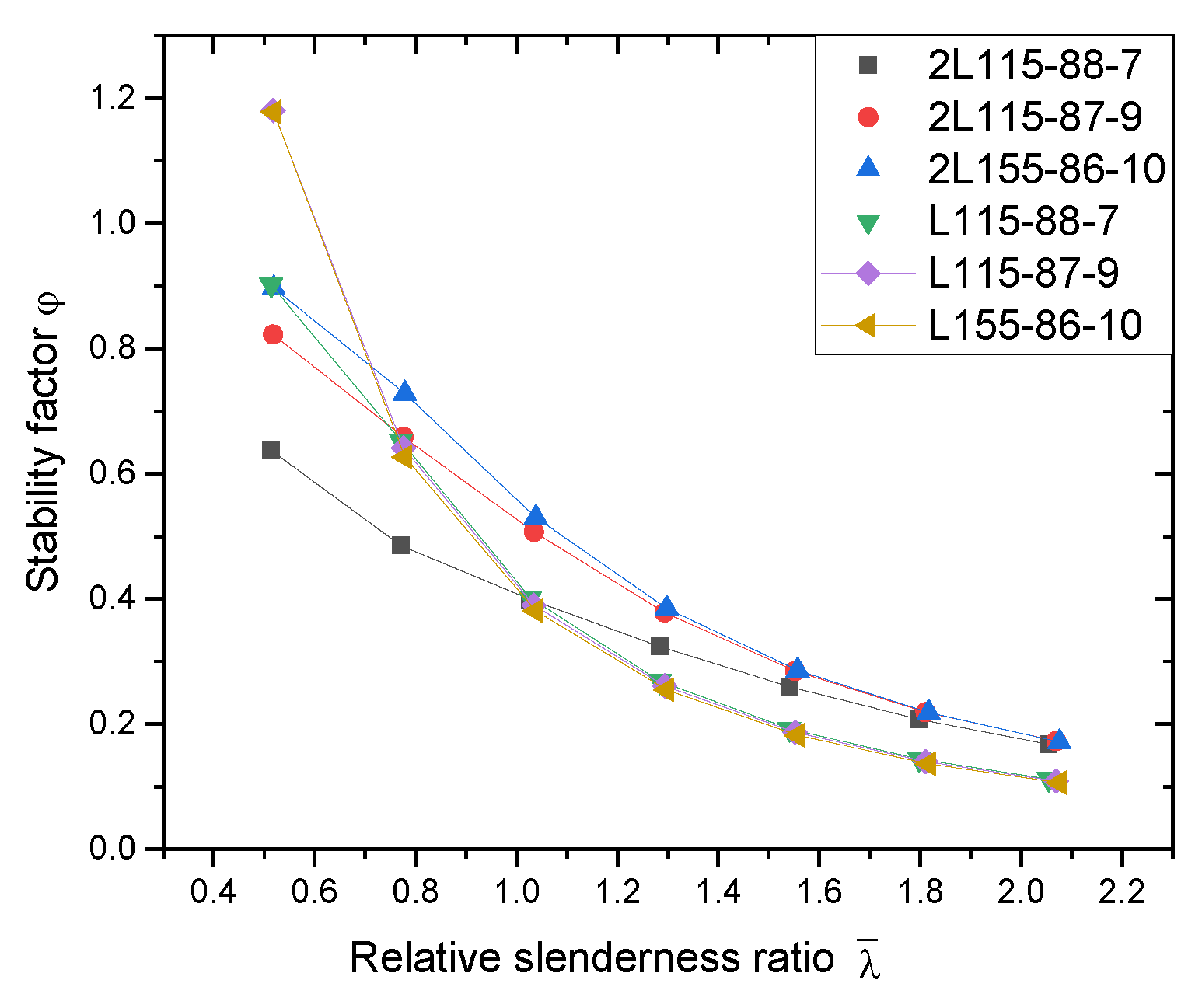
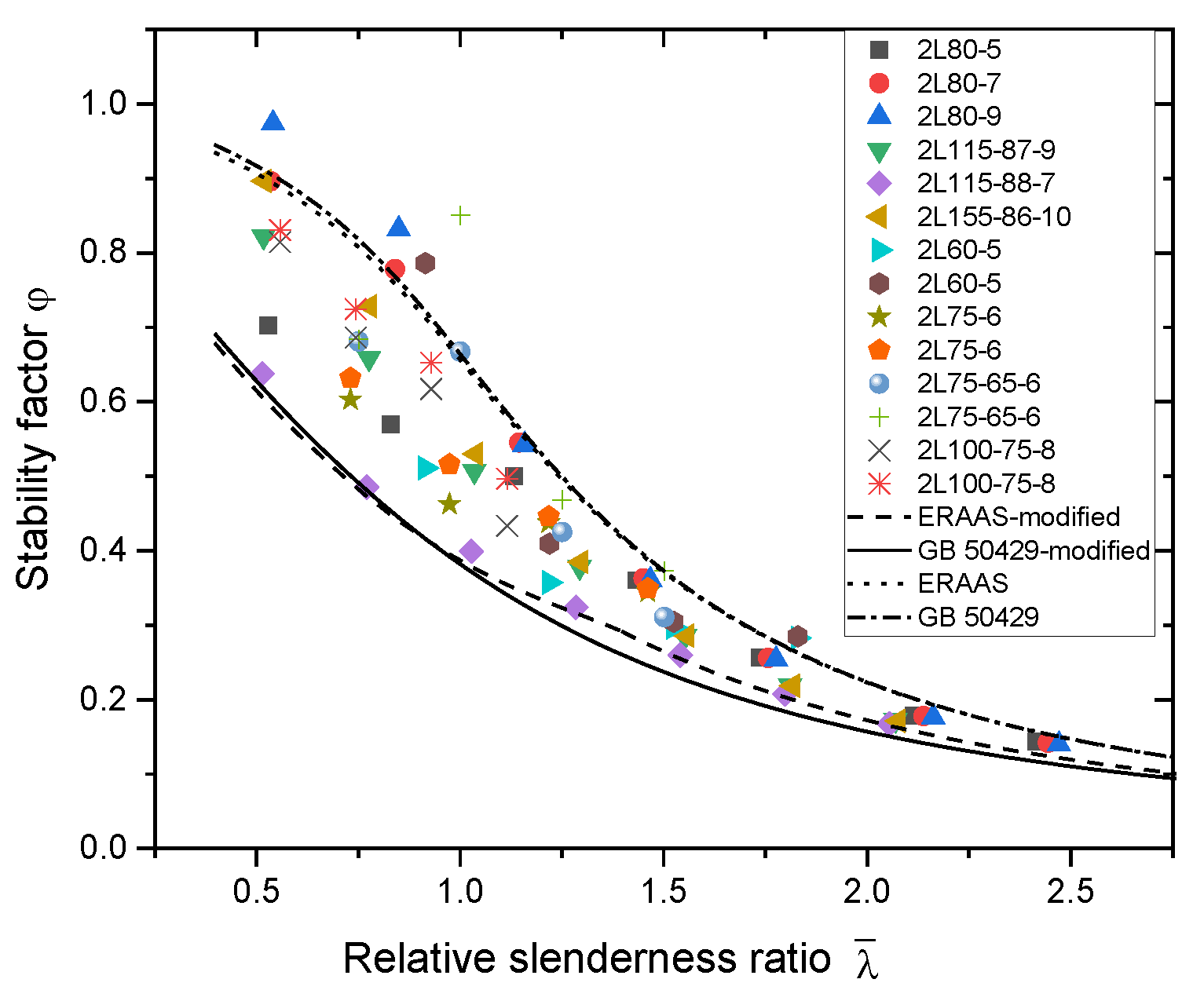
5.2. Study on the Formula for Calculating the Stability Coefficient of Axially Compressed Specimens
6. Conclusions
- (1)
- The experimental results indicate that, for equilateral and non-equilateral assembled T-shaped aluminum alloy components with clear strong and weak axes, primarily bending instability occurs, accompanied by local buckling of the plates when the aspect ratio is relatively small. For non-equilateral assembled T-shaped aluminum alloy components without clear strong and weak axes, torsional buckling instability occurs, accompanied by local deformation of the connecting limbs due to mutual compression.
- (2)
- The numerical model established in this paper can effectively simulate the mechanical properties of assembled T-shaped aluminum alloy components under axial compression.
- (3)
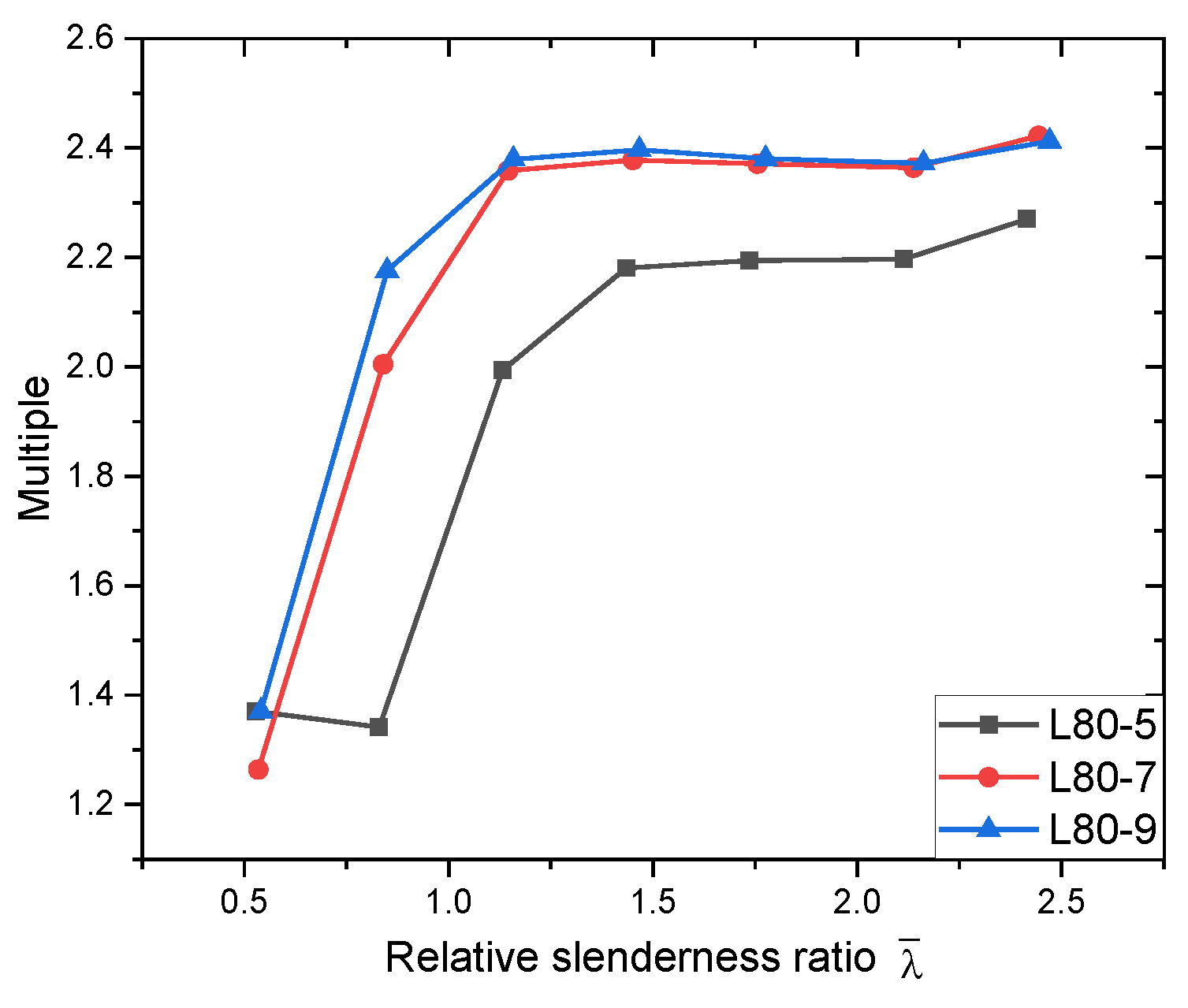
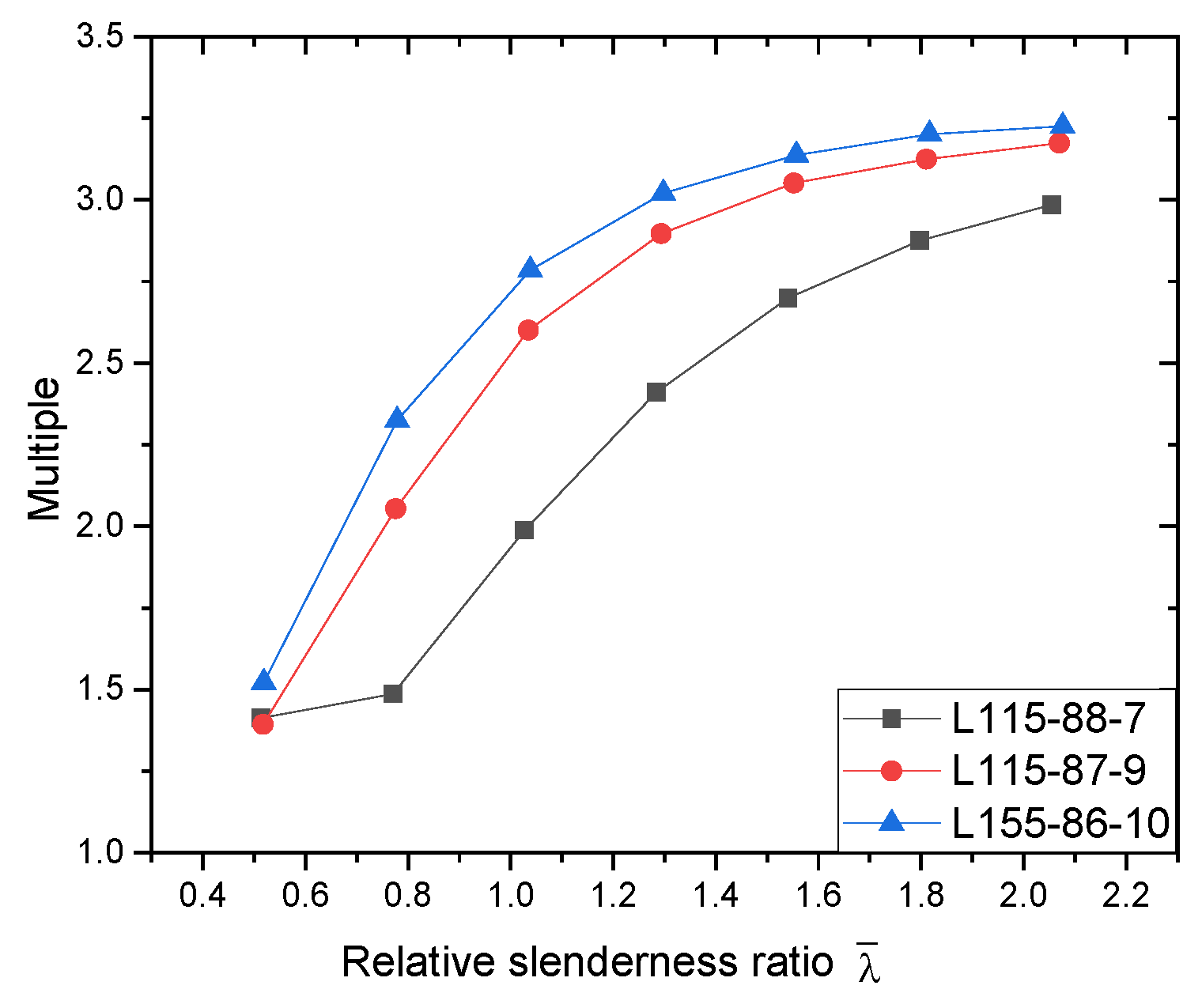
- Based on the numerical models, the composite performance of assembled T-shaped members was investigated. When the relative slenderness ratio of the members was less than 0.75, the boundary conditions of the plate components in the assembled T-shaped members changed, resulting in a tendency for local buckling of the plates and poor composite performance, with the bearing capacity found to be significantly lower than that of the double L-shaped aluminum alloy members. When the relative slenderness ratio was greater than 1.125, the assembled T-shaped aluminum alloy members exhibited good overall synergistic force performance, with the bearing capacity significantly greater than that of the double L-shaped aluminum alloy members (up to twice as much).
- (4)
- The experimental and numerical results were compared with Chinese and European standards, and it was found that the calculation methods in the standards tended to be unsafe. Parameters for calculating the defects of the members were modified based on Chinese and European standards. The modified column curve was the lower envelope of the numerical calculation results, which enabled a more accurate and safe prediction of the bearing capacity of the assembled T-shaped aluminum alloy members.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Wang, Y.; Sojeong, J.; Ouyang, Y. Experimental investigation and parametric analysis on overall buckling behavior of large-section aluminum alloy columns under axial compression. Thin-Walled Struct. 2018, 122, 585–596. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Yuan, H.X.; Chang, T.; Du, X.X.; Yu, M. Compressive buckling strength of extruded aluminum alloy I-section columns with fixed-pinned end conditions. Thin-Walled Struct. 2017, 119, 396–403. [Google Scholar] [CrossRef]
- Adeoti, G.O.; Fan, F.; Wang, Y.; Zhai, X. Stability of 6082-T6 aluminum alloy columns with H-section and rectangular hollow sections. Thin-Walled Struct. 2015, 89, 1–6. [Google Scholar] [CrossRef]
- Yuan, H.X.; Yuan, H.X.; Wang, Y.; Chang, T.; Du, X.; Bu, Y.; Shi, Y.J. Local buckling and post buckling strength of extruded aluminum alloy stub columns with slender I-sections. Thin-Walled Struct. 2015, 90, 140–149. [Google Scholar] [CrossRef]
- Guo, X.; Liang, S.; Shen, Z. Experiment on aluminum alloy specimens under axial compression. Front. Struct. Civ. Eng. 2015, 9, 48–64. [Google Scholar] [CrossRef]
- Zhi, X.; Wang, Y.; Zhang, Y.; Li, B.; Ouyang, Y. Study of local buckling performance of 7075-T6 high-strength aluminium alloy H-section stub columns. Thin-Walled Struct. 2022, 180, 109925. [Google Scholar] [CrossRef]
- Li, L.; Boissonnade, N. Local/global coupled instabilities of slender I-sections under compression. Thin-Walled Struct. 2022, 172, 108842. [Google Scholar] [CrossRef]
- Ali, S.B.; Georgantzia, E.; Kamaris, G.S.; Gkantou, M.; Kot, P. Experimental study of square and rectangular hollow section aluminum alloy columns. J. Phys. Conf. Ser. 2022, 2198, 012046. [Google Scholar] [CrossRef]
- Feng, R.; Wu, Z.; Haiying, W.; Chen, A.; Chen, Y. Tests of perforated aluminium alloy SHSs and RHSs under axial compression. Thin-Walled Struct. 2018, 130, 194–212. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhai, X.; Wang, J. Buckling behaviors and ultimate strength of 6082-T6 aluminum alloy columns with square and circular hollow sections under eccentric compression—Part II: Parametric study, design provisions and reliability analysis. Thin-Walled Struct. 2019, 143, 106208. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhai, X.; Sun, L. Test and design method for the buckling behaviors of 6082-T6 aluminum alloy columns with box-type and L-type sections under eccentric compression. Thin-Walled Struct. 2016, 100, 62–80. [Google Scholar] [CrossRef]
- Rong, B.; Guo, Y.; Li, Z. Study on the stability behavior of 7A04-T6 aluminum alloy square and rectangular hollow section columns under axial compression. J. Build. Eng. 2021, 45, 103652. [Google Scholar]
- Li, B.; Wang, Y.; Zhi, X.; Zhang, Y.; Baniotopoulos, C.C. Testing, modelling and design of 7A04-T6 high-strength aluminium alloy RHS columns under axial compression. J. Build. Eng. 2022, 57, 104910. [Google Scholar] [CrossRef]
- Zhi, X.; Wang, Y.; Li, B.; Zhang, Y.; Ouyang, Y. Axial compression behaviour of 7A04-T6 high-strength aluminium alloy SHS and RHS stub columns. Thin-Walled Struct. 2022, 180, 109816. [Google Scholar] [CrossRef]
- Hu, Y.; Rong, B.; Zhang, R.; Zhang, Y.; Zhang, S. Study of buckling behavior for 7A04-T6 aluminum alloy rectangular hollow columns. Thin-Walled Struct. 2021, 169, 108410. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, F.; Lin, S. Experimental investigation on the stability of aluminum alloy 6082 circular tubes in axial compression. Thin-Walled Struct. 2015, 89, 54–66. [Google Scholar] [CrossRef]
- Li, Z.Y.; Wang, C.X.; Li, J.J.; Ding, Y.J.; Rong, B. 7A04. Study on the axial compression stability of aluminum alloy circular tube specimens. J. Tianjin Univ. Nat. Sci. Eng. Technol. Ed. 2020, 10, 1036–1044. [Google Scholar]
- Zhu, J.; Young, B. Experimental investigation of aluminum alloy circular hollow section columns. Eng. Struct. 2006, 28, 207–215. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Hu, X.G.; Han, J.; Xing, H.J. Experimental study and parametric analysis on the stability behavior of 7A04 high-strength aluminum alloy angle columns under axial compression. Thin-Walled Struct. 2016, 108, 305–320. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Yun, X.; Gardner, L.; Hu, X. Experimental and Numerical Study of Fixed-Ended High-Strength Aluminum Alloy Angle-Section Columns. J. Struct. Eng. Asce. 2020, 146, 04020206. [Google Scholar] [CrossRef]
- Zhu, J.; Li, Z.; Su, M.; Young, B. Numerical study and design of aluminum alloy channel section columns with welds. Thin-Walled Struct. 2019, 139, 139–150. [Google Scholar] [CrossRef]
- Yuan, L.; Zhang, Q. Buckling behavior and design of concentrically loaded T-section aluminum alloy columns. Eng. Struct. 2022, 260, 114221. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Zhongxing, W.; Bu, Y.; Fan, S.; Zheng, B. Experimental investigation and numerical analysis of pin-ended extruded aluminum alloy unequal angle columns. Eng. Struct. 2020, 215, 110694. [Google Scholar] [CrossRef]
- Zhang, Y.; Bu, Y.; Wang, Y.; Wang, Z.; Ouyang, Y. Study of flexural–torsional buckling behavior of 6061-T6 aluminum alloy unequal-leg angle columns. Thin-Walled Struct. 2021, 164, 107821. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters. Vol. Technical; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943.
- Guo, X. Theoretical and Experimental Research on Aluminum Alloy Structural Members. Ph.D. Thesis, Tongji University, Shanghai, China, 2006. [Google Scholar]
- GB/T 50429-2007; Aluminum Alloy Structural Design Specification. China Planning Press: Beijing, China, 2007.
- GB50017-2017; Code for Design of Steel Structures. China Planning Press: Beijing, China, 2018.
- EN 1999 Eurocode 9; Design of Aluminum Structures: Part 1-1 to 1-5. CEN: Brussels, Belgium, 2007.
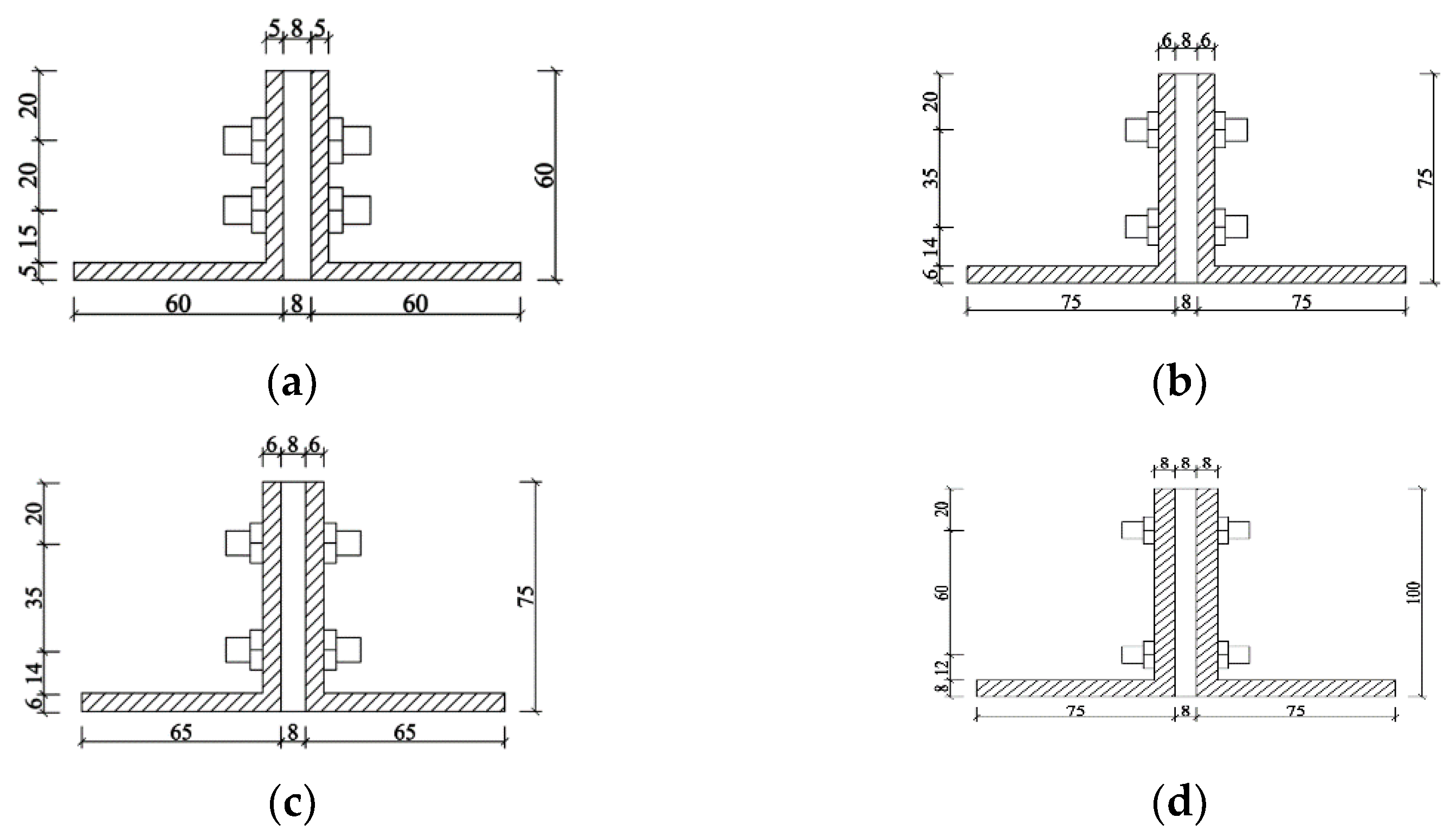

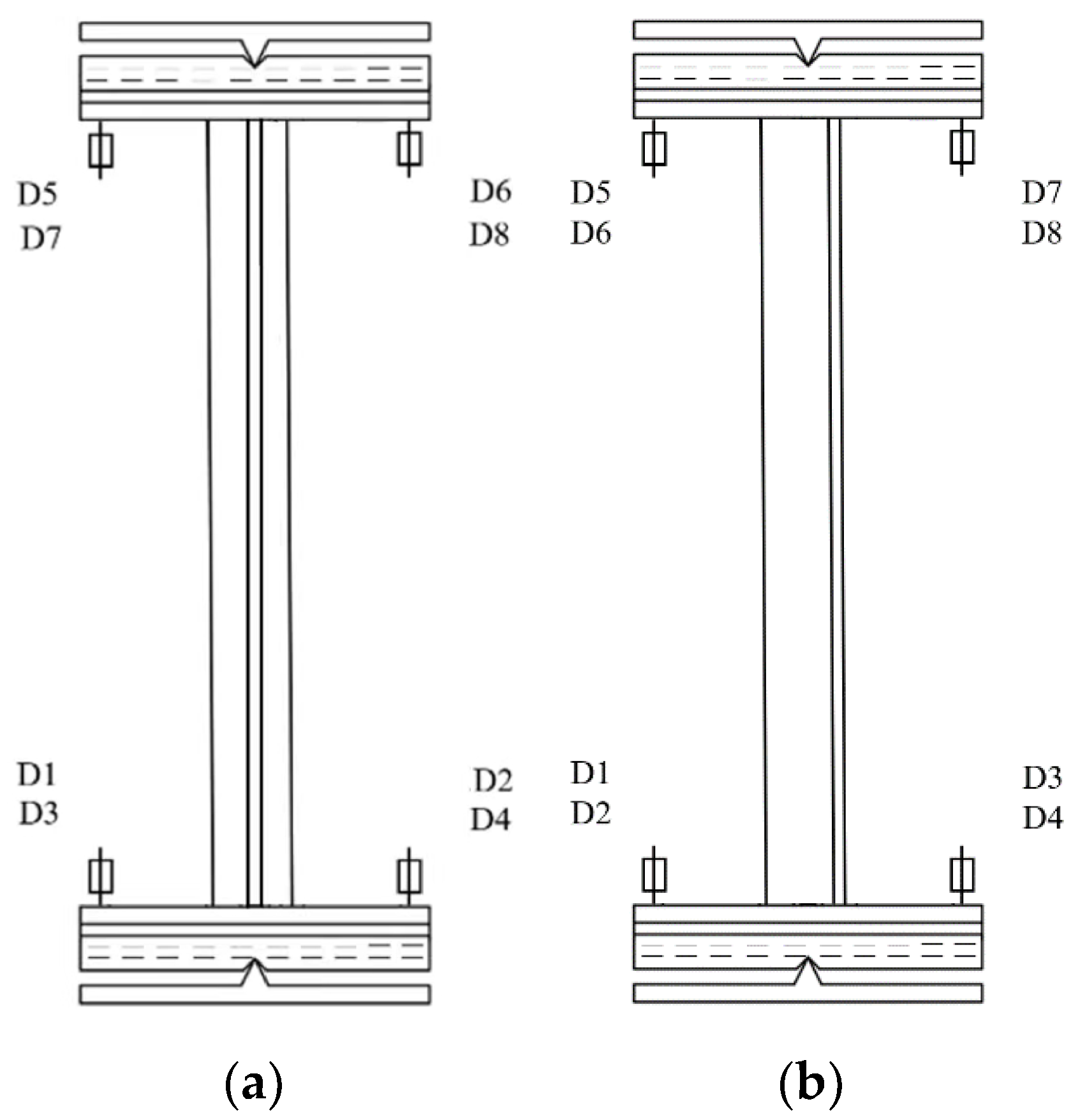




| Specimen Number | Length | A Limb Width | B Limb Width | A Limb Thickness | B Limb Thickness | Specimen Number | Length | A Limb Width | B Limb Width | A Limb Thickness | B Limb Thickness |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2L75-6-900A | 899 | 75.00 | 75.00 | 5.90 | 6.00 | 2L75-65-6-900A | 899 | 74.86 | 64.90 | 5.88 | 5.92 |
| 2L75-6-900B | 902 | 74.92 | 75.00 | 6.00 | 6.00 | 2L75-65-6-900B | 899 | 74.96 | 65.00 | 5.92 | 5.90 |
| 2L75-6-1200A | 1202 | 75.00 | 74.88 | 6.00 | 5.88 | 2L75-65-6-1200A | 1202 | 75.00 | 64.92 | 5.94 | 5.90 |
| 2L75-6-1200B | 1200 | 75.00 | 75.00 | 6.00 | 5.88 | 2L75-65-6-1200B | 1200 | 74.92 | 64.86 | 5.90 | 6.00 |
| 2L75-6-1500A | 1500 | 74.90 | 75.00 | 5.92 | 5.90 | 2L75-65-6-1500A | 1507 | 74.90 | 64.88 | 5.86 | 5.84 |
| 2L75-6-1500B | 1496 | 75.00 | 74.86 | 5.90 | 5.92 | 2L75-65-6-1500B | 1500 | 75.00 | 64.90 | 5.96 | 5.92 |
| 2L75-6-1800A | 1801 | 74.92 | 74.90 | 5.96 | 6.00 | 2L75-65-6-1800A | 1803 | 74.92 | 64.90 | 6.00 | 5.90 |
| 2L75-6-1800B | 1803 | 74.88 | 75.00 | 5.94 | 6.00 | 2L75-65-6-1800B | 1803 | 75.02 | 65.00 | 5.86 | 5.94 |
| 2L60-5-900A | 899 | 59.86 | 59.72 | 4.84 | 4.90 | 2L100-75-8-900A | 902 | 100.04 | 75.00 | 8.26 | 8.26 |
| 2L60-5-900B | 900 | 59.82 | 59.70 | 5.00 | 4.88 | 2L100-75-8-900B | 895 | 100.00 | 75.02 | 8.10 | 8.08 |
| 2L60-5-1200A | 1201 | 59.84 | 59.70 | 4.92 | 4.82 | 2L100-75-8-1200A | 1201 | 100.08 | 75.00 | 8.14 | 8.20 |
| 2L60-5-1200B | 1198 | 59.72 | 59.68 | 4.88 | 4.90 | 2L100-75-8-1200B | 1198 | 100.06 | 74.96 | 8.12 | 8.14 |
| 2L60-5-1500A | 1497 | 59.84 | 59.80 | 4.90 | 4.92 | 2L100-75-8-1500A | 1490 | 100.04 | 75.08 | 8.14 | 8.14 |
| 2L60-5-1500B | 1499 | 59.90 | 59.88 | 5.00 | 4.92 | 2L100-75-8-1500B | 1510 | 100.08 | 74.98 | 8.12 | 8.10 |
| 2L60-5-1800A | 1791 | 59.86 | 59.82 | 4.96 | 4.90 | 2L100-75-8-1800A | 1796 | 100.00 | 75.04 | 8.10 | 8.16 |
| 2L60-5-1800B | 1798 | 59.92 | 59.84 | 4.86 | 4.88 | 2L100-75-8-1800B | 1800 | 99.98 | 75.00 | 8.16 | 8.14 |
| Number | E0/MPa | f0.2/MPa | fu/MPa | n | Extreme Elongation (%) |
|---|---|---|---|---|---|
| L60-5 | 61,922 | 291 | 308 | 62.84 | 14.34 |
| L75-6 | 64,023 | 215 | 244 | 25.88 | 14.15 |
| L75-65-6 | 60,675 | 259 | 287 | 37.84 | 16.50 |
| L100-75-8 | 71,060 | 286 | 301 | 74.92 | 14.50 |
| Specimen Number | Ultimate Load Capacity Fexp (kN) | Destruction Mode |
|---|---|---|
| 2L60-5-900 | 144 | Bending Instability + Local Buckling |
| 2L60-5-1200 | 106 | Bending Instability |
| 2L60-5-1500 | 75 | Bending Instability |
| 2L60-5-1800 | 53 | Bending Instability |
| 2L75-6-900 | 266 | Bending Instability + Local Buckling |
| 2L75-6-1200 | 213 | Bending Instability + Local Buckling |
| 2L75-6-1500 | 175 | Bending Instability + Local Buckling |
| 2L75-6-1800 | 133 | Bending Instability |
| 2L75-65-6-900 | 283 | Bending Instability + Local Buckling |
| 2L75-65-6-1200 | 230 | Bending Instability + Local Buckling |
| 2L75-65-6-1500 | 182 | Bending Instability |
| 2L75-65-6-1800 | 147 | Bending Instability |
| 2L100-75-8-900 | 545 | Bending Instability + Local Buckling |
| 2L100-75-8-1200 | 472 | Bending Instability + Local Buckling |
| 2L100-75-8-1500 | 390 | Bending Instability + Local Buckling |
| 2L100-75-8-1800 | 308 | Bending Instability + Local Buckling |
| Mesh Size (mm) | Number of Nodes | Number of Elements | Calculation Time (s) | Load Bearing Capacity (kN) |
|---|---|---|---|---|
| 5 | 54,536 | 545,365,156 | 4440 | 148 |
| 10 | 15,882 | 9936 | 1520 | 147 |
| 20 | 5316 | 3190 | 920 | 143 |
| 30 | 3051 | 1780 | 565 | 249 |
| 40 | 2130 | 1214 | 387 | 247 |
| Specimen Number | Fexp (kN) | Ffe (kN) | Fexp/Ffe |
|---|---|---|---|
| 2L60-5-900 | 144 | 150 | 0.960 |
| 2L60-5-1200 | 106 | 108 | 0.981 |
| 2L60-5-1500 | 75 | 80 | 0.938 |
| 2L60-5-1800 | 53 | 60 | 0.883 |
| 2L75-6-900 | 266 | 246 | 1.081 |
| 2L75-6-1200 | 213 | 202 | 1.054 |
| 2L75-6-1500 | 175 | 168 | 1.042 |
| 2L75-6-1800 | 133 | 120 | 1.108 |
| 2L75-65-6-900 | 283 | 257 | 1.101 |
| 2L75-65-6-1200 | 230 | 214 | 1.075 |
| 2L75-65-6-1500 | 182 | 176 | 1.034 |
| 2L75-65-6-1800 | 147 | 135 | 1.089 |
| 2L100-75-8-900 | 545 | 550 | 0.991 |
| 2L100-75-8-1200 | 472 | 477 | 0.990 |
| 2L100-75-8-1500 | 390 | 396 | 0.985 |
| 2L100-75-8-1800 | 308 | 319 | 0.966 |
| Parameter | ERAAS | GB50429 |
|---|---|---|
| 0.2 | 0.2 | |
| 0.1 | 0.15 |
| Parameter | ERAAS-Modified | GB50429-Modified |
|---|---|---|
| 0.75 | 1 | |
| 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, Y.; Liu, H.; Ying, J.; Zhao, J.; Liu, X.; Liu, Z. Study on the Behavior of Assembled T-Shaped Aluminum Alloy Specimens under Axial Compression. Metals 2023, 13, 919. https://doi.org/10.3390/met13050919
Ouyang Y, Liu H, Ying J, Zhao J, Liu X, Liu Z. Study on the Behavior of Assembled T-Shaped Aluminum Alloy Specimens under Axial Compression. Metals. 2023; 13(5):919. https://doi.org/10.3390/met13050919
Chicago/Turabian StyleOuyang, Yuanwen, Hongbo Liu, Jiaojie Ying, Jianxiong Zhao, Xiaowei Liu, and Zhenfei Liu. 2023. "Study on the Behavior of Assembled T-Shaped Aluminum Alloy Specimens under Axial Compression" Metals 13, no. 5: 919. https://doi.org/10.3390/met13050919
APA StyleOuyang, Y., Liu, H., Ying, J., Zhao, J., Liu, X., & Liu, Z. (2023). Study on the Behavior of Assembled T-Shaped Aluminum Alloy Specimens under Axial Compression. Metals, 13(5), 919. https://doi.org/10.3390/met13050919






