Modeling Segregation of Fe–C Alloy in Solidification by Phase-Field Method Coupled with Thermodynamics
Abstract
:1. Introduction
2. Model Description and Numerical Implementations
2.1. Phase-Field Model for Alloy Solidification
2.2. Thermodynamic Description of the Fe–C Binary System
2.3. Numerical Implementations
3. Results and Discussion
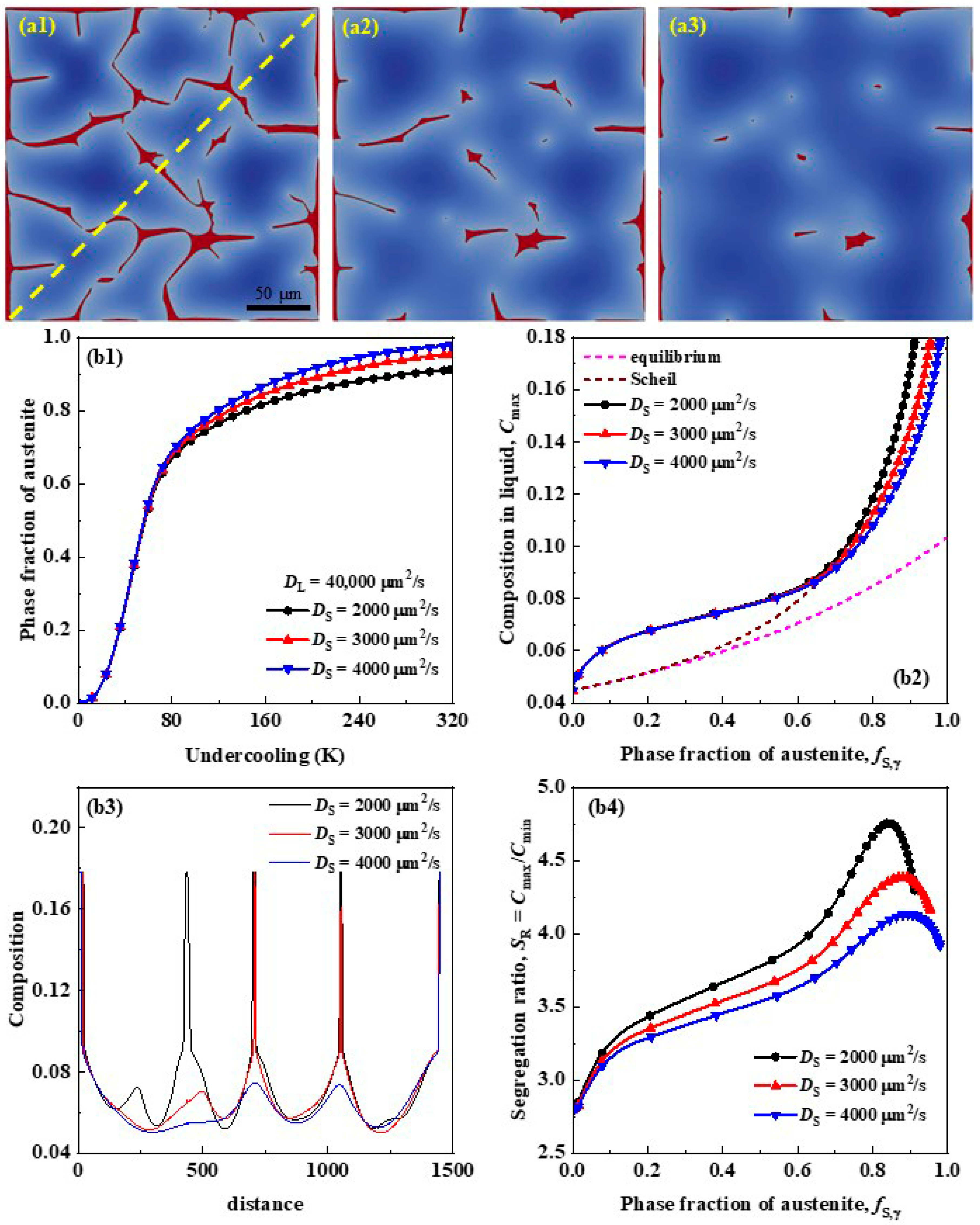
3.1. Effects of Solute Diffusivity on Segregation
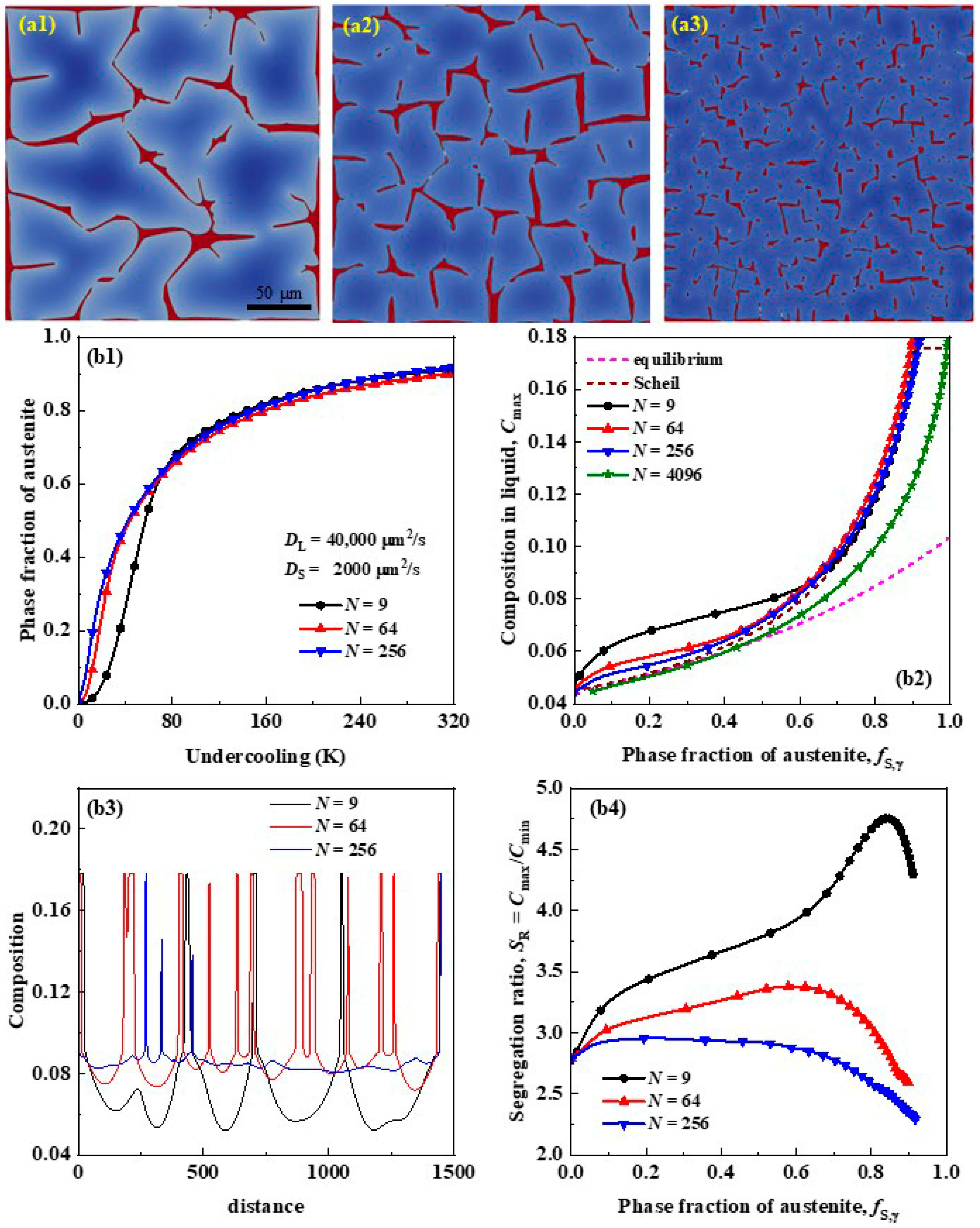
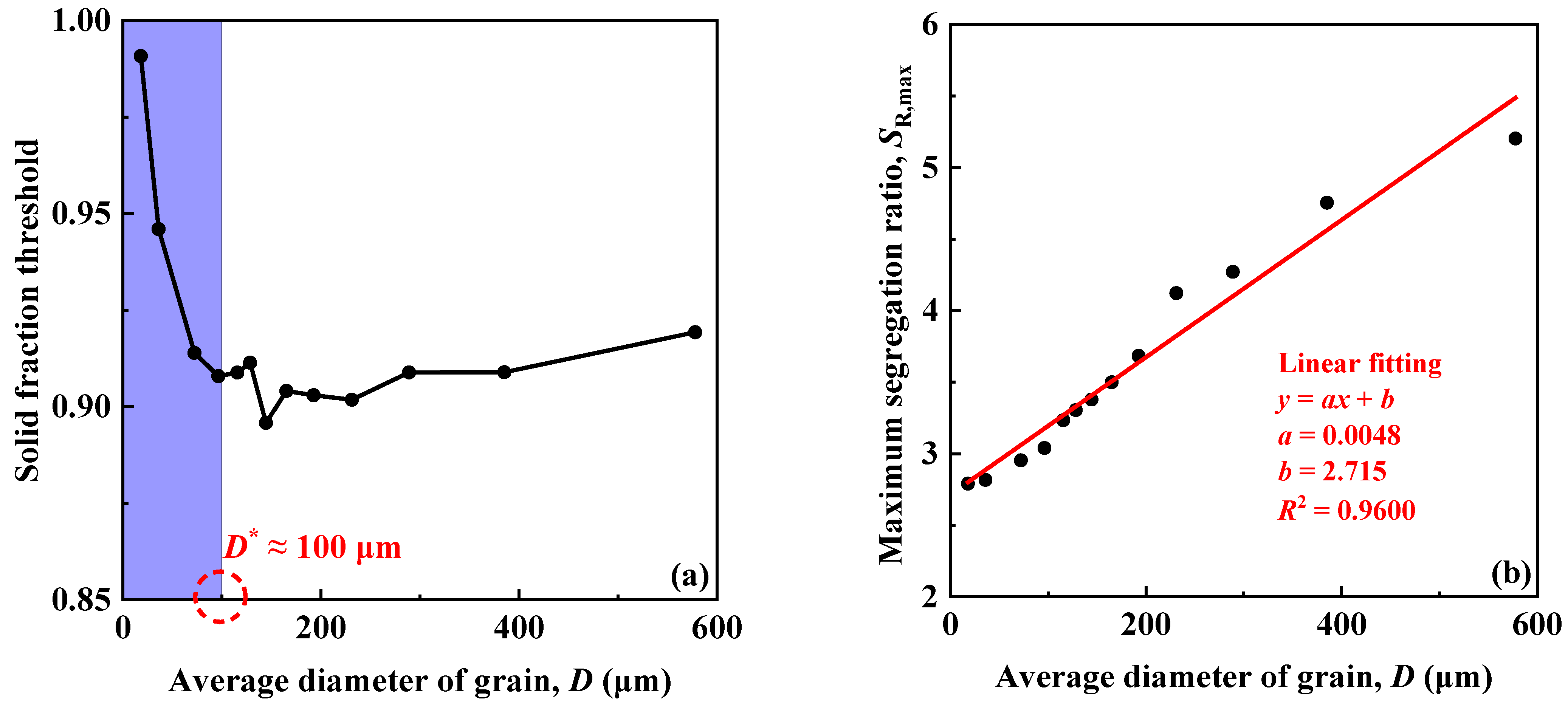
3.2. Effects of Grain Size on Segregation
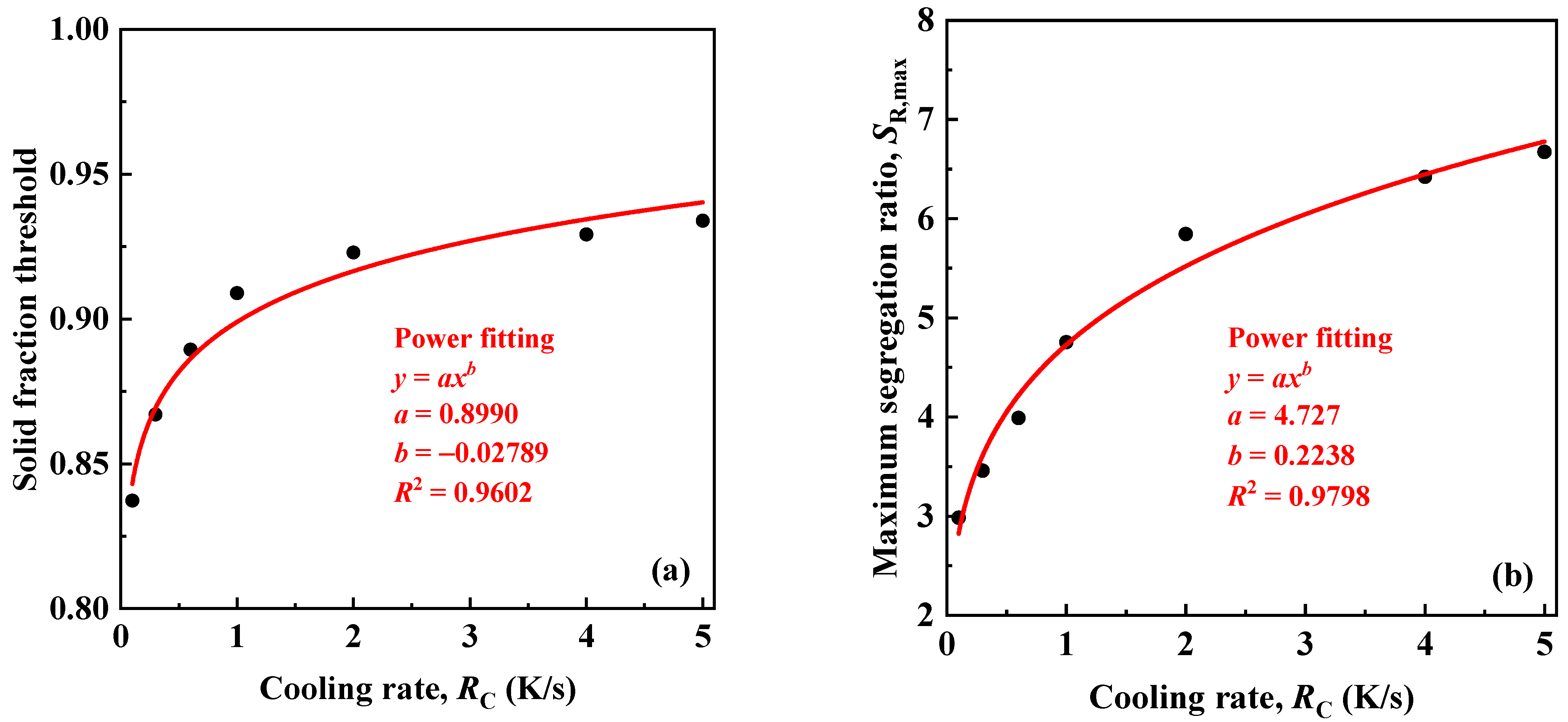
3.3. Effects of Cooling Rate on Segregation
4. Conclusions
- (1)
- By increasing the ratio of solute diffusivity in solid and liquid, the phase fraction threshold of primary austenite when the solute concentration in residual liquid reaches the eutectic composition increases as a logistic function, and the maximum segregation ratio decreases as a power function, both indicating that the solute segregation and cementite precipitation will be reduced.
- (2)
- By decreasing the grain size of primary austenite, the phase fraction threshold of primary austenite increases dramatically only when the grain size is lower than a certain value (revealed to be about 100 μm here), while the maximum segregation ratio is decreased monotonically in an approximate linear manner, and therefore the grain size of primary austenite must be reduced to small enough to improve the solute segregation and inhibit carbide precipitation by grain refinement.
- (3)
- By increasing the cooling rate (artificially ignoring the effect of the cooling rate on the nucleation rate), the phase fraction threshold of the primary austenite increases as a power function, indicating that even without considering the change in grain size, a higher cooling rate is still helpful to reduce solute segregation and carbide precipitation. However, although the segregation ratio increases with an increase in the cooling rate, the underlying reason is that the short solidification time leads to the heterogeneous solute distribution in solid, rather than the aggravating solute enrichment in liquid.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Chen, X.-Q.; Fu, P.; Ma, X.; Liu, H.; Chen, Y.; Cao, Y.; Luan, Y.; Li, Y. Inclusion flotation-driven channel segregation in solidifying steels. Nat. Commun. 2014, 5, 5572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silva, A. The effects of non-metallic inclusions on properties relevant to the performance of steel in structural and mechanical applications. J. Mater. Res. Technol. 2019, 8, 2408–2422. [Google Scholar] [CrossRef]
- Li, D.; Wang, P.; Chen, X.-Q.; Fu, P.; Luan, Y.; Hu, X.; Liu, H.; Sun, M.; Chen, Y.; Cao, Y.; et al. Low-oxygen rare earth steels. Nat. Mater. 2022, 21, 1137–1143. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, K.; Taniguchi, T.; Nakashima, K. Generation mechanisms of non-metallic inclusions in high-cleanliness steel. Tetsu Hagane-J. Iron Steel Inst. Jpn. 2007, 93, 743–752. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.J.; Bao, Y.P.; Wang, M.; Zhao, L.H. Effect of Mg and Ca treatment on behavior and particle size of inclusions in bearing steels. ISIJ Int. 2014, 54, 536–542. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.P.; Xiong, L.; Zhang, L.; Wang, Y.; Shu, Y.Y.; Zhou, Y.H. Investigation of RE-O-S-As inclusions in high carbon steels. Metall. Mater. Trans. B 2017, 48, 2849–2858. [Google Scholar] [CrossRef]
- Yang, C.Y.; Luan, Y.K.; Li, D.Z.; Li, Y.Y. Effects of rare earth elements on inclusions and impact toughness of high-carbon chromium bearing steel. J. Mater. Sci. Technol. 2019, 35, 1298–1308. [Google Scholar] [CrossRef]
- Zhang, S.C.; Yu, J.T.; Li, H.B.; Jiang, Z.H.; Geng, Y.F.; Feng, H.; Zhang, B.B.; Zhu, H.C. Refinement mechanism of cerium addition on solidification structure and sigma phase of super austenitic stainless steel S32654. J. Mater. Sci. Technol. 2022, 102, 105–114. [Google Scholar] [CrossRef]
- Sourmail, T. Precipitation in creep resistant austenitic stainless steels. Mater. Sci. Technol. 2001, 17, 1–14. [Google Scholar] [CrossRef]
- Yen, H.W.; Chen, P.Y.; Huang, C.Y.; Yang, J.R. Interphase precipitation of nanometer-sized carbides in a titanium-molybdenum-bearing low-carbon steel. Acta Mater. 2011, 59, 6264–6274. [Google Scholar] [CrossRef]
- Li, T.; Ma, Y.; Cai, Q.; Ma, J. Cause and control on unqualified UT of large-size high-carbon high-chromium bearing steel ring. Hot Work. Technol. 2013, 42, 230. [Google Scholar]
- Kim, K.H.; Park, S.D.; Bae, C.M. New approach to the soaking condition of 100Cr6 high-carbon chromium bearing steel. Met. Mater. Int. 2014, 20, 207–213. [Google Scholar] [CrossRef]
- Khan, F.A. The effect of soaking on segregation and primary-carbide dissolution in ingot-cast bearing steel. Metals 2018, 8, 800. [Google Scholar] [CrossRef] [Green Version]
- Li, S.S.; Chen, Y.; Gong, T.Z.; Chen, X.Q.; Fu, P.X.; Li, D.Z. Effect of cooling rate on the precipitation mechanism of primary carbide during solidification in high carbon-chromium bearing steel. Acta Metall. Sin. 2022, 58, 1024–1034. [Google Scholar]
- Xu, C.; Chen, Y.; Gong, T.; Shi, Y.; Wang, J.; Chen, X.-Q.; Liu, P.; Guo, Y.; Li, D. Ab initio study of local structures during cooling of liquid Fe-C and Fe-Cr-C alloys. Comput. Mater. Sci. 2022, 212, 111572. [Google Scholar] [CrossRef]
- Tian, Q.R.; Wang, G.C.; Yuan, X.H.; Wang, Q.; Sridhar, S. Complex precipitates of TiN-MCx in GCr15 bearing steel. Metals 2019, 9, 641. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wang, X.; Yang, S.; Chen, W.; Hou, H. The Morphology and solute segregation of dendrite growth in Ti-4.5% Al alloy: A phase-field study. Materials 2021, 14, 7257. [Google Scholar] [CrossRef]
- Mianroodi, J.R.; Shanthraj, P.; Svendsen, B.; Raabe, D. Phase-field modeling of chemoelastic binodal/spinodal relations and solute segregation to defects in binary alloys. Materials 2021, 14, 1787. [Google Scholar] [CrossRef]
- Guan, J.; Pu, Z.-P.; Zhao, S.-C.; Liu, D.-R. Three-dimensional modeling of segregation behavior during solidification of a Sn-6 wt.% Pb alloy. Materials 2022, 15, 1298. [Google Scholar] [CrossRef]
- Wang, K.L.; Yang, W.K.; Shi, X.C.; Hua, H.; Zhao, Y.H. Phase-field-method-studied mechanism of Cu-rich phase precipitation in AlxCuMnNiFe high-entropy alloy. Acta Phys. Sin. 2023, 72, 076102. [Google Scholar] [CrossRef]
- Kurz, W.; Rappaz, M.; Trivedi, R. Progress in modelling solidification microstructures in metals and alloys. Part II: Dendrites from 2001 to 2018. Int. Mater. Rev. 2021, 66, 30–76. [Google Scholar] [CrossRef]
- Kim, S.G.; Kim, W.T.; Suzuki, T.; Ode, M. Phase-field modeling of eutectic solidification. J. Cryst. Growth 2004, 261, 135–158. [Google Scholar]
- Eiken, J.; Böttger, B.; Steinbach, I. Multiphase-field approach for multicomponent alloys with extrapolation scheme for numerical application. Phys. Rev. E 2006, 73, 066122. [Google Scholar] [CrossRef] [PubMed]
- Steinbach, I. Phase-field models in materials science. Model. Simul. Mater. Sci. Eng. 2009, 17, 073001. [Google Scholar] [CrossRef]
- Fattebert, J.-L.; DeWitt, S.; Perron, A.; Turner, J. Thermo4PFM: Facilitating phase-field simulations of alloys with thermodynamic driving forces. Comput. Phys. Commun. 2023, 288, 108739. [Google Scholar] [CrossRef]
- Chen, Y.; Bogno, A.A.; Xiao, N.M.; Billia, B.; Kang, X.H.; Nguyen-Thi, H.; Luo, X.H.; Li, D.Z. Quantitatively comparing phase-field modeling with direct real time observation by synchrotron X-ray radiography of the initial transient during directional solidification of an Al-Cu alloy. Acta Mater. 2012, 60, 199–207. [Google Scholar] [CrossRef]
- Chen, Y.; Billia, B.; Li, D.Z.; Nguyen-Thi, H.; Xiao, N.M.; Bogno, A.A. Tip-splitting instability and transition to seaweed growth during alloy solidification in anisotropically preferred growth direction. Acta Mater. 2014, 66, 219–231. [Google Scholar] [CrossRef]
- Gong, T.Z.; Chen, Y.; Cao, Y.F.; Kang, X.H.; Li, D.Z. Fast simulations of a large number of crystals growth in centimeter-scale during alloy solidification via nonlinearly preconditioned quantitative phase-field formula. Comput. Mater. Sci. 2018, 147, 338–352. [Google Scholar] [CrossRef]
- Yamanaka, A.; Aoki, T.; Ogawa, S.; Takaki, T. GPU-accelerated phase-field simulation of dendritic solidification in a binary alloy. J. Cryst. Growth 2011, 318, 40–45. [Google Scholar] [CrossRef]
- Yang, C.; Xu, Q.Y.; Liu, B.C. GPU-accelerated three-dimensional phase-field simulation of dendrite growth in a nickel-based superalloy. Comput. Mater. Sci. 2017, 136, 133–143. [Google Scholar] [CrossRef]
- Clarke, A.J.; Tourret, D.; Song, Y.; Imhoff, S.D.; Gibbs, P.J.; Gibbs, J.W.; Fezzaa, K.; Karma, A. Microstructure selection in thin-sample directional solidification of an Al-Cu alloy: In situ X-ray imaging and phase-field simulations. Acta Mater. 2017, 129, 203–216. [Google Scholar] [CrossRef] [Green Version]
- Gong, T.Z.; Chen, Y.; Li, S.S.; Cao, Y.F.; Hou, L.Y.; Li, D.Z.; Chen, X.Q.; Reinhart, G.; Nguyen, H. Equiaxed dendritic growth in nearly isothermal conditions: A study combining in situ and real-time experiment with large-scale phase-field simulation. Mater. Today Commun. 2021, 28, 102467. [Google Scholar] [CrossRef]
- Gong, T.Z.; Chen, Y.; Chen, X.-Q.; Li, D.Z.; Reinhart, G.; Nguyen, H.; Debierre, J.-M. Scaling law for growth of misoriented equiaxed Al-Cu dendrites: A phase-field study with in situ experiment validation. Comput. Mater. Sci. 2023, 226, 112238. [Google Scholar] [CrossRef]
- Kim, S.G. A phase-field model with antitrapping current for multicomponent alloys with arbitrary thermodynamic properties. Acta Mater. 2007, 55, 4391–4399. [Google Scholar] [CrossRef]
- Böttger, B.; Apel, M.; Santillana, B.; Eskin, D.G. Relationship between solidification microstructure and hot cracking susceptibility for continuous casting of low-carbon and high-strength low-alloyed steels: A phase-field Study. Metall. Mater. Trans. A 2013, 44, 3765–3777. [Google Scholar] [CrossRef] [Green Version]
- Gustafson, P. A thermodynamic evaluation of the Fe-C system. Scand. J. Metall. 1985, 14, 259–267. [Google Scholar] [CrossRef]
- Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Gong, T.; Chen, Y.; Li, S.; Cao, Y.; Li, D.; Chen, X.-Q.; Reinhart, G.; Nguyen-Thi, H. Revisiting dynamics and models of microsegregation during polycrystalline solidification of binary alloy. J. Mater. Sci. Technol. 2021, 74, 155–167. [Google Scholar] [CrossRef]


| Parameter | Meaning | Value |
|---|---|---|
| DL | Diffusivity of C in liquid | 1 × 10−8~4 × 10−8 m2/s |
| DS | Diffusivity of C in solid | 1 × 10−9~4 × 10−9 m2/s |
| μL/γ | Interface mobility | 1 × 10−10 m4/(J∙s) |
| σL/γ | Interface energy | 0.06 J/m2 |
| δμ | Kinetic anisotropy coefficient | 0.05 |
| δσ | Static anisotropy coefficient | 0.05 |
| Vm | Molar volume | 6.7 × 10−6 m3/mol |
| η | Interface width | 1.0 μm |
| ∆x | Grid resolution | 0.25η |
| ∆t | Time step | 0.8∆x2/(4DL) |
| Phase | Thermodynamic Parameters |
|---|---|
| Liquid (C, Fe)1 | |
| Austenite (Fe)1(C, Va)1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, T.-Z.; Chen, Y.; Hao, W.-Y.; Chen, X.-Q.; Li, D.-Z. Modeling Segregation of Fe–C Alloy in Solidification by Phase-Field Method Coupled with Thermodynamics. Metals 2023, 13, 1148. https://doi.org/10.3390/met13061148
Gong T-Z, Chen Y, Hao W-Y, Chen X-Q, Li D-Z. Modeling Segregation of Fe–C Alloy in Solidification by Phase-Field Method Coupled with Thermodynamics. Metals. 2023; 13(6):1148. https://doi.org/10.3390/met13061148
Chicago/Turabian StyleGong, Tong-Zhao, Yun Chen, Wei-Ye Hao, Xing-Qiu Chen, and Dian-Zhong Li. 2023. "Modeling Segregation of Fe–C Alloy in Solidification by Phase-Field Method Coupled with Thermodynamics" Metals 13, no. 6: 1148. https://doi.org/10.3390/met13061148
APA StyleGong, T.-Z., Chen, Y., Hao, W.-Y., Chen, X.-Q., & Li, D.-Z. (2023). Modeling Segregation of Fe–C Alloy in Solidification by Phase-Field Method Coupled with Thermodynamics. Metals, 13(6), 1148. https://doi.org/10.3390/met13061148





