Review of Particle-Based Computational Methods and Their Application in the Computational Modelling of Welding, Casting and Additive Manufacturing
Abstract
1. Introduction
2. Lattice Boltzmann Method
2.1. LBM and Enthalpy Method
2.2. LBM and Cellular Automata Method
2.3. LBM and the Phase Field Method
2.4. Application of LBM Modelling
3. Smoothed Particle Hydrodynamics Modelling
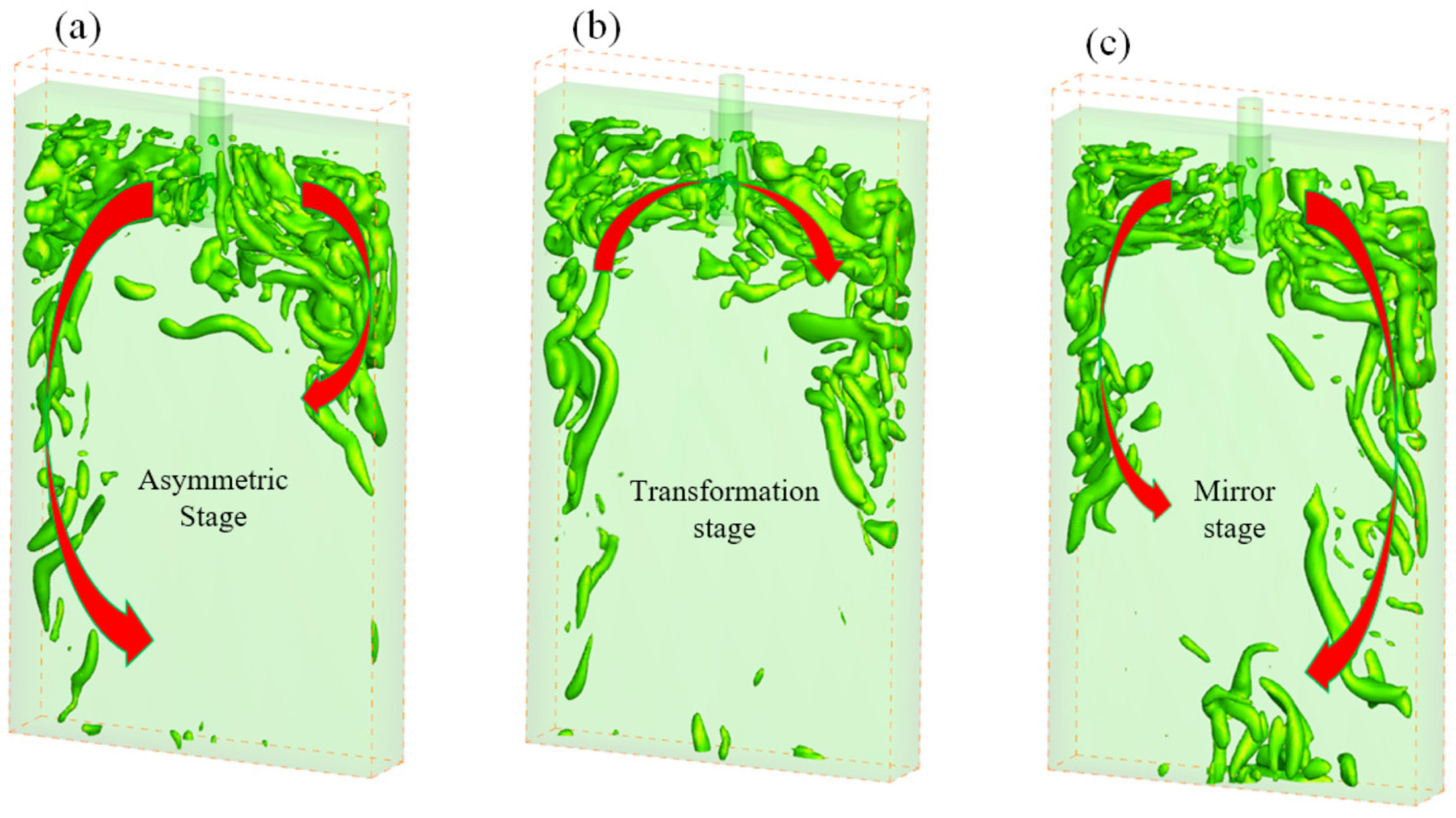
3.1. Application of SPH Modelling in Casting
3.2. Application of SPH Modelling in Welding
3.3. Application of SPH Modelling in Additive Manufacturing
4. Discrete Element Method
5. Particle Finite Element Method
6. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Chen, Z.; Liu, Y. The Material Point Method: A Continuum-Based Particle Method for Extreme Loading Cases; Academic Press: Beijing, China, 2016. [Google Scholar]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systems Simulia Corp.: Providence, RI, USA, 2009. [Google Scholar]
- Ruffoni, D.; Van Lenthe, G. 3.10 Finite Element Analysis in Bone Research: A Computational Method Relating Structure to Mechanical Function. Compr. Biomater. II 2017, 3, 169–196. [Google Scholar]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM and Matlab; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Osher, S.; Fedkiw, R. Level Set Methods: An Overview and Some Recent Results. J. Comput. Phys. 2001, 169, 463–502. [Google Scholar] [CrossRef]
- Blanc, C.; Aubert, I. Mechanics—Microstructure—Corrosion Coupling: Concepts, Experiments, Modeling and Cases; ISTE Press—Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Haff, P. Discrete Mechanics. In Granular Matter; Mehta, A., Ed.; Springer: New York, NY, USA, 1994. [Google Scholar]
- Tuckerman, M.; Martyna, G. Understanding Modern Molecular Dynamics: Techniques and Applications. J. Phys. Chem. B 2000, 104, 159–178. [Google Scholar] [CrossRef]
- Papanikolaou, M.; Salonitis, K.; Jolly, M.; Frank, M. Large-Scale Molecular Dynamics Simulations of Homogeneous Nucleation of Pure Aluminium. Metals 2019, 9, 1217. [Google Scholar] [CrossRef]
- Yang, H.; Yu, K.; Mu, X.; Wei, Y.; Guoa, Y.; Qi, H. Molecular dynamics studying on welding behavior in thermosetting polymers due to bond exchange reactions. RSC Adv. 2016, 6, 22476–22487. [Google Scholar] [CrossRef]
- Chang, Q.; Xie, J.; Mao, A.; Wang, W. Study on Interface Structure of Cu/Al Clad Plates by Roll Casting. Metals 2018, 8, 770. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Panagiotopoulou, V. Developing a Framework for Using Molecular Dynamics in Additive Manufacturing Process Modelling. Modelling 2022, 3, 189–200. [Google Scholar] [CrossRef]
- Mouvet, F.; Villard, J.; Bolnykh, V.; Rothlisberger, U. Recent Advances in First-Principles Based Molecular Dynamics. Acc. Chem. Res. 2022, 55, 221–230. [Google Scholar] [CrossRef]
- Harvey, J.; Asimow, P. Current limitations of molecular dynamic simulations as probes of thermo-physical behavior of silicate melts. Am. Mineral. 2015, 100, 1866–1882. [Google Scholar] [CrossRef]
- Mahgoub, A.; Ghani, S. Numerical and experimental investigation of utilizing the porous media model for windbreaks CFD simulation. Sustain. Cities Soc. 2021, 65, 102648. [Google Scholar]
- Bakhshian, S.; Hosseini, S.; Shokri, N. Pore-scale characteristics of multiphase flow in heterogeneous porous media using the lattice Boltzmann method. Sci. Rep. 2019, 9, 3377. [Google Scholar] [CrossRef] [PubMed]
- Neethling, S.; Barker, D. Using Smooth Particle Hydrodynamics (SPH) to model multiphase mineral processing systems. Miner. Eng. 2016, 90, 17–28. [Google Scholar] [CrossRef]
- Frissane, H.; Taddei, L.; Lebaal, N.; Roth, S. 3D smooth particle hydrodynamics modeling for high velocity penetrating impact using GPU: Application to a blunt projectile penetrating thin steel plates. Comput. Methods Appl. Mech. Eng. 2019, 357, 112590. [Google Scholar] [CrossRef]
- Snelling, B.; Piggott, M.; Collins, G.; Neethling, S. Using Smoothed Particle Hydrodynamics to investigate the effect of complex slide rheology on landslide generated waves. Geophys. Res. Abstr. 2018, 20, 8848. [Google Scholar]
- Idelsohn, S.; Oñate, E.; Pin, F.; Calvo, N. Fluid–structure interaction using the particle finite element method. Comput. Methods Appl. Mech. Eng. 2006, 195, 2100–2123. [Google Scholar] [CrossRef]
- Xu, L.; Luo, K.; Zhao, Y.; Fan, J.; Cen, K. Influence of particle shape on liner wear in tumbling mills: A DEM study. Powder Technol. 2019, 350, 26–35. [Google Scholar] [CrossRef]
- Raabe, D. Overview of the lattice Boltzmann method for nano- and microscale fluid dynamics in materials science and engineering. Model. Simul. Mater. Sci. Eng. 2004, 12, R13–R46. [Google Scholar] [CrossRef]
- Sudhakar, T.; Das, A.K. Evolution of Multiphase Lattice Boltzmann Method: A Review. J. Inst. Eng. India Ser. C 2020, 101, 711–719. [Google Scholar] [CrossRef]
- He, X.; Luo, L.S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811. [Google Scholar] [CrossRef]
- Perumal, D.A.; Dass, A.K. A Review on the development of lattice Boltzmann computation of macro fluid flows and heat transfer. Alex. Eng. J. 2015, 54, 955–971. [Google Scholar] [CrossRef]
- Semma, E.A.; Ganaoui, M.E.; Bennacer, R. Lattice Boltzmann method for melting/solidification problems. Comptes Rendus Mec. 2007, 335, 295–303. [Google Scholar] [CrossRef]
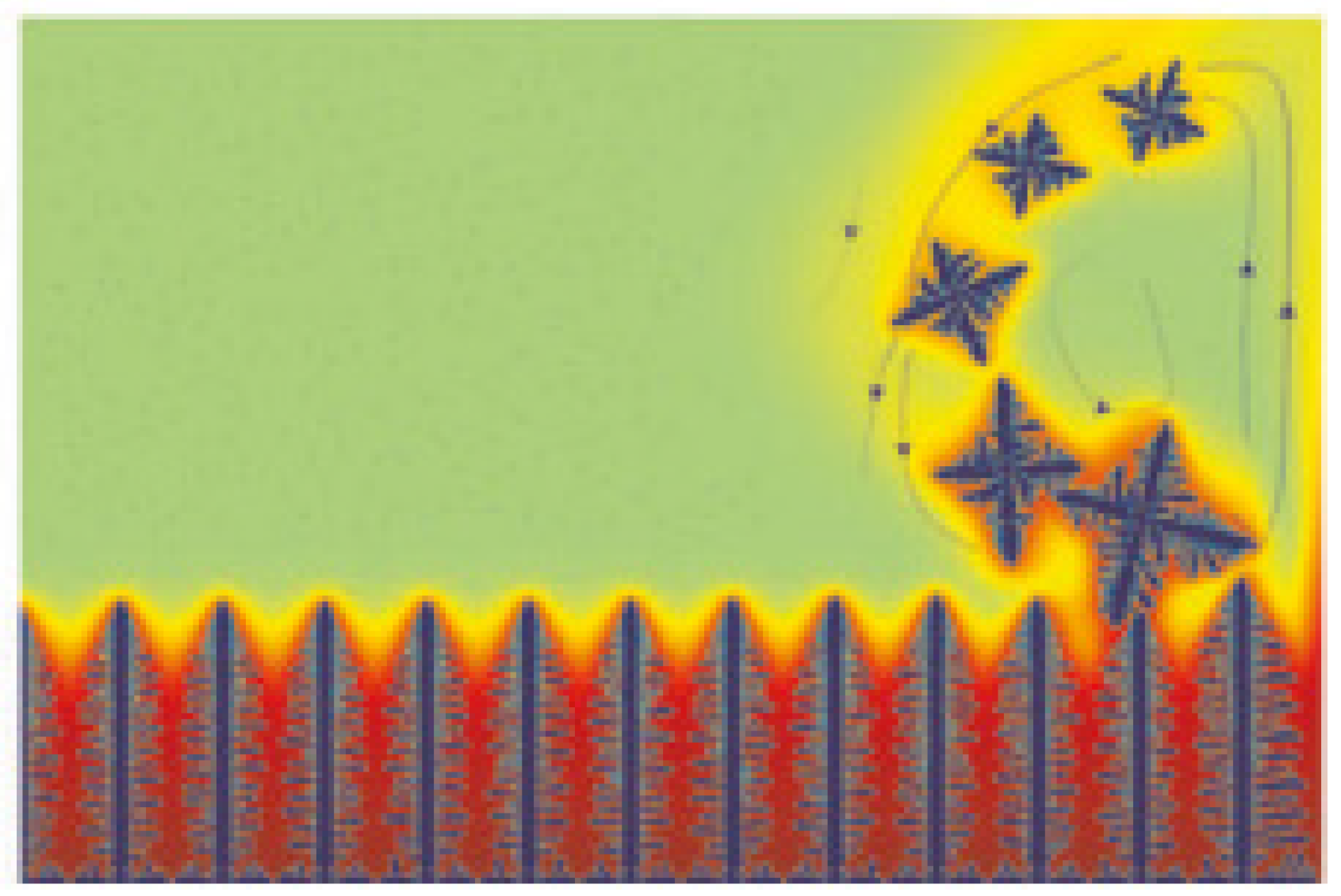
- Sun, D.; Zhu, M.; Pan, S.; Raabe, D. Numerical Modeling of Dendritic Growth in Alloy Solidification with Forced Convection. Int. J. Mod. Phys. B 2009, 23, 1609–1614. [Google Scholar] [CrossRef]
- Huang, R.; Wu, H. Phase interface effects in the total enthalpy-based lattice Boltzmann model for solid–liquid phase change. J. Comput. Phys. 2015, 294, 346–362. [Google Scholar] [CrossRef]
- Sun, D.K.; Zhu, M.F.; Pan, S.Y.; Yang, C.R.; Raabe, D. Lattice Boltzmann modeling of dendritic growth in forced and natural convection. Comput. Math. Appl. 2011, 61, 3585–3592. [Google Scholar] [CrossRef]
- Lee, W.; Bae, J.; Lee, H.; Kang, S.-H.; Yoon, J. Numerical simulation of dendritic growth and porosity evolution in solidification of Al-Cu alloy with lattice Boltzmann—Cellular automata method. J. Alloys Compd. 2022, 929, 167233. [Google Scholar] [CrossRef]
- Reuther, K.; Rettenmayr, M. Perspectives for cellular automata for the simulation of dendritic solidification—A review. Comput. Mater. Sci. 2014, 95, 213–220. [Google Scholar] [CrossRef]
- Rátkai, L.; Pusztai, T.; Gránásy, L. Phase-field lattice Boltzmann model for dendrites growing and moving in melt flow. Comput. Mater. 2019, 5, 113. [Google Scholar] [CrossRef]
- Zhan, C.; Chai, Z.; Shi, B.; Jiang, P.; Geng, S.; Sun, D. A diffuse-interface lattice Boltzmann method for the dendritic growth with thermosolutal convection. Commun. Comput. Phys. 2023, 33, 1164–1188. [Google Scholar] [CrossRef]
- Zhao, P.; Piao, R. Lattice Boltzmann Method Modeling of the Evolution of Coherent Vortices and Periodic Flow in a Continuous Casting Mold. Metals 2022, 12, 572. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Qian, X.W.; Zhou, J.X.; Yin, Y.J.; Shen, X.; Ji, X.Y.; Huang, J.L. Simulation of casting filling process using the lattice Boltzmann method. IOP Conf. Ser. Mater. Sci. Eng. 2019, 529, 012061. [Google Scholar] [CrossRef]
- Sirrell, B.; Holliday, M.; Campbell, J. Benchmark testing the flow and solidification modeling of AI castings. JOM 1996, 48, 20–23. [Google Scholar] [CrossRef]
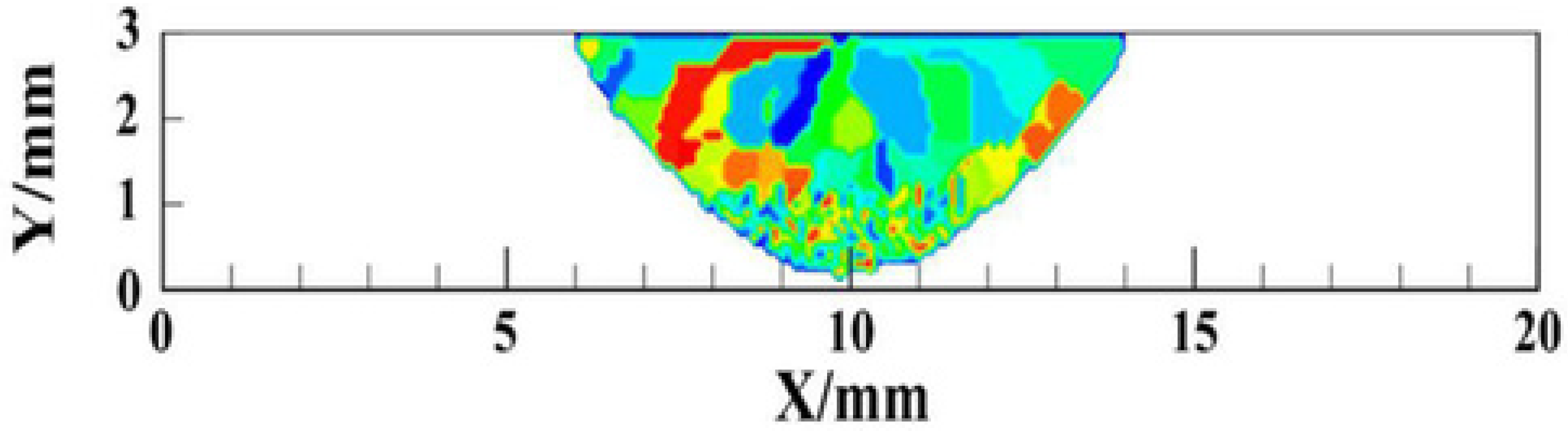
- Feng, Y.; Zhoua, J.; Cai, J.; Zhang, X.; Wu, C. A 3-D lattice Boltzmann analysis of weld pool dynamic behaviors in plasma arc welding. Appl. Therm. Eng. 2018, 139, 623–635. [Google Scholar] [CrossRef]
- Shi, F.; Zheng, Z.; He, M.; Lei, Y.; Guo, D.; Yu, J. Fluid flow behavior and solidification process of welding pool under rapid cooling condition based on cellular automata-lattice Boltzmann method (CA-LBM) couple model. Mater. Werkst. 2020, 51, 862–877. [Google Scholar] [CrossRef]
- Klassen, A.; Scharowsky, T.; Korner, C. Evaporation model for beam based additive manufacturing using free surface lattice Boltzmann methods. J. Phys. D Appl. Phys. 2014, 47, 275303. [Google Scholar] [CrossRef]
- Rausch, A.M.; Küng, V.E.; Pobel, C.; Markl, M. Predictive Simulation of Process Windows for Powder Bed Fusion Additive Manufacturing: Influence of the Powder Bulk Density. Materials 2017, 10, 1117. [Google Scholar] [CrossRef]
- Mark, M.; Ammer, R.; Rude, U.; Korner, C. Numerical investigations on hatching process strategies for powder-bed-based additive manufacturing using an electron beam. Int. J. Adv. Manuf. Technol. 2015, 78, 239–247. [Google Scholar] [CrossRef]
- Rai, A.; Mark, M.; Körner, C. A coupled Cellular Automaton–Lattice Boltzmann model for grain structure simulation during additive manufacturing. Comput. Mater. Sci. 2016, 124, 37–48. [Google Scholar] [CrossRef]
- Chen, D.; Chen, W.; Liu, Y.; Sun, D. A Two-Relaxation-Time Lattice Boltzmann Model for Electron Beam Selective Melting Additive Manufacturing. Front. Mater. 2022, 9, 885481. [Google Scholar] [CrossRef]
- McNamara, G.R.; Garcia, A.L.; Alder, B.J. A Hydrodynamically Correct Thermal Lattice Boltzmann Model. J. Stat. Phys. 1997, 87, 1111–1121. [Google Scholar] [CrossRef]
- Coreixas, C.; Wissocq, G.; Chopard, B.; Latt, J. Impact of collision models on the physical properties and the stability of lattice Boltzmann methods. Phil. Trans. R. Soc. A 2019, 378, 0397. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Xu, F.; Wang, J.; Yang, Y.; Wang, L.; Dai, Z.; Han, R. On methodology and application of smoothed particle hydrodynamics in fluid, solid and biomechanics. Acta Mech. Sin. 2023, 39, 722185. [Google Scholar] [CrossRef]
- Cleary, P.; Ha, J.; Prakash, M.; Nguyen, T. 3D SPH flow predictions and validation for high pressure die casting of automotive components. Appl. Math. Model. 2006, 30, 1406–1427. [Google Scholar] [CrossRef]
- Cleary, P.W.; Savage, G.; Ha, J.; Prakash, M. Flow analysis and validation of numerical modelling for a thin walled high pressure die casting using SPH. Comput. Part. Mech. 2014, 1, 229–243. [Google Scholar] [CrossRef]
- Cleary, P.W. Extension of SPH to predict feeding, freezing and defect creation in low pressure die casting. Appl. Math. Model. 2010, 34, 3189–3201. [Google Scholar] [CrossRef]
- Cleary, P.W.; Harrison, S.M.; Sinnott, M.D.; Pereira, G.G.; Prakash, M.; Cohen, R.C.Z.; Rudman, M.; Stokes, N. Application of SPH to Single and Multiphase Geophysical, Biophysical and Industrial Fluid Flows. Int. J. Comput. Fluid Dyn. 2021, 35, 22–78. [Google Scholar] [CrossRef]
- He, Y.; Zhou, Z.-Y.; Cao, W.-J.; Yang, D.-Z. Numerical Simulation of Solidification by SPH in Sand Cast Process. Adv. Mater. Res. 2011, 314–316, 614–619. [Google Scholar] [CrossRef]
- Ellingsen, K.; Coudert, T.; Hamdi, M.M. SPH based modelling of oxide and oxide film formation in gravity die castings. IOP Conf. Ser. Mater. Sci. Eng. 2015, 84, 012064. [Google Scholar] [CrossRef]
- Pineau, F.; D’Amours, G. Application of LS-DYNA SPH Formulation to Model Semi-Solid Metal Casting. In Proceedings of the 8th European LS-DYNA Conference, Strasbourg, France, 22–23 May 2011. [Google Scholar]
- Jeske, S.R.; Simon, M.S.; Semenov, O.; Kruska, J.; Mokrov, O.; Sharma, R.; Reisgen, U.; Bender, J. Quantitative evaluation of SPH in TIG spot welding. Comput. Part. Mech. 2023, 10, 1–18. [Google Scholar] [CrossRef]
- Das, R. Cleary, Three-dimensional modelling of coupled flow dynamics, heat transferand residual stress generation in arc welding processes using themesh-free SPH method. J. Comput. Sci. 2016, 16, 200–216. [Google Scholar] [CrossRef]
- Nassiria, A.; Kinseyc, B. Numerical studies on high-velocity impact welding: Smoothed particle hydrodynamics (SPH) and arbitrary Lagrangian–Eulerian (ALE). J. Manuf. Process. 2016, 24, 376–381. [Google Scholar] [CrossRef]
- Aval, H.J. Smoothed-Particle Hydrodynamics (SPH) Simulation of AA6061-AA5086 Dissimilar Friction Stir Welding. Metals 2023, 13, 906. [Google Scholar] [CrossRef]
- Russell, M.; Souto-Iglesias, A.; Zohdi, T. Numerical simulation of Laser Fusion Additive Manufacturing processes using the SPH method. Comput. Methods Appl. Mech. Eng. 2018, 341, 163–187. [Google Scholar] [CrossRef]
- Lee, Y.; Zhang, W. Modeling of heat transfer, fluid flow and solidification microstructure of nickel-base superalloy fabricated by laser powder bed fusion. Addit. Manuf. 2016, 12, 178–188. [Google Scholar] [CrossRef]
- Dao, M.H.; Lou, J. Simulations of Laser Assisted Additive Manufacturing by Smoothed Particle Hydrodynamics. Comput. Methods Appl. Mech. Eng. 2021, 373, 113491. [Google Scholar] [CrossRef]
- Fuchs, S.L.; Praegla, P.M.; Cyron, C.J.; Wall, W.A.; Meier, C. A versatile SPH modeling framework for coupled microfluid powder dynamics in additive manufacturing: Binder jetting, material jetting, directed energy deposition and powder bed fusion. Eng. Comput. 2022, 38, 4853–4877. [Google Scholar] [CrossRef]
- Afrasiabi, M.; Lüthi, C.; Bambach, M.; Wegener, K. Multi-Resolution SPH Simulation of a Laser Powder Bed Fusion Additive Manufacturing Process. Appl. Sci. 2021, 11, 2962. [Google Scholar] [CrossRef]
- Lüthi, C.; Afrasiabi, M.; Bambach, M. An adaptive smoothed particle hydrodynamics (SPH) scheme for efficient melt pool simulations in additive manufacturing. Comput. Math. Appl. 2023, 139, 7–27. [Google Scholar] [CrossRef]
- Cleary, P. Prediction of coupled particle and fluid flows using DEM and SPH. Miner. Eng. 2015, 73, 85–99. [Google Scholar] [CrossRef]
- Chen, H.; Sun, Y.; Yuan, W.; Pang, S.; Yan, W.; Shi, Y. A Review on Discrete Element Method Simulation in Laser Powder Bed Fusion Additive Manufacturing. Chin. J. Mech. Eng. Addit. Manuf. Front. 2022, 1, 100017. [Google Scholar] [CrossRef]
- Cummins, S.; Cleary, P.W.D.; Phua, A.; Sinnott, M.; Gunasegaram, D.; Davies, C. A Coupled DEM/SPH Computational Model to Simulate Microstructure Evolution in Ti-6Al-4V Laser Powder Bed Fusion Processes. Metals 2021, 11, 858. [Google Scholar] [CrossRef]
- Cremonesi, M.; Franci, A.; Idelsohn, S.; Oñate, E. A State of the Art Review of the Particle Finite Element Method (PFEM). Arch. Comput. Methods Eng. 2020, 27, 1709–1735. [Google Scholar]
- Bobach, B.-J.; Falla, R.; Boman, R.; Terrapon, V.; Ponthot, J. Phase change driven adaptive mesh refinement in PFEM. In Proceedings of the ESAFORM 2021, 24th International Conference on Material Forming, Online, 14–16 April 2021. [Google Scholar]
- Bobach, B.-J.; Boman, R.; Celentano, D.; Terrapon, V.E.; Ponthot, J.-P. Simulation of the Marangoni Effect and Phase Change Using the Particle Finite Element Method. Appl. Sci. 2021, 11, 11893. [Google Scholar] [CrossRef]
- Franci, A.; Oñate, E.; Carbonell, J.M.; Chiumenti, M. PFEM formulation for thermo-coupled FSI analysis. Application to Nuclear Core Melt Accident. Comput. Methods Appl. Mech. Eng. 2017, 325, 711–732. [Google Scholar] [CrossRef]
- Zhang, D.; Rodriguez, J.M. A Particle Finite Element Method for Additive Manufacturing Simulations. J. Comput. Inf. Sci. Eng. 2023, 23, 051008. [Google Scholar] [CrossRef]
- Xu, R.; Stansby, P.; Laurence, D. Accuracy and stability in incompressible SPH (ISPH) based on the projection method and a new approach. J. Comput. Phys. 2009, 228, 6703–6725. [Google Scholar] [CrossRef]
- Prins, J.H. Lattice Boltzmann Method with a Neural Network Collision Operator. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2022. [Google Scholar]
- Lu, L.; Gao, X.; Dietiker, J.; Shahnam, M.; Rogers, W. Machine learning accelerated discrete element modeling of granular flows. Chem. Eng. Sci. 2021, 245, 116832. [Google Scholar] [CrossRef]
- Marinho, E. A machine learning approach of finding the optimal anisotropic SPH kernel. J. Phys. Conf. Ser. 2021, 2090, 012115. [Google Scholar] [CrossRef]
- Liu, G.; Liu, M. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific Publishing Company: Singapore, 2003. [Google Scholar]
- Tong, Z.X.; Li, M.J.; Chen, X.; He, Y.L. Direct coupling between molecular dynamics and lattice Boltzmann method based on velocity distribution functions for steady-state isothermal flow. Int. J. Heat Mass Transf. 2017, 115, 544–555. [Google Scholar] [CrossRef]
- Murashima, T.; Urata, S.; Li, S. Coupling fnite element method with large scale atomic/molecular massively parallel simulator (LAMMPS) for hierarchical multiscale simulations. Eur. Phys. J. B 2019, 92, 211. [Google Scholar] [CrossRef]
- Chena, C.; Shi, W.; Shen, Y.; Chen, J.; Zhang, A. A multi-resolution SPH-FEM method for fluid–structure interactions. Comput. Methods Appl. Mech. Eng. 2022, 401, 115659. [Google Scholar] [CrossRef]
- Du, B.; Zhao, C.; Dong, G.G.; Bi, J. FEM-DEM coupling analysis for solid granule medium forming new technology. J. Mater. Process. Tech. 2017, 249, 108–117. [Google Scholar] [CrossRef]
- Adiaa, J.; Yvonnet, J.; He, Q.; Tran, N.; Sanahuja, J. A combined Lattice-Boltzmann-finite element approach to modeling unsaturated poroelastic behavior of heterogeneous media. J. Comput. Phys. 2021, 437, 110334. [Google Scholar] [CrossRef]

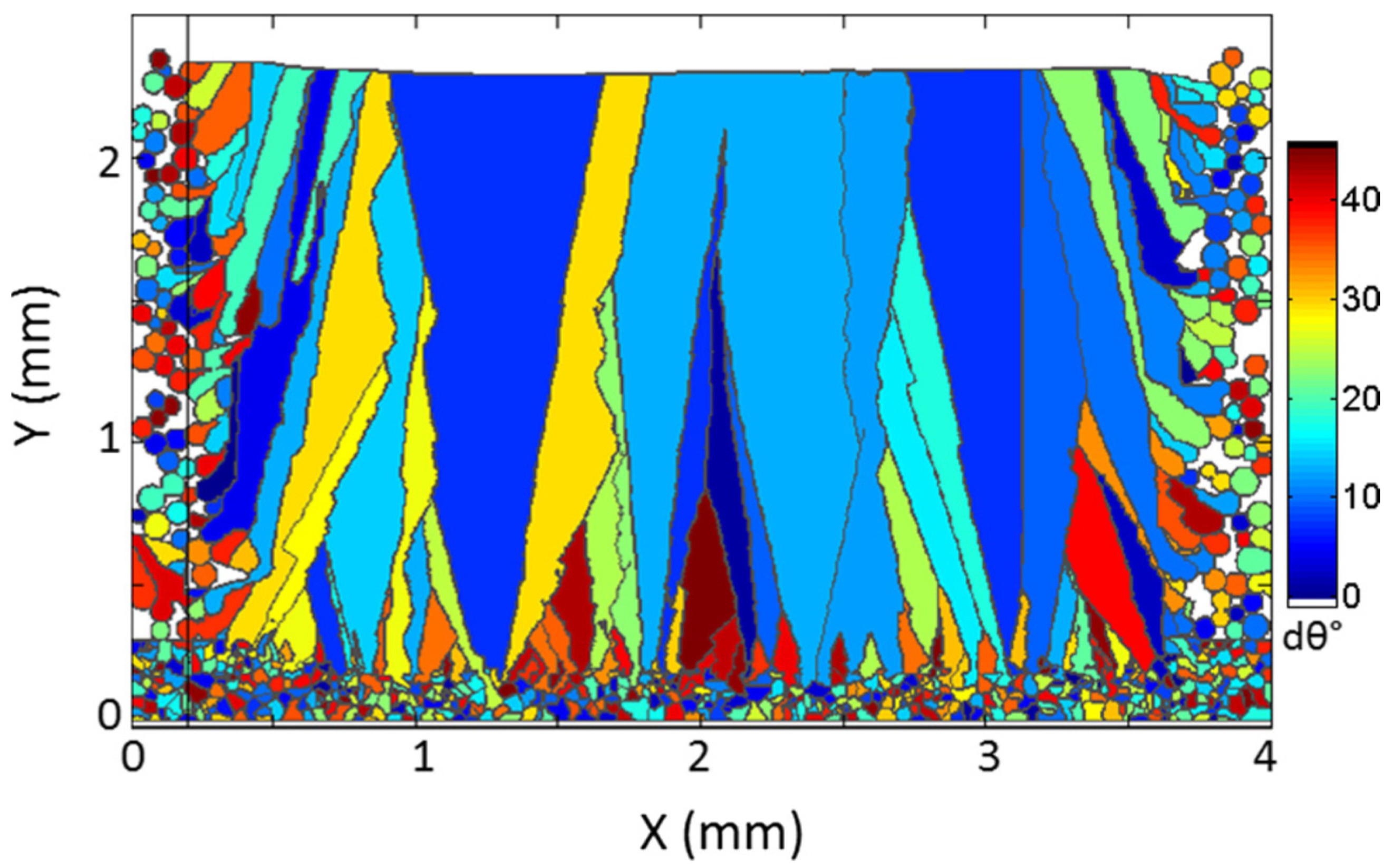
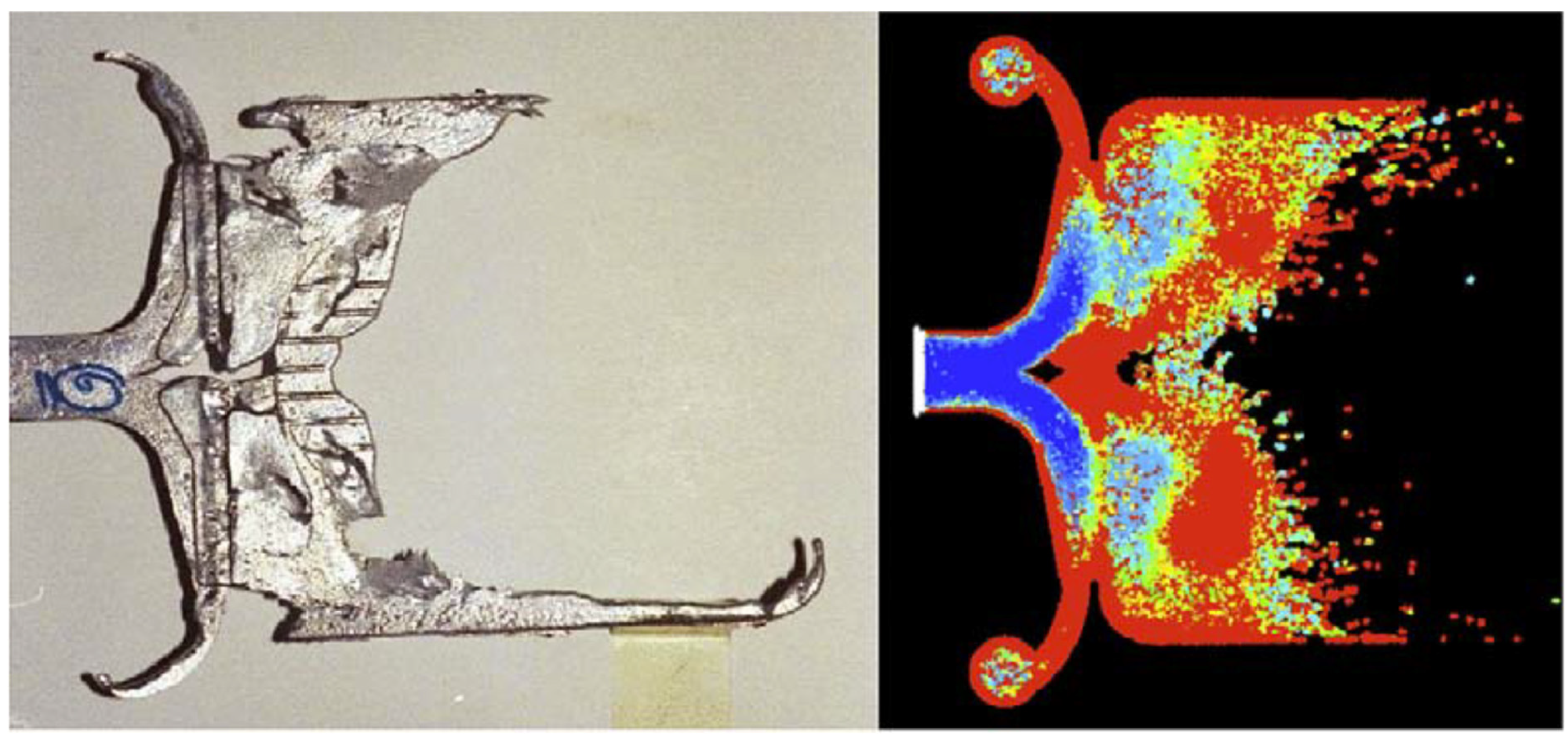

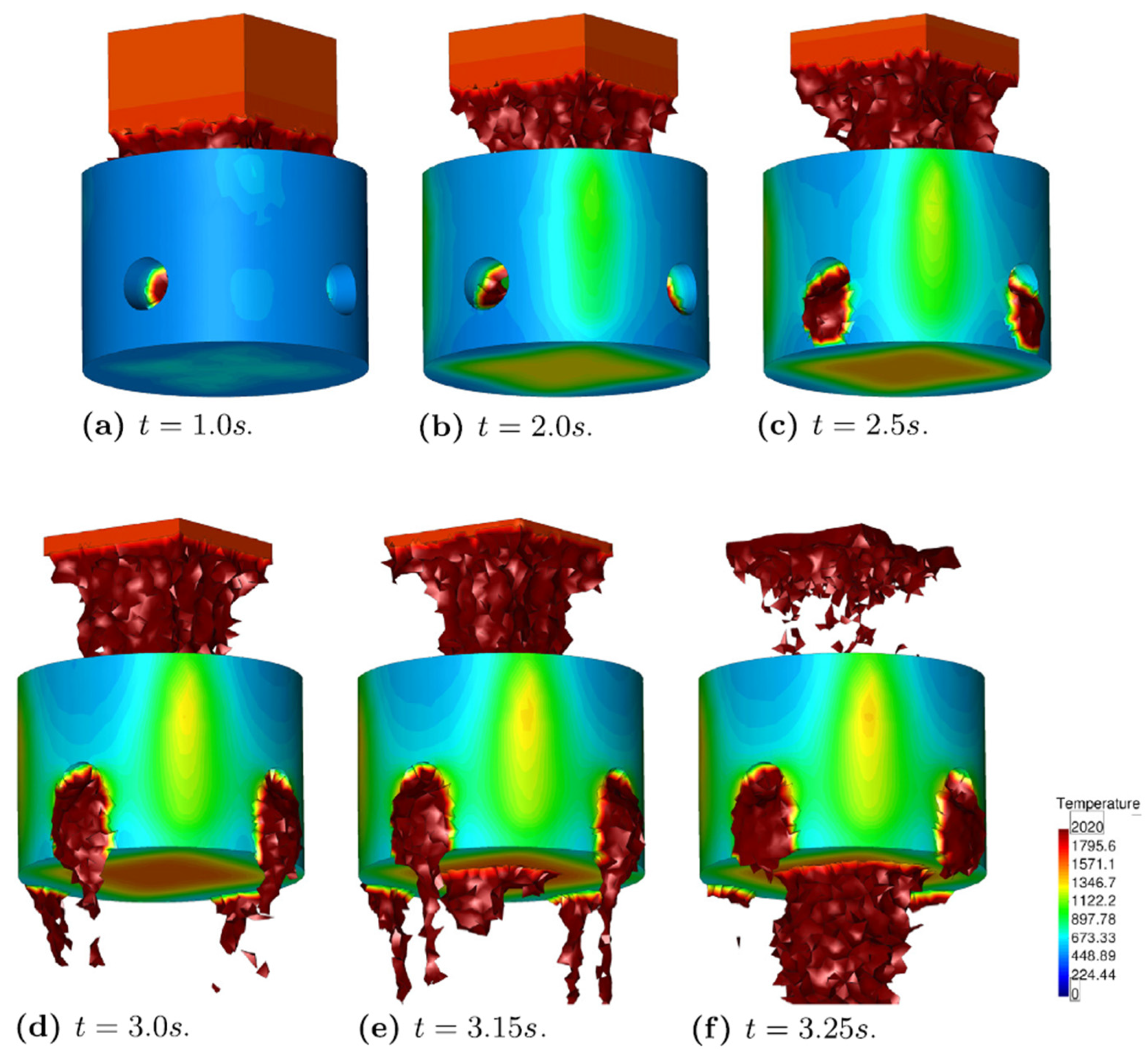
| Method | Mesh-Based or Meshless | Eulerian or Lagrangian | Target Materials | Some Accompanying Model of Phase Transformation |
|---|---|---|---|---|
| LBM | Mesh-based | Eulerian | Solid or fluid | Enthalpy, CA or PFM |
| SPH | Meshless | Lagrangian | Solid or fluid | Enthalpy |
| DEM | Meshless | Lagrangian | granular materials | Enthalpy |
| PFEM | Mesh-based | Lagrangian | solid or fluid | Enthalpy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, M. Review of Particle-Based Computational Methods and Their Application in the Computational Modelling of Welding, Casting and Additive Manufacturing. Metals 2023, 13, 1392. https://doi.org/10.3390/met13081392
Tong M. Review of Particle-Based Computational Methods and Their Application in the Computational Modelling of Welding, Casting and Additive Manufacturing. Metals. 2023; 13(8):1392. https://doi.org/10.3390/met13081392
Chicago/Turabian StyleTong, Mingming. 2023. "Review of Particle-Based Computational Methods and Their Application in the Computational Modelling of Welding, Casting and Additive Manufacturing" Metals 13, no. 8: 1392. https://doi.org/10.3390/met13081392
APA StyleTong, M. (2023). Review of Particle-Based Computational Methods and Their Application in the Computational Modelling of Welding, Casting and Additive Manufacturing. Metals, 13(8), 1392. https://doi.org/10.3390/met13081392





