Experimental and Simulation Studies of Micro-Swing Arc Welding Process for X80M Pipeline
Abstract
:1. Introduction
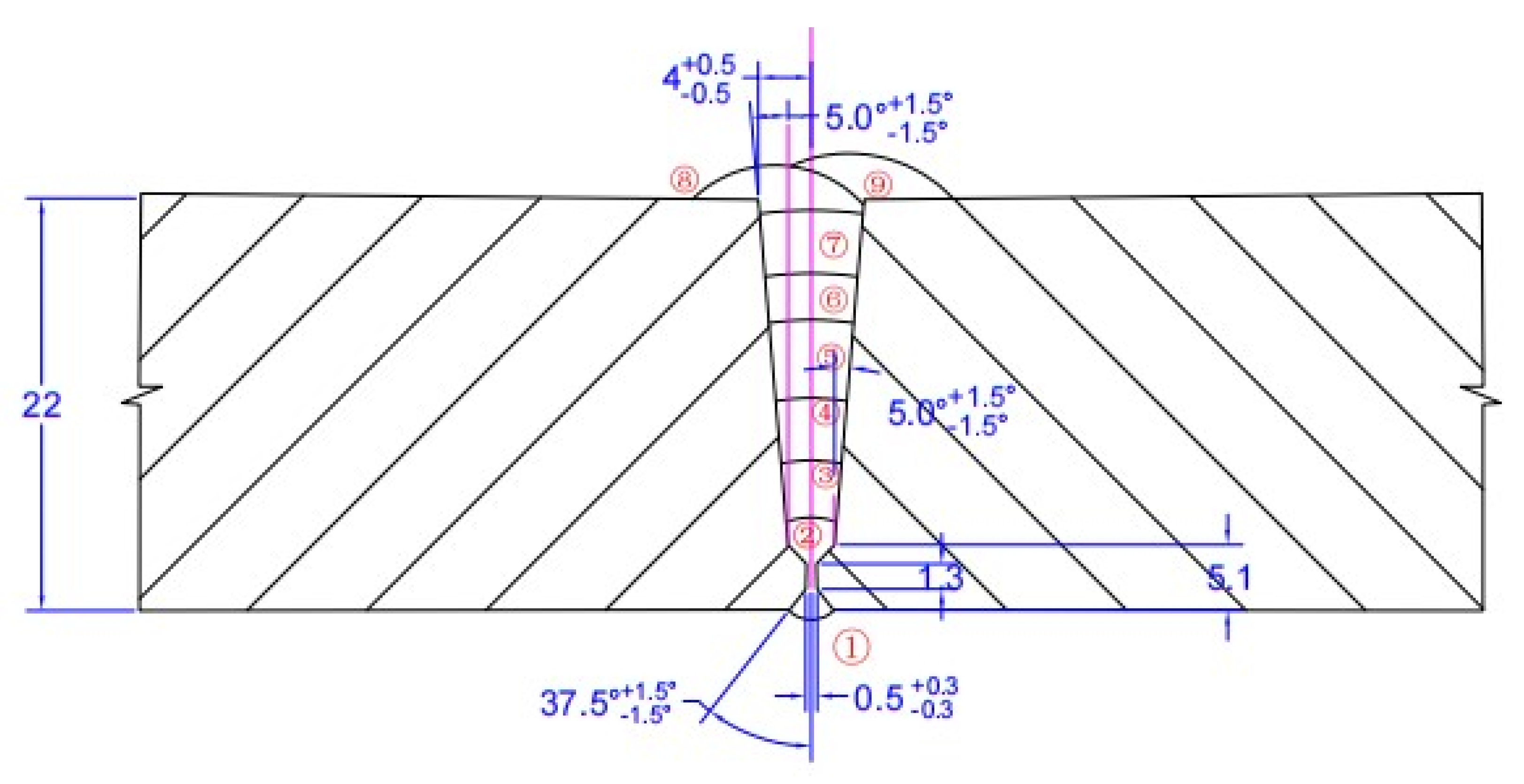
2. Test Method and Equipment
3. Numerical Simulation and Swing Welding Model
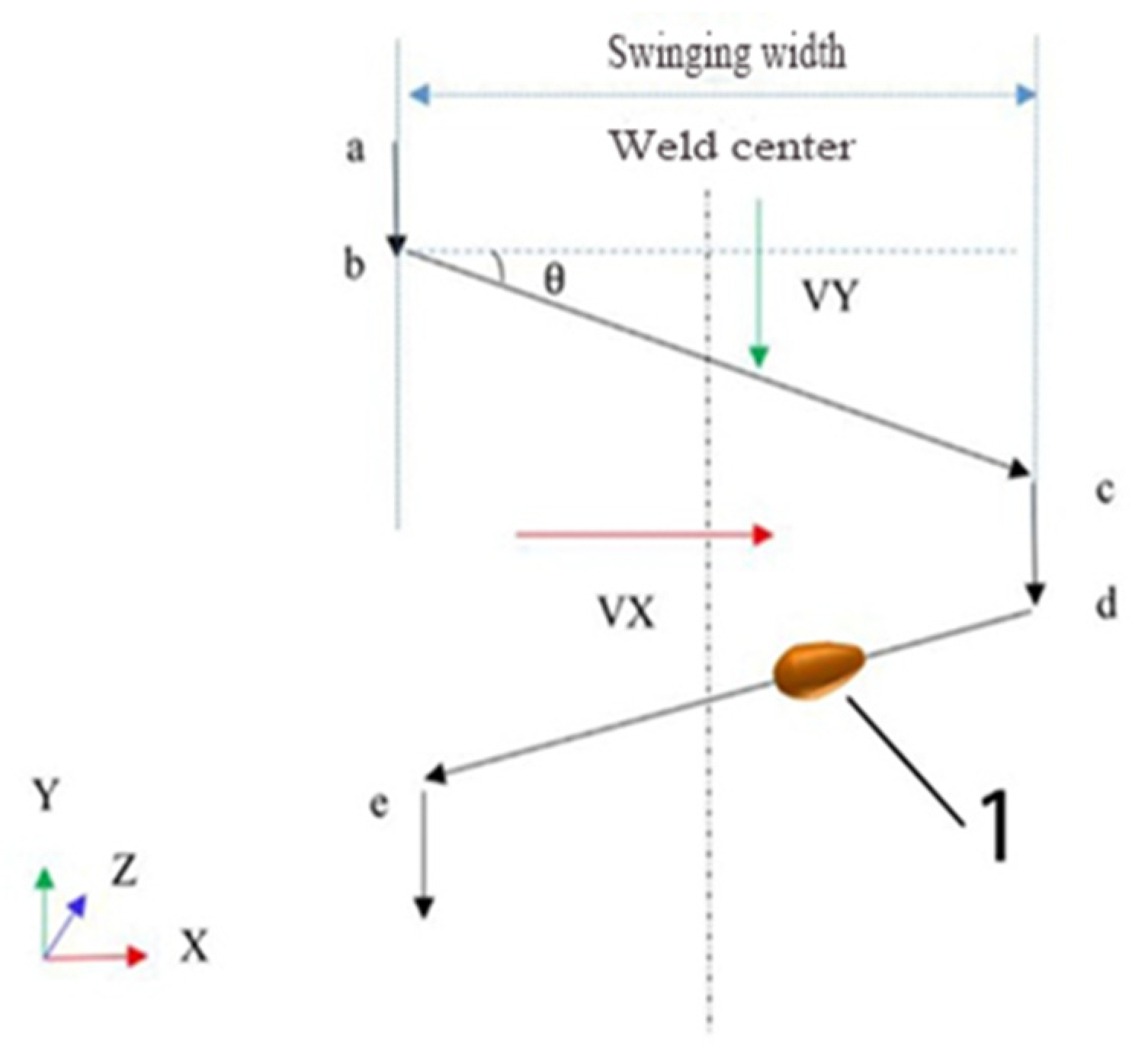
3.1. Welding Heat Source Model
- (1)
- The ab segment is the dwell stage on the left of the weld, in which VY is constant and VX is equal to 0;
- (2)
- The bc segment is the left-to-right swing stage, where VY remains unchanged, and VX is in the direction from left to right;
- (3)
- The cd segment maintains the constant VY, and VX is 0;
- (4)
- The de segment is the right-to-left swing stage, where the direction of VX is opposite to that in the bc segment.
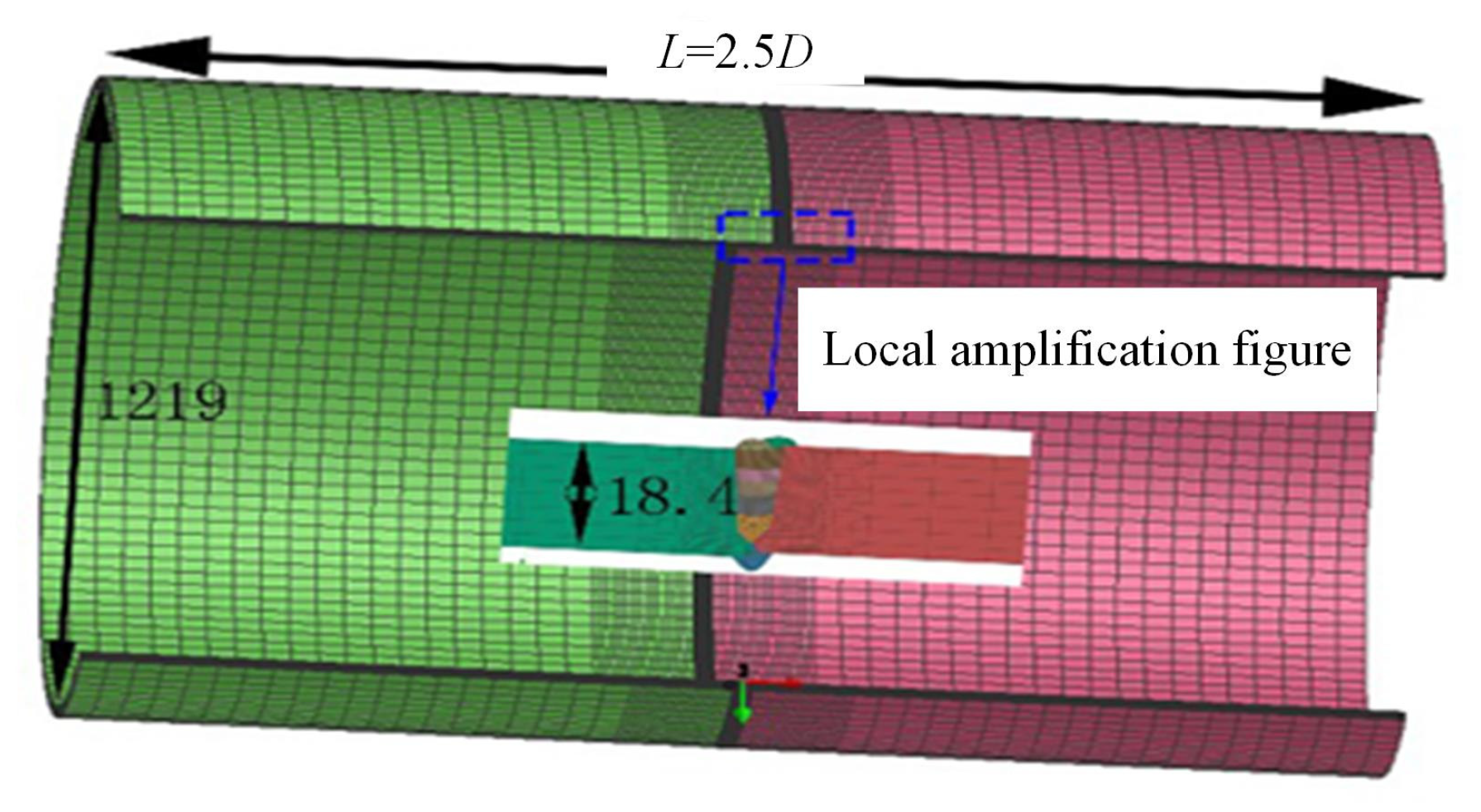
3.2. Finite Element Model
3.3. Governing Equation and Boundary Conditions
4. Results and Discussion
4.1. Melting Point Analysis Based on In Situ Laser Confocal System
4.2. Experimental Investigation of Pipeline Automatic Swing Welding
- (1)
- Welding process parameters
- (2)
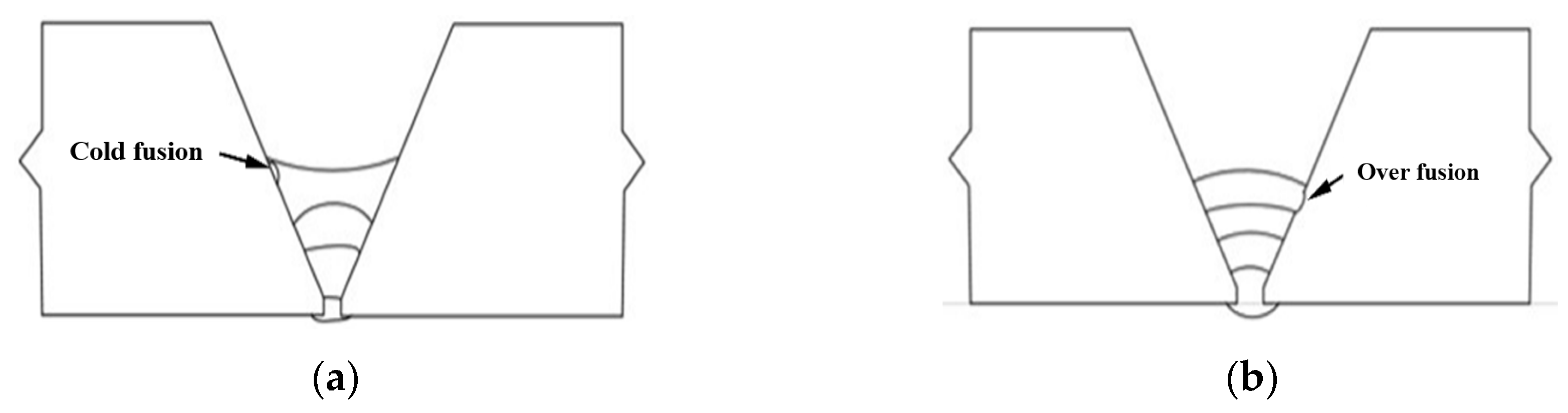
- Weld bead formation and incomplete fusion on sidewalls
- (3)
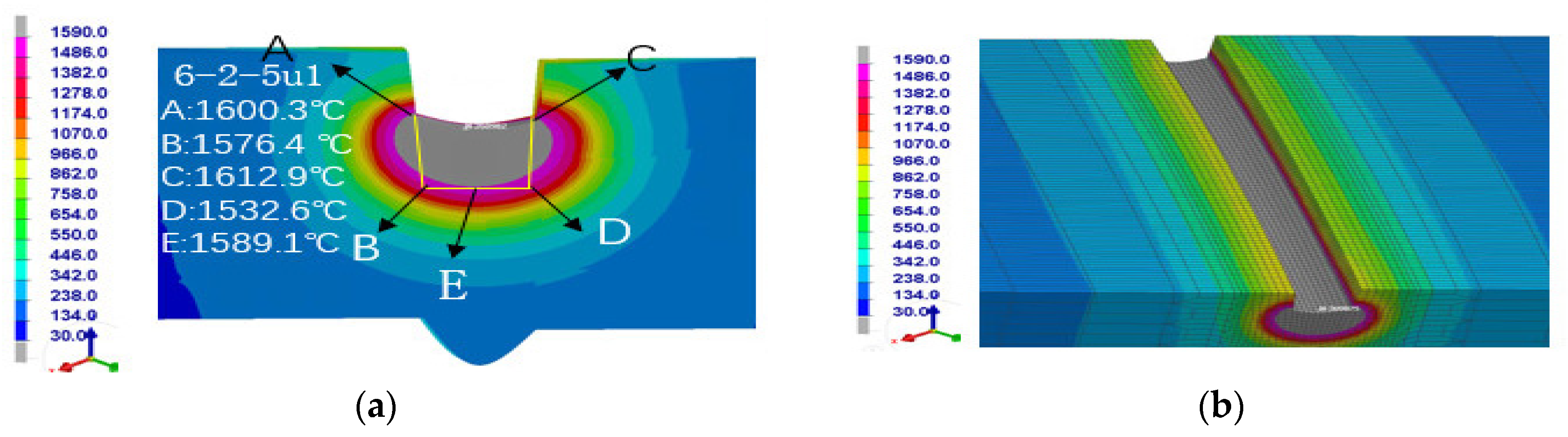
- Welding temperature field
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Quan, T. Application Status and Prospect of Automatic Welding Technology for Long Distance Oil and Gas Pipelines in China. Nat. Gas Ind. 2021, 33, 69–70. [Google Scholar]
- Lu, Y.; Shao, Q.; Sui, Y.; Feng, D. Girth welding technology for large-diameter high steel grade gas line pipes. Nat. Gas Ind. 2020, 40, 114–122. [Google Scholar]
- Xu, Q.; Zhang, L.; Wu, D. Automatic Welding Technology for the Sino-Russian Eastern Route Gas Pipeline. Nat. Gas Technol. Econ. 2017, 11, 37–39. [Google Scholar]
- Zhang, X.; Jiang, Q.; Zhan, S.; Gu, Q.; Jin, J.; Wang, Q. Design improvement measures for the automatic welding of high-steel-grade and large-diameter gas line pipes in the project of the China–Russian Eastern Gas Pipeline. Nat. Gas Ind. 2020, 40, 126–132. [Google Scholar]
- Zhang, F.; Liu, X.; Xu, X.; Zhang, Y.; Niu, L. Study on the equipment and techniques for automatic pipeline welding in mountain area. Electr. Weld. Mach. 2018, 48, 37–41. [Google Scholar]
- Sun, L. Construction resource allocation and economy analysis of automatic welding for long -distance pipeline. Electr. Weld. Mach. 2021, 51, 95–100. [Google Scholar]
- Ren, G.; Zhang, X.; Guo, J. Comparative analysis of automatic welding process for all positions of long distance pipeline. Weld. Cut. 2018, 807, 42–44. [Google Scholar]
- Shen, H.; Chen, Z.; Feng, Z. Simulation of temperature field in automatic welding of oil and gas pipeline. Pet. Petrochem. Mater. Procure. 2021, 25, 53–55. [Google Scholar]
- Zong, X.; Wu, B.; Zhang, L.; Li, W. Numerical simulation of temperature field in weaving welding based on ladder model. Trans. China Weld. Inst. 2014, 35, 9–12. [Google Scholar]
- Zhang, H.; Zhang, G.; Cai, C.; Wang, J.; Wu, L. Numerical simulation on temperature field of dynamic welding processing with weaving. Trans. China Weld. Inst. 2008, 29, 69–76. [Google Scholar]
- Qi, Z.; Yang, X. Welding defects characteristics and prevention on metal-cored wire all-position pipe welding. Electr. Weld. Mach. 2012, 42, 84–86. [Google Scholar]
- Zhang, J.; Tang, D.; Zhang, T.; Hou, Z. Causes of Frequently Appeared Defects in Pipeline Automatic Welding and Preventive Measures. Pet. Eng. Constr. 2005, 31, 44–47. [Google Scholar]
- Rihar, G.; Uran, M. Lack of Fusion Characterisation of Indications. Weld. World 2006, 50, 35–39. [Google Scholar] [CrossRef]
- Lv, C.; Lei, Z.; Xia, S. Analysis and Treatment of Welding Defect in Narrow Gap Automatic Welding pf primary Coolant pipeline of ACP1000 Demonstration Project. China Nucl. Power 2020, 13, 148–154. [Google Scholar]
- Bandhu, D.; Djavanroodi, F.; Shaikshavali, G.; Vora, J.J.; Abhishek, K.; Thakur, A.; Kumari, S.; Saxena, K.K.; Ebrahimi, M.; Attarilar, S. Effect of Metal-Cored Filler Wire on Surface Morphology and Micro-Hardness of Regulated Metal Deposition Welded ASTM A387-Gr. 11-Cl. 2 Steel Plates. Materials 2022, 15, 6661. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, S.; Zhang, T.; Zhou, X.; Li, S. Effects of post-weld heat treatment on the microstructure and mechanical properties of laser-welded NiTi/304SS joint with Ni filler. Mater. Sci. Eng. A 2020, 771, 138545. [Google Scholar] [CrossRef]
- Chen, Y.; Mao, Y.; Lu, W.; Peng, H. Investigation of welding crack in micro laser welded NiTiNb shape memory alloy and Ti6Al4V alloy dissimilar metals joints. Opt. Laser Technol. 2017, 91, 197–202. [Google Scholar]
- Zhang, Z.; Shao, C. Numerical simulation and visualization experiment of gas-liquid two phase flow in the centrifugal pump. J. Nanjing Tech Univ. (Nat. Sci. Ed.) 2020, 13, 148–154. [Google Scholar]
- Wang, G.; Jia, L.; Zhang, X. CFD numerical simulation of pulse-jet cleaning efficiency based on response surface method. J. Nanjing Tech Univ. (Nat. Sci. Ed.) 2022, 44, 132–140. [Google Scholar]
- Zhu, C.; Cheon, J.; Tang, X.; Na, S.-J.; Lu, F.; Cui, H. Effect of swing arc on molten pool behaviors in narrow-gap GMAW of 5083 Al-alloy. J. Mater. Process. Technol. 2018, 259, 243–258. [Google Scholar] [CrossRef]
- Xu, G.; Wang, J.; Li, P.; Zhu, J.; Cao, Q. Numerical analysis of heat transfer and fluid flow in swing arc narrow gap GMA welding. J. Mater. Process. Technol. 2017, 252, 260–269. [Google Scholar] [CrossRef]
- Panwisawas, C.; Sovani, Y.; Turner, R.P.; Brooks, J.W.; Basoalto, H.C.; Choquet, I. Modelling of thermal fluid dynamics for fusion welding. J. Mater. Process. Technol. 2017, 252, 176–182. [Google Scholar] [CrossRef]
- Yang, T.; Liu, J.F.; Zhang, Y.; Sun, K.; Chen, W. Studies on the formation mechanism of incomplete fusion defects in ultra-narrow gap laser wire filling welding. Opt. Laser Technol. 2020, 129, 1–7. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Zhang, B.; Liu, X.; Yan, H.; Wang, Z. Technology of causes and suppression of weld edge incomplete fusion for long-distance pipeline automatic welding. Electr. Weld. Mach. 2019, 49, 57–61. [Google Scholar]
- Zhao, W.; Jiang, W.; Zhang, H.; Han, B.; Jin, H.; Gao, Q. 3D finite element analysis and optimization of welding residual stress in the girth joints of X80 steel pipeline. J. Manuf. Process. 2021, 66, 166–178. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Han, T.; Bao, L.; Wu, Q.; Gu, S. Numerical and experimental investigation of the formation mechanism and the distribution of the welding residual stress induced by the hybrid laser arc welding of AH36 steel in a butt joint configuration. J. Manuf. Process. 2020, 51, 95–108. [Google Scholar] [CrossRef]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Li, Y.; Zhang, H.; Wang, P. Experimental and Simulation Studies of Micro-Swing Arc Welding Process for X80M Pipeline. Metals 2023, 13, 1228. https://doi.org/10.3390/met13071228
Luo Z, Li Y, Zhang H, Wang P. Experimental and Simulation Studies of Micro-Swing Arc Welding Process for X80M Pipeline. Metals. 2023; 13(7):1228. https://doi.org/10.3390/met13071228
Chicago/Turabian StyleLuo, Zhili, Yan Li, Hong Zhang, and Pengyu Wang. 2023. "Experimental and Simulation Studies of Micro-Swing Arc Welding Process for X80M Pipeline" Metals 13, no. 7: 1228. https://doi.org/10.3390/met13071228





