Efficiently Removing Hydrogen of H-Supersaturated Liquid Steel in the Vacuum Degasser with Various Gas Injection Modes
Abstract
1. Introduction
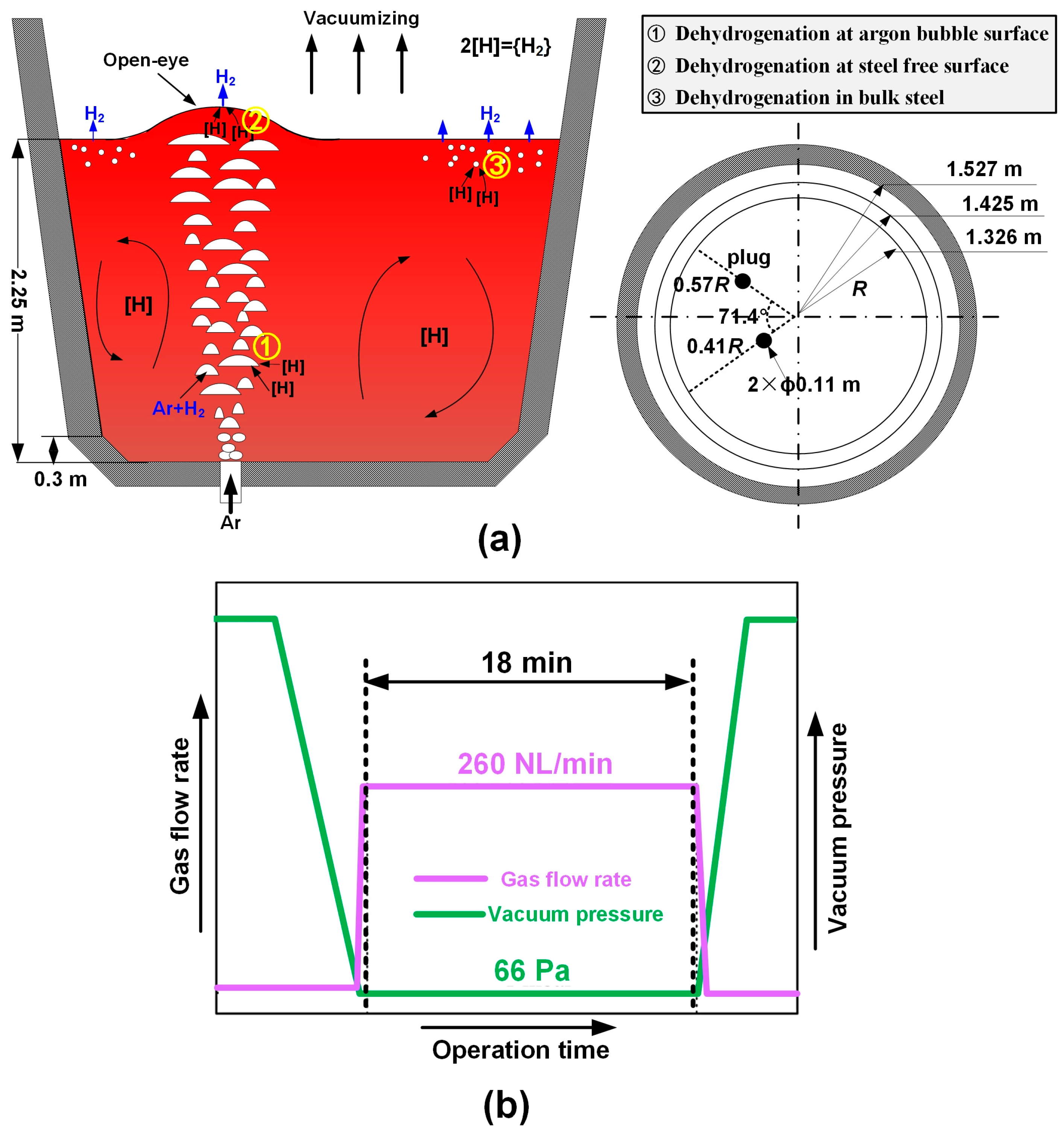
2. Numerical Model
3. Results
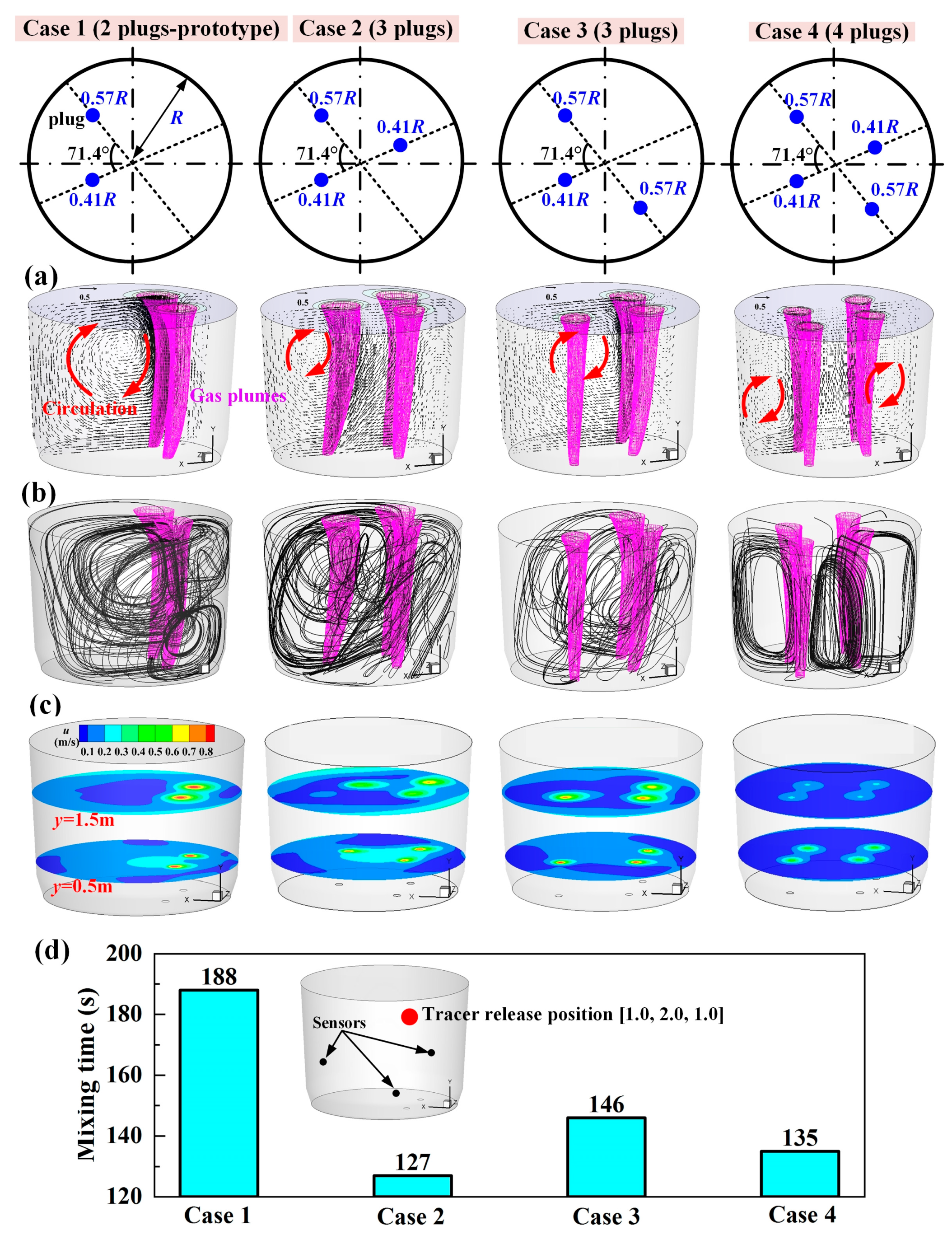
3.1. Number of Plugs
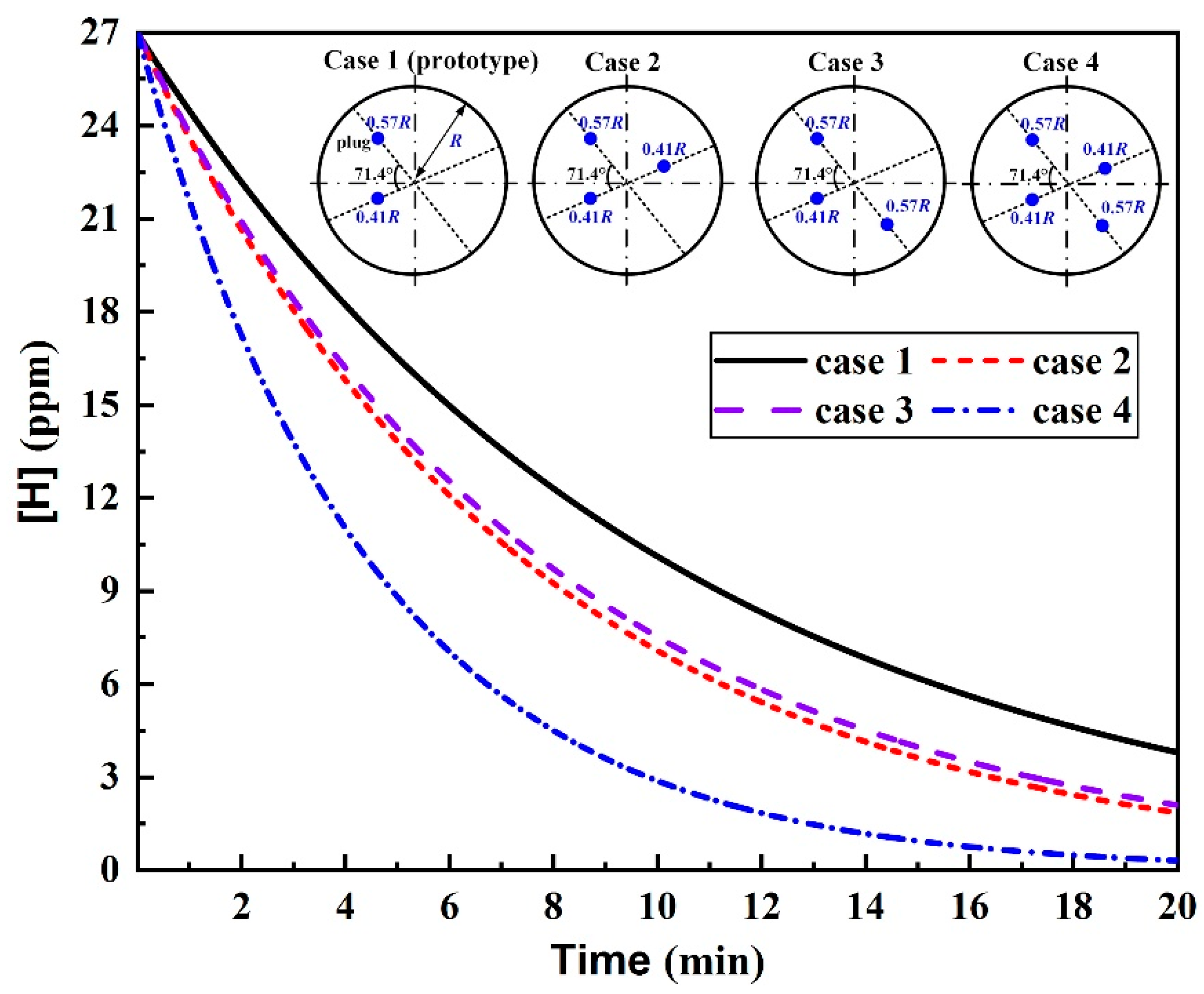
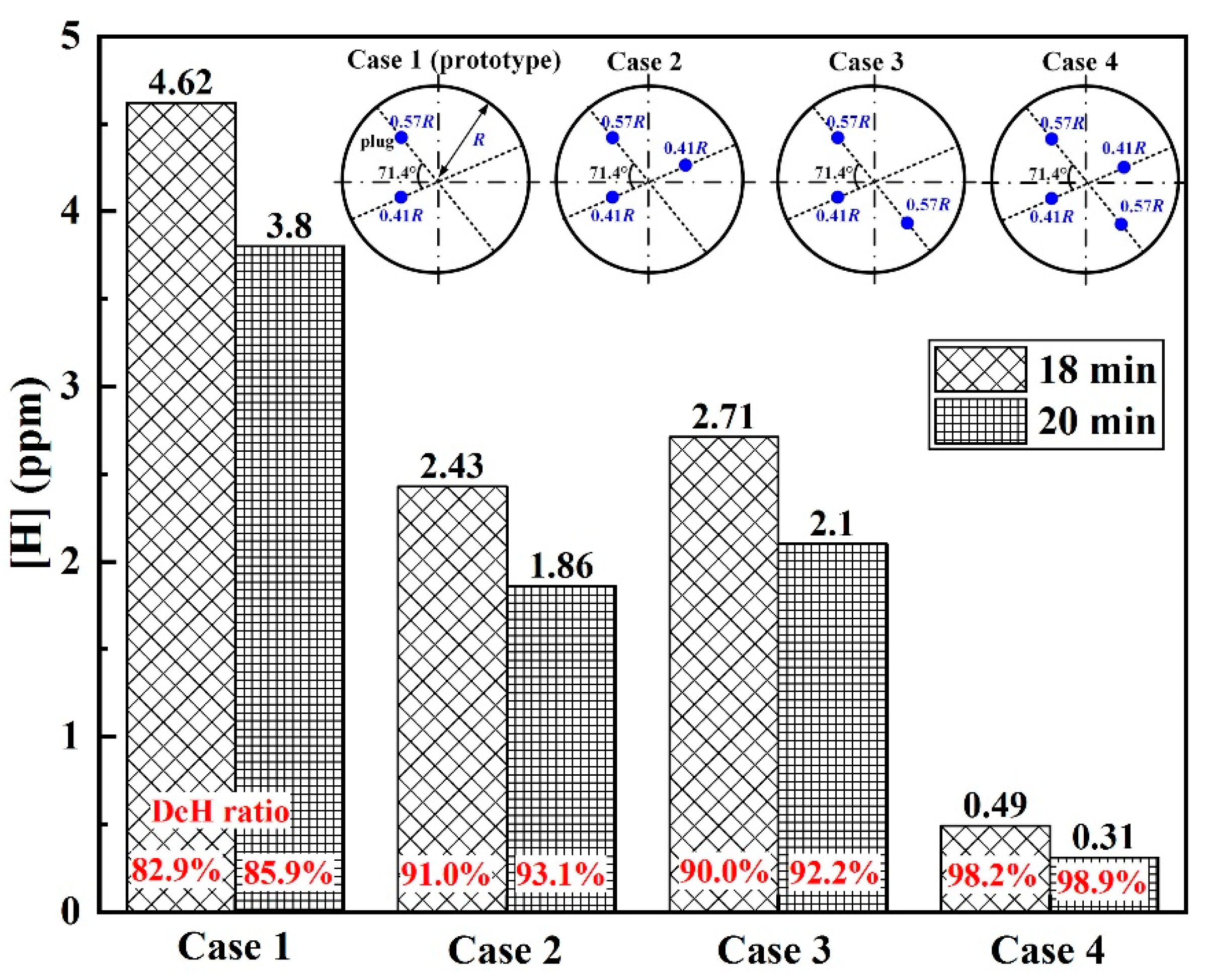
3.2. Plug Position
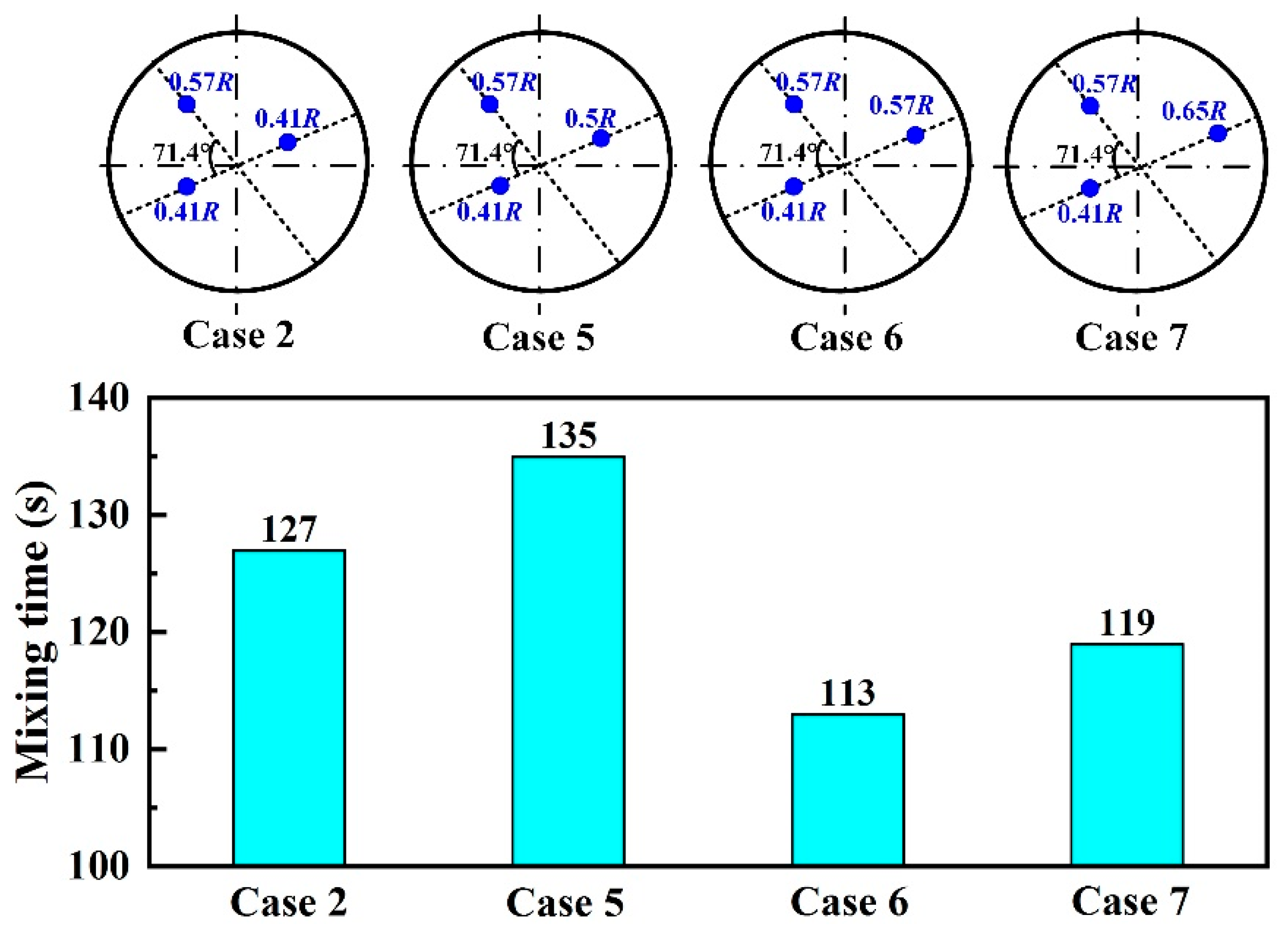
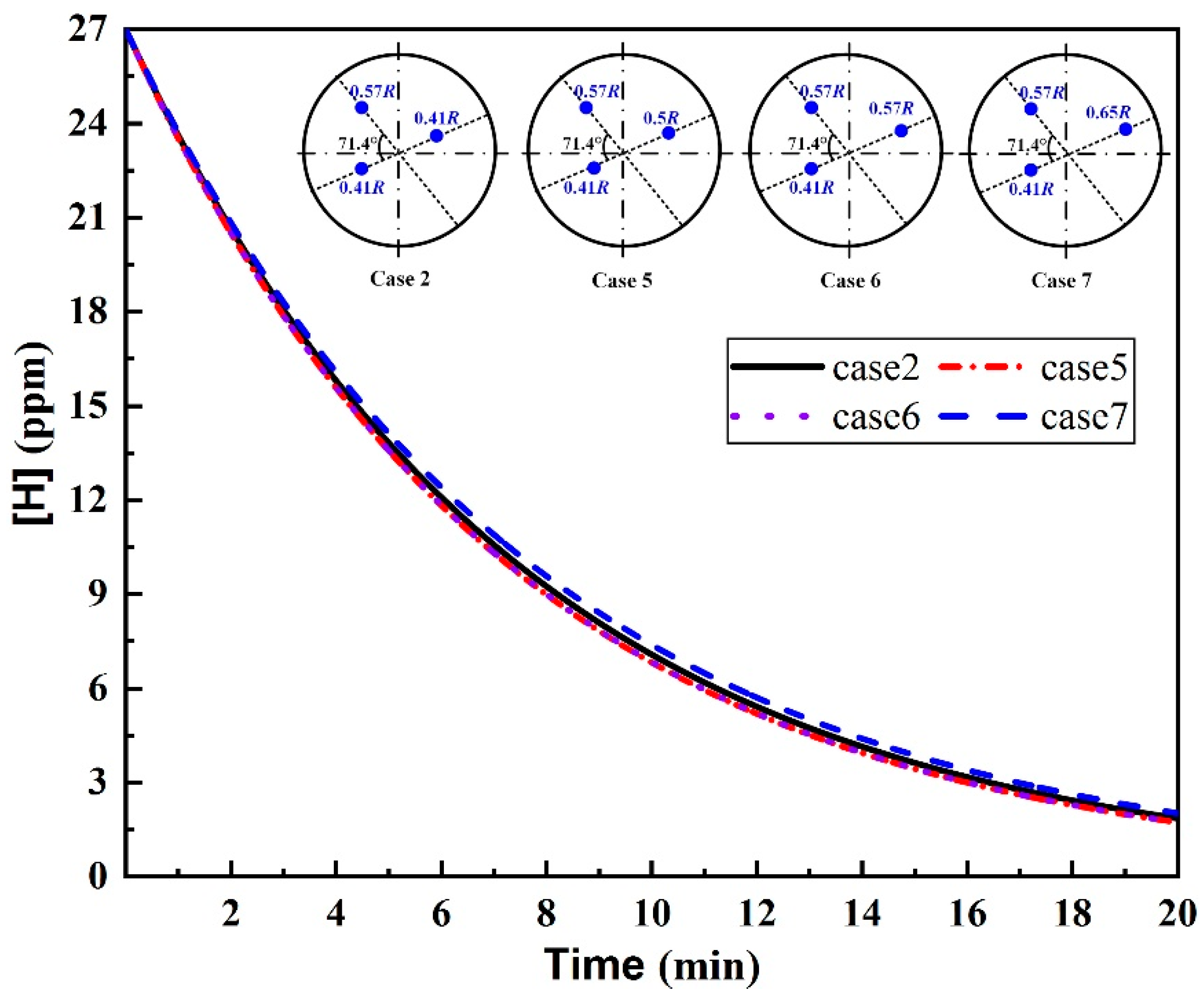
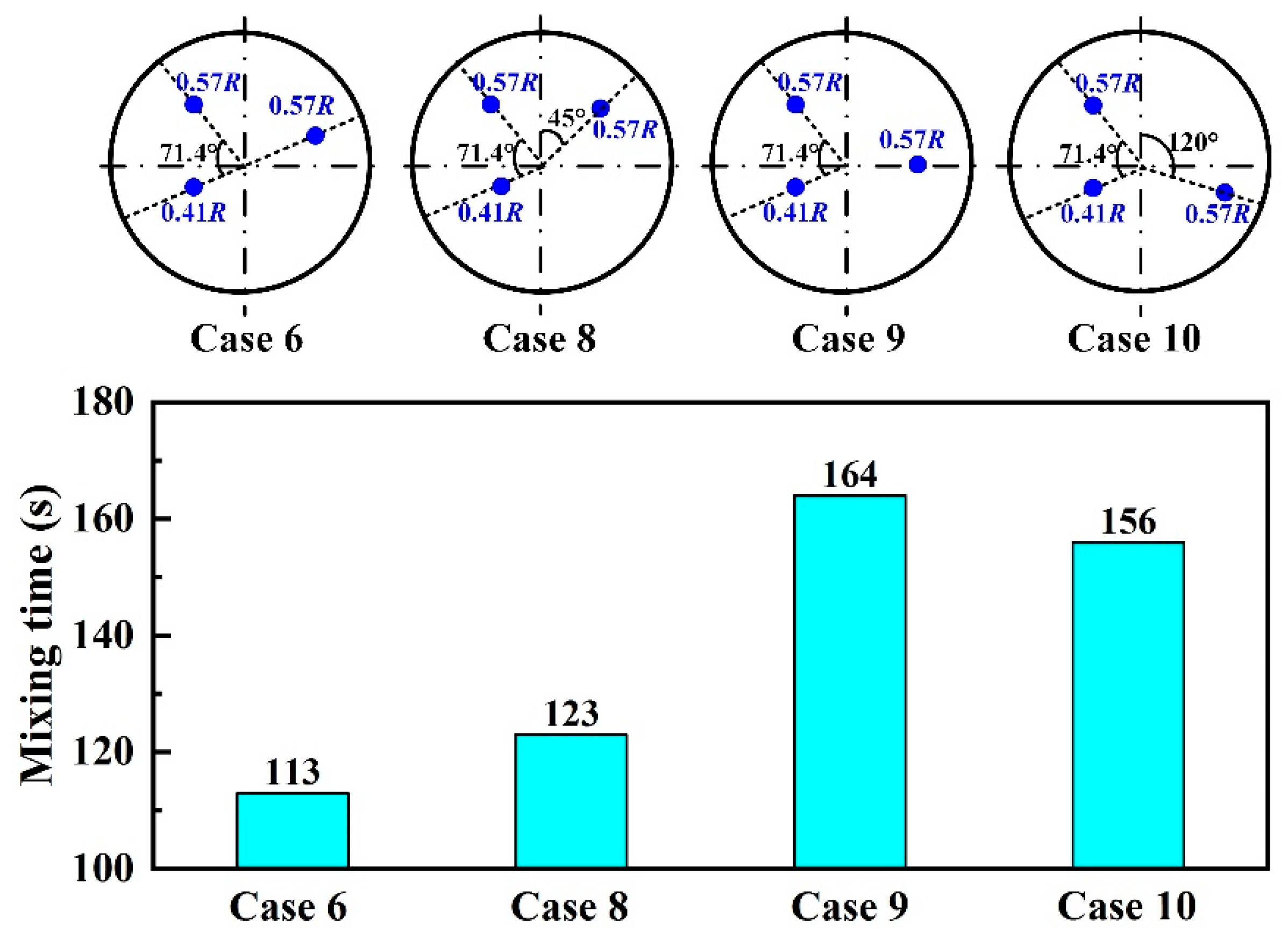
3.3. Plug Angle
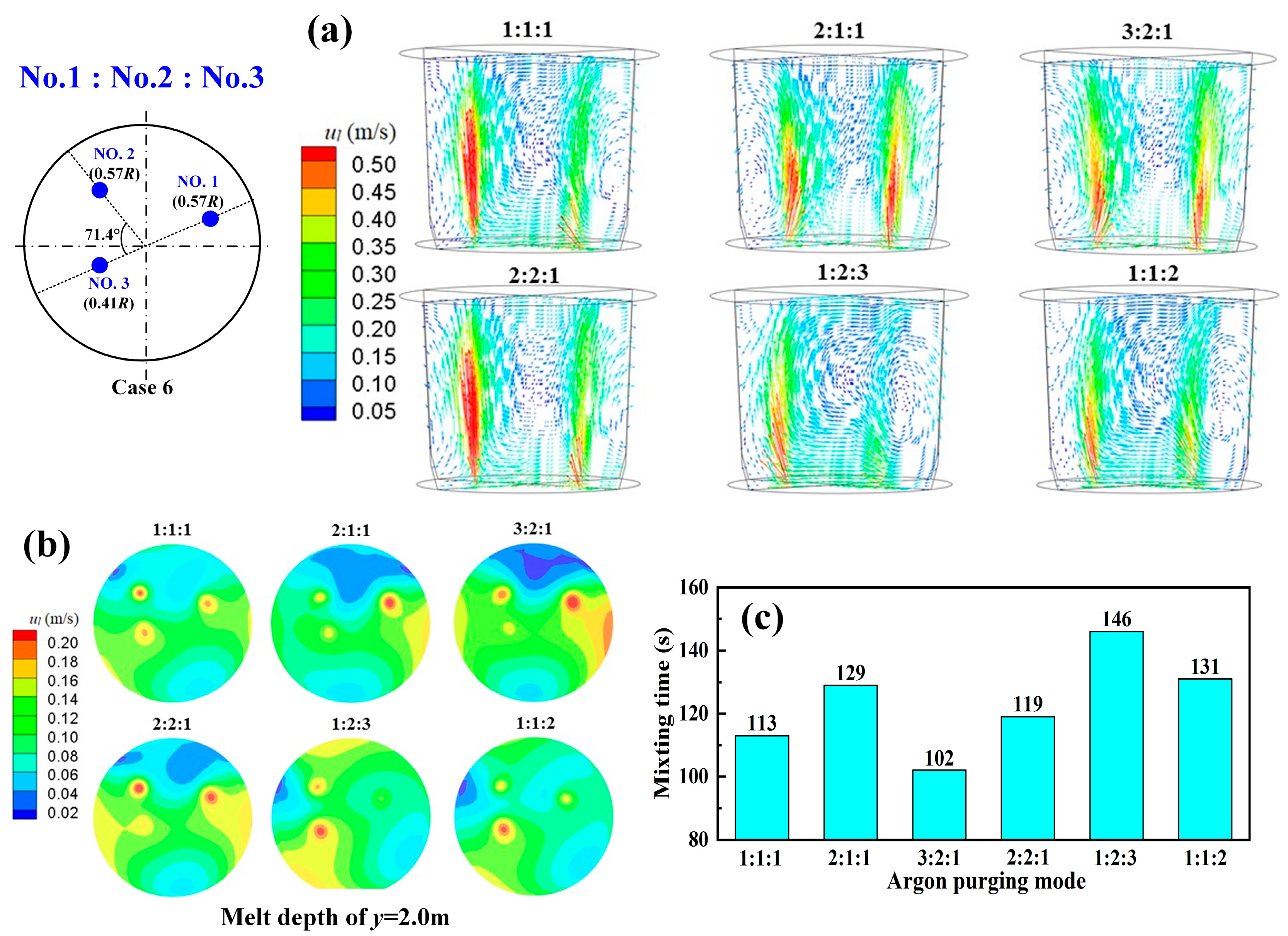
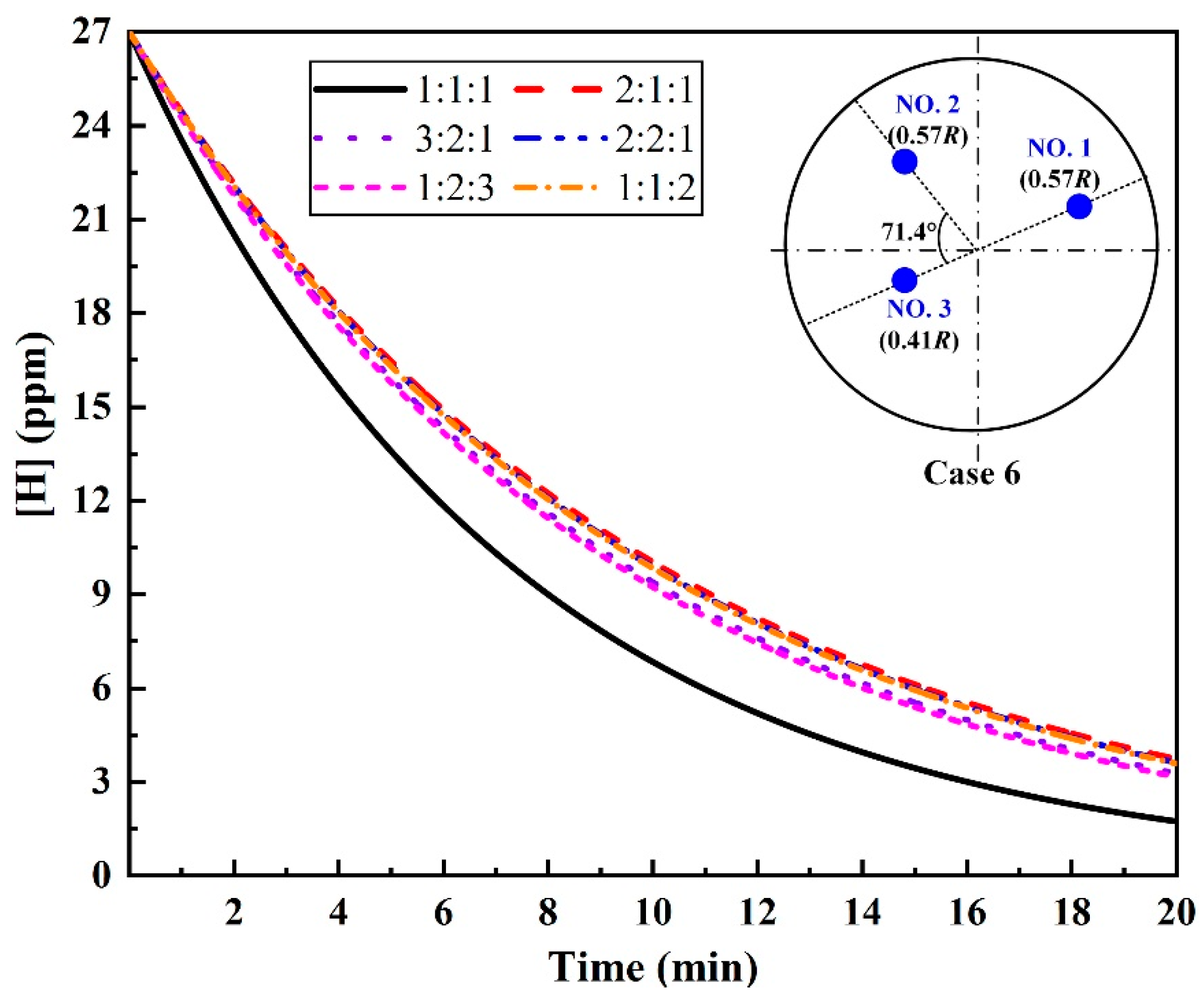
3.4. Argon-Purging Modes for Multi-Plugs
4. Conclusions
- (1)
- Increasing the number of plugs improved the dehydrogenation efficiency. For H-supersaturated liquid steel, the double- and triple-plug ladles were incapable of obtaining a desired dehydrogenation efficiency under the routine degassing operation conditions, whereas it was achieved using the quadruple-plug ladle or using some triple-plug ladles under the condition of slightly prolonging the routine degassing time.
- (2)
- For the triple-plug ladle, varying the plug position made no significant difference to the melt hydrodynamic conditions and the dehydrogenation efficiency, both of which, however, were greatly affected by the plug angle. The melt-mixing time lengthened, and the dehydrogenation efficiency decreased when the plug angle between the two plugs closer to the wall increased.
- (3)
- For the triple-plug ladle, the non-uniform argon-purging mode, increasing the argon flow rate of the plugs closer to the wall and decreasing that of those far from the wall, improved the melt hydrodynamic conditions. However, the optimal dehydrogenation performance was achieved with the uniform argon-purging mode.
- (4)
- Of all the ladle designs considered, the plug number had the greatest impact on the dehydrogenation efficiency. For highly efficient dehydrogenation of H-supersaturated liquid steel in the VD, the quadruple-plug ladle produced the highest efficiency, followed by the triple-plug ladle with the plug positions of 0.57R, 0.57R, and 0.41R, and the plug angles of 108.6° and 71.4°, using the uniform argon-purging flow rate.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sabat, K.C.; Rajput, P.; Paramguru, R.K.; Bhoi, B.; Mishra, B.K. Reduction of oxide minerals by hydrogen plasma: An overview. Plasma Chem. Plasma Process. 2014, 34, 1–23. [Google Scholar] [CrossRef]
- Sabat, K.C.; Murphy, A. Hydrogen plasma processing of iron ore. Metall. Mater. Trans. B 2017, 48, 1561–1594. [Google Scholar] [CrossRef]
- Seftejani, M.N.; Schenk, J. Thermodynamic of liquid iron ore reduction by hydrogen thermal plasma. Metals 2018, 8, 1051. [Google Scholar] [CrossRef]
- Behera, P.R.; Bhoi, B.; Paramguru, R.K.; Mukherjee, P.S.; Mishra, B.K. Hydrogen plasma smelting reduction of Fe2O3. Metall. Mater. Trans. B 2019, 50, 262–270. [Google Scholar] [CrossRef]
- Filho, I.R.S.; Springer, H.; Ma, Y.; Mahajan, A.; Silva, C.C.; Kulse, M.; Raabe, D. Green steel at its crossroads: Hybrid hydrogen-based reduction of iron ores. J. Clean Prod. 2022, 340, 130805. [Google Scholar] [CrossRef]
- Ren, X.C.; Chu, W.Y.; Su, Y.J.; Li, J.X.; Qiao, L.J. Effects of Atomic hydrogen and flaking on mechanical properties of wheel steel. Metall. Mater. Trans. B 2007, 38, 1004–1011. [Google Scholar] [CrossRef]
- Fan, J.K.; Chen, H.T.; Zhao, W.; Yan, L. Study on flake formation behavior and its influence factors in Cr5 steel. Materials 2018, 11, 690. [Google Scholar] [CrossRef]
- Sano, M.; Mori, K. Bubble Formation from Single Nozzles in Liquid Metals. Trans. ISIJ 1976, 17, 344–352. [Google Scholar] [CrossRef]
- Dembovsky, V. Thermodynamics of dissolution and liberation of gases in the atomization of molten metals by plasma-induced expansion. J. Mater. Process Technol. 1997, 64, 65–74. [Google Scholar] [CrossRef]
- Gedeon, S.A.; Eagar, T.W. Assessing hydrogen-assisted cracking fracture modes in high-strength steel weldments. Weld. J. 1990, 69, 213–220. [Google Scholar]
- Steneholm, K.; Andersson, M.; Tilliander, A.; Jönsson, P.G. Removal of hydrogen, nitrogen and sulphur from tool steel during vacuum degassing. Ironmak. Steelmak. 2013, 40, 199–205. [Google Scholar] [CrossRef]
- Zhang, G.L.; Cheng, G.G.; Dai, W.X.; Huang, Y.; Wang, Q.M. Study on dehydrogenation behaviour of molten steel in single snorkel refining furnace (SSRF) by a mathematical model. Ironmak. Steelmak. 2021, 48, 909–918. [Google Scholar] [CrossRef]
- Yu, S.; Louhenkilpi, S. Numerical simulation of dehydrogenation of liquid steel in the vacuum tank degasser. Metall. Mater. Trans. B 2013, 44, 459–468. [Google Scholar] [CrossRef]
- Yu, S.; Miettinen, J.; Shao, L.; Louhenkilpi, S. Mathematical modeling of nitrogen removal from the vacuum tank degasser. Steel Res. Int. 2015, 86, 466–477. [Google Scholar] [CrossRef]
- Karouni, F.; Wynne, B.P.; Talamantes-Silva, J.; Phillips, S. Hydrogen degassing in a vacuum arc degasser using a three-phase eulerian method and discrete population balance model. Steel Res. Int. 2018, 89, 1700550. [Google Scholar] [CrossRef]
- Karouni, F.; Wynne, B.P.; Talamantes-Silva, J.; Phillips, S. Modeling the effect of plug positions and ladle aspect ratio on hydrogen removal in the vacuum arc degasser. Steel Res. Int. 2018, 89, 1700551. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J.H.; Yu, S.J.; Su, X.F.; Yan, B.J.; Yang, H. Bubble growth and floating behavior during degassing process of molten steel/(N2, H2) system. ISIJ Int. 2020, 60, 470–480. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Chen, C.; Lin, W.M.; Yu, Y.C.; E, D.Y.; Wang, S.B. Numerical simulation of tracers transport process in water model of a vacuum refining unit: Single snorkel refining furnace. Steel Res. Int. 2020, 91, 2000022. [Google Scholar] [CrossRef]
- Ouyang, X.; Lin, W.; Luo, Y.; Zhang, Y.; Fan, J.; Chen, C.; Cheng, G. Effect of salt tracer dosages on the mixing process in the water model of a single snorkel refining furnace. Metals 2022, 12, 1948. [Google Scholar] [CrossRef]
- Geng, D.Q.; Zhang, X.; Liu, X.A.; Wang, P.; Liu, H.T.; Chen, H.M.; Dai, C.M.; Lei, H.; He, J.C. Simulation on flow field and mixing phenomenon in single snorkel vacuum degasser. Steel Res. Int. 2015, 86, 724–731. [Google Scholar] [CrossRef]
- Song, K.; Jokilaakso, A. CFD modeling of multiphase flow in an SKS furnace: The effect of tuyere arrangements. Metall. Mater. Trans. B 2021, 52, 1772–1788. [Google Scholar] [CrossRef]
- Xiao, J.B.; Yan, H.J.; Schubert, M.; Liu, L.; Döß, A.; Schleicher, E.; Hampel, U. Effect of nozzle geometry on centerline gas holdup in submerged gas injection. Metall. Mater. Trans. B 2021, 52, 4002–4011. [Google Scholar] [CrossRef]
- Li, Q.; Pistorius, P.C. Interface-resolved simulation of bubbles–metal–slag multiphase system in a gas-stirred ladle. Metall. Mater. Trans. B 2021, 52, 1532–1549. [Google Scholar] [CrossRef]
- Li, Q.; Pistorius, P.C. Toward multiscale model development for multiphase flow: Direct numerical simulation of dispersed phases and multiscale interfaces in a gas-stirred ladle. JOM 2021, 73, 2888–2899. [Google Scholar] [CrossRef]
- Haas, T.; Schubert, C.; Eickhoff, M.; Pfeifer, H. Numerical Modeling of the Ladle Flow by a LES-Based Eulerian–Lagrange Approach: A Systematic Survey. Metall. Mater. Trans. B 2021, 52, 903–921. [Google Scholar] [CrossRef]
- Villela-Aguilar, J.J.; Ramos-Banderas, J.; Hernández-Bocanegra, C.A.; Solorio-Díaz, G. Optimization of the mixing time using asymmetrical arrays in both gas flow and injection positions in a dual-plug ladle. ISIJ Int. 2020, 60, 1172–1178. [Google Scholar] [CrossRef]
- Li, M.M.; Yang, Y.; Yu, S.; Shao, L.; Zou, Z.S. A Numerical study on dehydrogenation of liquid steel supersaturated with hydrogen in a vacuum degasser (VD). Metall. Mater. Trans. B 2023, 1–12. [Google Scholar] [CrossRef]
- Sheng, Y.Y.; Irons, G.A. Measurement and modeling of turbulence in the gas/liquid two-phase zone during gas injection. Metall. Trans. B 1993, 24, 695–705. [Google Scholar] [CrossRef]
- Weinstein, M.; Elliott, J.F. Solubility of hydrogen in liquid iron alloys. Trans. Met. Soc. AIME 1963, 227, 378–382. [Google Scholar]
- Tang, H.Y.; Guo, X.C.; Wu, G.H.; Wang, Y. Effect of gas blown modes on mixing phenomena in a bottom stirring ladle with dual plugs. ISIJ Int. 2016, 56, 2161–2170. [Google Scholar]
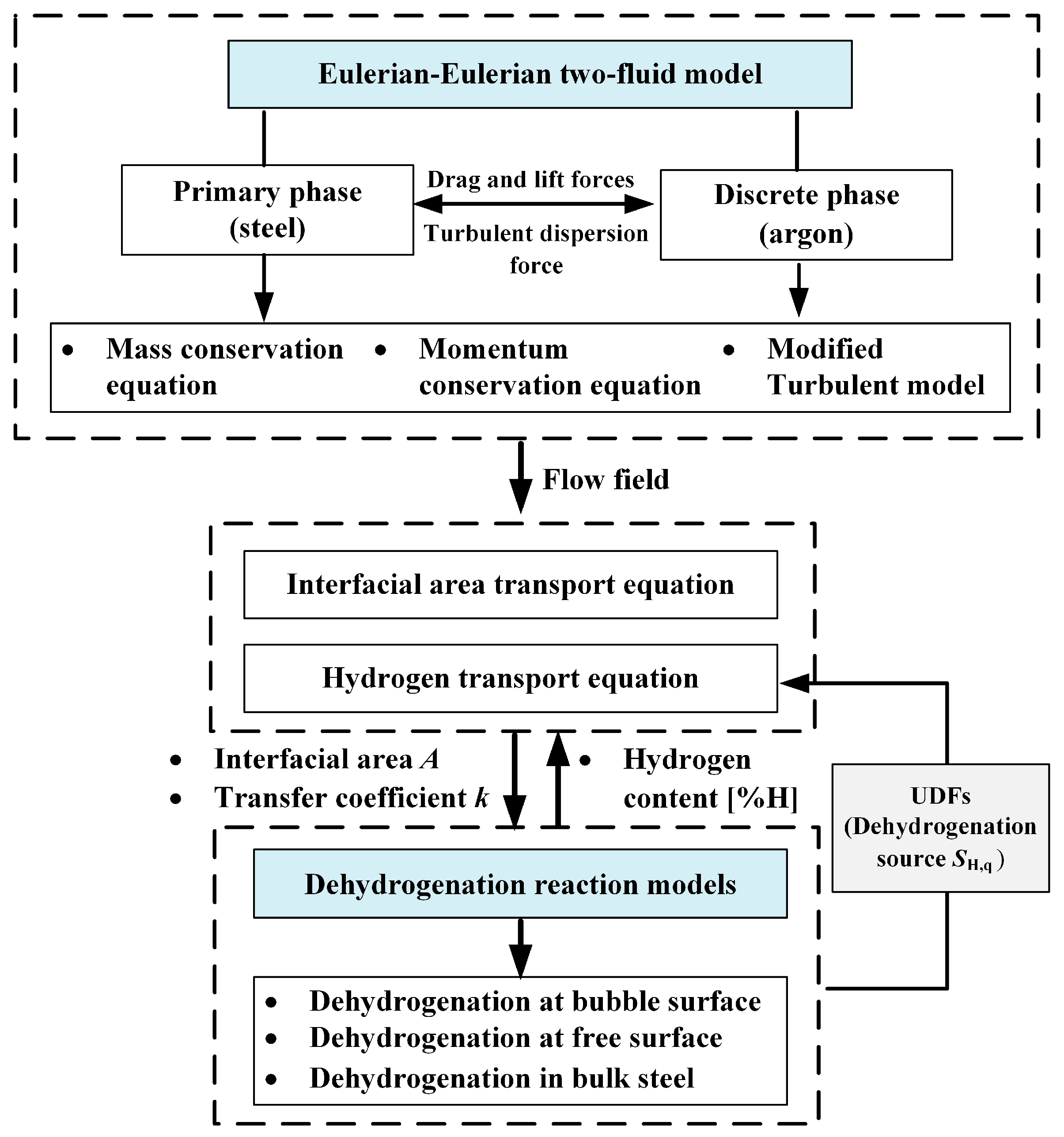

| Continuity equation | αq—volume fraction of phase q ρq—density of phase q uq—velocity of phase q p—pressure g—acceleration of gravity μeff—effective viscosity, μt—turbulent viscosity, μl—molecular viscosity Fpq—interfacial force Fdrag, Flift, FTD—drag, lift, and turbulent dispersion forces, respectively CL—lift coefficient, CL = 0.1 CD—drag coefficient db—bubble diameter Re—Reynolds number λRT—Rayleigh–Taylor instability wavelength | |
| Momentum equation | ||
| Turbulence model | Gk—production of turbulence kinetic energy Sk, Sε—source terms C1ε = 1.44, C2ε = 1.92 σk = 1.0, σε = 1.3 Ck1 = 6.0, Ck2 = 0.75 Cε1 = 4.0, Cε2 = 0.6 | |
| Hydrogen transport equation | Yi,q—mass fraction of hydrogen JH,q—diffusive flux SH,q—source term | |
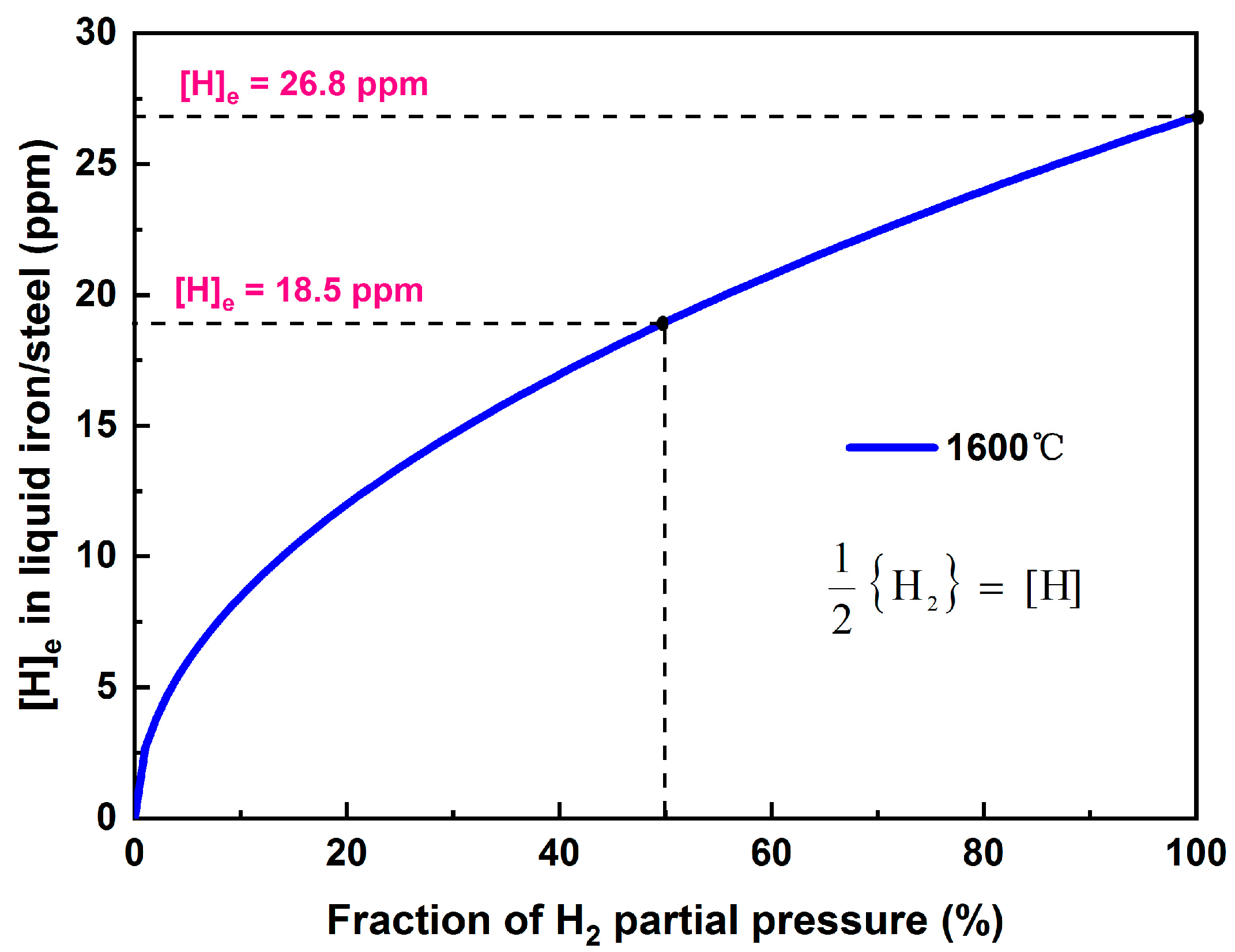
| Dehydrogenation rate at bubble surface | A—argon bubble surface area kH—mass transfer coefficient W—weight of liquid steel N—number of argon bubbles [%H]—hydrogen content in steel [%H]eq—equilibrium hydrogen content hcri—critical bath depth for nucleation | |
| Dehydrogenation rate at steel surface | ||
| Dehydrogenation rate in bulk steel |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, B.; Li, M.; Yang, Y.; Shao, L.; Zou, Z. Efficiently Removing Hydrogen of H-Supersaturated Liquid Steel in the Vacuum Degasser with Various Gas Injection Modes. Metals 2023, 13, 1229. https://doi.org/10.3390/met13071229
Dai B, Li M, Yang Y, Shao L, Zou Z. Efficiently Removing Hydrogen of H-Supersaturated Liquid Steel in the Vacuum Degasser with Various Gas Injection Modes. Metals. 2023; 13(7):1229. https://doi.org/10.3390/met13071229
Chicago/Turabian StyleDai, Bing, Mingming Li, Yu Yang, Lei Shao, and Zongshu Zou. 2023. "Efficiently Removing Hydrogen of H-Supersaturated Liquid Steel in the Vacuum Degasser with Various Gas Injection Modes" Metals 13, no. 7: 1229. https://doi.org/10.3390/met13071229
APA StyleDai, B., Li, M., Yang, Y., Shao, L., & Zou, Z. (2023). Efficiently Removing Hydrogen of H-Supersaturated Liquid Steel in the Vacuum Degasser with Various Gas Injection Modes. Metals, 13(7), 1229. https://doi.org/10.3390/met13071229







