Experimental and Numerical Investigation of the Buckling Behavior and Strength of Combined Opening Plate Girders in Passenger Ships
Abstract
:1. Introduction
2. Experimental Design
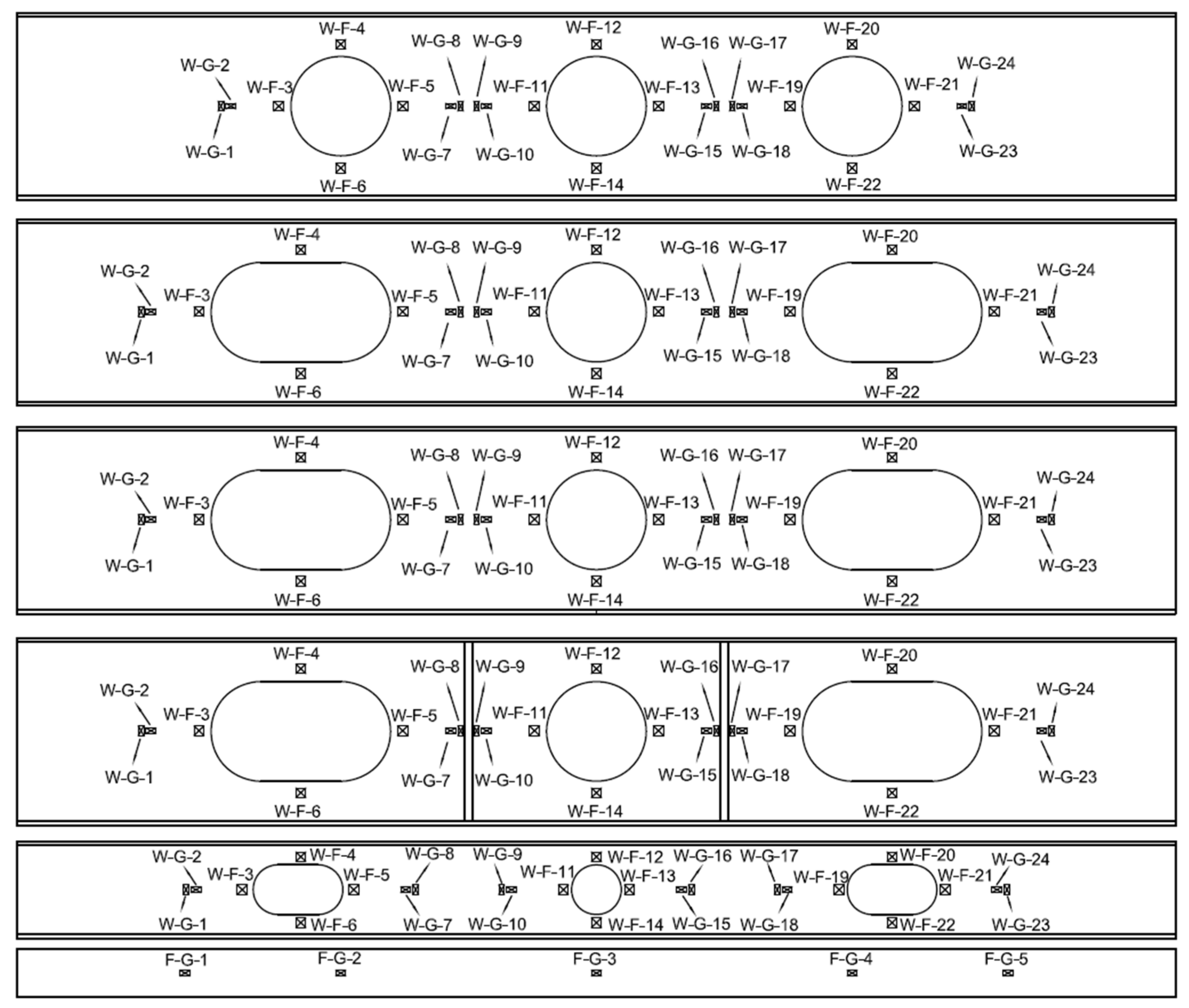
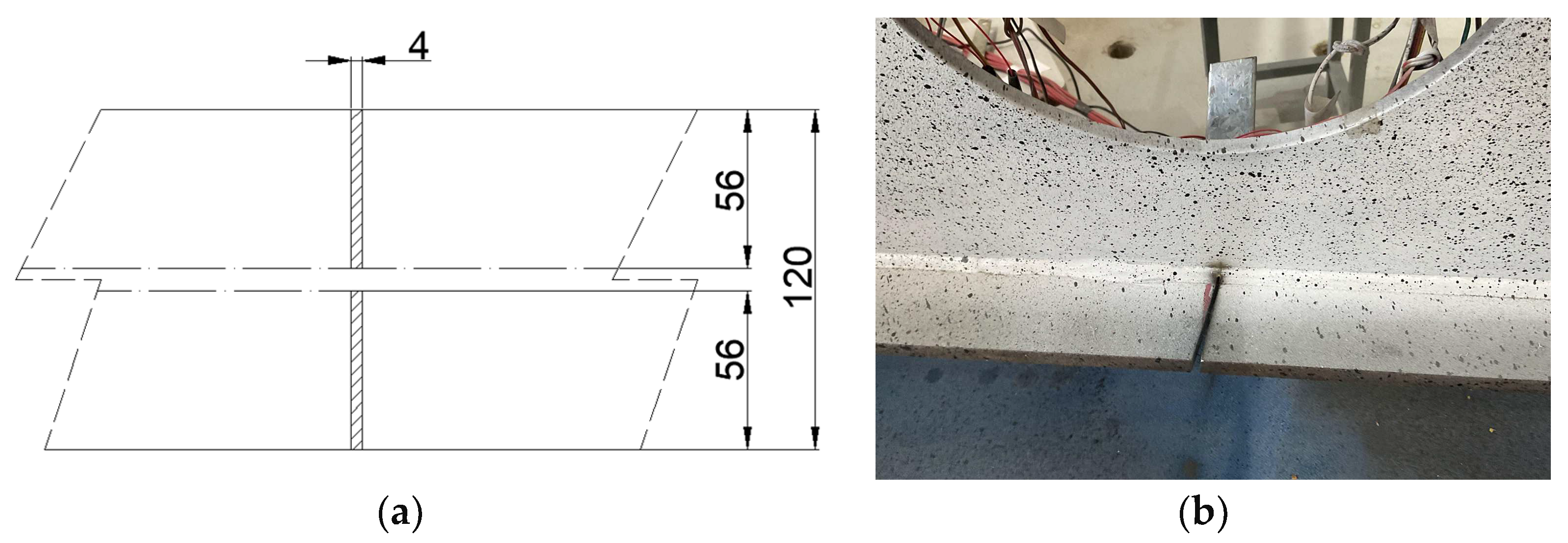
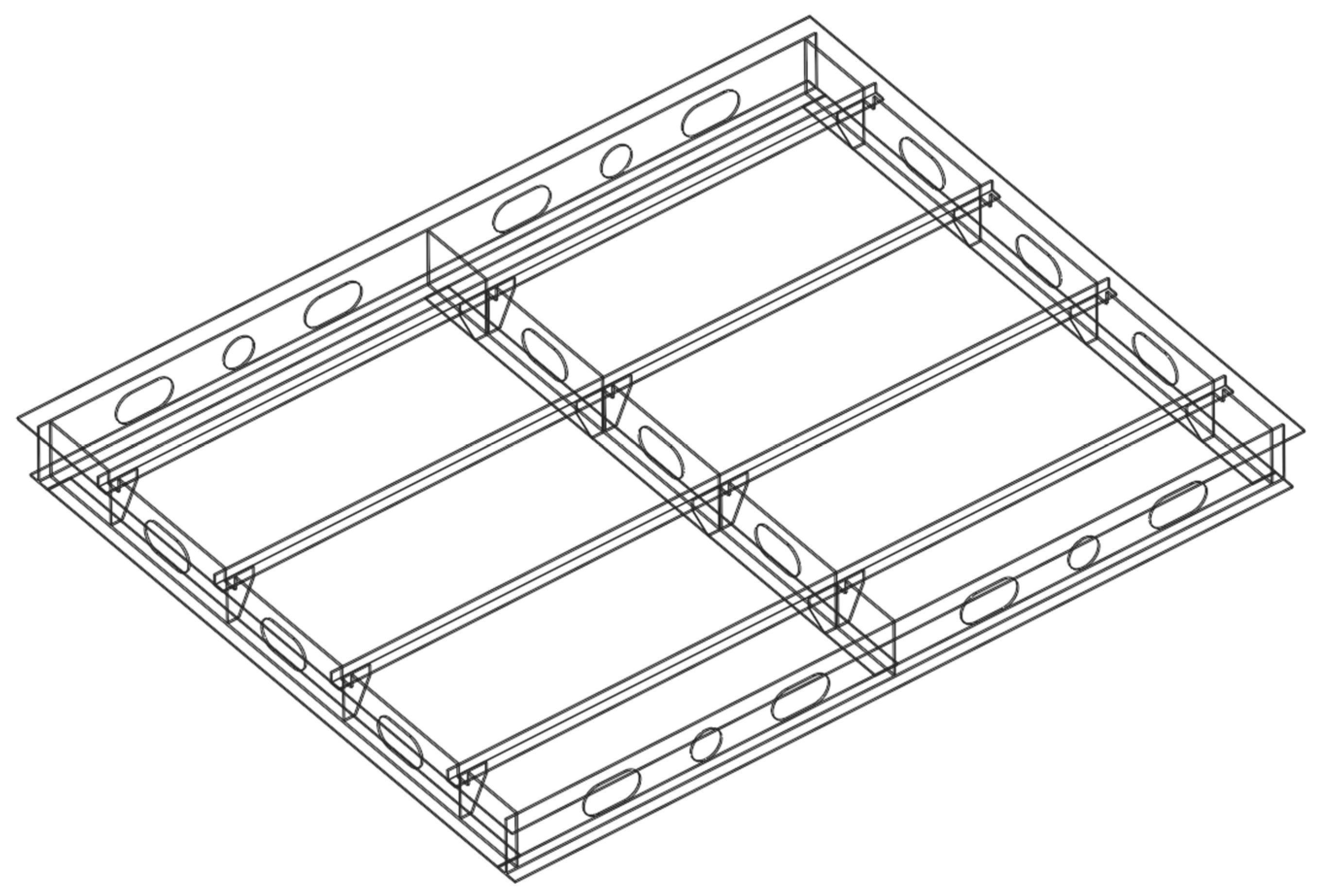
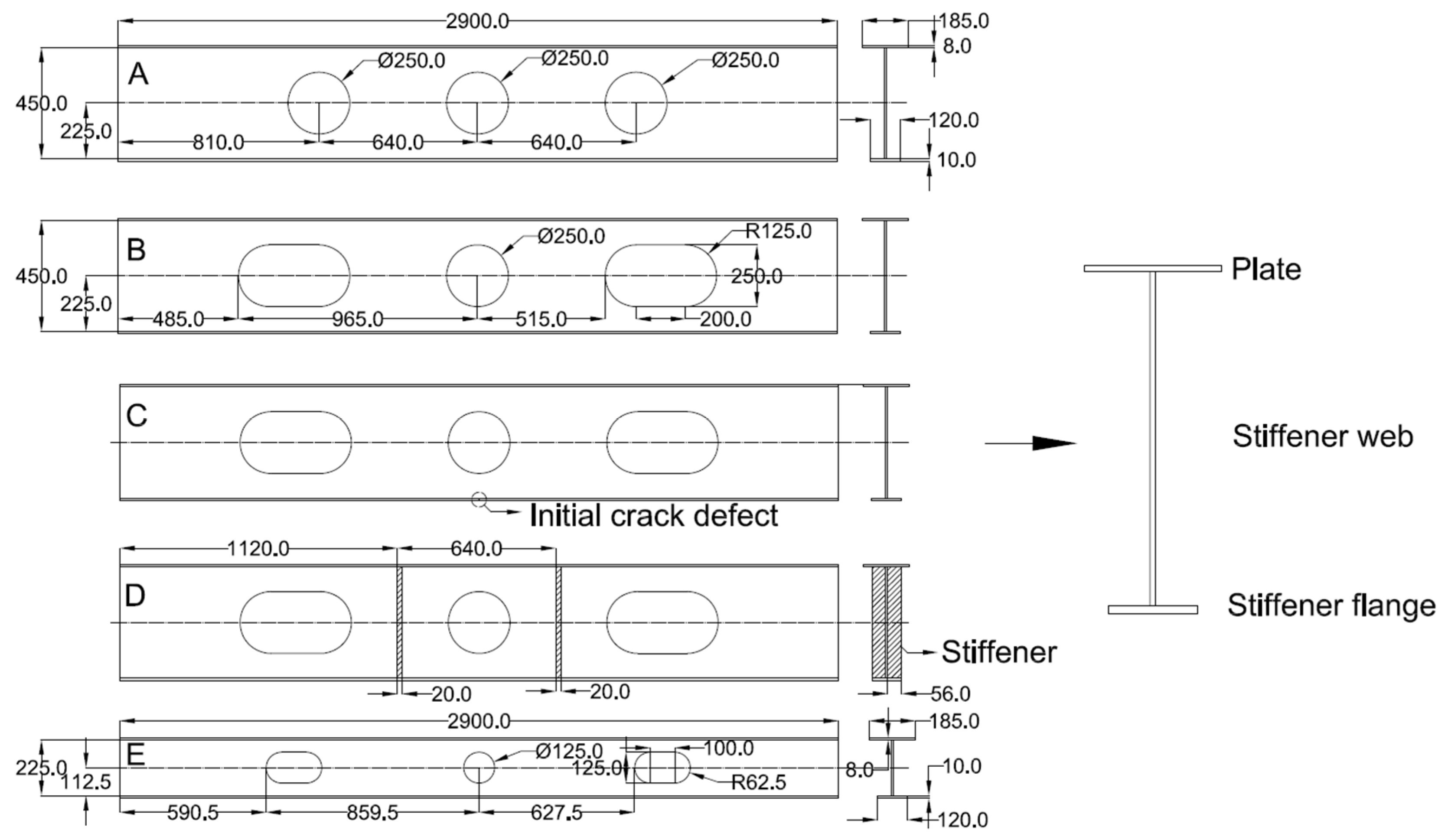
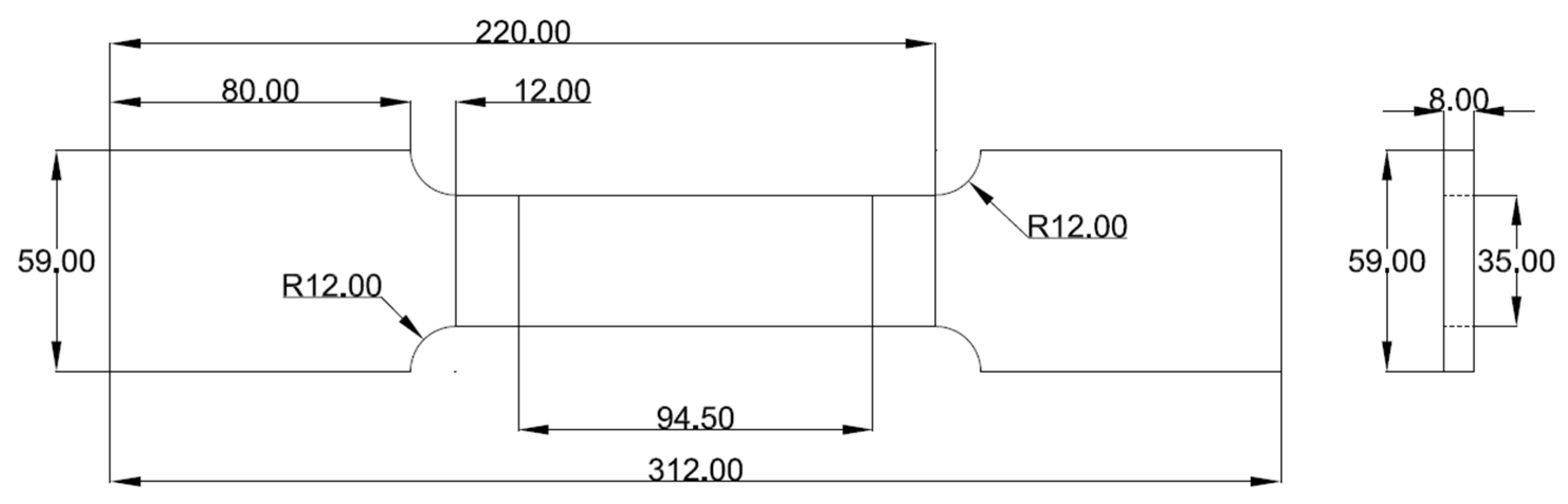
2.1. Specimen
2.2. Experimental Design
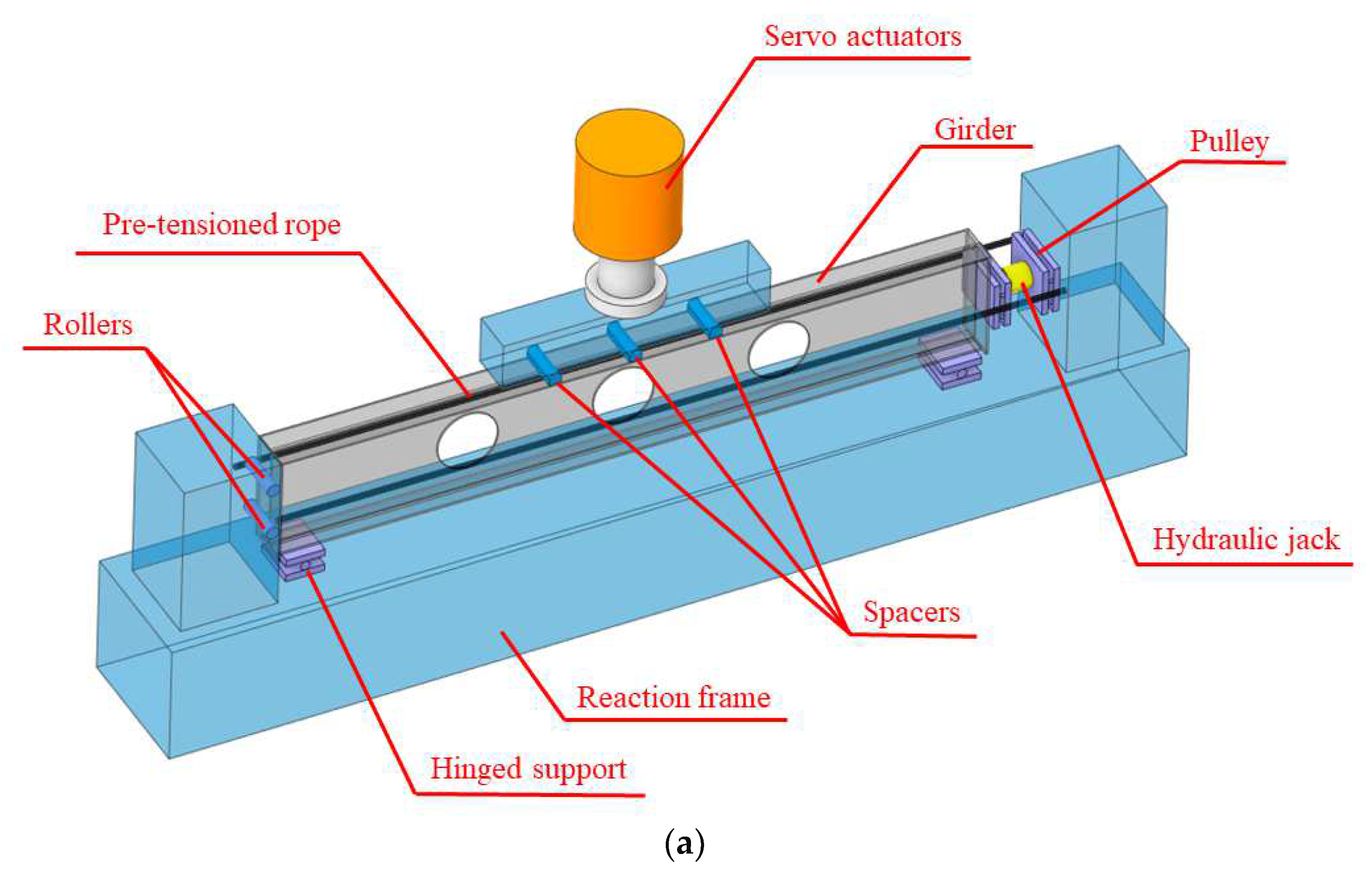
2.2.1. Equipment Arrangement
2.2.2. Material Properties
3. Experimental Results and Numerical Comparison
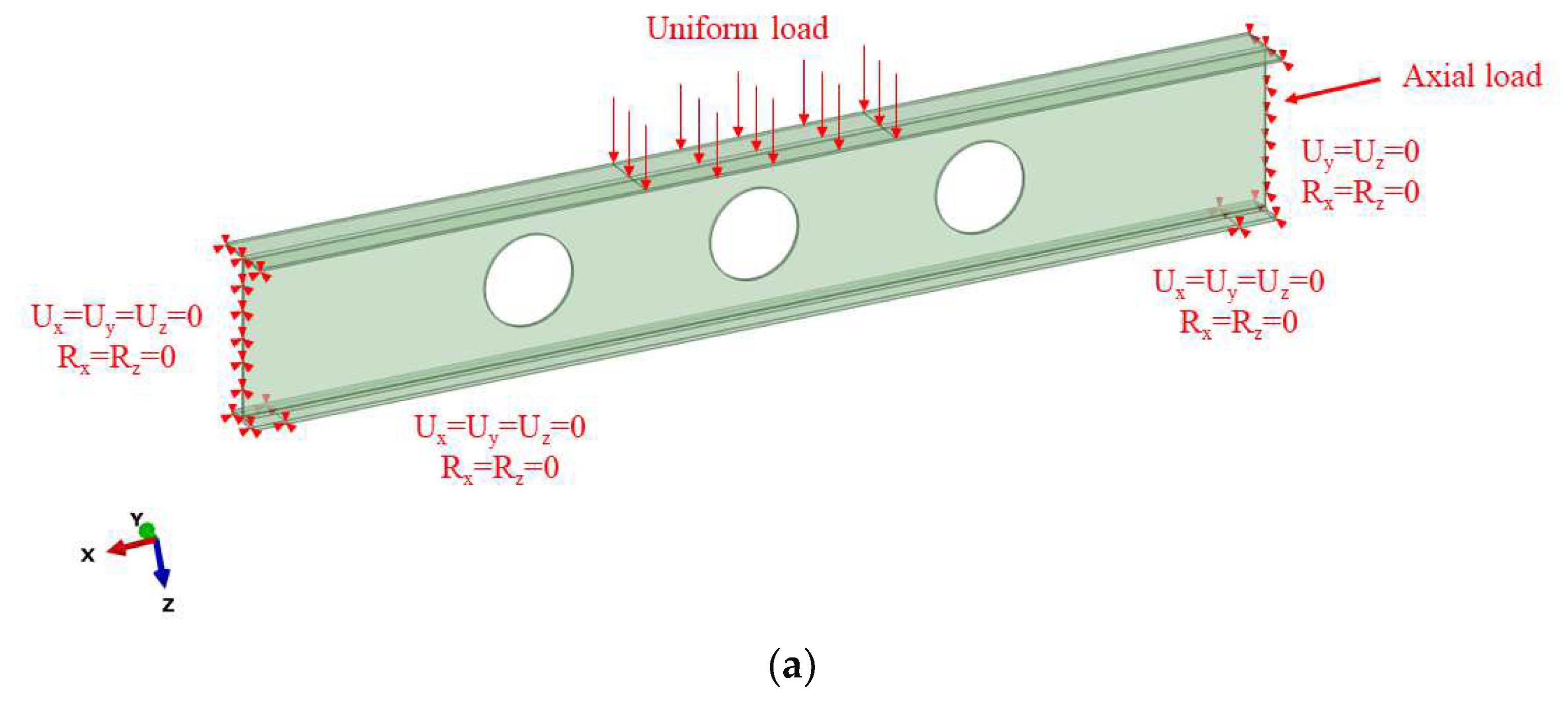
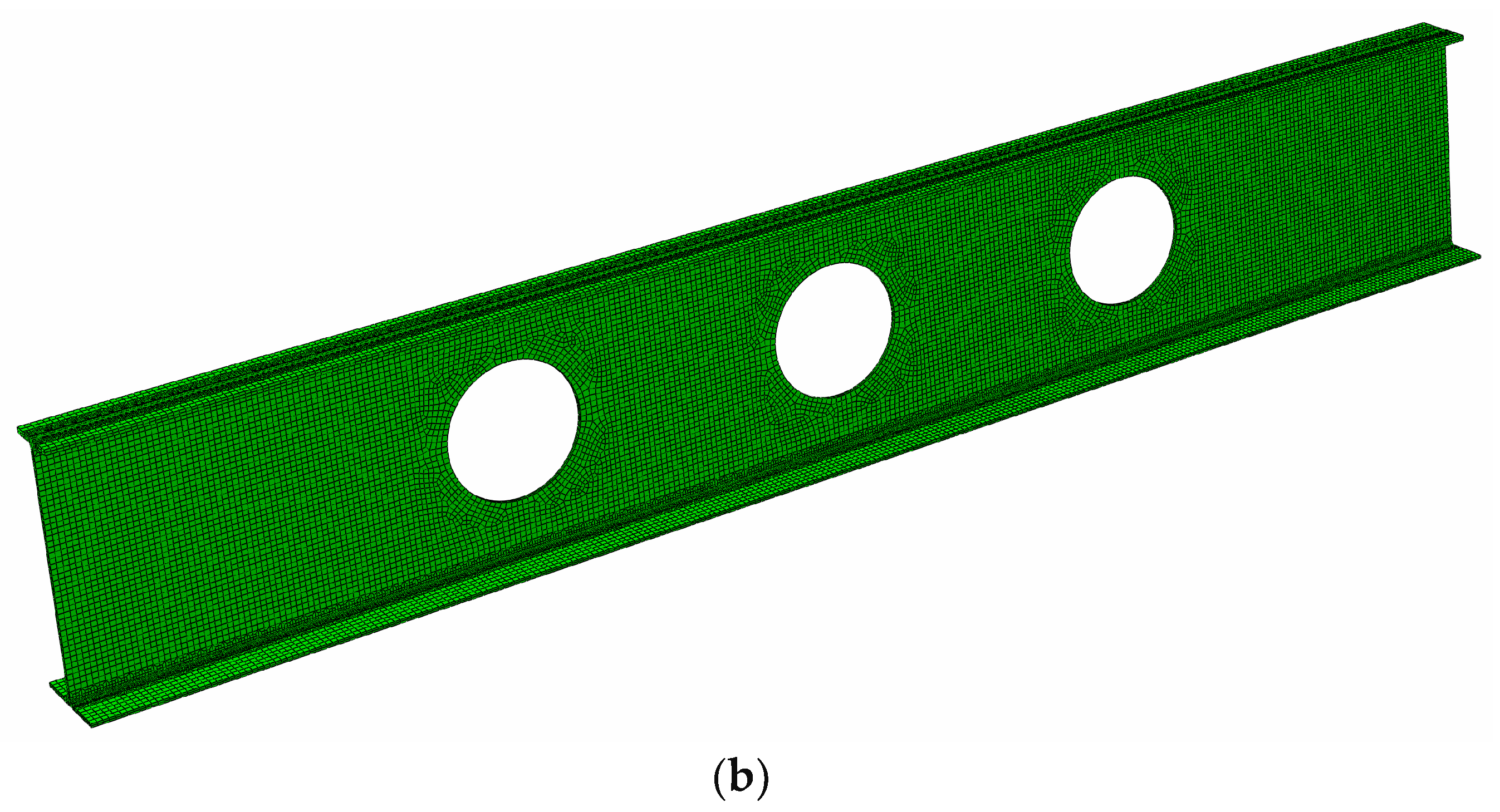
3.1. Numerical Simulation Settings
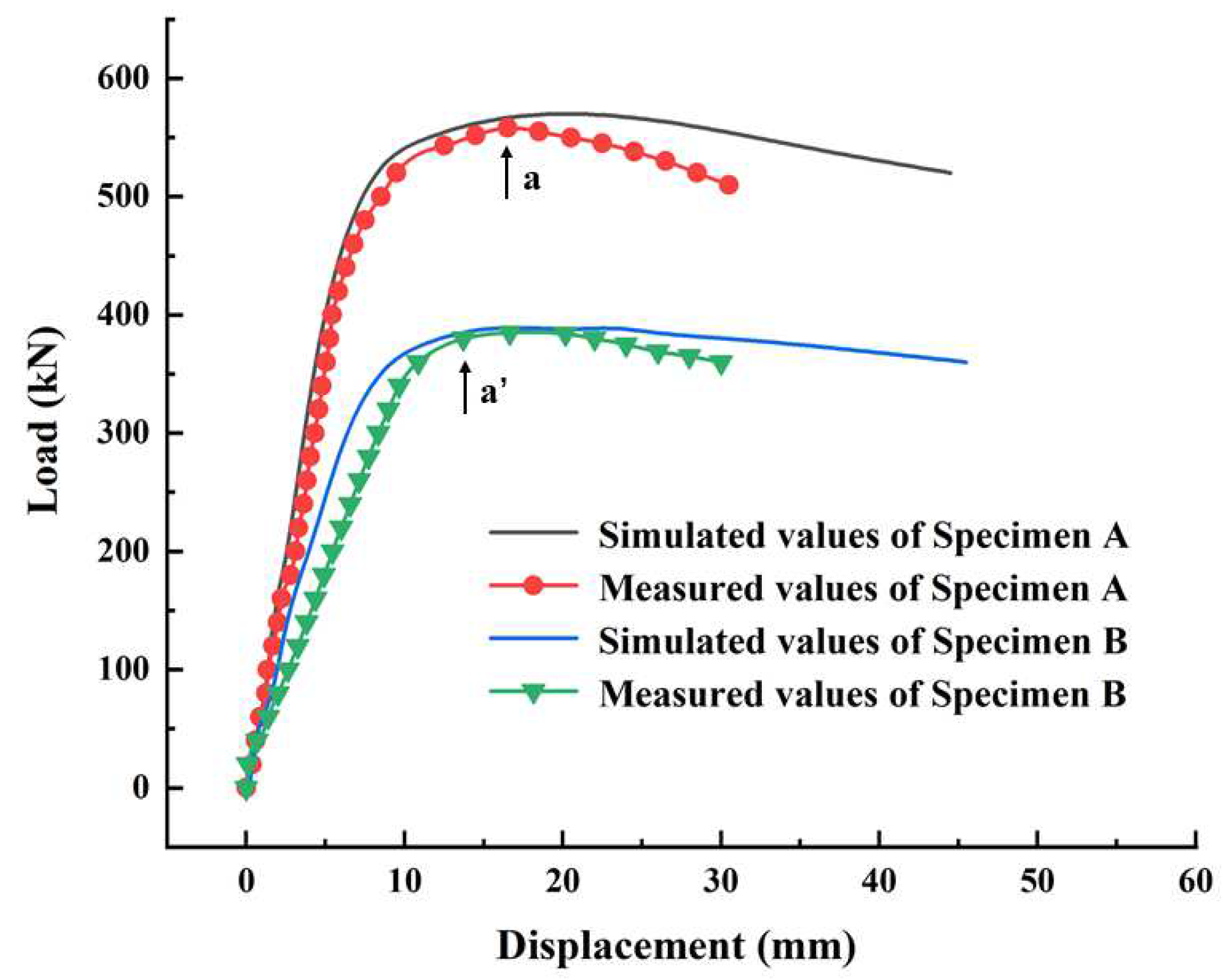
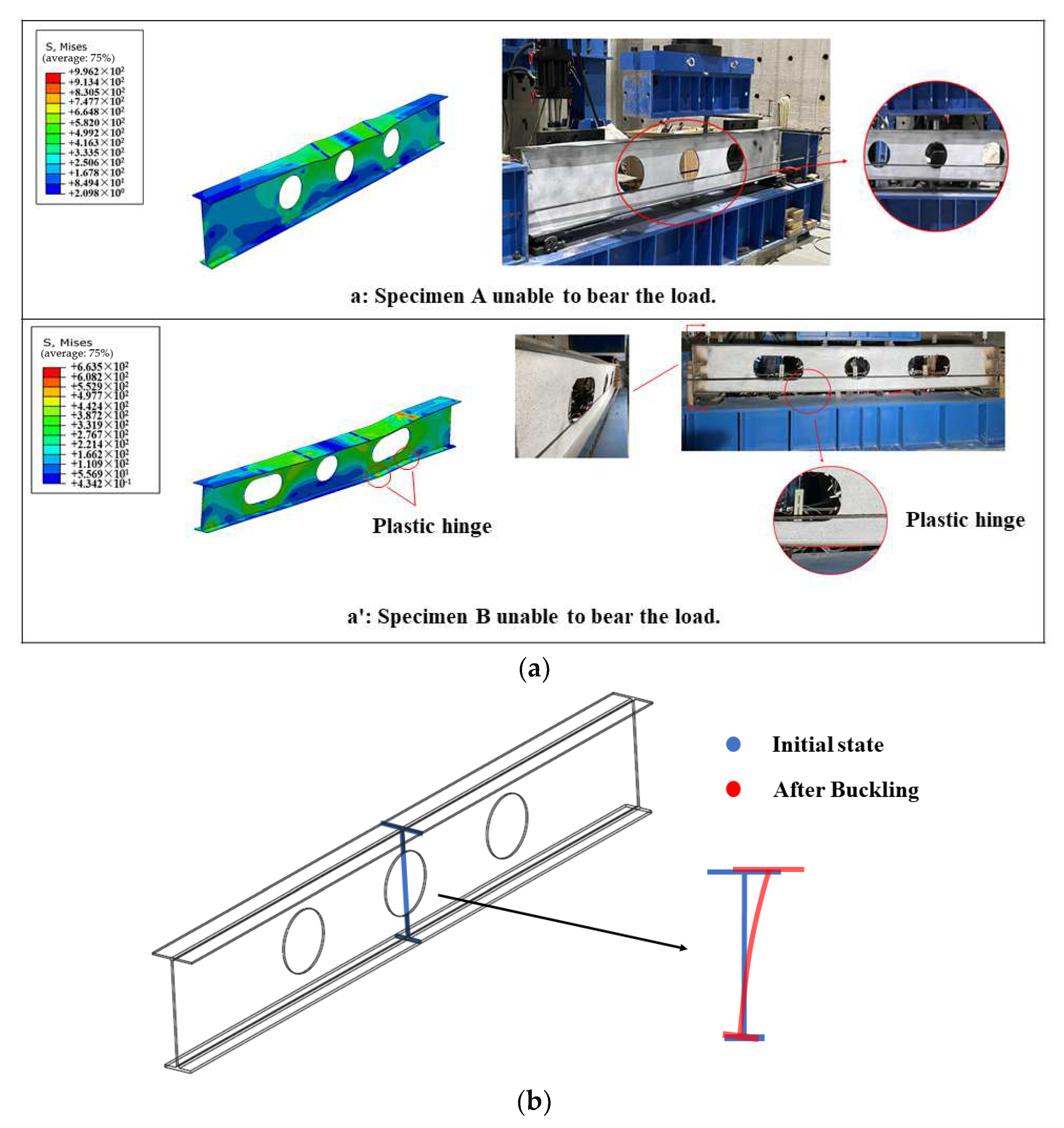
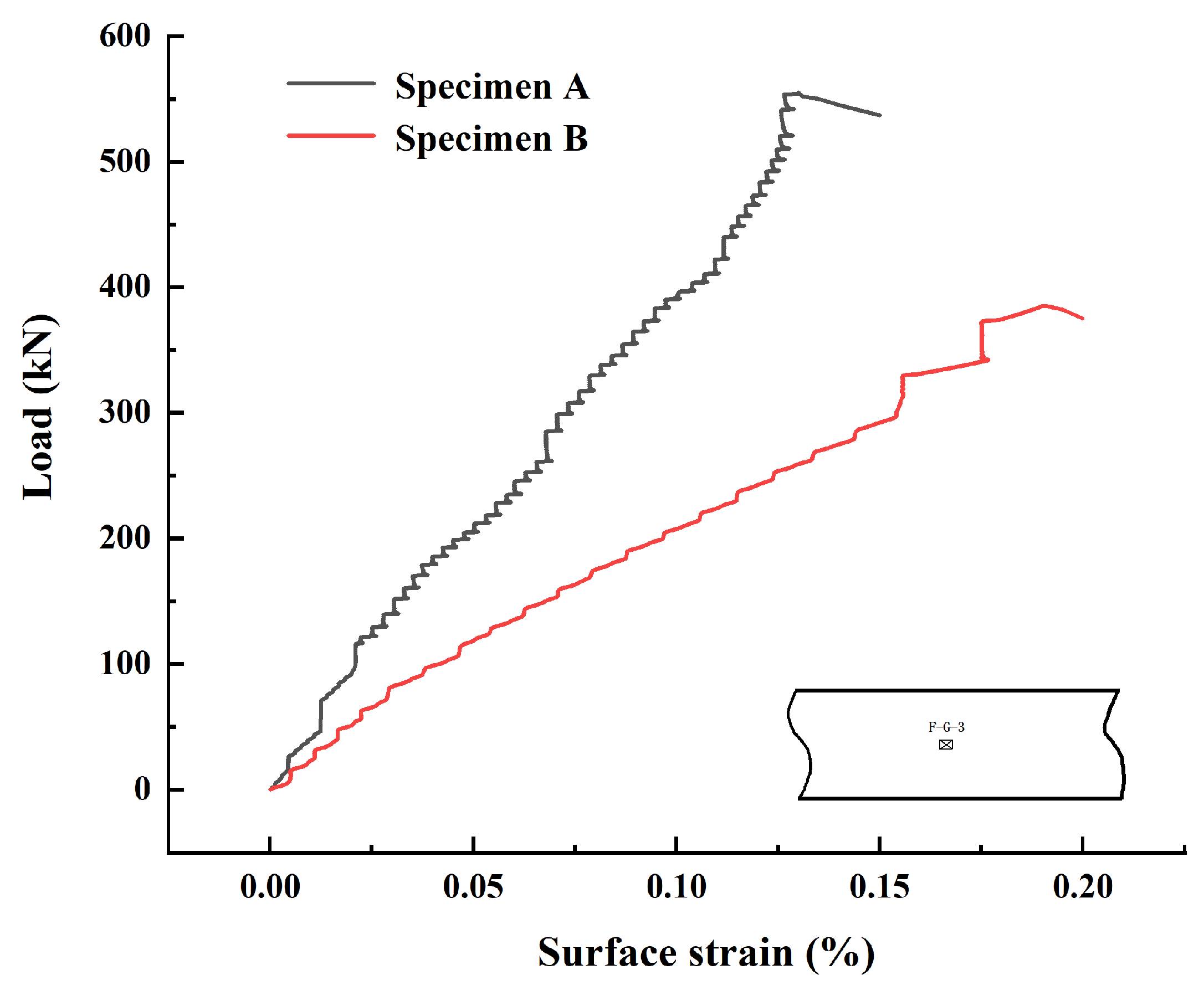
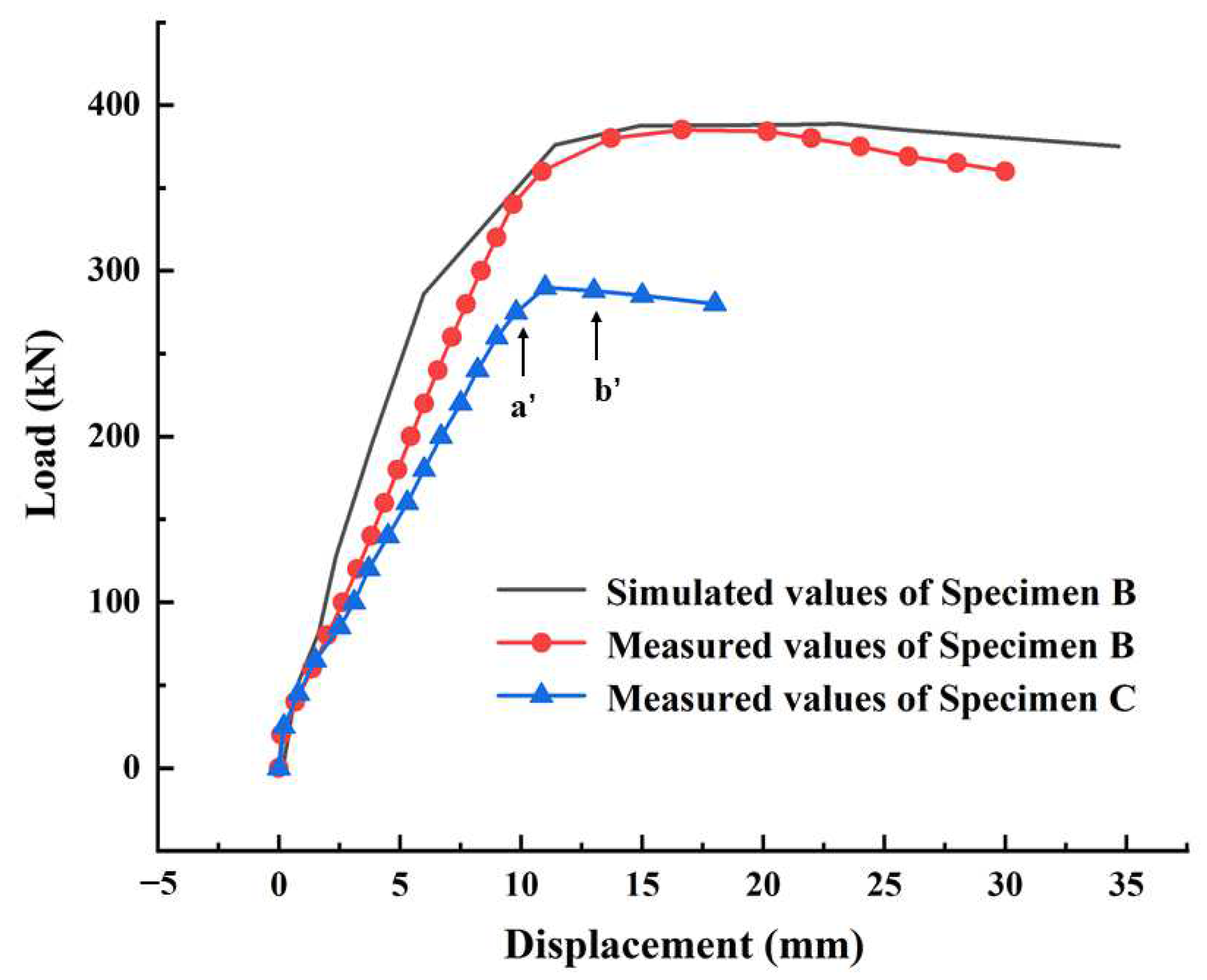
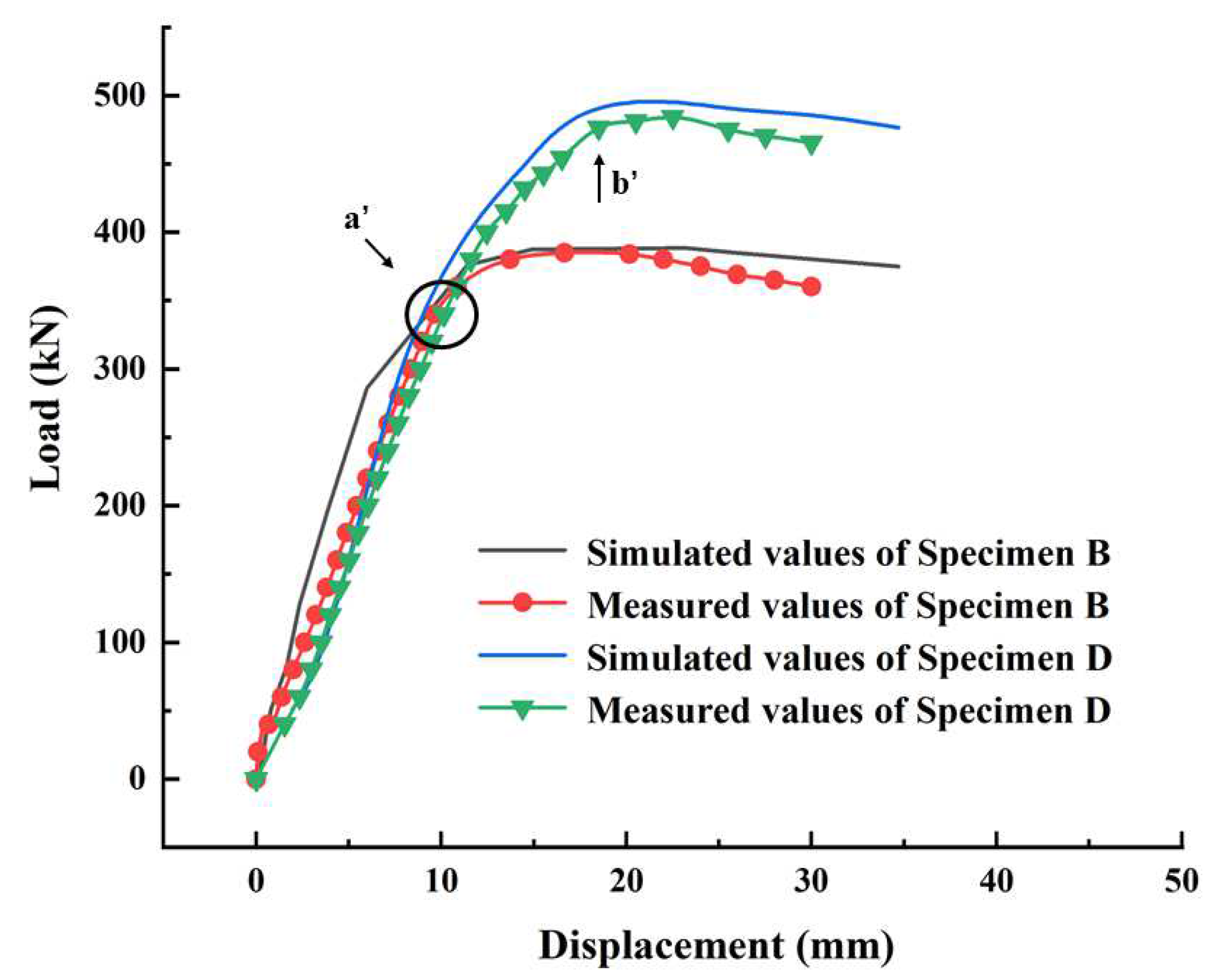
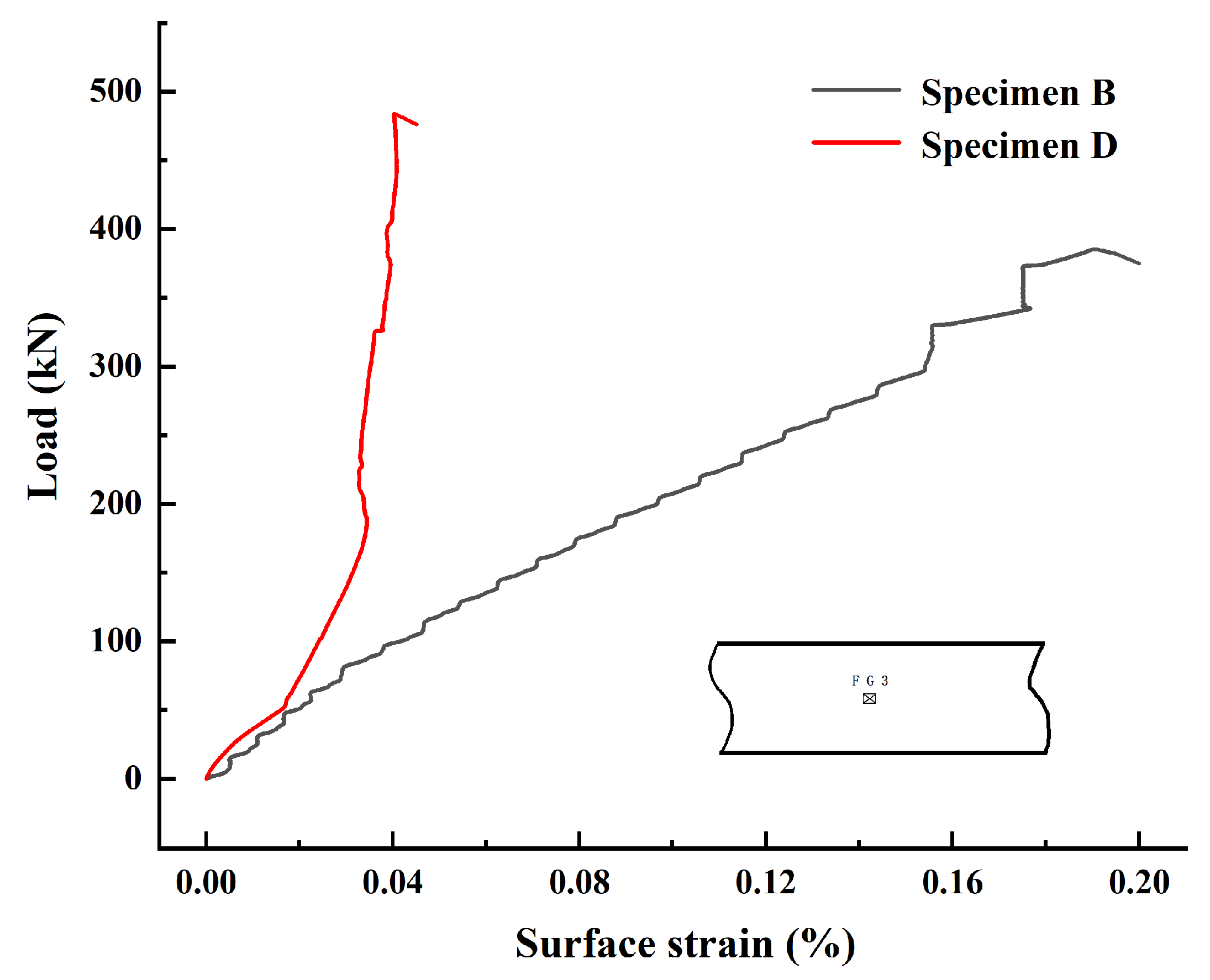
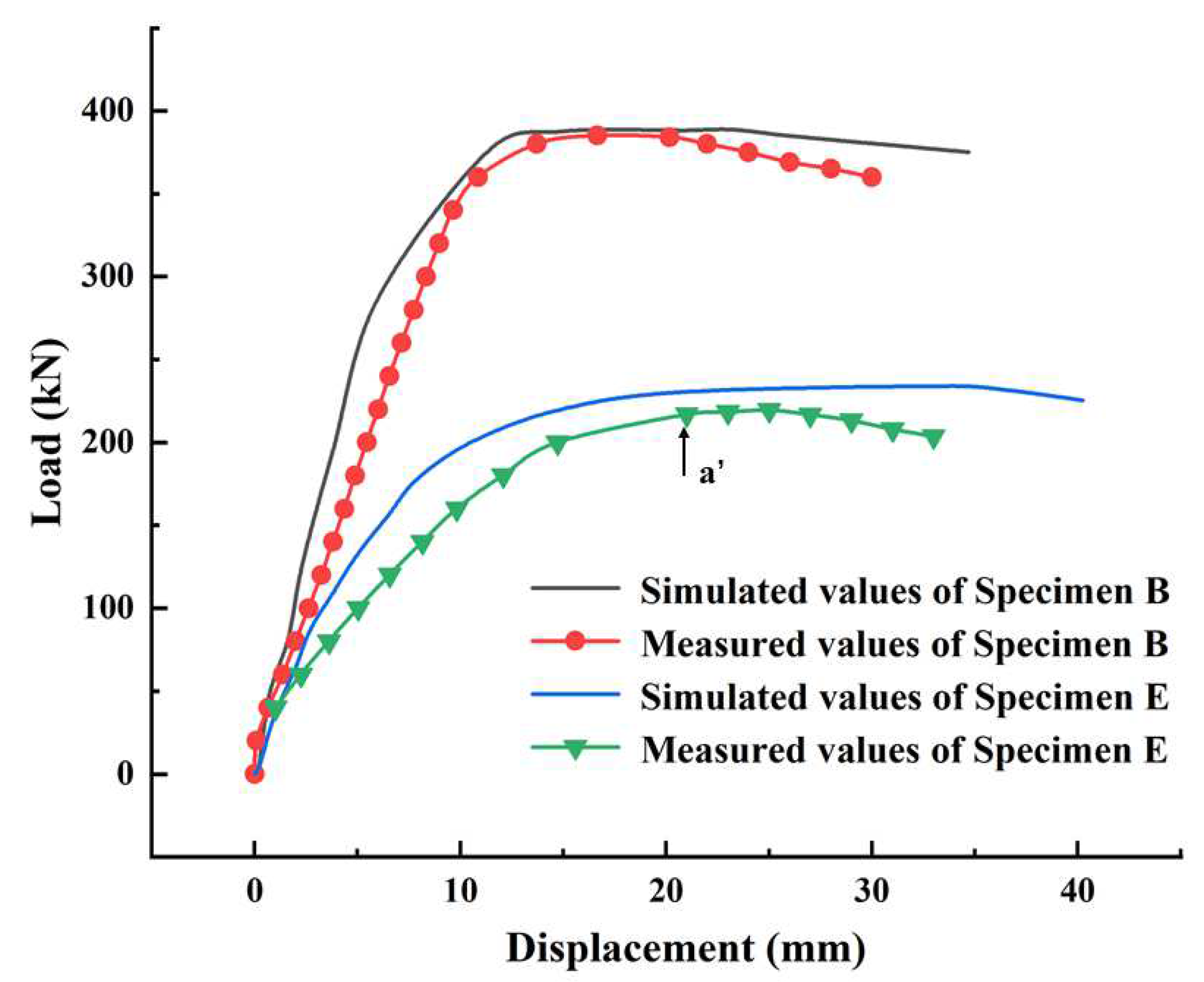
3.2. Effect of the Combined Opening Shapes
3.3. Effect of the Initial Crack Defects
3.4. Effect of the Strengthening Stiffeners
3.5. Effect of the Stiffener Web Height
4. Numerical Investigation of the Buckling Behavior of Combined Opening Plate Frame
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Andric, J.; Prebeg, P.; Palaversa, M.; Zanic, V. Influence of different topological variants on optimized structural scantlings of passenger ship. Mar. Struct. 2021, 78, 102981. [Google Scholar] [CrossRef]
- Yang, B.; Pei, Z.; Wu, W. Stress-distribution characteristics of cruise ship based on multiple-beam method. Ocean. Eng. 2022, 266, 112646. [Google Scholar] [CrossRef]
- Liu, B.; Yao, X.; Lin, Y.; Wu, W.; Guedes Soares, C. Experimental and numerical analysis of ultimate compressive strength of long-span stiffened panels. Ocean. Eng. 2021, 237, 109633. [Google Scholar] [CrossRef]
- Zhang, Z.; Gan, J.; Guo, G.; Wu, W. Research on the buckling characteristics of opening high web plate frame structures for large cruise ships. China Shipbuild. 2022, 63, 15–23. [Google Scholar]
- Zheng, H.; Qiao, H.; Chen, Y.; Yang, B.; Zhu, B.; Lai, L. Study on anti-progressive collapse performance of cellular steel frames with different web opening shapes. Structures 2023, 47, 338–357. [Google Scholar] [CrossRef]
- Peng, Y.; Kong, Z.; Dinh, B.H.; Nguyen, H.-H.; Cao, T.-S.; Papazafeiropoulos, G.; Vu, Q.-V. Web Bend-Buckling of Steel Plate Girders Reinforced by Two Longitudinal Stiffeners with Various Cross-Section Shapes. Metals 2023, 13, 323. [Google Scholar] [CrossRef]
- Sujitha, R.; Sunmathi, N.; Manikandan, R.K.; Arunprasad, J.; Rajkumar, S.; Sharma, S.; Sharma, K.; Li, C.; Tag Eldin, E.M. Analytical and Experimental Study on Cold-Formed Steel Built-Up Sections for Bending. Materials 2022, 15, 7140. [Google Scholar] [CrossRef]
- Brown, C.J.; Yettram, A.L. The elastic stability of square perforated plates under combinations of bending, shear and direct load. Thin-Walled Struct. 1986, 4, 239–246. [Google Scholar] [CrossRef]
- Brown, C. Elastic buckling of perforated plates subjected to concentrated loads. Comput. Struct. 1990, 36, 1103–1109. [Google Scholar] [CrossRef]
- Shakerley, T.; Brown, C. Elastic buckling of plates with eccentrically positioned rectangular perforations. Int. J. Mech. Sci. 1996, 38, 825–838. [Google Scholar] [CrossRef]
- Wang, G.; Sun, H.; Peng, H.; Uemori, R. Buckling and ultimate strength of plates with openings. Ships Offshore Struct. 2009, 4, 43–53. [Google Scholar] [CrossRef]
- Shanmugam, N.E.; Thevendran, V.; Tan, Y.H. Design formula for axially compressed perforated plates. Thin-Walled Struct. 1999, 4, 1–20. [Google Scholar] [CrossRef]
- Shanmugam, N.E.; Lian, V.T.; Thevendran, V. Finite element modelling of plate girders with web openings. Thin-Walled Struct. 2002, 40, 443–464. [Google Scholar] [CrossRef]
- El-Sawy, K.M.; Nazmy, A.S.; Martini, M.I. Elasto-plastic buckling of perforated plates under uniaxial compression. Thin-Walled Struct. 2004, 42, 1083–1101. [Google Scholar] [CrossRef]
- Paik, J.K. Ultimate strength of perforated steel plates under edge shear loading. Thin-Walled Struct. 2007, 45, 301–306. [Google Scholar] [CrossRef]
- Paik, J.K. Ultimate strength of steel plates with a single circular hole under axial compressive loading along short edges. Ships Offshore Struct. 2007, 2, 355–360. [Google Scholar] [CrossRef]
- Paik, J.K. Ultimate strength of perforated steel plates under combined biaxial compression and edge shear loads. Thin-Walled Struct. 2008, 46, 207–213. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Soares, C.G. Strength Assessment of Wash Plates Subjected to Combined Lateral and Axial. In Maritime Technology and Engineering; Taylor & Francis Group: London, UK, 2015; pp. 553–564. [Google Scholar]
- Saad-Eldeen, S.; Garbatov, Y.; Soares, C.G. Experimental investigation on the residual strength of thin steel plates with a central elliptic opening and locked cracks. Ocean Eng. 2016, 115, 19–29. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Soares, C.G. Experimental strength analysis of steel plates with a large circular opening accounting for corrosion degradation and cracks subjected to compressive load along the short edges. Mar. Struct. 2016, 48, 52–67. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Soares, C.G. Experimental compressive strength analyses of high tensile steel thin-walled stiffened panels with a large lightening opening. Thin-Walled Struct. 2017, 113, 61–68. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Soares, C.G. Buckling collapse tests of deteriorated steel plates with multiple circular openings. Ocean Eng. 2019, 172, 523–530. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Soares, C.G. Experimental failure assessment of high tensile stiffened plates with openings. Eng. Struct. 2020, 206, 110–121. [Google Scholar] [CrossRef]
- Moen, C.D.; Schafer, B.W. Elastic buckling of thin plates with holes in compression or bending. Thin-Walled Struct. 2009, 47, 1597–1607. [Google Scholar] [CrossRef]
- Chung, K.F.; Liu, C.H.; Ko, A.C.H. Steel beams with large web openings of various shapes and sizes: An empirical design method using a generalised moment-shear interaction curve. J. Constr. Steel Res. 2003, 59, 1177–1200. [Google Scholar] [CrossRef]
- Chung, K.F.; Liu, C.H.; Ko, A.C.H. Investigation on Vierendeel mechanism in steel beams with circular web openings. J. Constr. Steel Res. 2001, 57, 467–490. [Google Scholar] [CrossRef]
- Yingjiang, Z.; Renjun, Y.; Hongxu, W. Experimental and numerical investigations on plate girders with perforated web under axial compression and bending moment. Thin-Walled Struct. 2015, 97, 199–206. [Google Scholar] [CrossRef]
- Yingjiang, Z.; Renjun, Y.; Hongxu, W. Experimental Studies of Failure Behavior and Strength of H Beams with Stiffened Web Openings under Compression and Bending Loads. J. Ship Mech. 2016, 20, 315–322. [Google Scholar]
- Shen, W.; Zhao, Y.; Li, L.; Qiu, Y.; Liu, E. Assessment of residual ultimate strength on plate girders with web opening under compression-bending loadings. Ocean Eng. 2019, 187, 106147. [Google Scholar] [CrossRef]
- GB-T 228.1-2021; Tensile Testing of Metallic Materials Part 1: Room Temperature Test Method. National Standardization Management Committee: Beijing, China, 2021.
- Dieffenbach, T.; Treutler, K.; Wesling, V. High-speed tensile tests on high-manganese steel at low temperatures. Mater. Test. 2023, 65, 124–133. [Google Scholar] [CrossRef]


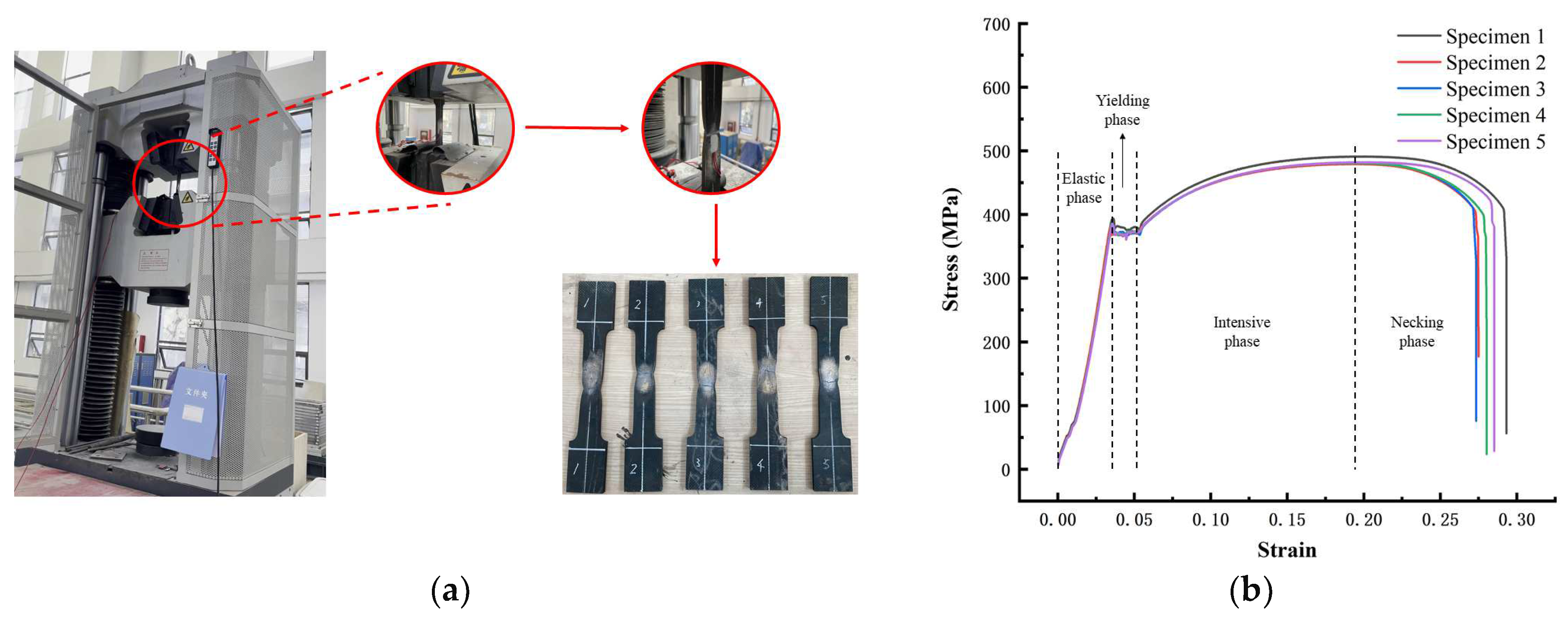



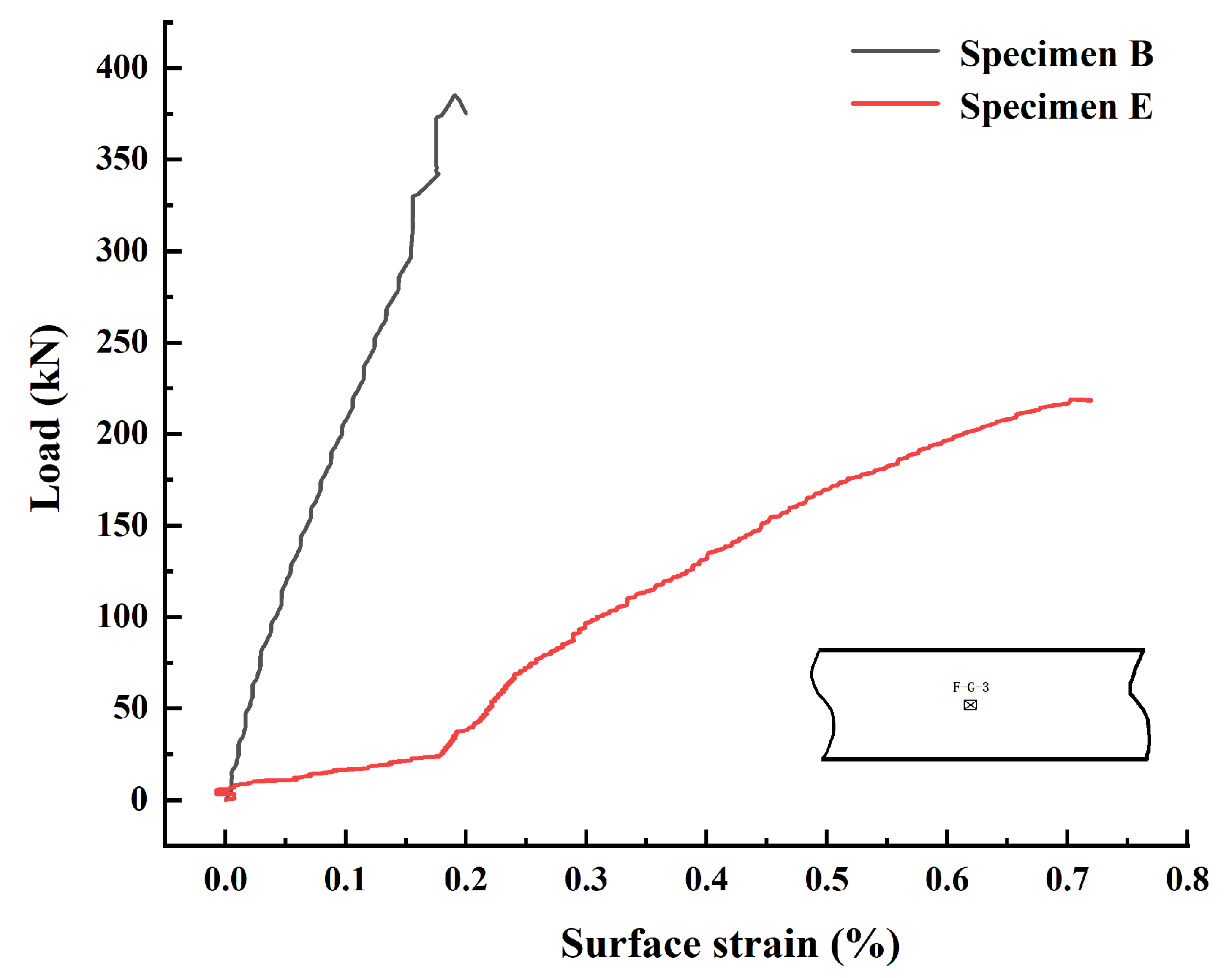
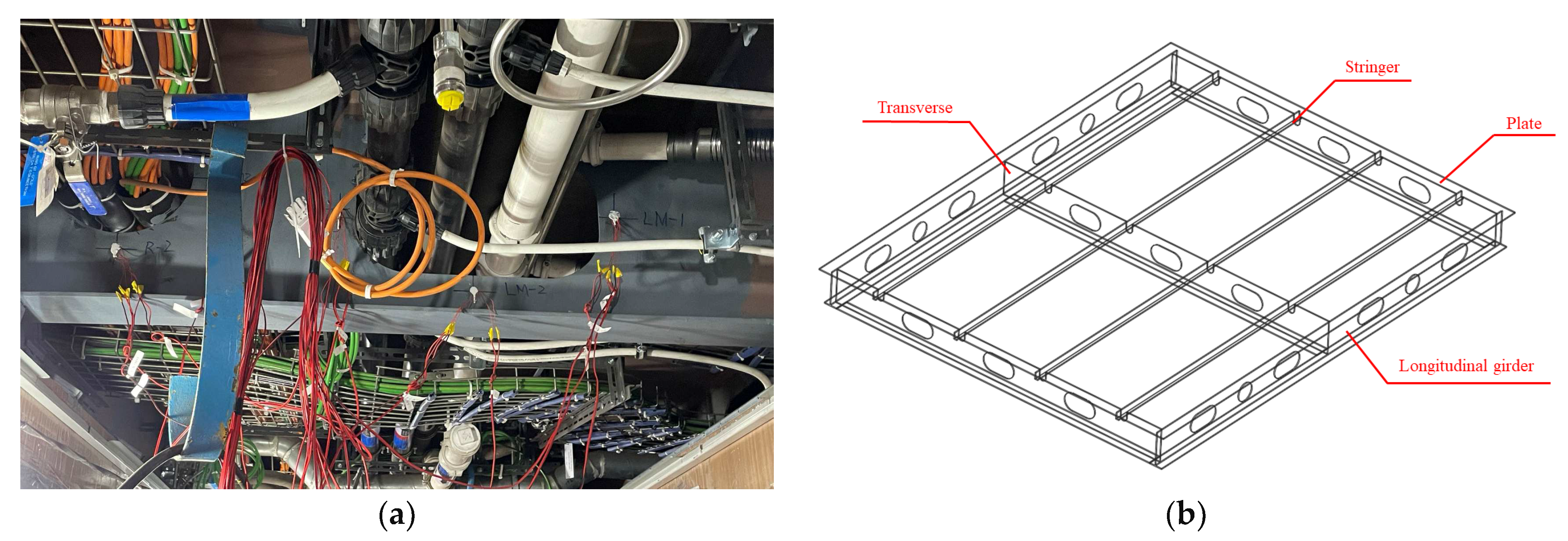
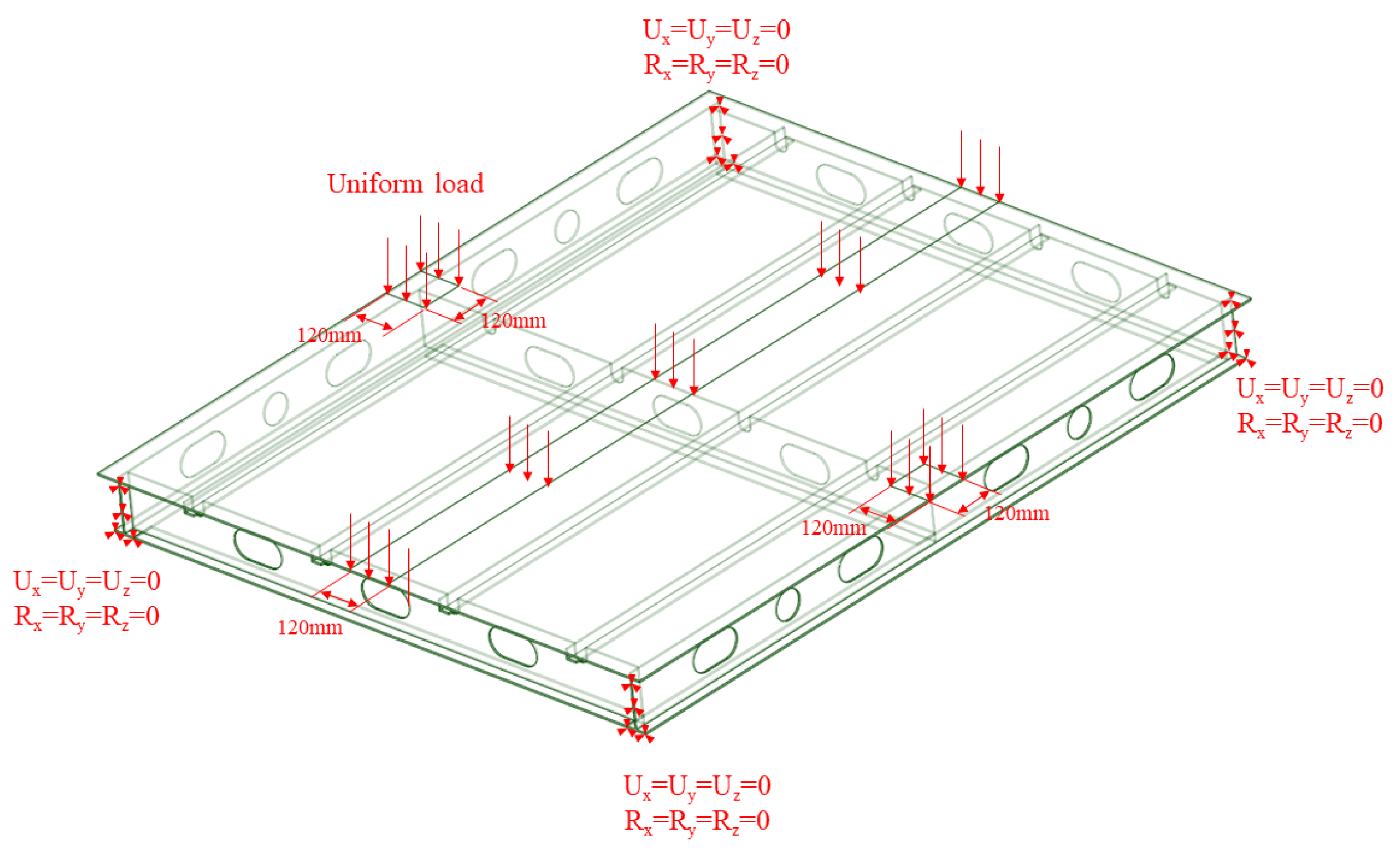

| No. | (%) | ||
|---|---|---|---|
| 1 | 383 | 490 | 26.98 |
| 2 | 372 | 479 | 25.93 |
| 3 | 377 | 480 | 24.87 |
| 4 | 376 | 480 | 27.51 |
| 5 | 371 | 482 | 26.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Zhou, H.; Lv, Z.; Ge, X.; Xu, X. Experimental and Numerical Investigation of the Buckling Behavior and Strength of Combined Opening Plate Girders in Passenger Ships. Metals 2023, 13, 1256. https://doi.org/10.3390/met13071256
Chen C, Zhou H, Lv Z, Ge X, Xu X. Experimental and Numerical Investigation of the Buckling Behavior and Strength of Combined Opening Plate Girders in Passenger Ships. Metals. 2023; 13(7):1256. https://doi.org/10.3390/met13071256
Chicago/Turabian StyleChen, Chen, Hong Zhou, Zhengda Lv, Xi Ge, and Xiao Xu. 2023. "Experimental and Numerical Investigation of the Buckling Behavior and Strength of Combined Opening Plate Girders in Passenger Ships" Metals 13, no. 7: 1256. https://doi.org/10.3390/met13071256
APA StyleChen, C., Zhou, H., Lv, Z., Ge, X., & Xu, X. (2023). Experimental and Numerical Investigation of the Buckling Behavior and Strength of Combined Opening Plate Girders in Passenger Ships. Metals, 13(7), 1256. https://doi.org/10.3390/met13071256






