Numerical Investigation of Residual Stress Formation Mechanisms in Flash-Butt Welded Rail
Abstract
1. Introduction
2. Material and Methods
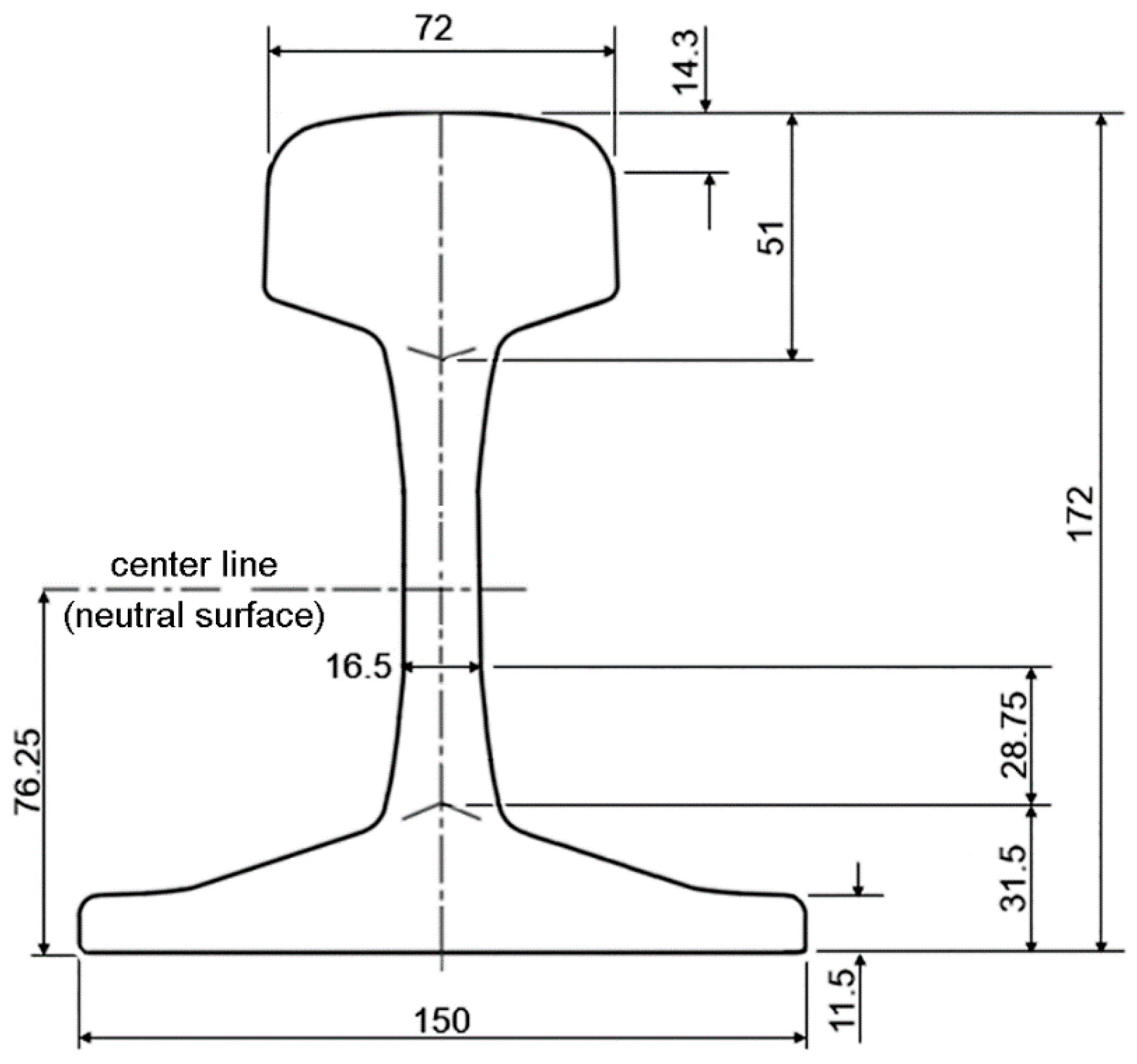
2.1. Flash-Butt Welded Rail
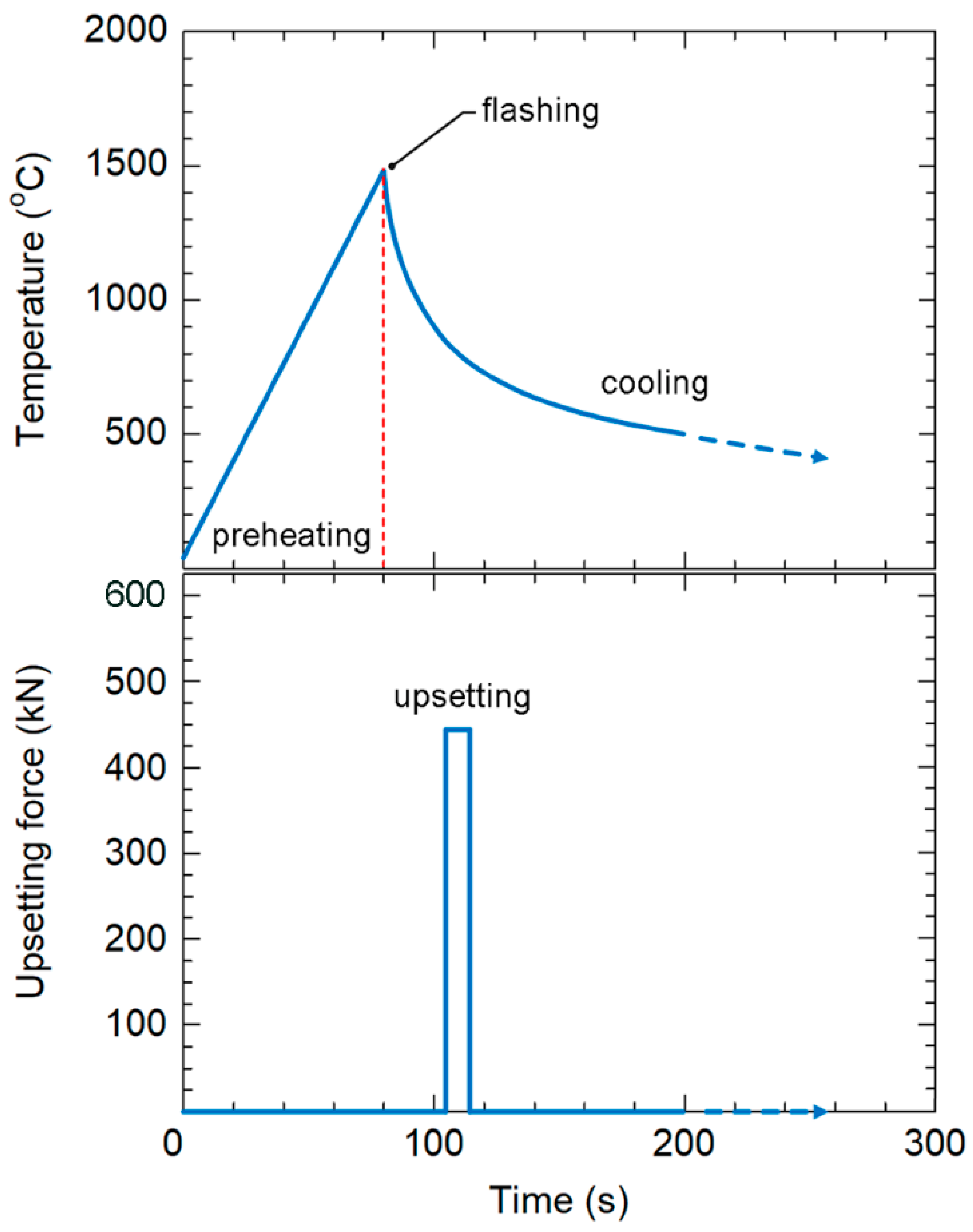
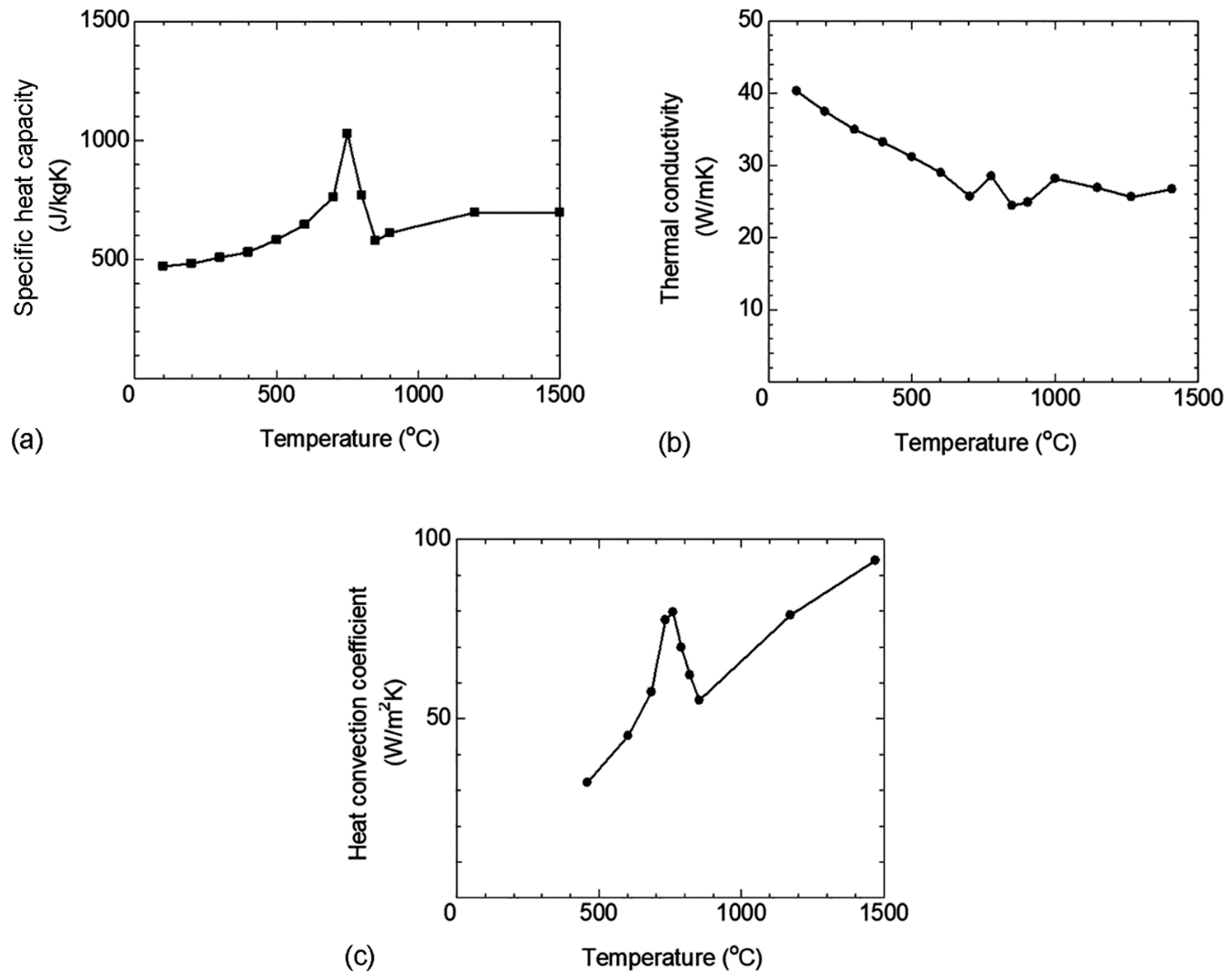
2.2. Governing Equations for Flash-Butt Welding
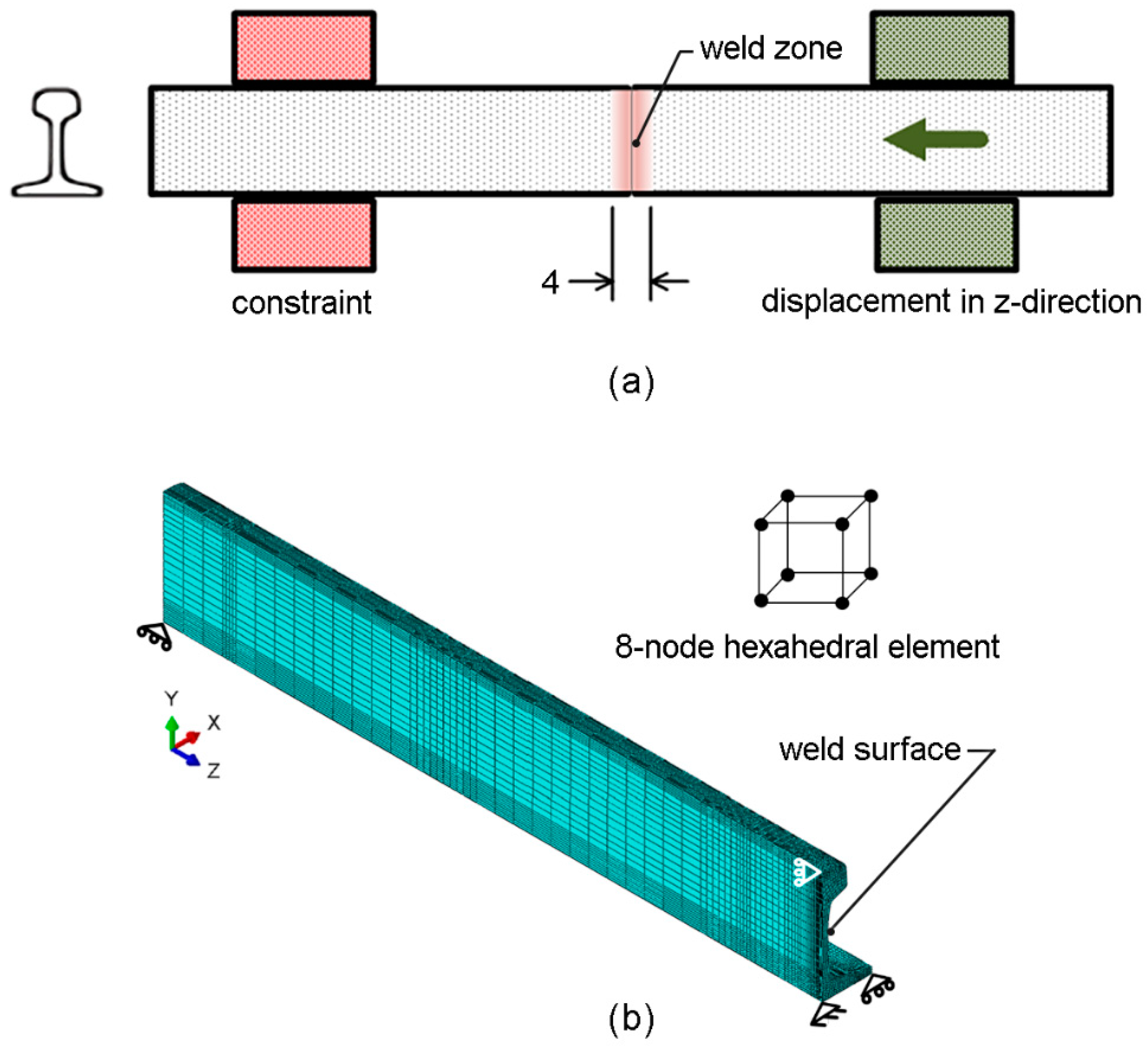
2.3. Finite Element Analysis
3. Results and Discussion
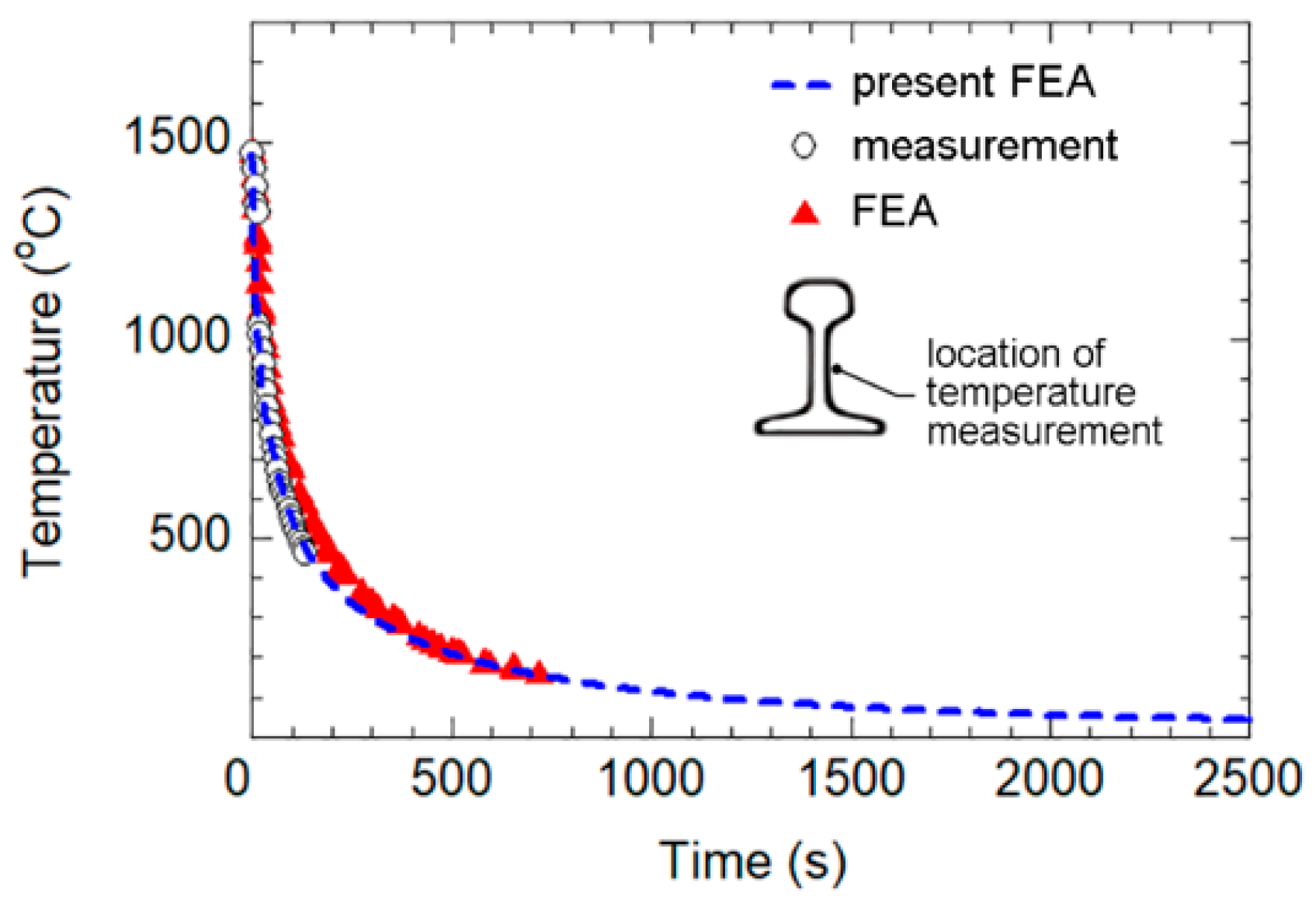
3.1. Cooling Temperature
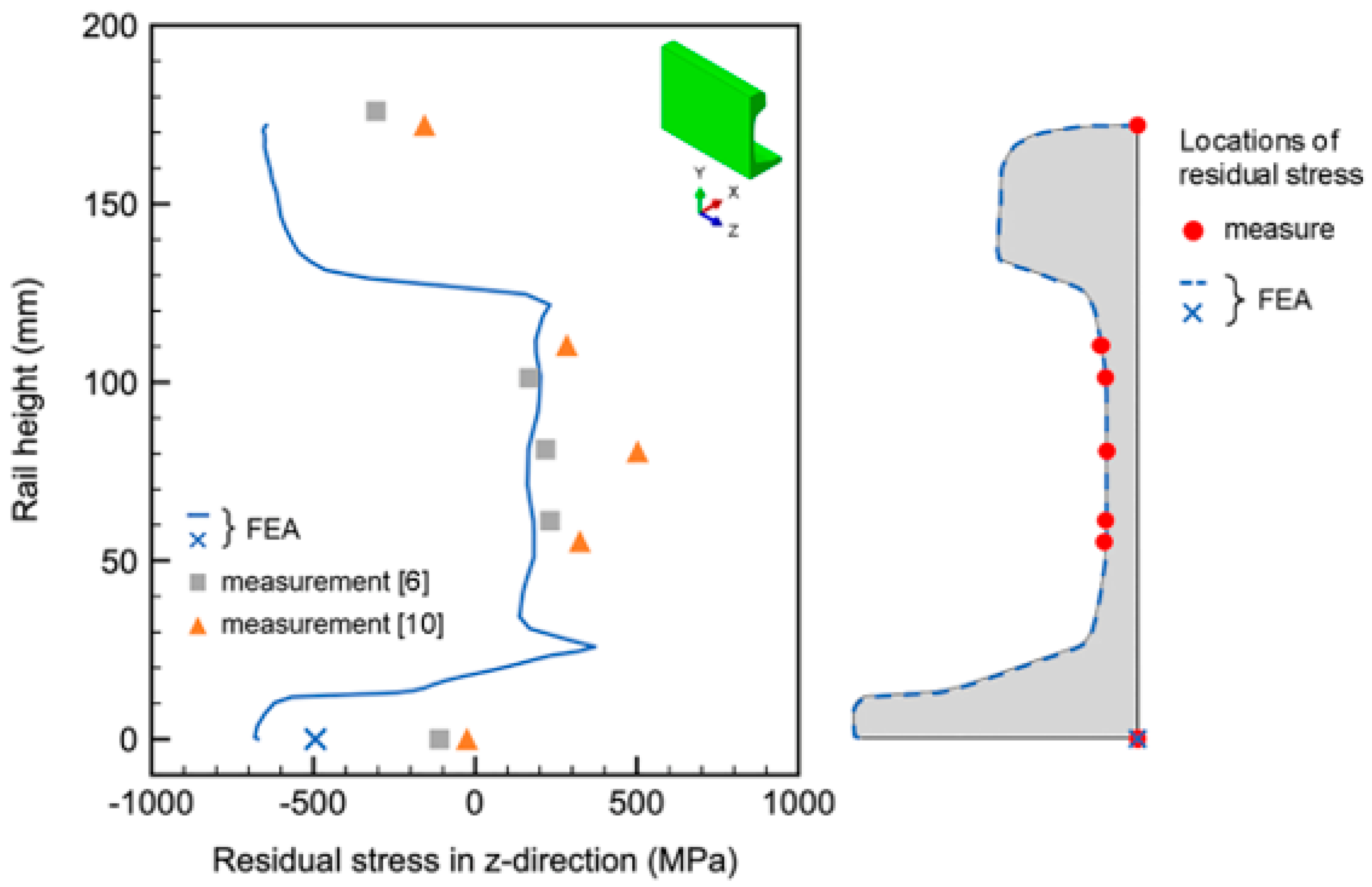
3.2. Residual Stress
3.3. Residual Stress Formation Mechanisms
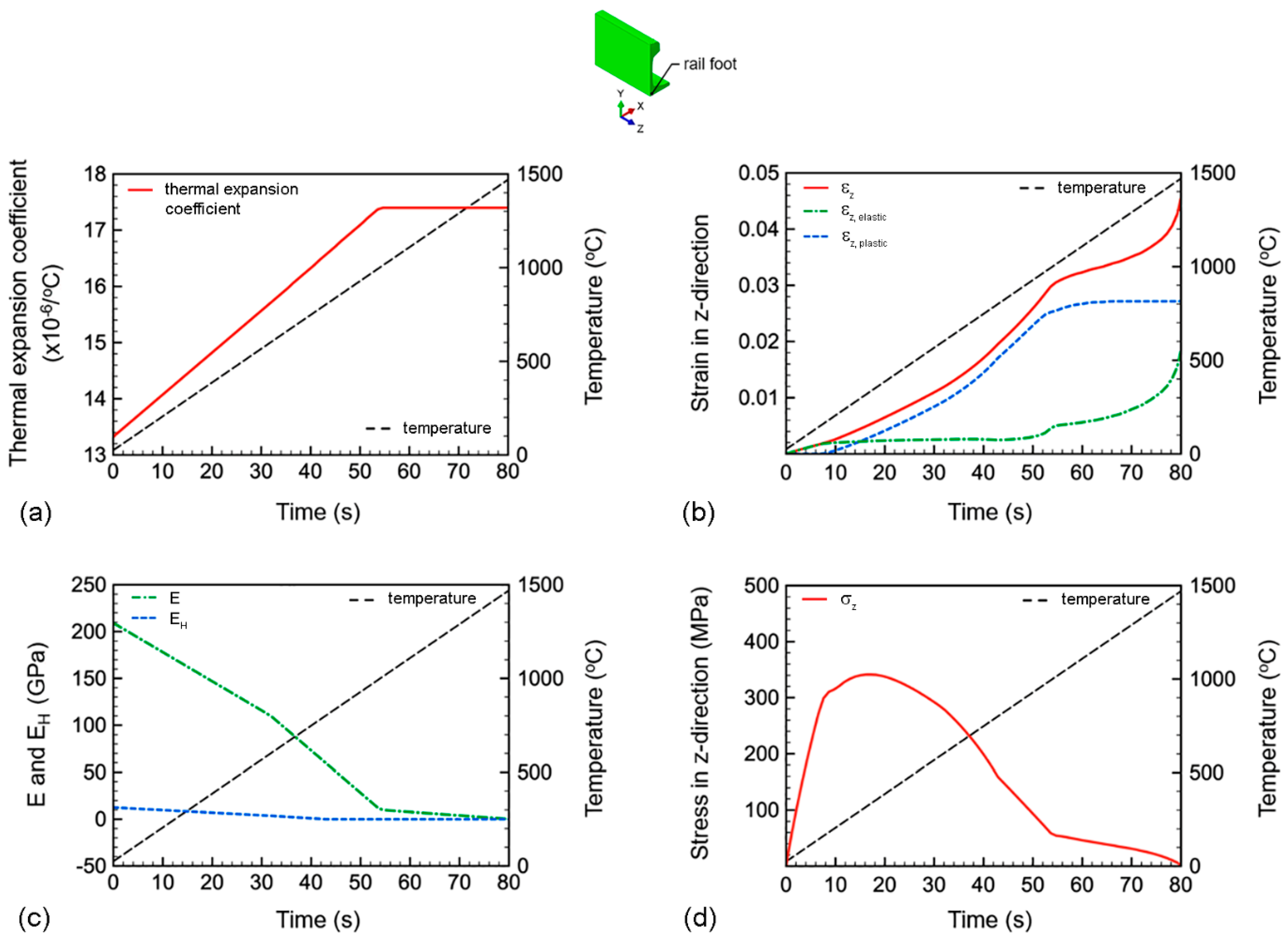
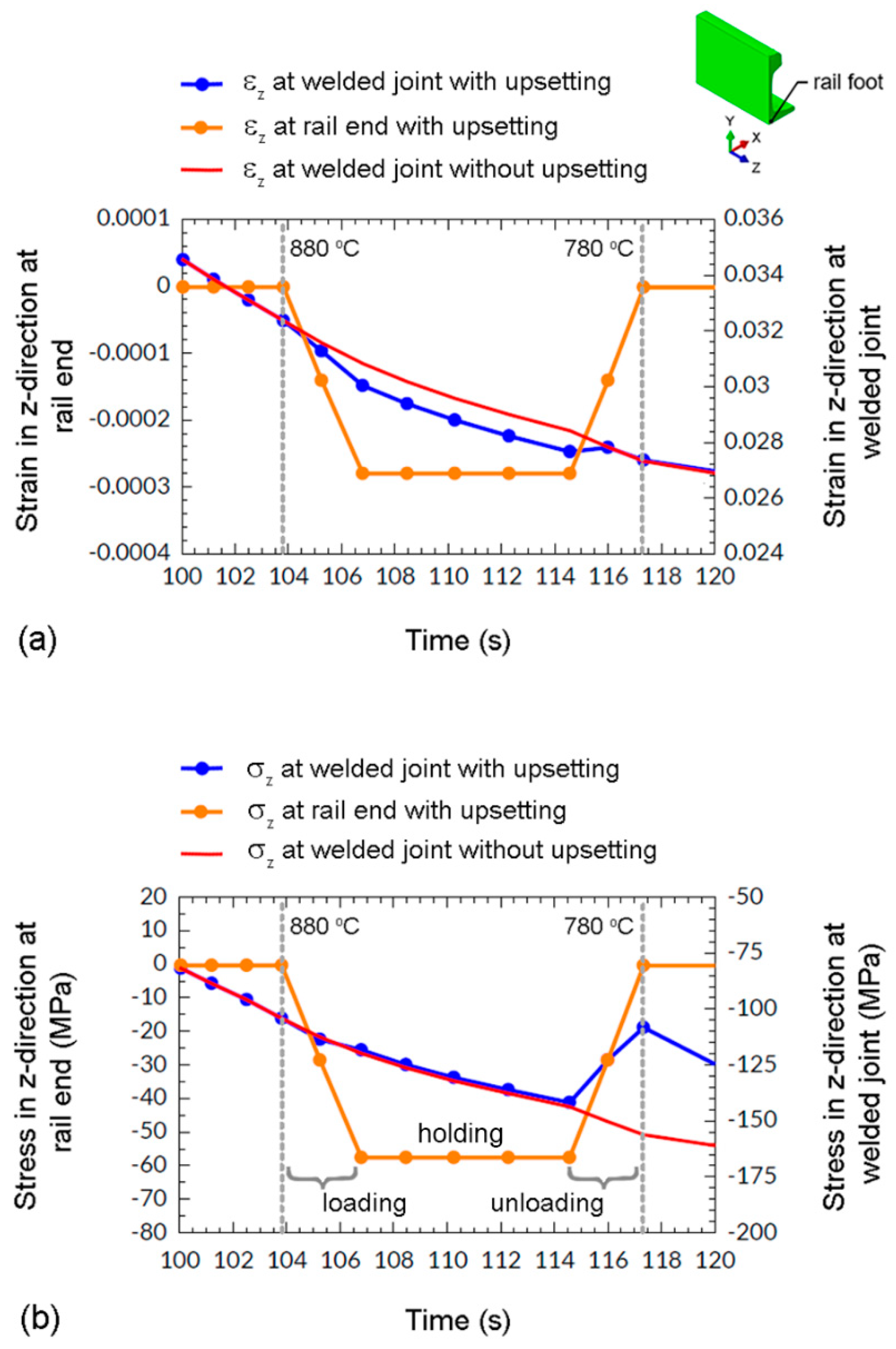
3.3.1. Heating Process
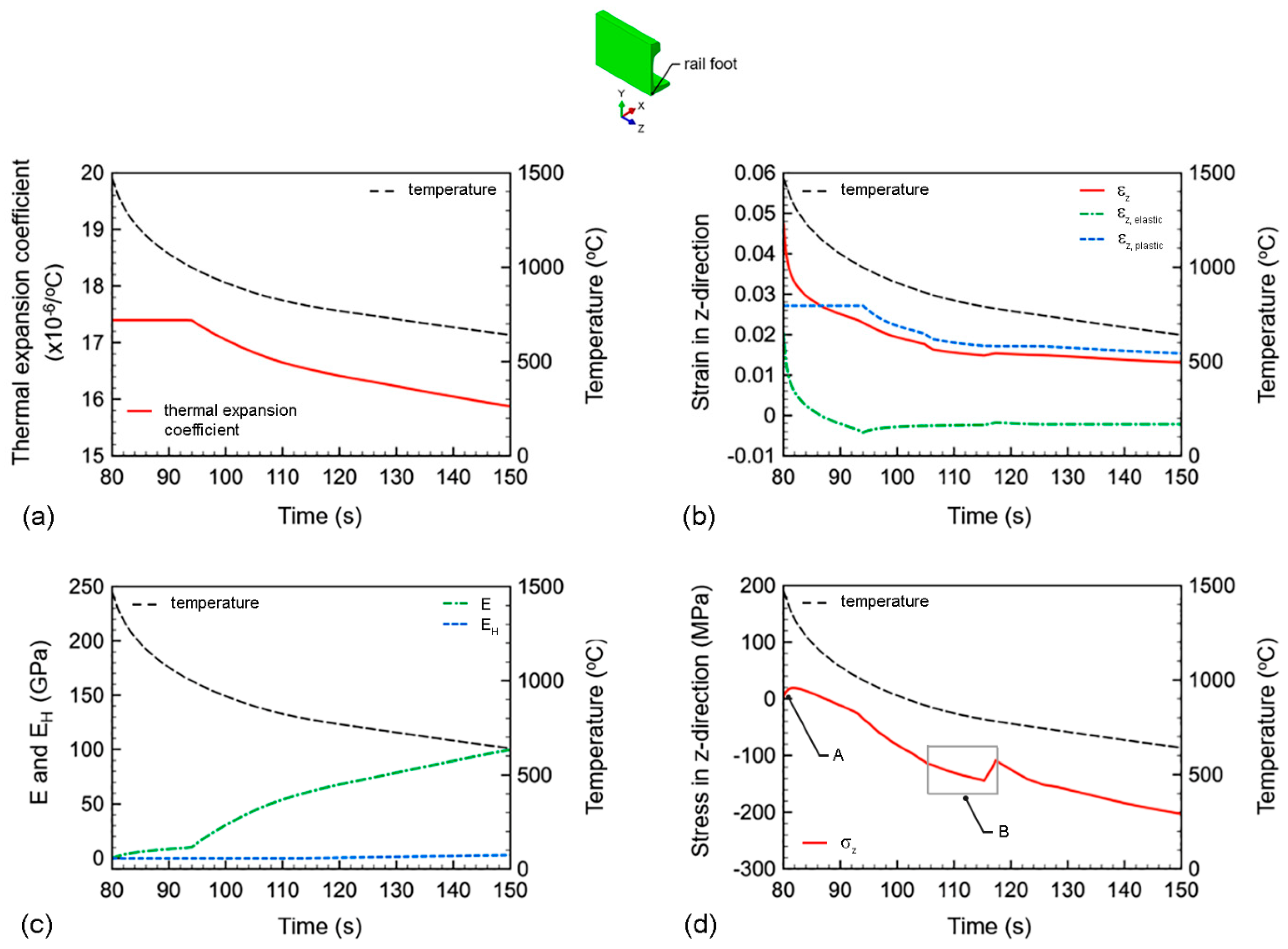
3.3.2. Cooling Process
3.4. Influence of Upsetting on Residual Stress Formation
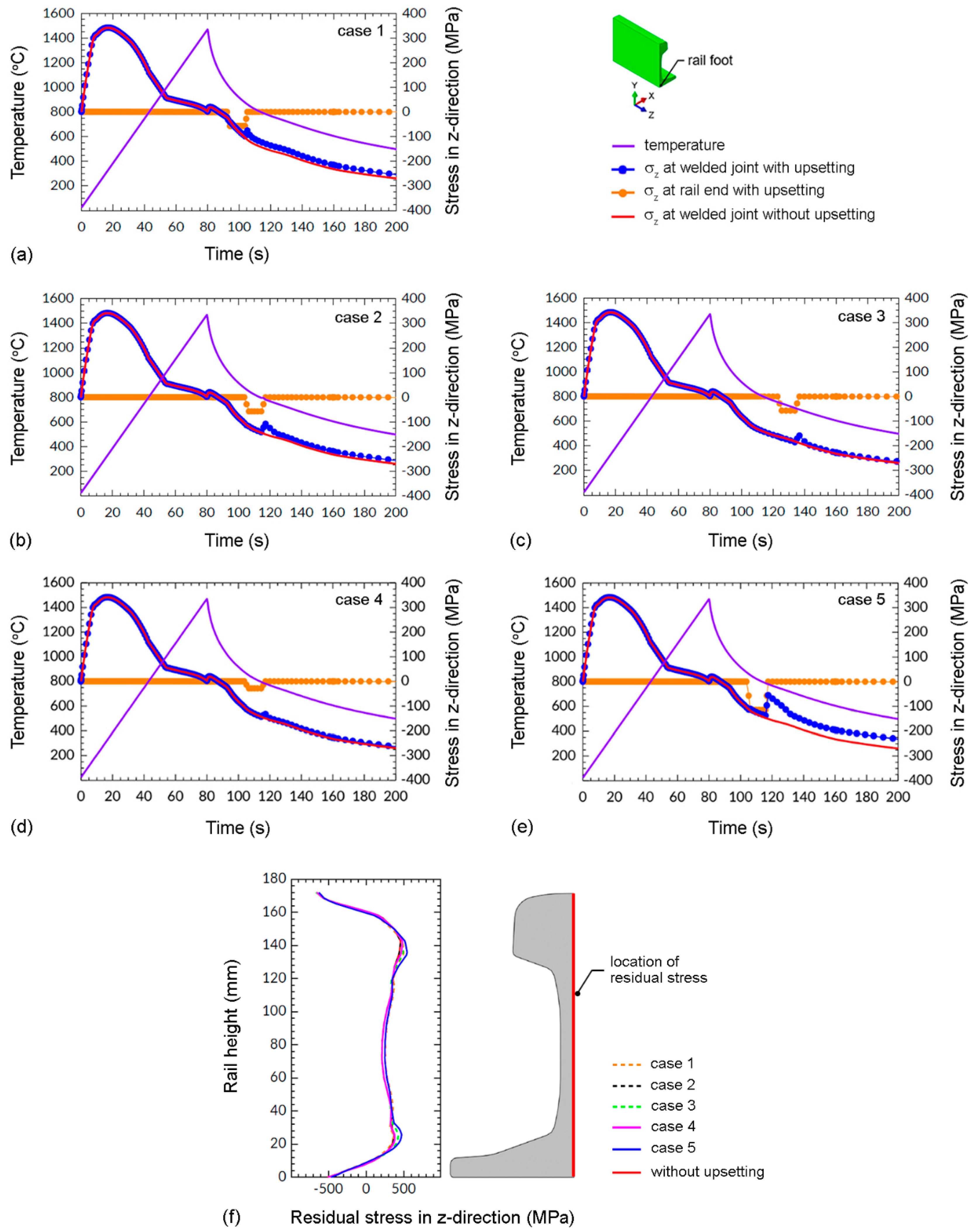
3.4.1. Upsetting Temperature Range
3.4.2. Upsetting Force
3.5. Discussion
4. Conclusions
- The calculated cooling temperature at the welded joint showed excellent agreement with the measured result. From 1470 to 450 °C, the cooling temperature experienced a rapid decline in approximately 150 s. Below 450 °C, the decrease in cooling temperature slowed down, eventually reaching the ambient temperature of 25 °C after a total cooling period of 3 h;
- The patterns of residual stresses obtained from the present FEA and the measurements using the hole-drilling strain-gage method exhibited similarities. The compressive residual stresses were observed around the rail head and the rail foot, while the tensile residual stresses were observed at the rail web;
- The formation mechanisms of residual stress involved the changes in thermal expansion coefficient, strain, and elastic modulus of the welded joint with temperature. The stress in the longitudinal direction of the rail was the main contribution of the residual stress around the rail head and the rail foot;
- At the end of heating process (i.e., the peak temperature of 1470 °C), the stresses of the welded joint reached zero. However, in contrast to the stresses, the strains remained in the welded joint. This retention of strains could potentially influence the development of residual strain and residual stress throughout the subsequent cooling process;
- The decreases in thermal expansion coefficient and strain and the increase in elastic modulus with decreasing temperature were the dominant factors for the formation mechanisms of residual stress during the cooling process. The stresses around the rail head and the rail foot decreased with decreasing temperature, and became compressive residual stresses before the end of the cooling process;
- Under the investigated ranges of upsetting temperature and upsetting forces, the yield stress and hardening modulus of rail steel were extremely low. Consequently, the applied compressive upsetting force primarily induced plastic deformation in the welded joint without significantly impacting stress alteration. The residual stresses in the welded joints with and without upsetting were nearly indistinguishable at the rail foot and the rail head. Thus, the investigated ranges of upsetting temperature and upsetting forces exerted an insignificant influence on the formation of residual stress.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AREMA | American Railway Engineering and Maintenance-of-Way Association |
| ASTM | American Society for Testing and Materials |
| α | thermal expansion coefficient |
| c | specific heat capacity |
| E | elastic modulus |
| EH | hardening modulus |
| ε | normal strain |
| εT | thermal strain |
| εx, εy, εz | normal strains in rectangular coordinate system |
| εY | yield strain |
| εz,elastic | elastic strain in the longitudinal direction of the rail |
| εz,plastic | plastic strain in the longitudinal direction of the rail |
| FEA | finite element analysis |
| HAZ | heat affected zone |
| hc | convection coefficient |
| k | thermal conductivity |
| ν | Poisson’s ratio |
| PWHT | post-weld heat treatment |
| Q | internal heat generation rate |
| q | heat flux vector |
| ρ | density of material |
| σ | normal stress |
| σv | Von Mises stress |
| σx, σy, σz | normal stresses in rectangular coordinate system |
| σY | yield stress |
| T | temperature |
| Tα | annealing temperature |
| To | ambient temperature |
| Ts | peak temperature at fusion line |
| t | time |
| x, y, z | rectangular coordinate system |
References
- Lewis, R.; Olofsson, U. Wheel-Rail Interface Handbook; Woodhead Publishing: New Delhi, India, 2009. [Google Scholar]
- Tzanakakis, K. The Railway Track and Its Long Term Behaviour; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2013. [Google Scholar]
- BS EN 14587-1; Railway Applications—Track—Flash Butt Welding of Rails—Part 1: New R220, R260, R260Mn and R350HT Grade rails in a Fixed Plant, in British-Adopted European Standard. British Standards Institution (BSI): London, UK, 2007.
- Ozakgul, K.; Piroglu, F.; Caglayan, O. An experimental investigation on flash butt welded rails. Eng. Fail. Anal. 2015, 57, 21–30. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, S.H.; Chang, Y.S.; Jun, H.K. Fatigue life assessment of railway rail subjected to welding residual and contact stresses. J. Mech. Sci. Technol. 2014, 28, 4483–4491. [Google Scholar] [CrossRef]
- Ma, N.; Cai, Z.; Huang, H.; Deng, D.; Murakawa, H.; Pan, J. Investigation of welding residual stress in flash-butt joint of U71Mn rail steel by numerical simulation and experiment. Mater. Des. 2015, 88, 1296–1309. [Google Scholar] [CrossRef]
- Yan, S.; Chen, H.; Gou, G.; Li, D.; Liu, Y.; Zhu, Z. Research on measurement of residual stresses in flash-butt-weld rails using X-ray diffraction. Adv. Mater. Res. 2011, 291–294, 934–940. [Google Scholar] [CrossRef]
- Ma, R.; Huang, D.; Zhang, J.; Zhang, Y.; Lv, Q. Effects of rail flash-butt welding and post-weld heat treatment processes meeting different national standards on residual stresses of welded joints. Int. J. Mater. Res. 2020, 111, 780–787. [Google Scholar] [CrossRef]
- ASTM E837-99; Standard Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method, in Annual Book of ASTM Standards. ASTM International: West Conshohocken, PA, USA, 1999.
- Skyttebol, A.; Josefson, B.L.; Ringsberg, J.W. Fatigue crack growth in a welded rail under the influence of residual stresses. Eng. Fract. Mech. 2005, 72, 271–285. [Google Scholar] [CrossRef]
- Ghazanfari, M.; Tehrani, P.H. Experimental and numerical investigation of the characteristics of flash-butt joints used in continuously welded rails. Proceedings of the Institution of Mechanical Engineers. Part F J. Rail Rapid Transit 2020, 234, 65–79. [Google Scholar] [CrossRef]
- Ghazanfari, M.; Tehrani, P.H. Investigation of residual stress and optimization of welding process parameters to decrease tensile residual stress in the flash butt welded UIC60 rail. Mech. Based Des. Struct. Mach. 2020, 50, 1580–1594. [Google Scholar] [CrossRef]
- Haibatollahi, S.P.; Tehrani, P.H. Prediction of residual stress distribution in flash butt welded rails using electro-thermo-mechanical simulation. Int. J. Veh. Struct. Syst. 2013, 5, 53–57. [Google Scholar] [CrossRef]
- Tawfik, D.; Kirstein, O.; Mutton, P.J.; Chiu, W.K. Verification of residual stresses in flash-butt-weld rails using neutron diffraction. Phys. B Condens. Matter 2006, 385–386, 894–896. [Google Scholar] [CrossRef]
- Tawfik, D.; Mutton, P.J.; Chiu, W.K. Modifying residual stress levels in rail flash-butt welds using localised rapid post-weld heat treatment and accelerated cooling. Int. Heat Treat. Surf. Eng. 2008, 2, 839–848. [Google Scholar] [CrossRef]
- Pereira, H.B.; EEcheverri, A.A.; Alves, L.H.D.; Goldenstein, H. Evaluation of the effect of heat input and cooling rate of rail flash-butt welding using finite element method simulation. Soldag. E Insp. 2022, 27, e2701. [Google Scholar] [CrossRef]
- BS EN 13674-1; Railway Applications—Track—Vignole Railway Rails 46 kg/m and above, in British-Adopted European Standard. British Standards Institution (BSI): London, UK, 2002.
- Manual for Railway Engineering; American Railway Engineering and Maintenance-of-Way Association: Chicago, IL, USA, 2010; Available online: https://pdfcoffee.com/manual-for-railway-engineering-structures-pdf-free.html (accessed on 1 January 2023).
- Cai, Z.; Nawafune, M.; Ma, N.; Qu, Y.; Cao, B.; Murakawa, H. Residual stresses in flash butt welded rail. Trans. Join. Weld. Res. Inst. 2011, 40, 79–87. [Google Scholar]
- Dowling, N.E. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue; Prentice-Hall International: Sicklerville, NJ, USA, 1993. [Google Scholar]
- Bhatti, A.A.; Barsoum, Z.; Murakawa, H.; Barsoum, I. Influence of thermo-mechanical material properties of different steel grades on welding residual stresses and angular distortion. Mater. Des. 2015, 65, 878–889. [Google Scholar] [CrossRef]
- ABAQUS User’s Manual; ABAQUS Inc.: Palo Alto, CA, USA, 2016; Available online: http://130.149.89.49:2080/v6.11/pdf_books/CAE.pdf (accessed on 1 January 2023).
- Żak, S.; Wozniak, D. The influence of changes in roll pass design on the state of residual stresses in raIlway raIls—summary. Arch. Metall. Mater. 2023, 68, 439–446. [Google Scholar]
- Zhao, C.; Li, J.; Fan, W.; Liu, Y.; Wang, W. Experimental and simulation research on residual stress for abrasive belt rail grinding. Int. J. Adv. Manuf. Technol. 2020, 109, 129–142. [Google Scholar] [CrossRef]
- Wang, W.; Li, J.; Wu, Y.; Fan, W. Experimental and simulation investigation into residual stress for rail grinding with abrasive belt. Diam. Abras. Eng. 2020, 40, 5–12. [Google Scholar]
- Kendall, O.; Abrahams, R.; Paradowska, A.; Reid, M.; Qiu, C.; Mutton, P.; Schläfer, T.; Yan, W. Influence of multi-layer laser cladding depositions and rail curvature on residual stress in light rail components. Eng. Fail. Anal. 2023, 150, 107330. [Google Scholar] [CrossRef]
- Roy, T.; Paradowska, A.; Abrahams, R.; Law, M.; Mutton, P.; Soodi, M.; Yan, W. Residual stress in laser cladded heavy-haul rails investigated by neutron diffraction. J. Mater. Process. Technol. 2020, 278, 116511. [Google Scholar] [CrossRef]
- Wang, K.; Ma, Q.; Xu, J.; Liao, T.; Wang, P.; Chen, R.; Qian, Y.; Li, L. Effect of material non-uniformity and residual stress on wear and transient rolling contact behaviour in laminar plasma quenched (LPQ) rails. Wear 2023, 523, 204767. [Google Scholar] [CrossRef]
- Mortazavian, E.; Wang, Z.; Teng, H. Finite element investigation of residual stresses during laser powder deposition process as an innovative technique to repair worn rails. Proceedings of the Institution of Mechanical Engineers. Part F J. Rail Rapid Transit 2023, 237, 21–32. [Google Scholar] [CrossRef]
- Fang, X.Y.; Zhang, H.N.; Ma, D.W.; Wu, Z.J.; Huang, W. Influence of welding residual stress on subsurface fatigue crack propagation of rail. Eng. Fract. Mech. 2022, 271, 108642. [Google Scholar] [CrossRef]
- Kang, C.; Wenner, M.; Marx, S. Experimental investigation on the rail residual stress distribution and its influence on the bending fatigue resistance of rails. Constr. Build. Mater. 2021, 284, 122856. [Google Scholar] [CrossRef]
- Liu, Y.; Tsang, K.S.; Subramaniam, N.A.; Pang, J.H.L. Structural fatigue investigation of thermite welded rail joints considering weld-induced residual stress and stress relaxation by cyclic load. Eng. Struct. 2021, 235, 112033. [Google Scholar] [CrossRef]



| Temperature (°C) | Elastic Modulus (GPa) | Yield Stress (MPa) | Hardening Modulus (GPa) | Poisson’s Ratio | Thermal Expansion Coefficient (×10−6/°C) |
|---|---|---|---|---|---|
| 20 | 210 | 430 | 12.7 | 0.3 | 13.3 |
| 600 | 110 | 242 | 3.7 | 0.3 | 15.7 |
| 1000 | 10 | 50 | 0 | 0.4 | 17.4 |
| 1470 | 0.1 | 20 | 0 | 0.4 | 17.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thadsoongnoen, K.; Hasap, A.; Noraphaiphipaksa, N.; Kanchanomai, C. Numerical Investigation of Residual Stress Formation Mechanisms in Flash-Butt Welded Rail. Metals 2023, 13, 1359. https://doi.org/10.3390/met13081359
Thadsoongnoen K, Hasap A, Noraphaiphipaksa N, Kanchanomai C. Numerical Investigation of Residual Stress Formation Mechanisms in Flash-Butt Welded Rail. Metals. 2023; 13(8):1359. https://doi.org/10.3390/met13081359
Chicago/Turabian StyleThadsoongnoen, Kotchaporn, Anat Hasap, Nitikorn Noraphaiphipaksa, and Chaosuan Kanchanomai. 2023. "Numerical Investigation of Residual Stress Formation Mechanisms in Flash-Butt Welded Rail" Metals 13, no. 8: 1359. https://doi.org/10.3390/met13081359
APA StyleThadsoongnoen, K., Hasap, A., Noraphaiphipaksa, N., & Kanchanomai, C. (2023). Numerical Investigation of Residual Stress Formation Mechanisms in Flash-Butt Welded Rail. Metals, 13(8), 1359. https://doi.org/10.3390/met13081359







