The Optimization of Welding Spots’ Arrangement in A-Pillar Patchwork Blank Hot Stamping
Abstract
:1. Introduction
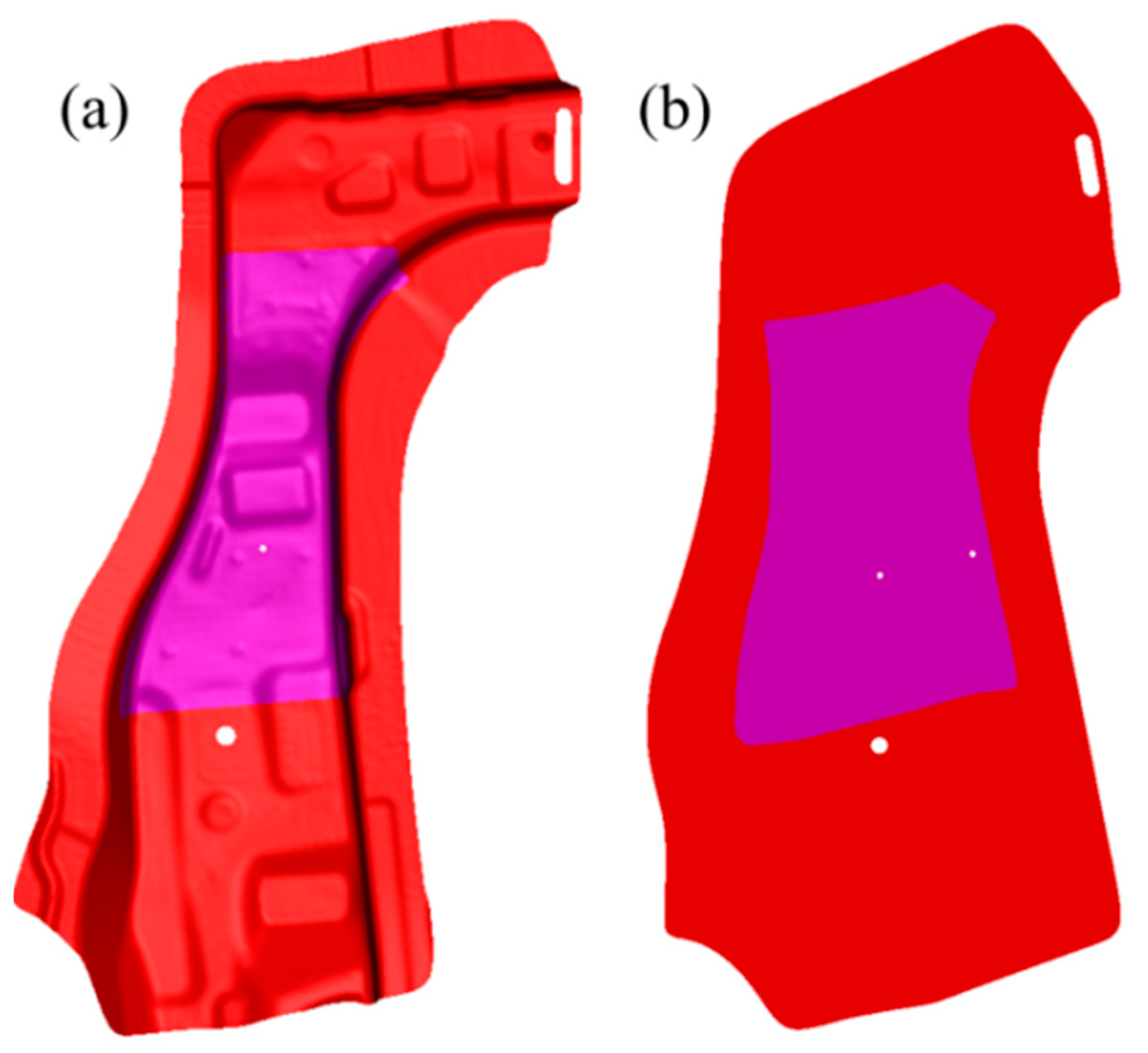
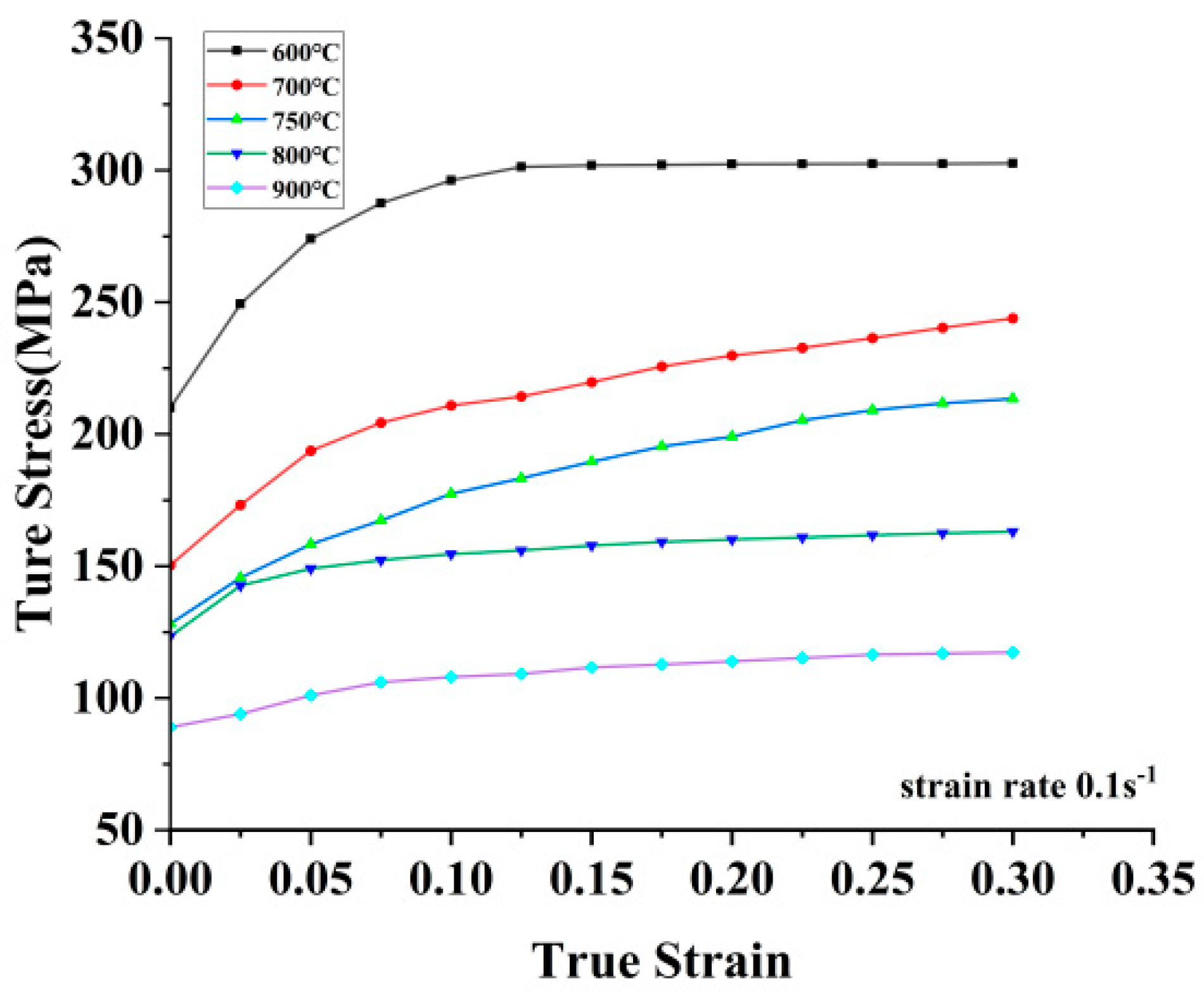
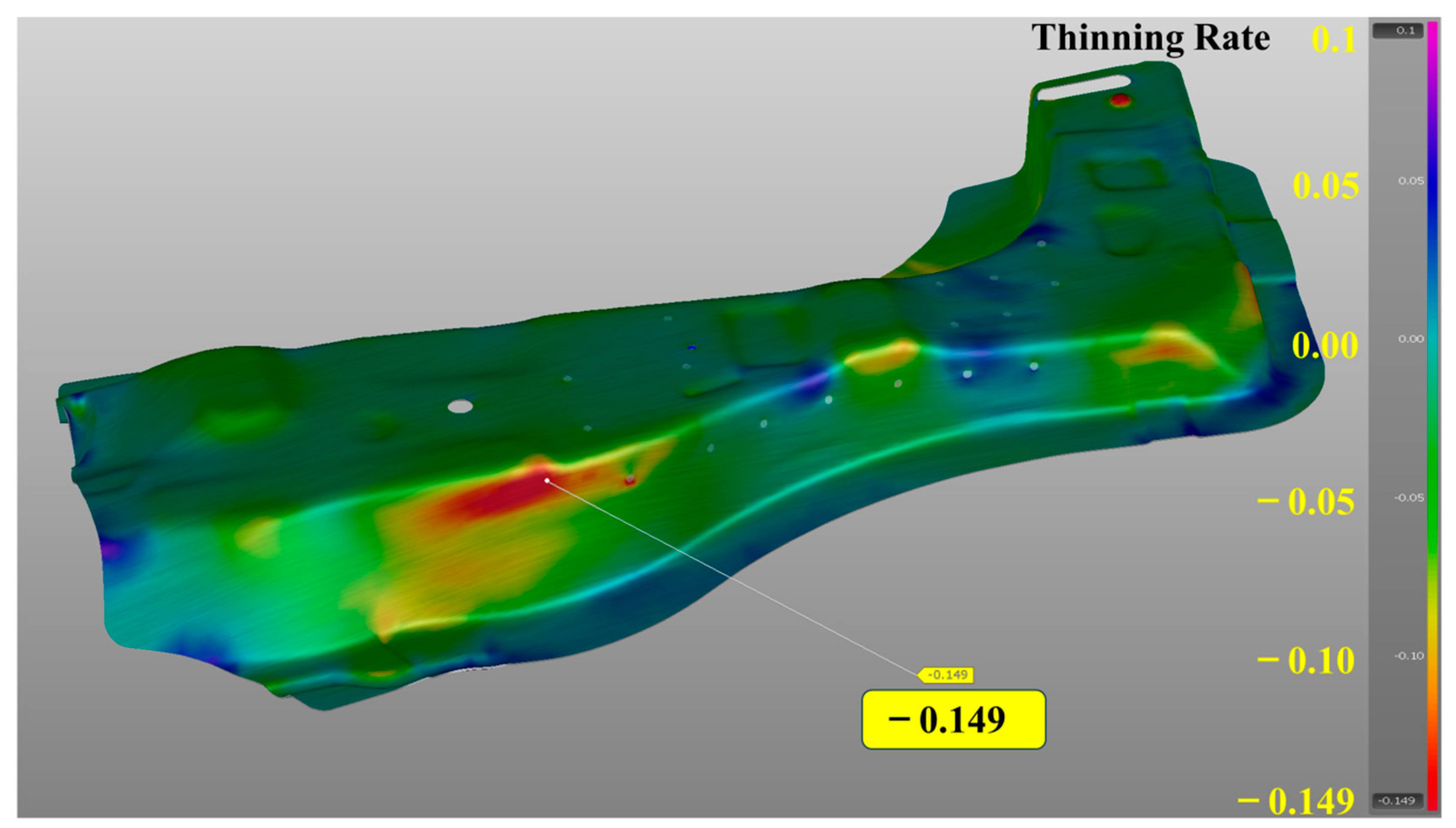
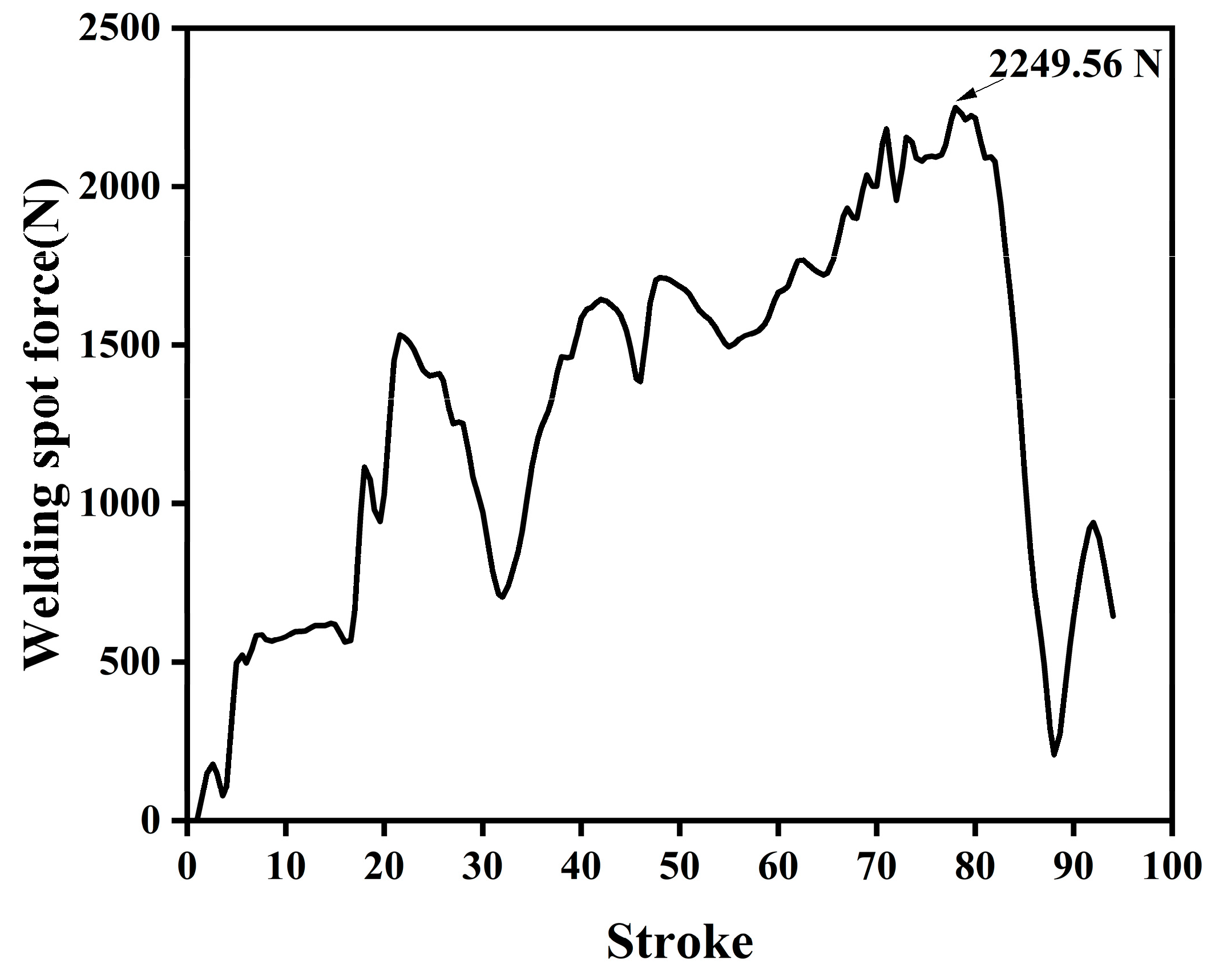
2. Establishment of Finite Element Model for A-Pillar Patchwork Blanks
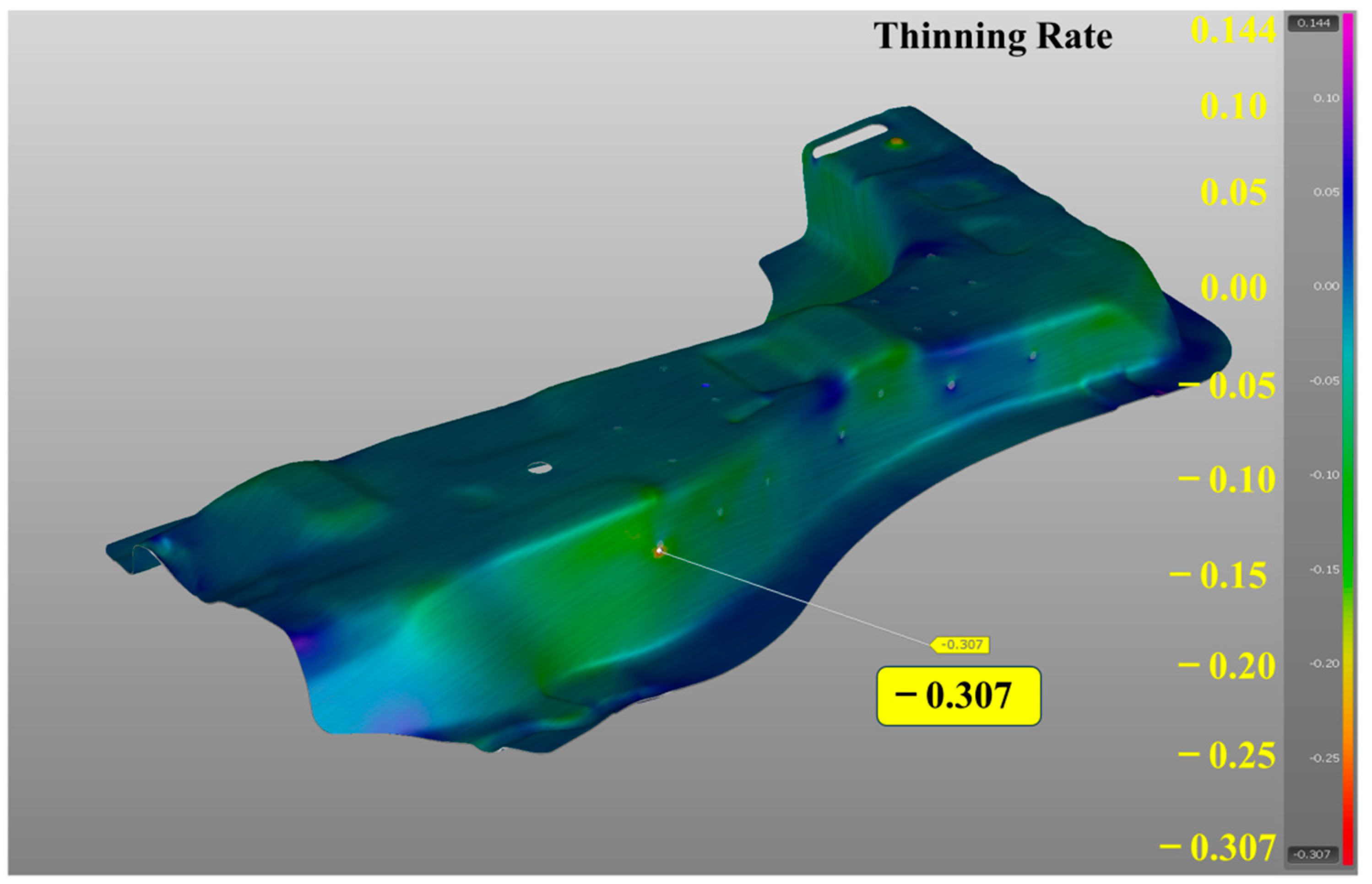
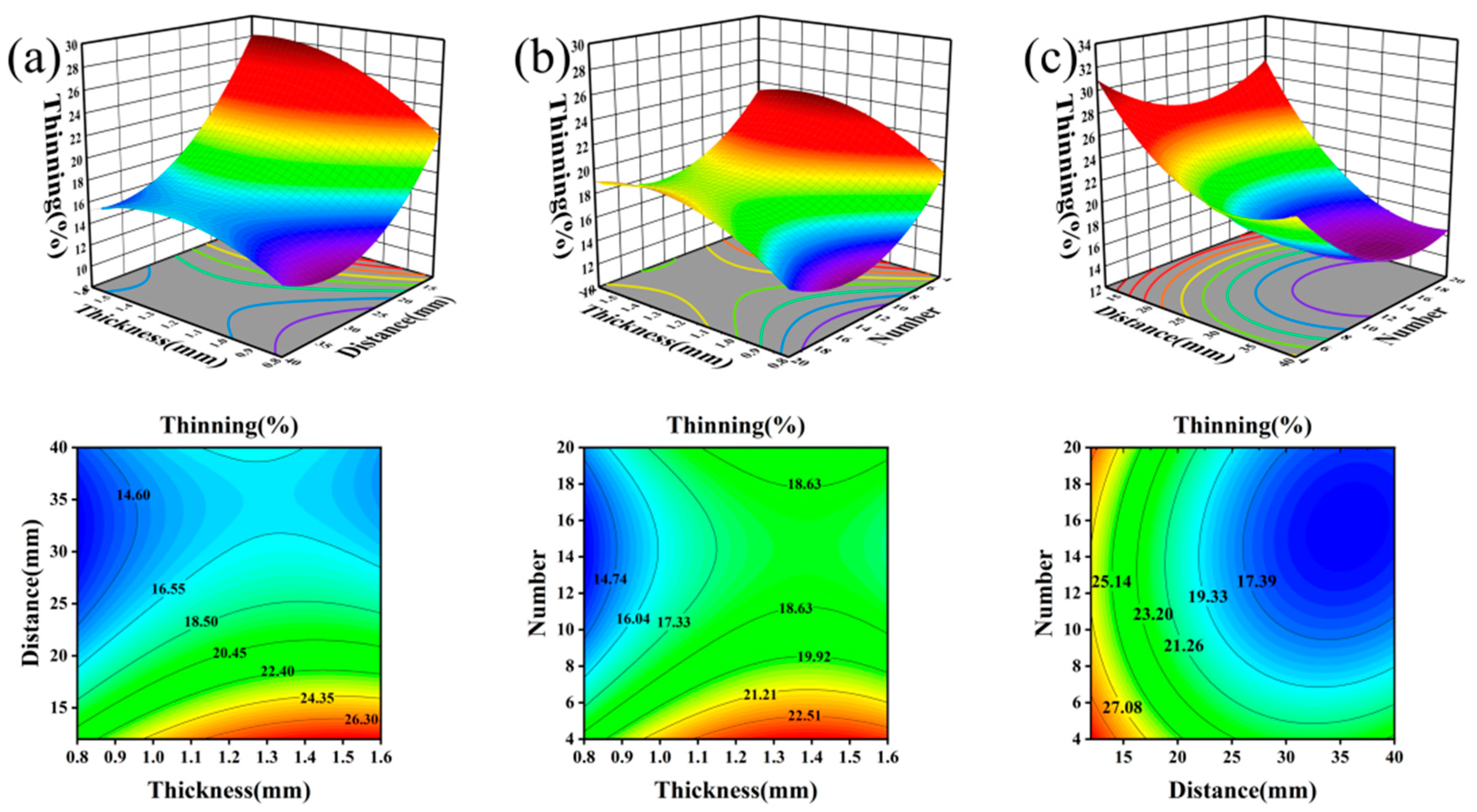
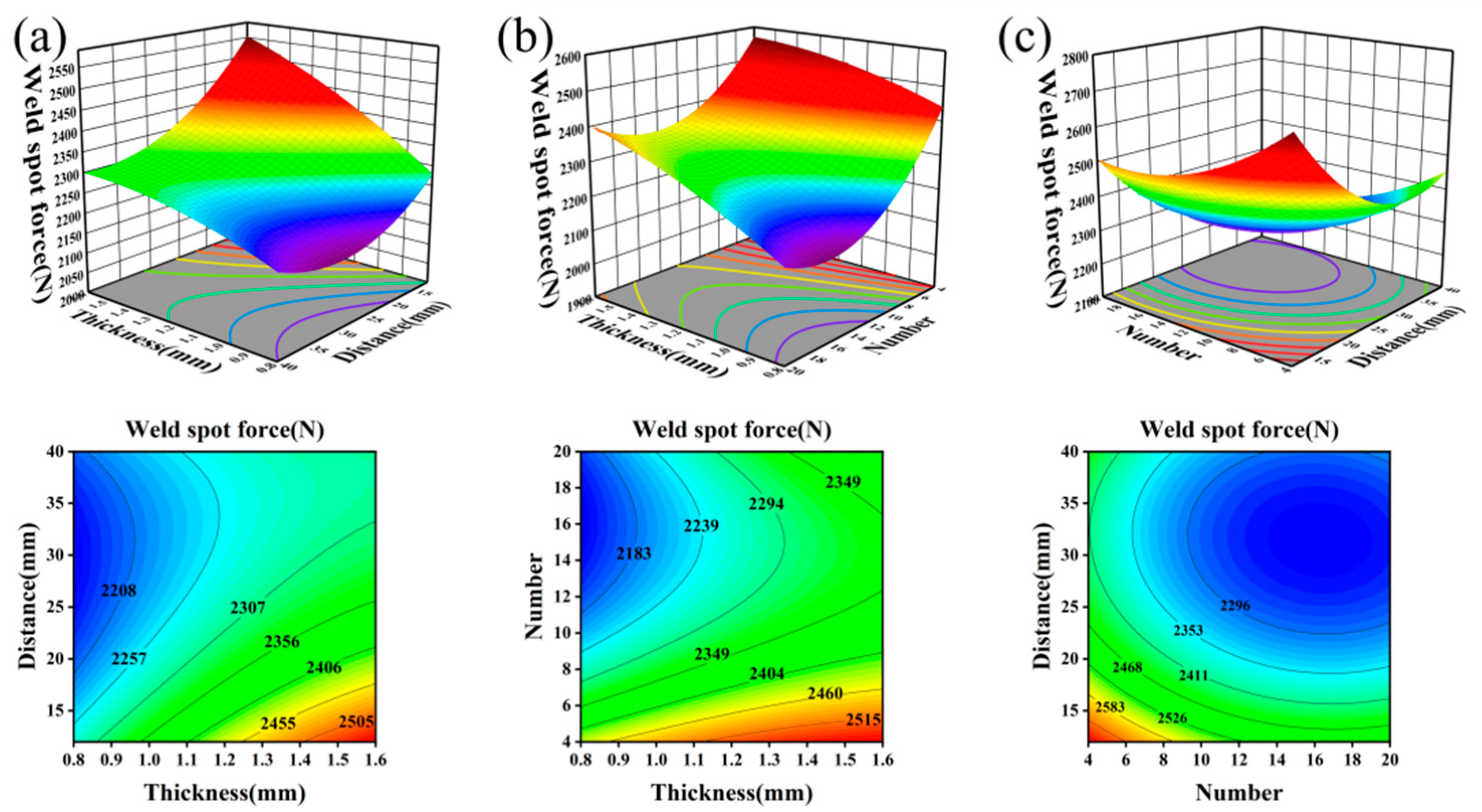
3. Response Surface Method Hot Stamping of A-Pillar Patchwork Blanks
4. Multi-Objective Optimization Based on the NSGA-II Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, W.; Tao, W.; Luo, H.W.; Yang, S.L. Effect of oscillation frequency on the mechanical properties and failure behaviors of laser beam welded 22MnB5 weld. J. Mater. Res. Technol. 2023, 22, 1436–1448. [Google Scholar] [CrossRef]
- Wang, Y.W.; Ding, Y.J.; Jiang, Y.H.; Wang, W.R.; Zhao, Y.Y.; Wei, X.C. The Effects of Die Temperature and Cooling Condition on Friction Behavior of Bare 22MnB5 Boron Steel in Hot Stamping. Tribol. Trans. 2022, 65, 519–530. [Google Scholar] [CrossRef]
- Li, S.S.; Luo, H.W. Medium-Mn steels for hot forming application in the automotive industry. Int. J. Min. Met. Mater. 2021, 28, 741–753. [Google Scholar] [CrossRef]
- Zhou, Q.; Guo, P.C.; Qin, F. Stress Response Behavior, Microstructure Evolution and Constitutive Modeling of 22MnB5 Boron Steel under Isothermal Tensile Load. Metals 2022, 12, 930. [Google Scholar] [CrossRef]
- Hirtler, M.; Unsal, I.; Buhl, J.; Bambach, M. Investigation of quench hardening behavior of directed energy deposited 22MnB5 steel for local reinforcement of hot stamping parts. CIRP J. Manuf. Sci. Technol. 2022, 39, 223–231. [Google Scholar] [CrossRef]
- Yuan, C.W.; Li, S.C.; Huang, J.J.; Lin, X.B.; Bian, X.Z.; Chen, J.M. Effect of hierarchical martensitic microstructure on fatigue crack growth behavior of ultra-high strength hot stamping steel. Mater. Charact. 2021, 174, 111041. [Google Scholar] [CrossRef]
- Esiyok, F.; Ertan, R.; Sevilgen, G.; Bulut, E.; Ozturk, F.; Alyay, I.; Abi, T.T. A Comparative Study on Conventional and Hybrid Quenching Hot Forming Methods of 22MnB5 Steel for Mechanical Properties and Microstructure. J. Mater. Eng. Perform. 2023, 32, 1347–1356. [Google Scholar] [CrossRef]
- Yogo, Y.; Kurato, N.; Iwata, N. Investigation of Hardness Change for Spot Welded Tailored Blank in Hot Stamping Using CCT and Deformation-CCT Diagrams. Metall. Mater. Trans. A 2018, 49A, 2293–2301. [Google Scholar] [CrossRef]
- Yang, J.; Xiao, M.; Wu, L.Q.; Li, Z.G.; Liu, H.B.; Zhao, Y.X.; Guo, W.; Tan, C.W. The influence of laser power on microstructure and properties of laser welding-brazing of Al alloys to Al-Si coated 22MnB5 steel. Opt. Laser. Technol. 2023, 162, 109318. [Google Scholar] [CrossRef]
- Almeida, D.T.; Clarke, T.G.R.; de Souza, J.H.C.; Haupt, W.; de Lima, M.S.F.; Mohrbacher, H. The effect of laser welding on microstructure and mechanical properties in heavy-gage press hardening steel alloys. Mat. Sci. Eng. A-Struct. 2021, 821, 141341. [Google Scholar] [CrossRef]
- Lei, C.; Xing, Z.; Xu, W.; Hong, Z.; Shan, D. Hot stamping of patchwork blanks: Modelling and experimental investigation. Int. J. Adv. Manuf. Technol. 2017, 92, 2609–2617. [Google Scholar] [CrossRef]
- Long, A.; Ge, R.; Zhang, Y.S.; Wei, X. Numerical Simulation of B-Pillar’s Hot Press Forming Process and its Shape Optimization. Appl. Mech. Mater. 2011, 138–139, 749–753. [Google Scholar] [CrossRef]
- Zhang, Z.; Ouyang, X.; Zhu, L. Study on the hot stamping simulation and experiment of A-pillar patchwork blanks. Int. J. Adv. Manuf. Technol. 2022, 122, 365–376. [Google Scholar] [CrossRef]
- Lamprecht, K.; Merklein, M.; Geiger, M. Hydroforming of Patchwork Blanks—Numerical Modeling and Experimental Validation. In Proceedings of the 6th International Conference and Workshop on Numerical Simulation of 3D Sheet Metal Forming Processes, Detroit, MI, USA, 15–19 August 2005. [Google Scholar]
- Xiancheng, G.; Dongfang, H.; Wende, L.; Peng, L.; Xiaolu, X. Hot stamping process of ultra high strength steel patchworks. Forg. Stamp. Technol. 2016, 41, 80–83. (In Chinese) [Google Scholar]
- Chenlei, W.; Yanjun, W.; Weili, X.; Aihui, L. Simulation and experiment of patchwork B-pillar hot forming. Die Mould Technol. 2016, 6, 10–13. (In Chinese) [Google Scholar]
- Zhao, Y.; Zhang, Y.; Lai, X. Analysis of Fracture Modes of Resistance Spot Welded Hot-Stamped Boron Steel. Metals 2018, 8, 764. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Cui, X.; Luo, Z.; Ao, S. Microstructure and Tensile-Shear Properties of Resistance Spot Welded 22MnMoB Hot-Stamping Annealed Steel. J. Mater. Eng. Perform. 2016, 26, 424–430. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, C.; Yi, R.; Ju, J. Optimization of Double-pulse Process in Resistance Spot Welding of Hot Stamped Steel Sheet. ISIJ Int. 2020, 60, 1284–1290. [Google Scholar] [CrossRef]
- Schwedler, O.; Zinke, M.; Jüttner, S. Determination of hydrogen input in welded joints of press-hardened 22MnB5 steel. Weld. World 2014, 58, 339–346. [Google Scholar] [CrossRef]
- Ribeiro, R.; Romão, E.L.; Luz, E.; Gomes, J.H.; Costa, S. Optimization of the Resistance Spot Welding Process of 22MnB5-Galvannealed Steel Using Response Surface Methodology and Global Criterion Method Based on Principal Components Analysis. Metals 2020, 10, 1338. [Google Scholar] [CrossRef]
- Güler, H.; Ertan, R.; Özcan, R. Investigation of the hot ductility of a high-strength boron steel. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2014, 608, 90–94. [Google Scholar] [CrossRef]
- Min, J.; Lin, J.; Min, Y.a.; Li, F. On the ferrite and bainite transformation in isothermally deformed 22MnB5 steels. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2012, 550, 375–387. [Google Scholar] [CrossRef]
- Merklein, M.; Lechler, J. Determination of Material and Process Characteristics for Hot Stamping Processes of Quenchenable Ultra-High-Strength Steels With Respect to a FE-Based Process Design. SAE Int. J. Mater. Manuf. 2008, 1, 411–426. [Google Scholar] [CrossRef]
- Hu, P.; Ying, L.; Jiang, D.X.; Shi, D.Y.; Shen, G.Z.; Zhang, X.K.; Liu, W.Q. The investigation of 3D temperature field numerical simulation in hot forming of high strength steel. In Proceedings of the 11th International Conference on Numerical Methods in Industrial Forming Processes (NUMIFORM), Shenyang, China, 6–10 July 2013. [Google Scholar]
- Palmieri, M.E.; Galetta, F.R.; Tricarico, L. Study of Tailored Hot Stamping Process on Advanced High-Strength Steels. Mater. Manuf. Process. 2022, 6, 11. [Google Scholar] [CrossRef]
- Merklein, A.; Lechler, J. Investigation of the thermo-mechanical properties of hot stamping steels. J. Mater. Process. Technol. 2006, 177, 452–455. [Google Scholar] [CrossRef]
- Liu, H.; Lu, X.; Jin, X.; Dong, H.; Shi, J. Enhanced mechanical properties of a hot stamped advanced high-strength steel treated by quenching and partitioning process. Scr. Mater. 2011, 64, 749–752. [Google Scholar] [CrossRef]
- Zheng, G.; Li, X.; Chang, Y.; Wang, C.; Dong, H. A Comparative Study on Formability of the Third-Generation Automotive Medium-Mn Steel and 22MnB5 Steel. J. Mater. Eng. Perform. 2018, 27, 530–540. [Google Scholar] [CrossRef]
- Ouyang, X.; Zhang, Z.; Jia, H.; Ren, M.; Sun, Y. Study on the Effect of Heat Treatment on Microstructures and High Temperature Mechanical Properties of Welding Spots of Hot Stamped Ultra-High Strength Steel Patchwork Blanks. Metals 2021, 11, 1033. [Google Scholar] [CrossRef]




| C | Si | Mn | P | B | Cr | Ti | Fe |
|---|---|---|---|---|---|---|---|
| ≤0.25 | 0.23 | 1.2 | ≤0.02 | 0.003 | ≤0.20 | ≤0.30 | Bal. |
| Temperature (°C) | 20 | 500 | 600 | 700 | 800 | 900 |
|---|---|---|---|---|---|---|
| Elasticity modulus E (MPa) | 212 | 158 | 150 | 142 | 134 | 126 |
| Poisson’s ratio ν | 0.284 | 0.303 | 0.301 | 0.317 | 0.325 | 0.334 |
| Thermal conductivity K (W/m °C) | 32.0 | 22.3 | 23.6 | 24.5 | 25.6 | 26.7 |
| Specific heat capacity Cp (J/kg °C) | 412 | 573 | 581 | 586 | 590 | 596 |
| Design Factors | Levels | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| X1 (mm) | 0.8 | 1.2 | 1.6 |
| X2 (mm) | 12 | 26 | 40 |
| X3 | 4 | 12 | 20 |
| Experiment Number | Design Factors | Thinning Rate | Welding Spot Force | ||
|---|---|---|---|---|---|
| X1 (mm) | X2 (mm) | X3 | Y1 (%) | Y2 (N) | |
| 1 | 0.8 | 12 | 4 | 24.7 | 2553 |
| 2 | 1.6 | 12 | 4 | 31.2 | 2785 |
| 3 | 0.8 | 40 | 4 | 20.6 | 2453 |
| 4 | 1.6 | 40 | 4 | 22.8 | 2501 |
| 5 | 0.8 | 12 | 20 | 23.1 | 2245 |
| 6 | 1.6 | 12 | 20 | 30.4 | 2584 |
| 7 | 0.8 | 40 | 20 | 14.5 | 2177 |
| 8 | 1.6 | 40 | 20 | 15.4 | 2352 |
| 9 | 0.8 | 26 | 12 | 14.6 | 2232 |
| 10 | 1.6 | 26 | 12 | 17.7 | 2375 |
| 11 | 1.2 | 12 | 12 | 29.9 | 2476 |
| 12 | 1.2 | 40 | 12 | 15.0 | 2327 |
| 13 | 1.2 | 26 | 4 | 23.9 | 2552 |
| 14 | 1.2 | 26 | 20 | 19.3 | 2373 |
| 15 | 1.2 | 26 | 12 | 17.3 | 2253 |
| 16 | 1.2 | 26 | 12 | 17.3 | 2253 |
| 17 | 1.2 | 26 | 12 | 17.3 | 2253 |
| 18 | 1.2 | 26 | 12 | 17.3 | 2253 |
| 19 | 1.2 | 26 | 12 | 17.3 | 2253 |
| 20 | 1.2 | 26 | 12 | 17.3 | 2253 |
| Source | Quadratic Sum | Degree of Freedom | Average Variance | F-Value | p-Value |
|---|---|---|---|---|---|
| Models | 521.08 | 9 | 57.9 | 31.55 | <0.0001 |
| X1 | 40 | 1 | 40 | 21.8 | 0.0009 |
| X2 | 260.1 | 1 | 260.1 | 141.74 | <0.0001 |
| X3 | 42.02 | 1 | 42.02 | 22.9 | 0.0007 |
| X1X2 | 14.31 | 1 | 14.31 | 7.8 | 0.019 |
| X1X3 | 0.0313 | 1 | 0.0313 | 0.017 | 0.8988 |
| X2X3 | 15.4 | 1 | 15.4 | 8.39 | 0.0159 |
| 12.77 | 1 | 12.77 | 6.96 | 0.0248 | |
| 47.26 | 1 | 47.26 | 25.75 | 0.0005 | |
| 29.87 | 1 | 29.87 | 16.28 | 0.0024 |
| Source | Quadratic Sum | Degree of Freedom | Average Variance | F-Value | p-Value |
|---|---|---|---|---|---|
| Models | 454,600 | 9 | 50,511.31 | 24 | <0.0001 |
| X1 | 87,796.9 | 1 | 87,796.9 | 41.72 | <0.0001 |
| X2 | 69,388.9 | 1 | 69,388.9 | 32.97 | 0.0002 |
| X3 | 123,900 | 1 | 123,900 | 58.86 | <0.0001 |
| X1X2 | 15,138 | 1 | 15,138 | 7.19 | 0.023 |
| X1X3 | 6844.5 | 1 | 6844.5 | 3.25 | 0.1015 |
| X2X3 | 882 | 1 | 882 | 0.4191 | 0.532 |
| 1602.05 | 1 | 1602.05 | 0.7612 | 0.4034 | |
| 15,003.55 | 1 | 15,003.55 | 7.13 | 0.0235 | |
| 50,017.55 | 1 | 50,017.55 | 23.76 | 0.0006 |
| Model | Correlation Coefficient R2 | Revised Correlation Coefficient Radj2 |
|---|---|---|
| Y1 | 0.9660 | 0.9354 |
| Y2 | 0.9558 | 0.9159 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Zhang, Z.; Jia, H.; Ren, M. The Optimization of Welding Spots’ Arrangement in A-Pillar Patchwork Blank Hot Stamping. Metals 2023, 13, 1409. https://doi.org/10.3390/met13081409
Li W, Zhang Z, Jia H, Ren M. The Optimization of Welding Spots’ Arrangement in A-Pillar Patchwork Blank Hot Stamping. Metals. 2023; 13(8):1409. https://doi.org/10.3390/met13081409
Chicago/Turabian StyleLi, Wenfeng, Zhiqiang Zhang, Hongjie Jia, and Mingwen Ren. 2023. "The Optimization of Welding Spots’ Arrangement in A-Pillar Patchwork Blank Hot Stamping" Metals 13, no. 8: 1409. https://doi.org/10.3390/met13081409
APA StyleLi, W., Zhang, Z., Jia, H., & Ren, M. (2023). The Optimization of Welding Spots’ Arrangement in A-Pillar Patchwork Blank Hot Stamping. Metals, 13(8), 1409. https://doi.org/10.3390/met13081409





