Abstract
In this paper, stress intensity factor (SIF) solutions of eccentric annular external cracks in elliptical notched round bars under tension loading have been obtained from 3D finite element analysis, along with their relation to the energy release rate obtained with the J-integral contour. The analysis variables have been the ligament diameter, its eccentricity, and the elliptical notch aspect ratio. The maximum SIF increases with the ligament eccentricity, the presence of the notch (compared to when the bar is smooth), and the elliptical notch axial semi-axis (for the same notch depth); it decreases with the ligament diameter. For external cracks, eccentricity induces bending of the bar subjected to tensile loading, which can produce partial and full contact of the crack surface, relevant phenomena in terms of the SIF value at the different points of the crack front.
1. Introduction
In circumferentially notched bars, different mechanisms can cause the appearance of external cracks with different configurations (almond-shaped crack, sickle-shaped crack, or annular crack) depending on aspects such as notch geometry, stress type, stress magnitude, etc. For fatigue-tested notched bars, a three-probe potential drop method (PDM) has been used to estimate the crack area, location, and configuration (circumferential or semi-elliptical) []. In a turbine rotor under loading conditions including bending and torsion, due to rotor weight and steam pressure, circumferential crack growth is observed due to the high cycle fatigue phenomenon []. In bolted joints under cyclic tensile loading, fatigue fracture usually happens at the root of the first notch inside the bolted joint, with a fatigue fracture surface showing a crescent moon geometry in the case of short cracks (high stress range) and evolving towards a nearly straight crack front in the case of long cracks (small stress range) [].
Analysis of the fracture surface topography of X8CrNiS18-9 austenitic stainless-steel specimens for different tensile-compression fatigue loading and notch radii showed that the root mean square height and the void volume (fracture surface parameters) increase with higher values of the stress amplitude and the notch radius, and decrease with increasing fatigue life []. In AW 6063 T6 aluminum alloy specimens subjected to rotary bending, a good correlation has been found between the stress concentration factor and the ratio between the area of the final fracture zone and the total cross-sectional area []. By performing hydrogen-assisted cracking (HAC) as a function of hydrogen pre-charging time, a method was employed to initiate highly symmetric circumferential cracks in circumferentially grooved round bars (in a controlled manner) without the need for fatigue pre-cracking [].
Commonly used methods for fatigue evaluation of notched metallic components are: nominal stress approaches, local stress-strain approaches, critical distance theories (CDT), and weighting control parameter-based approaches []. To consider the size effect in notch fatigue analysis, a modified stress field intensity (SFI) approach [] and a reformulation of CDT introducing the relative stress gradient (RSG) concept [] have been proposed. A probabilistic fatigue model for life evaluation (combining the weakest link theory with the concept of strain energy) has developed the concept of effective strain energy density (SED), to build the connection between the experimental data of the smooth samples and the SED of the notches within the critical damage region [].
Analysis of the stress distribution at the notch tip shows a pseudo-stress singularity characterized by the notch stress intensity factor (NSIF), whose critical value can be used to determine the fracture toughness of very brittle materials from notched specimens []. Studies on finite-width cracked and uncracked notched plates have concluded that from the existing empirical formulae for finite-width cracked unnotched plates, it is possible to estimate the NSIF in uncracked notched plates and the stress intensity factor (SIF) in cracked notched plates []. The peak stress method (PSM) has been used to obtain polynomial expressions to quickly estimate the NSIFs at the tips of V-notches [].
In ZK60-T5 magnesium alloy, the notch fracture toughness (NFT) was obtained by combining the NSIF and the CDT and by using a machining learning approach, the support vector machine (SVM), trained using experimental values []. Circumferentially notched round bar (CNRB) specimens and circumferentially cracked round bar (CCRB) specimens have been used to obtain the fracture toughness, the fatigue crack growth rates, the susceptibility to HAC, etc. [,,,,]. Tests with these specimens present certain advantages over more conventional ones: they are simple, quicker, and less expensive.
Circumferential external cracks (generated by rotating bending in a notched bar) usually present some eccentricity in relation to the bar axis [] that can be due to several causes: slight asymmetries regarding the sample, the grips, or the testing machine, as well as non-uniform material properties, residual stress effects, etc. [,]. In bars subjected to tensile load, external annular cracks that have a certain eccentricity propagate due to fatigue, increasing this parameter [].
In elliptical surface cracks located in a notched round bar subjected to tension loading, it has been observed that the SIF is strongly dependent on the stress concentration coefficient, while the influence of notch geometry is negligible for a given stress concentration coefficient []. Fatigue crack growth for various cracks in unnotched and notched round bars was directly modeled by using a step-by-step numerical simulation technique, which calculates the SIFs at a set of crack front points using the finite element method and then applies an appropriate fatigue crack growth law to this set of points to obtain a new crack front [].
When external cracks are generated in notched bars (at the notch root) by rotating bending fatigue, a significant amount of the ligaments are eccentric and some are non-circular []. These specimens (CCRB) are used in fracture, fatigue, and stress corrosion testing because of their simplicity and shorter testing time [,,,,]. In addition, these crack geometries appear in bolts and notched bars subjected to fatigue, stress corrosion cracking, or corrosion-fatigue with different load types [,,,,,]. For these geometries subjected to tensile loading, in the framework of linear elastic fracture mechanics, it is of interest to obtain solutions of the SIF (a key parameter when determining stresses in the crack tip). Thus, the aim of the present paper is to study the notch effect on the SIF of elliptically notched bars with external annular cracks that present a circular ligament with a certain eccentricity with respect to the bar axis. For this purpose, three elliptical notch geometries of equal depth and different axial semiaxis (aspect ratio of the ellipse) are analyzed, and the SIF results are compared with those of a smooth bar with the same crack configurations.
2. Numerical Procedure
The SIFs of eccentric circumferential external cracks located in the cross section of smooth and notched round bars subjected to tensile loading were calculated numerically with finite element analysis. The elliptically notched bar geometry (Figure 1 and Figure 2) is given by the outer diameter of the bar (D = 3 mm, the same as for the smooth bar), the elliptical notch radial semi-axis (b = 0.4 mm, the notch depth is the same for all notched bars), and the elliptical notch axial semi-axis c (Figure 2b). Four specimen geometries were studied (Figure 1): smooth bar (no notch), sharp notched bar (c/b = 0.5), circular notched bar (c/b = 1), and blunt notched bar (c/b = 2).
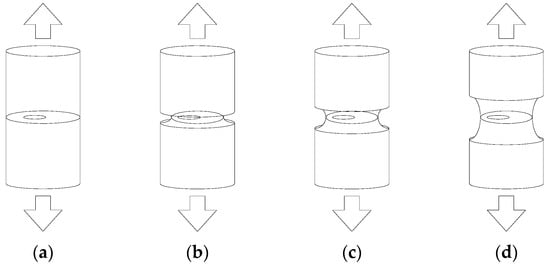
Figure 1.
Eccentric annular external cracks in: (a) smooth bar (no notch); (b) sharp notched bar (c/b = 0.5); (c) circular notched bar (c/b = 1); (d) blunt notched bar (c/b = 2).
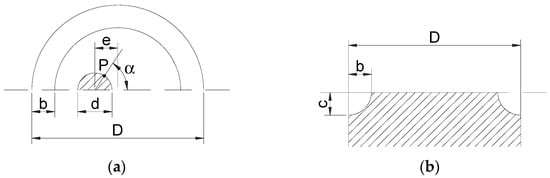
Figure 2.
Parameters defining the geometry of the elliptically notched bar with an eccentric annular external crack: (a) cross section of the bar at the notch root; (b) longitudinal section of the bar.
The geometry of the circumferential crack was characterized by the diameter of the resistant ligament d (which is considered circular) and its eccentricity with respect to the bar axis e (Figure 2a).
The cracks analyzed were those corresponding to relative ligament diameters d/D from 3/30 to 15/30 in 2/30 increments and relative ligament eccentricities e/D from 0 to ((15/60) − d/2D)) in 1/30 increments.
Figure 2a shows how the position of a crack front point P was characterized through the angle α, arc of the circle (corresponding to the crack front) measured from the greatest crack depth point to the point P. Thus, this angle α is 0° for the crack front point of greatest depth and 180° for the crack front point of least depth.
The three-dimensional finite element method (using MSC.Marc 2012 software) has been used to model a quarter of the bar with the appropriate boundary conditions, restraining the displacement in some directions of certain nodes (to simulate the problem symmetry), and applying a tension loading of 100 MPa at the bar end (Figure 3).
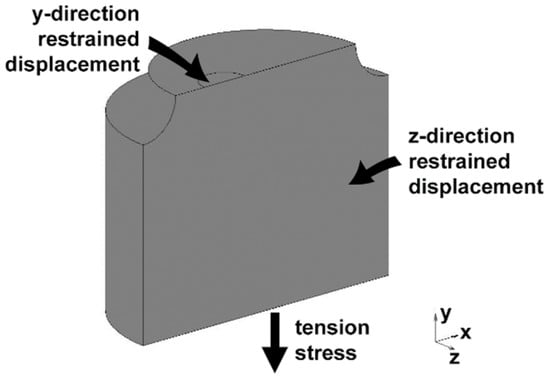
Figure 3.
A quarter of the bar with the appropriate boundary conditions (to simulate the problem symmetry) and the tension stress applied at the bar end.
20-node isoparametric hexahedral elements were used, with the nodes closest to the crack tip shifted to a ¼ position to simulate the stress singularity. The element type uses triquadratic interpolation functions, and the stiffness of this element is formed with a 27-point Gaussian integration. The mesh was further refined in the areas around the crack front (where the smallest elements of ~0.015D edge length are located) and the notch. Figure 4 shows the finite element mesh for the four specimens studied, and Figure 5 shows mesh details in some areas where the mesh is more refined. The models have between 17,972 and 26,477 nodes and between 4100 and 6000 elements.
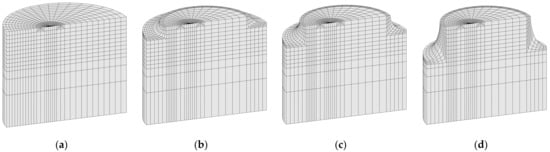
Figure 4.
Three-dimensional finite element meshes: (a) smooth bar (no notch); (b) sharp notched bar (c/b = 0.5); (c) circular notched bar (c/b = 1); (d) blunt notched bar (c/b = 2).
Figure 5.
Detailed finite element mesh: (a) at the crack tip; (b) around the crack; (c) in the notch.
SIF KI has been obtained from its relationship with the energy release rate, calculated using the J-integral (with a subroutine provided by the MSC.Marc 2012 software), through the following equation for plane strain []:
where E is the Young’s modulus and ν is the Poisson’s ratio, whose values for the calculations are typical for steel (200 GPa and 0.3, respectively). Using the J-integral method, knowledge of the exact displacement field in the crack tip vicinity is not required. The J-integral evaluation is based on the domain integration method. For the calculations, MSC.Marc 2012 software requires the nodes along the crack front, the shift vector, and the nodes of the rigid region. The crack front is defined by an unsorted list of nodes. The topology-based determination of the rigid region creates disks of increasing size at each crack front node from element faces. The shift vector at each crack front node is automatically determined to be perpendicular to both the tangent to the crack front and the normal to the crack face at each crack front node []. The J-integral was calculated at 21 equidistant points on the modeled crack front.
In addition, a convergence study of mesh size was carried out, decreasing the dimensions of the elements around the crack and the notch. It was performed for two specimens of circular notch (c/b = 1) with: d/D = 3/30 and e/D = 6/30; d/D = 13/30 and e/D = 1/30. The element numbers of the meshes used in the convergence study are shown in Table 1, and the results of the J-integral along the crack front are shown in Figure 6. The difference between the results of the J-integral for the most refined meshes, with respect to the mesh used in this paper, was less than 3%.

Table 1.
The element numbers of the meshes used in the convergence study.

Figure 6.
Finite element mesh convergence study: (a) d/D = 3/30 and e/D = 6/30; (b) d/D = 13/30 and e/D = 1/30.
The SIF has been dimensioned using the following expression in order to obtain the dimensionless SIF Y:
where σ is the tension stress applied to the bar ends.
3. Numerical Results
3.1. Stress Intensity Factors Solutions for Non-Eccentric Annular Cracks in Smooth Bars
For a smooth bar subjected to tensile loading with a non-eccentric circumferential external crack (e = 0), there are several SIF solutions in the scientific literature [,,,]. The Tada, Paris, and Irwin handbook [] provides the following expression:
Figure 7 shows the dimensionless SIF results obtained in the present paper and the Tada, Paris, and Irwin solution (versus relative ligament diameter). As the relative ligament diameter d/D becomes smaller, the relative crack depth and the SIF value increase. For d/D between 0.1 and 0.5, the results of the present paper are in perfect agreement with the solution of Tada, Paris, and Irwin [].
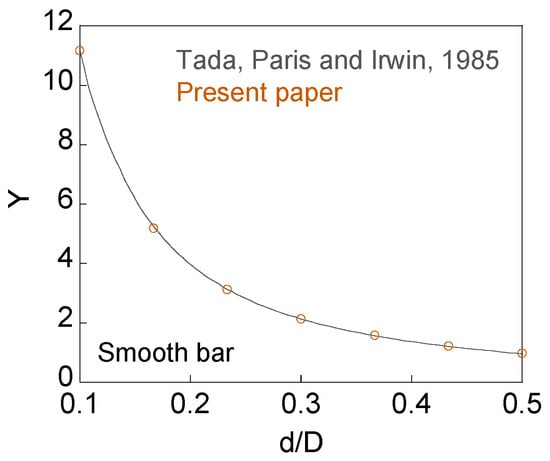
Figure 7.
Dimensionless SIF vs. relative ligament diameter for smooth bars with a non-eccentric annular external crack, present paper, and Tada, Paris, and Irwin solution [].
In the symmetrical case (non-eccentric cracks e = 0), for the studied crack geometries, the SIF results of notched bars match those of smooth bar since the distance from the crack front to the notch is too large for the notch to have any effect on the SIF and the relative crack depth (or relative ligament diameter) is the only determining parameter in the value of the dimensionless SIF. In a circumferentially notched round bar with a non-eccentric annular crack, for small crack depths, the SIF is lower than if there is no notch (smooth bar). Once the crack has reached a critical crack depth, the notch has no effect on the crack tip stress field, and the SIF of a smooth bar, where the notch depth has been added to the crack depth, is applicable []. In circular notches, both SIF values (for notched and unnotched bars) approach each other more quickly when the notch depth is lower and the notch radius is smaller []. On the other hand, in non-eccentric inner cracks, the notch affects the SIF value for the whole range of crack depths, increasing it with respect to that of the smooth bar and when the elliptical notch axial semi-axis is larger (for the same notch depth) [].
3.2. Stress Intensity Factors Solutions for Eccentric Annular Cracks
Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 show the dimensionless SIF along the crack front (Y–α curves) for smooth and notched bars (c/b = {0.5, 1, 2}) with circumferential external cracks characterized through the relative ligament diameter and the relative ligament eccentricity (d/D and e/D). Eccentricity causes the SIF value to vary along the crack front, increasing with the crack depth from the crack front point corresponding to α = 180° (shallowest depth) to the point associated with α = 0° (deepest depth). The variation of the SIF along the crack front is greater when the bar is notched than when it is smooth, and in the former case when the axial semi-axis of the elliptical notch increases (for the same notch depth). There is a greater difference between the Y–α curve of the smooth bar and that of the sharp notched bar than between the Y–α curve of the sharp notched bar and that of the circular notched bar; this difference is small and very similar to the one between the Y–α curve of the circular notched bar and the blunt notched bar.
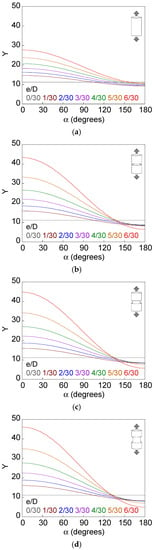
Figure 8.
Dimensionless SIF along the crack front, d/D = 3/30: (a) smooth bar; (b) sharp notched bar; (c) circular notched bar; (d) blunt notched bar.
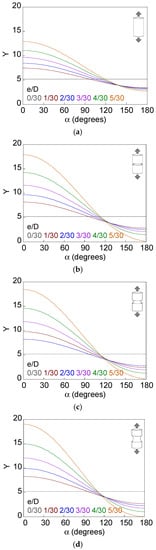
Figure 9.
Dimensionless SIF along the crack front, d/D = 5/30: (a) smooth bar; (b) sharp notched bar; (c) circular notched bar; (d) blunt notched bar.
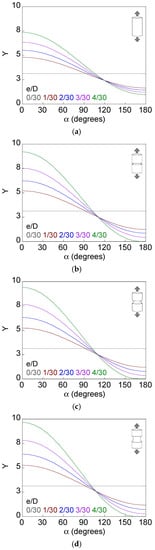
Figure 10.
Dimensionless SIF along the crack front, d/D = 7/30: (a) smooth bar; (b) sharp notched bar; (c) circular notched bar; (d) blunt notched bar.
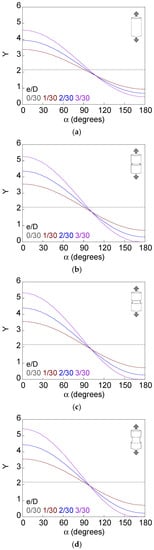
Figure 11.
Dimensionless SIF along the crack front, d/D = 9/30: (a) smooth bar; (b) sharp notched bar; (c) circular notched bar; (d) blunt notched bar.
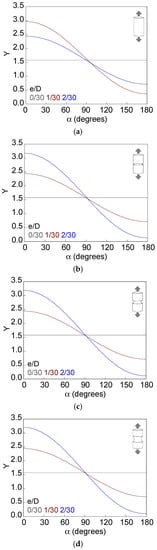
Figure 12.
Dimensionless SIF along the crack front, d/D = 11/30: (a) smooth bar; (b) sharp notched bar; (c) circular notched bar; (d) blunt notched bar.
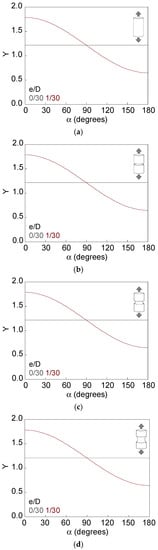
Figure 13.
Dimensionless SIF along the crack front, d/D = 13/30: (a) smooth bar; (b) sharp notched bar; (c) circular notched bar; (d) blunt notched bar.
Figure 14 and Figure 15 plot the maximum and minimum dimensionless SIF (Ymax and Ymin) versus the relative ligament eccentricity (e/D).

Figure 14.
Maximum dimensionless SIF vs. relative ligament eccentricity: (a) smooth bar; (b) sharp notched bar; (c) circular notched bar; (d) blunt notched bar.

Figure 15.
Minimum dimensionless SIF vs. relative ligament eccentricity: (a) smooth bar; (b) sharp notched bar; (c) circular notched bar; (d) blunt notched bar.
The maximum dimensionless SIF rises with decreasing relative ligament diameter and increasing relative ligament eccentricity. In addition, the presence of the notch in the bar increases the maximum SIF, also slightly increasing its value with the notch axial semi-axis. In contrast, the minimum dimensionless SIF decreases with the rise of the relative ligament diameter and the relative ligament eccentricity, except for d/D = 3/30 (where there is a pronounced decrease in the minimum dimensionless SIF for e/D = 1/30, with respect to the symmetrical case, that then increases slightly with eccentricity, and only in notched bars does it decrease again at high eccentricities). The presence of the notch and the increase in the elliptical notch axial semi-axis produce lower values of the minimum dimensionless SIF.
Figure 16 shows the initial and deformed specimens, after applying a high tensile loading at the bar ends, for a circular notch (c/b = 1) and cracks with d/D = 5/30 and e/D = {0/30, 1/30, 5/30}. The non-eccentric crack produces the same SIF value at all points on the crack front, with no contact at the cracked surface (Figure 16a). On the other hand, for the relative ligament diameters studied in the smooth and notched bars, the eccentricity of the crack (from a certain value) produces partial contact of the cracked surface in the area close to the shallowest crack front (Figure 16b), produced by the compression of part of the specimen. Moreover, only in notched bars, for some of the relative ligament diameters analyzed in this paper and for the maximum relative ligament eccentricities, the eccentricity causes full contact of the cracked surface in a zone close to the shallower crack front. The occurrence of a slight contact between the cracked surfaces drastically decreases the SIF [], and the full contact creates a null SIF value in the arc of the crack front where it occurs.

Figure 16.
Initial and deformed notched bar (c/b = 1 and d/D = 5/30): (a) no crack surface contact (e/D = 0/30); (b) crack surface partial contact (e/D = 1/30); (c) crack surface total contact (e/D = 5/30).
When there is eccentricity in the cracks, tensile load produces bar bending due to the lack of geometric symmetry, which significantly increases the dimensionless SIF in the deepest crack front area while decreasing it in the shallowest. Thus, in [], for an eccentric annular external cracked bar under tensile load, the SIF has been calculated based on the superposition principle from solutions for a non-eccentric annular external cracked bar subjected to tension loading and for the same geometry subjected to bending loading. The bending of the bar under tension loading significantly increases the variation of the SIF along the crack front in relation to the case of restrained bending. In most of the studied geometries, bar bending results in partial or full contact of the cracked surfaces in the shallower crack front zone, which drastically reduces the value of the dimensionless SIF in said area and causes differences between SIF values for smooth and notched bars.
Figure 17 shows the initial and deformed specimen for smooth and notched bars with a crack geometry of d/D = 3/30 and e/D = 6/30, observing how the bar bending is greater for the notched bars than for the smooth one and slightly higher as the ratio between notch semi-axes c/b increases. When the surface interference effect appears, the different crack contact (Figure 18, with d/D = 3/30 and e/D = 6/30), for the same crack geometry, between the smooth bar and the notched bars (due to the lack of material in the specimen because of the notch) and by increasing c/b (due to the lost constraint), causes the variations in the bar bending and with it in dimensionless SIFs.
Figure 17.
Initial and deformed bar (d/D = 3/30 and e/D = 6/30): (a) smooth bar; (b) sharp notched bar; (c) circular notched bar; (d) blunt notched bar.

Figure 18.
Crack contact surface (in yellow) on bar cross section (d/D = 3/30 and e/D = 6/30): (a) smooth bar; (b) sharp notched bar; (c) circular notched bar; (d) blunt notched bar.
4. Conclusions
The following conclusions have been obtained regarding the notch effect on the stress intensity factor (SIF) in eccentric annular external cracks located in the notch root of elliptically notched round bars under tensile loading:
- -
- The crack eccentricity with respect to the bar axis causes a difference in depth along the crack front and the bending of the bar, leading to a decrease in the dimensionless SIF value from the point of deepest crack depth (maximum SIF) to the point of shallowest crack depth (minimum SIF).
- -
- The maximum dimensionless SIF (associated with the maximum depth crack front point) and the difference between dimensionless SIFs along the crack front rise with decreasing relative ligament diameter, increasing relative ligament eccentricity, the presence of a notch in the bar, and the increase in the elliptical notch axial semi-axis.
- -
- The partial and full contact of the crack surface in the crack front zone of the shallowest crack depth is a constraint to the bar bending, reduces the dimensionless SIF values, and produces variations between the dimensionless SIF values of the smooth and notched bars due to contact differences caused by the bar geometries.
Author Contributions
Numerical modeling concept and design, J.T., B.G. and J.-C.M.; finite element modeling development, B.G., J.-C.M. and I.G.; data analysis, J.T., B.G., J.-C.M. and I.G.; writing and editing, J.T. and I.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the following Spanish Institutions: Ministry for Science and Technology (MICYT; Grant MAT2002-01831), Ministry for Education and Science (MEC; Grant BIA2005-08965), Ministry for Science and Innovation (MICINN; Grant BIA2008-06810), Ministry for Economy and Competitiveness (MINECO; Grant BIA2011-27870), Junta de Castilla y León (JCyL; Grants SA067A05, SA111A07, SA039A08, and SA132G18), and Fundación Samuel SolórzanoBarruso (Grant FS/9-2019) of the University of Salamanca (USAL).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. With regard to the research funds, the different institutions providing financial support for the scientific research had no role in the design of the study, in the collection, analysis, or interpretation of data, in the writing of the present manuscript, or in the decision to publish the results.
Nomenclature
| Symbols | |
| α | angle defining a crack front point |
| b | elliptical notch radial semi-axis (notch depth) |
| c | elliptical notch axial semi-axis |
| c/b | elliptical notch semi-axes ratio |
| d | ligament diameter |
| d/D | relative ligament diameter |
| D | outer diameter of the bar |
| e | ligament eccentricity with respect to the bar axis |
| e/D | relative ligament eccentricity |
| E | Young’s modulus |
| J | J-integral |
| KI | SIF in mode I |
| ν | Poisson’s ratio |
| P | crack front point |
| σ | tension stress applied to the bar ends |
| Y | dimensionless SIF |
| Ymax | maximum dimensionless SIF |
| Ymin | minimum dimensionless SIF |
| Abbreviations | |
| CCRB | circumferentially cracked round bar |
| CDT | critical distance theory |
| CNRB | circumferentially notched round bar |
| HAC | hydrogen-assisted cracking |
| NSIF | notch stress intensity factor |
| PDM | potential drop method |
| PSM | peak stress method |
| RSG | relative stress gradient |
| SED | strain energy density |
| SFI | stress field intensity |
| SIF | stress intensity factor |
| SVM | support vector machine |
References
- Campagnolo, A.; Bär, J.; Meneghetti, G. Analysis of crack geometry and location in notched bars by means of a three-probe potential drop technique. Int. J. Fatigue 2019, 124, 167–187. [Google Scholar] [CrossRef]
- Nikravesh, M.Y.; MeidanSharafi, M. Failure of a steam turbine rotor due to circumferential crack growth influenced by temperature and steady torsion. Eng. Fail. Anal. 2016, 66, 296–311. [Google Scholar] [CrossRef]
- Toribio, J.; González, B.; Matos, J.C.; Ayaso, F.J. Fatigue behaviour of bolted joints. Met. Mater. Int. 2012, 18, 553–558. [Google Scholar] [CrossRef]
- Macek, W.; Robak, G.; Żak, K.; Branco, R. Fracture surface topography investigation and fatigue life assessment of notched austenitic steel specimens. Eng. Fail. Anal. 2022, 135, 106121. [Google Scholar] [CrossRef]
- Strzelecki, P.; Wachowski, M. Effect of the stress concentration factor on the final fracture zone of aluminium AW 6063 T6 for rotating bending specimens. Mater. Today Commun. 2022, 31, 103766. [Google Scholar] [CrossRef]
- Brilz, M.; Hoche, H.; Oechsner, M. Hydrogen-assisted cracking (HAC) of high-strength steels as a function of the hydrogen pre-charging time. Eng. Fract. Mech. 2022, 261, 108246. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.-P.; Correia, J.A.F.O.; de Jesus, A.M.P.; Berto, F. Recent advances on notch effects in metal fatigue: A review. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 637–659. [Google Scholar] [CrossRef]
- Wu, Y.-L.; Zhu, S.-P.; He, J.-C.; Liao, D.; Wang, Q. Assessment of notch fatigue and size effect using stress field intensity approach. Int. J. Fatigue 2021, 149, 106279. [Google Scholar] [CrossRef]
- Ye, W.-L.; Zhu, S.-P.; Niu, X.; He, J.-C.; Correia, J.A.F.O. Fatigue life prediction of notched components under size effect using critical distance theory. Theor. Appl. Fract. Mech. 2022, 121, 103519. [Google Scholar] [CrossRef]
- Li, X.-K.; Zhu, S.-P.; Liao, D.; Correia, J.A.F.O.; Berto, F.; Wang, Q. Probabilistic fatigue modelling of metallic materials under notch and size effect using the weakest link theory. Int. J. Fatigue 2022, 159, 106788. [Google Scholar] [CrossRef]
- Pluvinage, G. Fatigue and fracture emanating from notch; the use of the notch stress intensity factor. Nucl. Eng. Des. 1998, 185, 173–184. [Google Scholar] [CrossRef]
- Lou, B.; Barltrop, N. Universal hybrid method and approximate closed-form solution for V-notched and V-notch-cracked plate under tensile and in-plane bending. Theor. Appl. Fract. Mech. 2020, 108, 102579. [Google Scholar] [CrossRef]
- Visentin, A.; Campagnolo, A.; Meneghetti, G. Analytical expressions to estimate rapidly the notch stress intensity factors at V-notch tips using the Peak Stress Method. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 1572–1595. [Google Scholar] [CrossRef]
- Alshaiji, A.; Albinmousa, J.; Peron, M.; AlMangour, B.; Ali, U. Analyzing quasi-static fracture of notched magnesium ZK60 using notch fracture toughness and support vector machine. Theor. Appl. Fract. Mech. 2022, 121, 103463. [Google Scholar] [CrossRef]
- Stark, H.L.; Ibrahim, R.N. Estimating fracture toughness from small specimens. Eng. Fract. Mech. 1986, 25, 395–401. [Google Scholar] [CrossRef]
- Ibrahim, R.N.; Kotousov, A. Eccentricity correction for the evaluation of fracture toughness from cylindrical notched test smallspecimens. Eng. Fract. Mech. 1999, 64, 49–58. [Google Scholar] [CrossRef]
- Bozkurt, F.; Schmidová, E. Fracture toughness evaluation of S355 steel using circumferentially notched round bars. Period. Polytech. Transp. Eng. 2019, 47, 91–95. [Google Scholar] [CrossRef]
- Fischer, J.; Freudenthaler, P.J.; Bradler, P.R.; Lang, R.W. Novel test system and test procedure for fatigue crack growth testing with cracked round bar (CRB) specimens. Polym. Test. 2019, 78, 105998. [Google Scholar] [CrossRef]
- Singh, D.K.; Raman, R.K.S.; Maiti, S.K.; Bhandakkar, T.K.; Pal, S. Investigation of role of alloy microstructure in hydrogen-assisted fracture of AISI 4340 steel using circumferentially notched cylindrical specimens. Mat. Sci. Eng. A 2017, 698, 191–197. [Google Scholar] [CrossRef]
- Poduška, J.; Hutař, P.; Frank, A.; Kučera, J.; Sadílek, J.; Pinter, G.; Náhlík, L. Numerical simulations of cracked round bar test: Effect of residual stresses and crack asymmetry. Eng. Fract. Mech. 2018, 203, 18–31. [Google Scholar] [CrossRef]
- Toribio, J.; González, B.; Matos, J.C. Crack tip field in eccentric circumferentially cracked round bar (CCRB) under tensile loading. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 2153–2161. [Google Scholar] [CrossRef]
- Guo, W.; Shen, H.; Li, H. Stress intensity factors for elliptical surface cracks in round bars with different stress concentration coefficient. Int. J. Fatigue 2003, 25, 733–741. [Google Scholar] [CrossRef]
- Lin, X.B.; Smith, R.A. Fatigue growth simulation for cracks in notched and unnotched round bars. Int. J. Mech. Sci. 1998, 40, 405–419. [Google Scholar] [CrossRef]
- Ibrahim, R.N.; Stark, H.L. Establishing Klc from eccentrically fatigue cracked small circumferentially grooved cylindrical specimens. Int. J. Fract. 1990, 44, 179–188. [Google Scholar] [CrossRef]
- Toribio, J. On the concept of micro-fracture map (MFM) and its role in structural integrity evaluations in materials science and engineering: A Tribute to Jorge Manrique. Procedia Struct. Integr. 2020, 28, 2432–2437. [Google Scholar] [CrossRef]
- Toribio, J.; Vergara, D. Influence of microstructural anisotropy on the hydrogen-assisted fracture of notched samples of progressively drawn pearlitic steel. Procedia Struct. Integr. 2020, 28, 2390–2395. [Google Scholar] [CrossRef]
- Toribio, J. Hydrogen-assisted microdamage of eutectoid steel in the presence of notches: The tearing topography surface. Metals 2023, 13, 1365. [Google Scholar] [CrossRef]
- Irwin, G.R. Analysis of stresses and strain near the end of a crack traversing a plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Marc Analysis Research Corporation. MARC User Information; Marc Analysis Research Corporation: Palo Alto, CA, USA, 1994. [Google Scholar]
- Benthem, J.P.; Koiter, W.T. Asymptotic approximations to crack problems. In Method of Analysis and Solutions of Crack Problems; Sih, G.C., Ed.; Noordhoft International Publishing: Croningen, The Netherlands, 1973; pp. 131–178. [Google Scholar]
- Gray, T.G.F. Convenient closed form stress intensity factors for common crack configurations. Int. J. Fract. 1977, 13, 65–75. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.C.; Irwin, G.R. The Stress Analysis of Cracks Handbook, 3rd ed.; ASME Press: New York, NY, USA, 1985. [Google Scholar]
- Smirnov, V.; Vidyushenkov, S. Stress intensity factor for cylindrical specimen with external circular crack under tension. In International Scientific Siberian Transport Forum-TransSiberia 2021; Manakov, A., Edigarian, A., Eds.; Springer: Cham, Switzerland, 2021; pp. 408–417. [Google Scholar]
- Lefort, P. Stress intensity factors for a circumferential crack emanating from a notch in a round tensile bar. Eng. Fract. Mech. 1978, 10, 897–904. [Google Scholar] [CrossRef]
- Toribio, J.; Matos, J.C.; González, B. Notch effect on the stress intensity factor in tension-loaded circumferentially cracked bars. Eng. Fract. Mech. 2018, 202, 436–444. [Google Scholar] [CrossRef]
- Toribio, J.; González, B.; Matos, J.C.; González, I. Notch effects on the stress intensity factor and on the fatigue crack path for eccentric circular internal cracks in elliptically notched round bars under tensile loading. Materials 2022, 15, 9091. [Google Scholar] [CrossRef] [PubMed]
- Meguid, S.A. Three-dimensional finite element analysis of circumferentially-cracked notched and un-notched cylindrical components. Eng. Fract. Mech. 1990, 37, 361–371. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).