Creep Behavior and Deformation Mechanism of a Third-Generation Single Crystal Ni-Based Superalloy at 980 °C
Abstract
:1. Introduction
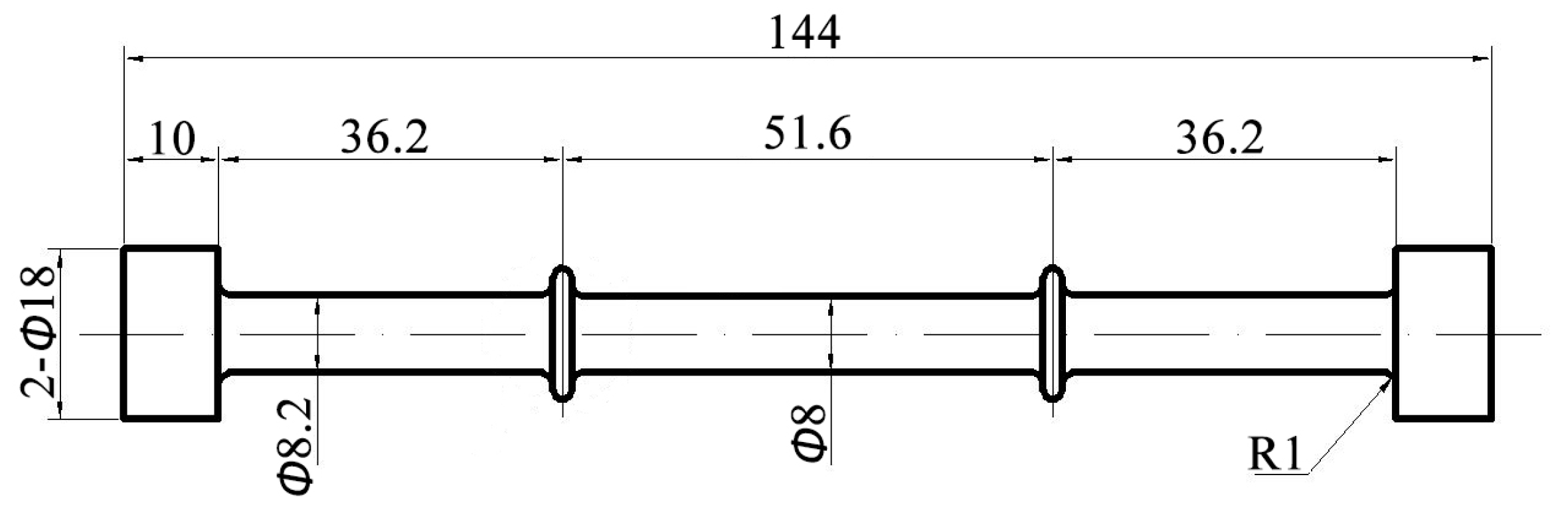
2. Materials and Methods
3. Results
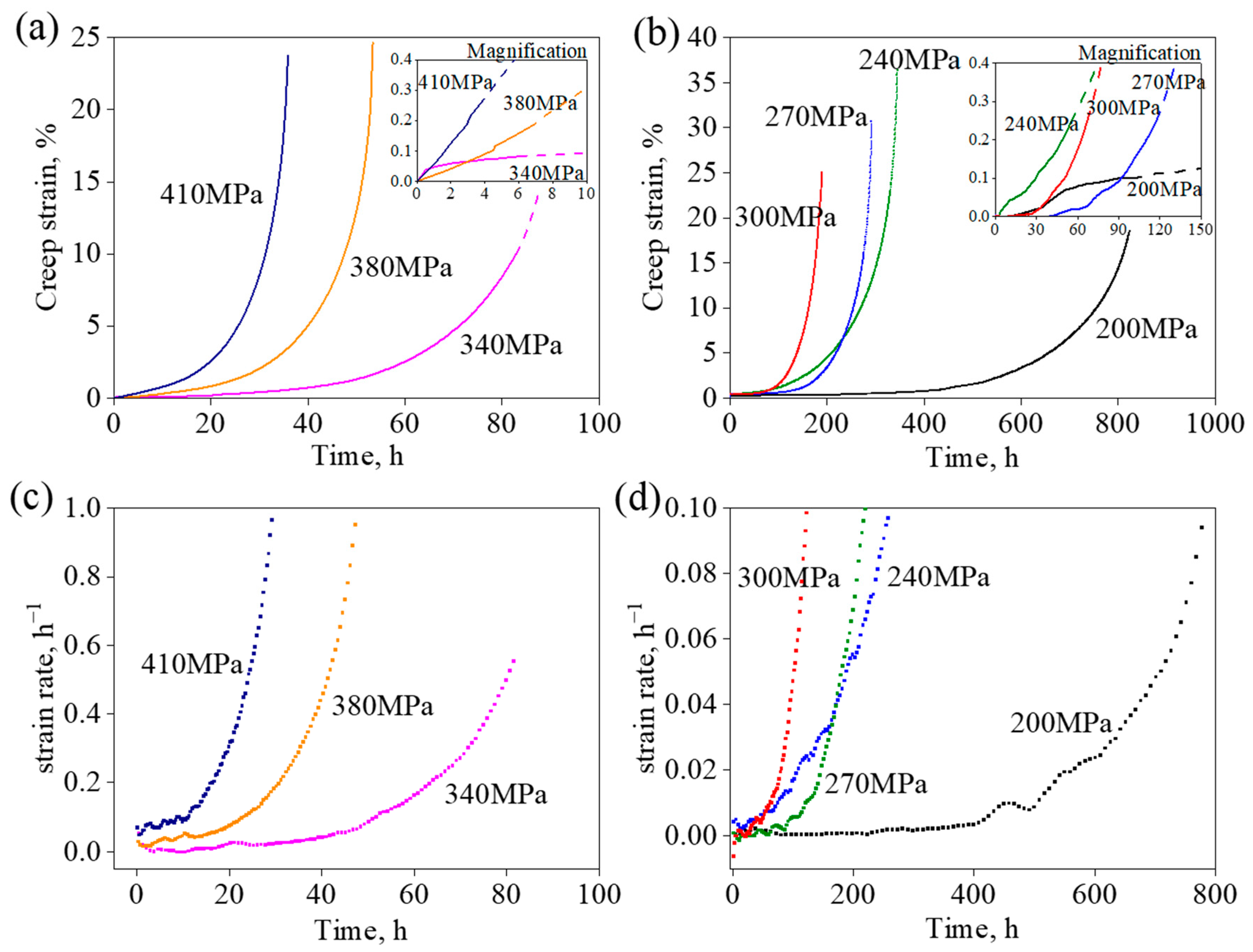
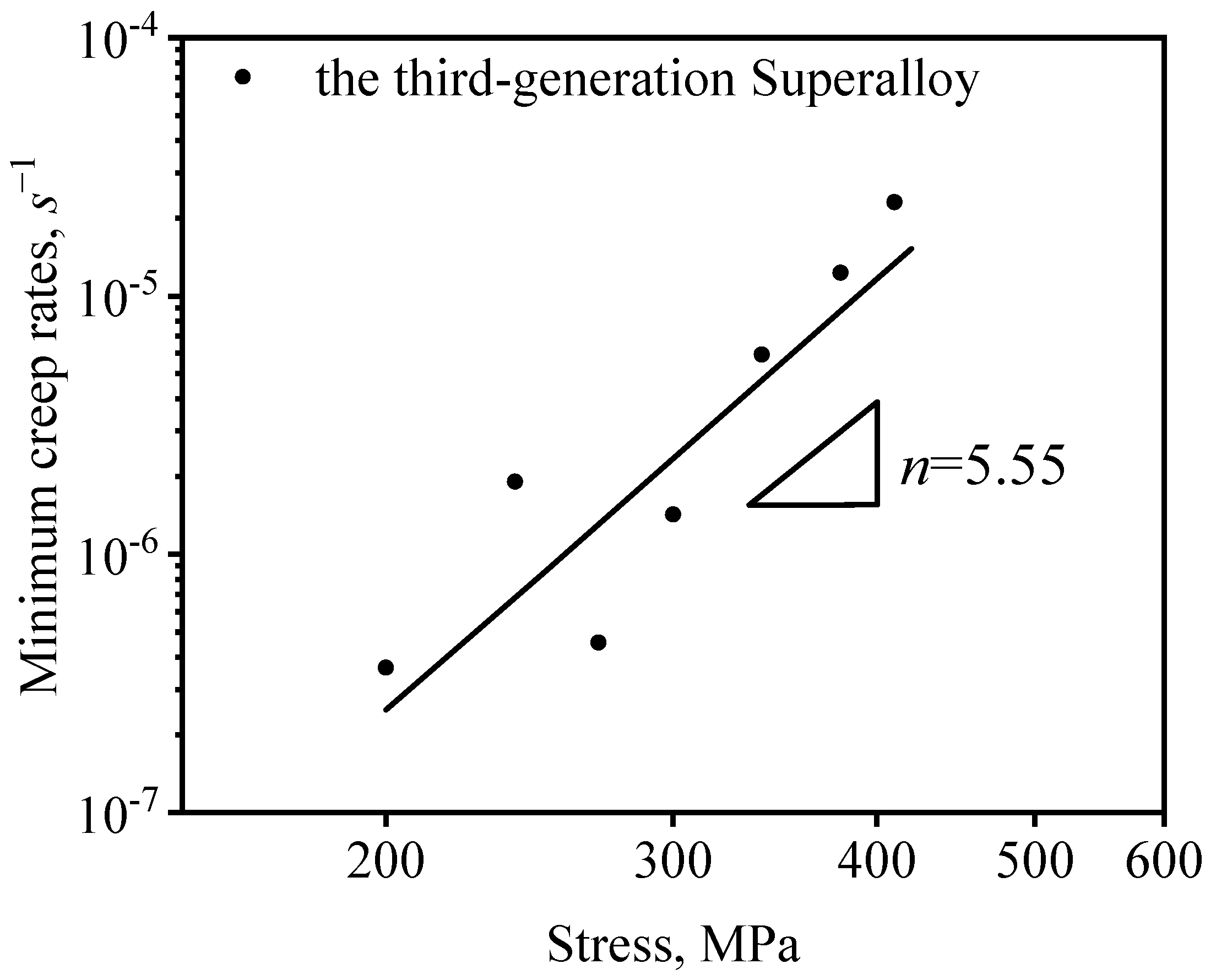
3.1. Creep Behavior and Analysis
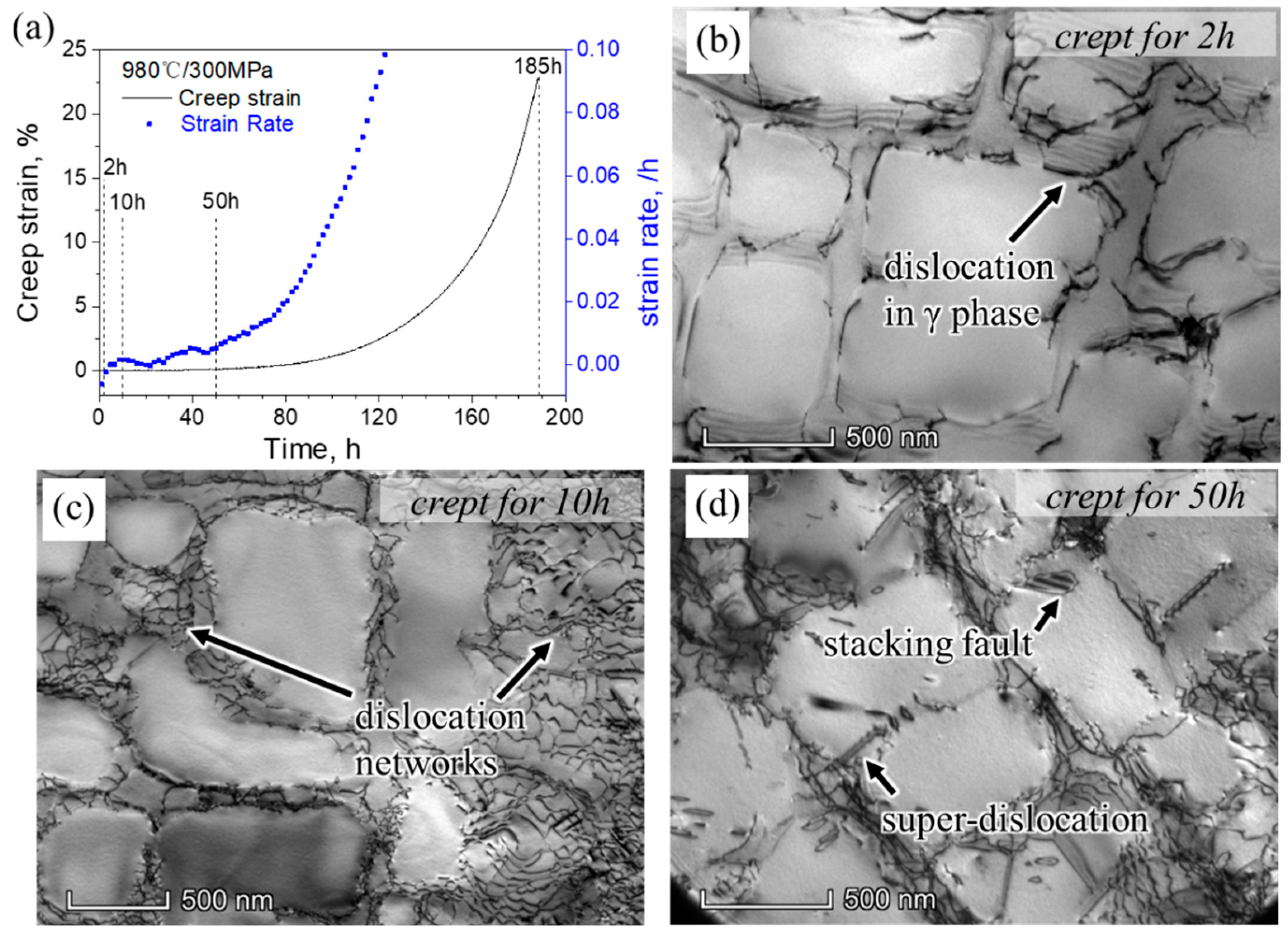
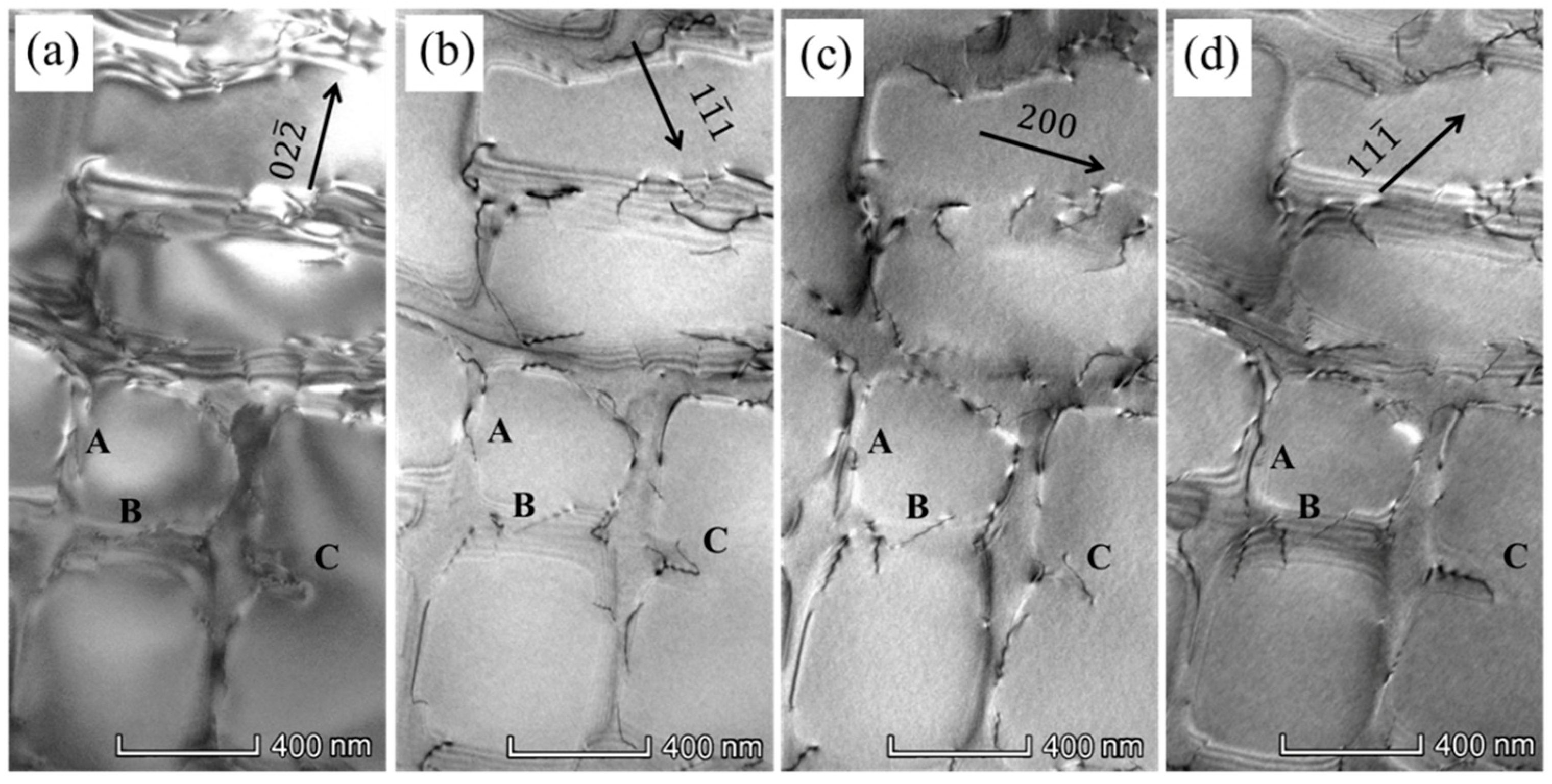
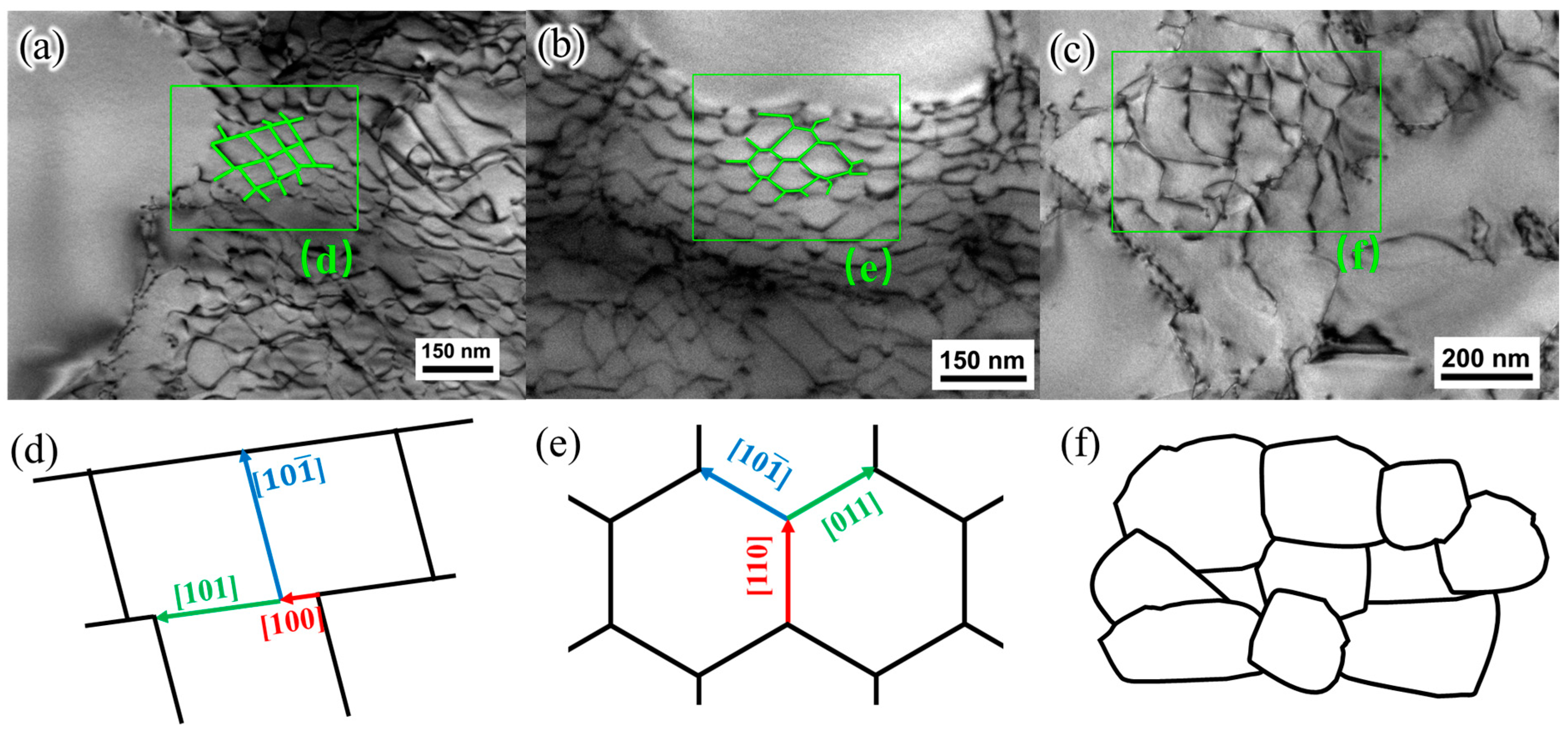
3.2. Microstructure and Dislocation Configuration
4. Discussion
4.1. Analysis of Dislocation Movement in γ Phase
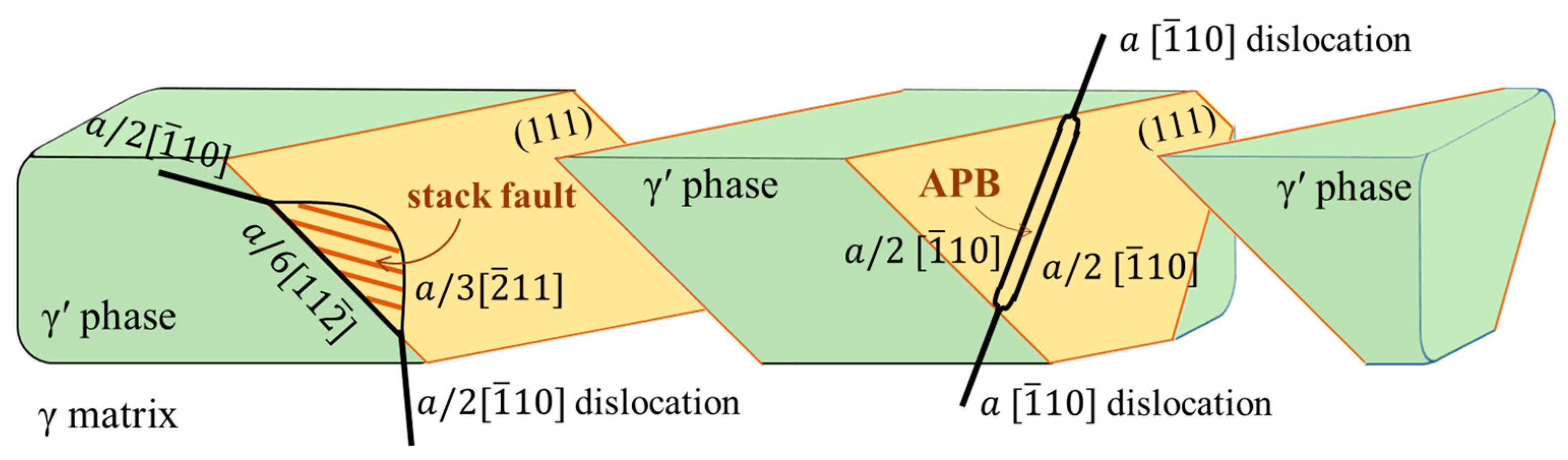
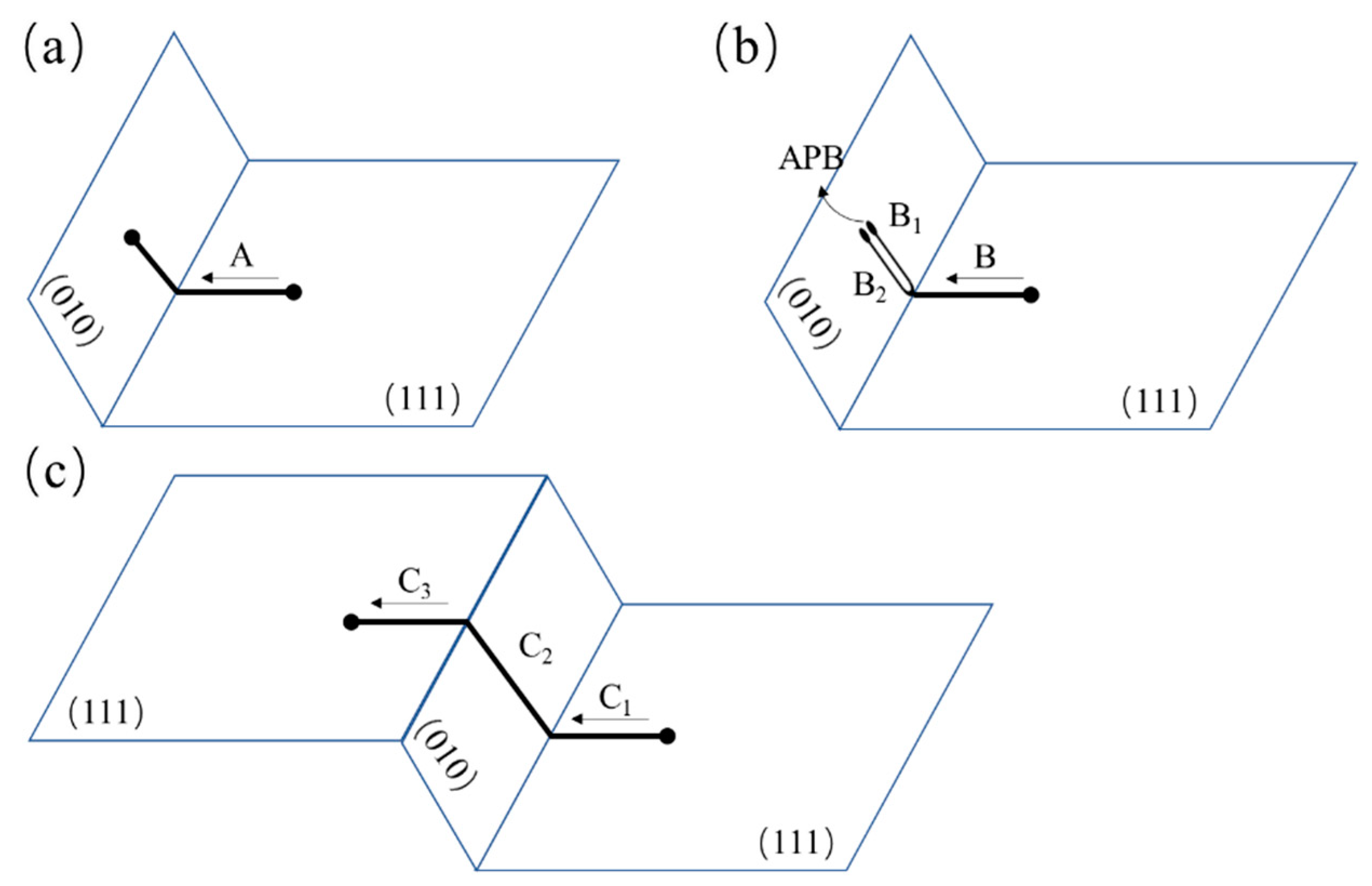
4.2. Mechanism of Dislocations Decomposing in γ′ Phase
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reed, R.C. The Superalloys Fundamentals and Applications; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Li, J.R.; Liu, S.Z.; Wang, X.G.; Shi, Z.X.; Zhao, J.Q. Development of A Low-Cost Third Generation Single Crystal Superalloy Dd9. Superalloys 2016, 2016, 55–63. [Google Scholar]
- Li, Y.; Wang, L.; Zhao, S.; Zhang, G.; Lou, L. Creep anisotropy of a 3rd generation nickel-base single crystal superalloy in the vicinity of [001] orientation. Mater. Sci. Eng. A 2022, 848, 143479. [Google Scholar] [CrossRef]
- Xia, W.; Zhao, X.; Yue, L.; Zhang, Z. Microstructural evolution and creep mechanisms in Ni-based single crystal superalloys: A review. J. Alloys Compd. 2020, 819, 152954. [Google Scholar] [CrossRef]
- Shang, Z.; Niu, H.; Wei, X.; Song, D.; Zou, J.; Liu, G.; Liang, S.; Nie, L.; Gong, X. Microstructure and tensile behavior of nickel-based single crystal superalloys with different Re contents. J. Mater. Res. Technol. 2022, 18, 2458–2469. [Google Scholar] [CrossRef]
- He, C.; Liu, L.; Huang, T.; Yang, W.; Wang, X.; Zhang, J.; Guo, M.; Fu, H. The effects of misfit and diffusivity on γ′ rafting in Re and Ru containing Nickel based single crystal superalloys—Details in thermodynamics and dynamics. Vacuum 2021, 183, 109839. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, Z.; Chen, J.; Zhang, H.; Zhang, Y.; Lu, H. Effect of refractory elements M (=Re, W, Mo or Ta) on the diffusion properties of boron in nickel-based single crystal superalloys. Vacuum 2023, 211, 111923. [Google Scholar] [CrossRef]
- Tian, S.; Zhu, X.; Wu, J.; Yu, H.; Shu, D.; Qian, B. Influence of Temperature on Stacking Fault Energy and Creep Mechanism of a Single Crystal Nickel-based Superalloy. J. Mater. Sci. Technol. 2016, 32, 790–798. [Google Scholar] [CrossRef]
- Probst-Hein, M.; Dlouhy, A.; Eggeler, G. Interface dislocations in superalloy single crystals. Acta Mater. 1999, 47, 2497–2510. [Google Scholar] [CrossRef]
- Boualy, O.; Clément, N.; Benyoucef, M. Analysis of dislocation networks in crept single crystal nickel-base superalloy. J. Mater Sci. 2018, 53, 2892–2900. [Google Scholar] [CrossRef]
- Jiang, L.; Cui, Y.; Wu, M.; Li, S.; Han, Y. Creep behavior and dislocation mechanism of Ni3Al based single crystal alloy IC6SX at °C. Prog. Nat. Sci. Mater. Int. 2021, 31, 755–761. [Google Scholar] [CrossRef]
- Lv, X.; Zhang, J. Core structure of a <100> interfacial superdislocations in a nickel-base superalloy during high-temperature and low-stress creep. Mater. Sci. Eng. A 2017, 683, 9–14. [Google Scholar]
- Lv, X.; Zhang, J. Three-dimensional geometry of “square-like” dislocation network in nickel-base single crystal superalloy. J. Alloys Compd. 2016, 688, 449–455. [Google Scholar] [CrossRef]
- Zhang, J.X.; Murakumo, T.; Harada, H.; Koizumi, Y. Dependence of creep strength on the interfacial dislocations in a fourth generation SC superalloy TMS-138. Scr. Mater. 2003, 48, 287–293. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; He, Y.; Zheng, W.; Lou, L.; Zhang, J. Role of interfacial dislocation networks during secondary creep at elevated temperatures in a single crystal Ni-based superalloy. Scr. Mater. 2022, 217, 114769. [Google Scholar] [CrossRef]
- Shu, D.L.; Tian, S.G.; Liang, S.; Zhang, S.B. Deformation and Damage Mechanism of a 4.5% Re-containing Nickel-based Single Crystal Superalloy During Creep at 980 °C. J. Mater. Eng. 2017, 45, 93–100. [Google Scholar]
- Chang, C.; Jiang, L.; Wu, M.; Li, S.; Han, Y. Effect of temperature and stress on high temperature creep behavior of Ni3Al-based single crystal superalloy. Prog. Nat. Sci. Mater. Int. 2022, 32, 267–271. [Google Scholar] [CrossRef]
- Lv, P.; Liu, L.; Zhao, G.; Guo, S.; Zhou, Z.; Chen, R.; Zhao, Y.; Zhang, J. Creep properties and relevant deformation mechanisms of two low-cost nickel-based single crystal superalloys at elevated temperatures. Mater. Sci. Eng. A 2022, 851, 143561. [Google Scholar] [CrossRef]
- Zhao, G.; Tian, S.; Zhang, S.; Tian, N.; Liu, L. Deformation and damage features of a Re/Ru-containing single crystal nickel base superalloy during creep at elevated temperature. Prog. Nat. Sci. 2019, 29, 210–216. [Google Scholar] [CrossRef]
- Hirsch, P.B. A new theory of the anomalous yield stress in l12 alloys. Philos. Mag. A 1992, 65, 569–612. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Liu, J.Y.S.; Shi, Z.; Yue, X. Tensile Anisotropy of Single Crystal Superalloy DD9. Acta Metall. Sin. 2015, 51, 1253–1260. [Google Scholar]
- Xu, R.; Li, Y.; Yu, H. Microstructure Evolution and Dislocation Mechanism of a Third-Generation Single-Crystal Ni-Based Superalloy during Creep at 1170 °C. Materials 2023, 16, 5166. [Google Scholar] [CrossRef] [PubMed]
- Wen, Z.; Zhang, D.; Li, S.; Yue, Z.; Gao, J. Anisotropic creep damage and fracture mechanism of nickel-base single crystal superalloy under multiaxial stress. J. Alloys Compd. 2017, 692, 301–312. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, J.; Kang, L.; He, Y.; Xu, W. Creep Behavior Characterization of Nickel-Based Single-Crystal Superalloy DD6 Thin-Walled Specimens Based on a 3D-DIC Method. Materials 2023, 16, 3137. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, A.K.; Bird, J.E.; Dorn, J.E. Experimental correlations for high-temperature creep. Trans. ASM 1969, 62, 155–163. [Google Scholar]
- Li, Y.; Wang, L.; Zhang, G.; Zheng, W.; Lou, L.; Zhang, J. On the role of topological inversion and dislocation structures during tertiary creep at elevated temperatures for a Ni-based single crystal superalloy. Mater. Sci. Eng. A 2021, 809, 140982. [Google Scholar] [CrossRef]
- Svoboda, J.; Lukas, P. Modelling of kinetics of directional coarsening in Ni-superalloys. Acta Mater. 1996, 44, 2557–2565. [Google Scholar] [CrossRef]
- Tang, Y.; Huang, M.; Xiong, J.; Li, J.; Zhu, J. Evolution of super dislocation structures during tertiary creep of a nickel-based single-crystal superalloy at high temperature and low stress. Acta Mater. 2017, 126, 336–345. [Google Scholar] [CrossRef]
- Bürger, D.; Dlouhý, A.; Yoshimi, K.; Eggeler, G. How Nanoscale Dislocation Reactions Govern Low-Temperature and High-Stress Creep of Ni-Base Single Crystal Superalloys. Crystals 2020, 10, 134. [Google Scholar] [CrossRef]




| Cr | Co | Mo | W | Ta | Re | Nb | Al | Hf | C | Y | Ni |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.5 | 7 | 2 | 6.5 | 7.5 | 4.5 | 0.5 | 5.6 | 0.1 | 0.008 | 0.001 | Bal. |
| Temperature (°C) | Orientation | UTS (MPa) | YS (MPa) | EL (%) | RA (%) | E (GPa) |
|---|---|---|---|---|---|---|
| 20 | [001] | 983 | 929 | 20.8 | 20.6 | 135.3 |
| 980 | [001] | 809 | 627 | 29.2 | 43.1 | 93.3 |
| Stress/MPa | 200 | 240 | 270 | 300 | 340 | 380 | 410 |
|---|---|---|---|---|---|---|---|
| Lifetime/h | 841 | 502 | 292 | 185 | 91 | 53 | 35 |
| 0.036 | 0.189 | 0.044 | 0.047 | 0.583 | 1.231 | 2.306 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.; Li, Y.; Yu, H. Creep Behavior and Deformation Mechanism of a Third-Generation Single Crystal Ni-Based Superalloy at 980 °C. Metals 2023, 13, 1541. https://doi.org/10.3390/met13091541
Xu R, Li Y, Yu H. Creep Behavior and Deformation Mechanism of a Third-Generation Single Crystal Ni-Based Superalloy at 980 °C. Metals. 2023; 13(9):1541. https://doi.org/10.3390/met13091541
Chicago/Turabian StyleXu, Ruida, Ying Li, and Huichen Yu. 2023. "Creep Behavior and Deformation Mechanism of a Third-Generation Single Crystal Ni-Based Superalloy at 980 °C" Metals 13, no. 9: 1541. https://doi.org/10.3390/met13091541
APA StyleXu, R., Li, Y., & Yu, H. (2023). Creep Behavior and Deformation Mechanism of a Third-Generation Single Crystal Ni-Based Superalloy at 980 °C. Metals, 13(9), 1541. https://doi.org/10.3390/met13091541





