A Molecular Dynamics Simulation to Shed Light on the Mechanical Alloying of an Al-Zr Alloy Induced by Severe Plastic Deformation
Abstract
:1. Introduction
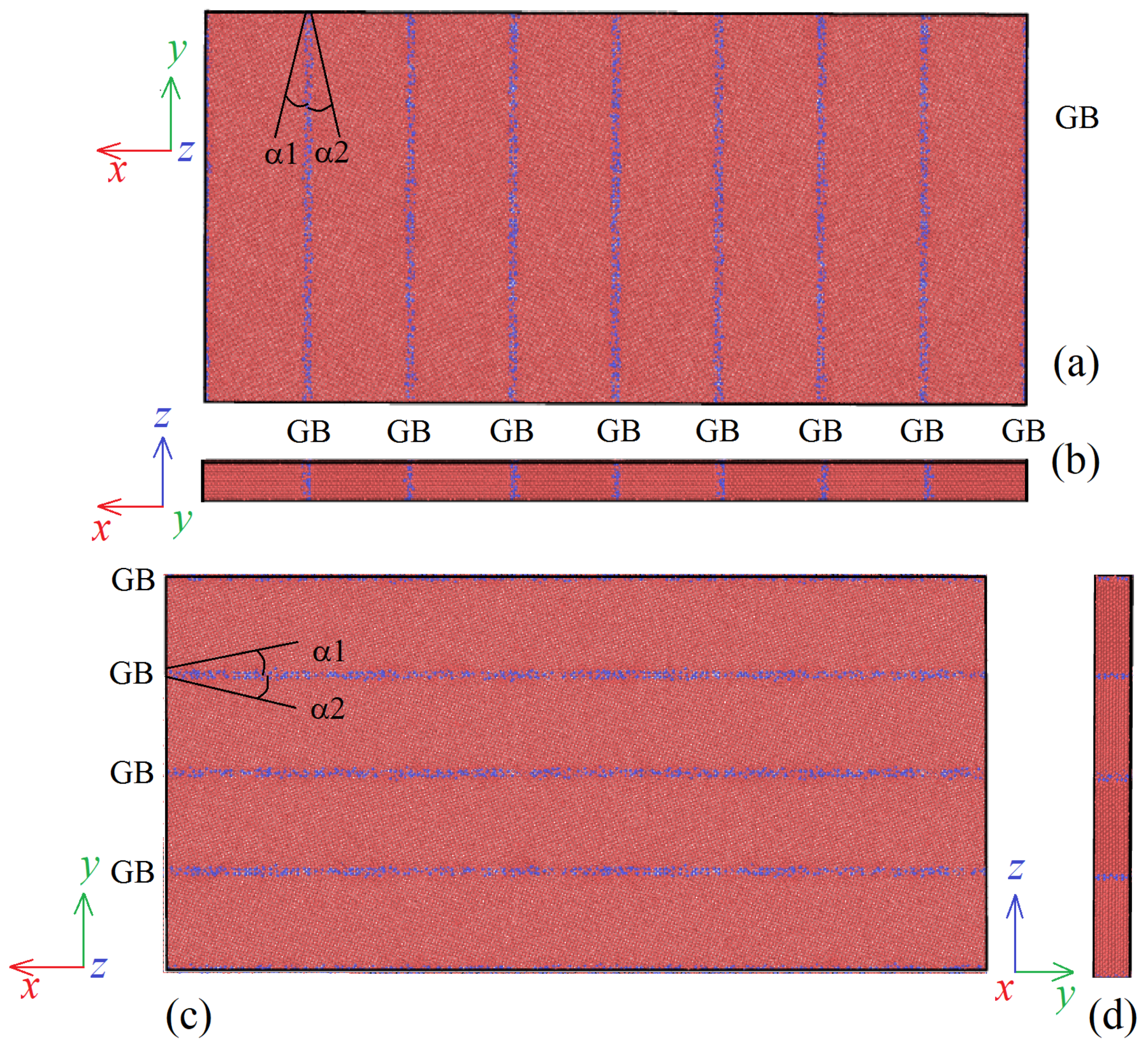
2. Simulation Details
3. Results and Discussion
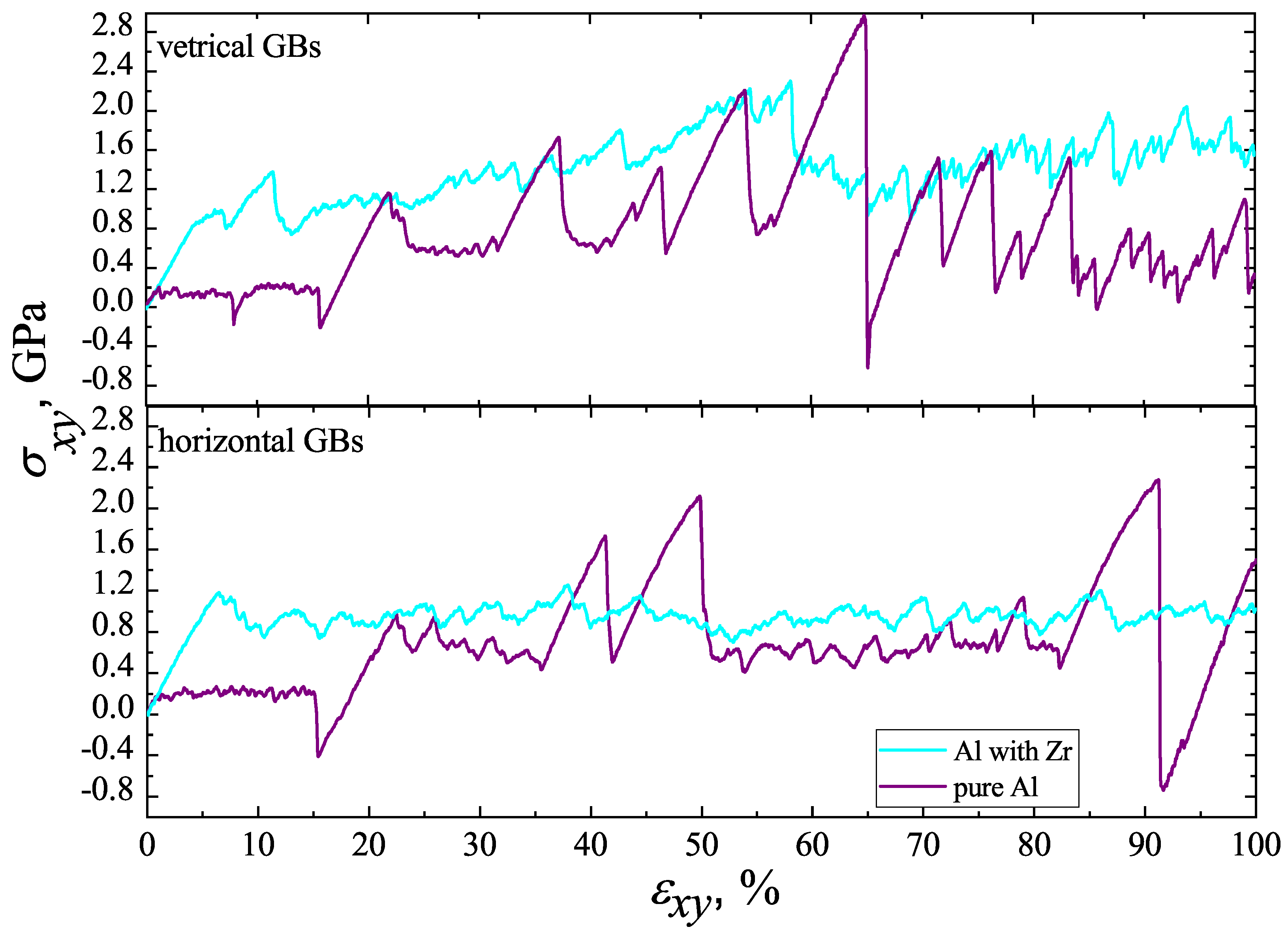
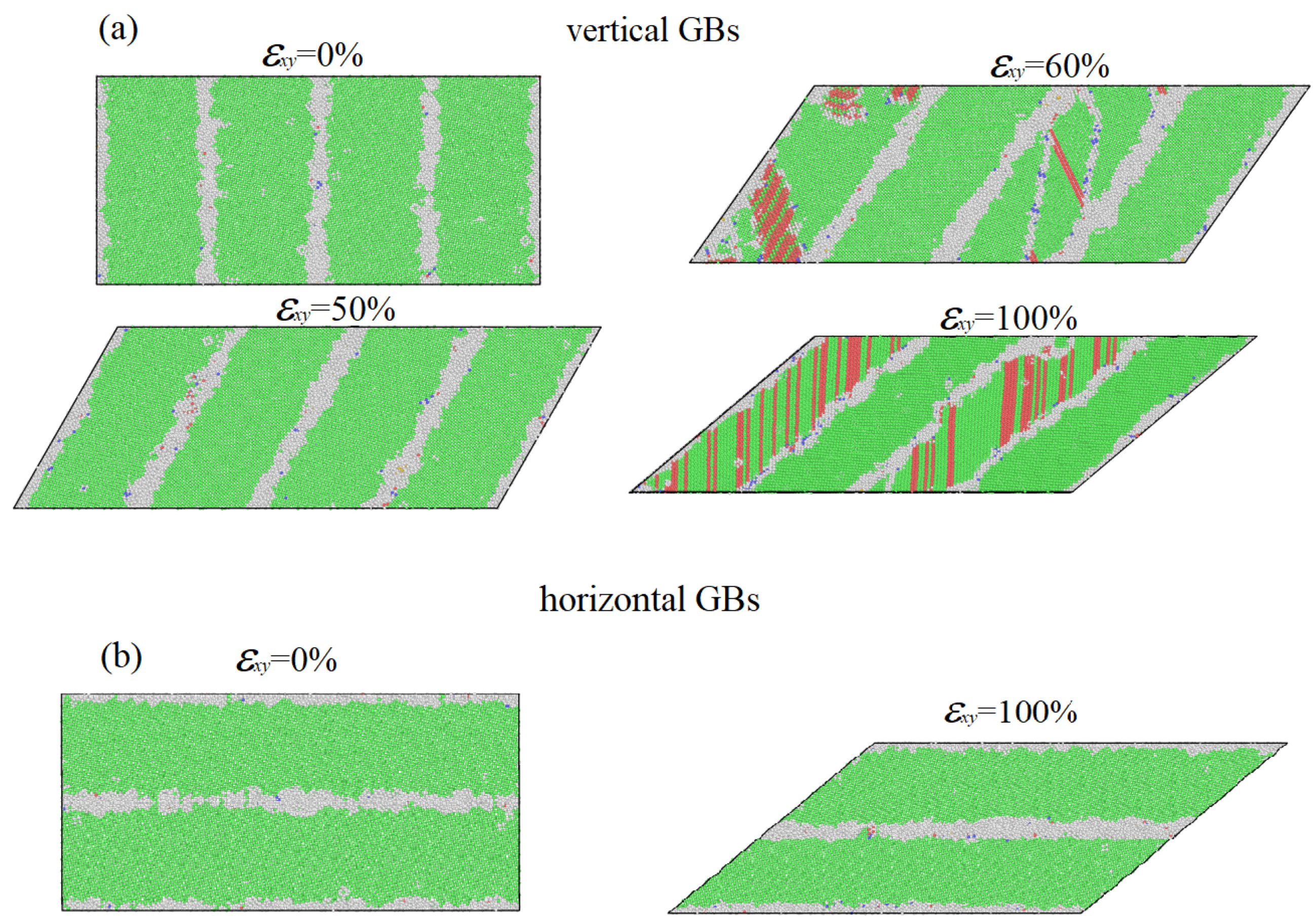
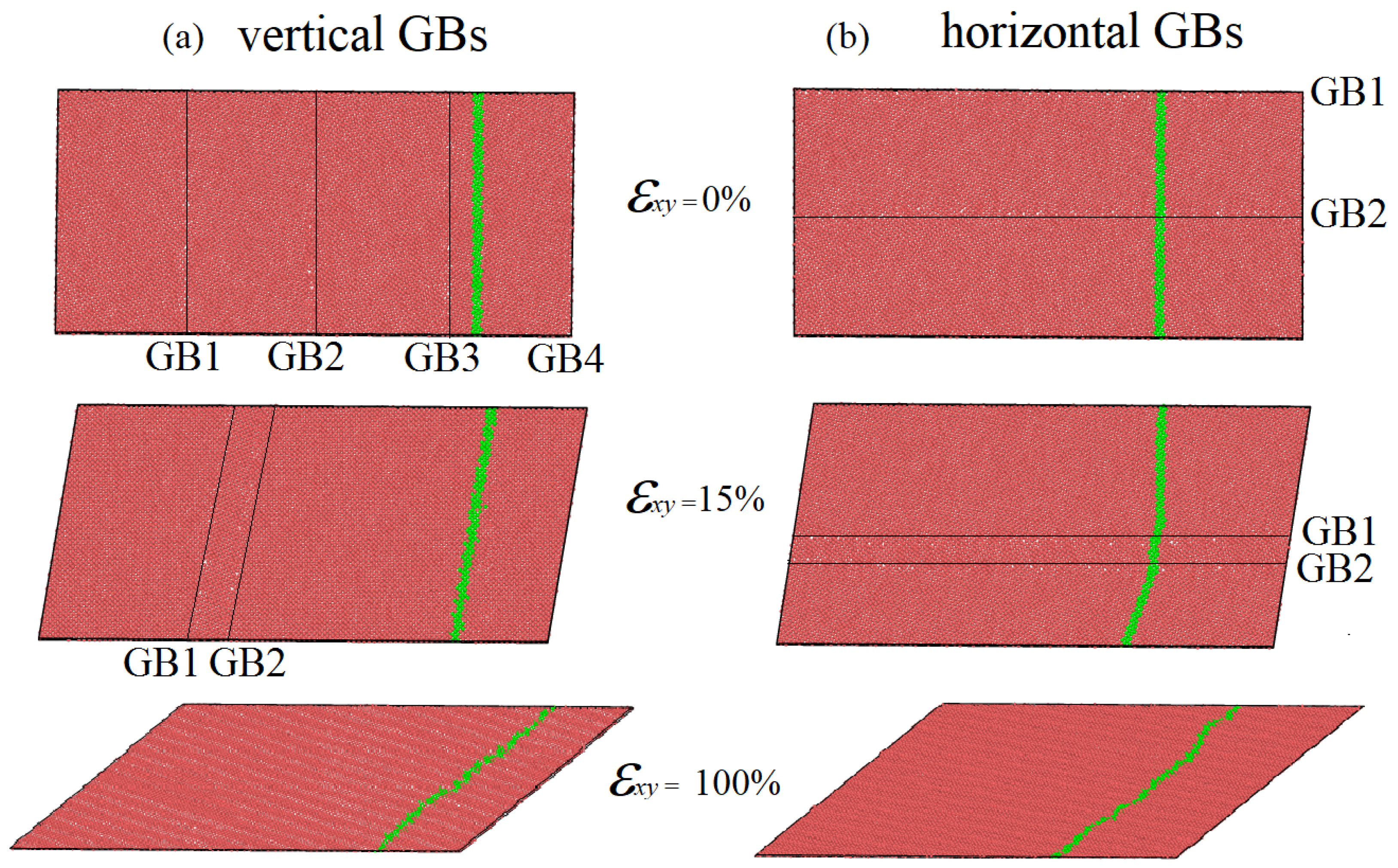
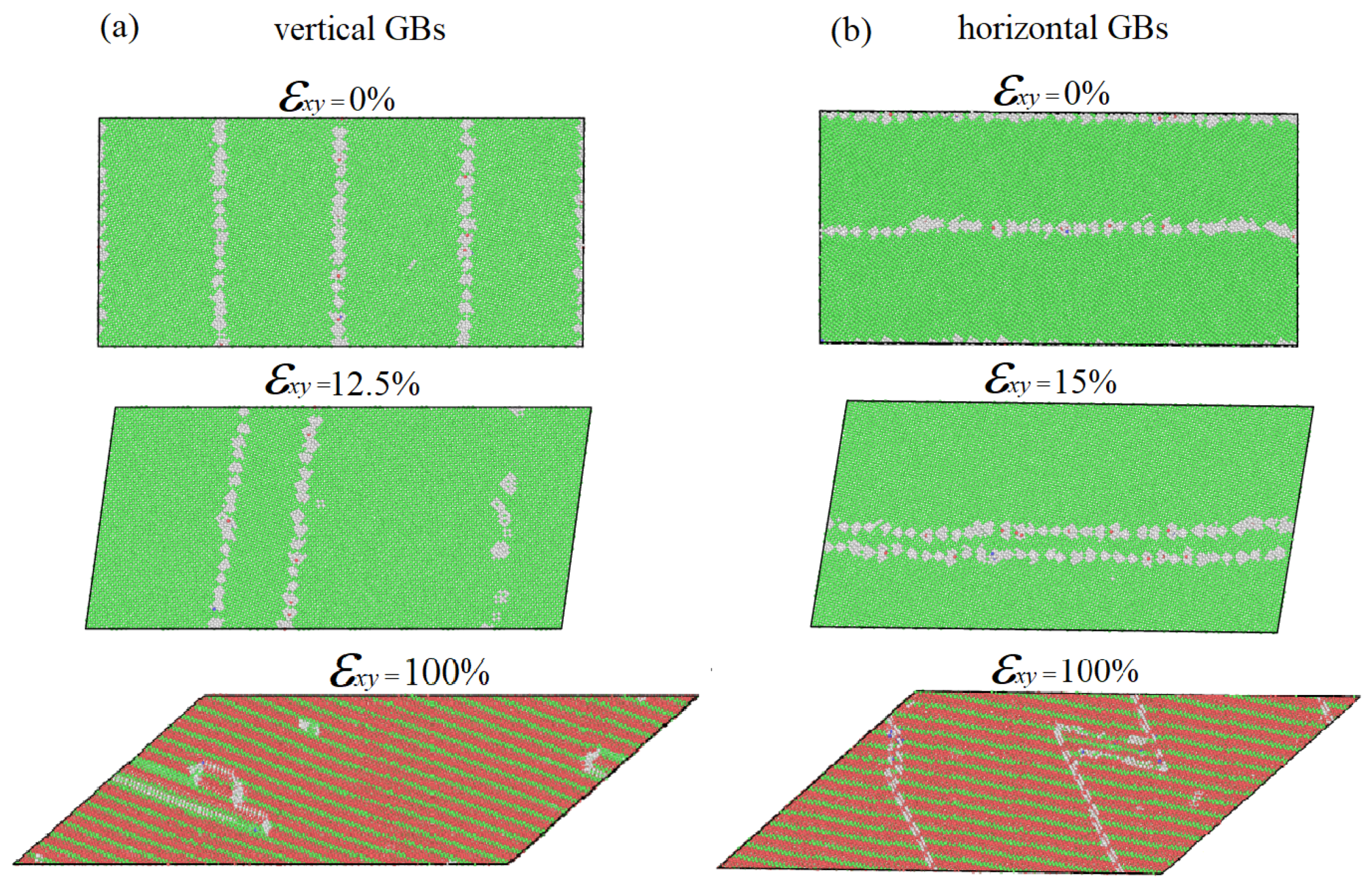
3.1. The Effect of GB Segregation of Zr on Shear Deformation Behavior
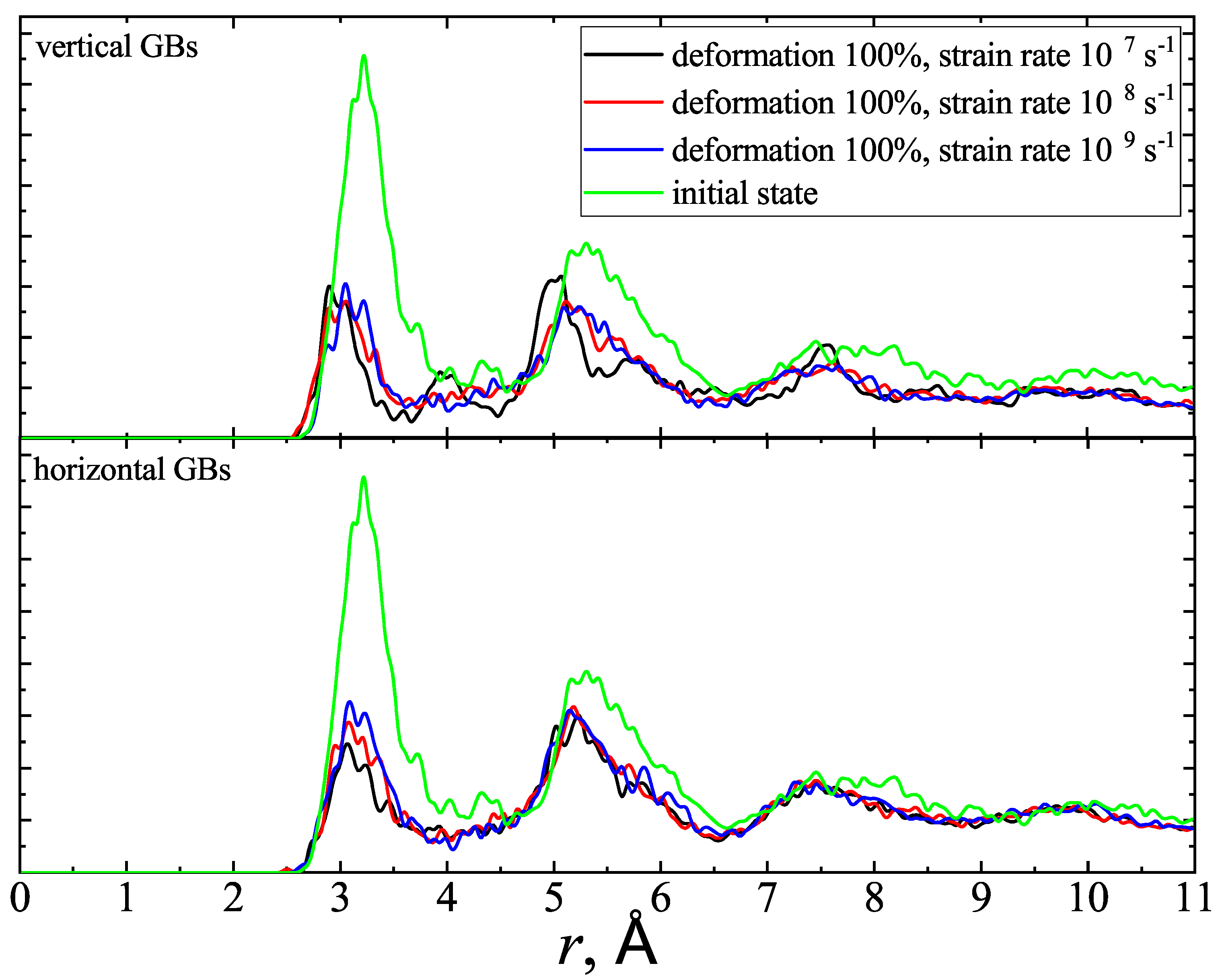
3.2. The Effect of Strain Rate
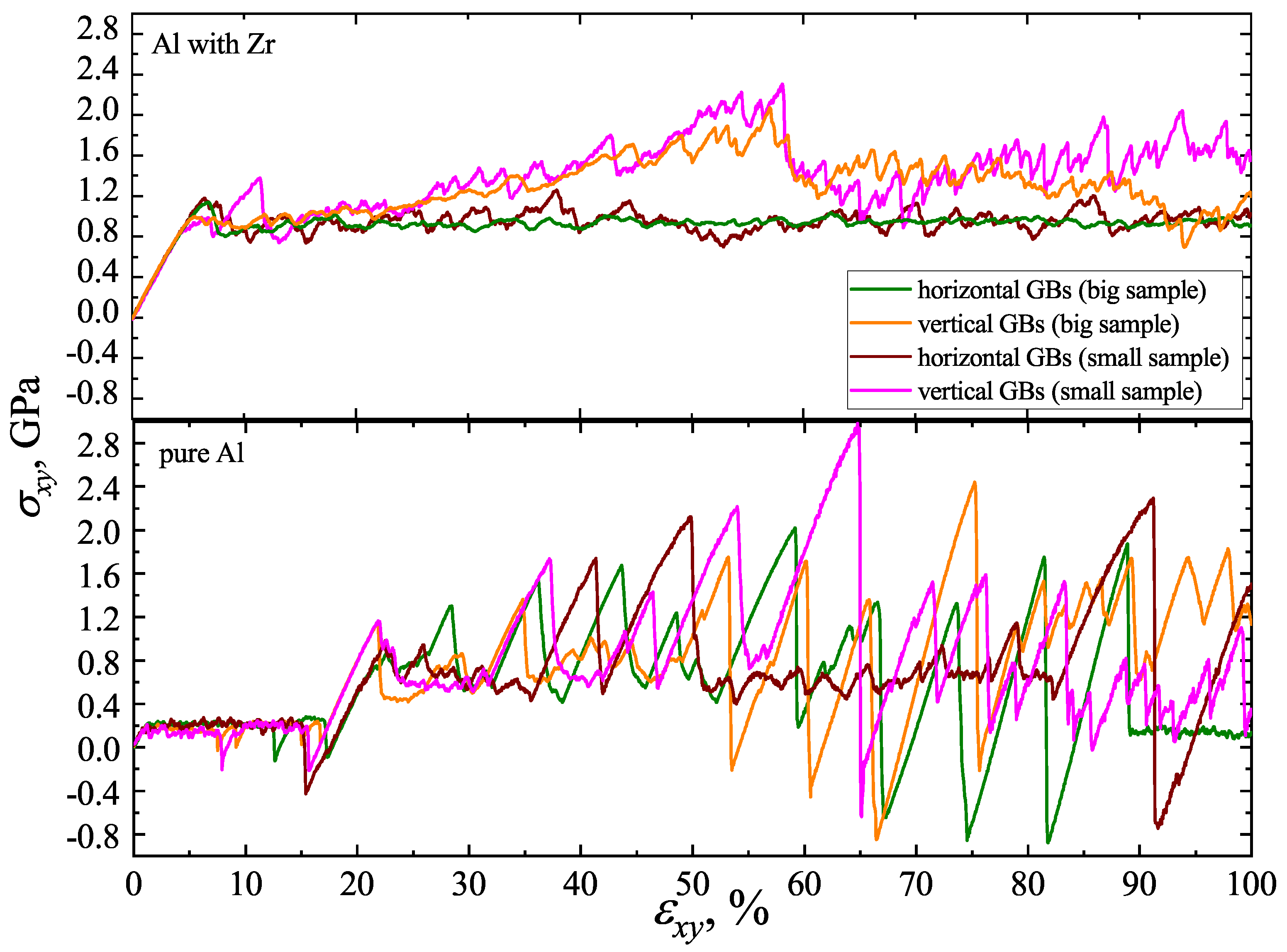
3.3. The Effect of Computational Cell Size
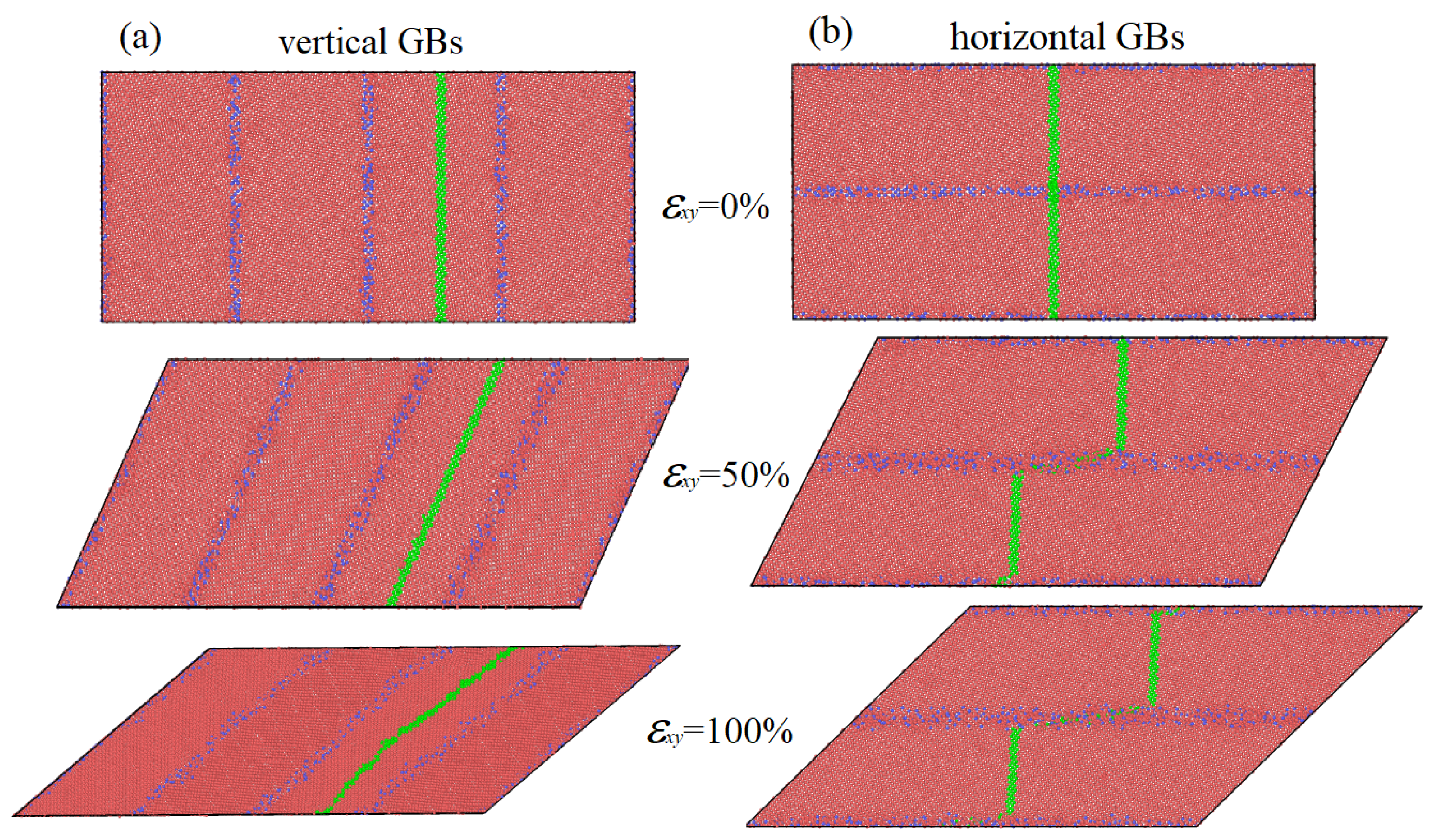
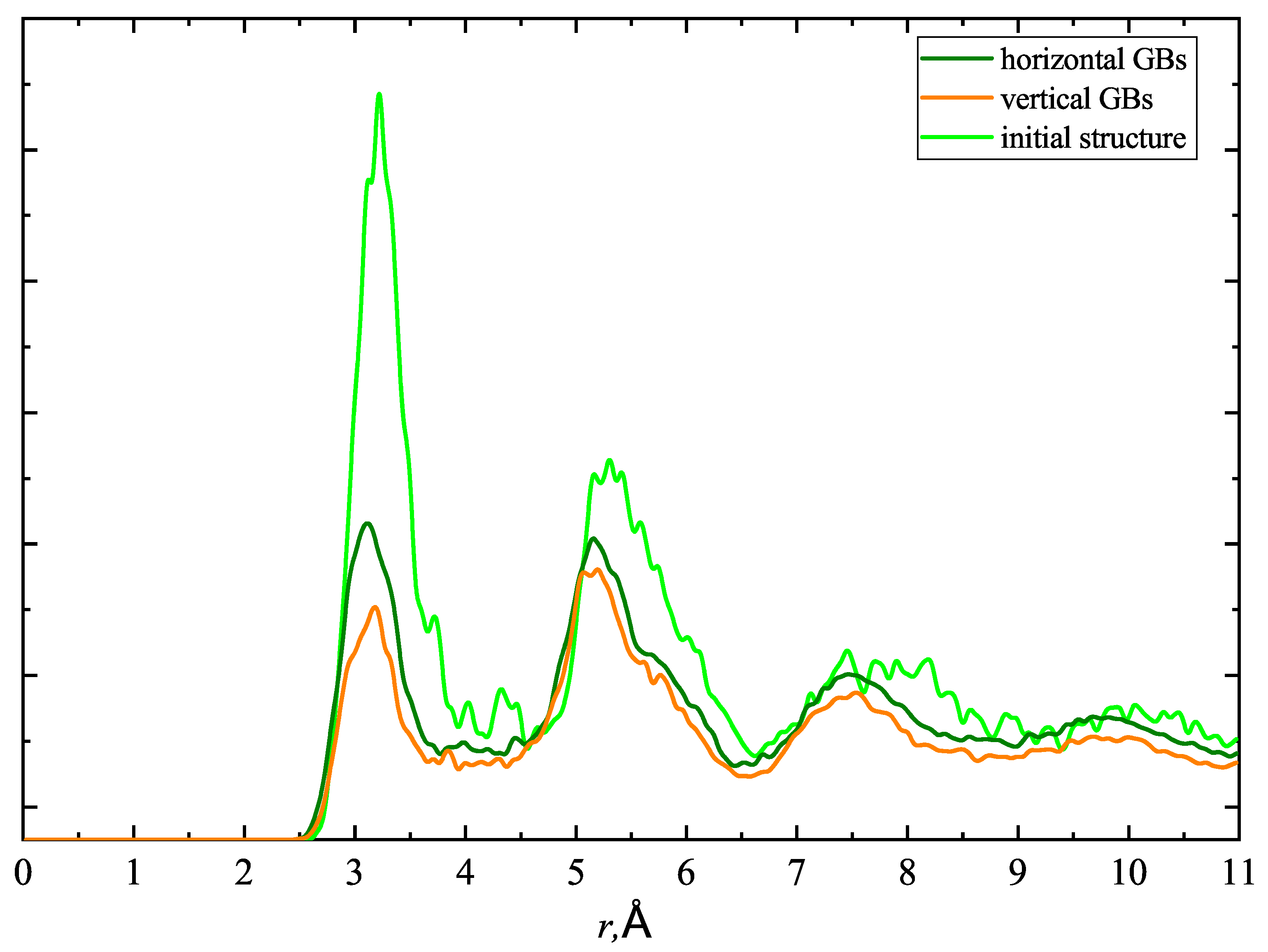
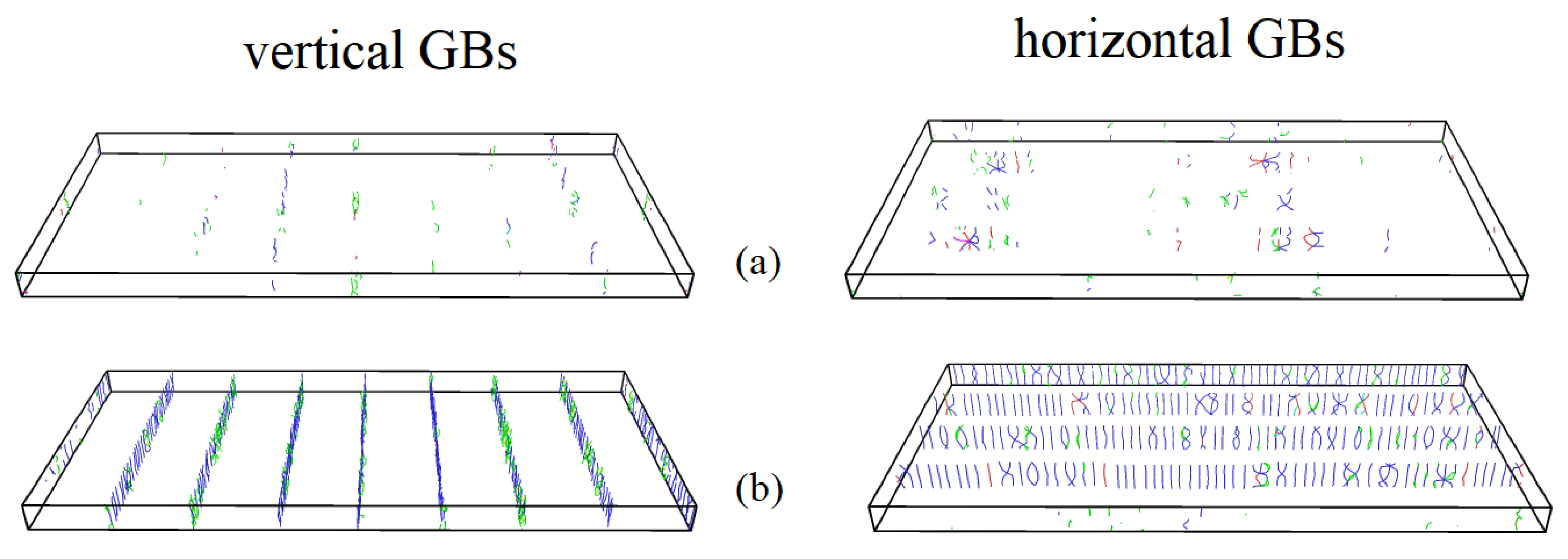
3.4. Structure Evolution Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kiessling, F.; Nefzger, P.; Nolasco, J.F.; Kaintzyk, U. Overhead Power Lines: Planning, Design, Construction; Springer: Berlin/Heidelberg, Germany, 2003; p. 759. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, L.; Niu, G.; Mao, J. Conductive Al Alloys: The Contradiction between Strength and Electrical Conductivity. Adv. Eng. Mater. 2021, 23, 2001249. [Google Scholar] [CrossRef]
- He, J.H. A new proof of the dual optimization problem and its application to the optimal material distribution of SiC/graphene composite. Rep. Mech. Eng. 2020, 1, 187–191. [Google Scholar] [CrossRef]
- Confalonieri, C.; Casati, R.; Gariboldi, E. Effect of Process Parameters on Laser Powder Bed Fusion of Al-Sn Miscibility Gap Alloy. Quantum Beam Sci. 2022, 6, 17. [Google Scholar] [CrossRef]
- Onyibo, E.C.; Safaei, B. Application of finite element analysis to honeycomb sandwich structures: A review. Rep. Mech. Eng. 2022, 3, 192–209. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Murashkin, M.Y.; Sabirov, I. A nanostructural design to produce high-strength Al alloys with enhanced electrical conductivity. Scr. Mater. 2014, 76, 13–16. [Google Scholar] [CrossRef]
- Edalati, K.; Bachmaier, A.; Beloshenko, V.A.; Beygelzimer, Y.; Blank, V.D.; Botta, W.J.; Bryła, K.; Čížek, J.; Divinski, S.; Enikeev, N.A.; et al. Nanomaterials by severe plastic deformation: Review of historical developments and recent advances. Mater. Res. Lett. 2022, 10, 163–256. [Google Scholar] [CrossRef]
- Murashkin, M.Y.; Enikeev, N.A.; Sauvage, X. Potency of severe plastic deformation processes for optimizing combinations of strength and electrical conductivity of lightweight Al-based conductor alloys. Mater. Trans. 2023, 64, 1833–1843. [Google Scholar] [CrossRef]
- Czerwinski, F. Thermal Stability of Aluminum Alloys. Materials 2020, 13, 3441. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Thermal-Resistant Aluminium Alloy Wire for Overhead Line Conductor IEC 62004; IEC: Geneva, Switzerland, 2007. [Google Scholar]
- Hamana, D.; Nebti, S.; Hamamda, S. Effect of the zirconium addition on the microstructure of Al+ 8 wt% Mg alloy. Scr. Metall. Mater. 1990, 24, 2059–2064. [Google Scholar] [CrossRef]
- Murray, J.L.; Peruzzi, A.; Abriata, J.P. The Al-Zr (aluminum-zirconium) system. J. Phase Equilib. 1992, 13, 277–291. [Google Scholar] [CrossRef]
- Wang, F.; Eskin, D.G.; Khvan, A.V.; Starodub, K.F.; Lim, J.J.H.; Burke, M.G.; Connolley, T.; Mi, J. On the occurrence of a eutectic-type structure in solidification of Al-Zr alloys. Scr. Mater. 2017, 133, 75–78. [Google Scholar] [CrossRef]
- Edalati, K. Superfunctional Materials by Ultra-Severe Plastic Deformation. Materials 2023, 16, 587. [Google Scholar] [CrossRef]
- Edalati, K. Metallurgical Alchemy by Ultra-Severe Plastic Deformation via High-Pressure Torsion Process. Mater. Trans. 2019, 60, 1221–1229. [Google Scholar] [CrossRef]
- Mohammadi, A.; Enikeev, N.A.; Murashkin, M.Y.; Arita, M.; Edalati, K. Developing age-hardenable Al-Zr alloy by ultra-severe plastic deformation: Significance of supersaturation, segregation and precipitation on hardening and electrical conductivity. Acta Mater. 2021, 203, 116503. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y.; An, J.; Chen, J.; Chen, T. The research on the essence of unsteady mechanical behavior of Fe14.6Ni (at%) nanocrystalline elastocaloric refrigeration alloy through molecular dynamics simulation. J. Mater. Res. Technol. 2022, 20, 3103–3113. [Google Scholar] [CrossRef]
- Muscati, I.A.; Jahwari, F.A.; Pervez, T. Effect of CNT’s volume fraction on the mechanical properties of CNT reinforced Al/Cu alloy nanocomposite using molecular dynamics simulation. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Rogachev, A.S.; Fourmont, A.; Kovalev, D.Y.; Vadchenko, S.G.; Kochetov, N.A.; Shkodich, N.F.; Baras, F.; Politano, O. Mechanical alloying in the Co-Fe-Ni powder mixture: Experimental study and molecular dynamics simulation. Powder Technol. 2022, 399, 117187. [Google Scholar] [CrossRef]
- Vasconcelos, I.F.; Figueiredo, R.S. Driving mechanisms on mechanical alloying: Experimental and molecular dynamics discussions. Nanostructured Mater. 1999, 11, 935–946. [Google Scholar] [CrossRef]
- Babicheva, R.I.; Evazzade, I.; Korznikova, E.A.; Shepelev, I.A.; Zhou, K.; Dmitriev, S.V. Low-energy channel for mass transfer in Pt crystal initiated by molecule impact. Comp. Mater. Sci. 2019, 163, 248–255. [Google Scholar] [CrossRef]
- Shepelev, I.A.; Dmitriev, S.V.; Kudreyko, A.A.; Velarde, M.G.; Korznikova, E.A. Supersonic voidions in 2D Morse lattice. Chaos Solitons Fractals 2020, 140, 110217. [Google Scholar] [CrossRef]
- Shepelev, I.A.; Bachurin, D.V.; Korznikova, E.A.; Dmitriev, S.V. Highly efficient energy and mass transfer in bcc metals by supersonic 2-crowdions. J. Nucl. Mater. 2022, 568, 153841. [Google Scholar] [CrossRef]
- Bayazitov, A.M.; Korznikova, E.A.; Bachurin, D.V.; Zinovev, A.V.; Dmitriev, S.V. Dynamics of supersonic N-crowdions in fcc metals. Rep. Mech. Eng. 2020, 1, 54–60. [Google Scholar] [CrossRef]
- Sitdikov, O.; Avtokratova, E.; Latypova, O.; Markushev, M. Structure, strength and superplasticity of ultrafine-grained 1570C aluminum alloy subjected to different thermomechanical processing routes based on severe plastic deformation. Trans. Nonferrous Met. Soc. China 2021, 31, 887–900. [Google Scholar] [CrossRef]
- Junaidi, S.; Amro, A.; Intan, F.M. Equal channel angular pressing of single crystal aluminum: A molecular dynamics simulation. J. Mater. Res. Technol. 2022, 17, 888–897. [Google Scholar] [CrossRef]
- Babicheva, R.I.; Dmitriev, S.V.; Zhang, Y.; Kok, S.W.; Srikanth, N.; Liu, B.; Zhou, K. Effect of grain boundary segregations of Fe, Co, Cu, Ti, Mg and Pb on small plastic deformation of nanocrystalline Al. Comp. Mater. Sci. 2015, 98, 410–416. [Google Scholar] [CrossRef]
- Babicheva, R.I.; Dmitriev, S.V.; Bai, L.; Zhang, Y.; Kok, S.W.; Kang, G.; Zhou, K. Effect of grain boundary segregation on the deformation mechanisms and mechanical properties of nanocrystalline binary aluminum alloys. Comp. Mater. Sci. 2016, 117, 445–454. [Google Scholar] [CrossRef]
- Babicheva, R.I.; Dmitriev, S.V.; Bachurin, D.V.; Srikanth, N.; Zhang, Y.; Kok, S.W.; Zhou, K. Effect of grain boundary segregation of Co or Ti on cyclic deformation of aluminium bi-crystals. Int. J. Fatigue 2017, 102, 270–281. [Google Scholar] [CrossRef]
- Babicheva, R.I.; Jarlöv, A.; Zheng, H.; Dmitriev, S.V.; Korznikova, E.A.; Ling Sharon Nai, M.; Ramamurty, U.; Zhou, K. Effect of short-range ordering and grain boundary segregation on shear deformation of CoCrFeNi high-entropy alloys with Al addition. Comp. Mater. Sci. 2022, 215, 111762. [Google Scholar] [CrossRef]
- Khalikov, A.R.; Korznikova, E.A.; Kudreyko, A.A.; Bebikhov, Y.V.; Dmitriev, S.V. Planar superstructure defects in ordered alloys with L10 structure. Met. Mater. Int. 2023, 29, 1712–1722. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sc. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Ma, E.; Sheng, H.W. Atomic level structure in multicomponent bulk metallic glass. Phys. Rev. Lett. 2009, 102, 245501. [Google Scholar] [CrossRef] [PubMed]
- EAM Potential Database. 2023. Available online: https://www.sites.google.com/site/eampotentials (accessed on 21 August 2023).
- Stillinger, F.H. A topographic view of supercooled liquids and glass formation. Science 1995, 267, 1935. [Google Scholar] [CrossRef] [PubMed]
- Sheng, H.W.; Kramer, M.J.; Cadien, A.; Fujita, T.; Chen, M.W. Highly optimized embedded-atom-method potentials for fourteen fcc metals. Phys. Rev. B 2011, 83, 134118. [Google Scholar] [CrossRef]
- Lee, M.; Lee, C.M.; Lee, K.R.; Ma, E.; Lee, J.C. Networked interpenetrating connections of icosahedra: Effects on shear transformations in metallic glass. Acta Mater. 2011, 59, 159–170. [Google Scholar] [CrossRef]
- Pippan, R. High-pressure torsion—Features and applications. In Bulk Nanostructured Materials; John Wiley Sons: Hoboken, NJ, USA, 2009; pp. 217–233. [Google Scholar] [CrossRef]
- Beygelzimer, Y.; Estrin, Y.; Davydenko, O.; Kulagin, R. Gripping prospective of non-shear flows under high-pressure torsion. Materials 2023, 16, 823. [Google Scholar] [CrossRef]
- Hou, Z.Y.; Tian, Z.A.; Mo, Y.F.; Liu, R.S.; Wang, J.G.; Shuai, X.M.; Dong, K.J. Atomic dynamics of grain boundaries in bulk nanocrystalline aluminium: A molecular dynamics simulation study. Comp. Mater. Sci. 2015, 108, 177–182. [Google Scholar] [CrossRef]
- Dang Thi, H.; Van-Khanh, T.; Van-Lam, N.; Le, V.; Van-Hai, D.; Trong-Giang, N. High strain-rate effect on microstructure evolution and plasticity of aluminum 5052 alloy nano-multilayer: A molecular dynamics study. Vacuum 2022, 201, 111104. [Google Scholar] [CrossRef]
- Xiaotao, L.; Wentao, M. Molecular dynamics simulation and theoretical modeling of free surface effect on nanocrack initiation induced by grain boundary sliding in nanocrystalline materials. Mater. Lett. 2021, 304, 130647. [Google Scholar] [CrossRef]
- Hoffrogge, P.W.; Barrales-Mora, L.A. Grain-resolved kinetics and rotation during grain growth of nanocrystalline aluminium by molecular dynamics. Comp. Mater. Sci. 2017, 128, 207–222. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Zhang, Y.; Kitipornchai, S.; Yang, J. Machine learning assisted prediction of mechanical properties of graphene/aluminium nanocomposite based on molecular dynamics simulation. Mater. Des. 2022, 213, 110334. [Google Scholar] [CrossRef]
- Li, Z.; Gao, Y.; Zhan, S.; Fang, H.; Zhang, Z. Molecular dynamics study on temperature and strain rate dependences of mechanical properties of single crystal Al under uniaxial loading. AIP Adv. 2020, 10, 075321. [Google Scholar] [CrossRef]
- Zeng, Q.; Wang, L.; Jiang, W. Molecular dynamics simulations of the tensile mechanical responses of selective laser-melted aluminum with different crystalline forms. Crystals 2021, 11, 1388. [Google Scholar] [CrossRef]
- Komanduri, R.; Chandrasekaran, N.; Raff, L. Molecular dynamics (MD) simulation of uniaxial tension of some single-crystal cubic metals at nanolevel. Int. J. Mech. Sci. 2001, 43, 2237–2260. [Google Scholar] [CrossRef]
- Xu, W.; Dávila, L.P. Size dependence of elastic mechanical properties of nanocrystalline aluminum. Mater. Sci. Eng. A 2017, 692, 90–94. [Google Scholar] [CrossRef]
- Xu, W.; Dávila, L.P. Tensile nanomechanics and the Hall-Petch effect in nanocrystalline aluminium. Mater. Sci. Eng. A 2018, 710, 413–418. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morkina, A.Y.; Babicheva, R.I.; Korznikova, E.A.; Enikeev, N.A.; Edalati, K.; Dmitriev, S.V. A Molecular Dynamics Simulation to Shed Light on the Mechanical Alloying of an Al-Zr Alloy Induced by Severe Plastic Deformation. Metals 2023, 13, 1595. https://doi.org/10.3390/met13091595
Morkina AY, Babicheva RI, Korznikova EA, Enikeev NA, Edalati K, Dmitriev SV. A Molecular Dynamics Simulation to Shed Light on the Mechanical Alloying of an Al-Zr Alloy Induced by Severe Plastic Deformation. Metals. 2023; 13(9):1595. https://doi.org/10.3390/met13091595
Chicago/Turabian StyleMorkina, Alina Y., Rita I. Babicheva, Elena A. Korznikova, Nariman A. Enikeev, Kaveh Edalati, and Sergey V. Dmitriev. 2023. "A Molecular Dynamics Simulation to Shed Light on the Mechanical Alloying of an Al-Zr Alloy Induced by Severe Plastic Deformation" Metals 13, no. 9: 1595. https://doi.org/10.3390/met13091595
APA StyleMorkina, A. Y., Babicheva, R. I., Korznikova, E. A., Enikeev, N. A., Edalati, K., & Dmitriev, S. V. (2023). A Molecular Dynamics Simulation to Shed Light on the Mechanical Alloying of an Al-Zr Alloy Induced by Severe Plastic Deformation. Metals, 13(9), 1595. https://doi.org/10.3390/met13091595






